The linear $k$-arboricity of digraphs

1.   Introduction

In this paper, a digraph is a finite loopless directed graph without parallel arcs (arcs with the same head and the same tail) and an undirected graph is also a finite and simple graph. A linear forest is a forest in which every connected component is a path. The linear arboricity of a graph $G$, defined by Harary ^[14], is the minimum number of linear forests that partition the edges of $G$ and is denoted by $la(G)$. Later, Habib and Péroche ^[13] introduced the linear $k$-arboricity of a graph $G$, which is the minimum number of $k$-linear forests (forests in which every connected component is a path of length at most $k$) required to partition the edges of $G$ and is denoted by $la_{k}(G)$. Moreover, Akiyama et al. ^[1] proposed a conjecture about the value of linear arboricity and Habib and Péroche ^[13] proposed a conjecture about the value of linear $k$-arboricity which subsumes Akiyama's conjecture. Aimed at these two conjectures, considerable works have been done over the years (see ^{[2,3,6,7,8,9,10,11,12,16,19,20,21,22]}).

It is natural to consider similar problems for digraphs. Let $D = (V(D), A(D))$ be a digraph. We denote $\Delta^{+}(D) = max\{d^{+}(v)|\ for\ all\ v \in V\}$, $\Delta^{-}(D) = max\{d^{-}(v)|\ for\ all\ v \in V\}$ and $\Delta(D) = max\{\Delta^{+}(D), \Delta^{-}(D)\}$. The underlying graph $S(D)$ of $D$ is the undirected simple graph with the same vertex set of $D$ by replacing each arc by an edge with the same ends. A linear diforest is a directed forest in which every connected component is a directed path. The linear arboricity of $D$, defined by Nakayama and Péroche ^[17], is the minimum number of linear diforests that partition the arcs of $D$ and is denoted by $\overrightarrow{la}(D)$. Nakayama and Péroche ^[17] also conjectured that $\overrightarrow{la}(D)\leq \Delta(D)+1$. Since every digraph can be a regular digraph by adding arcs, Nakayama-Péroche conjecture is equivalent to say that the linear arboricity of a $d$-regular digraph $D$ (i.e. every vertex in $D$ has in-degree $d$ and out-degree $d$) is $d+1$. In 2017, He et al. ^[15] found that the symmetric complete digraphs $K_3^*$ and $K_5^*$ have the linear arboricity $d+2\ (d = 2, 4$ respectively), which is contrary to Nakayama-Péroche conjecture. Then they conjectured that the linear arboricity of a $d$-regular digraph $D$ is $d+1$ except $D$ is $K_3^*$ or $K_5^*$.

In this paper, we study the linear $k$-arboricity for digraphs. The linear $k$-arboricity of a digraph $D$ is the minimum number of linear $k$-diforests (diforests in which every connected component is a directed path of length at most $k$) that partition the arcs of $D$ and is denoted by $\overrightarrow{la}_{k}(D)$.

This paper is organized as follows: In Section 2, we introduce some notations and obtain the upper bound and the lower bound of the linear $k$-arboricity for general digraphs. In Sections 3 and 4, we study the linear $3$-arboricity and linear $2$-arboricity for symmetric complete digraphs respectively. In Sections 5 and 6, we study the linear $3$-arboricity and linear $2$-arboricity for symmetric complete bipartite digraphs respectively.

2.   Preliminaries

For an undirected graph $G$ with $n$ vertices, Habib and Péroche ^[13] conjectured that $la_k(G)\leq \lceil \frac{\Delta(G) n+1}{2\lfloor kn/(k+1)\rfloor}\rceil$ when $\Delta(G) < n-1$ and $la_k(G)\leq \lceil \frac{\Delta(G) n}{2\lfloor kn/(k+1)\rfloor}\rceil$ when $\Delta(G) = n-1$. Based on the linear arboricity conjecture for digraphs in ^[15] and Habib-Péroche conjecture, we propose the following conjecture for the linear $k$-arboricity in digraphs.

Conjecture 2.1. For a digraph $D$ with $n$ vertices, if $k = n-1$,

If $k < n-1$,

It is easy to obtain the following lemmas.

Lemma 2.1. Let $H$ be a subdigraph of a digraph $D$. Then $\overrightarrow{la_{k}}(H) \leq \overrightarrow{la_{k}}(D)$.

Lemma 2.2. For a digraph $D$ with $n$ vertices,

Lemma 2.3. For a digraph $D = (V(D), A(D))$ with $n$ vertices,

If $D$ is a symmetric digraph, we just give two opposite directions to the linear forests of the minimum linear $k$-forests partition of $S(D)$ and get the following trivial upper bound for $\overrightarrow{la}_{k}(D)$.

Lemma 2.4. Let $D$ be a symmetric digraph. Then $\overrightarrow{la}_{k}(D)\leq 2la_{k}(S(D))$.

In this paper, we mainly study the linear $k$-arboricity for symmetric complete digraphs and symmetric complete bipartite digraphs. Fu et al.^[11,12,22] studied linear $2$-arboricity and $3$-arboricity of complete graphs $K_n$ and complete bipartite graphs $K_{n, n}$.

Theorem 2.1. ^[12]

Theorem 2.2. ^[12]

Theorem 2.3. ^[6,22]

Theorem 2.4. ^[11]

Let $K^{\ast}_{n, n}$ be a symmetric complete bipartite digraph with partite sets $X = \{x_{0}, x_{1}, ..., x_{n-1}\}$ and $Y = \{y_{0}, y_{1}, ..., y_{n-1}\}$. We define the bipartite difference of the undirected edge $x_{p}y_{q}$ in $S(K^{\ast}_{n, n})$ as the value $q-p(mod\ n)$. Those edges in $S(K^{\ast}_{n, n})$ with the same value of the bipartite difference must be a matching. In particular, we denote the set of edges of the bipartite difference $i$ in $S(K^{\ast}_{n, n})$ by $M_{i}$ $(i = 0, 1, ..., n-1)$. In $K^{\ast}_{n, n}$, for $i = 0, 1, ..., n-1$, we define $\overrightarrow{M}_{i} = \{x_{d}y_{d+i(mod\ n)}|d = 0, 1, ..., n-1\}$ and $\overleftarrow{M}_{i} = \{y_{d+i(mod\ n)} x_{d}|d = 0, 1, ..., n-1\}$. Thus, we can partition the arcs of $K^{\ast}_{n, n}$ into $2n$ pairwise arc-disjoint perfect matchings $\overrightarrow{M}_{0}$, $\overrightarrow{M}_{1}$, ..., $\overrightarrow{M}_{n-1}$, $\overleftarrow{M}_{0}$, $\overleftarrow{M}_{1}$, ..., $\overleftarrow{M}_{n-1}$. Similarly as in ^[12], we have the following two useful results.

Lemma 2.5. If $n\geq4$ is even and $\alpha\in\{0, 1, ..., n-3\}$, then the arcs in the union $\{\overrightarrow{M}_{\alpha}$, $\overleftarrow{M}_{\alpha+1}$, $\overrightarrow{M}_{\alpha+2}\}$in $K^{\ast}_{n, n}$ can form two arc-disjoint linear $3$-diforests and $\{\overleftarrow{M}_{\alpha}$, $\overrightarrow{M}_{\alpha+1}$, $\overleftarrow{M}_{\alpha+2}\}$can form another two arc-disjoint linear $3$-diforests.

Lemma 2.6. If $n\geq3$ is odd, $\alpha\in\{0, 1, ..., n-3\}$ and $e$ is an arc of $\overleftarrow{M}_{\alpha+1}$, then$\{\overrightarrow{M}_{\alpha}, \overleftarrow{M}_{\alpha+1}-\{e\}, \overrightarrow{M}_{\alpha+2}\}$ in $K^{\ast}_{n, n}$ can form two arc-disjoint linear $3$-diforests. And if$e$ is an arc of $\overrightarrow{M}_{\alpha+1}$, then $\{\overleftarrow{M}_{\alpha}, \overrightarrow{M}_{\alpha+1}-\{e\}, \overleftarrow{M}_{\alpha+2}\}$ can form anothertwo arc-disjoint linear $3$-diforests.

3.   Linear $3$-arboricity of symmetric complete digraphs

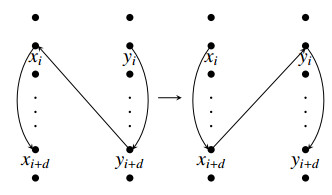
In this section, we determine the linear $3$-arboricity of $K^{\ast}_{n}$. Firstly, we propose an operation of replacing arcs in $K^{\ast}_{n, n}$. Let $X = \{x_{0}, x_{1}, ..., x_{n-1}\}$ and $Y = \{y_{0}, y_{1}, ..., y_{n-1}\}$ be partite sets of $K^{\ast}_{n, n}$. Suppose it exists the following directed $3$-path $y_{i}y_{i+d}x_{i}x_{i+d}$ by adding arcs $x_{i}x_{i+d}$ and $y_{i}y_{i+d}$ in $K^{\ast}_{n, n}$ as shown in Figure 1. Then we replace the arc $y_{i+d}x_{i}\in \overleftarrow{M}_{d}$ by the arc $x_{i+d}y_{i}\in \overrightarrow{M}_{n-d}$ and we get another directed $3$-path $x_{i}x_{i+d}y_{i}y_{i+d}$. We call this operation replacing arc operation. In this operation we can use the arcs in a matching to replace the arcs in another matching contained in some directed paths.

We need to mention that some of the proof in the following propositions are similar as the proof for the linear $3$-arboricity of $K_n$ ^[12], and we will omit some analogous and tedious proof in this section.

Proposition 3.1. $\overrightarrow{la}_{3}(K^{\ast}_{n}) \leq 2\lceil \frac{2n-2}{3}\rceil-1$ when $n\equiv0\; (mod\ 12)$.

Proof. Let $n = 12t$, $m = \frac{n}{2}$. In ^[12] it is proved that $S(K^{\ast}_{n})$ can be decomposed into $m-1$ pairwise edge-disjoint linear $3$-forests and couple of matchings. Thus, by giving two opposite directions to edges of those linear $3$-forests and matchings of $S(K^{\ast}_{n})$, in $K^{\ast}_{n}$, we have

(1) $2(m-1)$ pairwise arc-disjoint linear $3$-diforests;

(2) $m$ pairwise arc-disjoint perfect matchings $\overrightarrow{M}_{d} = \{x_{i}y_{i+d(mod\ m)}|i = 0, 1, ..., m-1\}$ $(d = 0, 1, 2, ...\frac{m}{2}-1)$, $\overleftarrow{M}_{d} = \{{y_{i+d(mod\ m)} x_{i}}|i = 0, 1, ..., m-1\}$ $(d = 0, 1, 2, ...\frac{m}{2}-1)$;

(3) $\overrightarrow{M}_{\frac{m}{2}} = \{x_{i}y_{i+\frac{m}{2}(mod\ m)}|i = 0, 1, ..., \frac{m}{2}-1\}$ and $\overleftarrow{M}_{\frac{m}{2}} = \{y_{i+\frac{m}{2}(mod\ m)}x_{i}|i = 0, 1, ..., \frac{m}{2}-1\}$.

By Lemma 2.5, we can construct $\frac{2m}{3}$ linear $3$-diforests using these matchings in (2).

Then for the directed $3$-paths $y_{i+\frac{m}{2}}y_{i}x_{i+\frac{m}{2}}x_{i}$, $i \in \{0, 1, ..., \frac{m}{2}-1\}$ from those $2(m-1)$ linear $3$-diforests in (1), by using the arcs in $\overrightarrow{M}_{\frac{m}{2}}$, we apply the replacing arc operation for $y_{i+\frac{m}{2}}y_{i}x_{i+\frac{m}{2}}x_{i}$ and get new paths $x_{i+\frac{m}{2}}x_{i}y_{i+\frac{m}{2}}y_{i}$. Note that in the whole operation, the arcs in the matching $\overleftarrow{M}^{'}_{\frac{m}{2}} = \{y_{i}x_{i+\frac{m}{2}(mod\ m)}|i = 0, 1, ..., \frac{m}{2}-1\}$ are removed from the paths. It is not hard to see that the arcs of $\overleftarrow{M}^{'}_{\frac{m}{2}}$ and $\overleftarrow{M}_{\frac{m}{2}}$ can form one linear $3$-diforest.

Accordingly, $\overrightarrow{la}_{3}(K^{\ast}_{n}) \leq 2(m-1)+\frac{2m}{3}+1 = 2\lceil \frac{2n-2}{3}\rceil-1$.

Proposition 3.2. $\overrightarrow{la}_{3}(K^{\ast}_{n}) \leq 2\lceil \frac{2n}{3}\rceil-1$ when $n\equiv2\; (mod\ 12)$.

Proof. Let $n = 12t+2$, $m = \frac{n-2}{2}$, $t \geq 1$ (when $t = 0$, it is trivial). In $K^{\ast}_{n}$, we have

(1) $2(m+1)$ pairwise arc-disjoint linear $3$-diforests;

(2) $m$ pairwise arc-disjoint perfect matchings $\overrightarrow{M}_{d} = \{x_{i}y_{i+d(mod\ m)}|i = 0, 1, ..., m-1\}$ $(d = 0, 1, 2, ...\frac{m}{2}-1)$, $\overleftarrow{M}_{d} = \{{y_{i+d(mod\ m)}}x_{i}|i = 0, 1, ..., m-1\}$ $(d = 0, 1, 2, ...\frac{m}{2}-1)$;

(3) $\overrightarrow{M}_{\frac{m}{2}} = \{x_{i}y_{i+\frac{m}{2}(mod\ m)}|i = 0, 1, ..., \frac{m}{2}-1\}$ and $\overleftarrow{M}_{\frac{m}{2}} = \{{y_{i+\frac{m}{2}(mod\ m)}}x_{i}|i = 0, 1, ..., \frac{m}{2}-1\}$.

By Lemma 2.5, we can construct $\frac{2m}{3}$ linear $3$-diforests using these matchings in (2).

Then, by the similar replacing arc operation in Proposition 1, we have $\overrightarrow{la}_{3}(K^{\ast}_{n}) \leq 2(m+1)+\frac{2m}{3}+1 = 2\lceil \frac{2n}{3}\rceil-1$.

Proposition 3.3. $\overrightarrow{la}_{3}(K^{\ast}_{n}) \leq 2\lceil \frac{2n}{3}\rceil-1$ when $n\equiv5\; (mod\ 12)$.

Proof. Let $n = 12t+5$, $m = \frac{n-1}{2}$, $t \geq 0$.

When $t = 0$, let $V(K^{\ast}_{5}) = \{x_{0}, x_{1}, x_{2}, x_{3}, x_{4}\}$. Then we can easily find $7$ arc-disjoint linear $3$-diforests to partition the arcs of $K^{\ast}_{5}$: $\{x_{1}x_{2}x_{0}x_{4}\}$, $\{x_{0}x_{3}x_{1}, x_{4}x_{2}\}$, $\{x_{0}x_{1}, x_{4}x_{3}x_{2}\}$, $\{x_{2}x_{1}x_{4}x_{0}\}$, $\{x_{1}x_{3}x_{0}, x_{2}x_{4}\}$, $\{x_{1}x_{0}, x_{2}x_{3}x_{4}\}$, $\{x_{0}x_{2}, x_{4}x_{1}\}$.

Now we assume that $t\geq 1$. In $K^{\ast}_{n}$, we have

(1) $2(m+1)$ pairwise arc-disjoint linear $3$-diforests;

(2) $\frac{m}{2}-1$ pairwise arc-disjoint perfect matchings $\overrightarrow{M}_{d} = \{x_{i}y_{i+d(mod\ m)}|i = 0, 1, ..., m-1\}$, $d = 0, 2, ...\frac{m}{2}-1$;

(3) $\frac{m}{2}-1$ pairwise arc-disjoint perfect matchings $\overleftarrow{M}_{d} = \{{y_{i+d(mod\ m)}x_{i}}|i = 0, 1, ..., m-1\}$, $d = 0, 2, ...\frac{m}{2}-1$;

(4) $\overrightarrow{M}_{\frac{m}{2}} = \{x_{i}y_{i+\frac{m}{2}(mod\ m)|i = 0, 1, ..., \frac{m}{2}-1}\}$ and $\overleftarrow{M}_{\frac{m}{2}} = \{y_{i+\frac{m}{2}(mod\ m)}x_{i}|i = 0, 1, ..., \frac{m}{2}-1\}$.

By Lemma 2.5, we can construct $\frac{2}{3}(m-8) = \frac{2m-16}{3}$ linear $3$-diforests by the matchings in (2) and (3) except the matchings $\overrightarrow{M}_{0}$, $\overleftarrow{M}_{0}$, $\overrightarrow{M}_{\frac{m}{2}-2}$, $\overleftarrow{M}_{\frac{m}{2}-2}$, $\overrightarrow{M}_{\frac{m}{2}-1}$, $\overleftarrow{M}_{\frac{m}{2}-1}$.

When $t$ is even and $t \geq 2$, $\overrightarrow{M}_{0}$, $\overleftarrow{M}_{\frac{m}{2}-2}$, $\overrightarrow{M}_{\frac{m}{2}-1}$ can form two linear $3$-diforests as

Similarly, $\overleftarrow{M}_{0}$, $\overrightarrow{M}_{\frac{m}{2}-2}$, $\overleftarrow{M}_{\frac{m}{2}-1}$ can form another two arc-disjoint linear $3$-diforests.

When $t$ is odd, $\overleftarrow{M}_{0}$, $\overrightarrow{M}_{\frac{m}{2}-1}$, $\overleftarrow{M}_{\frac{m}{2}-2}$ can form two linear $3$-diforests as

Similarly, $\overrightarrow{M}_{0}$, $\overleftarrow{M}_{\frac{m}{2}-1}$, $\overrightarrow{M}_{\frac{m}{2}-2}$ can form another two arc-disjoint linear $3$-diforests.

In addition, we apply the replacing arc operation for the arcs of the matching $\overrightarrow{M}_{\frac{m}{2}}$ in some linear $3$-diforests of (1) and obtain a new matching $\overleftarrow{M}^{'}_{\frac{m}{2}} = \{{y_{i}x_{i+\frac{m}{2}(mod\ m)}|i = 0, 1, ..., \frac{m}{2}-1}\}$. The arcs of $\overleftarrow{M}^{'}_{\frac{m}{2}}$ and $\overleftarrow{M}_{\frac{m}{2}}$ also can form one linear $3$-diforest.

Accordingly, $\overrightarrow{la}_{3}(K^{\ast}_{n}) \leq 2(m+1)+\frac{2m-16}{3}+4+1 = 2\lceil \frac{2n}{3}\rceil-1$.

Proposition 3.4. $\overrightarrow{la}_{3}(K^{\ast}_{n}) \leq 2\lceil \frac{2n}{3}\rceil-1$ when $n\equiv7\; (mod\ 12)$.

Proof. Let $n = 12t+7$, $m = \frac{n-1}{2}$, $t \geq 0$.

When $t = 0$, let $V(K^{\ast}_{7}) = \{x_{0}, x_{1}, x_{2}, x_{3}, x_{4}, x_{5}, x_{6}\}$. We can find $9$ arc-disjoint linear $3$-diforests to partition the arcs of $K^{\ast}_{7}$: $\{x_{4}x_{1}x_{0}, x_{3}x_{2}x_{5}x_{6}\}$, $\{x_{5}x_{0}x_{3}x_{1}, x_{6}x_{4}x_{2}\}$, $\{x_{0}x_{6}x_{1}x_{2}, x_{4}x_{3}x_{5}\}$, $\{x_{0}x_{1}x_{4}, x_{6}x_{5}x_{2}x_{3}\}$, $\{x_{1}x_{3}x_{0}x_{5}, x_{2}x_{4}x_{6}\}$, $\{x_{2}x_{1}x_{6}x_{0}, x_{3}x_{4}x_{5}\}$, $\{x_{3}x_{6}x_{2}x_{0}, x_{1}x_{5}x_{4}\}$, $\{x_{0}x_{4}, x_{5}x_{1}, x_{2}x_{6}x_{3}\}$, $\{x_{4}x_{0}x_{2}, x_{5}x_{3}\}$.

In $K^{\ast}_{n}$, we have

(1) $2m$ pairwise arc-disjoint linear $3$-diforests;

(2) $\frac{m-3}{2}$ pairwise arc-disjoint perfect matchings $\overrightarrow{M}_{d} = \{x_{i}y_{i+d(mod\ m)}|i = 0, 1, ..., m-1\}$, $d = 0, 1, 2, ...\frac{m-5}{2}$;

(3) $\frac{m-3}{2}$ pairwise arc-disjoint perfect matchings $\overleftarrow{M}_{d} = \{y_{i+d(mod\ m)}x_{i}|i = 0, 1, ..., m-1\}$, $d = 0, 1, 2, ...\frac{m-5}{2}$;

(4) $\overrightarrow{M}_{\frac{m-3}{2}} = \{x_{i}y_{i+d(mod\ m)}|i = 0, 1, ..., m-1\}$, $\overleftarrow{M}_{\frac{m-1}{2}} = \{y_{i+d(mod\ m)}x_{i}|i = 0, 1, ..., m-1\}$, and $\overleftarrow{M}_{\frac{m-3}{2}} = \{y_{i+d(mod\ m)}x_{i}|i = 0, 1, ..., m-1\}$, $\overrightarrow{M}_{\frac{m-1}{2}} = \{x_{i}y_{i+d(mod\ m)}|i = 0, 1, ..., m-1\}$.

Similarly to the proof of Proposition 3.7 in ^[12], we can construct $2m+\frac{2}{3}(m-3)$ arc-disjoint linear $3$-diforests using the linear $3$-diforests in (1) and the matchings in (2) and (3).

Next, we apply the replacing arc operation for the arcs of $\overleftarrow{M}_{\frac{m-1}{2}}$ in some linear $3$-diforests of (1) and obtain a new matching $\overrightarrow{M}_{\frac{m+1}{2}}$. Also, we obtain $\overleftarrow{M}_{\frac{m+3}{2}}$ by replacing the arcs of $\overrightarrow{M}_{\frac{m-3}{2}}$ in some linear $3$-diforests of (1).

Now there are only four matchings left: $\overleftarrow{M}_{\frac{m-3}{2}}$, $\overrightarrow{M}_{\frac{m-1}{2}}$, $\overrightarrow{M}_{\frac{m+1}{2}}$, $\overleftarrow{M}_{\frac{m+3}{2}}$. In the following, we prove that these four matchings can form three arc-disjoint linear $3$-diforests. For convenience, we denote these four matchings by $\overleftarrow{M}_{3t}$, $\overrightarrow{M}_{3t+1}$, $\overrightarrow{M}_{3t+2}$, $\overleftarrow{M}_{3t+3}$.

We partition $\overrightarrow{M}_{3t+1}$ into three pairwise arc-disjoint matchings $\overrightarrow{W}_{0} = \{x_{4t+3}y_{t+1}\}$, $\overrightarrow{W}_{1} = \{x_{i}y_{i+3t+1(mod\ 6t+3)}|i = 0, 2, 4, ..., 4t+2, 4t+5, 4t+7, ..., 6t+1\}$ and $\overrightarrow{W}_{2} = \{x_{i}y_{i+3t+1(mod\ 6t+3)}|i = 1, 3, 5, ..., 4t+1, 4t+4, 4t+6, ..., 6t+2\}$. Also, we partition $\overleftarrow{M}_{3t+3}$ into two arc-disjoint matchings $\overleftarrow{W}^{'}_{1} = \{y_{i+3t+3(mod\ 6t+3)}x_{i}|i = 0, 2, 4, ..., 4t+2, 4t+5, 4t+7, ..., 6t+1\}$ and $\overleftarrow{W}^{'}_{2} = \{y_{i+3t+3(mod\ 6t+3)}x_{i}|i = 1, 3, 5, ..., 4t+1, 4t+3, 4t+4, 4t+6, ..., 6t+2\}$. Then the arcs in $\overleftarrow{M}_{3t} \cup \overrightarrow{W}_{2}$, $\overrightarrow{M}_{3t+2} \cup \overrightarrow{W}^{'}_{1}$, $\overrightarrow{W}_{1} \cup \overleftarrow{W}^{'}_{2}$ can form three linear $3$-diforests, which are denoted by $L_{1}$, $L_{2}$ and $L_{3}$ respectively. We move the arc $y_{t+1}x_{4t+4}$ of $L_{1}$ into $L_{3}$, add $\overrightarrow{W}_{0}$ into $L_{1}$ and finally obtain three arc-disjoint linear $3$-diforests by using $\overleftarrow{M}_{3t}$, $\overrightarrow{M}_{3t+1}$, $\overrightarrow{M}_{3t+2}$, $\overleftarrow{M}_{3t+3}$.

Accordingly, $\overrightarrow{la}_{3}(K^{\ast}_{n}) \leq 2m+\frac{2m-6}{3}+3 = 2\lceil \frac{2n}{3}\rceil-1$.

Proposition 3.5. $\overrightarrow{la}_{3}(K^{\ast}_{n}) \leq 2\lceil \frac{2n}{3}\rceil-1$ when $n\equiv10\; (mod\ 12)$.

Proof. Let $n = 12t+10$, $m = \frac{n}{2} = 6t+5, t \geq 0$. In $K^{\ast}_{n}$, we have

(1) $2m$ pairwise arc-disjoint linear $3$-diforests;

(2) $\frac{m-1}{2}$ pairwise arc-disjoint matchings $\overrightarrow{M}_{d} = \{x_{i}y_{i+d(mod\ m)}|i = 0, 1, ..., m-1\}$, $d = 1, 2, ...\frac{m-1}{2}$;

(3) $\frac{m-1}{2}$ pairwise arc-disjoint matchings $\overleftarrow{M}_{d} = \{y_{i+d(mod\ m)}x_{i}|i = 0, 1, ..., m-1\}$, $d = 1, 2, ...\frac{m-1}{2}$.

We assume that $t$ is even. We partition the matchings in (2) and (3) into two groups $\mathcal{M}_1 = \{\overrightarrow{M}_{1}, \overleftarrow{M}_{2}, \overrightarrow{M}_{3}, ..., \overrightarrow{M}_{3t+1}, \overleftarrow{M}_{3t+2}\}$ and $\mathcal{M}_2 = \{\overleftarrow{M}_{1}, \overrightarrow{M}_{2}, \overleftarrow{M}_{3}, ..., \overleftarrow{M}_{3t+1}, \overrightarrow{M}_{3t+2}\}$. Then we apply the replacing arc operation for the arcs of the matchings of $\mathcal{M}_2$ in some linear $3$-diforests of (1) and obtain some new matchings which are put in a new group $\mathcal{M}_3 = \{\overrightarrow{M}_{6t+4}, \overleftarrow{M}_{6t+3}, \overrightarrow{M}_{6t+2}, ..., \overrightarrow{M}_{3t+4}, \overleftarrow{M}_{3t+3}\}$. Now the arcs not covered by linear $3$-diforests are either in the matchings of $\mathcal{M}_1$ or in the matchings of $\mathcal{M}_3$.

We claim that $\overrightarrow{M}_{1}$, $\overleftarrow{M}_{2}$, $\overleftarrow{M}_{6t+3}$, $\overrightarrow{M}_{6t+4}$ can form three pairwise arc-disjoint $3$-diforests. First, we partition $\overrightarrow{M}_{1}$ into two arc-disjoint matchings $\overrightarrow{W}_{1} = \{x_{i}y_{i+1}|i = 0, 2, 4, ..., 6t+4\}$ and $\overrightarrow{W}_{2} = \{x_{i}y_{i+1}|i = 1, 3, 5, ..., 6t+3\}$; we partition $\overleftarrow{M}_{6t+3}$ into two arc-disjoint matchings $\overleftarrow{W}^{'}_{1} = \{y_{i+6t+3}x_{i}|i = 0, 2, 4, ..., 6t+2\}$ and $\overleftarrow{W}^{'}_{2} = \{y_{i+6t+3}x_{i} \cup y_{6t+2}x_{6t+4}|i = 1, 3, 5, ..., 6t+3\}$. Then the arcs in $\overrightarrow{W}_{2} \cup \overleftarrow{M}_{2}$, $\overleftarrow{W}^{'}_{1} \cup \overrightarrow{M}_{6t+4}$, $\overrightarrow{W}_{1} \cup \overleftarrow{W}^{'}_{2}$ can form three linear $3$-diforests $L_{1}$, $L_{2}$ and $L$ respectively, where $L = \{x_{i}y_{i+1}x_{i+3} \cup x_{6t+2}y_{6t+3} \cup y_{6t+4}x_{1} \cup y_{6t+2}x_{6t+4}y_{0}|i = 0, 2, 4, ..., 6t\}$. Thus, we have proved our claim and it is easy to observe that $y_{i}(i \in \{2, 4, ..., 6t\})$ are not incident to any arcs in $L$.

Now we only need to construct linear $3$-diforests to cover the remain matchings: $\overrightarrow{M}_{3}$, $\overleftarrow{M}_{4}$, ..., $\overrightarrow{M}_{3t+1}$, $\overleftarrow{M}_{3t+2}$ and $\overleftarrow{M}_{3t+3}$, $\overrightarrow{M}_{3t+4}$, ..., $\overleftarrow{M}_{6t+1}$, $\overrightarrow{M}_{6t+2}$. Lemma 2.6 states that we can take away one arc from each $\overleftarrow{M}_{4+6i}$, $\overrightarrow{M}_{7+6i}$, $\overrightarrow{M}_{3t+4+6i}$, $\overleftarrow{M}_{3t+7+6i}$ $(i = 0, 1, ..., \frac{t}{2}-1)$ when $t$ is even and the remaining arcs can form $4t$ linear $3$-diforests. And those arcs that we took away are adjacent to some $y_{i} (i \in \{2, 4, ..., 6t\})$, so they can be moved into $L$ to form a new linear $3$-diforest.

Then we show how we select those arcs $\{e_{j}, j = 0, 1, ..., 2t-1\}$ of each $\overleftarrow{M}_{4+6i}$, $\overrightarrow{M}_{7+6i}$, $\overrightarrow{M}_{3t+4+6i}$, $\overleftarrow{M}_{3t+7+6i}$ $(i = 0, 1, ..., \frac{t}{2}-1)$ when $t$ is even.

Case 1.1. $t\neq 10k+2, 10k+6$ and $10k$, $k \geq 0$.

Let $e_{i}$ = $y_{t+6+10i}x_{t+2+4i} \in \overleftarrow{M}_{4+6i}$, $e_{\frac{t}{2}+i}$ = $x_{t+3+4i}y_{t+10+10i} \in \overrightarrow{M}_{7+6i}$,

$e_{t+i}$ = $x_{3t+3+4i}y_{2+10i} \in \overrightarrow{M}_{3t+4+6i}$, $e_{\frac{3t}{2}+i}$ = $y_{6+10i}x_{3t+4+4i} \in \overleftarrow{M}_{3t+7+6i}$, for all $i \in \{0, 1, 2, ..., \frac{t}{2}-1\}$.

Case 1.2. $t = 10k+2, k \geq 0$.

When $k \geq 1$, let $e_{i}$ = $y_{t+4+10i}x_{t+4i} \in \overleftarrow{M}_{4+6i}$, $e_{\frac{t}{2}+i}$ = $x_{t+1+4i}y_{t+8+10i} \in \overrightarrow{M}_{7+6i}$,

$e_{t+i}$ = $x_{3t+9+4i}y_{8+10i} \in \overrightarrow{M}_{3t+4+6i}$, $e_{\frac{3t}{2}+i}$ = $y_{12+10i}x_{3t+10+4i} \in \overleftarrow{M}_{3t+7+6i}$, for all $i \in \{0, 1, 2, ..., \frac{t}{2}-1\}$.

When $k = 0$, let $e_{0} = y_{8}x_{4}\in \overleftarrow{M}_{4}$, $e_{1} = x_{5}y_{12} \in \overrightarrow{M}_{7}$, $e_{2} = x_{9}y_{2} \in \overrightarrow{M}_{10}$, $e_{3} = y_{6}x_{10} \in \overleftarrow{M}_{13}$.

Case 1.3. $t = 10k, 10k+6, k \geq 0$.

When $t = 0$, $\overrightarrow{M}_{1}$, $\overleftarrow{M}_{2}$, $\overrightarrow{M}_{3}$, $\overleftarrow{M}_{4}$ can form three arc-disjoint linear $3$-diforests.

When $t\neq0$, let $e_{i}$ = $y_{t+4+10i}x_{t+4i} \in \overleftarrow{M}_{4+6i}$, $e_{\frac{t}{2}+i}$ = $x_{t+1+4i}y_{t+8+10i} \in \overrightarrow{M}_{7+6i}$,

$e_{t+i}$ = $x_{3t+3+4i}y_{2+10i} \in \overrightarrow{M}_{3t+4+6i}$, $e_{\frac{3t}{2}+i}$ = $y_{6+10i}x_{3t+4+4i} \in \overleftarrow{M}_{3t+7+6i}$, for all $i \in \{0, 1, 2, ..., \frac{t}{2}-1\}$.

Now we assume that $t$ is odd and partition the matchings in (2) and (3) into two groups $\mathcal{M}_1 = \{\overrightarrow{M}_{1}, \overleftarrow{M}_{2}, \overrightarrow{M}_{3}, ..., \overleftarrow{M}_{3t+1}, \overrightarrow{M}_{3t+2}\}$ and $\mathcal{M}_2 = \{\overleftarrow{M}_{1}, \overrightarrow{M}_{2}, \overleftarrow{M}_{3}, ..., \overrightarrow{M}_{3t+1}, \overleftarrow{M}_{3t+2}\}$. Similarly to the proof above, we need to select one arc from each $\overleftarrow{M}_{4+6i}$, $\overrightarrow{M}_{7+6i}$, $\overleftarrow{M}_{3t+4+6i}$, $\overrightarrow{M}_{3t+7+6i}$, $i \in \{0, 1, 2, ..., \frac{t-1}{2}-1\}$.

Case 2.1. $t\neq 10k+1, 10k+3$ and $10k+7$, $k \geq 0$.

Let $e_{i}$ = $y_{t+5+10i}x_{t+1+4i} \in \overleftarrow{M}_{4+6i}$, $e_{\frac{t-1}{2}+i}$ = $x_{t+2+4i}y_{t+9+10i} \in \overrightarrow{M}_{7+6i}$,

$e_{t-1+i}$ = $y_{2+10i}x_{3t+3+4i} \in \overleftarrow{M}_{3t+4+6i}$, $e_{\frac{3(t-1)}{2}+i}$ = $x_{3t+4+4i}y_{6+10i} \in \overrightarrow{M}_{3t+7+6i}$, for all $i \in \{0, 1, ..., \frac{t-1}{2}-1\}$.

$e_{2t-2} = y_{6t}x_{3t-1} \in \overleftarrow{M}_{3t+1}$, $e_{2t-1} = y_{6t-2}x_{6t+2} \in \overleftarrow{M}_{6t+1}$.

Case 2.2. $t = 10k+3, 10k+7, k \geq 0$.

Let $e_{i}$ = $y_{t+1+10i}x_{t-3+4i} \in \overleftarrow{M}_{4+6i}$, $e_{\frac{t-1}{2}+i}$ = $x_{t-2+4i}y_{t+5+10i} \in \overrightarrow{M}_{7+6i}$,

$e_{t-1+i}$ = $y_{6+10i}x_{3t+7+4i} \in \overleftarrow{M}_{3t+4+6i}$, $e_{\frac{3(t-1)}{2}+i}$ = $x_{3t+8+4i}y_{10+10i} \in \overrightarrow{M}_{3t+7+6i}$, for all $i \in \{0, 1, ..., \frac{t-1}{2}-1\}$.

$e_{2t-2} = y_{6t}x_{3t-1} \in \overleftarrow{M}_{3t+1}$, $e_{2t-1} = y_{6t-2}x_{6t+2} \in \overleftarrow{M}_{6t+1}$.

Case 2.3. $t = 10k+1, k \geq 0$.

When $k \geq 1$, let $e_{i}$ = $y_{t+1+10i}x_{t-3+4i} \in \overleftarrow{M}_{4+6i}$, $e_{\frac{t-1}{2}+i}$ = $x_{t-2+4i}y_{t+5+10i} \in \overrightarrow{M}_{7+6i}$,

$e_{t-1+i}$ = $y_{4+10i}x_{3t+5+4i} \in \overleftarrow{M}_{3t+4+6i}$, $e_{\frac{3(t-1)}{2}+i}$ = $x_{3t+6+4i}y_{8+10i} \in \overrightarrow{M}_{3t+7+6i}$, for all $i \in \{0, 1, ..., \frac{t-1}{2}-1\}$.

$e_{2t-2} = y_{6t}x_{3t-1} \in \overleftarrow{M}_{3t+1}$, $e_{2t-1} = y_{6t-2}x_{6t+2} \in \overleftarrow{M}_{6t+1}$.

When $k = 0$, let $e_{0} = y_{4}x_{0} \in \overleftarrow{M}_{4}$ and $e_{1} = y_{2}x_{6} \in \overleftarrow{M}_{7}$.

We have finished all the cases discussion and the arcs $\{e_{i}, i = 0, 1, ..., 2t-1\}$ are what we need. Accordingly, $\overrightarrow{la}_{3}(K^{\ast}_{n}) \leq 2(6t+5)+4t+3 = 2\lceil \frac{2n}{3}\rceil-1$.

Now we conclude the following result for the linear $3$-arboricity of $K^{\ast}_{n}$, which verifies Conjecture 2.1.

Theorem 3.1.

Proof. By Lemmas 2.3, 2.4 and Theorem 2.1, $\left \lceil \frac{n(n-1)}{\lfloor\frac {3n}{4}\rfloor} \right \rceil \leq \overrightarrow{la}_{3}(K^{\ast}_{n}) \leq 2la_{3}(K_{n})$. In addition, with the above five propositions, we have the result.

4.   Linear $2$-arboricity of symmetric complete digraphs

In this section, we study the linear $2$-arboricity of $K^{\ast}_{n}$. We first introduce $K_3$-factorization $\boldsymbol{F} = \{F_{1}, F_{2}, ..., F_{t}\}$ of $K_{n} (n \geq 3)$: $(1)$ $F_{i}$ is a spanning subgraph of $K_{n}$ and each component of $F_{i}$ is isomorphic to $K_{3}$; (2) each edge is in only one $F_{i}$ $(1\leq i\leq t)$. And we call each $F_{i}$ is a $K_3$-factor of $K_n$. Similarly, we can define the $\overrightarrow{K_3}$-factorization of $K^*_{n} (n \geq 3)$ and each component of the $\overrightarrow{K_3}$-factor is a directed $K_3$.

Lemma 4.1. Let $C^{\ast}_{n}$ be a symmetric directed cycle with $n$ vertices. If $n\equiv 0\; (mod\ 6)$, then $\overrightarrow{la}_{2}(C^{\ast}_{n}) = 3$.

Proof. Let $n = 6t$ and $C^{\ast}_{n} = (x_{0}, x_{1}, ..., x_{6t-1}, x_{0})$. The arcs of $C^{\ast}_{n}$ can be decomposed into three linear $2$-diforests: $\{x_{i}x_{i+1}x_{i+2}|i = 0, 6, ..., 6t-6\} \cup$$\{x_{i+2}x_{i+1}x_{i}|i = 3, 9, ..., 6t-3\}$, $\{x_{i}x_{i+1}x_{i+2}|i = 2, 8, ..., 6t-4\} \cup$$\{x_{i+2(mod\ 6t)}x_{i+1(mod\ 6t)}x_{i}|i = 5, 11, ..., 6t-1\}$ and $\{x_{i}x_{i+1}x_{i+2}|i = 4, 10, ..., 6t-2\} \cup$$\{x_{i+2}x_{i+1}x_{i}|i = 1, 7, ..., 6t-5\}$.

Proposition 4.1. $\overrightarrow{la}_{2}(K^{\ast}_{n}) \leq 2\left \lceil \dfrac{n(n-1)}{2\lfloor\dfrac{2n}{3}\rfloor} \right \rceil-1$ when $n\equiv0\; (mod\ 12)$.

Proof. Let $n = 12t$.

When $t = 1$, we know that $K^{\ast}_{12} = K^{\ast}_{6, 6}\cup2K^{\ast}_{6}$. Then $\overrightarrow{la}_{2}(K^{\ast}_{12}) \leq \overrightarrow{la}_{2}(K^{\ast}_{6, 6}) + \overrightarrow{la}_{2}(K^{\ast}_{6})$. Since $K^{\ast}_{6, 6}$ can be decomposed into three arc-disjoint symmetric directed cycles and each such cycle can form three linear $2$-forests by Lemma 4.1, $\overrightarrow{la}_{2}(K^{\ast}_{6, 6})\leq 9$. Let $V(K^{\ast}_{6}) = \{x_{0}, x_{1}, x_{2}, y_{0}, y_{1}, y_{2}\}$. We decompose $K^{\ast}_{6} = 2K^{\ast}_{3} \cup M^{\ast}_{0} \cup M^{\ast}_{1} \cup M^{\ast}_{2}$, where $M^{\ast}_{d} = \{x_{i}y_{i+d(mod\ 3)}, y_{i+d(mod\ 3)}x_{i}|i = 0, 1, 2\}$ $(d = 0, 1, 2)$. $M^{\ast}_{0} \cup M^{\ast}_{1}$ can form a symmetric directed cycle and thus form three linear $2$-diforests by Lemma 4.1. $2K^{\ast}_{3} \cup M^{\ast}_{2}$ contains a symmetric directed cycle $x_{1}x_{0}x_{2}y_{1}y_{2}y_{0}x_{1}$ and still can form three linear $2$-diforests by Lemma 4.1. In addition, $x_{1}x_{2}, x_{0}y_{2}, y_{0}y_{1}$ and $x_{2}x_{1}, y_{2}x_{0}, y_{1}y_{0}$ form two linear $2$-diforests. Thus, $\overrightarrow{la}_{2}(K^{\ast}_{12})\leq \overrightarrow{la}_{2}(K^{\ast}_{6, 6}) + \overrightarrow{la}_{2}(K^{\ast}_{6}) \leq 9+3+3+2 = 17$.

Now we assume $t\geq 2$. Baker and Wilson ^[5] proved that if $F$ is a perfect matching of $K_{n}$, $K_{n}-F$ can be decomposed into $6t-1$ $K_3$-factors if and only if $n = 0 (mod\ 12)$ and $t \geq 2$. So for two perfect matchings $F$ and $F^{'}$ in $K_n^*$, which are with opposite directions, we obtain $6t-1$ $\overrightarrow{K_3}$-factors $F_{1}, F_{2}, ..., F_{6t-1}$ and $6t-1$ $\overrightarrow{K_3}$-factors $F^{'}_{1}, F^{'}_{2}, ..., F^{'}_{6t-1}$ with opposite directions in $K_n^*-\{F, F^{'}\}$.

For the union of any two $\overrightarrow{K_3}$-factors, the directed triangles with a common vertex have two possibilities as in Figure 2. It is easy to check that both circumstances can be decomposed into three linear $2$-diforests. $F_{1}, F_{2}, ..., F_{6t-1}$ and $F^{'}_{1}, F^{'}_{2}, ..., F^{'}_{6t-1}$ can be partitioned into pairs of directed triangles with a common vertex, and then can form $3(6t-1)$ linear $2$-diforests. In addition, $F$ and $F^{'}$ also form two linear $2$-diforests in a trivial way.

So $\overrightarrow{la}_{2}(K^{\ast}_{n}) \leq 3(6t-1)+2 = 2\left \lceil \dfrac{n(n-1)}{2\lfloor\dfrac{2n}{3}\rfloor} \right \rceil-1$.

Proposition 4.2. $\overrightarrow{la}_{2}(K^{\ast}_{n}) \leq 2\left \lceil \dfrac{n(n-1)}{2\lfloor\dfrac{2n}{3}\rfloor} \right \rceil-1$ when $n\equiv3\; (mod\ 12)$ and $n > 3$.

Proof. Let $n = 12t+3.$ Ray-Chauduri and Wilson^[18] proved that $K_{n}$ can be decomposed into $6t+1$ $K_3$ factors if and only if $n = 3\; (mod\ 6)$. Thus, as in Proposition 6, we obtain $6t+1$ $\overrightarrow{K_3}$-factors $F_{1}, F_{2}, ..., F_{6t+1}$ and $6t+1$ $\overrightarrow{K_3}$-factors $F^{'}_{1}, F^{'}_{2}, ..., F^{'}_{6t+1}$ with opposite directions in $K_n^*$. $F_{1}, F_{3}, ..., F_{6t+1}$ and $F^{'}_{1}, F^{'}_{2}, ..., F^{'}_{6t+1}$ can form $3(6t+1)$ linear $2$-diforests.

Accordingly, $\overrightarrow{la}_{2}(K^{\ast}_{n}) \leq 3(6t+1) = 2\left \lceil \dfrac{n(n-1)}{2\lfloor\dfrac{2n}{3}\rfloor} \right \rceil-1$.

Proposition 4.3. $\overrightarrow{la}_{2}(K^{\ast}_{n}) \leq 2\left \lceil \dfrac{n(n-1)}{2\lfloor\dfrac{2n}{3}\rfloor} \right \rceil-1$ when $n\equiv2, 10\; (mod\ 12)$.

Proof. Since Alspach el al. ^[4] proved that $K_n$ has a Hamiltonian path decomposition when $n$ is even, $K^{\ast}_{n}$ can be decomposed into $\frac{n}{2}$ arc-disjoint symmetric directed $n$-paths. Each symmetric directed path can be decomposed into three linear $2$-forests. Thus, $K^{\ast}_{n}$ can form $\frac{3n}{2}$ arc-disjoint linear $2$-diforests.

Accordingly, $\overrightarrow{la}_{2}(K^{\ast}_{n}) \leq \frac{3n}{2} = 2\left \lceil \dfrac{n(n-1)}{2\lfloor\dfrac{2n}{3}\rfloor} \right \rceil-1$.

Proposition 4.4. $\overrightarrow{la}_{2}(K^{\ast}_{n}) \leq 2\left \lceil \dfrac{n(n-1)}{2\lfloor\dfrac{2n}{3}\rfloor} \right \rceil-1$ when $n\equiv7\; (mod\ 12)$.

Proof. Let $n = 12t+7$ and $\{v_0, v_1, v_2, ..., v_{12t+6}\}$ be the vertex set of $K^{\ast}_{n}$. Since Alspach el al. ^[4] proved that $K_n$ has a Hamiltonian cycle decomposition when $n$ is odd, $K^{\ast}_{n}$ can be decomposed into $6t+3$ symmetric directed Hamiltonian cycles

$C^{\ast}_{i} = v_{12t+6}v_{i}v_{12t+5+i(mod\ 12t+6)}v_{i+1}v_{12t+4+i(mod\ 12t+6)}...v_{6t+2+i}v_{6t+3+i}v_{12t+6}$ $(0 \leq i \leq 6t+2)$.

Next, we construct symmetric directed paths from $C^{\ast}_{i}$ by removing two kinds of symmetric arcs $v_{3t+1+i}v_{9t+4+i(mod\ 12t+6)}, v_{9t+4+i(mod\ 12t+6)}v_{3t+1+i}$ $(0 \leq i \leq 6t+2)$. Those removed arcs form two matchings and thus form two arc-disjoint linear $2$-diforests. In addition, each symmetric directed paths can form three arc-disjoint linear $2$-diforests.

Accordingly, $\overrightarrow{la}_{2}(K^{\ast}_{n}) \leq 3(6t+3)+2 = 2\left \lceil \dfrac{n(n-1)}{2\lfloor\dfrac{2n}{3}\rfloor} \right \rceil-1$.

Proposition 4.5. $\overrightarrow{la}_{2}(K^{\ast}_{n}) \leq 2\left \lceil \dfrac{n(n-1)}{2\lfloor\dfrac{2n}{3}\rfloor} \right \rceil-1$ when $n\equiv5\; (mod\ 12)$.

Proof. Let $n = 12t+5$. $K^{\ast}_{n}$ can be decomposed into $6t+2$ symmetric directed Hamiltonian cycles

$C^{\ast}_{i} = v_{12t+4}v_{i}v_{12t+3+i(mod\ 12t+4)}v_{i+1}v_{12t+2+i(mod\ 12t+4)}...v_{6t+1+i}v_{6t+2+i}v_{12t+4}$ $(0 \leq i \leq 6t+1)$.

We obtain symmetric directed paths from $C^{\ast}_{i}$ by removing the symmetric arcs $v_{3t+1+i}v_{9t+3+i(mod\ 12t+4)}$, $v_{9t+3+i(mod\ 12t+4)}v_{3t+1+i}$ $(0 \leq i \leq 6t+1)$. Next, for each such path, we relabel these vertices as $x_{0}, x_{1}, x_{2}, ..., x_{12t+4}$ along the direction: $x_{0}$ on behalf of the vertex $v_{9t+3+i(mod\ 12t+4)}$; $x_{12t+4}$ on behalf of the vertex $v_{3t+1+i}$. Then for each such path, we decompose it into three linear $2$-diforests $F_{1}$, $F_{2}$, $F_{3}$ as follows:

$F_{1} = \{x_{i}x_{i+1}x_{i+2}|i = 0, 6, ..., 12t\} \cup \{x_{i+5}x_{i+4}x_{i+3}|i = 0, 6, ..., 12t-6\} \cup \{x_{12t+3}x_{12t+4}\}$;

$F_{2} = \{x_{i+3}x_{i+2}x_{i+1}|i = 0, 6, ..., 12t\} \cup \{x_{i+4}x_{i+5}x_{i+6}|i = 0, 6, ..., 12t-6\}$;

$F_{3} = \{x_{i+2}x_{i+3}x_{i+4}|i = 0, 6, ..., 12t\} \cup \{x_{i+7}x_{i+6}x_{i+5}|i = 0, 6, ..., 12t-6\} \cup \{x_{1}x_{0} \}$.

And we move the arcs $x_{12t+4}x_{0} = v_{3t+1+i}v_{9t+3+i(mod\ 12t+4)}$ into $F_{2}$ to form a new linear $2$-diforest. In addition, the arcs $\{v_{9t+3+i(mod\ 12t+4)}v_{3t+1+i}|i = 0, 1, ..., 6t+1\}$ form a matching and then also a trivial linear $2$-diforest.

Accordingly, $\overrightarrow{la}_{2}(K^{\ast}_{n}) \leq 3(6t+2)+1 = 2\left \lceil \dfrac{n(n-1)}{2\lfloor\dfrac{2n}{3}\rfloor} \right \rceil-1$.

Now we have the following result for the linear $2$-arboricity of $K^{\ast}_{n}$, which verifies Conjecture 2.1.

Theorem 4.1. For $K^{\ast}_{n} (n > 3)$,

Proof. By Lemmas 2.3, 2.4 and Theorem 2.3, we know that $\left \lceil \frac{n(n-1)}{\lfloor\frac {2n}{3}\rfloor} \right \rceil \leq \overrightarrow{la}_{2}(K^{\ast}_{n}) \leq 2la_{2}(K_{n})$. With all the propositions in this section, we have the result.

5.   Linear $3$-arboricity of symmetric complete bipartite digraphs

Let $K^{\ast}_{n, n}$ be a symmetric complete bipartite digraph with partite sets $X = \{x_{0}, x_{1}, ..., x_{n}\}$ and $Y = \{y_{0}, y_{1}, ..., y_{n}\}$. We decompose the arc set of $K^{\ast}_{n, n}$ into $2n$ pairwise disjoint perfect matchings $\overrightarrow{M}_{d} = \{x_{i}y_{i+d(mod\ n)}|i = 0, 1, ..., n-1\}$ and $\overleftarrow{M}_{d} = \{y_{i+d(mod\ n)}x_{i}|i = 0, 1, ..., n-1\}$ $(d = 0, 1, 2, ...n-1)$.

Proposition 5.1. $\overrightarrow{la}_{3}(K^{\ast}_{n, n}) \leq 2\lceil \frac{2n}{3}\rceil-1$ when $n\equiv2\; (mod\ 6)$.

Proof. Let $n = 6t+2$. We partition the $2n$ pairwise arc-disjoint perfect matchings of $K^{\ast}_{n, n}$ into the following three groups:

(1) $\overrightarrow{M}_{2}$, $\overleftarrow{M}_{3}$, $\overrightarrow{M}_{4}$, ..., $\overrightarrow{M}_{6t}$, $\overleftarrow{M}_{6t+1}$;

(2) $\overleftarrow{M}_{0}$, $\overrightarrow{M}_{1}$, $\overleftarrow{M}_{2}$, ..., $\overleftarrow{M}_{6t-2}$, $\overrightarrow{M}_{6t-1}$;

(3) $\overrightarrow{M}_{0}$, $\overleftarrow{M}_{1}$, $\overleftarrow{M}_{6t}$, $\overrightarrow{M}_{6t+1}$.

By Lemma 2.5, the perfect matchings in $(1)$ and $(2)$ can form $8t$ arc-disjoint linear $3$-diforests.

In addition, we claim that the remaining matchings $\overrightarrow{M}_{0}$, $\overleftarrow{M}_{1}$, $\overleftarrow{M}_{6t}$, $\overrightarrow{M}_{6t+1}$ can form three arc-disjoint linear $3$-diforests. We partition $\overleftarrow{M}_{1}$ into two matchings $W_{1} = \{y_{i+1}x_{i}|i = 0, 2, ..., 6t\}$ and $W_{2} = \{y_{i+1}x_{i}|i = 1, 3, ..., 6t+1\}$. And we partition $\overrightarrow{M}_{6t+1}$ into two matchings $W^{'}_{1} = \{x_{i}y_{6t+1+i(mod\ 6t+2)}|i = 0, 2, ..., 6t\}$ and $W^{'}_{2} = \{x_{i}y_{6t+1+i(mod\ 6t+2)}|i = 1, 3, ..., 6t+1\}$. Then $W_{1} \cup W^{'}_{2}$, $W_{2} \cup \overrightarrow{M}_{0}$, $W^{'}_{1} \cup \overleftarrow{M}_{6t}$ form three arc-disjoint linear $3$-diforests.

Accordingly, $\overrightarrow{la}_{3}(K^{\ast}_{n, n}) \leq 8t+3 = 2\lceil \frac{2n}{3}\rceil-1$.

Proposition 5.2. $\overrightarrow{la}_{3}(K^{\ast}_{n, n}) \leq 2\lceil \frac{2n+2}{3}\rceil-1$ when $n\equiv3\; (mod\ 6).$

Proof. Let $n = 6t+3$. We partition the $2n$ pairwise arc-disjoint perfect matchings of $K^{\ast}_{n, n}$ into the following two groups:

(1) $\overrightarrow{M}_{0}$, $\overleftarrow{M}_{1}$, $\overrightarrow{M}_{2}$, ..., $\overleftarrow{M}_{6t+1}$, $\overrightarrow{M}_{6t+2}$;

(2) $\overleftarrow{M}_{0}$, $\overrightarrow{M}_{1}$, $\overleftarrow{M}_{2}$, ..., $\overrightarrow{M}_{6t+1}$, $\overleftarrow{M}_{6t+2}$.

Let $e_{i} = y_{4i}x_{6t+2-2i} \in \overleftarrow{M}_{1+6i} (i = 0, 1, ..., t)$,

$e_{t+1+i} = x_{6t+1-2i}y_{4i+2} \in \overrightarrow{M}_{4+6i} (i = 0, 1, ..., t-1)$,

$e_{2t+1+i} = x_{4t+1-2i}y_{4t+2+4i(mod\ 6t+3)} \in \overrightarrow{M}_{1+6i} (i = 0, 1, ..., t)$,

$e_{3t+2+i} = y_{4t+4+4i(mod\ 6t+3)}x_{4t-2i} \in \overleftarrow{M}_{4+6i} (i = 0, 1, ..., t-1)$.

Then we remove the arcs $\{e_{j}|j = 0, 1, ..., 4t+1 \}$ from those perfect matchings. By Lemma 2.6, the perfect matchings of $(1)$ and $(2)$ other than the removed arcs can form $8t+4$ arc-disjoint linear $3$-diforests. In addition, the removed arcs can form another one linear $3$-diforests.

Accordingly, $\overrightarrow{la}_{3}(K^{\ast}_{n, n}) \leq 8t+5 = 2\lceil \frac{2n+2}{3}\rceil-1$.

We have the following result for the linear $3$-arboricity of $K^{\ast}_{n, n}$, which verifies Conjecture 2.1.

Theorem 5.1.

Proof. By Lemmas 2.3, 2.4 and Theorem 2.2, $\left \lceil \frac{2n^{2}}{\lfloor\frac {6n}{4}\rfloor} \right \rceil \leq \overrightarrow{la}_{3}(K^{\ast}_{n, n}) \leq 2la_{3}(K_{n, n})$. With all the propositions in this section, we have the result.

6.   Linear $2$-arboricity of symmetric complete bipartite digraphs

Proposition 6.1. $\overrightarrow{la}_{2}(K^{\ast}_{n, n}) \leq 2\left \lceil \dfrac{n^{2}}{\lfloor\dfrac{4n}{3}\rfloor} \right \rceil-1$ when $n\equiv3\; (mod\ 12)$.

Proof. Let $n = 12t+3$. We partition the $2n$ pairwise arc-disjoint perfect matchings of $K^{\ast}_{n, n}$ into two groups:

(1) $\overrightarrow{M}_{i}$, $\overleftarrow{M}_{i}$, $\overrightarrow{M}_{i+1}$, $\overleftarrow{M}_{i+1}$, $i = 0, 2, 4, ..., 12t$;

(2) $\overleftarrow{M}_{12t+2}$, $\overrightarrow{M}_{12t+2}$.

For $i \in \{0, 2, 4, ..., 12t\}$, $\overrightarrow{M}_{i}$, $\overleftarrow{M}_{i}$, $\overrightarrow{M}_{i+1}$, $\overleftarrow{M}_{i+1}$ can form a symmetric directed cycle and such cycle can be decomposed into three linear $2$-diforests by Lemma 4.1. In addition, $\overleftarrow{M}_{12t+2}$ and $\overrightarrow{M}_{12t+2}$ form another two linear $2$-diforests.

Accordingly, $\overrightarrow{la}_{2}(K^{\ast}_{n, n}) \leq 3(6t+1)+2 = 2\left \lceil \dfrac{n^{2}}{\lfloor\dfrac{4n}{3}\rfloor} \right \rceil-1$.

Proposition 6.2. $\overrightarrow{la}_{2}(K^{\ast}_{n, n}) \leq 2\left \lceil \dfrac{n^{2}}{\lfloor\dfrac{4n}{3}\rfloor} \right \rceil-1$ when $n\equiv4\; (mod\ 12)$.

Proof. Let $n = 12t+4$. $K^{\ast}_{n, n}$ can be decomposed into $2n$ pairwise arc-disjoint perfect matchings and every four matchings $\overrightarrow{M}_{i}$, $\overleftarrow{M}_{i}$, $\overrightarrow{M}_{i+1}$, $\overleftarrow{M}_{i+1}$ $(i = 0, 2, ..., 12t+2)$ form a symmetric directed cycle $C^{\ast}_{j} (j = \frac{i}{2})$.

We claim that if $C$ is a symmetric directed cycle with $V(C) = \{x_{0}, x_{1}, ..., x_{24t+7}\}$ and $e$ is an arc of $C$, then $C-\{e\}$ can form three arc-disjoint linear $2$-diforests. Without loss of generality, we assume that $e = x_{0}x_{24t+7}$. The three linear $2$-diforests $F_{1}, F_{2}, F_{3}$ are $F_{1} = \{x_{i}x_{i+1}x_{i+2}|i = 0, 6, ..., 24t\} \cup$$\{x_{i+2}x_{i+1}x_{i}|i = 3, 9, ..., 24t+3\} \cup$$\{x_{24t+6}x_{24t+7}\}$, $F_{2} = \{x_{i+2}x_{i+1}x_{i}|i = 1, 7, ..., 24t+1\} \cup$$\{x_{i}x_{i+1}x_{i+2}|i = 4, 10, ..., 24t+4\} \cup$$\{x_{24t+7}x_{0}\}$ and $F_{3} = \{x_{i}x_{i+1}x_{i+2}|i = 2, 8, ..., 24t+2\} \cup$$\{x_{i+2}x_{i+1}x_{i}|i = 5, 11, ..., 24t+5\} \cup$$\{x_{1}x_{0}\}$.

Let $e_{j} = x_{n-1-j}y_{j} \in C^{\ast}_{j}$ $(j = 0, 1, ...6t+1)$. By the claim above, $C^{\ast}_{j}-\{e_{j}\}$ can form three linear $2$-diforests. Furthermore, $\{e_{j}|i = 0, 1, ..., 6t+1\}$ is a matching and thus form one linear $2$-diforest.

Accordingly, $\overrightarrow{la}_{2}(K^{\ast}_{n, n}) \leq 3(6t+2)+1 = 2\left \lceil \dfrac{n^{2}}{\lfloor\dfrac{4n}{3}\rfloor} \right \rceil-1$.

Proposition 6.3. $\overrightarrow{la}_{2}(K^{\ast}_{n, n}) \leq 2\left \lceil \dfrac{n^{2}}{\lfloor\dfrac{4n}{3}\rfloor} \right \rceil-1$ when $n\equiv5\; (mod\ 12)$.

Proof. Let $n = 12t+5$. We partition the $2n$ pairwise disjoint perfect matchings of $K^{\ast}_{n, n}$ into two groups:

(1) $\overrightarrow{M}_{i}$, $\overleftarrow{M}_{i}$, $\overrightarrow{M}_{i+1}$, $\overleftarrow{M}_{i+1}$, $(i = 0, 2, ..., 12t+2)$;

(2) $\overleftarrow{M}_{12t+4}$, $\overrightarrow{M}_{12t+4}$.

Every four matchings $\overrightarrow{M}_{i}$, $\overleftarrow{M}_{i}$, $\overrightarrow{M}_{i+1}$, $\overleftarrow{M}_{i+1}$ $(i \in \{0, 2, ..., 12t+2\})$ form a symmetric directed cycle $C^{\ast}_{j} (j = \frac{i}{2})$.

We claim that if $C$ is a symmetric directed cycle with $V(C) = \{x_{0}, x_{1}, ..., x_{24t+9}\}$, and $e = x_{0}x_{24t+9}$, $e^{'} = x_{3}x_{2}$ are two arcs of $C$, then $C-\{e, e^{'}\}$ can form three arc-disjoint linear $2$-diforests, which are $F_{1} = \{x_{i}x_{i+1}x_{i+2}|i = 3, 9, ..., 24t+3\} \cup$$\{x_{i+2}x_{i+1}x_{i}|i = 6, 12, ..., 24t+6\} \cup$$\{x_{24t+9}x_{0}x_{1}\}$, $F_{2} = \{x_{i}x_{i+1}x_{i+2}|i = 1, 7, ..., 24t+7\} \cup$$\{x_{i+2}x_{i+1}x_{i}|i = 4, 10, ..., 24t+4\}$ and $F_{3} = \{x_{i}x_{i+1}x_{i+2}|i = 5, 11, ..., 24t+5\} \cup$$\{x_{i+2}x_{i+1}x_{i}|i = 8, 14, ..., 24t+2, t \geq 1\} \cup \{x_{2}x_{1}x_{0}\} \cup \{x_{4}x_{3}\} \cup$$\{x_{24t+9}x_{24t+8}\}$.

Let $e_{j} = x_{2j}y_{4j(mod\ n)}$, $e^{'}_{j}$ $= y_{4j+2(mod\ n)}x_{2j+1} \in C^{\ast}_{j}$, $(j = 0, 1, ...6t+1)$. From our claim above $C^{\ast}_{j}-\{e_{j}, e^{'}_{j}\}$ form three linear $2$-diforests. Furthermore, $\{e_{j}|j = 0, 1, ..., 6t+1\}\cup \{e_{j}^{'}|j = 0, 1, ..., 6t+1\}$ is a matching and thus form a linear $2$-diforest.

In addition, the remaining matchings $\overleftarrow{M}_{12t+4}$, $\overrightarrow{M}_{12t+4}$ also form two linear $2$-diforests.

Accordingly, $\overrightarrow{la}_{2}(K^{\ast}_{n, n}) \leq 3(6t+2)+1+2 = 2\left \lceil \dfrac{n^{2}}{\lfloor\dfrac{4n}{3}\rfloor} \right \rceil-1$.

Proposition 6.4. $\overrightarrow{la}_{2}(K^{\ast}_{n, n}) \leq 2\left \lceil \dfrac{n^{2}}{\lfloor\dfrac{4n}{3}\rfloor} \right \rceil-1$ when $n\equiv6\; (mod\ 12)$.

Proof. Let $n = 12t+6$. For $i \in \{0, 2, ..., 12t+4\}$, the matchings $\overrightarrow{M}_{i}$, $\overleftarrow{M}_{i}$, $\overrightarrow{M}_{i+1}$, $\overleftarrow{M}_{i+1}$ can form a symmetric directed cycle and such cycle can decomposed into three linear $2$-diforests by Lemma 4.1.

Accordingly, $\overrightarrow{la}_{2}(K^{\ast}_{n, n}) \leq 3(6t+3) = 2\left \lceil \dfrac{n^{2}}{\lfloor\dfrac{4n}{3}\rfloor} \right \rceil-1$.

Proposition 6.5. $\overrightarrow{la}_{2}(K^{\ast}_{n, n}) \leq 2\left \lceil \dfrac{n^{2}}{\lfloor\dfrac{4n}{3}\rfloor} \right \rceil-1$ when $n\equiv8\; (mod\ 12)$.

Proof. Let $n = 12t+8$. For $i \in \{0, 2, ..., 12t+6\}$, every four matchings $\overrightarrow{M}_{i}$, $\overleftarrow{M}_{i}$, $\overrightarrow{M}_{i+1}$, $\overleftarrow{M}_{i+1}$ form a symmetric directed cycle $C^{\ast}_{j} (j = \frac{i}{2})$.

We claim that if $C$ is a symmetric directed cycle with $V(C) = \{x_{0}, x_{1}, ..., x_{24t+15}\}$, and $e = x_{0}x_{24t+15}$, $e^{'} = x_{3}x_{2}$ are two arcs of $C$, then $C-\{e, e^{'}\}$ can form three arc-disjoint linear $2$-diforests, which are $F_{1} = \{x_{i}x_{i+1}x_{i+2}|i = 3, 9, ..., 24t+9\} \cup$$\{x_{i+2}x_{i+1}x_{i}|i = 6, 12, ..., 24t+12\} \cup$$\{x_{24t+15}x_{0}x_{1}\}$, $F_{2} = \{x_{i}x_{i+1}x_{i+2}|i = 1, 7, ..., 24t+13\} \cup$$\{x_{i+2}x_{i+1}x_{i}|i = 4, 10, ..., 24t+10 \}$ and $F_{3} = \{x_{i}x_{i+1}x_{i+2}|i = 5, 11, ..., 24t+11\} \cup \{x_{i+2}x_{i+1}x_{i}|i = 8, 14, ..., 24t+8\} \cup$$\{x_{2}x_{1}x_{0}\} \cup$$\{x_{4}x_{3}\} \cup \{x_{24t+15}x_{24t+14}\}$. And if we choose $e = x_{24t+15}x_{0}$, $e^{'} = x_{2}x_{3}$, we have the same claim.

Let $e_{j} = x_{2j}y_{4j(mod\ n)}$, $e^{'}_{j}$ $= y_{4j+2(mod\ n)}x_{2j+1}$ $\in C^{\ast}_{j}$, $(j = 0, 1, ..., 3t+1)$; $e_{j} = y_{4j(mod\ n)}x_{2j}$, $e^{'}_{j}$ $= x_{2j+1}y_{4j+2(mod\ n)}$ $\in C^{\ast}_{j}$, $j = 3t+2, 3t+3, ..., 6t+3$. By the claim above, $C^{\ast}_{j}-\{e_{j}, e^{'}_{j}\}$ form three linear $2$-diforests. Furthermore, the arcs $\{e_{j}|j = 0, 1, ..., 6t+3\}\cup \{e_j^{'}|j = 0, 1, ..., 6t+3\}$ form a linear $2$-diforest $\{x_{2j}y_{4j}x_{6t+4+2j}|j = 0, 1, ..., 3t+1\} \cup$$\{x_{6t+5+2j}y_{4j+2}x_{2j+1}|j = 0, 1, ..., 3t+1\}$.

Accordingly, $\overrightarrow{la}_{2}(K^{\ast}_{n, n}) \leq 3(6t+4)+1 = 2\left \lceil \dfrac{n^{2}}{\lfloor\dfrac{4n}{3}\rfloor} \right \rceil-1$.

We have the following result for the linear $2$-arboricity of $K^{\ast}_{n, n}$, which verifies Conjecture 2.1.

Theorem 6.1.

Proof. By Lemmas 2.3, 2.4 and Theorem 2.4, $\left \lceil \frac{2n^{2}}{\lfloor\frac {4n}{3}\rfloor} \right \rceil \leq \overrightarrow{la}_{2}(K^{\ast}_{n, n}) \leq 2la_{2}(K_{n, n})$. With all Propositions in this section, we have the result.

Note that, in Theorem 6.1, we missed one case when $n\equiv 7\; (mod\ 12)$. We believe that $\overrightarrow{la}_{2}(K^{\ast}_{n, n}) = 2\left \lceil \dfrac{n^{2}}{\lfloor\dfrac{4n}{3}\rfloor} \right \rceil-1$ in this case, but we can only prove that $\overrightarrow{la}_{2}(K^{\ast}_{n, n})\leq 2\left \lceil \dfrac{n^{2}}{\lfloor\dfrac{4n}{3}\rfloor} \right \rceil$ by Lemma 2.4 and Theorem 2.4.

7.   Conclusions

In this paper, we determine the linear $3$-arboricity for symmetric complete digraphs and symmetric complete bipartite digraphs, and also determine the linear $2$-arboricity for symmetric complete digraphs. All these results verify Conjecture 2.1.

Acknowledgments

The authors would like to thank anonymous referees for helpful comments and suggestions which improved the original version of the paper. This work was supported by Guangdong Basic and Applied Basic Research Foundation (No. 2021A1515012047) and Science and Technology Program of Guangzhou (No. 202002030401).

Conflict of interest

The authors declare that they have no competing interests.