Sharp bounds on the zeroth-order general Randić index of trees in terms of domination number

1.   Introduction

Let $G$ be a graph with vertex set $V_{G}$ and edge set $E_{G}$. The general Randić index is defined as

where $d_v$ denotes the degree of a vertex $v\in V(G)$, and $\alpha$ is an arbitrary real number. It's widely known that $R_{-\frac{1}{2}}$, i.e., the Randić index in original sense, was introduced by the chemist Milan Randić ^[19] under the name connectivity index or branching index in 1975, which has a good correlation with a variety of physico-chemical properties of alkanes, such as enthalpy of formation, boiling point, parameters in the Antoine equation, surface area and solubility in water, etc. In the past 30 to 40 years, the Randić index has been widely utilized in physics, chemistry, biology and complex networks ^[5,20], and many interesting mathematical properties have been obtained ^[4,11,12,14]. In 1998, Bollobás and Erdös ^[1] generalized this index by replacing $-\frac{1}{2}$ with a real number $\alpha$, and called it the general Randić index, denoted by $R_{\alpha} = R_{\alpha}(G)$.

Moreover, there are also many variants of Randić index ^[6,9,21]. In ^[8], Kier and Hall proposed the zeroth-order Randić index, denoted by $^0R$. The explicit formula of $^0R$ is

In some bibliographies, $^0R$ is also called the modified first Zagreb index ($^mM_1$). Pavlović ^[17] determined the extremal $(n, m)$-graphs of $^0R$ with maximum value. Almost at the same time, Lang et al. considered similar problems in ^[13] for the first Zagreb index ($M_1$), which is defined as

In 2005, Li and Zheng ^[15] constructed the zeroth-order general Randić index, written as $^0R_{\alpha}$, which is the sum of items $(d_v)^{\alpha}$ over all vertices $v\in V_G$, where $\alpha$ is a pertinently chosen real number. Note that $^0R_{-\frac{1}{2}} = {^0R} = {^mM_1}$, and $^0R_{2} = M_1$ in the mathematical sense. For the zeroth-order general Randić index of trees, Li and Zhao ^[16] determined the first three maximum and minimum values with exponent $\alpha_0, -\alpha_0, \dfrac{1}{\alpha_0}, -\dfrac{1}{\alpha_0}$, where $\alpha_0\geq 2$ is an integer. In 2007, Hu et al. ^[7] investigated connected $(n, m)$-graphs with extremal values of $^0R_{\alpha}$. Two years later, in ^[18], Pavlović et al. corrected some errors in the work of Hu et al.

Recently, the relationships between Randić-type indices and the domination number have attracted much attention of many researchers. In 2016, Borovićanin and Furtula ^[2] gave the precise upper and lower bounds on the first Zagreb index ($M_1$) of trees in terms of domination number and characterized the corresponding extremal trees. Later, Bermudo et al. ^[3] and Liu et al. ^[10] answered the same question regarding the Randić index ($R_{-\frac{1}{2}}$) and the modified first Zagreb index ($^mM_1$), respectively. Motivated by ^[2,3,10], in this paper, we intend to establish some connections between the zeroth-order general Randić index of trees and the domination number.

For convenience, we first introduce some graph-theoretic terminology and notions. The number of vertices and edges of graph $G$ are called the order and size of $G$, respectively. For each $v\in V_G$, the set of neighbours of this vertex is denoted by $N(v) = \left\lbrace u\in V_G|\; uv\in E_G \right\rbrace$. A vertex $v$ for which $d_v = 1$ is called a pendent vertex or a leaf vertex. The maximum vertex degree in $G$ is denoted by $\Delta(G)$. The diameter path of a tree is the longest path between two pendent vertices. A dominating set $D$ of graph $G$ is a vertex subset in $V_G$ such that every vertex in $V_G\setminus D$ is adjacent to at least one vertex in $D$. A subset $D$ is called a minimum dominating set of $G$ if $D$ contains the least vertices among all dominating sets. The domination number $\gamma$ is defined as $\gamma = \min\limits_{D\subseteq {V_G}}\left\lbrace|D|\right\rbrace$.

Based on the above consideration, the structure of this paper is arranged as below. In Section 2, we prove a fundamental lemma and simplify the mathematical formula of bounds on $^0R_{\alpha}$ of trees. Then in Sections 3 and 4, sharp upper and lower bounds on $^0R_{\alpha}$ of trees with a given domination number for $\alpha\in(-\infty, 0)\cup(1, \infty)$ and $\alpha\in(0, 1)$ are obtained, respectively. Furthermore, the corresponding extremal trees are characterized.

2.   Preliminaries

Now, we present a basic lemma, and then show the simplified mathematical formula of bounds on $^0R_{\alpha}$ of trees.

Lemma 2.1. Let the function $f(x_1, x_2, \dots, x_k) = x_{1}^{\alpha}+x_{2}^{\alpha}+\dots+x_{k}^{\alpha}$, where $\left\lbrace x_1, x_2, \dots, x_k\right\rbrace$ are all positive integers, and $\sum_{i = 1}^{k}x_i = N$ be a fixed positive integer. If there exist $x_i$ and $x_j$ such that $x_i-x_j\geq2$, $i, j\in\left\lbrace1, 2, \dots, k \right\rbrace$, then

(ⅰ) $f(x_1, \dots, x_i, \dots, x_j, \dots, x_k) < f(x_1, \dots, x_i-1, \dots, x_j+1, \dots, x_k)$, for $\alpha\in(0, 1)$,

(ⅱ) $f(x_1, \dots, x_i, \dots, x_j, \dots, x_k) > f(x_1, \dots, x_i-1, \dots, x_j+1, \dots, x_k)$, for $\alpha\in(-\infty, 0)\cup(1, \infty)$.

Proof. From the definition of function $f(x_1, x_2, \dots, x_k)$, we consider the following function $g(x_i, x_j, \alpha)$,

Note that $x_i-x_j\geq2$, we let $x_i = x_j+r$, where $r\geq2$ is an integer. Hence, $g(x_i, x_j, \alpha) = g(x_j, r, \alpha) = (x_j+r)^{\alpha}+x_{j}^{\alpha}-(x_j+r-1)^{\alpha}-(x_j+1)^{\alpha}$. Suppose $r$ is a continuous variable, then we get $\frac{\partial g(x_j, r, \alpha)}{\partial r} = \alpha(x_j+r)^{\alpha-1}-\alpha(x_j+r-1)^{\alpha-1}$ is positive if $\alpha\in(-\infty, 0)\cup(1, \infty)$, and negative if $\alpha\in(0, 1)$. By the Lagrange mean-value theorem, we have

(ⅰ) for $\alpha\in(0, 1)$,

where $x_j < \xi_2 < x_j+1 < \xi_1 < x_j+2$ and $\xi_2 < \eta < \xi_1$.

(ⅱ) for $\alpha\in(-\infty, 0)\cup(1, \infty)$,

where $x_j < \xi_2 < x_j+1 < \xi_1 < x_j+2$ and $\xi_2 < \eta < \xi_1$.

This completes the proof.

By repeating Lemma 2.1, finally, we can obtain the following corollary.

Corollary 2.2. Assume the function $f(x_1, x_2, \dots, x_k)$ is defined as above. Then

(ⅰ) for $\alpha\in(0, 1)$, $f(x_1, x_2, \dots, x_k)$ attains its maximum value if the difference between any two integers in $\left\lbrace x_1, x_2, \dots, x_k\right\rbrace$ at most one, and

(ⅱ) for $\alpha\in(-\infty, 0)\cup(1, \infty)$, $f(x_1, x_2, \dots, x_k)$ attains its minimum value if the difference between any two integers in $\left\lbrace x_1, x_2, \dots, x_k\right\rbrace$ at most one.

Suppose $D$ is a minimum dominating set in a tree $T$ with order $n$ and domination number $\gamma$, and $\overline{D} = V(T)\backslash D$. Let $E_1 = \left\lbrace uv\in E_T|\; u\in D, \; v\in \overline{D} \right\rbrace$, $E_{2} = \left\lbrace uv\in E_T|\; u\in D, \; v\in D\right\rbrace$, $E_{3} = \left\lbrace uv\in E_T|\; u\in \overline{D}, \; v\in \overline{D}\right\rbrace$ be three subsets of $E_T$, and $l_1 = |E_1|$, $l_2 = |E_2|$, $l_3 = |E_3|$. It's obvious that

Now the zeroth-order general Randić index $^0R_{\alpha}(T)$ can be given by

Since each $v\in\overline{D}$ is adjacent to at least one vertex of $D$, we have $l_1\geq n-\gamma$. By calculation, we obtain $l_2+l_3\leq\gamma-1$, implying

If $\alpha\in(0, 1)$, by Corollary 2.2, we can see the sum $\sum\limits_{v\in D}(d_{v})^{\alpha}$ necessarily attains its maximum when degree $d_{v}\in\left\lbrace\lfloor\frac{l_1+2l_2}{\gamma}\rfloor, \lceil\frac{l_1+2l_2}{\gamma}\rceil \right\rbrace$ for any vertex $v\in D$, and the sum $\sum\limits_{v'\in \overline{D}}(d_{v'})^{\alpha}$ attains its maximum when degree $d_{v'}\in\left\lbrace\lfloor\frac{l_1+2l_3}{n-\gamma}\rfloor, \lceil\frac{l_1+2l_3}{n-\gamma}\rceil \right\rbrace$ for any vertex $v'\in\overline{D}$.

Therefore, we let $l_1+2l_2 = q\gamma+t$ ($0\leq t\leq \gamma-1$) and $l_1+2l_3 = q'(n-\gamma)+t'$ $(0\leq t'\leq n-\gamma-1)$, where $q = \lfloor\frac{l_1+2l_2}{\gamma}\rfloor$, $t = l_1+2l_2-\gamma\lfloor\frac{l_1+2l_2}{\gamma}\rfloor$, $q' = \lfloor\frac{l_1+2l_3}{n-\gamma}\rfloor$ and $t' = l_1+2l_3-(n-\gamma)\lfloor\frac{l_1+2l_3}{n-\gamma}\rfloor$. Bearing in mind previous discussion, one can check that the formula shown in (2.2) might attain its maximum if $D$ contains $t$ vertices with degree $q+1$ and $\gamma-t$ vertices with degree $q$, and $\overline{D}$ contains $t'$ vertices with degree $q'+1$ and $n-\gamma-t'$ vertices with degree $q'$. Thus, we have

and

which implies that

For fixed $n$ and $\gamma$, the right-hand side of the inequality (2.4) can be viewed as the function $h(l_2-l_3)$, i.e. $^0R_{\alpha}(T)\leq h(l_2-l_3)$ for $\alpha\in(0, 1)$.

Analogously, if $\alpha\in(-\infty, 0)\cup(1, \infty)$, we can derive the inequality $^0R_{\alpha}(T)\geq h(l_2-l_3)$. So far, we have obtained a simplified formula of bounds on $^0R_{\alpha}(T)$.

3.   Bounds for the $^0R_{\alpha}$ with $\alpha\in(0, 1)$ of trees in terms of domination number

In this section, several upper and lower bounds for the zeroth-order general Randić index $^0R_{\alpha}$ with $\alpha\in(0, 1)$ of trees are determined. To characterize extremal $n$-vertex trees of $^0R_{2}$ with a given domination number $\gamma$, Borovićanin and Furtula ^[2] defined three trees family, denoted by $\mathcal{F}_{1}(n, \gamma)$, $\mathcal{F}_{2}(n, \gamma)$ and $\mathcal{F}_{3}(n, \gamma)$ in this paper.

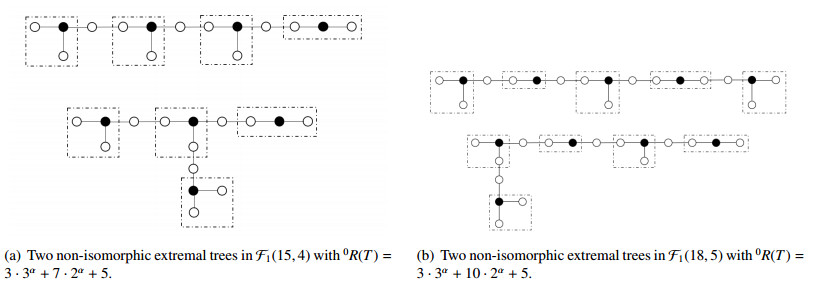
Definition 3.1. (ⅰ) $\mathcal{F}_{1}(n, \gamma)$ is a graph family contains all paths of order $3k$ ($P_{3k}$), where $k = \frac{n}{3}$ is a positive integer, and contains some $n$-vertex trees with domination number $\gamma$ which consists of stars of orders $\lfloor\frac{n-\gamma}{\gamma}\rfloor$ and $\lceil\frac{n-\gamma}{\gamma}\rceil$ with exactly $\gamma-1$ pairs of adjacent pendent vertices in neighbouring stars (See Figure 1).

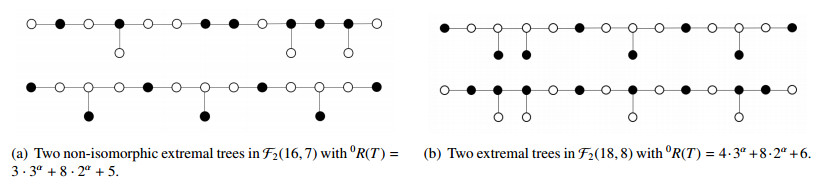
(ⅱ) $\mathcal{F}_{2}(n, \gamma)$ is a graph family contains some $n$-vertex trees $T$ with domination number $\gamma$ such that each vertex in $V_T$ has at most one pendent neighbour and $T$ satisfies: (1) There exists a minimum dominating set $D$ of $T$ which has $3\gamma-n-2$ vertices with degree $3$ and $2(n-2\gamma)$ vertices with degree $2$, while $\overline{D}$ has $n-2\gamma+2$ vertices with degree $2$ and $3\gamma-n$ pendent vertices, or (2) there exists a minimum dominating set $D$ of $T$ which has $n-2\gamma$ vertices with degree $2$ and $3\gamma-n$ pendent vertices, while $\overline{D}$ has $2(n-2\gamma+1)$ vertices with degree $2$, $3\gamma-n-2$ with degree $3$, and each vertex in $\overline{D}$ has only one neighbour in the dominating set $D$ (See Figure 2).

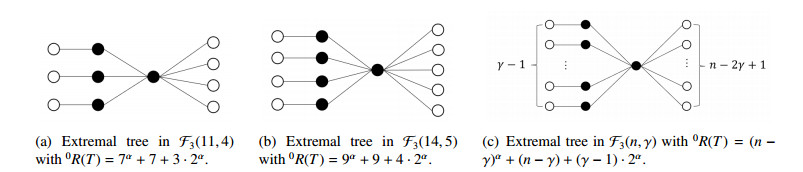
(ⅲ) $\mathcal{F}_{3}(n, \gamma)$ is a set of trees with order $n$ and domination number $\gamma$, which are obtained from the star $S_{n-\gamma+1}$ by attaching a pendant edge to its $\gamma-1$ pendent vertices (See Figure 3).

Next, we will give two theorems to prove that graph family $\mathcal{F}_{i}(n, \gamma)$ ($i = 1, 2, 3$) are also extremal trees of $^0R_{\alpha}(T)$ with a given domination number $\gamma$, for $\alpha\in(0, 1)$.

Theorem 3.2. Let $T$ be an $n$-vertex tree with domination number $\gamma$, $\alpha\in(0, 1)$, then

(ⅰ)

for $1\leq\gamma\leq\frac{n}{3}$, with equality holding if and only if $T\in\mathcal{F}_{1}(n, \gamma)$.

(ⅱ)

with equality holding if and only if $T\in\mathcal{F}_{2}(n, \gamma)$.

Proof. (ⅰ) For path $P_3$, the theorem holds. Suppose $n\geq3$. By $1\leq\gamma\leq\frac{n}{3}$, we get $n-\gamma\geq\frac{2n}{3}$, i.e. $\frac{\gamma-1}{n-\gamma}\leq\frac{n-3}{2n} < \frac{1}{2}$. Combining (2.3), yields

implying

Then by $\frac{n-1+l_2-l_3}{\gamma}\geq\frac{n-1-\gamma+1}{\gamma} = \frac{n-\gamma}{\gamma}\geq\frac{2n}{n} = 2$, we have $q = \lfloor\frac{n-1+l_2-l_3}{\gamma}\rfloor\geq2$. Now, the function $h(l_2-l_3)$ can be expressed as

There are two possible cases.

Case 1. $0\leq l_2-l_3\leq\gamma-1$. In such a case, $\frac{n-1}{\gamma}\leq\frac{n-1+l_2-l_3}{\gamma}\leq\frac{n-1+\gamma-1}{\gamma} < \frac{n-1}{\gamma}+1$, implying

Since $\alpha\in(0, 1)$, one can check that $h(l_2-l_3)$ always decreases in interval $\left[ 0, \gamma\lfloor \frac{n-1}{\gamma} \rfloor+\gamma-n\right]$ and $\left[ \gamma\lfloor \frac{n-1}{\gamma} \rfloor+\gamma-n+1, \gamma-1\right]$. Thus, $h(l_2-l_3)$ will attain its maximum if $l_2-l_3 = 0$ or $l_2-l_3 = \gamma\lfloor \frac{n-1}{\gamma} \rfloor+\gamma-n+1$. We consider the difference

See $\frac{n-1}{\gamma}\geq\frac{n-1}{n/3}\geq2+\frac{n-3}{n}$, we have $\lfloor \frac{n-1}{\gamma} \rfloor\geq2$. Hence,

for any $\alpha\in(0, 1)$. Combining (3.2) and (3.3), yields $h\left(\gamma\lfloor \frac{n-1}{\gamma} \rfloor+\gamma-n+1\right) < h(0)$. Then the function $h(0)$ becomes

Case 2. $1-\gamma\leq l_2-l_3\leq 0$. Note that $\frac{n-\gamma-1}{\gamma} < \frac{n-\gamma}{\gamma}\leq\frac{n-1+l_2-l_3}{\gamma}\leq\frac{n-1}{\gamma}$. From (2.3), we get

Analogously, we conclude that $h(l_2-l_3)$ will attain its maximum if $l_2-l_3 = \gamma\lfloor \frac{n-1}{\gamma} \rfloor-n+1$ or $l_2-l_3 = 1-\gamma$. Consider the difference $h\left(\gamma\lfloor \frac{n-1}{\gamma} \rfloor-n+1 \right)-h(1-\gamma)$, which is given by

Since $n-\gamma-\gamma\lfloor\frac{n-1}{\gamma}\rfloor\leq0$, for $\gamma\geq2$ and $\left(\lfloor\frac{n-1}{\gamma}\rfloor \right)^{\alpha}- \left(\lfloor\frac{n-1}{\gamma}\rfloor-1 \right)^{\alpha}+1-2^{\alpha} \leq0$, for $\alpha\in(0, 1)$ and $\lfloor\frac{n-1}{\gamma}\rfloor\geq2$, we have $h\left(\gamma\lfloor \frac{n-1}{\gamma} \rfloor-n+1 \right)\leq h(1-\gamma)$. In addition, if $n = \gamma\lfloor\frac{n-1}{\gamma}\rfloor+\gamma$, then only the inequality (3.5) holds. Note that $\left(\lfloor\frac{n-1}{\gamma}\rfloor \right)^{\alpha}- \left(\lfloor\frac{n-1}{\gamma}\rfloor-1 \right)^{\alpha} = 2^{\alpha}-1$ if and only if $\lfloor\frac{n-1}{\gamma}\rfloor = 2$, implying $2\gamma+1\leq n < 3\gamma+1$. Hence, $n = 3\gamma$. It's easy to conclude that the corresponding extremal tree is $P_{3\gamma}$ (See Figure 4), which belongs to $\mathcal{F}_1(n, \gamma)$.

To find the feasible maximum value of $h(l_2-l_3)$, we just need to calculate the value of $h(0)-h(1-\gamma)$,

Note that $0 < \left(\lfloor \frac{n-1}{\gamma} \rfloor+1\right)^{\alpha}-\left(\lfloor \frac{n-1}{\gamma} \rfloor\right)^{\alpha} < \left(\lfloor \frac{n-1}{\gamma} \rfloor\right)^{\alpha}-\left(\lfloor \frac{n-1}{\gamma} \rfloor-1\right)^{\alpha}$ for $\alpha\in(0, 1)$. Then we have

The inequality is strict. Thus,

for $\alpha\in(0, 1)$ and $1\leq\gamma\leq\frac{n}{3}$. Equality holds if and only if $l_2-l_3 = 1-\gamma$. Combining (2.1) and (2.2), yields $l_1 = n-\gamma$, $l_2 = 0$ and $l_3 = \gamma-1$. One can easily check that the corresponding extremal trees in such a case all belong to $\mathcal{F}_{1}(n, \gamma)$.

(ⅱ) For $\gamma = \lceil\frac{n}{3}\rceil$, the path $P_n$ is the unique tree such that $^0R_{\alpha}(T)$ with $\alpha\in(0, 1)$ attains its maximum. Then we suppose $\gamma\geq\frac{n+3}{3}$. Now, it holds $2\gamma\leq n\leq 3\gamma-3$, implying $n\geq6$ and $\gamma\geq3$. Since

which implies that $q' = \lfloor\frac{n-1+l_3-l_2}{n-\gamma}\rfloor = 2$ or $q' = \lfloor\frac{n-1+l_3-l_2}{n-\gamma}\rfloor = 1$. Then we consider the following two cases.

Case 1. $q' = \lfloor\frac{n-1+l_3-l_2}{n-\gamma}\rfloor = 1$. In this case, one can see $l_3-l_2 < n-2\gamma+1$, implying $l_2-l_3\geq 2\gamma-n$. Note that $\gamma\leq\frac{n}{2}$, thus, $2\gamma-n\leq0$. For convenience, we divide $2\gamma-n\leq0$ into $2\gamma-n\leq-1$ and $2\gamma-n = 0$.

Case 1.1. $2\gamma-n\leq-1$. Obviously, $2\leq\frac{n-1}{\gamma}\leq\frac{n-1}{n/3+1} < 3$, then we have $\lfloor\frac{n-1}{\gamma}\rfloor = 2$. Assume that $2\gamma-n\leq l_2-l_3\leq0$. Similarly, we obtain

Since $q' = \lfloor\frac{n-1+l_3-l_2}{n-\gamma}\rfloor = 1$ and $\gamma\geq\frac{n+3}{3}$, then the only relation (3.8) holds. Hence,

Now, we suppose $0\leq l_2-l_3\leq\gamma-1$. Analogously, we get

implying

and

Then by (3.10) and (3.11), we obtain

See $h(3\gamma-n+1)-h(3\gamma-n) = (3^{\alpha}-2\cdot2^{\alpha}+1) < 0$ for any $\alpha\in(0, 1)$, we just need to consider the relation (3.12).

Note that $^0R_{\alpha}(T)$ with $\alpha\in(0, 1)$ attains its maximum if and only if $T$ is a path (See ^[14] Theorem 4.2), we conclude that an extremal $T$, whose zeroth-order general Randić index with $\alpha\in(0, 1)$ is maximum, only consists of vertices with degree $1$–$3$. To determine a sharp upper bound on $^0R_{\alpha}(T)$, we must investigate further to find a feasible value of $l_2-l_3$. For a minimum dominating set $D$ of tree $T$, the number of vertices with degree $2$ and $3$ are denoted by $s_2$ and $s_3$, respectively. Also, for the set $\overline{D}$, the number of vertices with degree $1$ and $2$ are denoted by $s'_{1}$ and $s'_{2}$, respectively. It holds

Combining $\sum_{v\in V_T}d_v = 2(n-1) = 2(s_2+s_3+s'_1+s'_2-1) = s'_1+2(s_2+s'_2)+3s_3$, yields $s_3 = s'_1-2$ and $s_2-s'_2 = 2\gamma-n+2$. From (3.13), we get

By (2.4) and system (3.14), the function $h(l_2-l_3)$ becomes

Case 1.2. $2\gamma-n = 0$, i.e., $\gamma = \frac{n}{2}$ if $n$ is even.

Then $1\leq\frac{n-1}{\gamma} = 1+\frac{\gamma-1}{\gamma} < 2$, which implies $\lfloor\frac{n-1}{\gamma}\rfloor = 1$. One can easily check that the following relations hold.

By the analogous derivation, the function $h(l_2-l_3)$ can be given by

In ^[2], Borovićanin and Furtula have proved that $s'_1\geq 3\gamma-n$ for trees, and $s'_1 > 3\gamma-n$ always holds if there exists a vertex in $V_T$ which has two pendent neighbours. It's obvious that $^0R_{\alpha}$ of trees attains its maximum value if $s'_1 = 3\gamma-n$, i.e., $l_2-l_3 = 5\gamma-2n+1$. In such a case, one can check that corresponding extremal trees all belong to $\mathcal{F}_2(n, \gamma)$. Now, the function $h(l_2-l_3)$ becomes

Case 2. $q' = \lfloor\frac{n-1+l_3-l_2}{n-\gamma}\rfloor = 2$. Since $2\leq\frac{n-1+l_3-l_2}{n-\gamma} < 3$, we have $l_2-l_3\leq2\gamma-n+1 < 0$. It holds

implying $q = \lfloor \frac{n-1+l_2-l_3}{\gamma} \rfloor = 1$. If $l_3-l_2 = n-2\gamma+1$, we have $\frac{n-1+l_3-l_2}{n-\gamma} = 2$, implying all vertices in $\overline{D}$ has degrees 2, where $D$ is an arbitrary minimum dominating set. Consequently, all vertices in $D$ have degree 1 and 2, i.e., $T\cong P_n$, a contradiction, since $\gamma\geq\frac{n+3}{3}$.

Next, we assume $l_3-l_2\geq n-2\gamma+2$, then by (2.4), we get

Analogously, we have to find the minimum realizable value of $l_2-l_3$. For an arbitrary minimum dominating set $D$ of $T$, the number of vertices with degree 1 and 2 are denoted by $s_1$ and $s_2$, respectively, and for the set $\overline{D}$, the number of vertices with degree 2 and 3 are denoted by $s'_2$ and $s'_3$, respectively. Apparently, it holds $s_2-s'_2 = 2\gamma-n-2$ and $l_2-l_3 = 2\gamma-n-s_1+1$. Hence, the function $h(l_2-l_3)$ can be given by

Based on previous discussions, we can determine the only possible value of $s_1$, that is $3\gamma-n$, implying $l_2-l_3 = 1-\gamma$, such that there exists a corresponding extremal tree with order $n$ and domination number $\gamma$, where $\frac{n+3}{3}\leq\gamma\leq\frac{n}{2}$, satisfying its all vertices in an arbitrary minimum dominating set $D$ have degree 1 and 2, while all vertices in $\overline{D}$ have degree 2 and 3. Then the function $h(l_2-l_3)$ becomes

At this time, we have $l_1 = n-\gamma$, $l_2 = 0$ and $l_3 = \gamma-1$. Based on previous considerations, one can check that the corresponding extremal trees all belong to $\mathcal{F}_2(n, \gamma)$.

This completes the proof.

Theorem 3.3. Let $T$ be an $n$-vertex tree with domination number $\gamma$, $\alpha\in(0, 1)$, then

with equality holding if and only if $T\in\mathcal{F}_{3}(n, \gamma)$.

Proof. Assume first that $\Delta(T) = 2$, implying $T$ is a path and $\gamma(T) = \lceil\frac{n}{3}\rceil$. It holds $T_2\in\mathcal{F}_3(2, 1)$ ($\cong P_2$), $T_3\in\mathcal{F}_3(3, 1)$ ($\cong P_3$) and $T_4\in\mathcal{F}_3(4, 2)$ ($\cong P_4$). If $n\geq5$, the inequality in (3.15) is strict.

For $\Delta(T)\geq3$, we take an arbitrary diameter path in $T$, denoted by $v_1v_2\dots v_d$ ($d\geq4$). It holds $\Delta(T)\leq n-\gamma$. Then we prove this theorem by induction on $n$. Suppose the inequality in (3.15) holds for $|V_T| = n-1$. If $|V_T| = n$, we let $T_{-1} = T-\left\lbrace v_1 \right\rbrace$ and consider the following two cases.

Case 1. $\gamma(T_{-1}) = \gamma(T)$. By calculation, we get

All equalities in (3.16) hold if and only if $d_{v_2} = \Delta(T) = n-\gamma$, implying $T\in\mathcal{F}_{3}(n, \gamma)$.

Case 2. $\gamma(T_{-1}) = \gamma(T)-1$. By the definition of domination set, one can see $d_{v_2} = 2$. Hence,

Equality in (3.17) holds if and only if $T_{-1}\in\mathcal{F}_{3}(n-1, \gamma-1)$, i.e., $T\in\mathcal{F}_{3}(n, \gamma)$.

This completes the proof.

4.   Bounds for the $^0R_{\alpha}$ with $\alpha\in(-\infty, 0)\cup(1, \infty)$ of trees in terms of domination number

Next, we will show two theorems to clarify the sharp upper and lower bounds on $^0R_{\alpha}(T)$ with $\alpha\in(-\infty, 0)\cup(1, \infty)$. Based on the Corollary 2.2 and proofs in Section 3, we can derive the following two theorems by a straightforward procedure.

Theorem 4.1. Let $T$ be an $n$-vertex tree with domination number $\gamma$, $\alpha\in(-\infty, 0)\cup(1, \infty)$, then

(ⅰ)

for $1\leq\gamma\leq\frac{n}{3}$, with equality holding if and only if $T\in\mathcal{F}_{1}(n, \gamma)$.

(ⅱ)

with equality holding if and only if $T\in\mathcal{F}_{2}(n, \gamma)$.

Theorem 4.2. Let $T$ be an $n$-vertex tree with domination number $\gamma$, $\alpha\in(-\infty, 0)\cup(1, \infty)$, then

with equality holding if and only if $T\in\mathcal{F}_{3}(n, \gamma)$.

See the results in ^[2] and ^[10], Theorems 4.1 and 4.2 can be directly verified.

5.   Conclusions

The extremal properties of the zeroth-order general Randić index ${^0}R_{\alpha}$ of trees with a given domination number are established in this paper. In Section 3, for $\alpha\in(0, 1)$, we propose some sharp bounds on ${^0}R_{\alpha}$ of trees in terms of the number of vertices and the domination number. Then by Corollary 2.2, for $\alpha\in(-\infty, 0)\cup(1, \infty)$, we obtain some sharp bounds on ${^0}R_{\alpha}$ of trees with a given domination number easily. In each case, extremal graphs are characterized. In the future, one can find the more extremal properties related to the zeroth-order general Randić index and other graph parameters in chemical trees, unicyclic graphs, bicyclic graphs, etc.

Acknowledgements

The authors would like to express their sincere gratitude to all the referees for their careful reading and insightful suggestions. This work was supported by the National Natural Science Foundation of China [61773020] and Postgraduate Scientific Research Innovation Project of Hunan Province [CX20200033].

Conflict of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.