Application of a tripled fixed point theorem to investigate a nonlinear system of fractional order hybrid sequential integro-differential equations

1.   Introduction

Given an open bounded domain $\Omega\subset \mathbb{R}^d$ which has a smooth boundary $\Gamma$, and a positive real number $T$. We consider the non-linear hyperbolic partial different equation with the strong damping $\alpha \Delta^2 u_t$, as follows

associated with the final value functions

and the Dirichlet boundary condition

where $\alpha, \beta$ are positive constants, and the source $\mathcal{F}(x, t, u)$ is a given function of the variable $u$.

As we all know, the amplitude of a wave is related to the amount of energy it carries. A high amplitude wave carries a large amount of energy and vice versa. A wave propagates through a certain environment, its energy will decrease as time goes on, so wave amplitude also decreases (called damped wave). The damped wave equations are widely used in science and engineering, especially in physics. They can describe how waves propagate. It applies to all kinds of waves, from water waves ^[8] to sound and vibrations ^[13,21], and even light and radio waves ^[10].

Let us briefly describe some previous results related to the Problem (1.1). In recent years, much attention has been paid to the study on the properties and asymptotic behavior of the solution on Problem (1.1) subject to the initial conditions $u(x, 0) = \rho(x)$, $u_t(x, 0) = \xi(x)$ (pioneering works ^[1,2,5,9,15]). However, to the best of our knowledge, there are not any result on backward problem (1.1)–(1.3).

In practice we usually do not have these final value functions, instead they are suggested from the experience of the researcher. A more reliable way is to use their observed values. However, we all know that observations always come with random errors, these errors are derived from the ability of the measuring device (measurement error). It is therefore natural that observations are observed usually in the presence of some noise. In this paper, we will consider the case where these perturbation are an additive stochastic white noise

where $\epsilon$ is the amplitude of the noise and $W(x)$ is a Gaussian white noise process. Suppose further that even the observations (1.4) cannot be observed exactly, but they can only be observed in discretized form

where $\{\varphi_p\}$ is a orthonormal basic of Hilbert space $\mathcal{H}$; $\langle, \rangle$ denotes the inner product in $\mathcal{H}$; $W_p: = \langle W, \varphi_p \rangle$ are standard normal distribution; and $\langle \rho^\epsilon, \varphi_p \rangle$ are independent random variables for orthonormal functions $\varphi_p$. For more detail on the white noise model see, ^[3,11,12].

It is well-known that Problem (1.1)–(1.4) is ill-posed in the sense of Hadamard (if the solution exists, then it does not depend continuously on the final values), and regularization methods for it are required. The aim of this paper is to recover the unknown final value functions $\rho$, $\xi$ from indirect and noisy discrete observations (1.5) and then we use them to establish a regularized solution by the Fourier truncation method. To the best of our knowledge, the present paper may be the fist study for ill-posed problem for hyperbolic equations with Gaussian white noise. We have learned more ideas from these articles^{[14,17,18,20]}, but the detailed technique is different.

The organizational structure of this paper is as follows. Section 2 introduces some preliminary materials. Section 3 uses the Fourier series to obtain the mild solution and analyse the ill-posedness of problem. Section 4 presents an example of an ill-posed problem with random noise. In Section 5, we draw into main results: first we propose a new regularized solution, and then we give the convergent estimates between a mild solution and a regularized solution under some priori assumptions on the exact solution. To end this section, we discuss a regularization parameter choice rule. Finally, Section 6 reports numerical implementations to support our theoretical results and to show the validity of the proposed reconstruction method.

2.   Preliminaries

Throughout this paper, let us denote the Hilbert space $\mathcal{H} : = L^2(\Omega)$, and $\langle\cdot, \cdot\rangle$ is the inner product of $\mathcal{H}$. Since $\Omega$ is the bounded open set, there exists a Hilbert orthonormal basic $\{\varphi_p\}_{p = 1}^\infty$ in $\mathcal{H}$ ($\varphi_p \in \mathcal{H}^1_0(\Omega) \cap C^\infty(\Omega)$) and a sequence $\{\lambda_p\}_{p = 1}^\infty$ of real, $0\leq \lambda_1\leq \lambda_2\leq \ldots\leq \lim\limits_{p\to \infty}\lambda_p = +\infty$, such that $-\Delta \varphi_p(x) = \lambda_p \varphi_p(x)$ for $x \in \Omega$ and $\varphi_p(x) = 0$ for $x\in \partial \Omega$. We say that $\lambda_p$ are the eigenvalues of of $-\Delta$ and $\varphi_p$ are the associated eigenfunctions. The Sobolev class of function is defined as follows

It is a Hilbert space endowed with the norm $\| f\|_{\mathcal{H}^\mu }^2 = \sum_{p = 1}^\infty \lambda_p^\mu \langle f, \varphi_p\rangle ^2$. For $\tau, \nu > 0$, following ^[4,6], we introduce the special Gevrey classes of functions

We remark that ${G}_{\sigma, \nu}$ is also the Hilbert space endowed with the norm $\| f\|_{{G}_{\sigma, \nu} }^2 = \sum_{p = 1}^{\infty } e^{\sigma \lambda_p} \lambda_p^\nu\langle f, \mathrm{e}_i \rangle^2$.

Definition 2.1 (Bochner space ^[22]). Given a probability measure space $(\widetilde \Omega, \mathcal{M}, \mu)$, a Hilbert space $\mathcal{H}$. The Bochner space $L^2(\widetilde \Omega, \mathcal{H})\equiv L^2((\widetilde \Omega, \mathcal{M}, \mu); \mathcal{H})$ is defined to be the functions $u : \widetilde \Omega \mapsto \mathcal{H}$ such that the corresponding norm is finite

Definition 2.2 (Reconstruction of the final value functions). Given $\rho, \xi\in \mathcal{H}^\mu$ ($\mu > 0$), which have sequences of $n$ (is known as sample size) discrete observations $\langle \rho^\epsilon, \varphi_p \rangle$ and $\langle \xi^\epsilon, \varphi_p \rangle$, $p = 1, \ldots, n$. Non-parametric estimation of $\rho$ and $\xi$ are suggested as

Lemma 2.1. Given $\rho, \xi \in \mathcal{H}^\mu$ ($\mu > 0$), then the estimation errors are

Here $n(\epsilon): = n$ depends on $\epsilon$ and satisfies that $\lim_{\epsilon \to 0^+}n(\epsilon) = +\infty$.

Proof. Our proof starts with the observation that

The assumption $W_p = \langle W, \varphi_p\rangle\stackrel{iid}{\sim} N(0, 1)$ implies that $\mathbb{E}W_p^2 = 1$. We then have the desired the first result. The same conclusion can be drawn for the remaining case.

3.   Mild solution

Taking the inner product on both side of (1.1) and (1.2) with $\varphi_p$, and set $u_p(t) = \langle u(\cdot, t), \varphi_p\rangle$, $\rho_p(t) = \langle \rho, \varphi_p\rangle$, $\xi_p(t) = \langle \xi, \varphi_p\rangle$, and $\mathcal{F}_p(u) = \langle \mathcal{F}(\cdot, t, u(\cdot, t)), \varphi_p\rangle$, then

In this work we assume that $\Delta_p: = \alpha^2\lambda_p^4-4\beta \lambda_p^2 > 0$ then a quadratic equation $k^2 -\alpha \lambda_p^2 k+\beta \lambda_p^2 = 0$ has two different solutions $k_p^- = \frac{ \alpha \lambda_p^2 - \sqrt{\Delta_p }}{2}, k_p^+ = \frac{ \alpha \lambda_p^2 + \sqrt{\Delta_p }}{2}.$ Multiplying both sides the first equation of System (3.1) by $\phi_p(\tau) = \frac{\mathrm{e}^{(\tau-t)k^+_p} - \mathrm{e}^{(\tau-t)k^-_p}}{\sqrt{\Delta_p}}$, and integrating both sides from $t$ to $T$,

The left hand side of (3.2) now becomes

Since $k^-_p$, $k^+_p$ satisfy the equation $k^2 -\alpha \lambda_p^2 k+\beta \lambda_p^2 = 0$, then $\phi''(\tau) -\alpha\lambda_p^2 \phi_p'(\tau) +\beta\lambda_p^2 = 0$. Hence, (3.2) becomes

It is worth noticing that $\phi_p(t) = 0$, $\phi'_p(t) = 1$ and $-\phi'_p(T) + \alpha \lambda_p^2 \phi_p(T) = \frac{ k^{-}_p \mathrm{e}^{(T-t) k^{+}_p } - k^{+}_p \mathrm{e}^{(T-t) k^{-}_p } }{\sqrt{\Delta_p}}$. Therefore, (3.3) now becomes

Lemma 3.1. Let $\rho, \xi \in \mathcal{H}$. Suppose that the given problem $(1.1)–(1.3)$ has a solution $u\in C([0, T], \mathcal{H})$, then the mild solution is represented in terms of the Fourier series as follows

where the operators ${\bf{R}} (t) f$ and ${\bf{S}} (t) f$ are

4.   The ill-posedness of the problem

In this section, we present an example of Problem (1.1)–(1.3) with random noise (1.4) which is ill-posed in the sense of Hadamard (does not depend continuously on the final data). We consider the particular case as follows

where $\mathcal{F}(\tilde u^n)(x, t) = \sum_{p = 1}^\infty \frac{\mathrm{e}^{-\alpha \lambda_p^2 T}}{2{T^2}} \langle \tilde u^n(\cdot, t), \varphi_p \rangle \varphi_p(x)$. For simple computation, we assume that $\Omega = (0, \pi)$. It immediately follows that $\lambda_p = p^2$. We assume further that the function $\xi(x) = 0$ (unknown) has observations $\langle \xi^\epsilon, \varphi_p \rangle = \epsilon\langle W, \varphi_p \rangle$, $p = 1, \ldots, n$. Then the statistical estimate of $\xi(x)$ is in the form.

Using Lemma 3.1, System (4.1) has the mild solution

We first show that this nonlinear integral equation has unique solution $\tilde u^n \in {L^\infty([0, T]; L^2(\tilde \Omega, \mathcal{H}))}$. Indeed, let us denote

Let $u_1, u_2\in {L^\infty([0, T]; L^2(\tilde \Omega, \mathcal{H}))}$. Using the Hölder inequality and Parseval's identity, we obtain

Since $\left| \mathrm{e}^{-(\tau-t) k^{-}_p } - \mathrm{e}^{-(\tau-t) k^{+}_p } \right| \leq (\tau - t) | k^{+}_p - k^{-}_p|\leq T \sqrt{\Delta_p}$ and $(\tau-t)(k^+_p+k^-_p) \leq T \alpha \lambda_p^2$, then

From defining the function $\mathcal{F}$ as above, it follows that ${\bf{\Pi}}_p^\mathcal{F}(\tau) = \frac{\mathrm{e}^{-\alpha\lambda_p^2 T}}{2 {T^2}} \langle u_1(\cdot, \tau)-u_2(\cdot, \tau), \varphi_p \rangle$. Thus

Hence, we have that $\| {\bf{\Phi}}(u_1) - {\bf{\Phi}}(u_2) \|^2_{L^\infty([0, T]; L^2(\tilde \Omega, \mathcal{H}))} \leq \frac{1}{4} \|u_1- u_2 \|^2_{L^\infty([0, T]; L^2(\tilde \Omega, \mathcal{H}))}.$ This means that ${\bf{\Phi}}$ is a contraction. The Banach fixed point theorem leads to a conclude that ${\bf{\Phi}}(u) = u$ has a unique solution $u\in {L^\infty([0, T]; L^2(\tilde \Omega, \mathcal{H}))}$.

We then point out that System (4.1) does not depend continuously on the final data. We start by

It is easy to verify that

This leads to

It is worth recalling that $\mathbb{E } \langle \widetilde \xi_n^\epsilon, \varphi_p \rangle^2 = \epsilon^2$, so

We note that $k_n^+ -k_n^- = \sqrt{\Delta_p} = \sqrt{\alpha^2\lambda_n^4-\beta\lambda_n^2} > \sqrt{\alpha^2\lambda_1^4-\beta\lambda_1^2}$, then we have

The function $h (t) = \mathrm{e}^{(T-t) k_n^+} \Big[1- \mathrm{e}^{-(T-t) \sqrt{\alpha^2\lambda_1^4-4\beta \lambda_1^2}} \Big]$ is a decreasing function with respect to variable $t\in [0, T]$, so $\sup_{0\leq t\leq T} h(t) = h(0)$. This leads to

Combining (4.7)–(4.9) yields

Let us choose $n(\epsilon) : = n = \sqrt{\frac{1}{2T}\ln(\frac{1}{\epsilon^3})}$. When $\epsilon \to 0^+$, we have $\mathbb{E}\| \widetilde \xi_n^\epsilon\|^2_\mathcal{H} = \epsilon^2n(\epsilon) \to 0$. However,

Thus, we can conclude that Problem (1.1)–(1.3) with random noise (1.4) which is ill-posed in the sense of Hadamard.

5.   Main results

To come up with a regularized solution, we first denote a truncation operator $\mathbb{1}_N f = \sum_{p = 1 }^N \langle f, \varphi_p \rangle \varphi_p(x)$ for all $f\in \mathcal{H}.$ Now, let us consider a problem as follows

where $\widetilde \rho_n(x)$, $\widetilde \xi_n^\epsilon(x)$ as in Definition 2.2 and $N$, $n$ are called the regularized parameter and the sample size respectively. Applying Lemma 3.1, Problem (5.1) has the mild solution

where

The non-linear integral equation is called the regularized solution of Problem (1.1)–(1.3) with the perturbation random model (1.4). And $N$ serves as the regularization parameter.

Lemma 5.1 (^[16,19]). Given $f \in \mathcal{H}$ and $t\in [0, T]$. We have the following estimates:

where ${{\bf{C}}_{\bf{R}}}$, ${{\bf{C}}_{\bf{S}}}$ are constants dependent on $\alpha$, $T$.

Theorem 5.1. Given the functions $\rho, \xi \in \mathcal{H}$. Assume that $\mathcal{F} \in C(\Omega\times [0, T]\times \mathbb{R})$ satisfies the globally Lipschitz property with respect to the third variable i.e., there exists a constant ${\bf{L}} > 0$ independent of $x, t, u_1, u_2$ such that

Then the nonlinearintegral equation $(5.2)$ has a unique solution $\widetilde U^N\in L^{\infty}([0, T], L^2(\widetilde \Omega; \mathcal{H}))$.

Proof. Define the operator ${\bf{P}}: L^{\infty}([0, T], L^2(\widetilde \Omega; \mathcal{H})) \mapsto L^{\infty}([0, T], L^2(\widetilde \Omega; \mathcal{H}))$ as following

For integer $m\geq 1$, we shall begin with showing that for any $v_1, v_2\in L^{\infty}([0, T], L^2(\widetilde \Omega; \mathcal{H}))$

We now proceed by induction on $m$. For the base case $(m = 1)$,

where we apply Lemma 5.1 and the Lipschitz condition of $\mathcal{F}$. Thus it is correct for $m = 1$. For the inductive hypothesis, it is true for $m = m_0$. We show that (5.5) is true for $m+1$.

From the inductive hypothesis, we have

Hence, by the principle of mathematical induction, Formula (5.5) holds. We realize that,

and therefore, there will exist a positive number $m = m_0$, such that ${\bf{P}}^{m_0}$ is a contraction. It means that ${\bf{P}}^{m_0}({\widetilde U}^N) = {\widetilde U}^N$ has a unique solution ${\widetilde U}^N \in {\bf{L}}^\infty \big([0, T]; L^2(\widetilde \Omega, \mathcal{H})\big)$. This leads to ${\bf{P}}\big({\bf{P}}^{m_0}(\widetilde U^N)\big) = {\bf{P}}(\widetilde U^N)$. Since ${\bf{P}}\big({\bf{P}}^{m_0}(\widetilde U^N)\big) = {\bf{P}}^{m_0}\big({\bf{P}}(\widetilde U^N)\big)$, it follows that ${\bf{P}}^{m_0}\big({\bf{P}}(\widetilde U^N)\big) = {\bf{P}}(\widetilde U^N)$. Hence ${\bf{P}}(\widetilde U^N)$ is a fixed point of ${\bf{P}}^{m_0}$. By the uniqueness of the fixed point of ${\bf{P}}^{m_0}$, we conclude that ${\bf{P}}(\widetilde U^N) = \widetilde U^N$ has a unique solution $\widetilde U^N \in {\bf{L}}^\infty \big([0, T]; L^2(\widetilde \Omega, \mathcal{H})\big)$.

Theorem 5.2. Let $\rho, \xi\in \mathcal{H}^\mu$, $(\mu > 0)$. Assume that System $(1.1)–(1.3)$ has the exact solution $u\in C([0, T]; \mathcal{G}_{\sigma, 2})$, where $\sigma > 2\alpha T$. Given $\varepsilon > 0$, the following estimate holds

where the regularization parameter $N(\epsilon): = N$ and the sample size $n(\epsilon): = n$ are choosen such that

Remark 5.1. The order of convergence of $(5.7)$ is

There are many ways to choose the parameters $n(\epsilon), N(\epsilon)$, that satisfies $(5.8)$. Since $\lambda_{n(\epsilon)} \sim (n(\epsilon))^{2/d}$ ^[7], one of the ways we can do by choosing the regularization parameter $N(\epsilon)$ such that $\lambda_{N(\epsilon)}$ satisfies $\mathrm{e}^{2\alpha T \lambda_{N(\epsilon)}^2} = (n(\epsilon))^a$, where $\quad 0 < a < 2\mu/d.$ Then we obtain $\lambda_{N(\epsilon)}^2 = \frac{a}{2\alpha T }\ln(n(\epsilon))$. The sample size $n(\epsilon)$ is chosen as $n(\epsilon) = \left(1/\epsilon\right) ^{b/(a+1)},$ $(0 < b < 2)$. In this case, the error will be of order

Proof of Theorem 5.2. Let us define the integral equation

Then, we have

For easy tracking, we divide the above estimate into two main steps:

Step 1. We have

By Höder's inequality and the results in Lemma 5.1, we have

Use the results of Lemma 2.1 and the Lipschitz property of $\mathcal{F}$, we have

Multiplying both sides (5.11) to $\mathrm{e}^{2\alpha t \lambda_N^2}$, we derive that

Gronwall's inequality leads to

Step 2. To evaluate the remining term, we define the truncation version of the solution $u$ as following

Then, we have

Sub-step 1.1. By Höder's inequality, Lemma 5.1 and the Lipschitz property of $\mathcal{F}$, we have

Since $u\in C([0, T]; \mathcal{G}_{\sigma, 2})$, then

Substituting (5.14) and (5.15) into (5.13), we have

Multiplying both sides above formula to $\mathrm{e}^{2\alpha t \lambda_N}$, we have

Using Gronwall's inequality, we obtain

The proof is completed by combining (5.10), (5.12) and (5.16).

6.   Numerical experiments

We propose the general scheme of our numerical calculation. For simplicity, we fix $T = 1$ and $\Omega = (0, \pi)$. The eigenelements of the Dirichlet problem for the Laplacian in $\Omega$ have the following form:

6.1.   General numerical scheme

To find a numerical solution to Eq (5.2), we first need to define a set of $Nx\times Nt$ grid points in the domain $\Omega\times [0, T]$. Let $\Delta x = \pi/Nx$ is the time step, $\Delta t = 1/Nt$ is the spatial step, the coordinates of the mesh points are $x_j = j\Delta x$, $j = 0, \ldots, Nx$, and $t_i = i\Delta t$, $i = 0, \ldots, Nt$, and the values of the regularized solution $\widetilde U^N(x, t)$ at these grid points are $\widetilde U^N(x_j, t_i) \approx \widetilde U_{ij}$, where we denote $\widetilde U_{ij}$ by the numerical estimate of the regularized solution $\widetilde U^N(x, t)$ of at the point $(x_j, t_i)$.

Initialization step. The numerical process starts when time $t = T$. Since $\widetilde U^N(x, T) = {\bf{R}}^N(0)\widetilde \rho_n^\epsilon$, then

Iteration steps. For $t_i < T$, we want to determine

where ${\bf{I}}(t_i)$ is performed in backward time as following

It is worth pointing out that, the Simpson's rule leads to the approximation

where

Error estimation. We use the absolute error estimation between the regularized solution and the exact solution as follows

6.2.   Test case

In this example, we fixed $\alpha = 0.3$, $\beta = 0.01$ and present the inputs

and source data $\mathcal{F}(x, t, u) = f(x, t) +\frac{1}{1+u^2}$, where

It is easy to check that the exact solution of Problem (1.1)–(1.3) is given by $u(x, t) = \mathrm{e}^{-t}\sin 2x + \mathrm{e}^{-2t}\sin x.$

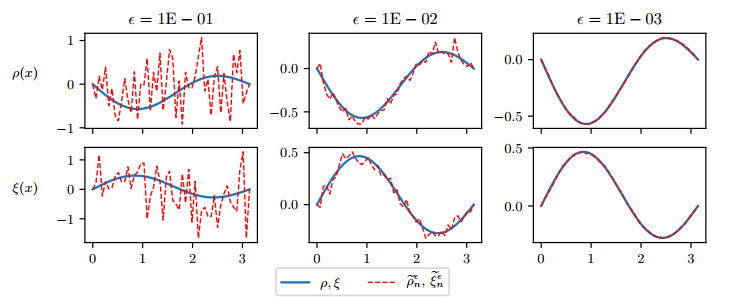
Figure 1 compares $\rho(x)$, $\xi(x)$ with their estimates $\widetilde \rho_n^\epsilon(x)$, $\widetilde \xi_n^\epsilon(x)$, respectively. When $\epsilon$ tends to 0, the estimates are consistent with that of the exact ones. Figure 2 presents a 3D graph of the exact solution $u$ and the regularized solution for the case $\epsilon = \mathrm{1E-03}$. Figure 3 displays the numerical convergence for different values of $\epsilon$ and t.

Table 1 shows the values of ${\bf{Err}}(t)$ from (6.3) calculated numerically. As a conclusion, our proposed regularization method works properly and the numerical solution method is also feasible in practice.

Acknowledgements

This research is supported by Industrial University of Ho Chi Minh City (IUH) under grant number 130/HD-DHCN. Nguyen Anh Tuan thanks the Van Lang University for the support.

Conflict of interest

The authors declare no conflict of interest.