1.
Introduction
The study of differential equations in the complex domain is a consolidated field in the general theory of differential equations [1,2,3,4]. The rigorous analysis of this type of differential equations involves profound tools, including Nevanlinna theory [5] and the Painlevé transcendents [6]. Some recent advances about equations in the complex domain also include difference and integral equations and their strong relationship with differential equations [7].
The aim of this paper is to contribute to the analysis of complex differential equations with uncertainties. According to [8, Sec. 4.7], we first point out that in the extant literature one mainly distinguishes two classes of differential equations, namely, stochastic differential equations (SDEs) [9,10], and random differential equations (RDEs) [11,12]. SDEs are those whose uncertainty is driven by a stochastic process having highly irregular trajectories (e.g., nowhere differentiable). In the case that uncertainty is modelled by the Wiener process, they are termed Itô type SDEs. Solving this class of SDEs requires using special tools as Itô calculus and, particularly, its cornerstone result, the so called Itô lemma. The formulation of these equations can be motivated from its deterministic counterpart by considering Gaussian perturbations of some model parameters, that may be affected by uncertainties. SDEs have demonstrated to be useful tools to model some real-world problems, specifically in Finance and Biology [13].
Complementary to SDEs, RDEs are those in which random effects are directly manifested in their coefficients, initial/boundary conditions and/or source terms (hereinafter referred to as input data), which are assumed to have a regular sample behaviour (e.g., differentiable) with respect to the independent variable (usually time and/or space) [11,12].
As indicated in [8, p. 96], the techniques and tools required to rigorously analyze SDEs and RDEs are distinctly different. Throughout this paper, we will deal with RDEs only. Despite the considerable influence of RDEs [14], to the best of our knowledge, there are not previous studies dealing with these equations in the case that their input data are complex random variables. So, as a first step, we here deal with the simplest case corresponding to the non-homogeneous first-order linear RDE
with initial condition
Here, the coefficient a(ω), the non-homogeneous term, b(ω), and the initial condition, z0(ω), are assumed to be complex absolutely continuous random variables defined in a common complete probability space (Ω,F,P). So, it is important to observe that we are dealing with problem (1.1)–(1.2) where the parameters are complex random variables and the solution is a complex stochastic process parametrized with the real parameter t. Recall that a complex random variable, say x=x(ω), is defined as x:Ω⟶C that can be written as x(ω)=xR(ω)+ixC(ω), where the real and the imaginary (or complex) contributions, xR(ω) and xC(ω), are real random variables, and i=√−1 is the imaginary unit. In other words, any complex random variable can always be regarded as a pair whose components are two random variables, the so-called real and the imaginary parts. As a consequence, the distribution of any complex random variable can be considered as the joint distribution of two real random variables [15]. For convenience, hereinafter we will utilize this representation. So, the probabilistic information of a complex random variable is given by the joint probability density function (PDF), fRC(xR,xC), of the random vector (xR(ω),xC(ω)), [15,16,17,18]. Complex random variables are applied in a number of disciplines, including information theory and digital signal processing [19]. Notice that, the full probabilistic analysis of the initial value problem (IVP) (1.1)–(1.2), where the parameters of the first order differential equation and the initial condition are assumed to be real absolutely continuous random variables, has been done in a previous contribution [20]. Further studies about random ordinary differential equation on the real domain can be found in [11,12].
For the sake of generality, in our subsequent analysis for the random IVP formulated in (1.1)–(1.2), we will assume that the random vector
has a joint PDF, f0(z0R,z0C,bR,bC,aR,aC), i.e. independence between input data, z0(ω), a(ω) and b(ω) is not assumed, including the real and complex parts of everyone of the foregoing random variables. Obviously, here z0(ω)=z0R(ω)+iz0C(ω), b(ω)=bR(ω)+ibC(ω) and a(ω)=aR(ω)+iaC(ω).
As in the deterministic theory, a main goal when dealing with its random counterpart is to obtain the solution of the random IVP (1.1)–(1.2). However, as in our context the solution, say z(t;ω), is a stochastic process (or random function), obtaining z(t;ω) to the IVP (1.1)–(1.2) is not enough, so one further needs to determine the main probabilistic properties of z(t;ω), mainly the mean and the variance. In the complex case, the mean of z(t;ω) is defined as
where E[⋅] denotes the expectation operator, and, zR(t;ω) and zC(t;ω) stands for the real and imaginary parts of z(t;ω), respectively. So, notice that the expectation of z(t;ω) does not exist if the expectation of its real or complex part do not. The mean function satisfies the following property
where, for w∈C, ¯w stands for the complex conjugate. Indeed,
Using property (1.4) and that |z(t;ω)|2=z(t;ω)¯z(t;ω), it is easy to check that the variance function can be calculated by
From this property, one can obtain the following representation of the variance function of a complex stochastic process in terms of the variances of its real and complex parts (which are real stochastic processes),
As we shall see later, this formula will be more fruitful throughout our subsequent development To prove (1.6), let us observe that
In this paper, we will go a step further by determining an explicit expression of the first probability density function (1-PDF) of the solution, f1(z;t). For each t, f1(z;t) is defined as the joint PDF of the random vector (zR(t;ω),zC(t;ω)), i.e. f1(z;t):=f1(zR,zC;t). Notice that the 1-PDF of the real and complex contributions, denoted by fR1(zR;t) and fC1(zC;t), respectively, can be calculated by marginalizing f1(zR,zC;t) as follows
Then, the expectations of the real stochastic processes zR(ω;t) and zC(ω;t) are
Furthermore, thanks to the representation (1.6) of the variance σ2z(t) of z(t;ω), in terms of the variances, σ2zR(t) and σ2zC(t), of the real random processes, zR(t;ω) and zC(t;ω), respectively, we can see that σ2z(t) can also be calculated as
The previous development clearly shows the importance of determining f1(zR,zC;t), that will be our main goal henceforth. Apart from the mean and the variance, and similarly as it happens in the real setting, the 1-PDF, f1(zR,zC;t), also permits calculating any one-dimensional moment of the random stochastic process, z(t;ω) at every time instant t, provided they exist. For t=ˆt fixed, the PDF, f1(zR,zC;ˆt), allows us to calculate the probability that the solution at t=ˆt lies in any specific region, say S⊂R2, of interest
Finally, we also point out that f1(zR,zC;t) can also be applied to construct confidence regions at any confidence level 1−α, with α∈(0,1) and t=ˆt fixed. To this end, we look for ζ>0 such that
Then, the confidence region is given by the interior points limited by the plane curve {(zR,zC)∈R2:f1(zR,zC;ˆt)=ζ}. One typically takes α=0.05, then f1(zR,zC;ˆt)=ζ determines a set in the plane with (1−α)×100=95% of confidence level.
To obtain an expression of the 1-PDF of the solution z(t;ω), and also of the real and complex contributions, we will extensively apply the Random Variable Transformation (RVT) technique. This method is a very powerful technique which allows us to compute the PDF of a random vector that results after transforming another random vector whose PDF is known [11,21,22,23].
Theorem 1 (Random Variable Transformation method, [11]). Let u(ω)=(u1(ω),…,un(ω)) and v(ω)=(v1(ω),…,vn(ω)) be two n-dimensional absolutely continuous random vectors. Let r:Rn→Rn be a one-to-one deterministic transformation of u into v, i.e., v=r(u). Assume that r is continuous in u and has continuous partial derivatives with respect to u. Then, if fU(u) denotes the joint PDF of vector u(ω), and s=r−1=(s1(v1,…,vn),…,sn(v1,…,vn)) represents the inverse mapping of r=(r1(u1,…,un),…,rn(u1,…,un)), the joint PDF of vector v(ω) is given by
where |Jn| is the absolute value of the Jacobian, which is defined by
The paper is organized as follows. Section 2 is devoted to obtain the 1-PDF of the solution stochastic process, z(t;ω), to the random IVP (1.1)–(1.2). For sake of completeness, in Section 2, explicit expressions for the 1-PDF for the real and imaginary components of the solution are also determined. The study is divided into two cases for the sake of clarity, namely the so-called exponential solution (Subsection 2.1) and the linear solution (Subsection 2.2). In Subsection 2.3, an analysis of the probabilistic stability of the solution is discussed in terms of the densities. Section 3 is addressed to illustrate the theoretical results obtained in Subsection 2 by means of several numerical examples. Conclusions and future work are presented in Section 4.
2.
Determining an explicit expression for the first probability density function of the solution stochastic process
As it has been indicated in Section 1, a RDE in the complex domain is a natural generalization of its deterministic counterpart. Therefore, for the first-order IVP (1.1)–(1.2), its solution is similarly obtained as in the deterministic case [2, Sec. 5.1]
where, as usual, "w.p.'' stands for "with probability''. Since a(ω) is assumed to be an absolutely continuous random variable, the first case (exponential solution) will happen w.p. 1, while the second case correspond to the linear solution and it corresponds to the case that the random IVP whose RDE is z′(t;ω)=b(ω), ω∈Ω. For the sake of clarity, henceforth, we separately study each case.
2.1. Exponential solution
In order to determine the 1-PDF of z(t;ω), we first rewrite (2.1) in terms of the real and complex parts of each random variable in (1.1), i.e. z0R(ω), z0C(ω), bR(ω), bC(ω), aR(ω) and aC(ω). From the properties of complex numbers, in particular the Euler's formula, exR+ixC=exR(cos(xC)+isin(xC)), after some algebra calculations, the real and complex components of z(t;ω) can be expressed as
where
Let t>0 fixed, we apply the RVT method to compute the PDF of the random vector v(ω)=(v1(ω),v2(ω),v3(ω),v4(ω),v5(ω),v6(ω))=(zR(t;ω),zC(t;ω),aR(ω),aC(ω),bR(ω),bC(ω)) in terms of the known PDF of the (random) input data, f0(u), where u=(z0R,z0C,aR,aC,bR,bC). First, for the sake of clarity, we rewrite formulas (2.2) and (2.3) as follows
being
and hi, i=1,2,3,4, given in (2.4). Let us define the deterministic mapping r:R6→R6
where zR(t) and zC(t) are given in (2.2) and (2.3), respectively. Isolating z0R and z0C (which appear in the definitions of zR(t) and zC(t)), the inverse of the mapping r, s:R6→R6, is
Denoting by I4 the identity matrix of size 4, the Jacobian of the inverse mapping s=r−1 is given by
Notice that we have used that h23+h24=e2v3t. Then, applying the RVT technique (stated in Theorem 1.1), the joint PDF of the random vector v(ω), in terms of the PDF, f0(⋅), of the random input parameters, u(ω), is
As, for each time instant t, we are interested in the PDF of the complex random variable z(t;ω), which is given by the joint PDF of the random vector (zR(t;ω),zC(t;ω)). So, it is obtained by marginalizing the joint PDF, fv(v), given in formula (2.5), with respect to (v3(ω),v4(ω),v5(ω),v6(ω))=(aR(ω),aC(ω),bR(ω),bC(ω)),
Then, taking t>0 arbitrary, the 1-PDF of the solution stochastic process, z(t;ω), of the random IVP (1.1)–(1.2) is
Remark 1. Assuming independence between the complex RV z0(ω), with PDF fz0(z0R,z0C), and the random vector (aR(ω),aC(ω),bR(ω),bC(ω)), the 1-PDF given by the integral expression (2.6) can be rewritten in terms of the expectation operator
Notice that E(aR,aC,bR,bC)[⋅] stands for the expectation with respect to the random vector (aR(ω),aC(ω),bR(ω),bC(ω)). Thus, taking samples of the random vector (aR(ω),aC(ω),bR(ω),bC(ω)), the 1-PDF, f1(zR,zC;t), can be approximated by computing the mean of fz0(s1(zR,zC,aR,aC,bR,bC),s2(zR,zC,aR,aC,bR,bC))e−2aCt over all the samples. Recall that the absolute error of the approximation decreases as 1/√N, being N the number of simulations.
Remark 2. Recall that from expression (2.6), we can also calculate the 1-PDF of the real and complex components, denoted by fR1(zR;t) and fC1(zR;t), respectively, as it was shown in (1.7).
2.2. Linear solution
In this case, the RDE writes
The solution stochastic process of the random IVP (2.7) and (1.2) is
To compute the 1-PDF, ˆf1(z;t), of z(t;ω), we first fix t>0, and then we will determine the PDF of the random vector of the auxiliary random vector v(ω)=(bR(ω)t+z0R(ω),bC(ω)t+z0C(ω),bR(ω),bC(ω)) in terms of the PDF of the random vector u(ω)=(z0R(ω),z0C(ω),bR(ω),bC(ω)), denoted by ˆf0(u)=ˆf0(z0R,z0C,bR,bC). To this end, we define the following mapping
Denoting v=(v1,v2,v3,v4), then the inverse mapping s:R4→R4 of r and its Jacobian, J4, are
Therefore, according to Theorem 1.1, the PDF of the random vector v(ω) is
Since this argument is valid for any t, to obtain the 1-PDF of z(t;ω), we marginalize with respect to the random variables bR(ω) and bC(ω)
Remark 3. Assuming independence between the complex RVs z0(ω) and b(ω), the 1-PDF given by the integral expression (2.9) can be rewritten in terms of the expectation operator with respect to the random vector (bR(ω),bC(ω))
where ˆfz0(z0R,z0C)=∫R2ˆf0(z0R,z0C,bR,bC)dbRdbC. Expression (2.10) permits approximating the 1-PDF via the Monte Carlo method by sampling the vector (bR(ω),bC(ω)), ω∈Ω.
2.3. Analysis of probabilistic stability
The study of stability of the solution stochastic process is presented for the exponential solution, since in the linear case the solution tends to infinity when t→∞. Otherwise, the solution is stable only when P[{ω∈Ω:b(ω)=0}]=1. In such case, the equilibrium state is the initial condition, z∗(ω)=z0(ω), and the PDF of the equilibrium point is directly obtained via f0(z0R,z0C).
The stability of the exponential solution can be deduced from the expression of the solution stochastic process z(t;ω)=zR(t;ω)+izC(t;ω), where the real and complex contributions are given in (2.2)–(2.4). We observe that the stability depends on the behaviour of the stochastic processes h3(aR(ω),aC(ω);t) and h4(aR(ω),aC(ω);t). Let ω∈Ω be fixed, then
since it is the limit of an exponential times a bounded (trigonometric) function, and the exponential tends to zero provided the exponent is negative. Then, as we are dealing with random variables, we will have stability with a certain probability
If the solution does not converge, it diverges oscillating, since the divergence depends on the real sine and cosine trigonometric functions.
In case of stability, we observe that the distribution of the equilibrium point, which is a complex random variable, z∗(ω)=z∗R(ω)+iz∗C(ω), is determined by the joint PDF of the random vector (z∗R(ω),z∗C(ω)) defined by
Now, we take advantage of RVT method (Theorem 1.1) to determine an exact expression for the joint PDF of the equilibrium point given in (2.12). To this end, let us fix ω∈Ω and define
Let r:R4→R4 be the deterministic mapping
The inverse mapping s:R4→R4 is
The Jacobian of s is J4=v21+v22≠0. Therefore, the joint PDF of the random vector v(ω) is
As we are interested in the joint PDF of the random vector (z∗R(ω),z∗C(ω)), we marginalize the last expression with respect to aR(ω) and aC(ω), then obtaining the desired PDF
Notice that from the very beginning, we are assuming that we know the joint PDF, f0(⋅), of the random vector (z0R(ω),z0C(ω),aR(ω),aC(ω),bR(ω),bC(ω)). Then, the PDF of the random vector (aR(ω),aC(ω),bR(ω),bC(ω)) is the marginal of f0(⋅) with respect the random vector (z0R(ω),z0C(ω)). As a consequence, the PDF of the equilibrium point finally writes
Remark 4. To calculate the PDF of the equilibrium point, given by (2.13), the Monte Carlo method can be applied under certain hypotheses. For example, assuming independence between the random vectors (bR(ω),bC(ω)) and (z0R(ω),z0C(ω),aR(ω),aC(ω)), expression (2.13) can be rewritten as
3.
Numerical examples
In this section, the theoretical results established in Section 2 are applied in three numerical examples. In the first example, statistical dependence between some input data is considered, while in the second and in the third examples, we assume independence between all the input data. In all the examples, after fixing of the probabilistic distributions of input data, we compute the 1-PDF, f1(z;t), of the solution stochastic process, z(t;ω); the 1-PDFs, fR1(zR;t) and fC1(zC;t), of the real and complex contributions, zR(t;ω) and zC(t;ω), respectively, as well as the mean and the variance of these stochastic processes. In the examples, statistical quantities of interest such as the mean, variance and confidence regions are also calculated in order to account for the probabilistic evolution of the solution over the time. Finally, the probability of stability, p∗, is also determined.
In the first numerical example, we have chosen an appropriate distribution of random variable aR(ω) to assure the solution is stable, w.p. 1, i.e. p∗=1. Therefore, in this example we show that the mean and the variance of the solution tend to the one corresponding to the equilibrium state, which is a random variable. In addition, for the sake of clarity, we show that the distributions of the real and complex stochastic processes tend to the distribution of the real and complex components, respectively, of the equilibrium as time increases.
In the second example, we have chosen the distribution of the random input a(ω) so that 0<p∗< is small. Therefore, the computations show that stability will not likely take place.
In the third example, we consider the linear solution, i.e. a(ω)=0 w.p. 1. The probabilistic analysis corresponding to this case has been shown in Subsection 2.2. In this case, the solution stochastic process is unstable. We will show this behaviour by means of the PDF of the solution and its main statistics (mean, variance and confidence regions).
Finally, we point out that a wide range of probability distributions has been selected to carry out the numerical experiments to better illustrate the applicability of the theoretical results.
3.1. Example 3.1
In this example, we consider that some input data are dependent random variables. In particular, we have chosen the following probability distributions:
● (aR(ω),aC(ω)) follows an Uniform distribution on the rectangle [−10.1,−10]×[−0.5,0.5], i.e., (aR(ω),aC(ω))∼U([−10.1,−10]×[−0.5,0.5]).
● (z0R(ω),z0C(ω)) has a multivariate Gaussian distribution with mean μz0=(0,0) and variance-covariance matrix
Then, (z0R(ω),z0C(ω))∼N(μz0,Σz0).
● bR(ω) has a Triangular distribution on the interval [1.7,2.5] with mode at 2, i.e., bR(ω)∼Tr([1.7,2.5],2).
● bC(ω) has a Gamma distribution with shape and scale parameters 3 and 2, respectively, i.e., bC(ω)∼Ga(3;2).
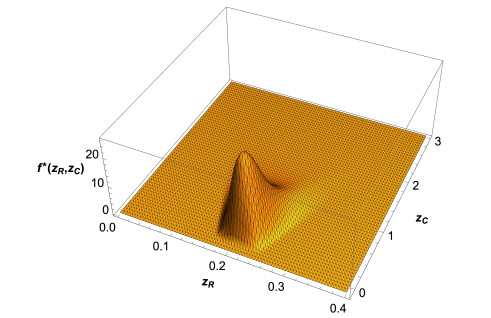
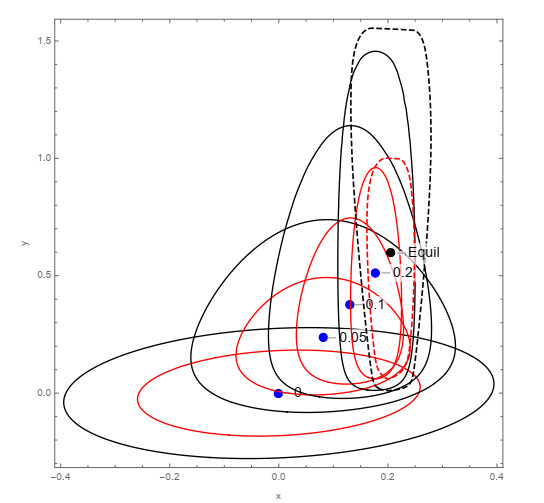
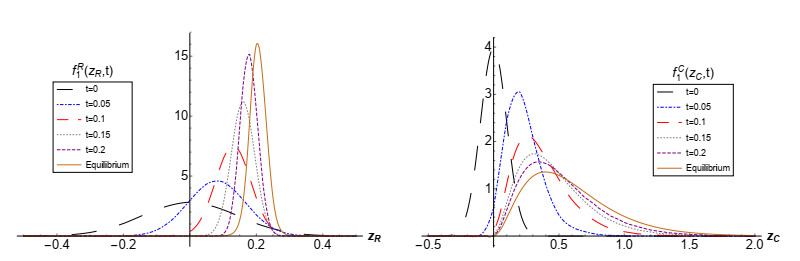
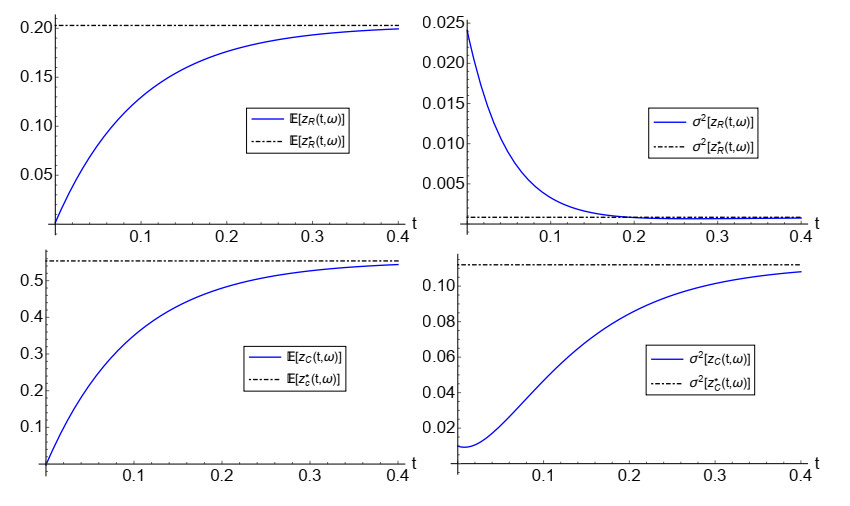
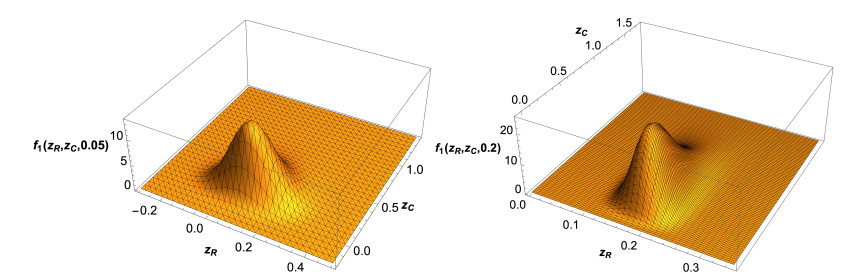
In Figure 1, we show 3D graphical representations for the 1-PDF, f1(zR,zC;t), at the time instants t=0.05 and t=0.2. Calculations have been carried out from expression (2.6). Since aR lies in negative interval w.p. 1, then z(t;ω)⟶(z∗R(ω),z∗C(ω)) as t→∞, where, the equilibrium point (z∗R(ω),z∗C(ω)), given by (2.12), is asymptotically stable. In Figure 2, we have plotted the PDF of (z∗R(ω),z∗C(ω)) using (2.13). Comparing the plots shown in Figures 1 and 2, we can graphically observe that convergence of PDF f1(zR,zC;t) to f1(z∗R,z∗C) is fast. Finally, in Figure 3, we show the evolution of the mean of the solution E[z(t;ω)] (blue points) at different time instants, t∈{0,0.05,0.1,0.2}, together with 50% and 90% confidence regions. They have been computed by expressions (1.3) and (1.8) for the mean, and (1.10) with α=0.5 and α=0.1 for the confidence regions (red and black solid curves, respectively). The same statistics are also shown for the equilibrium point (z∗R(ω),z∗C(ω)) (black point). We can observe that both the mean and confidence regions of z(t;ω) rapidly approximate the corresponding ones (plotted by dashed curves) associated to (z∗R(ω),z∗C(ω)) as t increases, thus illustrating stability. It is interesting to observe the full agreement between the shapes and scales of confidence regions observed in Figure 3 at the time instants: t=0.05 and Figure 1 (left panel); t=0.2 and Figure 1 (right panel), and t=∞, corresponding to the equilibrium (Figure 2). We complete the graphical analysis by plotting in Figure 4 the evolution of the PDF of the real component, fR1(zR;t) (left panel), and of the imaginary component, fC1(zR;t) (right panel), at the time instants t∈{0,0.05,0.1,0.15,0.2}, together with the corresponding PDFs of the components of the equilibrium. From these plots we can graphically confirm the stability, as expected. Again, it must be pointed out that the results shown in Figures 1–3 and in Figure 4 are in full agreement. In Figure 5 we show the expectation and the variance of the real and complex parts of the solution stochastic process together with the corresponding statistics of the equilibrium state. Observe that these graphical results completely agree with the ones shown in Figure 4.
3.2. Example 3.2
In this example we assume independence between all the input data. Specifically, we consider the following probability distributions for each random variable:
● aR(ω) has an Uniform distribution, defined on the interval [−0.02,0.4], i.e., aR(ω)∼U([−0.02,0.4]).
● aC(ω) has a Beta distribution with shape parameters 2 and 5, i.e., Be(2;5).
● The real component of the initial condition has a triangular distribution with mode 0 and defined on the interval [−0.2,0.1], i.e., z0R(ω)∼T([−0.2,0.1];0).
● The complex component of the initial condition has a Gamma distribution with parameters 2 and 0.2, i.e., z0C(ω)∼Ga(2;0.2).
● The parameter bR(ω) has a Gaussian distribution with mean −1 and standard deviation 0.01 truncated on the interval T=[−2,0], i.e., bR(ω)∼NT(−1;0.012).
● bC(ω) is uniformly distributed on the interval [−2,−1.8], i.e., bC(ω)∼U([−2,−1.8]).
Because of independence of input data, the joint PDF of them can be expressed as the product of the corresponding marginals PDFs, i.e.
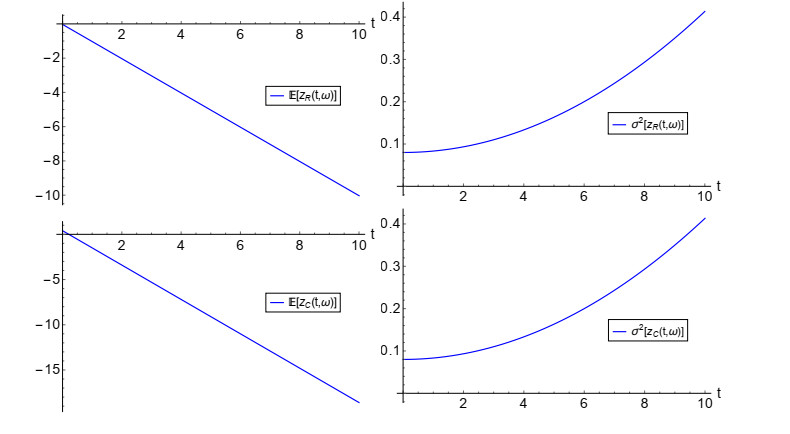
In Figure 6, we have plotted the 1-PDF of the solution stochastic process, f1(zR,zC;t), at the time instants t=0.5 and =1.5. In Figure 7, we have represented the mean (blue points) and confidence regions at 50% (red curves) and at 90% (blue curves) at the time instants t∈{0,0.5,1,1.5,2}. From this plot we can see that variability increases over the time. The PDFs of the real and imaginary components, corresponding to the above time instants, are shown in Figure 8. Notice that the aforementioned increasing of the variability as time goes on, is in full agreement with these graphical representations. This feature indicates that in the long run the solution tends to become unstable. Indeed, the probability of reaching stability can be exactly computed via (2.11)
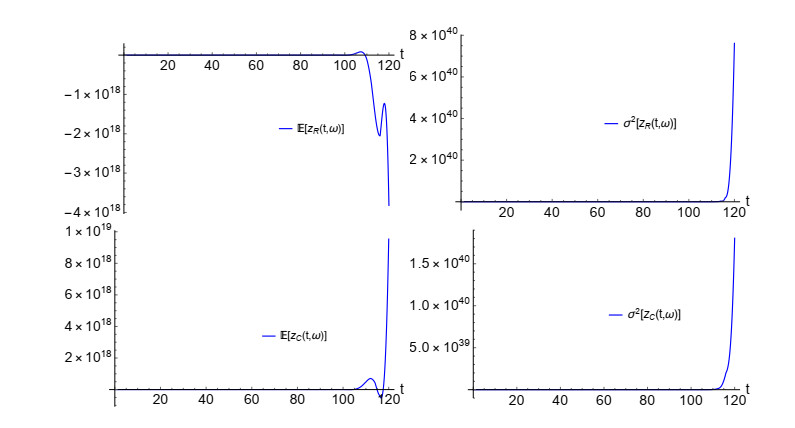
which is small. This situation is illustrated through the mean and the variance of the real and complex components, which are shown in Figure 9. In Figure 10, the same statistics are shown over the larger domain [0,120].
3.3. Example 3.3
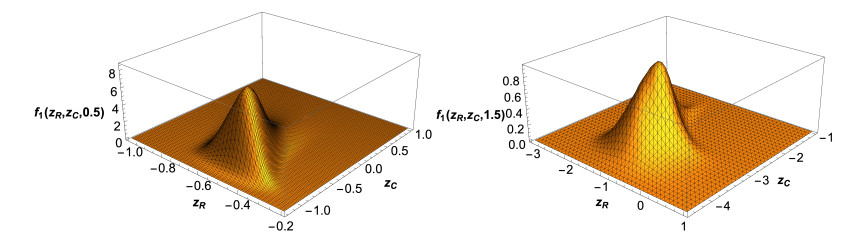
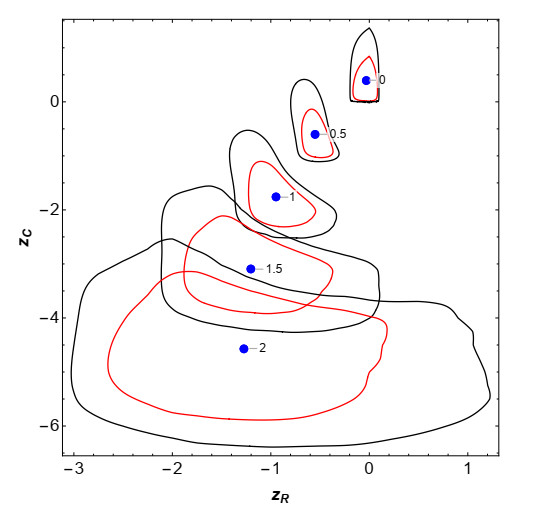
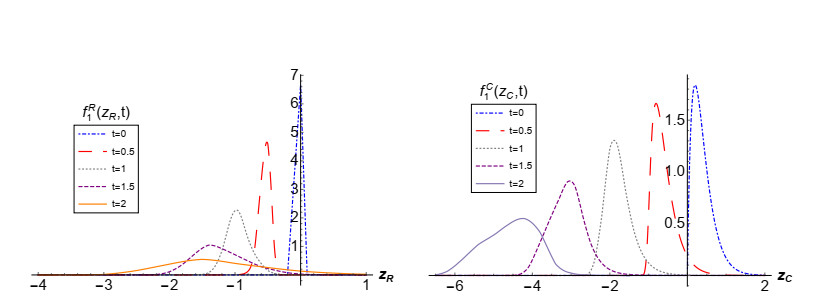
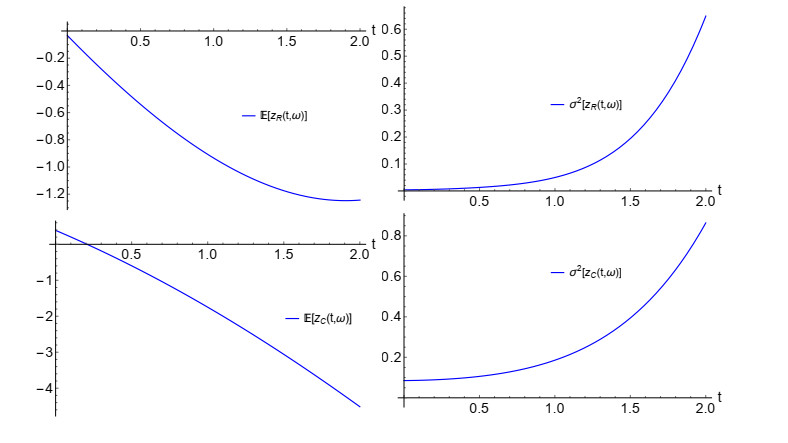
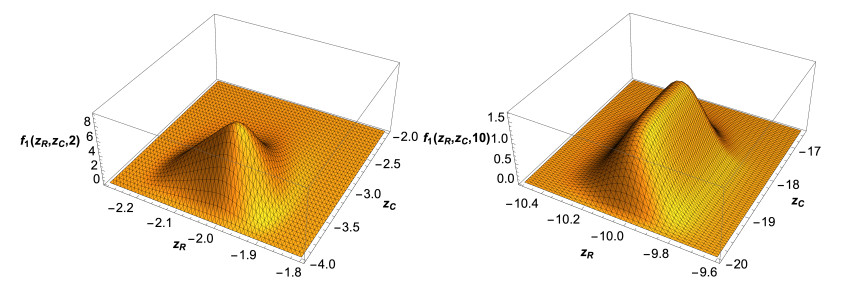
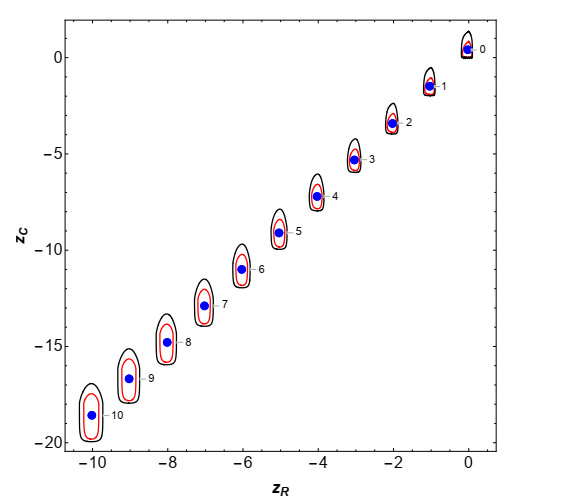
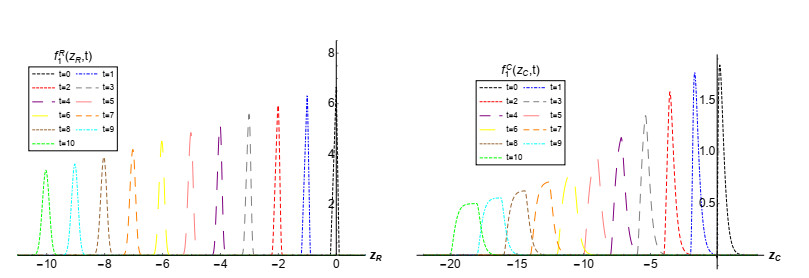
As previously indicated, in this example we shall assume that a(ω)=0 w.p. 1, so the linear solution, given in (2.8), is considered. We will choose the same probability distributions as in Example 3.2 for the input data, which are also assumed to be independent. In Figure 11, we show 3D graphical representation of the 1-PDF of the solution process, f1(zR,zC;t) at the time instants t=2 (left) and t=10 (right). We can see that the PDF moves the coordinates of its real and imaginary part towards greater (in absolute value) numbers as times increases. This fact is consistently also observed in Figure 12, where the mean (blue points) and 50% (red curves) and 90% (black curves) confidence regions have been plotted at the time instants t∈{0,1,…,10}. From this plot we also observe that the variability increases as t does. In Figure 13, the evolution of the PDFs of the real (left) and imaginary (right) components of the solution over the aforementioned time instants are shown. Notice that the plots are in full agreement with the ones shown in Figures 11 and 12. We complete the graphical analysis showing, in Figure 14, the plots of the mean (left panels) and of the variance (right panels) of the real and imaginary parts of the solution stochastic processes. It is clearly observed from these statistics that the solution is unstable. {Observe that it is in full agreement with the fact that this example corresponds to the case termed "linear solution'' (see Section 2.2) whose solution is a linear stochastic process (see expression (2.8)) such that P[{ω∈Ω:b(ω)=0}]≠1 (see also the discussion at the beginning of Section 2.3), so the solution diverges as t tends to infinite, i.e., is unstable.}
4.
Conclusion
In this paper, we have performed a probabilistic study of first order linear differential equations whose coefficients and the initial condition are complex random variables. The solution is a complex valued stochastic process parametrized with respect to a real parameter (identified with the time as usual). We have provided an exact expression for the probability density function of the solution stochastic process under very general hypotheses on the model parameters. Furthermore, our study has included a probabilistic analysis of the stability. Despite the simplicity of the differential equation, to the best of our knowledge, this is the first contribution in this direction and the ideas exhibited throughout the paper can open new avenues for studying other families of differential equations with uncertainties.
Acknowledgments
This work has been supported by the Spanish Ministerio de Economía, Industria y Competitividad (MINECO), the Agencia Estatal de Investigación (AEI) and Fondo Europeo de Desarrollo Regional (FEDER UE) grant PID2020-115270GB-I00 and Generalitat Valenciana (Grant AICO/2021/302).
We give our deepest thanks to the four anonymous referees that have improved the final version of the paper with their valuable comments.
Conflict of interest
The authors declare that there are not conflict of interest.









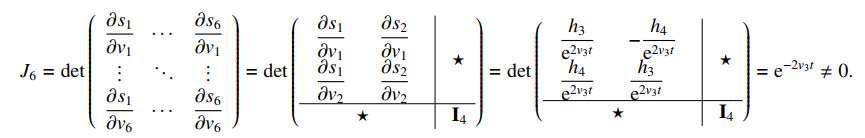
 DownLoad:
DownLoad: