On stochastic accelerated gradient with non-strongly convexity

1.   Introduction

In the era of 'big data', machine learning algorithms that only need to process each observation only once, or a few times, are desirable. Stochastic approximation algorithms such as stochastic gradient descent (SGD) and stochastic proximal gradient descent (SPGD), have been widely studied for this specific task and they have been successfully applied in various scenarios ^{[2,3,4,5,6,7,8,9,10,11,12,13,14,15,16]}. Regression and classification are effective analysis methods in machine learning, and have been successfully applied in practical problems. With the wide application of deep learning, these two methods are often used to train the parameters. In this paper, we consider stochastic approximation algorithms that consider minimizing a convex function where only the unbiased estimates of its gradients at the observations are assumed available.

The convex function defined on a closed convex set in Euclidean space is usually given by $f(\theta) = \frac{1}{2}\mathbb{E}\left[\ell\left(y_i, \langle\theta, x_i\rangle\right)\right]$, where $(x_i, y_i)\in {\cal X} \times {\cal Y}$ denotes the sample data which is assumed to be i.i.d., $\ell$ denotes a loss function that is convex and $\mathbb{E}$ represents the expectation under the second variable. This loss function includes such as the least square and logistic regression. In the stochastic approximation framework, the samples appear sequentially according to an unknown probability measure $\rho$ and the predictor defined by $\theta$ is updated after each pair is seen.

Robbins and Monro ^[1] were the first authors who proposed the stochastic approximation (SA) on the gradient descent method. From then on, algorithms based on SA have been widely used in stochastic optimisation and machine learning. Polyak ^[2] and Polyak and Juditsky ^[3] developed an important improvement of SA by using longer step-sizes with consequent averaging of the obtained iterates. The mirror-descent SA was developed by Nemirovski et al. ^[6] who showed that the mirror-descent SA exhibited an un-improvable expected rate for solving non-strongly convex programming problems. Shalev-Shwartz et al. ^[5] and Nemirovski et al. ^[6] studied an averaged stochastic gradient descent method for the least-square regression.

Theoretical studies on SGD for the least-square and logistic regression have shown that the convexity and smoothness of the loss function and the step-size policy play a critical role on the convergence rate. It was found that under strong-convexity assumption (i.e., the loss function is twice differentiable, the Hessians of the loss function is lower bounded by a constant $c$), the convergence rate of averaged SGD with proper step-size is of $O(1/c n)$ ^[5,6], while it is only of $O(1/\sqrt{n})$ in non-strongly-convex case ^[6]. By using the smoothness property of the loss function, it was shown in ^[10] that the averaged SGD with constant-step-size can achieve a convergence rate of $O(1/n)$ without requiring the strong-convexity assumption.

D. P. Kingma ^[24] propose Adam, a method for efficient stochastic optimization that only requires first-order gradients with little memory requirement. The method computes individual adaptive learning rates for different parameters from estimates of first and second moments of the gradients; the name Adam is derived from adaptive moment estimation.

Z. A. Zhu ^[25] introduced Katyusha, a direct, primal-only stochastic gradient method to fix this issue. It has a provably accelerated convergence rate in convex (off-line) stochastic optimization. It can be incorporated into a variance-reduction based algorithm and speed it up, both in terms of sequential and parallel performance.

In this paper, we develop two stochastic accelerated gradient algorithms for the consider least-square and logistic regressions aiming to improve the convergence rate without assuming strong-convexity. Our development is inspired by the work in the area of accelerated gradient method for general stochastic non-linear programming (NLP) ^{[17,18,19,20,21,22,23]}. In the stochastic NLP setting, different from the consider problem where the gradient can be estimated unbiased at certain points, the gradient is noisy and available through a stochastic oracle. That is, random vectors with unknown distribution are associated with each gradient at certain points. For such problem, recently developed stochastic accelerated gradient method proposed by Ghadimi and Lan ^[22] showed that for convex smooth function with Lipschitz continuous gradients achieves a convergence rate of $O(1/n^2)$.

In this paper, we prove that without the Lipschitz continuous gradient and strong-convexity assumption, the developed algorithms achieve a convergence rate of $O(1/ n^2)$ by using non-asymptotic analysis. Experimental studies on synthetic data and benchmarks justify our theoretical results and show a faster convergence rate than classical SGD and constant-step-size averaged SGD ^[10].

The rest of the paper is organised as follows. In Section 2, we present the accelerated gradient algorithm for the least square regression. In Section 3, we study the accelerated gradient algorithm for the logistic regression. Section 4 empirically verify the obtained theoretical results. Section 5 concludes the paper.

2.   Stochastic accelerated gradient algorithm for least square regression

In this section, we consider the least square regression. Let $(X, d)$ be a compact metric space and $Y = \mathbb{R}$. Assume $\rho$ be a probability distribution on $Z = \mathcal{X}\times {\cal Y}$ and $(X, Y)$ be corresponding random variable. We further assume:

(a) The training data $(x_k, y_k), k \geq 1$ are i.i.d. sampled from $\rho$.

(b) $\mathbb{E}\|x_k\|^2$ is finite, i.e., $\mathbb{E}\|x_k\|^2\leq M$ for any $k\geq 1$.

(c) The global minimum of $f(\theta) = \frac{1}{2}\mathbb{E}[\langle\theta, x_{k}\rangle^2-2y_{k}\langle\theta, x_{k}\rangle]$ is attainable at a certain point $\theta^{*}\in \mathbb{R}^d$.

(d) In the following, we denote $\xi_{k} = \left(y_{k}-\langle\theta^{k}, x_{k}\rangle\right)x_{k}$ as the residual. We assume that $\mathbb{E}\|\xi_{k}\|^2\leq M_{1}$ for every $k$ and $\overline{\xi}_{k} = \frac{1}{k}\sum_{i = 1}^{k}\xi_{i}$.

These assumptions are standard in stochastic approximation ^[9,10]. However, compared with the work in ^[10], we do not make assumptions on the covariance operator $\mathbb{E}(x_k \bigotimes x_k)$ and $\mathbb{E}[\xi_k\bigotimes\xi_k]$.

In the following, we present the accelerated stochastic gradient algorithm for least square regression learning in Algorithm 1. The algorithm takes a stream of data $(x_k, y_k)$ as input, and an initial guess of the parameter $\theta_0$. The other requirements include $\{\alpha_{k}\}$ which satisfies $\alpha_{1} = 1$ and $\alpha_{k} > 0$ for any $k\geq 2$, $\beta_{k} > 0$, and $\lambda_{k} > 0$. The algorithm involves two intermediate quantities $\theta^{ag}$ (which is initialised to be $\theta_0$) and $\theta^{md}$. $\theta^{md}$ is updated as a linear combination of $\theta^{ag}$ and the current estimation of the parameter $\theta$ when a data comes in (line 1), where $\alpha_k$ is the coefficient. The parameter $\theta$ is estimated in line 1 taking $\lambda_k$ as a parameter. The residue and the average residue of previous residues up to the $k$-th data are computed in line 1. $\theta^{ag}$ is then updated by taking $\beta_k$ as a parameter in line 1. The process continues whenever a new pair of data is seen.

2.1.   Notes on the algorithm

The unbiased estimate of the gradient, i.e., $\left(\langle \theta_{k}^{md}, x_{k}\rangle x_{k}-y_{k}x_{k}\right)$ for each data point $(x_k, y_k)$ is used in line 1. From this perspective, it is seen that the update of $\theta_k$ (line 1) is actually the same as in the stochastic gradient descent (also called least-mean-square, LMS) algorithm if we set $\alpha_k = 1$.

During optimizing, the residue $\xi_k$ is computed (line 1). All the residues up to now are averaged and the averaged residue takes effect on the update of $\theta_k^{ag}$ (line 1). It differs from the accelerated stochastic gradient algorithm in ^[22] where no residue is computed and used in the optimizing.

2.2.   Non-asymptotic analysis on convergence rate

This section we establish the convergence rate of the developed algorithm. The goal is to estimate the bound on the expectation $\mathbb{E}[f(\theta_n^{ag}) - f(\theta^*)]$. It turns out that the developed algorithm is able to achieve a convergence rate of $O(1/n^2)$ without strong convexity and Lipschitz continuous gradient assumptions.

To establish the convergence rate of the developed gradient algorithm, we need the following Lemma (see Lemma 1 of ^[22]).

Lemma 1. Let $\alpha_{k}$ be a sequence of step sizes in the accelerated gradient algorithm and the sequence $\{\eta_{k}\}$ satisfies $\eta_{k}\leq(1-\alpha_{k})\eta_{k-1}+\tau_{k}, \ \ k = 1, 2, \ldots,$ where

Then we have $\eta_{k}\leq \Gamma_{k}\sum_{i = 1}^{k}\frac{\tau_{i}}{\Gamma_{i}}$ for any $k\geq 1$.

Proof. Noting that $\alpha_{1} = 1$ and $\alpha_{k}\in(0, 1]$, we obtain

and

The result then immediately follows by summing up the above inequalities and rearranging the terms.

Applying Lemma 1, we can obtain the convergence rate of the developed algorithm as explained in Theorem 1.

Theorem 1. Let $\{\theta_{k}^{md}, \theta_{k}^{ag}\}$ be computed by the accelerated gradient algorithm and $\Gamma_{k}$ be defined in (2.1). Assume (a–d). If $\{\alpha_{k}\}, \{\beta_{k}\}, \{\lambda_{k}\}$ are chosen such that

then for any $n\geq 1$, we have

Proof. By Taylor expansion of the function $f$, Algorithm1 (line 3) and (line 6), we have:

where the last inequality holds due to assumption (b). Since

we have

where the inequality follows from the positive semi-definition of matrix $\mathbb{E}(x_{k}x_{k}^\intercal)$. By Algorithm 1 (line 2) and (2.2), we have

So we obtain

It follows from Algorithm 1 (line 4) that

Then we have

While

Combining (2.4) and (2.5), we obtain

The above inequality is equal to

Using Lemma 1, we have

Since

then

So we obtain

where the inequality follows from the assumption

Under assumption (d), we have

Taking expectation on both sides of the inequality (2.6) with respect to $(x_{i}, y_{i})$, we obtain for $\theta\in \mathbb{R}^d$,

Now, fixing $\theta = \theta^{*}$, we have

This finishes the proof of the theorem.

In the following, we apply the results of Theorem 1 to some particular selections of $\{\alpha_{k}\}, \{\beta_{k}\}$ and $\{\lambda_{k}\}$. We obtain the following Corollary 1.

Corollary 1. Suppose that $\alpha_{k}$ and $\beta_{k}$ in the accelerated gradient algorithm for regression learning are set to

then for any $n\geq 1$, we have

Proof. In the view (2.1) and (2.7), we have for $k\geq 2$

It is easy to check

Then we obtain

From the result of Theorem 1, we have

This finishes the proof of the Collorary.

3.   The accelerated stochastic gradient algorithm for logistic regression learning

In this section, we develop the accelerated gradient algorithm for logistic regression. For the logistic regression, we consider the logistic loss function: $l(\theta) = \mathbb{E}[\log(1+\exp(-y\langle x, \theta\rangle))]$. Assume the observations $(x_{i}, y_{i})\in \mathcal{F}\times \{-1, 1\}$ are independent and identically distributed from unknown distribution $\rho$ where $\mathcal{F}$ is a $d-$dimension Euclidean space, with $d\geq 1$. Further, we denote by $\theta^{*}\in \mathbb{R}^d$ a global minimiser of $l$ and assume its existence. Let $\xi_{i} = \left(y_{i}-\langle\theta^{k}, x_{i}\rangle\right)x_{i}$ denote the residual. We denote $\bar{\xi}_{k} = \frac{1}{k}\sum_{i = 1}^{k}\xi_{i}$ the average residue up until $k$ input data. To analyse the algorithm, we make the following assumptions:

(B1) $\mathbb{E}\|x_{i}\|^2$ is finite, i.e., $\mathbb{E}\|x_{i}\|^2\leq M$ for any $i\geq 1$.

(B2) $\mathbb{E}\|\xi_{i}\|^2\leq M_{1}$ for every $i$.

Again, unlike the algorithm by Bach et al. ^[10], we make no assumption on the Hessian operator at the global optimum $\theta^*$.

The developed accelerated stochastic gradient algorithm for the logistic regression is presented in Algorithm 2. In the algorithm, $\theta_0 \in {\cal F}$ is an initial guess, and

It can be seen that the basic framework of Algorithm 2 is the same as Algorithm 1 except that the unbiased estimation to the gradient is different due to the loss functions.

3.1.   Non-asymptotic analysis on convergence rate

In this section, we also provide the non-asymptotic analysis on the convergence rate of the developed algorithm in expectation. Theorem 2 describes the convergence rate.

Theorem 2. Let $\{\theta_{k}^{md}, \theta_{k}^{ag}\}$ be computed by the accelerated gradient algorithm and $\Gamma_{k}$ be defined in (2.1). Assume (B1 and B2). If $\{\alpha_{k}\}, \{\beta_{k}\}, \{\lambda_{k}\}$ are chosen such that

then for any $n\geq 1$, we have

Proof. By Taylor expansion of the function $l$, there exists a $\vartheta$ such that

In the equation, we know

It is easy to verify the matrix

is positive semidefinite and its largest eigenvalue satisfies

Combining with Algorithm 2 (line 6) and (3.1), we have

Similar to (3.1), there exists a $\zeta\in \mathbb{R}^d$ satisfying

we have

where the inequality follows from the positive semi-definition of matrix. Similar to (2.2), we have

So we obtain

It follows from Algorithm 2 (line 4) that

Combining the above two inequalities, we obtain

The above inequality is equal to

Using Lemma 1, we have

Since

then

So we obtain

where the inequality follows from the assumption

Under the assumption (B4), we have

Taking expectation on both sides of the inequality (3.2) with respect to $(x_{i}, y_{i})$, we obtain for $\theta\in \mathbb{R}^d$,

Now, fixing $\theta = \theta^{*}$, we have

This finishes the proof of the theorem.

Similar to Corollary 1, we specialise the result of Theorem 2 for some particular selections of $\{\alpha_{k}\}, \{\beta_{k}\}$ and $\{\lambda_{k}\}$.

Corollary 2. Suppose that $\alpha_{k}$ and $\beta_{k}$ in the accelerated gradient algorithm for regression learning are set to

then for any $n\geq 1$, we have

4.   Experiment results

In this section, we empirically investigate the performance of our algorithms on synthetic data and some benchmarks widely used by the machine learning community.

4.1.   Least square regression

We consider normally distributed inputs, with covariance matrix $H$ that has random eigenvectors and eigenvalues $1/k$, $k = 1, \ldots, d$. The outputs are generated from a linear function with homoscedastic noise with various signal to noise-ratio $\sigma$. We consider $d = 20$ and $100000$ samples using mini-batch size of 100.

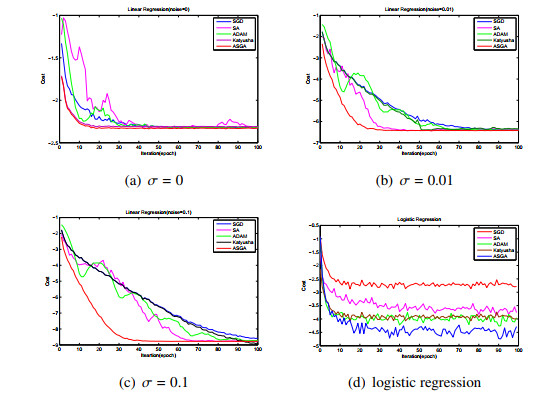
We compare SGD, stochastic approximation (SA) with averaging ^[10], ADAM ^[24], Katyusha ^[25] and ASGA on synthetic noisy datasets with different noise levels: $\sigma = 0, 0.1$ and $0.01$. For SGD and SA we choose the step size $\rho = 1/2R^{2}$ and $\gamma_{n} = 1/2R^{2}\sqrt{n})$ where $R^2 = trace(H)$, respectively. The loss function is defined as $\log_{10}[f({\theta})-f(\theta^{*})]$. The average loss function value over 100 runs on the training data is shown in Figure 1 (a)–(c). It can be seen that ASGA converges much faster than SGD, SA and ADAM. The results also verify our theoretical improvement on the convergence rate of ASGA.

4.2.   Logistic regression

For logistic regression, we consider the same input data as for the least-squares, but outputs are generated from the logistic probabilistic model. Comparison results are shown in Figure 1 (d). A step size $\gamma_{n} = 1/(2R^{2}\sqrt{n})$ is chosen for SA with averaging for an optimal performance. For ADAM, its step size $\alpha$ is adjusted by $1/\sqrt{n}$ decay as suggested in ^[24]. From Figure 1 (d), it is clearly seen that ASGA converges significantly faster than all the compared algorithms.

4.3.   Benchmarks

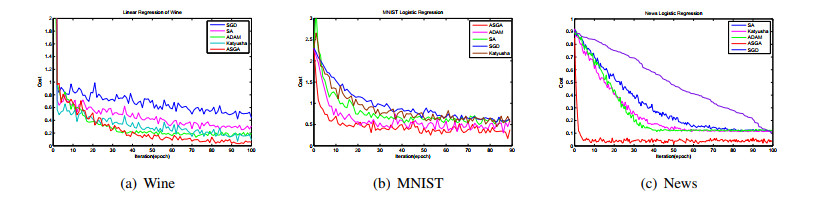
We evaluate ASGA on the MNIST, Wine dataset and News dataset. In our experiments, the raw features of the datasets are used directly as the input to the classifier. For MNIST, 9000/1000 data points are used as training/test dataset, the numbers are 4000/898 for Wine, while the numbers are 18000/846 for News. We compare SGD, stochastic approximation (SA) with averaging ^[10], ADAM ^[24], Katyusha ^[25] and ASGA using mini-batch size of 90 in MINST, using mini-batch size of 100 in Wine and News. Figure 2 shows the training procedure of ASGA on these three datasets by averaging 50 runs. From Figure 2, it is seen that ASGA obtains better the loss values with faster convergence rate. This clearly demonstrates the effectiveness of ASGA. Table 1 summarizes the prediction accuracies of the obtained optimal parameters of the logistic regression model on the test datasets by the compared algorithms. The $p$-values obtained by t-test at $5\%$ significance level are also given in the subscripts of the compared algorithms. From the table, it is seen that ASGA achieves significantly better accuracies that the other algorithms ($p < 0.05$).

5.   Conclusions

In this paper, we proposed two accelerated stochastic gradient algorithms (ASGA) for least-square and logistic regression in which the averaged residue is used to adjust the parameter estimation. An asymptotic analysis proved that ASGA can achieve a convergence rate of ${\cal O}(1/n^2)$ which is much tighter than the state-of-the-art rate under non-strongly convexity assumptions. Experimental results on synthetic data and benchmark datasets justified our theoretical results.

Acknowledgments

The authors acknowledge the financial supports from the National Natural Science Foundation of China [No.61573326], Support project for outstanding young talents in Colleges and universities in Anhui Province [No.gxyq2018076], Natural science research project of colleges and universities in Anhui Province [No.KJ2018A0455], scientific research project of Chaohu University [No.XLY-201903].

Conflict of interest

The authors declare that they have no competing interests.