Prominent interior GE-filters of GE-algebras

1.   Introduction

The relationship between predator and prey is the most common biological system in nature. Its basic mathematical model is the Lotka-Volterra system, which is an ordinary differential equation system proposed by mathematicians Lotka and Volterra in the 1920s. By building on its basic idea, Lotka-Volterra systems have been extensively studied ^[1,2,3,4,5]. It has been applied to model various phenomena, including predator harvesting, impulse control strategies, anti-predatory behavior, spatiotemporal patterns, the fear effect ^{[6,7,8,9,10,11,12]}.

Predator-prey systems in nature can be associated with a variety of different factors that can cause dramatic predator or prey populations change to undergo changes. In this study, we investigate the effect of impulsive control strategies on predator-prey relationships by employing the Lotka-Volterra model. Two types of impulsive control, i.e., periodic impulse and state-dependent impulse, have been widely studied in literature ^[13,14,15]. The periodic impulsive control strategy is to harvest or capture the predators or prey periodically, which can be modeled by using fixed-time impulsive differential equations ^[16,17,18]. A disadvantage of the periodic pulse control strategy is that the timing of the pulses does not take into account the actual changing population density. Therefore, the state-dependent impulsive control strategy has been introduced, which can be modeled by using state-dependent differential equations ^[19,20,21]. In nature, there exists the phenomenon of a high population density but slow growth and low population density but fast growth. Therefore, scholars are now paying more attention to state-dependent impulsive differential equations with nonlinear threshold control ^{[20,22,23,24]}.

State-dependent impulsive differential equations with nonlinear threshold control have been widely applied to analyze real-life problems, including modeling the population dynamics ^[25,26], tumor control ^[27,28], and viral dynamics ^[29,30]. Meanwhile, the theoretical development of the state-dependent impulsive differential equations has continued to advance, particularly in the realms of the invariant and limit sets ^[31,32] and the Poincaré-Bendixson theorem ^[31]. Tang and Cheke^[14] obtained the maximum invariant set of the system by using a Lyapunov function, and they studied the properties of the order-1 periodic solution and sufficient conditions for stability. Bonotto and Federson ^[31] studied the biological phenomena of predator-prey systems by using the Poincaré-Bendixson theorem.

In 2005, Tang and Cheke^[14] studied the following impulse differential equation with a fixed threshold:

x(t) and $y(t)$ denote the prey (pest) and predator (natural enemy) densities, respectively. $r$ represents the inherent growth rate of the prey, $\beta$ represents the capturing rate, $\eta$ denotes the effective conversion rate of natural enemies, $\delta$ indicates the mortality rate of natural enemies, $1-p$ denotes the survival rate of pests, and $\tau$ denotes the total number of predators released at regular intervals. $ET$ is a positive number and the threshold for impulse control. In ^[14], the scholars discuss the existence of periodic solutions of order 1 or 2 for the system (1.1) and show that with the exception of a special case, there are no periodic solutions of order greater than order 2. Zhang and Tang ^[19] in 2021 considered more realistic factors by replacing $ET$ in system (1.1) with the action threshold $AT$ and investigated the stability and existence of the order-1 periodic solution. Further, Tian and Tang^[21] studied a predator-prey system with nonlinear impulse functions and nonlinear threshold control and discussed the existence and stability of the order-1 periodic solution. It is worth noting that the order 1 periodic solution is very significant for studies on controlling policy decisions. It ensures that, when the control measures are implemented, they are able to maintain the population of the prey or predators below a given $AT$ level.

In a number of studies, scholars have focused on modeling the anti-predatory behavior in nature, where prey can attack predators, i.e., the prey population indirectly reduces the predator population ^[33,34]. Anti-predatory behavior is typical; for example, the adult prey can kill juvenile predators or eat them; examples include crustaceans and sea snails, predatory and herbivorous mites, and 'predatory' mites and thrips 'prey' ^[35,36]. Mathematically, a predator-prey model with anti-predatory behavior was proposed by Tang and Xiao ^[37], in which adult prey can attack immature predators and cause harm to the predators. Tian and Tang ^[21] also studied the effect of anti-predatory behavior on the changes in the system.

Kent et al. ^[38] and van Voorn et al. ^[39] obtained the effect of predators on the predator-prey system. The results showed that the invasion of predators into a prey network can fail and lead to the collapse of the system or maintain the coexistence of the prey and predator populations. In other words, predator invasion can alter the dynamic behavior of the system. Threshold control for the number of predators was considered in the predator-prey system proposed by Wei and Chen ^[40]. The authors considered the situation whereby the number of predators could be detected, and the population in the system was controlled through harvesting when the predator density reached a fixed threshold. The unique order-1 periodic solution was derived.

According to the existing literature, few scholars have studied state-dependent models from the perspective of the predators. However, from the above discussion, we can get that the influence of predators on population relations is also crucial. Therefore, in this paper, we apply the action threshold, which is closely related to the size of the predator population and the rate of continuous predator development. The influence of the threshold change on the system and the resulting complex biodynamics are studied.

This study applied the assumption that the predator population size is large and detectable. The decrease in predator density is assumed to be caused by anti-predatory behavior. The control strategy is implemented by releasing a certain number of predators that capture the corresponding prey when the predator density and rate of change reach given values. Therefore, a predator-prey system that integrates anti-predatory behavior and the nonlinear threshold is proposed; the threshold control of the predator-prey system is modeled by a nonlinear function of the predator density and rate of change. We explore the effects of predator density and rate of change threshold control on the system and discuss how to achieve economic benefits on the basis of the proposed predator-prey system.

The paper is organized as follows. In Section 2, a predator-prey model with anti-predator behavior is proposed, and the nonlinear threshold control depends on the number and growth rate of predators. The situation without impulsive control is discussed. In Section 3, the exact impulse set and the exact phase set of the model are obtained and the expressions of the Poincaré map are defined. The monotonicity of the Poincaré map and the extreme value points are analyzed in Section 4. In Section 5, we work on analyzing the nature of the periodic solutions to the model. The parameters are given values in Section 6, and the results show that the predator-prey system can demonstrate several interesting phenomena. Finally, we conclude the article with a summary of the content.

2.   Model formulation

2.1.   Presentation of system (2.1)

According to the above discussion, we present a nonlinear state-dependent feedback control model with an action threshold based on ^[21]:

Let us represent by x(t) and $y(t)$ the densities of prey (pest) and predator (natural enemy), respectively. $r$ denotes the intrinsic velocity of the growing prey, the carrying capacity of the environment is denoted by $K$, $\beta$ represents the efficiency of prey capture by the predators, $\eta$ denotes the effective conversion rate of the predators, $\varepsilon x(t)y(t)$ represents anti-predatory behavior (satisfying the restriction $\eta\beta-\varepsilon > 0$), and $\delta$ represents the mortality rate of the predators. The parameters $\alpha_1$, $\alpha_2$ and $ET$ are all positive numbers satisfying that $\alpha _1 + \alpha _2 = 1$. Let $ET$ be a threshold value such that if the density of the predator population and its speed of growth are equal to or below this value, impulse control is applied to the system immediately. In system (2.1) the carrying capacity of the environment is involved, so the condition ${x \in [0, K], y \in [0, K]}$ holds.

In the early studies of state-dependent impulse differential equations, the control threshold was assumed to be a fixed number of organisms in a given population. However, in terms of the actual growth of living species, the control of fixed threshold does not accurately reflect the real changes in a population. In recent years, scholars have considered an action threshold that incorporates population size and rate of change. Therefore, we consider the action threshold based on the number of predator populations and their rates of change, i.e., impulse control measures for both populations in the system when the number of predators and the rate of change reach our given threshold ($\alpha _1 y(t) + \alpha _2 \frac{{dy(t)}}{{dt}} = ET$).

We still employ the nonlinear impulse functions associated with population density and the capture rate as follows.

Here, $\sigma$ and $\mu$ represent the highest prey acquisition rate and the semi-saturation parameter, respectively, $\tau$ shows the largest number of released predators, and $\omega$ is the morphological coefficient. In this study, we suppose that the density of the predator population and its rate of change satisfy the condition $({{\alpha _1}y(t) + {\alpha _2}\frac{{dy(t)}}{{dt}} > ET})$. When the predator population density decreases to the action threshold $\alpha _1 y(t) + \alpha _2 \frac{{dy(t)}}{{dt}} = ET$, the prey is captured via control measures to reach $x(t) - \frac{{\sigma x^2 (t)}}{{x(t) + \mu }}$ (i.e., $x(t^ +)$) and the predator will be released to bring the density to $y(t) + \frac{\tau }{{1 + \omega y(t)}}$ (i.e., $y(t^ +)$).

2.2.   Analysis of the equilibrium point

Without the feedback control, the ordinary differential equation is as follows:

The two nullclines of system (2.2) are denoted by $L_1$ and $L_2$, where

Obviously, we can get three equilibrium points, which are the zero equilibrium point $(0, 0)$, boundary equilibrium point $(K, 0)$, and positive equilibrium spot ${E^*}\left({{x^*}, {y^*}} \right) = \left({\frac{\delta }{{\eta \beta - \varepsilon }}, \frac{{r\left({K(\eta \beta - \varepsilon) - \delta } \right)}}{{\beta K(\eta \beta - \varepsilon)}}} \right)$ when $K > \frac{\delta }{{\eta \beta - \varepsilon }}$. For the system (2.2) the equilibrium point is studied as shown below, which helps us to analyze the nature of the system (2.1).

Lemma 2.1. For the system (2.2), the trivial equilibrium point $(0, 0)$ is the saddle point. There is no positive equilibrium point if $K < \frac{\delta }{{\eta \beta - \varepsilon }}$ and $(K, 0)$ is a globally stable node. If $K > \frac{{\delta + \sqrt {\delta (\delta + r)} }}{{2(\eta \beta - \varepsilon)}}$, the point $E^*(x^*, y^*)$ is a globally stable focus. If $\frac{\delta }{{\eta \beta - \varepsilon }} < K < \frac{{\delta + \sqrt {\delta (\delta + r)} }}{{2(\eta \beta - \varepsilon)}}$, the equilibrium point $E^*(x^*, y^*)$ is a globally stable node.

Proof. The Jacobian matrix of system (2.2) can be obtained as follows:

Substituting $(0, 0)$, $(K, 0)$ and $E^*(x^*, y^*)$ into $J_{am} (x, y)$ respectively, we get

From this, $(0, 0)$ is a saddle point, and the equilibrium point $(K, 0)$ is a globally stable node when $K < \frac{\delta }{{\eta \beta - \varepsilon }}$ and a saddle point when $K > \frac{{\delta + \sqrt {\delta (\delta + r)} }}{{2(\eta \beta - \varepsilon)}}$. The characteristic polynomial of $J_{am} (x^*, y^*)$ is given by

thus yielding the eigenvalues: $\lambda _{1, 2} = \frac{{ - \frac{{\delta r}}{{K(\eta \beta - \delta)}} \pm \sqrt {\Delta _0 } }}{2}$, where

Since the real part of the eigenvalue $\lambda _{1, 2}$ is below zero, the equilibrium point $E^*(x^*, y^*)$ is locally stable. In addition, the inequality $\Delta _0 < 0$ can be expressed as

Therefore, if $K > \frac{{\delta + \sqrt {\delta (\delta + r)} }}{{2(\eta \beta - \varepsilon)}}$ then $\Delta _0 < 0$ and $K > \frac{\delta }{{\eta \beta - \varepsilon }} = x^*$, which signifies that the equilibrium point $E^*(x^*, y^*)$ is a focal spot. If $\frac{\delta }{{\eta \beta - \varepsilon }} < K < \frac{{\delta + \sqrt {\delta (\delta + r)} }}{{2(\eta \beta - \varepsilon)}}$ and $\Delta _0 > 0$, this implies that the equilibrium point $E^*(x^*, y^*)$ is a node. Furthermore, the equilibrium spot $E^*(x^*, y^*)$ is also globally stable on the interval in which the system is located, as proven below:

Let

Constructing a Dulac function $B(x, y) = \frac{1}{{xy}},$ we have that $\frac{{\partial (PB)}}{{\partial x}} + \frac{{\partial (QB)}}{{\partial y}} = - \frac{r}{{yK}} < 0$. By the Bendixson-Dulac discriminant, there is no limit cycle in the positive xy-plane, i.e., the point $E^*(x^*, y^*)$ is globally stable. The proof is complete.

As a result, we can know that $E^*$ is a stable focus or node when $\frac{\delta }{{\eta \beta - \varepsilon }} < K$. When $\frac{\delta }{{\eta \beta - \varepsilon }} > K$, there is no internal equilibrium point. In our following study, we consider the case in which the equilibrium point $E^*$ is stable, i.e., $\frac{\delta }{{\eta \beta - \varepsilon }} < K$.

3.   Construction of the Poincaré map

Regarding the biological significance, our study is limited to the range $R_ + ^2 = \{ (x, y):x \ge 0, y \ge 0\}.$ From $\alpha _1 y + \alpha _2 \frac{{dy}}{{dt}} = ET$ and $\frac{{dy(t)}}{{dt}} = (\eta \beta - \varepsilon)x(t)y(t) - \delta y(t)$, we can get

represented by $L_M$. By calculating the $x^ + = x - \frac{{\sigma x^2 }}{{x + \mu }}$, we can get

Substituting the above equation into the equation for $L_M$, we obtain

Let

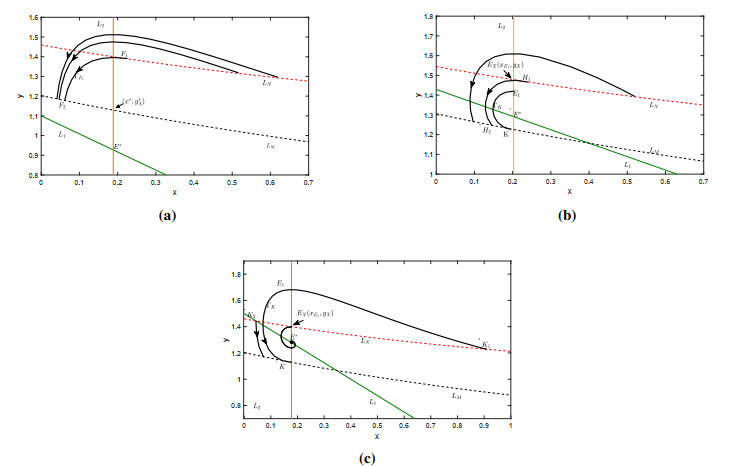
which is denoted by $L_N$. We assume that the curves $L_M$ and $L_N$ intersect the vertical coordinates in the right-angle coordinate system at the points ${Q_1}(0, {Y_1})$ and ${Q_2}(0, {Y_2})$, respectively. In the following discussion, we suppose that the starting point $p_0^ + (x_0^ +, y_0^ +)$ are on $L_N$, unless there are special cases. Because the initial values taken are different, the trajectories from the $L_N$ may not reach the curve $L_M$. Therefore, from the phase diagram of the system (2.1) and the relationship between the locations of the equilibrium points, we can obtain the concrete ranges of the curve $L_M$ and the curve $L_N$ (see Figure 1).

Case (A). $y^* \le y_A^*$.

The curve $L_2$ with the vertical coordinate of the equilibrium point $E^*$ intersects the impulse curve $L_M$ at the point $(x^*, y_A^*)$. Because $y^* \le y_A^*$, there is a curve $\Gamma _{F_1 }$ that is tangential to the curve $L_N$ at the point $F_1 (x_{F_1 }, y_{F_1 })$ and intersecting the curve $L_M$ at $F_2 (x_{F_2 }, y_{F_2 })$ (see Figure 1(a)). From Figure 1(a), we can get that the trace from the phase set will definitely arrive at the arrival pulse set after a certain period of time. Thus, considering this circumstance, we can obtain the concrete ranges of the impulse set and phase set as expressed below:

Here $(x, y)$ is the point in the impulse curve $L_M$ and $(x^ +, y^ +)$ is the spot in the phase curve $L_N$.

Case (B). $y^* > y_A^*$.

In this case, because $y^* > y_A^*$, there must exist a curve $\Gamma _K$ that is tangential to the impulse curve $L_M$ at point $K(x_K, y_K)$ and intersecting the curve $L_2$ at point $E_1 (x_{E_1 }, y_{E_1 })$. The curve $L_2$, where the longitudinal coordinates of point $E_1 (x_{E_1 }, y_{E_1 })$ are located, intersects the phase curve $L_N$ at point $E_X (x_{E_1 }, y_X)$. Thus, we have the following two cases:

(B1) $y_{E_1 } \le y_X$. Since $y_{E_1 } \le y_X$, this circumstance is similar to Case (A). Under this condition, the curve $\Gamma _K$ has no intersection with the phase curve $L_N$. From the phase set, all points can arrive at the pulse set. There exists a curve $\Gamma _{H_1 }$ that lies tangent to the phase curve $L_N$ with the point $H_1 (x_{H_1 }, y_{H_1 })$ and intersects the impulse curve at the point $H_2 (x_{H_2 }, y_{H_2 })$ (see Figure 1(b)). Therefore, the corresponding impulse set and phase set are expressed as follows:

respectively.

(B2) $y_{E_1 } > y_X$. In this case, as $y_{E_1 } > y_X$, which cause the curve $\Gamma _K$ to intersect the phase set at points $K_1 (x_{K_1 }, y_{K_1 })$ and $K_2 (x_{K_2 }, y_{K_2 })$ for $x_{K_2 } < x_{K_1 }$. Hence, none of the initial points on the phase curve $L_N$ from between points $K_1$ and $K_2$ can reach the impulse curve $L_M$ (see Figure 1(c)). From this, we can determine the scope of the impulse set and phase set as below:

respectively.

From the above discussion, we can construct the following Poincaré map. Provided an initial point $P_0^ + (x_0^ +, y_0^ +)$ belonging to the phase curve $L_N$, we can determine the path that starts from point $P_0^ +$ as follows:

As for $P_i^ + (x_i^ +, y_i^ +)$ belonging to the phase set, point $P_i^ +$ arrives at the impulse set becoming point $P_{i + 1} (x_{i + 1}, y_{i + 1})$ after time ${\tilde t}$. The corresponding formulation is as follows:

where $x_{i + 1} = x^ + (\tilde t, x_i^ +, y_i^ +)$. By the Cauchy-Lipschitz theorem, we learn that $x_{i + 1}$ is uniquely denoted by $x^ +$. By the definition $x_{i + 1} = \xi (x_i^ +)$, we have

The following scalar differential equation for the system (2.1) is considered:

From the system (2.1) we know that the function $e(y, x)$ is continuously differentiable. In addition, we set $y_0^ + = U, x_0^ + = V$ and $P_0^ + (x_0^ +, y_0^ +) \in N$. Let

The data variants of $y$ are between the curve $L_N$ and the curve $L_M$. Solving (3.2) we obtain

Therefore, from (3.1) and (3.4), we can get the expression for the Poincaré map:

4.   The nature of E(V)

In this section, we will discuss the properties of $E(V)$.

Theorem 4.1. Assume that $y^* \le y_A^*$. We obtain the following properties of $E(V)$ (see Figure 2):

(i) The domain of definition of $E(V)$ is $(0, + \infty)$. Moreover, $E(V)$ is decreasing monotonically in the interval $(0, x_{F_1 }]$ and increasing monotonically in the interval $[x_{F_1 }, + \infty)$.

(ii) $E(V)$ is continuously differentiable in the interval $(0, + \infty)$, and it follows that there is a unique fixed point.

Proof. (ⅰ) When ${y^{*}} \le y_A^*$, there exists a point ${F_1}({x_{{F_1}}}, {y_{{F_1}}}) \in {L_N}$ such that the curve ${\Gamma _{{F_1}}}$ is tangent to ${L_N}$ and ${\Gamma _{{F_1}}}$ intersects ${L_M}$ at the point ${F_2}({x_{{F_2}}}, {y_{{F_2}}})$. It follows that any trajectory starting from ${L_N}$ can reach ${L_M}$ after some time. Therefore, the Poincaré map is defined within the range $(0, + \infty)$. This means that $E(V)$ is significant within $(0, + \infty)$.

Assume that there exists $P_{{a_1}}^ + (x_{{a_1}}^ +, y_{{a_1}}^ +), P_{{a_2}}^ + (x_{{a_2}}^ +, y_{{a_2}}^ +) \in {L_N}$. By the dynamical behaviour of the system (2.1), at the elapsed time $\tilde t$, we can obtain that $\Gamma (\tilde t, x_i^ +, y_i^ +) = \Gamma (\tilde t, {x_{i + 1}}, {y_{i + 1}})$. If $x_{{a_1}}^ +, x_{{a_2}}^ + \in (0, {x_{{F_1}}}]$ and $x_{{a_1}}^ + < x_{{a_2}}^ +$, because of the uniqueness of the solution, we obtain that ${x_{{a_1} + 1}} > {x_{{a_2} + 1}}$. From the formulation of $E(V)$, we get that $E({x_{{a_1} + 1}}) > E({x_{{a_2} + 1}})$. Therefore, $E(V)$ is monotonically decreasing within the range $(0, x_{F_1 }]$.

When $x_{{a_1}}^ +, x_{{a_2}}^ + \in [{x_{{F_1}}}, + \infty)$ and $x_{{a_1}}^ + < x_{{a_2}}^ +$, the initial points $P_{{a_1}}^ +$ and $P_{{a_2}}^ +$ return to the curve ${L_N}$ at points ${{P'}_{{a_1}}}({{x'}_{{a_1}}}, {{y'}_{{a_1}}})$ and ${{P'}_{{a_2}}}({{x'}_{{a_2}}}, {{y'}_{{a_2}}})$ after a period of impulses. We easily get that ${{x'}_{{a_1}}} < {{x'}_{{a_2}}}$. By the uniqueness of the solution, we get that ${\rm{E(}}{{x'}_{{a_1}}}) < E({{x'}_{{a_2}}})$. Therefore, $E(V)$ is monotonically increasing within the range $[{x_{{F_1}}}, + \infty)$.

(ⅱ) From (3.2), it is obvious that the function $e(y, x)$ is continuously differentiable. By the theorems on continuity and differentiability for differential equations, we gain that $E(V)$ is continuously differentiable within the range $(0, + \infty)$.

The curve ${\Gamma _{{F_1}}}$ from the point ${F_1}$ reaches ${L_M}$ at the point ${F_2}$ and is impulsed to ${L_N}$ at the spot $F_2^ + (x_{{F_2}}^ +, y_{{F_2}}^ +)$ after some more time. If $E({x_{{F_1}}}) < {x_{{F_1}}}$, then $x_{{F_2}}^ + = E({x_{{F_1}}}) \in (0, {x_{{F_1}}}]$ and $x_{{F_2}}^ + < {x_{{F_1}}}$. And since $E(V)$ is monotonically decreasing within the range $(0, {x_{{F_1}}}]$, we have that $E(x_{{F_2}}^ +) > E({x_{{F_1}}}) = x_{{F_2}}^ +$. By the existence theorem for zeros of the function $E(V)$ and continuous differentiability, we can obtain that there exists $\bar x \in (x_{{F_2}}^ +, {x_{{F_1}}})$ such that $E(\bar x) = \bar x$. Therefore, there exists a unique immobile point of $E(V)$ in the zone $(0, + \infty)$, as shown in Figure 2(a). The proof for the case in Figure 2(b) is obvious.

When $y^* > y_A^*$ and $y_{E_1 } \le y_X$, the characteristics of $E(V)$ are similar to those in Case (A). For this reason, we discuss the nature of $E(V)$ when $y^* > y_A^*$ and $y_{E_1 } > y_X$.

Theorem 4.2. When $y^* > y_A^*$ and $y_{E_1 } > y_X$, the Poincaré map $E(V)$ possesses the following nature (see Figure 3):

(i) The domain of the definition of $E(V)$ is $(0, x_{K_2 }] \cup [x_{K_1 }, + \infty)$, with $E(V)$ decreasing monotonically in the interval $(0, x_{K_2 }]$ and increasing monotonically in the interval $[x_{K_1 }, + \infty)$.

(ii) $E(V)$ is continuously differentiable in the interval $(0, x_{K_2 }] \cup [x_{K_1 }, + \infty)$.

(iii) If $E(V)$ satisfies that $E(x_{K_2 }) < x_{K_2 }$ at point $x_{K_2 }$, then there is only one immobile point of $E(V)$ in the interval $(0, x_{K_2 }]$. However, when $E(V)$ is at point $x_{K_1 }$ at $E(x_{K_1 }) > x_{K_1 }$, there is no fixed point over the entire domain of the definition.

Proof. (ⅰ) When the condition $y_{E_1 } > y_X$ is satisfied, the curve $\Gamma _K$ which is tangent to the impulse curve $L_M$ intersects with the phase curve $L_ N$ at the points ${K_1 }$ and ${K_2 }$, respectively. Considering the following: $\forall P_i (x_i, y_i) \in N$, if $x_i^ + \in (x_{K_2 }, x_{K_1 })$, none of the trajectories from the phase curve $L_N$ can arrive at the curve $L_M$. Therefore, we denote the domain of the definition of $E(V)$ as $(0, x_{K_2 }] \cup [x_{K_1 }, + \infty)$.

Assume that there exists $P_{h_1 }^ + (x_{h_1 }^ +, y_{h_1 }^ +), P_{h_2 }^ + (x_{h_2 }^ +, y_{h_2 }^ +) \in L_N$; if $x_{h_1 }^ +, x_{h_2 }^ + \in [x_{K_1 }, + \infty)$, let $x_{h_1 }^ + < x_{h_2 }^ +$. From the previous discussion, we can know that the trajectory from point $x_i^ +$ to point $x_{i + 1}$ after time ${\tilde t}$ can be denoted as $\Gamma (\tilde t, x_i^ +, y_i^ +) = \Gamma (\tilde t, x_{i + 1}, y_{i + 1})$. By the sole nature of the solution, we obtain that $x_{h_1 + 1} < x_{h_2 + 1}$. Under the equation of the Poincaré map $E(V)$, we then obtain that $E(x_{h_1 + 1}) < E(x_{h_2 + 1})$. As a consequence, we obtain the Poincaré map $E(V)$ that is monotonically increasing in the interval $[x_{K_1 }, + \infty)$.

When $x_{h_1 }^ +, x_{h_2 }^ + \in (0, x_{K_2 }]$ and $x_{h_1 }^ + < x_{h_2 }^ +$, we obtain the paths of points $P_{h_1 }^ +, P_{h_2 }^ +$ passing through the curve $L_2$ and respectively intersecting the phase curve $L_N$ at points $P'_{h_1 } (x'_{h_1 }, y'_{h_1 }), P'_{h_2 } (x'_{h_2 }, y'_{h_2 })$ where $x'_{h_1 } > x'_{h_2 }$. Under the equation of the Poincaré map $E(V)$, we then obtain that $E_M (x'_{h_1 }) > E_M (x'_{h_2 })$. As a consequence, we obtain the Poincaré map $E(V)$ that is monotonically decreasing in the interval $(0, x_{K_2 }]$.

(ⅱ) Based on (3.2) given earlier, we can know that the function $e(y, x)$ is continuously differentiable. By the theorems of continuity and differentiability for the differential equations, we therefore easily obtain that $E(V)$ is continuously differentiable in the interval $(0, x_{K_2 }] \cup [x_{K_1 }, + \infty)$.

(ⅲ) The trajectory $\Gamma _K$ moves from the point $K_2$ to the impulse curve $L_M$ at the point $K$, and then to the phase curve $L_N$ at the point $K^ + (x_K^ +, y_K^ +)$, according to which we have that $x_K^ + = E(x_{K_2 }) \in (0, x_{K_2 }]$ holds. Since the Poincaré map $E(V)$ is monotonically decreasing in the interval $(0, x_{K_2 }]$, we have that $E(x_K^ +) > E(x_{K_2 }) = x_K^ +$ holds. If $E(x_{K_2 }) < x_{K_2 }$, then by the zero theorem there is $\bar x \in (x_K^ +, x_{K_2 })$ such that $E(\bar x) = \bar x$. Accordingly, the Poincaré map $E(V)$ holds a uniquely fixed point in the interval $(0, x_{K_2 }]$.

If $E(x_{K_1 }) > x_{K_1 }$ holds when $x = x_{K_1 }$, for any $x_i$ belonging to the interval $[x_{K_1 }, + \infty)$, the orbit from the spot $P_i (x_i, y_i)$ arrives at the impulse curve $L_M$ at the point $P_{i + 1} (x_{i + 1}, y_{i + 1})$ and is then pulsed to the phase curve $L_N$ at the spot $P_{i + 1}^ + (x_{i + 1}^ +, y_{i + 1}^ +)$. By the dynamical behavior of the system (2.1), we can work out that $x_i < x_{i + 1} < x_{i + 1}^ +$. As a result, there is no $\bar x \in [x_{K_1 }, + \infty)$ such that $E(\bar x) = \bar x$ holds, i.e., there is no indefinite point of $E(V)$ in the interval $[x_{K_1 }, + \infty)$. The proof is completed.

5.   Periodic solutions

From the previous discussion, we know that the system (2.1) has an order-1 periodic solution. In the following theorem, we will consider its stability and other possibilities.

Theorem 5.1. In Case (A), i.e., $y^* \le y_A^*$, the system (2.1) has an order-1 periodic solution, and in addition, we know that

(i) if $E(x_{F_1 }) > x_{F_1 }$, the order-1 periodic solution of the system (2.1) is globally stable;

(ii) if $E(x_{F_1 }) < x_{F_1 }$, the order-1 periodic solution of the system (2.1) is globally stable if and only if $E^2 (x_0^ +) < x_0^ +$ for $\forall x_0^ + \in [\bar x, x_{F_1 }]$.

Proof. From (3.1), we get that $x_{i + 1}^ + = \xi (x_i^ +) - \frac{{\sigma \xi (x_i^ +)^2 }}{{\xi (x_i^ +) + \mu }} = E_M (x_i^ +)$. Thus, the starting point $P_0^ + (x_0^ +, y_0^ +)$ from the phase curve $L_N$ arrives at the impulse curve $L_M$ at the point $P_1 (x_1, y_1)$, and after a period of action pulses in the impulse curve $L_M$ arrives at the phase curve $L_N$ at the point $P_1^ + (x_1^ +, y_1^ +)$. This process can be expressed as $E(x_0^ +) = \xi (x_0^ +) - \frac{{\sigma \xi (x_0^ +)^2 }}{{\xi (x_0^ +) + \mu }} = x_i^ +$. By a similar process, we obtain that $E[E(x_0^ +)] = E(x_1^ +) = x_2^ + = E^2 (x_0^ +)$. In more depth, we obtain that $E^k (x_0^ +) = x_k^ +$.

(ⅰ) For Case (A), if $E(x_{F_1 }) > x_{F_1 }$ is satisfied at $x = x_{F_1 }$, the Poincaré map has a single immovable point ${\bar x}$ within the zone $[x_{F_1 }, + \infty)$. Two cases are discussed according to different positional relations of $x_0^ +$:

a. If $x_0^ + \in (x_{F_1 }, \bar x]$, from the previous discussion, we know that the Poincaré map $E(V)$ is monotonically increasing within this interval. For $x_{F_1 } < x_0^ + < \bar x$, we have that $x_{F_1 } < E(x_{F_1 }) < E(x_0^ +) < E(\bar x) = \bar x$. By the monotonicity of the Poincaré map $E(V)$, we have that $E(x_0^ +) < E(x_1^ +) < E(\bar x) = \bar x$. Repeating the above process, it can be deduced that

which shows that the formula $E^k (x_0^ +)$ is a monotonically increasing function in the interval $(x_{F_1 }, \bar x]$ and $\mathop {\lim }\limits_{k \to \infty } E^k (x_0^ +) = \bar x$.

b. If $x_0^ + \in (\bar x, + \infty)$, analogous to the discussion above, we have that $\bar x = E(\bar x) < E(x_0^ +) < x_0^ +$ and $\bar x = E(\bar x) < E(x_1^ +) < E(x_0^ +) < x_0^ +$ is established. After that, we can get

Therefore, we get to know that the equation for $E^k (x_0^ +)$ is a decreasing monotonic function in the zone $(\bar x, + \infty)$, so we have that $\mathop {\lim }\limits_{k \to \infty } E^k (x_0^ +) = \bar x$. It can be seen that it is globally stable when $E(x_{F_1 }) > x_{F_1 }$.

(ⅱ) Sufficient condition: If we have that $E(x_{F_1 }) < x_{F_1 }$ at point $x = x_{F_1 }$; we learn from Theorem 4.1 that the Poincaré map $E(V)$ has a single immovable point $\bar x$ within the zone $(0, x_{F_1 }]$ and is decreasing monotonically in this zone. It follows that when $E^2 (x_0^ +) < x_0^ +$ for any $x_0^ + \in [\bar x, x_{F_1 }]$, there exist $\bar x = E(\bar x) > E(x_0^ +) > E(x_{F_1 })$ and $\bar x = E(\bar x) < E^2 (x_0^ +) < x_0^ +$, i.e., $E(x_{F_1 }) < E(x_0^ +) < \bar x = E(\bar x) < E^2 (x_0^ +) < x_0^ + < x_{F_1 }$. Repeating the above process, we get

According to the monotone convergence theorem for the function, we obtain that $\mathop {\lim }\limits_{k \to \infty } E^{2k + 2} (x_0^ +) = \mathop {\lim }\limits_{k \to \infty } E^{2k + 1} (x_0^ +) = \bar x$, i.e., our theorem holds.

Necessary condition: When $E(x_{F_1 }) < x_{F_1 }$ and the order-1 periodic solution ${\bar x}$ of the system (2.1) is globally stable, suppose that the existence of a point $\tilde x_1^ + \in (\bar x, x_{F_1 }]$ yields $E(\tilde x_1^ +) \ge \tilde x_1^ +$. From the stability of a point ${\bar x}$, we know that there exists a point $\tilde x_2^ + \in (\bar x - \varepsilon, \bar x + \varepsilon)$ that yields $E^2 (\tilde x_2^ +) < \tilde x_2^ +$ for $\varepsilon$ sufficiently small. From the continuity of the Poincaré map $E(V)$, we learn that there exists at least one $\bar x' \in (\tilde x_1^ +, \tilde x_2^ +)$ such that $E(\bar x') = \bar x'$ holds, which contradicts our previous assumptions. Consequently, if Theorem 5.1 holds, $E^2 (x_0^ +) < x_0^ +$ holds for $\forall x_0^ + (\bar x, x_{F_1 }]$.

Theorem 5.2. In Case (B), the order-1 periodic solution of the system (2.1) is globally stable when $E(x_{K_2 }) < x_{K_2 }$ and $E^2 (x_0^ +) < x_0^ +$ for $\forall x_0^ + \in (\bar x, x_{K_2 }]$.

Proof. In accordance with Theorem 4.2, we get that when $E(x_{K_1 }) > x_{K_1 }$, the Poincaré map $E(V)$ has no fixed point in the domain of the definition, and when $E(x_{K_2 }) < x_{K_2 }$, there is a unique fixed point, so the fixed point $\bar x \in (0, x_{K_2 }]$. By the previous discussion, the Poincaré map $E(V)$ is monotonically decreasing in the interval $(0, x_{K_2 }]$ and $E^k (x_0^ +) = x_k^ +$. For any $x_0^ + \in (\bar x, x_{K_2 }]$, i.e., $x_{K_2 } \ge x_0^ + > \bar x$, it follows that $E(x_{K_2 }) \le E(x_0^ +) = x_1^ + < E(\bar x) = \bar x$ holds. If $E^2 (x_0^ +) < x_0^ +$, then we have that $x_{K_2 } > x_0^ + > x_2^ + > \bar x$. By further computation, we have

Thus, we get that $\mathop {\lim }\limits_{k \to \infty } x_{2k}^ + = \mathop {\lim }\limits_{k \to \infty } x_{2k + 1}^ + = \bar x$. This means that Theorem 5.2 holds if $E(x_{K_2 }) < x_{K_2 }$ and $E^2 (x_0^ +) < x_0^ +$ for $\forall x_0^ + \in (\bar x, x_{K_2 }]$.

Theorem 5.3. In Case (A), if $E(x_{F_1 }) < x_{F_1 }$ and $E^2 (x_{F_1 }) < x_{F_1 }$, the system (2.1) has a stable order-1 or order-2 periodic solution.

Proof. For any one point $P_0^ + (x_0^ +, y_0^ +) \in L_N$, where $x_0^ + > 0$ and $y_0^ + {{ > 0}}$, from the previous discussion, we have that ${\rm{E}}^{\rm{k}} {\rm{(}}x_0^ + {\rm{) = }}x_k^ +$. According to Theorem 4.1, we obtain the Poincaré map $E(V)$ that is increasing monotonically in the region $[x_{F_1 }, + \infty)$ and without fixed points. So, there is a point $q$ such that $x_q^ + < x_{F_1 }$ and $x_{q - 1}^ + > x_{F_1 }$; then, $x_q^ + {\rm{ = E(}}x_{q - 1}^ +) > E(x_{F_1 })$, i.e., $E(x_{F_1 }) < x_q^ + < x_{F_1 }$. By the monotonicity of the Poincaré mapping and condition $E^2 (x_{F_1 }) < x_{F_1 }$, we have that $E[E(x_{F_1 }), x_{F_1 }] = [E(x_{F_1 }), E^2 (x_{F_1 })] \subset [E(x_{F_1 }), x_{F_1 }].$ So we just focus on the periodic solutions for the interval $[E(x_{F_1 }), x_{F_1 }]$. Let $E(x_0^ +) = x_1^ + \ne x_0^ +$ and $E^2 (x_0^ +) = x_2^ + \ne x_0^ +$, which can be used to obtain the system (2.1) with order-1 or order-2 periodic solution. Depending on the placement of the initial point, we discuss the next four cases:

(ⅰ) $x_{F_1 } \ge x_2^ + > x_0^ + > x_1^ + \ge E(x_{F_1 })$, i.e., $x_{F_1 } \ge E^2 (x_0^ +) > x_0^ + > E(x_0^ +) \ge E(x_{F_1 })$. By the monotonicity of the Poincaré map $E(V)$, we have that $x_3^ + = E^3 (x_0^ +) < E(x_0^ +) = x_1^ +$ and $x_4^ + = E^4 (x_0^ +) > E^2 (x_0^ +) = x_2^ +$, i.e., $x_{F_1 } \ge x_4^ + > x_2^ + > x_0^ + > x_1^ + > x_3^ + > E(x_{F_1 })$. Applying mathematical induction and repeating the above process, we can obtain

(ⅱ) $x_{F_1 } \ge x_0^ + > x_2^ + > x_1^ + \ge E(x_{F_1 })$, then $x_{F_1 } \ge x_0^ + > E^2 (x_0^ +) > E(x_0^ +) \ge E(x_{F_1 })$. By the monotonicity of the Poincaré map $E(V)$, we have that $x_1^ + = E(x_0^ +) < E^3 (x_0^ +) = x_3^ +$ and $x_2^ + = E^2 (x_0^ +) > E^4 (x_0^ +) = x_4^ +$, i.e., $x_{F_1 } \ge x_0^ + > x_2^ + > x_4^ + > x_3^ + > x_1^ + \ge E(x_{F_1 })$. Furthermore, we get

(ⅲ) $x_{F_1 } \ge x_1^ + > x_2^ + > x_0^ + \ge E(x_{F_1 })$. Analogous to the previous discussion, we have

(ⅳ) $x_{F_1 } \ge x_1^ + > x_0^ + > x_2^ + \ge E(x_{F_1 })$. By a similar discussion we have

Accordingly, in Cases (ⅱ) and (ⅲ), we have that $\bar x \in (E(x_{F_1 }), x_{F_1 })$; thus, $\mathop {\lim }\limits_{k \to \infty } x_{2k + 1}^ + = \mathop {\lim }\limits_{k \to \infty } x_{2k + 2}^ + = \bar x$, i.e., there is a stable order-1 periodic solution for the system (2.1).

For Cases (ⅰ) and (ⅳ), there exists $\bar x_1, \bar x_2 \in (E(x_{F_1 }), x_{F_1 })$ such that $\mathop {\lim }\limits_{k \to \infty } x_{2k + 1}^ + = \bar x_1$ and $\mathop {\lim }\limits_{k \to \infty } x_{2k + 2}^ + = \bar x_2$, where $\bar x_1 \ne \bar x_2$. This implies that in both cases, the predator-prey system has a stable order-2 periodic solution. There is no order-$k$ $(k > 2)$ periodic solution for the system (2.1) ^[14].

6.   Numerical simulation and discussion

In this paragraph, we assign some values to the parameters to verify the theoretical consequences given earlier and analyze some dynamic behavior of the system (2.1).

We set $r = 1.1, \beta = 1.2, \eta = 0.63$, $\varepsilon = 0.1, \delta = 0.1$, $K = 1.2, \sigma = 0.2, \mu = 3$, $\tau = 1.8, \omega = 5.$ When the parameters $\alpha _1 = 1, \alpha _2 = 0$, the impulse line and the phase line become two direct lines that run parallel to the horizontal coordinate of the coordinate axis, which is comparable to the results on many of our prior studies (Figure 4(a)). For this situation, the threshold is controlled only by dependence on the size of the predator population density. When we modify the weighting factor for the action threshold, we can observe that the slope of the impulse and phase lines changes (Figure 4(b), (c)). On the other hand, under the control of an action threshold with predator population density and its rate of change, the system (2.1) can still be obtained with a stable order-1 periodic solution.

For Case (A), we set $r = 1.1, \beta = 1.23, \eta = 0.72, \varepsilon = 0.1, \delta = 0.1, K = 1.2, AT = 0.55, \sigma = 0.2, \mu = 3, \tau = 1.8, \omega = 5.$ By Theorem 5.1, the system (2.1) has a stable order-1 periodic solution when $y^* \le y_A^*$. We can look at Figure 5, where Figure 5(a) indicates that the system (2.1) has an order-1 stable periodic solution, and Figure 5(b), (c) indicate the time series plots for the prey and predator, respectively. For Case (B)(B2), let $r = 1.8, \beta = 1.26, \eta = 0.63, \varepsilon = 0.3, \delta = 0.1, K = 1.2, ET = 0.7, \sigma = 0.2, \mu = 3, \tau = 1.8, \omega = 5.$ When $E(x_{K_2 }) < x_{K_2 }$, we can know that the system (2.1) has a stable order-1 periodic solution, as shown in Figure 6. When $E(x_{K_1 }) > x_{K_1 }$, i.e., $r = 1.1, \beta = 1, \eta = 0.72, \sigma = 0.5, \mu = 0.8$, we can observe Figure 7 to obtain that after impulse control, the system (2.1) has no periodic solution, but the system solution stabilizes at a fixed value.

The trajectories of the system (2.1) obtained for various starting points in Cases (A) and (B)(B2) are shown in Figures 8 and 9, respectively. We can ascertain from Figures 8 and 9 that the trajectories from various starting spots converge to a stable order-1 periodic solution. In Figure 10, we let $r = 1.7, \beta = 1.2, \eta = 0.63, \varepsilon = 0.3, \delta = 0.1, K = 8, ET = 0.7, \sigma = 0.2, \mu = 3, \tau = 1.8, \omega = 5.$ At this point, we can ascertain from Figure 10 that system (2.1) has no periodic solution, but the trajectories from various starting points eventually converge to the same point and stabilize at that point.

7.   Conclusions

The state dependent impulsive semi-dynamical system, among non-smooth systems is one of the most discontinuous type of system; it has been studied in many fields, such as cancer and diabetes treatment, neuronal dynamics, HIV and infectious disease control, integrated pest management, neuronal dynamics, etc. In recent years, research on such systems has made substantial progress in terms of application, qualitative analysis, and analytical techniques. In this study, we have modeled predator-prey state impulse feedback control based on predator density and the rate of change, taking into account the capture of prey and release of predators, where the control point depends on whether the weights of the predator number and its growth rate reach ET. We have studied the dynamical behavior of the model comprehensively and analyzed the biological significance of the system (2.1).

First, the model was introduced and the significance of each parameter in the model was analyzed. The existence condition and stability of the equilibrium point of the model without impulse have been proved by applying the Jacobian matrix and Bendixson-Dulac Discriminative theorem. Second, the model of $E(V)$ was defined and the main properties of $E(V)$ were studied. Moreover, we discussed the existence and stability conditions of the periodic solutions. Finally, the theoretical results were verified through the use of numerical examples.

In this study, the monotonicity, continuity, immobility points, and polar values of system (2.1) were studied by using a Poincaré map. We have demonstrated the existence and stability of an order-1 periodic solution in the system (2.1). According to Figures 5–9, we find that the prey population density and predator population density remain in periodic oscillation. Although there is no periodic solution in Figure 10, we can see that the points originating from different initial points eventually converge to the same value. Therefore, under the control of the action threshold in this study, using the method of Poincaré map, and after implementing effective impulse control, we can get that the prey and predator populations maintain periodic oscillations, i.e., they are stable within a small interval, which means that the biological populations have reached a state of coexistence. This is of ecological and economic significance for those who study control strategies for predator-prey systems.

The novelty of this study is the use of an action threshold, which is a function of the predator population number and the current rate of predator development. The fixed threshold is a special case of the dynamic threshold, where the dynamic threshold is an extension of the fixed threshold. Under this action threshold, we use the state feedback control strategy of increasing the predator and capturing the prey when the predator density and rate of change decrease to a certain amount. The control methods and control models used in this study are more general, which allows the models to demonstrate more complex dynamical behaviors that are more consistent with the development of biological populations.

In the future, we will focus on the effects of parameter changes on the predator and prey system and on studying the mutual restrictions between populations.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The authors would like to thank the editor and anonymous referees for their valuable comments and suggestions which have led to improvement of the paper.

This study was partially supported by the National Natural Science Foundation of China (Grant Nos. 12261033).

Conflict of interest

The authors declare that they have no conflict of interest.