Some weighted estimates for the commutators of $p$-adic Hardy operator on two weighted $p$-adic Herz-type spaces

1.   Introduction

Nowadays, with the rapid development of network and information technology, the distance between people is shortened by the network. The common way of information transmission has also changed from the traditional face-to-face transmission to online social networks (OSN), such as Facebook, Twitter, etc. At the same time, the spread of inaccurate information, or rumors^[1,2], through OSN has become very rapid. The spread of rumors will bring economic losses and adverse political effects to the society^[3]. Therefore, it is of practical importance to effectively control the spread of rumors.

Scholars at home and abroad have conducted in-depth research on the spread of rumors on the Internet. In recent years, some scholars have used game theory to discuss the antagonistic game relationship between rumor and anti-rumor^[4,5,6,7]; some scholars have used graph convolution to study the rumor propagation model^[8,9]; some scholars have extracted the characteristics of user behavior from the big data in social networks and studied the rumor propagation law through deep learning algorithm^[10,11,12]; using biological models including infectious disease models to study the mechanism of rumor transmission is also a major research method^{[13,14,15,16,17]}.

When spreading information (whether rumor or truth) on social networks, users can post comments representing their own views under the topic. The direction of public opinion will affect the spread of rumors or truth. In view of this situation, this paper establishes a node-based rumor propagation model under the comment mechanism by using the infectious disease model theory. The main contributions of this paper are as follows:

● First, we establish a node-level rumor-truth mixed propagation model based on the comment mechanism, so as to measure the influence of comment on rumors.

● Secondly, on this basis, we model the rumor-truth mixed problem based on comments as an optimal control problem, which is called uncertain-rumor-truth-comment (URTC) model.

● Thirdly, we prove that the model has the optimal control and obtain the optimal system for solving the model.

● Fourthly, by solving the corresponding optimal system, some optimal control strategies are given.

● Finally, through the sensitivity analysis of the relevant parameters of comments, the influence of comments on rumor propagation is further discussed.

This work is conducive to better suppressing the spread of rumors. The main organization of this paper is as follows: In Section 2, we review some of the relevant work. In Section 3, we modeled the node-level URTC model for the rumor-truth propagation problem, and modeled the URTC problem into the optimal control problem. Section 4 makes a theoretical analysis of the optimal control problem and gives a strategy to control rumors through comments. Some optimal URTC strategies are given in Section 5. In Section 6, the influence of comments on rumor propagation is further revealed through the sensitivity analysis of parameters. The work is closed by Section 7.

2.   Related work

In this section, in order to illustrate the novelty of this work, we review the work related to this paper.

Pioneering research on rumor propagation based on infectious disease models was conducted in 1964, when the first classic rumor propagation model DK model was proposed by Daley and Kendal ^[18,19]. Later, some scholars improved the DK model for different network structures, and the common point of these models is to assume that the network structures are homogeneous. In fact, with the improvement of people's cognition of the Internet, empirical findings have shown that many real world networks are highly structured and heterogeneous since the end of last century. Under the guidance of this cognition, Zanette^[20,21] first proposed the rumor propagation model based on small-world network in 2001. In 2004, Moreno^[22] built a mathematical model based on rumor propagation in a scale-free complex network. Many researchers^{[23,24,25,26,27,28,29,30,31,32]} have conducted in-depth studies on rumor propagation in heterogeneous network structures.

Since 2009, some scholars have studied the spread of infectious diseases^[33,34,35], network security^[36,37,38], software security^[39,40,41] and other aspects based on the individual-level modeling method. Recently, some scholars have proposed a node-based rumor propagation model^[42,43,44] by using the modeling method based on individual level. Compared with the rumor propagation model on heterogeneous networks, the node-level rumor propagation model not only considers the statistical data of topological attributes of the underlying network, but also the entire network structure, so it deeply reflects the influence of specific network structure on rumor propagation. Inspired by the node-level rumor propagation model, this paper considers the influence of comments on rumor propagation. Once an individual or organization publishes information online, ordinary people cannot judge whether the information is true or false. People may believe and spread the information, whether it is rumor or not. In fact, publicizing the truth is the main way to suppress rumor. In addition to choosing their own attitudes and disseminating them, some people who are exposed to information also post comments on the Internet to support their views and positions, and these comments will also influence the subsequent positions of people who are newly exposed to information. In other words, comments have an important impact on rumor propagation. On this basis, we establish a mixed rumor-truth propagation model based on comments. And it is modeled as an optimal control problem.

3.   The modeling of URTC problem

In this section we consider the issue of rumor propagation on OSN with comments. Suppose that in the process of spreading rumors, some people will comment that represent their own views. And those comments may influence the opinions of those exposed to the rumor. This section is dedicated to this problem according to the following procedures: First, introduce the basic terms and symbols. Secondly, the node-level model of URTC rumor spreading model is established. Finally, the URTC problem is modeled as an optimal control problem.

3.1.   Terms and notations

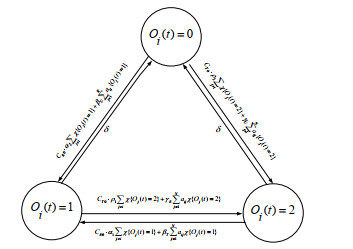
Assume that the number of nodes in the network is constant and the total number of users on the OSN is $N$, let $G = (V, E)$ denote the topology of this network. Where $V = (V_1, V_2, ..., V_N)$ represents the nodes of the network, $N$ is the number of nodes in the network. $E_{ij} = \{V_i, V_j\}\in E$ represents node $V_j$ can sent messages to node $V_i$, so G is a directed network. Where $A = (a_{ij})_{N\times N}$ represents the adjacency matrix of network $G$. When $a_{ij} = 1$, node $V_j$ can forward rumors or truth to node $V_i$ through the link. $a_{ij} = 0$ means that node $V_j$ cannot spread information to node $V_i$, whether it is rumors or truth.

Suppose that the rumor and the truth are spread in the network $G$ in the finite time horizon $[0, T]$. Assuming that at any time $t$ in the time horizon, the state of a node can only be one of three states: uncertain, rumor-spreading and truth-spreading. The uncertain state means that the node cannot make a choice, neither believes in rumor nor the truth, so no information will be spread. The state of rumor-spreading is to believe and spread rumor. The state of truth-spreading is the belief and transmission of truth. Let $O_i(t) = 0, 1$ and $2$ respectively indicate that node $V_i$ is an uncertain state, rumor-spreading and truth-spreading at time $t$. Let

In order to solve the problem of rumor propagation under the comment mechanism, we introduce the following hypotheses:

(1) Due to the influence of neighbor nodes who believe the rumor, an uncertain node $V_i$ becomes rumor-spreading with probability $\beta_U\sum\limits_{j = 1}^{N}a_{ij}\chi\{O_j(t) = 1\}$ on average.

(2) Due to the influence of neighbor nodes who believe the truth, an uncertain node $V_i$ becomes truth-spreading with probability $\gamma_U\sum\limits_{j = 1}^{N}a_{ij}\chi\{O_j(t) = 2\}$ on average.

(3) Due to the influence of neighbor nodes who believe the rumor, a truth-spreading node $V_i$ becomes rumor-spreading with probability $\beta_T\sum\limits_{j = 1}^{N}a_{ij}\chi\{O_j(t) = 1\}$ on average, $\beta_U\geq\beta_T$.

(4) Due to the influence of neighbor nodes who believe the truth, a rumor-spreading node $V_i$ becomes truth-spreading with probability $\gamma_R\sum\limits_{j = 1}^{N}a_{ij}\chi\{O_j(t) = 2\}$ on average, $\gamma_U\geq\gamma_R$.

(5) Due to the attenuation of memory, a rumor-spreading node becomes uncertain with probability $\delta$ on average.

(6) The average probability of comments supporting rumor posted on the network is $C_{R0}$.

(7) The average probability of comments supporting truth posted on the network is $C_{T0}$.

(8) Due to the influence of comments supporting the rumor, a truth-spreading node $V_i$ is transformed into rumor-spreading with probability $\alpha_1$ on average.

(9) Due to the influence of comments supporting the rumor, an uncertain node $V_i$ is transformed into rumor-spreading with probability $\alpha_2$ on average. Obviously, $\alpha_1\leq\alpha_2$.

(10) Due to the influence of comments supporting the truth, a rumor-spreading node $V_i$ is transformed into truth-spreading with probability $\rho_1$ on average.

(11) Due to the influence of comments supporting the truth, an uncertain node $V_i$ is transformed into truth-spreading with probability $\rho_2$ on average. Obviously, $\rho_1\leq\rho_2$.

The above assumptions are independent of each other, and the state transition diagram of the node is shown in Figure 1. In practice, parameters $\beta_U, \gamma_U, \beta_T, \gamma_R, \delta, C_{R0}, C_{T0}, \alpha_1, \alpha_2, \rho_1, \rho_2$ can be estimated from the information of the network.

Then the vector $O(t)$ represents the state of $N$ nodes in the network at time $t$. Since some nodes will also publish comments representing their own opinions while spreading rumor and truth, this causes the status of nodes to change over time. Let $U_i(t), R_i(t), T_i(t)$ denote the expected probabilities of node $V_i$ being uncertain, rumor-spreading and truth-spreading at time $t$, respectively.

Note that $U_i(t)+R_i(t)+U_i(t) = 1$. The vector

represents the expected state of node in the network at time $t$, where

3.2.   A rumor-truth model with comments mechanism

The rumor-truth hybrid with comments propagation model to be derived below conforms to the above hypothesis. The following system gives an equivalent form of the exact URTC model.

with the initial condition $\textbf{E}(0) = \textbf{E}_0$.

The system (3.5) may be written in system as

3.3.   The optimal control modeling of the URTC problem

Let $C(t) = (C_R(t), C_T(t)), 0\leq t\leq T$, consider $C(t)$ as the control variable of the URTC problem, where $C_R(t)$ represents the rumor control variable and $C_T(t)$ represents the truth control variable. The upper limit of this strategy is determined as shown in the following remarks:

Remark 3.1. The upper limit $\overline{C}_R$ of $C_R(t)$ is determined by basic human rights, and $C_R(t)$ is controlled on the basis of comments $C_{R0}$ spontaneously generated by rumor in the network, that is $0\leq C_R(t)\leq \overline{C}_R\leq 1$. When $C_R(t) = 0$, there is no human interference in rumor comments in the network. At this time, the comments supporting the rumor in the network are determined by the initial comments of the node. When $C_R(t) = 1$, comments supporting the rumor will disappear at time $t$.

Remark 3.2. The manual intervention to the comments supporting the truth takes the form of increasing the number of comments supporting the truth, denoted as $C_T(t)$. The upper bound $\overline{C}_T$ of $C_T(t)$ is determined by the cost of increasing comments that agree with the truth, and by the size of the network.

So we assume that the URTC strategy is

where $L[0, T]$ represents the set of all Lebesgue integrable functions defined on $[0, T]$^[45].

In order to solve the problem of rumor control with a comment mechanism, we first evaluate the loss caused by the negative impact of rumor. First, assuming that the unit loss caused by the spreading rumor node $V_i$ per unit time is a constant $\theta_{1i}$. Then the total loss caused by the spreading of rumor in the time horizon $[0, T]$ can be expressed as

The vector $\theta_1 = (\theta_{11}, \theta_{12}, ..., \theta_{1N})$ represents the unit loss caused by the rumor of each node.

Secondly, assuming that the unit cost of controlling the comments supporting rumor per unit time is $\theta_2$. The cost of controlling the comments supporting rumor in the time horizon $[0, T]$ can be expressed as

Finally, assuming that the unit cost of pushing the comments supporting truth per unit time is $\theta_3$. The scale of the number of artificially increased comments is $\zeta N$, where $N$ is the number of nodes in the network and $\zeta$ is the ratio of increased comments. The cost of pushing the comments supporting the truth in the time horizon $[0, T]$ can be expressed as

Remark 3.3. The parameter $\theta_1$ is estimated by the adverse social impact caused by the spread of rumor, and the parameter $\theta_2$ is estimated by deleting the comments supporting the rumor in the OSN; the parameter $\theta_3$ is estimated by sending or publishing comments on supporting the truth.

In summary, the expected loss of rumor spread is

where

Based on the above discussion and assumptions, this URTC problem is modeled as the following optimal control problem

The associated rumor spreading model can be recast in matrix notation as

We refer to this optimal control problem as the URTC* problem. This model can be described as the following 20-tuple problem:

4.   Theoretical study of the URTC* control problem

4.1.   Solvability of the URTC* problem

First, we first prove that this problem is an optimal control problem and can be solved. So we derive the following Lemma^[46]:

Lemma 4.1. The URTC^* problem is an optimal control if the following five conditions are held simultaneously.

(1) $\mathbb{C}$is convex and closed.

(2) There exists $C\in\mathbb{C}$ such that the system (3.13) is solvable.

(3) $\mathbf{f}_2(\mathbf{E}, C)$ is bounded by a linear function in $\boldsymbol{E}$.

(4) $\mathbf{F}(\mathbf{E}, C)$ is convex on $\mathbb{C}$.

(5) There exist $\rho > 1, d_1 > 0,$ and $d_2$ such that $\mathbf{F}(\boldsymbol{E}, C)\geq d_1\|C\|_2^\rho+d_2$.

Then we can conclude the following Theorem.

Theorem 4.1. This URTC* problem is an optimal control problem.

Proof. First, let $C(t) = (C_R(t), C_T(t))$ be a limit point of $\mathbb{C}$. Then there exists a sequence of points of $\mathbb{C}$, $C^{(n)}(t) = (C_R^{(n)}(t), C_T^{(n)}(t)), n = 1, 2, ...,$ that approaches $C(t)$. Since

Hence, $\mathbb{C}$ is closed. Let $C^{(1)}, C^{(2)}\in\mathbb{C}, 0 < \eta < 1, \hat{C} = (1-\eta)C^{(1)}+\eta C^{(2)}$. As $L[0, T]^2$ is a real vector space, we have $\hat{C}\in L[0, T]^2$ and $0\leq (1-\eta)C_R^{(1)}(t)+\eta C_R^{(2)}(t)\leq \overline{C}_R, 0\leq (1-\eta)C_T^{(1)}(t)+\eta C_T^{(2)}(t)\leq \overline{C}_T, 0\leq t\leq T.$ Hence, $\mathbb{C}$ is convex. Secondly, let $C^*(t) = (C_R^*(t), C_T^*(t)),$ then $C^*\in \mathbb{C}$. As $\textbf{f}_2(\textbf{E}, C^*)$ is continuously differentiable, it follows by the Continuation Theorem for Differentiable Systems^[47] that the corresponding state evolution state is solvable.

Thirdly, it follows from (3.13) that for $1\leq i\leq N$. As $U_i(t) = 1-R_i(t)-T_i(t),$ then we have

In inequality group (4.1),

Hence, $\textbf{f}_2(\textbf{E}, C)$ is bounded by a linear function in $\textbf{E}$.

Finally, $\textbf{F}(\textbf{E}, C)\geq0\geq(C_R^2(t)+C_T^2(t))-(\overline{C}_R^2+\overline{C}_T^2) = \|C\|_2^2-(\overline{C}_R^2+\overline{C}_T^2)$. Then there exists $d_1 = 1, \rho = 2, d_2 = -(\overline{C}_R^2+\overline{C}_T^2)$ such that $\textbf{F}(\textbf{E}, C)\geq d_1\|C\|_2^\rho+d_2$. By Lemma 4.1, the Theorem 4.1 is proved.

4.2.   The optimality system

According to the optimal control theory, the Hamilton function of the URTC* problem is

where $X(t) = (\lambda(t), \mu(t), \nu(t)) = (\lambda_1, \lambda_2, ..., \lambda_N, \mu_1, \mu_2, ..., \mu_N, \nu_1, \nu_2, ..., \nu_N)$ is the adjoint of $H$. We give the necessary condition for the optimal control of the URTC* problem as follows.

Theorem 4.2. Suppose $C = (C_R(t), C_T(t))$ is an optimal control of the URTC* problem (3.12), $\mathbf{E}$ is the solution to the associated rumor spreading model (3.13). Then there exists an adjoint function $X(t) = (\lambda(t), \mu(t), \nu(t))$ such that the following equation hold.

Moreover, let

Then, for $0\leq t\leq T$, we have

Proof. According to Pontryagin Minimum Principle^[46], there exists $(\lambda, \mu, \nu)$ such that

The first $3N$ equations in the system (4.3) follow by direct calculations. Since the terminal cost is unspecified and the final state is free, we have $\lambda(T) = \mu(T) = \nu(T) = 0.$ Based on Pontryagin Maximum Principle, we have

Equations (4.4)-(4.6) follow by direct calculations.

By optimal control theory, Eqs (3.12) and (4.3) constitute the optimality system for the URTC model. We refer to the control in each solution to the optimality system as a potential optimal control (POC) of URTC* problem. It is seen from Eqs (4.5) and (4.6) that the optimality system may have more than one POC.

5.   Examples of the potential optimal control

In the previous section, we introduced the notion of potential optimal control for the URTC model. In this section, we focus our attention on some examples of the potential control. First, in order to solve the problem of calculating the potential optimal control of the URTC model, we designed a POC algorithm, see Table 1: Algorithm POC. Here, POC is the acronym of the phrase "potential optimal control". Now solving the optimality system (3.13) and (4.4)-(4.6) by using Runge-Kutta and backward Runge-Kutta fourth order iterative procedure, where $K = 10^3$^[48,49]. The time computing complexity of Algorithm 1 is shown in Theorem 5.1. Suppose that the basic comment $C_0 = (C_{R0}, C_{T0}) = (0.1, 0.1)$ in the network. That is, the spontaneous comment ratio of network nodes at the initial moment. The control variables $C_R(t)$ and $C_T(t)$ are controlled on the basis of spontaneous comments.

Theorem 5.1. The time complexity of the Algorithm 1 is $O(TKN^2)$, where $N$ is the number of nodes, $T$ is the total number of controls the finite time horizon $[0, T]$.

Proof. According to the algorithms we give in the original version of our paper, the analysis of their time complexity is given as follows. Assume that we perform our Algorithm 1 in a social network graph $G(V, E)$ of $N$ users and $|E|$ connections. At time $t$, because solving each differential equation requires traversing the adjacency matrix of nodes. Therefore, the Runge-Kutta and backward Runge-Kutta fourth order iterative procedure has time complexity of $O(N^2)$. Because the maximum number of iterations of the Algorithm is $K$, and the number of control is $T$ in the finite time horizon $[0, T]$. Therefore, the time complexity of Algorithm 1 is $O(TKN^2)$.

In order to generate a large number of URTC examples, two types of networks are selected: Synthetic networks include scale-free networks and small-world networks; real networks include Email network, Facebook network and Twitter network. The principle of parameter selection follows Table 2. In addition, the influence of different values of parameters on loss cost under $C_{poc}$ will be discussed in Section 6 for the parameters estimated according to the actual situation in the network.

Experiment 1: Optimal control strategies in synthetic and real networks.

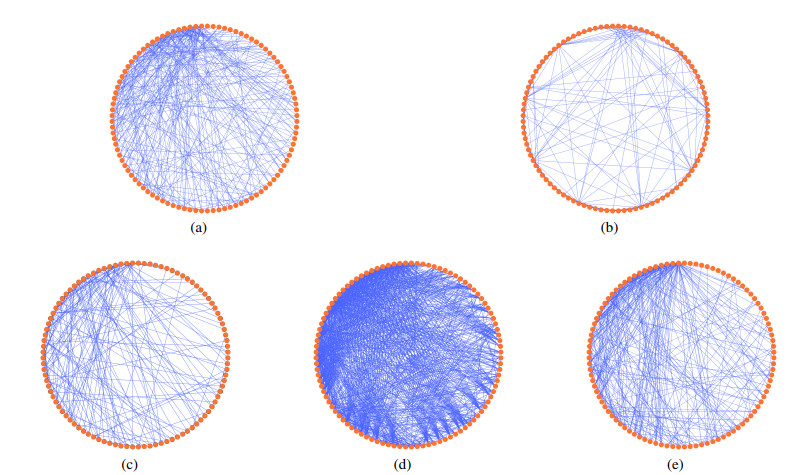
The synthetic network selects classic complex network, scale-free network^[52] and small-world network^[53]. We get a synthetic scale-free network $G_{SF}$ and a small-world network $G_{SW}$ with $N = 100$ nodes by software MATLAB, which is shown in Figure 2(a), (b). Let $A_{SF}$ and $A_{SW}$ denote the adjacency matrix of $G_{SF}$ and $G_{SW}$. Subnetworks of real networks such as Email, Facebook and Twitter are selected, and their nodes are set as $N = 100$. Their topological network graphs $G_{EM}, G_{FA}, G_{TW}$ are shown in Figure 2(c), (d), (e), and their corresponding adjacency matrices are $A_{EM}, A_{FA}, A_{TW}$.

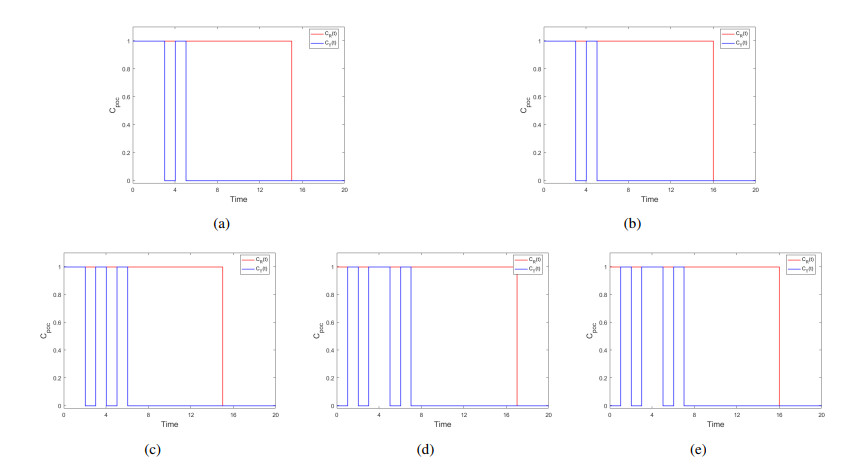
Suppose $\beta_U = 0.1, \beta_T = 0.05, \gamma_U = 0.08, \gamma_R = 0.05, \delta = 0.02$, $\overline{C}_R = \overline{C}_T = \theta_2 = \theta_3 = 1$, $\xi = 0.05, \alpha_1 = \rho_1 = 0.1, \alpha_2 = \rho_2 = 0.2$, $T = 20, \theta_1 = (1, ..., 1)$, $\textbf{E}_0 = (U_0, R_0, T_0) = (0.8, ..., 0.8, 0.1, ..., 0.1, 0.1, ..., 0.1)$. The optimal control $C_{poc}$ is obtained by solving the optimal system, as shown in Figure 3.

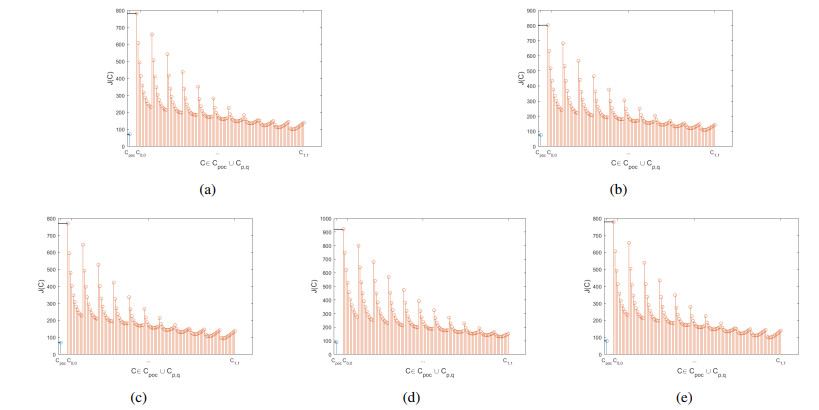
Experiment 2: The cost-effectiveness between $C_{poc}$ and $C_{p, q}$.

Suppose the parameters are the same as Experiment 1. Figure 4 shows the comparison of cost effectiveness between optimal strategy $C_{poc}$ and uniform control strategy $C_{p, q}$ for URTC* problem. In the uniform control strategy, $C_R = p, C_T = q$, where $p = (0, 0.1, 0.2, ..., 1), q = (0, 0.1, 0.2, ..., 1)$. It is seen that $C_{poc} < C_{p, q}$ for all $p, q$. $C_{poc}$ is superior to all the controls in both synthetic and real networks in terms of the cost effectiveness. In the above two experiments and 100 similar experiments, and in terms of cost-effectiveness, it is worth emphasizing that $C_{poc}$ outperforms all static controls in performance across all networks, confirming the optimality of $C_{poc}$.

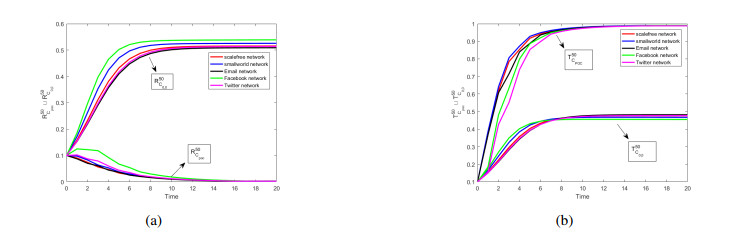
Experiment 3: The changes of node state under optimal control strategy $C_{poc}$.

Suppose the parameters are the same as Experiment 1. In terms of the effect of rumor control, the following numerical simulation experiments are carried out. Taking node No. 50 as an example, we compare the change curves of the expected probabilities of rumor-spreading and truth-spreading under optimal control and uncontrolled control in synthetic and real networks. Under the optimal control $C_{opc}$, along with the development of the time, rumor-spreading expected probability obviously decrease, truth expected probability obviously improved as shown in Figure 5. Among them, in Figure 5, It is clear that by controlling the comments we can make the rumor disappear and the probability of spreading the truth increase significantly.

6.   The impact of parameters on cost-effectiveness

In this section, we discuss the effect of the parameters related to comments on the expected cost-effectiveness under the optimal strategy through simulation experiments.

Experiment 4: The influence of spontaneous comments number $C_{R0}$ and $C_{T0}$ on rumor control.

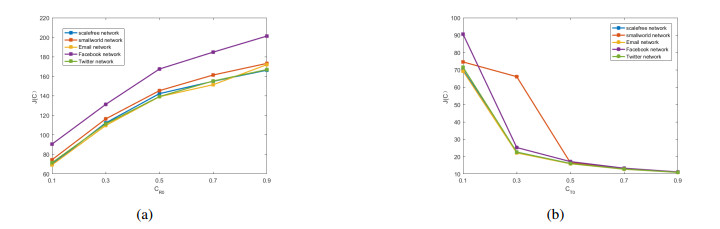
The parameter $C_{R0}$ represents the spontaneous comments in favor of rumor in the network, and $C_{T0}$ represents the spontaneous comments in favor of the truth in the network. Let $C_{R0} = {(0.1, 0.3, 0.5, 0.7, 0.9)}$, $C_{T0} = 0.1$ and other parameters are the same as Experiment 1. Figure 6(a) expressed the change of cost-effectiveness under $C_{poc}$ as $C_{R0}$ increases. Obviously, with the increase of $C_{R0}$, the cost-effectiveness increases sharply, because the number of nodes believing rumor increases significantly due to the large number of spontaneous comments. In this case, the loss caused by rumor increases, and the efforts to control rumor also increase, so the cost-effectiveness increases significantly. That is, when the spontaneous comment of the rumor is large enough, that is, when the rumor has developed into public opinion, the cost of controlling the rumor will increase sharply. Another case, when $C_{T0} = (0.1, 0.3, 0.5, 0.7, 0.9), C_{R0} = 0.1$ and other parameters are the same as Experiment 1. Figure 6(b) expressed the change of cost-effectiveness under $C_{poc}$ as $C_{T0}$ increase. When believe the truth of the initial comments increases, will cause a lot of nodes under the influence of public opinion to increase a lot believe the truth of the node, then the probability of rumor of nodes is greatly reduced at the same time. As can be seen from the Figure 6(b), when $C_{T0}$ is large enough, the cost-effectiveness caused by rumor becomes sharply smaller. This is because rumors will die out without any control.

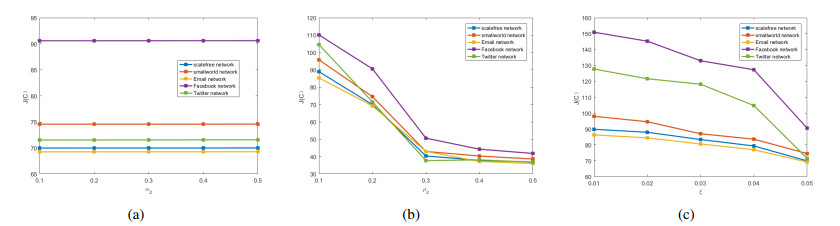
Experiment 5: The effect of parameters $\alpha_2$ and $\rho_2$ on the cost-effectiveness.

Let (1) $\alpha_2 = (0.1, 0.2, 0.3, 0.4, 0.5), \rho_2 = 0.2$; (2)$\rho_2 = (0.1, 0.2, 0.3, 0.4, 0.5), \alpha_2 = 0.2$, and other parameters are the same as Experiment 1. Figure 7 expressed the change of cost-effectiveness under $C_{poc}.$ As shown in Figure 7(a), it is worth noting that at this time, $C_{R0} = C_{T0} = 0.1$ for the spontaneous comments, that is, when the rumor does not develop into public opinion, the cost of rumor control will hardly increase when $\alpha_2$ increases. Combined with the conclusion of Experiment 4, it can be seen that once rumor develop into public opinion, the loss of rumor control will increase greatly. Therefore, rumor control must be carried out at the early stage of rumor development. As shown in Figure 7(b), when $\rho_2$ increases, the nodes that contact the comments of the truth position are more easily transformed into nodes that spread the truth. When $\rho_2$ increases to a certain degree, there is no need to control the rumor, and the rumor will naturally die out, so the cost-effectiveness caused by rumor becomes smaller.

Experiment 6: The effect of parameters $\xi$ on the cost-effectiveness.

Let $\xi = (0.01, 0.02, 0.03, 0.04, 0.05)$, and other parameters are the same as Experiment 1. $\xi$ indicates the percentage of invested comments that support the truth. This value is often determined by the rumor control budget. In fact, it is obvious that the higher the ratio of input to support the truth, the higher the cost consumed, but the higher the ratio of input, the influence of these comments will lead to the increase of the nodes spreading the truth, so as to achieve the purpose of rumor control. As can be seen from Figure 7(c), with the increase of $\xi$, the cost-effectiveness decreases obviously.

7.   Conclusions

In this paper, a rumor-truth hybrid propagation node-level model based on comment mechanism is introduced to minimize the impact of rumor by developing comment strategies. On this basis, we model the original problem as the optimal control problem. Finally, we derive the optimal system for solving the optimal control problem. In the future, there are still many problems to be solved. In the node-level rumor propagation model, it is also worth studying how to select some nodes to control rumor, locate the location of rumor propagation sources and the influence of network community structure on rumor propagation.

Acknowledgements

This work is supported by the National Natural Science Foundation of China under Grant Nos.61807028, 61772449, 61572420 and 61802332, the Natural Science Foundation of Hebei Province China under Grant No. F2019203120. The authors are grateful to valuable comments and suggestions of the reviewers.

Conflict of interest

All authors declare no conflicts of interest in this paper.