Bifurcation results of positive solutions for an elliptic equation with nonlocal terms

1.   Introduction

In this paper, we consider the elliptic problem with nonlocal terms

where $\Omega$ is a bounded domain of ${\mathbb{R}}^{N}$ with a smooth boundary, $N \geq 2$; $n$ is the outward unit normal to $\partial \Omega$; $m(x)$, $h(x)\in {C^\alpha }({\bar \Omega })$ for some $\alpha \in (0, 1)$ and $m(x)$, $h(x)$ may change sign in $\Omega$; $p, \; \beta > 1$ and $p < \frac{{N + 2}}{{N - 2}}$ for $N\geq3$, $\lambda \in \mathbb{R}$ is a parameter.

Many physical phenomena were formulated into nonlocal mathematical models ^{[1,2,3,11,12]} and studied by many authors. For example, J. Bebernes and A. Bressan ^[11] studied an ignition model similar to (1.1) for a compressible reactive gas which is a nonlocal reaction-diffusion equation. In ^[11], $u$ is the temperature perturbation of the gas and nonlocal term is due to the compressibility of the gas. Subsequently, some researchers ^[2,3,12] discussed the parabolic problems related to the equation

This type of problem is frequently encountered in nuclear reaction process, where it is known that the reaction is very strong, say like $f(x, u) = \lambda m(x)u + h(x){u^p}$ with $p > 1$ and constant functions $m(x)$ and $h(x)$, but the rate with respect to this power is unknown, say like $g\left({\int_\Omega {{u^\beta }} } \right) = \int_\Omega {{u^\beta }}$. The above mathematical problem can also be used to population dynamics and biological science where the total mass is often conserved or known, but the growth of a certain cell is known to be of some form (see ^[12]). Thus, the problem (1.1) is worthy to be considered.

Mathematically, the problem (1.1) combines local and nonlocal terms. It is well known ^[2,3] that the authors discussed that the case $m(x) = 0$, $h(x) \equiv {h_0} < 0$, $\beta > 1$ and $p \ge 1$. In two articles, the parabolic problem related to the equation was studied and the authors showed that the value $p = \beta$ represents a critical blow-up exponent. They proved that if $\beta > p$ or $\beta = p$ and $h_0 > - \left| \Omega \right|$, the blow-up phenomenon can occur in finite time. If $\beta < p$ or $\beta = p$ and $h_0 \le - \left| \Omega \right|$, all the solutions are global and bounded. The authors also proved the existence of positive solution for $h_0$ small in the particular case $h_0 < 0$, $p > \beta > 1$. In ^[1], F. Corr$\hat{\text{e}}$a and A. Su$\acute{\text{a}}$rez made a further study for the problem and proved the existence, uniqueness, stability and asymptotic properties of positive solutions for some values of $p \geq 1$ and $\beta > 0$.

We want to further consider the global bifurcation structure of the positive solutions set of the problem (1.1) when the function $m(x)$ and $h(x)$ are nonconstant functions because for general function $h(x)$, especially sign-changing function, comparing with the local elliptic equation, we see that many methods that prove the boundedness of positive solutions cannot be used in nonlocal elliptic equation, such as the extremum principle, parameter control. Finally, we can obtain the existence, multiplicity and nonexistence of the positive solution for the problem (1.1) when a bounded connected branch of the positive solutions set is established by the global bifurcation theory.

In an early paper, K. J. Brown ^[4] studied the local and global bifurcation of the semilinear elliptic boundary value problem

where $1 < \gamma < \frac{{N + 2}}{{N - 2}}$, $m(x)$, $b(x)$ may change sign in $\Omega$. The cases where $\int_{\Omega }{m(x)dx}\ne 0$ and $\int_{\Omega }{m(x)dx} = 0$ were discussed respectively and the author concluded that there are continua of positive solutions of (1.2) connecting $\lambda = 0$ to the other principal eigenvalue for $\int_{\Omega }{m(x)dx}\ne 0$ when $m(x)$ and $b(x)$ are under suitable conditions. It was also showed that the closed loops of positive solutions occur naturally and properties of these loops are investigated.

In this paper, we are interested in the problem (1.1), namely, the problem (1.2) added a nonlocal term. We want to investigate whether the local and global structures of positive solutions set for the problem (1.1) have similar properties to the problem (1.2). We also investigate sufficient conditions for a bounded continuum of positive solutions. In Theorem 2.2, we see that the direction of bifurcation curve is related to $\beta$ and $p$. In Theorem 3.1, we get a priori bound of positive solution when $m(x)$ is under suitable conditions and $\beta > \max \left\{ {p, {{N(p - 1)} \mathord{\left/ {\vphantom {{N(p - 1)} 2}} \right. } 2}} \right\}$ by using upper and lower solution method, blow-up technique and boot-strapping method. Moreover, another way of proving boundedness shows that the priori bound still exists when $\beta > \max \left\{ {p, {{N(p - 1)} \mathord{\left/ {\vphantom {{N(p - 1)} 2}} \right. } 2}} \right\}$ vanishes.

Before proceeding to the study of local and global nature of positive solutions, we need to introduce some notations. If $u > 0$ in $\Omega$, we say $u$ is a positive solution of the problem (1.1). $(\lambda, u)$ is called a nonnegative solution of the problem (1.1) if $u$ is a nonnegative solution of the problem (1.1) with $\lambda$. Obviously, $(\lambda, 0)$ is a nonnegative solution of the problem (1.1), we say it is a trivial solution.

To investigate the bifurcation of problem (1.1) at the trivial solution $(\lambda, 0)$, we discuss the linear eigenvalue problem

where $m(x)$ changes sign in $\Omega$. According to ^[5], we have the following results.

(i) If $\int_\Omega {m < 0}$, the problem (1.3) has the principal eigenvalues ${\lambda _ + } > 0$ and ${\lambda _0} = 0$.

(ii) If $\int_\Omega {m > 0}$, the problem (1.3) has the principal eigenvalues ${\lambda _ - } < 0$ and ${\lambda _0} = 0$.

(iii) If $\int_\Omega {m = 0}$, the problem (1.3) has the unique principal eigenvalue ${\lambda _0} = 0$.

The usual norms of the space ${L^p}(\Omega)$ for $p \in [1, \infty)$ and $C({\bar \Omega })$ are, respectively,

Let

We use the following hypothesis.

$({{\rm{H}}_1}) \; \Lambda = \left\{ {u \in H_0^1(\Omega _ + ^h):\int_{\Omega _ + ^h} {m{u^2}} > 0} \right\} \neq \varnothing$.

If $m(x)$ changes sign in $\Omega _ + ^h$ and $({{\rm{H}}_1})$ holds, then the equation

has unique positive principal eigenvalue ^[5,6].

We have the following main global results of positive solutions in two cases where $\int_{\Omega }{m} < 0$ and $\int_\Omega m > 0$ by using priori bounds, global bifurcation theory.

Theorem 1.1. Assume $\int_\Omega m < 0$ and

where ${\varphi _1}$ is the positive eigenfunction of ${\lambda _+}$. Then there exists a continuous curve $\left({\lambda (s), u(s)} \right)$ of $s \in (0, \varepsilon)$ such that $\left({\lambda (0), u(0)} \right) = ({\lambda _ + }, 0), \; \lambda (s) > {\lambda _ + }$, $\left({\lambda (s), u(s)} \right)$ are positive solutions of the problem (1.1), and for any positive solution $(\lambda, u)$ of the problem (1.1) in a neighborhood of $({\lambda _ + }, 0)$, we have $(\lambda, u) = \left({\lambda (s), u(s)} \right)$.

Moreover, if $m(x)$ changes sign in $\Omega _ + ^h$ and $({\rm{H}}_1)$ holds, then the connected branch ${C^ + }$ of positive solutions set containing $\left({\lambda (s), u(s)} \right)$ satisfies the following conclusions.

(i) The projection of ${C^ + }$ on ${\lambda }$-axis is bounded, that is,

More generally, there is no positive solution of the problem (1.1) for any sufficiently large $\left| \lambda \right|$.

(ii) If $(\lambda, u) \in {C^ + }$, then $u$ is bounded in ${C}(\bar \Omega)$.

(iii) The closure $\overline {{C^ + }}$ of ${C^ + }$ in $\mathbb{R} \times {C}(\bar \Omega)$ satisfies

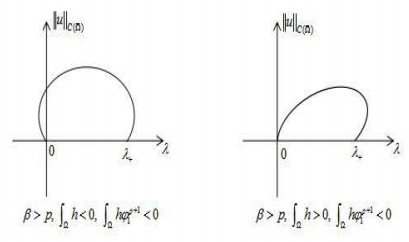
The assertions of Theorem 1.1 may be illustrated by the bifurcation diagram shown in Figure 1.

Remark 1.1. (i) Theorem 1.1 shows the conditions that the connected branch is supercritical at $\left({{\lambda _ + }, 0} \right)$. In fact, according to Theorem 2.2, we obtain the conditions that the connected branch is supercritical or subcritical at $(0, 0)$. In Figure 1, it is clear that if $\beta > p$, $\int_\Omega h < 0$ (resp. $\beta > p$, $\int_\Omega h > 0$), the connected branch at $(0, 0)$ is subcritical (resp. supercritical). Furthermore, by using Rabinowitz global bifurcation theory, we have that ${C^ + }$ bifurcates from $({\lambda _ + }, 0)$ and backs to $(0, 0)$.

(ii) Comparing with the results of ^[4], we see that directions of bifurcation curve depend on not only the sign of $\int_\Omega m$ and ${h\varphi _1^{p + 1}}$ but also the relationship of $\beta$ and $p$. In Theorem 1.1, we only show the case of $\beta > p$, while the cases of $\beta < p$ and $\beta = p$ can also be listed.

(iii) According to Theorem 1.1, we can obtain the existence, multiplicity and nonexistence of positive solutions for the problem (1.1). For example, the conditions of Theorem 1.1 hold and $\int_\Omega h < 0$, then there exist constants $\sigma _1 < 0 < \lambda _ + < \sigma _2$, such that

$\bullet$ the problem (1.1) has at least one positive solution for $\lambda \in [0, {\lambda _ + }]$;

$\bullet$ the problem (1.1) has at least two positive solutions for $\lambda \in (\sigma _1, 0) \cup ({\lambda _ + }, \sigma _2)$.

$\bullet$ the problem (1.1) has no positive solution for $\lambda \in (-\infty, \sigma _1) \cup (\sigma _2, +\infty)$.

These results are clearly shown in Figure 1.

Similarly, we have the global bifurcation of the positive solutions set for $\int_\Omega m > 0$.

Theorem 1.2. Assume $\int_\Omega m > 0$ and

where ${\varphi _1}$ is the positive eigenfunction of ${\lambda _-}$. Then there exists a continuous curve $\left({\lambda (s), u(s)} \right)$ of $s \in (0, \varepsilon)$ such that $\left({\lambda (0), u(0)} \right) = ({\lambda _ - }, 0), \; \lambda (s) < {\lambda _ - }$, $\left({\lambda (s), u(s)} \right)$ are positive solutions of the problem (1.1), and for any positive solution $(\lambda, u)$ of the problem (1.1) in a neighborhood of $({\lambda _ - }, 0)$, we have $(\lambda, u) = \left({\lambda (s), u(s)} \right)$.

Moreover, if $m(x)$ changes sign in $\Omega _ + ^h$ and $({\rm{H}}_1)$ holds, then the connected components ${C^ + }$ of positive solutions set containing $\left({\lambda (s), u(s)} \right)$ satisfies the claims (i), (ii) of Theorem 1.1 and the closure $\overline {{C^ + }}$ of ${C^ + }$ in $\mathbb{R} \times {C}(\bar \Omega)$ satisfies

The assertions of Theorem 1.2 may be illustrated by the bifurcation diagram shown in Figure 2.

Next, we consider the case $\int_\Omega m = 0$. We shall then study the global bifurcation of positive solutions for the problem (1.1) by the approximation method. Let ${m_\varepsilon }(x) = m(x) - \varepsilon$ for $\varepsilon > 0$, we have the following conclusions.

Theorem 1.3. Assume $\int_\Omega m = 0$, $p = 2$ or $3$, $m(x)$ changes sign in $\Omega _ + ^h$ and ${\rm{(}}{{\rm{H}}_1})$ holds. If

then there exists a connected components $C^ +$ of positive solutions set for the problem (1.1), which bifurcates from the origin and backs to the origin in $\lambda$-norm plane, namely, the closure $\overline {C ^ + }$ of $C^ +$ in $\mathbb{R} \times C(\bar \Omega)$ is a closed loop.

Remark 1.2. For the case $\int_\Omega m = 0$, the hypotheses for the Crandall and Rabinowitz theorem are no longer satisfied, and we use the Lyapunov-Schmidt technique to investigate how bifurcation occurs at $(\lambda, u) = (0, 0)$. Moreover, comparing with the global bifurcation results of ^[4], we see that the relationship of $p$ and nonlocal term power $\beta$ also has influence on the continuum.

The assertions of Theorem 1.3 may be illustrated by the bifurcation diagram shown in Figure 3.

The rest of this article is organized as follows. In Section 2, we discuss the local properties of positive solutions set in the cases where $\int_{\Omega }{m}\ne 0$ and $\int_{\Omega }{m} = 0$ by using the local bifurcation theory, Liapunov-Schmidt reduction technique. In Section 3, we show that a priori estimate of positive solutions by using the blow-up technique, global bifurcation theory and upper and lower solution. In Section 4, we complete the proof of main results in two cases.

2.   Local bifurcation results

Let's investigate local bifurcation in the cases where $\int_\Omega m \ne 0$ and $\int_\Omega m = 0$, respectively.

2.1.   Local bifurcation when $\int_\Omega m \ne 0$

If $\int_\Omega m < 0$, let ${\lambda _1} = {\lambda _ + }$ or ${\lambda _0}$; if $\int_\Omega m > 0$, let ${\lambda _1} = {\lambda _ - }$ or ${\lambda _0}$. Let ${\varphi _1}$ be the positive eigenfunction of ${\lambda _1}$. If ${\lambda _1} = 0$, ${\varphi _1}$ is a constant and we take ${\varphi _1} = 1$. Let $0 < \varepsilon \ll 1$ be a constant. We have the following result.

Theorem 2.1. Assume $\int_\Omega m \ne 0$, then there exists a bifurcation curve $\left({\lambda (s), u(s)} \right)$ of positive solutions of the problem (1.1) at $\left({{\lambda _1}, 0} \right)$ parameterized by $s \in (0, \varepsilon)$, which satisfies

Here, $\gamma (0) = 0$, $z(0) = 0$. $\gamma (s)$ and $z(s)$ is analytic at $s = 0$.

Proof. We define the mapping

where $X = \left\{ {u \in {C^{2 + \theta }}(\Omega):\frac{{\partial u}}{{\partial n}} = 0, x \in \partial \Omega } \right\}$.

For any $w \in X$, we have

then

Thus, we have

The range of ${F_u}({\lambda _1}, 0)$ is $R\left({{F_u}({\lambda _1}, 0)} \right) = \left\{ {u \in {C^\theta }\left(\Omega \right):\int_\Omega {u{\varphi _1}} = 0} \right\}$, so

Next, we prove

Since ${F_{\lambda u}}({\lambda _1}, 0)[{\varphi _1}] = m(x){\varphi _1}$, we have

(i) if ${\lambda _1} = 0$, then ${\varphi _1} = 1$ and $m(x){\varphi _1} \notin R\left({{F_u}({\lambda _1}, 0)} \right)$;

(ii) if ${\lambda _1} \ne 0$, then $\int_\Omega {{{\left| {\nabla {\varphi _1}} \right|}^2}} = {\lambda _1}\int_\Omega {m\varphi _1^2} > 0$, namely $\int_\Omega {m\varphi _1^2} \ne 0$. Thus, we have $m(x){\varphi _1} \notin R\left({{F_u}({\lambda _1}, 0)} \right)$.

Hence, we get (2.2). By virtue of the Crandall-Rabinowitz local bifurcation theory, we obtain Theorem 2.1.

Next, we discuss the direction of bifurcation.

Theorem 2.2. Assume $\int_\Omega m \ne 0$. $\left({\lambda (s), u(s)} \right)$ for $s \in (0, \varepsilon)$ is a bifurcation curve of positive solutions obtained by Theorem 2.1, then we have the following conclusions.

(1) ${\lambda _1} = 0$.

(i) $\beta = p$, then

If $|\Omega {|^2} + \int_\Omega h$ and $\int_\Omega m$ have same (resp. opposite) sign, then the bifurcation curve at $({\lambda _1}, 0)$ is subcritical (resp. supercritical).

(ii) $\beta < p$, then

If $\int_\Omega m > 0 \; (resp. < 0)$, then the bifurcation curve at $({\lambda _1}, 0)$ is subcritical (resp. supercritical).

(iii) $\beta > p$, then

If $\int_\Omega h$ and $\int_\Omega m$ have same (resp. opposite) sign, then the bifurcation curve at $({\lambda _1}, 0)$ is subcritical (resp. supercritical).

(2) ${\lambda _1} \ne 0$.

(i) $\beta = p$, if $\int_\Omega {h\varphi _1^{p + 1}} + \int_\Omega {{\varphi _1}} \int_\Omega {\varphi _1^p}$ and $\int_\Omega m$ have opposite (resp. same) sign, then the bifurcation curve at $({\lambda _1}, 0)$ is subcritical (resp. supercritical).

(ii) $\beta < p$, if $\int_\Omega {{\varphi _1}} \int_\Omega {\varphi _1^\beta }$ and $\int_\Omega m$ have opposite (resp. same) sign, then the bifurcation curve at $({\lambda _1}, 0)$ is subcritical (resp. supercritical).

(iii) $\beta > p$, if $\int_\Omega {h\varphi _1^{p + 1}}$ and $\int_\Omega m$ have opposite (resp. same) sign, then the bifurcation curve at $({\lambda _1}, 0)$ is subcritical (resp. supercritical).

Proof. Since $\left({\lambda (s), u(s)} \right)$ is a positive solution of the problem (1.1), we have

then

Multiplying the Eq (2.3) by $\varphi _1$, integrating in $\Omega$, and using the Green formula, it follows that

(i) If $\beta = p$, we get

So

(ii) If $\beta < p$, we get

So

(iii) If $\beta > p$, we get

So

Since $\int_\Omega {m\varphi _1^2}$ and $\int_\Omega m$ have opposite sign, then we get Theorem 2.2.

2.2.   Local bifurcation when $\int_\Omega m = 0$

If $\int_\Omega m = 0$, (2.2) doesn't work, then the hypotheses for the Crandall and Rabinowitz theorem are no longer satisfied. However we can use the Lyapunov-Schmidt technique to investigate how bifurcation occurs.

Assume $u \in X$ is the solution of the problem (1.1), let $u = s + w$, where $s$ is a constant and $\int_\Omega w = 0$. Let $Q$ be the projection of $X$ onto $W$, where $W = \left\{ {w \in X, \int_\Omega w = 0} \right\}$. Then $w = Q[u] = u - \frac{1}{{\left| \Omega \right|}}\int_\Omega u$, so $u = s + w$ is the solution of the problem (1.1) if and only if

The condition

implies that

The condition

implies that

We consider $F(\lambda, s, w) = 0$. Here $F: \mathbb{R}\times \mathbb{R} \times W \to W$,

Note that $F(0, 0, 0) = 0$, ${F_w}(0, 0, 0)w = - \Delta w$: $W \; \to \; W$ is homeomorphism, by using implicit function theorem, there exists a unique solution $w = w(\lambda, s)$ of the equation $F(\lambda, s, w) = 0$ around $(\lambda, s, w) = (0, 0, 0)$, being analytic at $(0, 0)$ and having the condition $w(0, 0) = 0$.

Since $W$ is complete, so $w$ satisfies $\int_\Omega {\frac{{{\partial ^k}w}}{{\partial {s^{k - l}}\partial {\lambda ^k}}}(0, 0)} = 0$, namely $\frac{{{\partial ^k}w}}{{\partial {s^{k - l}}\partial {\lambda ^k}}}(0, 0) \in W$. We substitute $w = w(\lambda, s)$ for (2.5), then

where $(\lambda, s)$ is in a neighborhood of $(0, 0)$ and $\Phi (\lambda, s)$ is analytic at $(0, 0)$.

Let ${w_m}$ be the solution of the problem

We have the following conclusions.

Theorem 2.3. Assume $\int_\Omega m = 0$, $p = 2$ or $3$. If $\beta = p$, let $\left| \Omega \right| + \int_\Omega h < 0$; if $\beta > p$, let $\int_\Omega h < 0$. Then there exists a continuous curve $\left({\lambda (s), u(s)} \right)$ of $s \in (0, \varepsilon)$ such that $\left({\lambda (0), u(0)} \right) = (0, 0)$, $\left({\lambda (s), u(s)} \right)$ are positive solutions of the problem (1.1), and for any positive solution $(\lambda, u)$ of the problem (1.1) in a neighborhood of $(0, 0)$, we have $(\lambda, u) = \left({\lambda (s), u(s)} \right)$. Moreover, if $\beta = p$, we have

If $\beta > p$, we have

Proof. We shall solve that $\Phi (\lambda, s) = 0$ by considering the Taylor expansion of $\Phi$ at $(\lambda, s) = (0, 0)$. Since $w(0, 0) = 0$, we have $\Phi (0, 0) = 0$. From $F(\lambda, s, w) = 0$, we can calculate the partial derivative of $w = w(\lambda, s)$ with respect to $\lambda$ and $s$ at $(0, 0)$ respectively.

Calculating derivative of $F(\lambda, s, w) = 0$ with respect to $\lambda$, when $\lambda = 0$ and $s = 0$, we have

So ${w_\lambda }(0, 0)$ is a constant. By virtue of $\frac{{{\partial ^k}w}}{{\partial {s^{k - l}}\partial {\lambda ^k}}}(0, 0) \in W$, we get ${w_\lambda }(0, 0) = 0$. Similarly, we have

Calculating derivative of $F(\lambda, s, w) = 0$ with respect to $s$, when $\lambda = 0$ and $s = 0$, we get

where ${w_p}$ is the solution of the equation

Moreover, we have

Next, we calculate partial derivative of $\Phi (\lambda, s)$ with respect to $\lambda$ and $s$ at $(0, 0)$ respectively. By direct calculations, we have

(i) $\beta = p$,

(ii) $\beta > p$,

(iii) $\beta < p$,

Moreover, we have

Therefore, the Taylor expansion of $\Phi$ at $(0, 0)$ is $\Phi (\lambda, s) = s\psi (\lambda, s)$.

(1) $p = 2$.

(i) If $\beta = 2$, then

(ii) If $\beta > 2$, then

(2) $p = 3$.

(i) If $\beta = 2$, then

(ii) If $\beta = 3$, then

(iii) If $\beta > 3$, then

For (1) (i), we note that ${\psi _s}(0, 0) = \left| \Omega \right| + \int_\Omega h < 0$, and that by using implicit function theorem, there exists a unique solution $s = s(\lambda)$ of the equation $\psi (\lambda, s) = 0$ around $(0, 0)$, which satisfies

So

Moreover, we have

Therefore, combining the above two equations, we obtain (2.6).

For (1) (ii), ${\psi _s}(0, 0) = \int_\Omega h < 0$, using a similar argument as that of (1) (i), we have

For (2) (i), since $\left| \Omega \right| > 0, \; \int_\Omega {{{\left| {\nabla {w_m}} \right|}^2}} > 0$, so the problem (1.1) is no positive solution in the neighborhood of $(0, 0)$.

For (2) (ii), since

by using the Morse lemma, we see that for any $s > 0$, $\psi (\lambda, s) = 0$ has a unique solution $s = s(\lambda)$ in a neighborhood of $(0, 0)$ and we have

So we get the conclusion.

For (2) (iii), since

using a similar argument as that of (2) (ii), we get

3.   A priori estimate

We first prove that under the suitable conditions, the problem (1.1) has no positive solution for any sufficiently large $\left| \lambda \right|$. More precisely, we have the following results.

Proposition 3.1. Assume that $m(x)$ changes sign in $\Omega _ + ^h$, $({{\rm{H}}_1})$ holds and $\left({\lambda, u} \right)$ is a positive solution of the problem (1.1). Then $\lambda \in (\lambda _1^ -, \lambda _1^ +)$, where $\lambda _1^ - < 0$ and $\lambda _1^ + > 0$ are the principal eigenvalue of the equation

Proof. If $(\tilde \lambda, \tilde u)$ is a positive solution of the problem (1.1), then

thus, we have

It follows that the principal eigenvalue ${\mu _1}({\tilde \lambda })$ of the eigenvalue problem

is positive. Then $\lambda _1^ - < \tilde \lambda < \lambda _1^ +$.

Assume $m(x)$ changes sign in $\Omega _ + ^h$, $({{\rm{H}}_1})$ holds. For any $\lambda \in \left({\lambda _1^ -, \lambda _1^ + } \right)$, ${e_\lambda }$ is the unique positive solution of the equation

We have the following lemma.

Lemma 3.1. Assume $m(x)$ changes sign in $\Omega _ + ^h$, $({{\rm{H}}_1})$ holds and $(\lambda, u)$ is a positive solution of the problem (1.1). Then

Proof. If $(\lambda, u)$ is a positive solution of the problem (1.1), then $\lambda \in \left({\lambda _1^ -, \lambda _1^ + } \right)$, and we have

so

Thus, we have $\frac{u}{{\int_\Omega {{u^\beta }} }} \ge {e_\lambda }$, namely, $u \ge {e_\lambda }\int_\Omega {{u^\beta }}$ for $x \in \Omega _ + ^h$.

We will use the method of Gidas-Spruck ^[7] to discuss the priori estimate of positive solutions.

Lemma 3.2. Assume $m(x)$ changes sign in $\Omega _ + ^h$, $({{\rm{H}}_1})$ holds and $\left\{ {({\lambda _k}, {u_k})} \right\}$ is a sequence of positive solutions of the problem (1.1) with ${\left\| {{u_k}} \right\|_{C\left({\bar \Omega _ + ^h} \right)}} \to \infty$ as $k \to \infty$. Then there exists a constant $C > 0$ such that ${\left\| {{u_k}} \right\|_{C\left({\bar \Omega _ + ^h} \right)}} \le Ct_k^{\frac{1}{p}}$ for sufficiently large $k$, where ${t_k} = \int_\Omega {u_k^\beta }$.

Proof. If $({\lambda _k}, {u_k})$ is a positive solution of the problem (1.1), then ${\lambda _k} \in \left({\lambda _1^ -, \lambda _1^ + } \right)$. Choose ${x_k}\in\bar \Omega _ + ^h$ such that

and let ${M_k} = {u_k}({x_k})$. Assume ${M_k}t_k^{ - \frac{1}{p}} \to \infty$ as $k \to + \infty$. Take a change of variables

where ${\rho _k} = M_k^{\frac{{p - 1}}{2}}$, $y \in {\Omega _k}: = {\rho _k}(\Omega_+^h - \{ {x_k}\})$. It is clear that $0 < {v_k} \le 1$, ${v_k}(0) = 1$. Substituting (3.1) into the problem (1.1), by direct calculations, we have

where ${\bar m_k}(y) = m(\rho _k^{ - 1}y + {x_k})$, ${\bar h_k}(y) = h(\rho _k^{ - 1}y + {x_k})$. Since $\bar \Omega _ + ^h$ is compact, then there exists a subsequence of $\{ {x_k}\}$, still denoted by $\{ {x_k}\}$, such that ${x_k} \to {x_0} \in \bar \Omega _ + ^h$. Now, we distinguish two cases.

Case 1. ${x_0} \in \Omega _ + ^h$. It is seen in this case that ${\Omega _k} \to {\mathbb{R}}^{N}$ as $k \to \infty$. Hence, for any compact subset $\mathbb{K}_1$, we have $\mathbb{K}_1 \subset \Omega_k$ for sufficiently large $k$. Since $0 < {v_k} \le 1$, there exist a positive constant $C_2$, such that

By using the regularity theory of the elliptic equation, we know that, there exists a subsequence of $\left\{ {{v_k}} \right\}$, still denoted by itself, such that

where $v \in {C^1}({\mathbb{K}_1})$. Since ${\mathbb{K}_1} \subset \subset {\Omega _k}$ is arbitrarily given, by a diagonal process, we can choose a subsequence, still denoted by $\left\{ {{v_k}} \right\}$, such that

Thus, we have

Note that $v(0) = 1$, by (3.3) and a linear change of coordinates, we find that there exists a nontrivial non-negative function $w \in {C^2}({\mathbb{R}}^{N})$ satisfying $- \Delta w = {w^p}$, which contradicts ^[7].

Case 2. ${x_0} \in \partial \Omega _ + ^h$. By an additional change of coordinates, we can assume that a neighborhood of ${x_0}$ in $\partial \Omega _ + ^h$ is a hyperplane ${x^N} = 0$ and $\bar \Omega _ + ^h \subset H = \{ x \in {\mathbb{R}}{^N}, {x^N} > 0\}$. Hence, given $R > 0$, there exists ${k_R}$ such that for $k \ge {k_R}$, ${v_k}$ is well defined on

Now, we have the following three cases.

(i) $\left\{ M_k^{\frac{{p - 1}}{2}}x_k^N \right\}$ is not bounded from upper. Assume without loss of generality that $M_k^{\frac{{p - 1}}{2}}x_k^N \to \infty$. Then, we have

We may argue exactly as in Case 1.

(ii) $\left\{ M_k^{\frac{{p - 1}}{2}}x_k^N \right\}$ is not bounded from below. Assume without loss of generality that $M_k^{\frac{{p - 1}}{2}}x_k^N \to 0$. Then, we have

Arguing as in Case 1, there exists $v \; \in \; {C^2}(\bar H)$ such that $v \ge 0$, $v(0) = 1$, and $v$ satisfies

This contradicts Corollary 2.1 of ^[7].

(iii) $\left\{ M_k^{\frac{{p - 1}}{2}}x_k^N \right\}$ is bounded from below. Assume without loss of generality that $M_k^{\frac{{p - 1}}{2}}x_k^N \to s, \; s > 0$. Then, we have

We can proceed as in (ii) and there exists $v \; \in \; C_{loc}^2({H_s})$ such that $v \ge 0$, $v(0) = 1$, and $v$ satisfies

Taking a change of variable through ${y^N} = - s$, we have that $v \in {C^2}(\bar H)$, $v \ge 0$, $v(0) = 1$, and $v$ satisfies

a contradiction.

Lemma 3.3. Assume $m(x)$ changes sign in $\Omega _ + ^h$ and $({{\rm{H}}_1})$ holds, then there exists a constant $C > 0$ such that ${\left\| u \right\|_{C\left({\bar \Omega _ + ^h} \right)}} \le C$ for any positive solution $(\lambda, u)$ of the problem (1.1).

Proof. If $({\lambda _k}, {u_k})$ is a positive solution of the problem (1.1), then ${\lambda _k} \in \left({\lambda _1^ -, \lambda _1^ + } \right)$. Assume

By virtue of Lemma 3.2, we have

where ${t_k} = \int_\Omega {u_k^\beta }$. Moreover, we have ${t_k} \to \infty$. But by using Lemma 3.1, we have ${u_k} \ge {e_{{\lambda _k}}}{t_k}$, a contradiction. Therefore, there exists a constant $C > 0$ such that ${\left\| u \right\|_{C\left({\bar \Omega _ + ^h} \right)}} \le C$.

Theorem 3.1. Assume $m(x)$ changes sign in $\Omega _ + ^h$, $({{\rm{H}}_1})$ holds and $\beta > \max \left\{ {p, {{N(p - 1)} \mathord{\left/ {\vphantom {{N(p - 1)} 2}} \right. } 2}} \right\}$. Then there exists a constant $C > 0$ such that ${\left\| u \right\|_{C(\bar \Omega)}} \le C$ for any positive solution $(\lambda, u)$ of the problem (1.1).

Proof. Let $f(u) = \lambda m(x)u + h(x){u^p} + \int_\Omega {{u^\beta }}$. By Lemma 3.3, there exists a constant ${C_ 1 } > 0$, such that $u \le {\left\| u \right\|_{C\left({\bar \Omega _ + ^h} \right)}} \le {C_ 1 }, {\rm{ }}x \in \Omega _ + ^h$. It follows that $\int_\Omega {{u^\beta }}$ is bounded by Lemma 3.1, so $f(u)$ is bounded in ${L^{{\beta \mathord{\left/ {\vphantom {\beta p}} \right. } p}}}(\Omega)$. Thus, $u$ is bounded in ${W^{2, {\beta \mathord{\left/ {\vphantom {\beta p}} \right. } p}}}(\Omega)$. By using boot-strapping method ^[1], it follows that there exists a constant $C > 0$, such that ${\left\| u \right\|_{C(\bar \Omega)}} \le C$.

Next, we give another way of proving boundedness. We first show two results about eigenvalue problem. We consider the eigenvalue problem

where

$\partial \Omega = {\Gamma _1}(\Omega) \cup {\Gamma _2}(\Omega)$, ${\Gamma _1}(\Omega)$ is nonempty. ${\sigma _1}(- \Delta + a(x), {B_\Omega }, \Omega)$ is the principal eigenvalue of problem (3.4). Generally, we denote ${B_\Omega }$ by $B$. We have the following results.

(1) If $a(x) \le \tilde a(x)$, then ${\sigma _1}(- \Delta + a(x), B, \Omega) \le {\sigma _1}(- \Delta + \tilde a(x), B, \Omega)$.

Proof. Let $\tilde a(x) = a(x) + b(x)$, then $b(x) \ge 0$. Let $F(u) = \int_\Omega {|\nabla u{|^2}} + \int_\Omega {a{u^2}}$, $\tilde F(u) = \int_\Omega {|\nabla u{|^2}} + \int_\Omega {\tilde a{u^2}}$, then

(2) If $\Omega \subset {\Omega ^*}$ and ${\mathop{\rm int}} (\Omega ^*) \cap {\Gamma _2}(\Omega) = \emptyset$, then

Proof. Let ${F_\Omega }(u) = \int_\Omega {|\nabla u{|^2}} + \int_\Omega {a{u^2}}$, $\tilde u$ denote that the function $u \in {H^1}(\Omega)$ extends to ${\Omega ^*}$ and ${\mathop{\rm int}} (\Omega ^*) \cap {\Gamma _2}(\Omega) = \emptyset$. Then $\tilde u$ satisfies ${\left. {\tilde u} \right|_{\partial {\Omega ^*}\backslash \partial \Omega }} = 0$, ${\left. {{B_{{\Omega ^*}}}\tilde u} \right|_{\partial {\Omega ^*} \cap \partial \Omega }} = 0$. Therefore,

Let $S$ is the positive solution set of the problem (1.1) and ${\Lambda _S}: = \left\{ {\lambda \in R; (\lambda, u) \in S} \right\}$ is bounded. we have

Theorem 3.2. If $\mathop {\sup }\limits_{(\lambda, u) \in S} \mathop {\sup }\limits_{\Omega _ + ^h} {\rm{u}} < \infty$, then $\mathop {\sup }\limits_{(\lambda, u) \in S} \mathop {\sup }\limits_\Omega u < \infty$.

Proof. If $(\lambda, u)$ is a positive solution of the problem (1.1), then

where ${\Gamma _1}(\Omega \backslash \bar \Omega _ - ^h) \subset \Omega$, ${\Gamma _2}(\Omega \backslash \bar \Omega _ - ^h) \subset \partial \Omega$, ${\Gamma _1}(\Omega)$ is nonempty. Then $(\lambda, u)$ is a strict upper solution of the equation

so

By $\Omega _0^h \subset \Omega \backslash \bar \Omega _ - ^h$ and result $(2)$, we have

Let

then ${\Omega _\delta } \to \Omega _0^h$ when $\delta \to 0$. So there exists a sufficiently small $\delta > 0$, such that ${\sigma _1}(- \Delta - \lambda m(x), B, {\Omega _\delta }) > 0$, so that ${\sigma _1}(- \Delta - \lambda m(x), B, {\Omega _\delta }) > 0$ satisfies the strong maximum principle.

Let $M = \mathop {\sup }\limits_{(\lambda, u) \in S} \mathop {\sup }\limits_{\Omega _ + ^h} u$ and $\psi$ be the unique solution of

Since ${\sigma _1}(- \Delta - \lambda m(x), B, {\Omega _\delta }) > 0$, we have $\psi > 0, x \in {\Omega _\delta }$ by the strong maximum principle. Denote by $w$ an extension of ${\left. \psi \right|_{{\Omega _{{\delta \mathord{\left/ {\vphantom {\delta 2}} \right. } 2}}}}}$ with $\mathop {\min }\limits_{\bar \Omega } w > 0$, ${\left. {{\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{\partial w}}{{\partial n}}} \right|_{{\Gamma _2}(\Omega)}} = 0$. Then $\bar u = kw$ is for sufficiently large $k > 0$ a positive strict upper solution of

where ${k_2} > \int_\Omega {{u^\beta}}$. Indeed, in ${\Omega _{{\delta \mathord{\left/ {\vphantom {\delta 2}} \right. } 2}}}$ we have

In ${\Sigma _\delta } = \left\{ {x \in \Omega _ - ^h:d(x, \partial \Omega _ - ^h) \ge \frac{\delta }{2}} \right\}$, since $w(x)$ and $- h(x)$ are positive and bounded away from zero, then $h(x){k^{p - 1}}{w^p} \to - \infty$ as $k \to \infty$, namely

On ${\Gamma _1}(\Omega \backslash \bar \Omega _ + ^h)$, since $\mathop {\min }\limits_{\bar \Omega } w > 0$, we know $kw \ge M$; on ${\Gamma _2}(\Omega \backslash \bar \Omega _ + ^h)$, we have $\frac{{\partial kw}}{{\partial n}} = 0$. Thus $\bar u = kw$ is a positive strict upper solution. Moreover, by the relationship between the strict upper solution and the principal eigenvalues, we have

If $(\lambda, u) \in S$ then it follows that $v = \bar u - u$ satisfies

Indeed, in $\Omega \backslash \bar \Omega _ + ^h$, since

so

Thus by result (1) we have

By the relationship between the principal eigenvalues and the strong maximum principle, we have $u \le \bar u$. The proof is completed.

4.   Proof of main results

proof of Theorem 1.1. If $\int_\Omega m < 0$, by virtue of Theorem 2.1, we obtain the bifurcation curve of positive solutions of the problem (1.1), and the direction of bifurcation is given by Theorem 2.2. When $m(x)$ changes sign in $\Omega _ + ^h$ and ${\rm{(}}{{\rm{H}}_1})$ holds, we have (i) by Proposition 3.1. Finally, we have (ii) by the priori estimate of positive solutions of Theorem 3.2.

Next, we prove (iii). We assume by contradiction that $({\lambda _k}, {u_k})$ are positive solutions of the problem (1.1), and $({\lambda _k}, {u_k}) \to (\gamma, 0)$ in $\mathbb{R} \times {C}(\bar \Omega)$, where $\gamma \ne {\lambda _ + }$ and 0. Let ${v_k} = \frac{{{u_k}}}{{{{\left\| {{u_k}} \right\|}_{C(\bar \Omega)}}}}$, by the problem (1.1), we have

By virtue of the regularity theory of the elliptic equation, we know that there is a subsequence, still denoted by $\{ {v_k}\}$, such that ${v_k} \to {v_0}$ in ${C^2}({\bar \Omega })$, ${v_0}$ is a solution of the equation

So $\gamma = {\lambda _ + }$ or $0$, a contradiction. Moreover, by using Rabinowitz global bifurcation theory, we see that ${C^ + }$ bifurcates from $({\lambda _ + }, 0)$ and backs to $(0, 0)$.

Similarly, we obtain the global bifurcation results of the problem (1.1) for $\int_\Omega m > 0$.

proof of Theorem 1.3. Since $m(x)$ changes sign in $\Omega _ + ^h$ and ${m_\varepsilon }(x) = m(x) - \varepsilon$ for $\varepsilon > 0$, so ${m_\varepsilon }$ changes sign and $\int_\Omega {{m_\varepsilon }} < 0$ for sufficiently small $\varepsilon$. Thus, we know that

has the principal eigenvalue $0$ and ${\lambda _ + }({m_\varepsilon }) > 0$. Substituting ${m_\varepsilon }(x)$ for $m(x)$, we can see that $u$ is bounded in ${C}(\bar \Omega)$ with ${m_\varepsilon }(x)$ through the proof of a priori estimate of positive solutions. By Theorem 1.1, we see that the problem (1.1) with ${m_\varepsilon }$ has a connected branch $C_\varepsilon ^ +$ of positive solutions set in $\mathbb{R} \times C(\bar \Omega)$ such that its closure $\overline {C_\varepsilon ^ + }$ contains $(0, 0)$ and $\left({{\lambda _ + }({m_\varepsilon }), 0} \right)$. Suppose that ${\varphi _\varepsilon } > 0$ is the principal eigenfunction corresponding to ${\lambda _ + }({m_\varepsilon })$ normalized so that ${\left\| {{\varphi _\varepsilon }} \right\|_{{W^{1, 2}}(\Omega)}} = 1$. According to ^[4], we have $\mathop {\lim }\limits_{\varepsilon \to 0} {\lambda _ + }({m_\varepsilon }) = 0$ and ${\varphi _\varepsilon } \to C$ in ${W^{1, 2}}(\Omega)$, where $C$ is a positive constant.

If $\beta > p$ and $\int_\Omega h < 0$, then $C_\varepsilon ^ +$ is subcritical at $(0, 0)$ by Theorem 2.2. Since ${\lambda _ + }({m_\varepsilon }) \to 0$ and ${\varphi _\varepsilon } \to C$, so for sufficiently small $\varepsilon$, we have $\int_\Omega {h\varphi _1^{p + 1}}$ and $\int_\Omega h$ have same sign for $\beta > p$. So $C_\varepsilon ^ +$ is supercritical at $\left({{\lambda _ + }({m_\varepsilon }), 0} \right)$ for $\beta > p$ and $\int_\Omega h < 0$. Therefore, $\overline {C_\varepsilon ^ + }$ is likely to approach a closed loop as $\varepsilon \to 0$, which bifurcates from the origin and backs to the origin, as Figure 3.

We now investigate $\overline {C_\varepsilon ^ + }$ as $\varepsilon \to 0$. Although it seems likely in Figure 3 that $\overline {C_\varepsilon ^ + }$ approaches a closed loop joining the origin to itself as $\varepsilon \to 0$, this seems difficult to establish. We can, however, prove that $\overline {C_\varepsilon ^ + }$ does not shrink to a point. For sets ${E_n}$, $n \in \mathbb{N}$, we define

$\mathop {\lim }\limits_{n \to \infty } \inf {E_n} = \{x:$ there exists ${{N_0} \in \mathbb{N}}$ such that any neighborhood of $x$ intersects ${E_n}$ for all ${n \ge {N_0}} \; \}$,

$\mathop {\lim }\limits_{n \to \infty } \sup {E_n} = \{x:$ any neighborhood of $x$ intersects ${E_n}$ for infinitely many $n \; \}$.

According to ^[8], if ${ \cup _{n \ge 1}}{E_n}$ is precompact in $M$ and $\mathop {\underline {\lim } }\limits_{n \to \infty } {E_n} \ne \emptyset$, then $\mathop {\overline {\lim } }\limits_{n \to \infty } {E_n}$ is non-empty, closed and connected. Here, $\{ {E_n}\}$ is a sequence of connected sets in a complete metric space $M$.

Obviously, $(0, 0) \in \overline {C_\varepsilon ^ + }$, so $(0, 0) \in \mathop {\underline {\lim } }\limits_{\varepsilon \to 0} C_\varepsilon ^ +$. It follows from the results of the priori bounds that ${ \cup _{\varepsilon > 0}}C_\varepsilon ^ +$ is precompact in ${C^2}({\bar \Omega })$. Then $\mathop {\overline {\lim } }\limits_{\varepsilon \to 0} C_\varepsilon ^ +$ is non-empty, closed and connected. We note that $(0, 0) \in \mathop {\overline {\lim } }\limits_{\varepsilon \to 0} C_\varepsilon ^ +$, and also, from the definition, that $\mathop {\overline {\lim } }\limits_{\varepsilon \to 0} C_\varepsilon ^ +$ consists of nonnegative solutions of the problem (1.1).

Since $\overline {C_\varepsilon ^ + }$ joining $(0, 0)$ and $\left({{\lambda _ + }({m_\varepsilon }), 0} \right)$ is subcritical at $(0, 0)$ and supercritical at $\left({{\lambda _ + }({m_\varepsilon }), 0} \right)$, then $\overline {C_\varepsilon ^ + }$ must join $(0, {u_\varepsilon })$, ${u_\varepsilon }$ is a positive solution of the equation

By a priori estimate of positive solutions, we see that ${u_\varepsilon }$ is bounded. By virtue of the regularity theory of the elliptic equation, it follows that $\{ {u_\varepsilon }\}$ must have a convergent subsequence in ${C^2}({\bar \Omega })$ converging to $u$, where $u$ is a solution of the Eq (4.1). Moreover, we have $(0, u) \in \overline {\mathop {\lim }\limits_{\varepsilon \to 0} } C_\varepsilon ^ +$.

Next, we prove $u \not \equiv 0$. Otherwise, we have ${u_\varepsilon } \to 0$. Let ${v_\varepsilon } = \frac{{{u_\varepsilon }}}{{\left\| {{u_\varepsilon }} \right\|}}$, by the Eq (4.1), we see that

then

Thus, we have $\int_\Omega {{{\left| {\nabla {v_\varepsilon }} \right|}^2}} \to 0$ as $\varepsilon \to 0$. Since ${v_\varepsilon }$ is bounded, so we may assume that ${v_\varepsilon } \rightharpoonup {v_0}$ in ${W^{1, 2}}(\Omega)$, ${v_\varepsilon } \to {v_0}$ in ${L^{p + 1}}(\Omega)$ and ${L^\beta }(\Omega)$, hence, we claim that ${v_\varepsilon } \to {v_0}$ in ${W^{1, 2}}(\Omega)$. Otherwise, we have

a contradiction, so ${v_0}$ is a positive constant $c$, then ${v_\varepsilon } \to c$ in ${L^{p + 1}}(\Omega)$ and ${L^\beta }(\Omega)$. Thus, when $\varepsilon$ is sufficiently small, we have $\int_\Omega {{v_\varepsilon }} \int_\Omega {v_\varepsilon ^\beta } < 0$ for $\beta > p$, but this is impossible because of the equality in (4.2).

Therefore, under the conditions of the Theorem 1.3, there exists a connected components $C^ +$ of positive solutions set such that its closure $\overline {{C^ + }}$ includes $\mathop {\overline {\lim } }\limits_{\varepsilon \to 0} C_\varepsilon ^ +$, which bifurcates from the origin and backs to the origin, namely, $\overline {{C^ + }}$ is a closed loop.

Acknowledgments

The authors would like to thank the referees for their valuable comments and suggestions. This paper is partially supported by NSFC, PR China 11871250.

Conflict of interest

The authors declare no conflict of interest.