Construction of $BCK$-neighborhood systems in a $d$-algebra

1.   Introduction

Imai and Iséki introduced two classes of abstract algebras: $BCK$-algebras and $BCI$-algebras ^[5,6]. Neggers and Kim introduced the notion of $d$-algebras which is another useful generalization of $BCK$-algebras, and they investigated several relations between $d$-algebras and $BCK$-algebras ^[10]. Allen et al. ^[1] developed a theory of companion $d$-algebras in sufficient detail to demonstrate considerable parallelism with the theory of $BCK$-algebras as well as obtaining a collection of results of a novel type. Allen et al. ^[2] introduced the notion of deformation in $d/BCK$-algebras. Using such deformations they constructed $d$-algebras from $BCK$-algebras in such a manner as to maintain control over properties of the deformed $BCK$-algebras via the nature of the deformation employed, and observed that certain $BCK$-algebras cannot be deformed at all, leading to the notion of a rigid $d$-algebra, and consequently of a rigid $BCK$-algebra as well. Kim et al. ^[7] explored properties of the set of $d$-units of a $d$-algebra. Moreover, they discussed the notions of a $d$-integral domain and a left-injectivity.

Since the notion of a $d$-algebra was defined simply by deleting two complicated axioms from a $BCK$-algebra, $d$-algebras became a wider class than the class of $BCK$-algebras. The following question arises: Can a $d$-algebra $X$ which is not a $BCK$-algebra be a union of its subsets $U_{\alpha}$ which satisfy the two complicated $BCK$-axioms, i.e., $(U_{\alpha}\cup\{0\}, *, 0)$ forms a $BCK$-algebra? In the sense of this concept, we introduce the notion of a $BCK$-neighborhood system of a $d$-algebra. In this paper, we introduce 3 different cases of the $BCK$-neighborhood system in different $d$-algebras.

In this paper, we introduce $BCK$-neighborhood systems in $d$-algebras as measures of distance of these algebras from $BCK$-algebras. We find examples of various cases and situations related to the general theory, as well as a complicated analytical example of one of particular interest in the theory of pseudo-$BCK$-algebras. It appears also that a digraph theory may play a constructive role in this case as it dose in the theory of $BCK$-algebras.

There are many algebraic structures which are generalizations of $BCK$-algebras in the literature, e.g., $BCH$-algebras, $BCI$-algebras, $BE$-algebras, $BF$-algebras, etc.. If we use the notion of the $BCK$-neighborhood system to such algebras, then we can develop the theory of $BCK$-algebras and general algebraic structures also. There will be some interesting results.

2.   Preliminaries

A $d$-algebra ^[9,10] is a non-empty set $X$ with a constant $0$ and a binary operation "$*$" satisfying the axioms:

(D1) $x*x = 0$,

(D2) $0*x = 0$,

(D3) $x*y = 0$ and $y*x = 0$ imply $x = y$, for all $x, y \in X$.

A $d$-algebra $X$ is said to be edge if $x*0 = x$ for all $x\in X$.

For brevity, we also call $X$ a $d$-algebra. In $X$ we can define a binary relation "$\leq$" by $x \leq y$ if and only if $x*y = 0$. A non-empty subset $I$ of a $d$-algebra $X$ is a $d$-subalgebra of $X$ if $x, y \in I$ implies $x*y \in I$.

A $BCK$-algebra ^[3,4,8] is a $d$-algebra $(X, *, 0)$ satisfying the following additional axioms:

(D4) $((x*y)*(x*z)*(z*y) = 0$,

(D5) $(x*(x*y))*y = 0$, for all $x, y, z \in X$.

3.   $BCK$-neighborhood systems

There are many $d$-algebras which are not $BCK$-algebras. Among them, we can find some $d$-algebras which can be divided into its subsets satisfying all $BCK$-axioms. We formulate this concept as below:

Definition 3.1. Let $(X, *, 0)$ be a $d$-algebra. A family $\{ U_{\alpha} \}_{\alpha \in \Sigma}$ of subsets of $X$ is said to be a $BCK$-neighborhood system of $X$ if

(N1) $\underset{\alpha \in \Sigma} \cup U_{\alpha} = X$,

(N2) $\forall\alpha \in \Sigma$, $\forall x, y \in U_{\alpha}$, $(x*(x*y))*y = 0$,

(N3) $\forall\alpha \in \Sigma$, $\forall x, y, z \in U_{\alpha}$, $((x*y)*(x*z))*(z*y) = 0$.

Such examples of $BCK$-neighborhood systems can be found in Examples 5.4 and 6.4 below.

Proposition 3.2. Let $(X, *, 0)$ be an edge $d$-algebra. If $\Sigma: = X$ and $U_x : = \{ x \}, \; \forall x \in X$, then $N_0 : = \{ U_x | x\in X \}$ is a $BCK$-neighborhood system of $X$.

Proof. Straightforward.

By Proposition 3.2, we have the following corollary.

Corollary 3.3. Every edge $d$-algebra $X$ permits a $BCK$-neighborhood system.

Example 3.4. Let $\{ U_{\alpha} \}_{\alpha \in \Sigma}$ be a $BCK$-neighborhood system of $X$ where $\Sigma: = \{0\}$ and $U_0 : = X$. Then $X$ is a $BCK$-algebra.

Let $X$ be a non-empty set and "$\leq$" be a binary relation on $X$. A system $(X, \leq)$ is said to be a quasi ordered set if $\leq$ is reflexive and transitive.

Proposition 3.5. Let $N: = \{U_{\alpha} \}_{\alpha \in \Sigma}$ be a $BCK$-neighborhood system of $X$ and let $M: = \{V_{\beta} \}_{\beta \in T}$ be a system of subsets of $X$ such that

(i) $\underset{\beta \in T} {\cup} V_{\beta} = X$,

(ii) $\forall\, \, V_{\beta} \in M, \; \exists U_{\alpha} \in N$ such that $V_{\beta} \subseteq U_{\alpha}$.

Then $M$ is also a $BCK$-neighborhood system of $X$.

Proof. (N1) By (i), we have $\underset{\beta \in T} \cup V_{\beta} = X$.

(N2) If $x, y \in V_{\beta}$ ($\beta \in T$), then there exists $U_{\alpha} \in N$ such that $V_{\beta} \subseteq U_{\alpha}$. Hence $x, y \in U_{\alpha}$. Since $\{U_{\alpha} \}_{\alpha \in \Sigma}$ is a $BCK$-neighborhood system of $X$, we have $(x*(x*y))*y = 0$.

(N3) If $x, y, z \in V_{\beta}$ ($\beta \in T$), then there exists $U_{\alpha} \in N$ such that $V_{\beta} \subseteq U_{\alpha}$. Hence $x, y, z \in U_{\alpha}$. Since $\{U_{\alpha} \}_{\alpha \in \Sigma}$ is a $BCK$-neighborhood system of $X$, we have $((x*y)*(x*z))*(z*y) = 0$. Hence $M$ is a $BCK$-neighborhood system of $X$.

In Proposition 3.5, we denote it by $M \leq N$. We call $M$ a sub-$BCK$-neighborhood system of $N$. We denote the set of all $BCK$-neighborhood systems of $X$ by $BCK(X)$.

Proposition 3.6. $(BCK(X), \leq)$ is a quasi ordered set. The $BCK$-neighborhood system $N_0$ in Proposition 3.2 is the unique minimal $BCK$-neighborhood system of $BCK(X)$.

Proof. Clearly, $(BCK(X), \leq)$ is a quasi ordered set. Let $N$ be any $BCK$-neighborhood system of $BCK(X)$. We show that $N_0 \leq N$. The first two conditions hold trivially. Since $N_0 = \{\{x\} | x\in X\}$, we have $V_{\beta} = \{\beta \},$ for any $V_{\beta} \in N_0$. Since $N$ is a $BCK$-neighborhood system of $X$, there exists $U_{\alpha}$ in N such that $\beta \in U_{\alpha}$. Hence $V_{\beta} \subseteq U_{\alpha}$. Therefore $N_0 \leq N$. It completes the proof.

4.   Constructions of $BCK$-neighborhood systems

In this section, we construct the $BCK$-neighborhood systems using analytic methods. We give a main assumption that $X: = [0, \infty)$ is a set of all positive real numbers, and "$*$" is a binary operation defined on $X$ as follows: For any $x, y \in X$,

Proposition 4.1. $(X, *, 0)$ is an edge $d$-algebra.

Proof. Clearly, we have $x*x = 0 = 0*x$ for any $x\in X$. We claim that if $x*y = 0$, then $x\leq y$. In fact, if we assume that $x*y = 0$ and $x > y$ for some $x, y \in X$. Then $\frac{2x}{\pi}\; \tan^{-1} (\ln \; \frac{x}{y}) = x*y = 0$. It follows that either $x = 0$ or $\tan^{-1} (\ln \; \frac{x}{y}) = 0$, i.e., $\ln\; \frac{x}{y} = 0$. Therefore either $x = 0$ or $y = x$, which is a contradiction to $y < x$. Assume that $x*y = 0 = y*x$ for any $x, y \in X$. Then, by claim, we obtain $x\leq y$ and $y\leq x$. Therefore $x = y$. Thus $(X, *, 0)$ is a $d$-algebra. For any $x\in X$, we have $x*0 = \frac{2x}{\pi}\; \tan^{-1}(\ln\frac{x}{0}) = \frac{2x}{\pi}\frac{\pi}{2} = x$. Hence $(X, *, 0)$ is an edge $d$-algebra.

We want to find a $BCK$-neighborhood system $\{ U_{\alpha} \}_{\alpha \in \Sigma}$ based on Proposition 4.1. By analytic method, we search to find such an $U_{\alpha}$.

Proposition 4.2. Let $x\in X$ with $x > 0$ and $y = \frac{1}{\lambda}x \; (\lambda > 1)$. Then $x*y \leq x$.

Proof. For such $x$ and $y$ in $X$, we have

Since $x*y \leq x$, we obtain

Lemma 4.3. Let $x\in X$ with $x > 0$ and $y = \frac{1}{\lambda}x \; (\lambda > 1)$. Then

Proof. If $x*y = 0$, then $x*(x*y) = x* 0 = x\geq 0$. If $x*y \not = 0$, then $\frac{x}{x*y} \geq 1$, since $x*y \leq x$. It follows that $\ln(\frac{x}{x*y})\geq \ln 1 = 0$, and hence $\tan^{-1}(\ln \frac{x}{x*y}) \geq \tan^{-1}0 = 0$. This shows that $x*(x*y) = \frac{2x}{\pi}\tan^{-1}(\ln \frac{x}{x*y}) \geq \frac{2x}{\pi}\tan^{-1}0 = 0$.

Theorem 4.4. Let $x\in X$ with $x > 0$ and let $y = \frac{1}{\lambda}x \; (\lambda > 1)$. Then the condition $x*(x*y)\leq y$ is equivalent to the following inequality.

Proof. Since $y = \frac{1}{\lambda}x$, by (1), we have

We compute $\ln\frac{x}{x*y}$ as follows:

where $\lambda = e^{\tau}, \tau > 0$ as in Proposition 4.2. Hence the condition $x*(x*y)\leq y$ is equivalent to the inequality (3).

Remark. Consider (3). If we let $\lambda: = 1$ in (3), then $\tan (\frac{\pi}{2 \lambda}) = \tan \frac{\pi}{2} = \infty$. Hence the inequality (3) holds. If we let $\tau \rightarrow \infty$, since $\lambda = e^{\tau}$ and $\tau > 0$, we have $\lambda \rightarrow \infty$ and so $\tan (\frac{\pi}{\lambda}) = 0$. On the while, $\ln \pi -\ln 2 - \ln (\tan^{-1} \tau) = \ln \pi -\ln 2 - \ln (\frac{\pi}{2}) = 0.$ Therefore the inequality (3) holds.

Theorem 4.5. Let $x\in X$ with $x > 0$ and let $y = \frac{1}{\lambda}x \; (\lambda > 1)$. Then there exists $\lambda_0$ such that if $\lambda \leq \lambda_0$, then $(x*(x*y))*y = (x*(x*\frac{1}{\lambda}x))*\frac{1}{\lambda}x = 0$.

Proof. If we let $\alpha: = \ln\pi -\ln 2 - \ln(\tan^{-1}\tau)$ and $\beta: = \tan(\frac{\pi}{2\lambda})$, then, by using L'H${\rm \widehat{o}}$pital's rule, we obtain

It follows that there exists $\lambda_0 \in X$ such that if $\lambda > \lambda_0$, then $\alpha > \beta$, i.e., $\exists \lambda_0$ such that $\lambda > \lambda_0$ implies $x*(x*y) > y$. This shows that $\lambda \leq \lambda_0$ implies $x*(x*y) \leq y$. Therefore there exists $\lambda_0 \in X$ such that

Remark. It is a problem to determine $\lambda_0$ exactly. A partial answer is that if we take $\tau: = 0.824$, then $\lambda = e^{\tau} = e^{0.824} \doteqdot 2.2796$. Let $\lambda_0: = 2.2796$.

We construct a $BCK$-neighborhood system $\mathscr{A} = \{ U_x | x\in X \}$, where $U_x: = [\frac{x}{\sqrt{\lambda_0 }}, \sqrt{\lambda_0 }x]$. Here we use the real number $\lambda_0$ which is obtained from Theorem 4.5.

Lemma 4.6. If $a, b \in U_x = [\frac{x}{\sqrt{\lambda_0 }}, \sqrt{\lambda_0 }x]$, then $(a*(a*b))*b = 0$.

Proof. If $a\leq b$, then $(a*(a*b))*b = (a*0)*b = a*b = 0$ by Proposition 4.1. If $a > b$, then there exists $\lambda > 1$ such that $b = \frac{a}{\lambda}$. Since $a, b \in U_x$, we have $\frac{x}{\sqrt{\lambda_0}} \leq b \leq a \leq \sqrt{\lambda_0} x$ and so

i.e., $\frac{a}{\lambda} = b \geq \frac{1}{\lambda_0 }a$. Hence $\lambda \leq \lambda_0$. By applying Theorem 4.5, we prove that $(a*(a*b))*b = 0$.

Given $x, y, z \in X$ with $y \leq x\leq z$ in $X$, we have the following:

Lemma 4.7. If $y \leq x \leq z$, then $x*y \leq z*y$.

Proof. If $y \leq x \leq z$, then $\ln(\frac{x}{y}) \leq \ln(\frac{z}{y})$, and hence $\tan^{-1}(\ln \frac{x}{y}) \leq \tan^{-1}(\ln \; \frac{z}{y})$. Since $x\leq z$, we obtain $x*y = \frac{2x}{\pi}\; \tan^{-1}(\ln \frac{x}{y}) \leq \frac{2z}{\pi}\tan^{-1}(\ln \; \frac{z}{y}) = z*y$. It completes the proof.

Lemma 4.8. If $z \leq y \leq x$, then $x*y \leq x*z$.

Proof. The proof is similar to Lemma 4.7, and we omit it.

Let $y \leq z \leq x$ in $X$. By Lemma 4.8, we obtain $x*z \leq x*y$. It follows that

and

In order to satisfy the condition $(N3)$, we need to show that $(5) \leq (6)$, i.e.,

If $y = z$ or $x = z$ in $y\leq z \leq x$, then the condition $((x*y)*(x*z))*(z*y) = 0$ holds trivially. We may assume $y < z < x$. Let $y: = \alpha x, \; z: = \beta x$, where $\alpha < \beta, \; \beta = \lambda \alpha < 1$. Then $1\leq \lambda \leq \frac{1}{\alpha}$. Therefore, we have

and hence

and

Note that $\frac{1}{\tan^{-1} (\ln \; \lambda)} \geq \frac{2}{\pi}$, since $\tan^{-1} (\ln \; \lambda) \leq \frac{\pi}{2}$. If we let

then

By formula (10), we see that $A$ is a function of $\lambda$ and so we replace $A$ by $A(\lambda)$.

Note that if $A(\lambda) = 0$, then

It follows that either $\tan^{-1}(\ln\alpha) = 0$ or $\tan^{-1}[\ln \frac{\; \tan^{-1}(\ln \; \alpha)}{\; \tan^{-1}(\ln \; \lambda \alpha)}] = 0$, and hence either $\alpha = 1$ or $\lambda = 1$. Since $\lambda\alpha < 1$, we conclude $\lambda \doteqdot 1$ is an approximate solution of $A(\lambda) = 0$. We denote such a solution by $\lambda_1$.

Pick $\alpha$ near zero and $\beta = \lambda\alpha$ near 1. Then we simplify the bracket expression of (11) to the following:

Hence $A(\lambda) \geq \frac{1}{\lambda} \frac{1}{\alpha} = \frac{1}{\beta} > 1$. Take $\lambda$ so that $\frac{1}{\alpha} > \lambda$, say $\lambda \alpha : = 1-\epsilon$ for some $\epsilon > 0$. Then $\lambda = \frac{1- \epsilon}{\alpha} < \frac{1}{\alpha}$. Hence $A(\lambda) > 1$ is possible for some $\lambda$.

Let $\lambda: = e$ in $A(\lambda)$. Then we get

Since $\lambda = e$ and $1 < \lambda < \frac{1}{\alpha}$, we have $0 < \alpha < \frac{1}{\lambda} = \frac{1}{e} < 1$ and so $\ln \; \alpha < 0$. Hence we get

Since $y = \tan^{-1} x$ is a monotone increasing function, we obtain $\tan^{-1} (\ln \; \alpha) < \tan^{-1} (\ln \; \alpha+1)$ and hence $\frac{\tan^{-1} (\ln \; \alpha)}{\tan^{-1} (\ln \; \alpha+1)} < 1$. If we take a logarithm, then $\ln\; (\frac{\tan^{-1} (\ln \; \alpha)}{\tan^{-1} (\ln \; \alpha+1)}) < 0$. Therefore we get

By (12)–(14), we obtain

From the observation, we see that $A(\lambda)$ is a continuous function and $A(\lambda) > 1$ is possible for some $\lambda$. Moreover, we showed that $A(e)\geq -\frac{1}{2e}$. Hence there exists $\lambda_2$ such that $A(\lambda_2) = 1$. Let $\lambda_3\in X$ such that $\lambda_2 < \lambda_3 < \lambda_1$ and let $\widehat{U_a} : = [\frac{a}{\sqrt{\lambda_3 }}, a \sqrt{\lambda_3}]$ where $a\in X$. The largest spread is $y = \frac{a}{ \sqrt{\lambda_3 }}, z = a\sqrt{\lambda_3}(1-\epsilon), x = a\sqrt{\lambda_3}$ for some $\epsilon > 0$. This shows that $\widehat{U_a}$ satisfies the conditions $(N2)$ and $(N3)$. Therefore we have the following theorem.

Theorem 4.9. Let $\lambda_1$ be a solution of $A(\lambda) = 0$ as in (10) and let $\lambda_2$ be a solution of $A(\lambda) = 1$. Given $\lambda_3\in X$ such that $\lambda_2 < \lambda_3 < \lambda_1$, define a set $\widehat{U_a}: = [\frac{1}{\sqrt{\lambda_3 }}, a\sqrt{\lambda_3}]$ where $a\in X$. Then the conditions $(N2), (N3)$ hold on $\widehat{U_a}$.

Now, we show that $\mathscr{A} = \{ \widehat{U_a }| a\in X \}$ forms a $BCK$-neighborhood system on $(X, *)$.

Given $x, y, z\in X$, we have 6 cases: (i) $x \leq y \leq z$, (ii) $x \leq z \leq y$, (iii) $y \leq x\leq z$, (iv) $z \leq x \leq y$, (v) $z \leq y \leq x$, (vi) $y \leq z \leq x$. If $x*y = 0$, i.e., cases (i), (ii), (iv), then the condition (N3) holds, since $(X, *)$ is an edge $d$-algebra. For the case (iii), we have $x*z = 0$, and hence $(x*y)*(x*z) = (x*y)*0 = x*y \leq z*y$ by Lemma 4.7. Hence we obtain $((x*y)*(x*z))*(z*y) = 0$. We consider (v) $z \leq y \leq x$. Since $z*y = 0$, by Lemma 4.8, we obtain $((x*y)*(x*z))*(z*y) = ((x*y)*(x*z))*0 = (x*y)*(x*z) = 0$. Finally, we consider the case (vi) $y \leq z \leq x$. It was already proved by Theorem 4.9. We summarize:

Theorem 4.10. Let $\lambda_1$ be a solution of $A(\lambda) = 0$ as in (10) and let $\lambda_2$ be a solution of $A(\lambda) = 1$. Given $\lambda_3\in X$ such that $\lambda_2 < \lambda_3 < \lambda_1$, define a set $\widehat{U_a}: = [\frac{1}{\sqrt{\lambda_3 }}, a\sqrt{\lambda_3}]$ where $a\in X$. Then $\mathscr{A} = \{ \widehat{U_a }| a\in X \}$ forms a $BCK$-neighborhood system on $(X, *)$.

5.   Another construction

Theorem 5.1. $X: = [0, \infty)$ be a set. Define a binary operation "$*$" on $X$ by

(i) $x*x = 0 = 0*x$,

(ii) if $x \neq 0, x \neq y$, we define $x*y: = \varphi(x, y)$ and $\varphi(x, y)\geq x+y$, where $\varphi:X \times X \rightarrow X$ is a map,

(iii) $x*0 = x$

for all $x, y \in X$. Then $(X, *, 0)$ is an edge $d$-algebra.

Proof. It is enough to show the anti-symmetry law holds. Assume that there exist $a, b \in X$ such that $a*b = 0 = b*a, a \neq b$. If $a \not = 0$, then $0 = a*b = \varphi(a, b) \geq a + b \geq a > 0$, a contradiction. If $b \not = 0$, then $0 = b*a = \varphi(b, a)\geq b + a\geq b > 0$, a contradiction. If $a = 0$, then $0 = b*a = b*0 = b$, a contradiction. Similarly, if $b = 0$, then $0 = a*b = a*0 = a$, a contradiction.

We construct a $BCK$-neighborhood system on the $d$-algebra $(X, *)$ as in Theorem 5.1.

Theorem 5.2. Let $(X, *, 0)$ be an edge $d$-algebra as in Theorem 5.1. Define a set $U_x$ by

for any $x\in X$. Then $\mathscr{A}: = \{ U_x | x \in X\}$ is a $BCK$-neighborhood system of $X$.

Proof. (N1) $\cup \mathscr{A} = \underset{x\in X}\cup U_x = \underset{x\in X} \cup \{x, 0\} = \underset{x\in X} \cup \{x\} = X.$

(N2) For any $x, y \in U_{\alpha}$ with $\alpha \neq 0$, we have 3 cases: (i) $x = y = \alpha$; (ii) $x = \alpha, y = 0$; (iii) $x = 0, y = \alpha$. If $x = y = \alpha$, then $(x*(x*y))*y = (\alpha*(\alpha * \alpha))*\alpha = (\alpha * 0)* \alpha = \alpha* \alpha = 0$, since $(X, *, 0)$ is an edge $d$-algebra. If $x = \alpha, y = 0$, then $(x*(x*y))*y = (\alpha*(\alpha*0))*0 = \alpha*(\alpha*0) = \alpha*\alpha = 0$. If $x = 0, y = \alpha$, then $(x*(x*y))*y = (0*(0*\alpha))*\alpha = 0$.

(N3) Given $x, y, z \in U_{\alpha} = \{ 0, \alpha\}$ with $\alpha \neq 0$, we have 8 cases. We consider one case, and the other cases are similar, and so we omit it. If $x = \alpha, y = z = 0$, then $((x*y)*(x*z))*(z*y) = ((\alpha *0)((\alpha *0))*(0*0) = ((\alpha *0)*(\alpha*0))*(0*0) = (\alpha*\alpha)*0 = 0$. Hence $\mathscr{A}: = \{ U_x | x \in X\}$ is a $BCK$-neighborhood system of $X$.

Proposition 5.3. Let $(X, *, 0)$ be an edge $d$-algebra as in Theorem 5.1. Let $\mathscr{A}: = \{ U_x | x \in X \}$, where

Then $\mathscr{A}: = \{ U_x | x \in X\}$ is a unique maximal $BCK$-neighborhood system of $X$, i.e., if $\mathscr{B}$ is a $BCK$-neighborhood system of $X$ such that $\mathscr{A} \subseteq \mathscr{B}$, then $\mathscr{A} = \mathscr{B}$.

Proof. Assume that there exists a $BCK$-neighborhood system $\mathscr{B}$ of $X$ such that $\mathscr{A} \subsetneq \mathscr{B}$. Then $\mathscr{B}$ contains a neighborhood $U$ such that $|U| \geq 3$. Let $x, y, 0\in U$ such that $x \neq y, x \neq 0 \neq y$. Then $x*(x*y) = x*\varphi(x, y)$. Since $\varphi(x, y)\geq x+y > x$, we have $x \neq \varphi(x, y)$. Hence we obtain

Since $x\neq y$, we get $x*(x*y)\neq y$. Hence we obtain

This shows that $(x*(x*y))*y = 0$ does not hold for $x\neq y$ in $U$. Hence $\mathscr{B}$ is not a $BCK$-neighborhood system of $X$, a contradiction. Therefore $\mathscr{A}$ is a unique maximal $BCK$-neighborhood system of $(X, *, 0)$.

Example 5.4. Let $X: = [0, \infty)$ be a set. Define a binary operation "$*$" on $X$ by $x*x = 0*x = 0$, $x*0 = x$, and $x*y : = x +y$ if $x\not = y$ and $x\not = 0$ for all $x, y \in X$, where $+$ is the usual addition of real numbers. Then it is easy to see that $(X, *, 0)$ is an edge $d$-algebra. Given $x\in X$, if we define $U_x: = \{x, 0\}$ and $\mathscr{A} : = \{U_x\, |\, x\in X\}$, then $\mathscr{A}$ is a $BCK$-neighborhood system of $(X, *, 0)$.

Theorem 5.5. Let $(X, *, 0)$ be a $d$-algebra. Let $\mathscr{A}: = \{ U_{\alpha} | \alpha \in \Lambda \}$ be a $BCK$-neighborhood system of $X$. If we define a class of sets

then $\widehat{\mathscr{A}}$ is a $BCK$-neighborhood system of $X$.

Proof. (N1). Given $x\in X$, since $\mathscr{A}$ is a $BCK$-neighborhood of $X$, there exists $U_{\alpha} \in \mathscr{A}$ such that $x\in U_{\alpha}$. Let $\widehat{U_{\alpha}}: = U_{\alpha} \cap U_{\alpha}$. Then $\widehat{U_{\alpha}} \neq \emptyset$ and $\widehat{U_{\alpha}} \in \widehat{\mathscr{A}}$. Hence $x\in \underset{\alpha \in \Lambda} \cup \widehat{U_{\alpha}} \subseteq \cup \{ \widehat{U_{\alpha}}| \widehat{U_{\alpha}} \in \widehat{\mathscr{A}} \}$. Therefore $X = \cup \{ \widehat{U_{\alpha}} | \widehat{U_{\alpha}} \in \widehat{\mathscr{A}} \}$.

(N2) and (N3). Given $\widehat{U_{\alpha}} \in \widehat{\mathscr{A}}$, there exist $U_{\alpha_1}, \cdots, \; U_{\alpha_n} \in \widehat{\mathscr{A}}$ such that $\widehat{U_{\alpha}} = U_{\alpha_1} \cap U_{\alpha_2} \cap \cdots U_{\alpha_n } \neq \emptyset.$ If $x, y, z \in \widehat{U_{\alpha}}$, then $x, y, z \in U_{\alpha_i}$ for all $i = 1, \cdots, m$. Since $\mathscr{A}$ is a $BCK$-neighborhood system of $X$, we get $(x*(x*y))*y = 0$ and $((x*y)*(x*z))*(z*y) = 0$ for all $i = 1, \cdots, m$, and hence the equations hold for $\widehat{U_{\alpha}}$. Hence $\widehat{\mathscr{A}}$ is a $BCK$-neighborhood system.

6.   Prism $d$-algebras

Proposition 6.1. Let $(X^{\prime}, \rightarrow)$ be a digraph and let $0\not\in X^{\prime}$. Let $0 \rightarrow x$ for any $x\in X'$, and let $X: = X' \cup \{0\}$. Define a binary operation "$*$" on $X$ by

(i) $x*x = 0 = 0*x$,

(ii) $x *0 = x$,

(iii) $x*y = 0, y*x = y$ if $x \rightarrow y$,

(iv) $x*y = x, y*x = y$ if there is no arrow between $x$ and $y$

for any $x, y \in X$ Then $(X, *, 0)$ is an edge $d$-algebra.

Proof. It is enough to show that "$\leq$" is anti-symmetry. Assume that there exist $x, y \in X$ such that $x*y = 0 = y*x$, $x\neq y$. If one of $x, y$ is zero, say $x = 0, y \neq 0$, then $0 = y*x = y*0 = y$ by (ii), which is a contradiction. Assume $x\neq 0 \neq y$. If $x\rightarrow y$, then we have $x*y = 0, y*x = y$ by using (iii). It leads to $0 = y*x = y$, a contradiction. Similarly, if $y\rightarrow x$, then it leads to $x = 0$, a contradiction. If there is no arrow between $x$ and $y$, then we have $x*y = x, y*x = y$ by (iv). Since $x*y = 0 = y*x$, we obtain $x = 0 = y$, which is a contradiction. Hence $(X, *, 0)$ is an edge $d$-algebra.

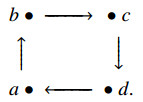
Example 6.2. Consider a digraph $(X^{\prime}: = \{a, b, c, d \}, \rightarrow)$ with the following digraph:

Adjoin $0$ to $X'$ so that $0 \rightarrow \alpha$ for all $\alpha \in X'$. Let $X: = X^{\prime} \cup \{0\}$. By Proposition 6.1, we obtain an edge $d$-algebra $(X, *, 0)$ as follows:

In Example 6.2, we call such an algebra $(X, *, 0)$ a prism $d$-algebra of order $4$.

Theorem 6.3. Every prism $d$-algebra $(X, *, 0)$ has a $BCK$-neighborhood system.

Proof. We consider two cases: (i) $X$ is a finite set; (ii) $X$ is an infinite set. Case (i): $|X| < \infty$. We consider two cases. Subcase (i)-1: $|X| = 2n \; (n \in \Bbb{N})$. Let $X: = \{x_1, x_2, \cdots, x_{2n-1}, x_{2n} \}$ such that $x_1 \rightarrow x_2 \rightarrow x_3 \rightarrow \cdots \rightarrow x_{2n-1} \rightarrow x_{2n} \rightarrow x_1$ and $0 \rightarrow x_i$ for all $i = 1, \cdots, 2n$. Let $N_1 : = \{0, x_1, x_2 \}, N_3 : = \{0, x_3, x_4 \}, \cdots, N_{2n-1}: = \{0, x_{2n-1}, x_{2n} \}$. Then $X = N_1 \cup \cdots \cup N_{2n-1}$. Since $0 \rightarrow x_{2i+1} \rightarrow x_{2i+2}$, we have

Then it is easy to see that $(N_{2i+1}, *, 0)$ is a $BCK$-algebra, and so the conditions (N2) and (N3) of Definition 3.1 hold for $N_{2i+1}$. Then $\{N_1, \cdots, N_{2n-1} \}$ is a $BCK$-neighborhood system. Subcase (i)-2: $|X| = 2n+1 \; (n \in \Bbb{N})$. Let $X: = \{x_1, x_2, \cdots, x_{2n}, x_{2n+1} \}$ such that $x_1 \rightarrow x_2 \rightarrow x_3 \rightarrow \cdots \rightarrow x_{2n} \rightarrow x_{2n+1} \rightarrow x_1$ and $0 \rightarrow x_i$ for all $i = 1, \cdots, 2n+1$. Let $N_2 : = \{0, x_1, x_2 \}, N_4 : = \{0, x_3, x_4 \}, \cdots, N_{2n}: = \{0, x_{2n-1}, x_{2n} \}$ and $N_{2n+1}: = \{0, x_{2n+1} \}.$ Then $X = N_2 \cup \cdots \cup N_{2n}\cup N_{2n+1}$. It is already shown that $N_{2i}$ is a $BCK$-algebra. Since $0 \rightarrow x_{2n+1}$, we have

Then $(N_{2n+1}, *, 0)$ is a $BCK$-algebra. Hence $\{N_2, N_{4}, \cdots, N_{2n}, N_{2n+1} \}$ is a $BCK$-neighborhood system of $X$.

Case (ii): $|X| = \infty$. Assume $X = \{x_n | n \in \Bbb{N} \}$ such that $x_1 \rightarrow x_2 \rightarrow \cdots \rightarrow x_n \rightarrow x_{n+1} \rightarrow \cdots$ and $0 \rightarrow x_i$ for all $i \in \Bbb{N}$. Let $N_{2i-1}: = \{ 0, x_{2i-1}, x_{2i} \} \; (i = 1, 2, \cdots)$. Then $X = \cup N_{2i-1}$ and $N_{2i-1}$ is a $BCK$-algebra. Therefore $X$ has a $BCK$-neighborhood system.

Example 6.4. In Example 6.2, we take $N_1 : = \{0, a, b \}$, $N_2 : = \{0, c, d \}$. Then $(N_i, *, 0)$ is a $BCK$-algebra $(i = 1, 2)$ and $X = N_1 \cup N_2$. Then $\{ N_1, N_2 \}$ is a $BCK$-neighborhood system of $X$. Also $(X, *, 0)$ in Example 6.2 is not a $BCK$-algebra, since $((b*d)*(b*c))*(c*d) = (b*0)*0 = b \neq 0$.

Remark 6.5. There exists a $BCK$-neighborhood system $\mathscr{A}: = \{N_i | i\in \Lambda\}$ such that there exist $N_1, N_2 \in \mathscr{A}$ such that $|N_1 \cap N_2 | \geq 2$.

Example 6.6. Let $X: = \{0, a, b, c, d, e\}$ be a set satisfying the conditions: $a \rightarrow b\rightarrow c \rightarrow d \rightarrow e \rightarrow a$ and $0\rightarrow x$ for all $x\in X$. Then we obtain the following table:

by applying Proposition 6.1, and we get $(X, *, 0)$ is an edge $d$-algebra. If we take $N_1 : = \{0, a, b \}, N_2 : = \{0, c, d \}$, and $N_3 : = \{0, d, e \}$, then $X = N_1 \cup N_2 \cup N_3$. We see that $N_i$ ($i = 1, 2, 3$) are $BCK$-algebras and $|N_2 \cap N_3| = 2$.

7.   Conclusions and future works

As part of the development of a general theory of groupoids (binary systems) a fundamental problem would be to try to determine how much a certain groupoid approximates a certain known type of interest, e.g., a group, a commutative group, a semigroup, etc.. Among these types a very significant type is that of $BCK$-algebra which may be very closely related to Boolean algebras, partially ordered sets with minimal element 0, and other subclasses. One way of dealing with providing an answer is to consider using the block product $(X, \Box) = (X, *)\Box (X, \bullet)$ of groupoids. It was shown that the block product of strong $d$-algebras is a strong $d$-algebra. It is also true that the block product of groups is not a group, but a groupoid which has properties in common with groups and are objects worth investigating in this way. $BCK$-algebras can be studied using the same tool. Another approach to deal with this question which is also promising is the following stated for example for groups (not yet done): Given a groupoid $(X, *)$, a group neighborhood system $\{(X_{\alpha}, *_{\alpha}, e_{\alpha})\}_{\alpha\in \bigwedge}$ has the property that $\cup_{\alpha\in \bigwedge} X_{\alpha} = X$ and if $x, y, z\in X_{\alpha}, (x*y)*z = x*(y*z)$, and $x\in X_{\alpha}$ implies that there is an element $x_{\alpha}^{-1} \in X_{\alpha}$ such that $x *_{\alpha} x_{\alpha}^{-1} = x_{\alpha}^{-1} *_{\alpha} x = e_{\alpha}$. Obviously, if there is a group neighborhood system containing only one element then the groupoid $(X, *)$ is a group. There will be a detailed investigation of group neighborhood systems.

In the development of a theory of this nature for a class of groupoids, our first choice has been the class of $BCK$-algebras. In order to obtain a "strickter" system with a better chance of obtaining sufficiently interesting results, we took the groupoid $(X, *)$ to be a $d$-algebra (i.e., already somewhat close to a $BCK$-algebra) and we let $0_{\alpha} = 0_{\beta} = 0$ for all $\alpha, \beta \in \bigwedge$, for a "better fit" of the $BCK$-algebras $X_{\alpha}$ in the $BCK$-neighborhood system, where it is obvious that if the system is a sigleton $\{(X, *_1, 0_1)\}_{\bigwedge = \{1\}}$, then $(X, *) = (X, *_1, 0_1) = (X, *, 0)$ is a $BCK$-algebra. As far as applications of these results, it is known that $BCK$-algebras as algebras of logic ^[4] already play a role in the design of both hardware networks and software algorithms. It is necessary to allow a more flexible approach to deal with groupoids (e.g., $d$-algebras) which have $BCK$-neighborhood systems of low cardinality.

From a purely theoretical viewpoint, it is clear that these "neighborhood systems" approaches are of interest on their own as well as resulting in more general information becoming available for deeper understanding of the structure principles governing the class/variety of groupoids $(X, *)$ for arbitrary sets $X$ and arbitrary products $x*y$ on these sets.

Conflict of interest

The authors hereby declare that there are no conflicts of interest regarding the publication of this paper.