Existence and multiplicity of solutions for generalized asymptotically linear Schrödinger-Kirchhoff equations

1.   Introduction

In this paper, we introduce a numerical method based on the spectral collocation method to solve nonlinear fractional quadratic integral equations

where $\Gamma (\cdot)$ is the gamma function, $y(x)$ is the unknown function and $a:[0, 1]\rightarrow \mathbb{R}$ is a given function. The functions $f$ and $g$ satisfy the following conditions:

$(1)$ The functions f, g: $[0, 1]\times \mathbb{R}\rightarrow \mathbb{R}$ in (1.1) are continuous and bounded functions with

$(2)$ The functions f and g satisfy the Lipschitz condition with respect to the second variable, i.e., there exist constants $L_{1} > 0$ and $L_{2} > 0$ such that, for all $(x, y_{1})$ and $(x, y_{2})$, we have

Integral equations are used to model some practical physical problems in the theory of radiative transfer, kinetic theory of gases, neutron transport, and traffic theory ^{[12,17,28,30,33]}. Also, some applications in the load leveling problem of energy systems, airfoils and optimal control problems can be found in ^{[24,25,39,40,41]}. Existence and uniqueness theorems and some other properties of quadratic integral equations have been studied in ^{[6,16,17,19,48]}. So far, various numerical methods for solving quadratic integral equations have been introduced: Adomian decomposition method ^[17,18,60], repeated trapezoidal methods ^[18], modified hat functions method ^[37], piecewise linear functions method ^[38], Chebyshev cardinal functions method ^[27], etc.

Spectral methods are a class of reliable techniques in solving various mathematical modeling of real-life phenomena. The general framework of these methods is based on approximating the solutions of the problems using a finite series of orthogonal polynomials as $\sum_{}^{}c_{i}\xi_{i}$, where $\xi_{i}$ are called basis functions and can be considered as Legendre, Chebyshev, Hermit, Jacobi polynomials and so on. Spectral methods have been developed to solve various types of fractional differential equations, such as ^{[1,8,14,21,23,44,53,55,59]}. The spectral collocation method is a powerful approach that provides high accuracy approximations for the solutions of both linear and nonlinear problems provided that these solutions are sufficiently smooth ^[9,11,22,58]. The spectral collocation methods based on some extended class of B-spline functions and finite difference formulation have been investigated to find the approximate solutions of time fractional partial differential equations ^{[2,3,4,32,50]}. In the last years, the extension of spectral methods based on fractional order basis functions have been developed for solving fractional differential and integral problems ^{[5,20,29,35,52,56,57]}. In these works, the authors constructed the fractional order basis functions by writing $x\rightarrow x^{\gamma}$, $(0 < \gamma < 1)$ in the standard basis functions.

The Chelyshkov orthogonal polynomials were introduced in ^[10] and then used to solve various classes of differential and integral equations, mixed functional integro-differential equations ^[43], weakly singular integral equations ^[46,52], nonlinear Volttera-Hammerstian integral equations ^[7], multi-order fractional differential equations ^[51], two-dimensional Fredholm-Volterra integral equation ^[49], systems of fractional delay differential equations ^[36], Volterra-Hammerstein delay integral equations ^[47]. Some properties of Chelyshkov polynomials can be listed as follows:

● The Chelyshkov polynomials $C_{N, n}(x)$ can be expressed in terms of the Jacobi polynomials $P_{m}^{(\gamma, \delta)}(x)$ ^[9] by the following relation

In the set $\lbrace C_{N, n}(x)\rbrace_{n = 0}^{N}$, every member has degree $N$ with $N-n$ simple roots. Hence, for every $N$ if the roots of the polynomial $C_{N, 0}(x)$ are chosen as collocation points, then an accurate numerical collocation method can be derived (for more details see ^[10]).

● The Chelyshkov polynomials (1.2) are orthogonal on the interval $[0, 1]$ with respect to the weight function $w(x) = 1$, i.e.,

About the structure of numerical methods in solving the fractional quadratic integral equations there are various researches, however some of them have not considered the singular behavior of the solutions. Most of these methods that were considered lie in the class of spectral methods and attempt to solve the problem via integer-order polynomial basis. Nevertheless, the obtained numerical solutions do not provide good approximations, and hence the convergence rates of the obtained numerical solutions are not be acceptable. Therefore, these methods cannot be considered as a comprehensive tool in solving fractional integral equations of the form of Eq (1.1) due to the singular behavior of their solutions. These disadvantages motivated us to overcome this drawback by developing a spectral method based on proper basis functions such that covers both smooth and non-smooth solutions of Eq (1.1). In this paper, we introduce a spectral collocation method via implementing a sequence of fractional-order Chelyshkov polynomials as basis functions to produce the numerical solution of Eq (1.1) regarding the singular behavior of the exact solution. These polynomials are constructed by writing $x\rightarrow x^{\gamma}$, $(0 < \gamma < 1)$ in the standard Chelyshkov polynomials ^[10]; i.e.,

which have both integer and non-integer powers. In this paper, we first convert the Eq (1.1) into a system of integral equation with linear integral operator. Then, the numerical method is implemented to reduce this problem to a set of nonlinear algebraic equations. This allows us to determine the approximate solution of the Eq (1.1) with a high order of accuracy versus results of other numerical methods based on standard orthogonal basis functions.

The contribution of this paper can be summarized as follows:

● In Theorems 4.1 and 4.2, we construct the operational matrices of fractional integration and multiplication based on fractional-order Chelyshkov polynomials with a simple calculative technique that is easy to implement in computer programming.

● The upper bound for the error vectors of the operational matrices is discussed in Theorems 4.4 and 4.5.

● The proposed numerical method is applied to an equivalent system of integral equations of the form (5.3), which includes a linear integral terms, to reduce the problem to a system of algebraic equations. This method is based on using simple operational matrix techniques so that, unlike other methods, it does not require any discretization, linearization, or perturbation (see Section 5).

● The approximate solution is expressed as a linear combination of fractional order terms of the form $x^{i\gamma}$ such that overcomes the drawback of the poor rate of convergence of the method. The accuracy of the method for solving the Eq (1.1) with non-smooth solutions is confirmed through theoretical and numerical results.

● The convergence analysis and numerical stability of the method are investigated.

The content of this paper is organized as follows: Section 2 contains some necessary definitions that are used in the rest of the paper. The fractional order Chelyshkov polynomials and their properties are investigated in Section 3. The operational matrices of integration and product of the fractional order Chelyshkov polynomials are derived in Section 4. In Section 5, we explain the application of operational matrices with spectral collocation method to obtain the numerical solution of Eq (1.1). The convergence analysis of the method is studied in Section 6. In Section 7, some numerical results are presented to illustrate the accuracy and efficiency of the method. Section 8 is devoted to conclusion and future works.

2.   Preliminaries

In this section, we recall some preliminary results which will be needed throughout the paper. With the development of theories of fractional derivatives and integrals, many definitions appear, such as Riemann-Liouville ^[45], which are described as follows:

For $u\in L_{1}[a, b]$, the Riemann-Liouville fractional integral of order $\gamma\in \mathbb{R}^{+}_{0}: = \mathbb{R}^{+}\cup \lbrace 0 \rbrace$ is defined as

For $\gamma = 0$, set $J_{a}^{0}: = I$, the identity operator. Let $u(x) = (x-a)^{\beta}$ for some $\beta > -1$ and $\gamma > 0$. Then

Let $m = \lceil \alpha\rceil$, the operator $D_{a}^{\alpha}$ defined by

is called the Riemann-Liouville fractional differential operator of order $\gamma$. For $\gamma = 0$, set $D_{a}^{0}: = I$, the identity operator. The Caputo fractional differential operator of order $n$ is defined by

whenever $D_{a}^{\gamma}[u(x)-T_{m-1}[u(x); a]]$ exists, where $T_{m-1}[u(x); a]$ denotes the Taylor polynomial of degree $m-1$ of the function $u$ around the point $a.$ In the case $m = 0$ define $T_{m-1}[u(x); a]: = 0$. Under the above conditions it is easy to show that,

For more details, see ^[13,45].

Theorem 2.1. ^[42] (Generalized Taylor's formula). Suppose that $D_{*0}^{k\gamma}u(x)\in C(0, 1]$ for $k = 0, 1, ...,$ $N+1$. Then, we can write

with $0 < \xi \leq x$, $\forall x\in (0, 1]$. Also, we have

provided that $\vert D_{*0}^{(N+1)\gamma}u(\xi) \vert \leq \mathcal{M}_{\gamma}$.

3.   Fractional order Chelyshkov polynomials

This section includes the definition of fractional Chelyshkov polynomials (FCHPs) and some of its essential properties that will be used in the next sections. The FCHPs on the interval $[0, 1]$ are defined as ^[52]

These polynomials are orthogonal with respect to the weight function $w(x) = x^{\gamma-1}$:

For $N = 5$, we have

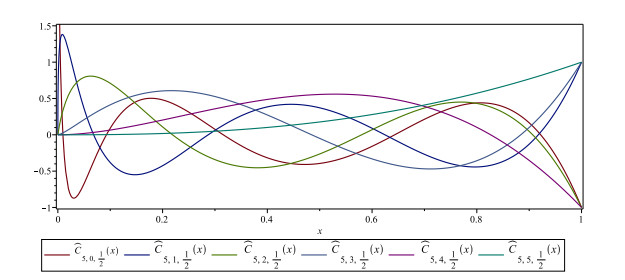
It is shown that, every member in the set $\lbrace \widehat{C}_{5, i, \gamma}(x)\rbrace$ has degree $5\gamma$. Figure 1 shows the graphs of these polynomials for $\gamma = \frac{1}{2}$ on the interval $[0, 1]$.

Lemma 3.1. The fractional order Chelyshkov polynomial $\widehat{C}_{N, 0, \gamma}(x)$, has precisely $N$ zeros in the form $x_{i}^{\frac{1}{\gamma}}$ for$i = 1, ..., N$, where $x_{i}$ are zeros of the standard Chelyshkov polynomial$C_{N, 0}(x)$ defined in (1.2).

Proof. The Chelyshkov polynomial $C_{N, 0}(x)$ can be written as

Changing the variable $x = t^{\gamma}$, yields

so, the zeros of $\widehat{C}_{N, 0, \gamma}(t)$ are

Let $M_{N} = span\lbrace\widehat{C}_{N, 0, \alpha}(x), \widehat{C}_{N, 1, \gamma}(x), ..., \widehat{C}_{N, N, \gamma}(x)\rbrace$ be a subspace of the Hilbert space $L_{2}[0, 1]$. Since $M_{N}$ is a finite dimensional space, for every $u \in L_{2}[0, 1]$ there exists a unique best approximation $u_{N}\in M_{N}$ such that

and there exist unique coefficients $a_{0}, a_{1}, ..., a_{N}$, such that

where

and

Lemma 3.2. Suppose that $D_{*0}^{k\gamma}u\in C(0, 1]$ for $k = 0, 1, ..., N$, and $u_{N}$ is the bestapproximation of $u$ defined by (3.3). Then, we have

provided that $\vert D_{*0}^{(N+1)\gamma}u(\xi) \vert \leq \mathcal{M}_{\gamma}$.

Proof. From Theorem 2.1, we have

Due to the fact that $u_{N}\in M_{N}$ is the best approximation of $u$, we obtain

This yields

Corollary 3.1. From Lemma 3.2, for the approximate solution $u_{N}(x)$ (3.3), we have the following error bound

4.   Operational matrices

In this section, we obtain the operational matrix of fractional integration $\widehat{\mathbf{\Phi}}(x)$ and the one of the product of vectors $\widehat{\mathbf{\Phi}}(x)$ and $\widehat{\mathbf{\Phi}}^{T}(x)$. These operational matrices have major role in reducing the Eq (1.1) to a system of algebraic equations.

Theorem 4.1. Let $\widehat{\mathbf{\Phi}}(x)$ be the FCHPs vector defined in (3.4) and suppose $\gamma\in(0, 1]$. Then,

with $P$ is the $(N+1)\times(N+1)$ fractional integral operational matrix and is given by

where

and

Proof. According to the definition of fractional integral (2.1), we have

Now, by approximating $x^{j\gamma+\alpha}$ in terms of $\widehat{\mathbf{\Phi}}(x)$, we have

where

Therefore, we derive from (4.2) and (4.3) that

This leads to the desired result.

Theorem 4.2. If $V = [v_{0}, v_{1}, ..., v_{N}]^{T}$, then

where

and $v_{l}$, $\mu_{i, l, j}$ will be introduced through the proof.

Proof. Let

By approximating $\widehat{C}_{N, i, \gamma}(x)\widehat{C}_{N, j, \gamma}(x)$ in terms of $\widehat{\mathbf{\Phi}}(x)$, we have

where

On the other hand, we can write $\widehat{\mathbf{\Phi}}(x) = \mathbf{D}\widehat{X}(x)$, where $\widehat{X}(x) = [1, x^{\gamma}, ..., x^{N\gamma}]^{T}$ and $\mathbf{D}$ is an upper triangular coefficient matrix (see ^[51] for details). Let $\mathbf{D}_{i}$ denote the $i$-th row of $\mathbf{D}$. Therefore, we achieve

where $\mathbf{K}$ is the $(N+1)\times(N+1)$ matrix given by

for $r, s, k = 0, ..., N$. From (4.8) and (4.9), we obtain

for $i = 0, 1, ..., N$. This leads to the desired result.

Now, we find the upper bound for the error vector of the operational matrix $P$ defined in Theorem 4.1. To this end, first we state the following theorems:

Theorem 4.3. ^[31]Suppose that $H$ is a Hilbert space and $U = span\lbrace u_{1}, u_{2}..., u_{N}\rbrace$ is a closed subspace of $H$. Let $u$ be an arbitrary element in $H$ and $u^{*}\in U$ be the unique best approximation to $u\in H$. Then,

where

Theorem 4.4. Let

be the error vector of the operational matrix $P$ defined in Theorem 4.1. Then,

and

where $e_{j, \alpha}(x)$ is the j-th component of $E_{I, \alpha}(x)$ and $\Vert E_{I, \alpha}\Vert_{2}: = \bigg(\sum_{j} \Vert e_{j, \alpha}\Vert^{2}_{2}\bigg)^{{\frac{1}{2}}}$.

Proof. We have

for $j = 0, 1, ..., N$. From Theorem 4.3, we can write

From (4.15) and (4.16), we obtain

By considering the above results and Lemma 3.2, we can conclude that

Theorem 4.5. Let

be the error vector of the operational matrix of $\widehat{V}$ defined in Theorem 4.2. Then, a similar proof for $\Vert E_{P, \alpha}\Vert_{2}$ can be obtained, since from (4.9) and Theorem 4.3, we have

For example, for $N = 5$, $\alpha = \gamma = \frac{1}{2}$, the following upper bound for components of $E_{I, \frac{1}{2}}(x)$ can be achieved:

Hence,

5.   Description of the method

By using the definition of Riemann-Liouville fractional integral in (2.1) we can rewrite the Eq (1.1) in the form

Based on the implicit collocation method ^[15], let

From Eqs (5.1) and (5.2), we have

The integral operator in (5.3) is linear and therefore application of the operational matrices becomes straightforward. The functions $w_{1}(x)$ and $w_{2}(x)$ can be approximated as follows

where $\mathbf{W}_{i} = [w_{i, 0}, w_{i, 1}, ..., w_{i, N}]^{T}$ are the unknown coefficient vectors for $i = 1, 2$. By applying Theorems 4.1 and 4.2, we get

From (5.4) and (5.5), the system (5.3) can be written as follows:

By collocating Eq (5.6) at the points $\widehat{x}_{i} = x_{i}^{\frac{1}{\gamma}}$, the zeros of $\widehat{C}_{N+1, 0, \gamma}(x)$, we obtain the following system of nonlinear algebraic equations

This nonlinear system can be solved for the unknown vectors $\mathbf{W}_{1}$ and $\mathbf{W}_{2}$. We employed the "fsolve" command in Maple for solving this system. Finally, the approximate solution of the Eq (1.1) is obtained as follows:

We present the algorithm of the method which is used to solve the numerical examples:

Algorithm:

Input: The numbers $\alpha$, $\gamma$; the functions $a(.)$, $f(., .)$ and $g(., .)$.

Step 1. Choose $N$ and construct the vector basis $\widehat{\mathbf{\Phi}}$ using relation (3.1).

Step 2. Compute the operational matrices $P$ and $\widehat{V}$ using Theorems 4.1 and 4.2.

Step 3. Compute the relation (5.5).

Step 4. Generate $\widehat{x}_{i}$ for $i = 0, ..., N$, the roots of $\widehat{C}_{N+1, 0, \gamma}(x)$ (5.5).

Step 5. Construct the nonlinear system of algebraic Eq (5.7) by using the nodes $\widehat{x}_{i}$.

Step 6. Solve the system obtained in Step 5 to determine the vectors $\mathbf{W}_{1}$ and $\mathbf{W}_{2}$.

Output: The approximate solution (5.8).

6.   Convergence analysis

In this section, we investigate the convergence of the proposed method in the space $L_{2}[0, 1]$.

Theorem 6.1. Assume that $w_{i}(x)$ and $w_{i, N}(x)$ are the exact and approximate solutions of Problems $(5.3)$ and $(5.6)$, respectively, and that Conditions (1) and (2) are satisfied. Then,

provided that

in which $e_{i, N}: = w_{i}-w_{i, N}$ are called the error functions.

Proof. By subtracting (5.6) from (5.3) and using Condition (2), we get

The Relation (6.2) can be written as

where

From Theorems 4.4 and 4.5, we can conclude that $\Vert \mathcal{E}_{\alpha}\Vert_{2}\rightarrow 0$ as $N\rightarrow \infty$. Using Condition (1) and the Cauchy-Schwarz inequality, we get

therefore, from (6.3) and (6.4), we can write

By ignoring the term $\Vert e_{1}\Vert\Vert e_{2}\Vert_{2}$ in (6.5), we obtain

which yields

Now according to inequalities expressed in (6.1), the proof is complete.

Theorem 6.2. Suppose that $y(x)$ and $y_{N}(x)$ are the exact solution and approximate solution of Eq (1.1), respectively and that Conditions (1), (2) and Relation (6.1) hold. Then, we have

Proof. By subtracting (5.8) from (5.1), we get

Therefore, from Theorem 6.1 we can conclude that (6.6) is valid.

7.   Numerical results

In this section, we provide some numerical examples to illustrate the efficiency and accuracy of the method. All calculations are performed in Maple 2018. The results are compared to the ones obtained using spectral collocation based on standard Chelyshkov basis polynomials $(\gamma = 1)$ ^[43], Taylor-collocation method ^[54] and Chebyshev cardinal functions method ^[27]. The computational error norm $(\Vert E_{N}\Vert_{2})$ is calculated in order to test the accuracy of the method as:

To investigate the numerical stability of the method, we solve the perturbed Eq (1.1) of the form

with $\epsilon = 10^{-3}, 10^{-6}, 10^{-9}$.

Example 7.1. Consider the fractional quadratic integral equation

in which $BesselJ(\cdot, \cdot)$ denotes the Bessel function of the first kind. The exact solution of this problem is $y(x) = \sin(\sqrt{x})$. In Table 1, the $\Vert E_{N}\Vert_{2}$-errors for $\gamma = \frac{1}{4}, \frac{1}{2}$ and $\gamma = 1$ (standard Chelyshkov polynomials ^[43]) are given, and also the CPU-times are computed. From this table, we see that fractional order basis functions get approximate solutions with higher accuracy than the integer order basis functions.

Table 2 presents a comparison between the numerical results given by our method and the ones obtained using Taylor-collocation method ^[54] and Chebyshev cardinal functions method ^[27].

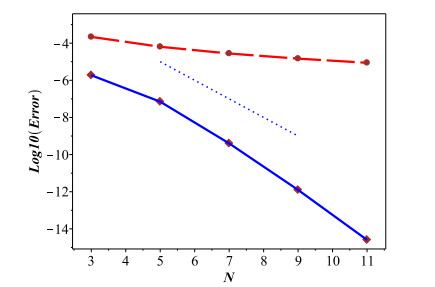
Figure 2 shows that the spectral accuracy of our method with $\gamma = \frac{1}{2}$ is achieved because the semi-logarithmic representation of the errors has almost similar behavior with the test line (dash-dot line). This line is the semi-logarithmic graph of $exp(-N)$.

In Table 3, we solved the perturbed problem with $\epsilon = 10^{-3}, 10^{-6}, 10^{-9}$ to investigate the stability of our method. The obtained numerical results in this example confirm the high-order rate of convergence and stability of the proposed method, as well as the agreement with the obtained theoretical results.

Example 7.2. Consider the fractional quadratic integral equation

The exact solution for $\alpha = 1$ is $y(x) = x^{3}$.

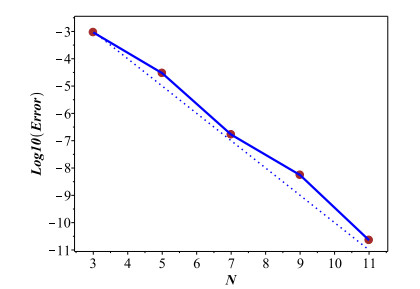
In this example, we study the applicability of the proposed method when the exact solution does not exist. Table 4 shows the numerical results for $N = 10$ and various values of $\alpha$, $\gamma$. From these results, it is seen that the approximate solution converges to the exact solution as $\alpha\rightarrow1$. The semi-log representation of errors for different values of $N$ with $\alpha = \gamma = 1$ confirm the spectral (exponential) rate of convergence of our method in Figure 3.

8.   Conclusions

Obtaining the analytical solution for integral equations is limited to a certain class of them. Therefore, it is required to derive appropriate numerical methods to solve them. A numerical method based on spectral collocation method is presented for solving nonlinear fractional quadratic integral equations. We used a new (fractional order) version of orthogonal Chelyshkov polynomials as basis functions. Also, the convergence of the method is investigated. The numerical results show the accuracy of the proposed method. Utilizing the new non-integer basis functions produces numerical results with high accuracy. The proposed method for problems on a large interval was not considered. As future work, this limitation may be considered by dividing the domain of the problem into sub-domains and applying the numerical method on them ^[26,34]. Also, this method can be applied to other kinds of integral equations such as cordial integral equations of quadratic type, quadratic integral equations systems and delay quadratic integral equations.

Conflict of interest

The authors declare no conflict of interest.