Modeling the co-infection of HTLV-2 and HIV-1 in vivo

1.   Introduction

Persistent viral infections, such those brought on by two different families of retroviruses human immunodeficiency viruses (HIVs) and the human T-lymphotropic viruses (HTLVs), are one of the largest clinical problems. In addition to sharing an in vivo preference for immune system cells, particularly T lymphocytes, the viruses are known to transmit along both vertical and horizontal pathways ^[1]. UNAIDS 2024 reports that in 2023, there were 630,000 HIV-related deaths, 1.3 million new HIV infections, and 39.9 million HIV-positive people globally ^[2]. HIV comes in two varieties: HIV-1 and HIV-2 ^[3]. HIV-2 has a slower rate of development and spread than HIV-1, despite the fact that both impair immunity by infecting and destroying the cental component of the adaptive immune response, CD4⁺ T cells. Certain drugs that are used to treat HIV-1 do not work on HIV-2. Acquired immune deficiency syndrome (AIDS) can result from either HIV-1 or HIV-2 ^[3]. In a healthy person, the expected number of CD4⁺ T cells is 1000 cells/mm³. Following HIV-1 infection, there is a reduction in CD4⁺ T cells that can last for years. An individual is considered to have acquired immunodeficiency syndrome (AIDS) when the count of these cells falls below 200 cells/mm^{3 [4]}.

Of the four HTLV types, only two—HTLV-1 and HTLV-2—have been connected to diseases ^[5]. Both HTLV-1 and HTLV-2 are closely related retroviruses that share shared mechanisms of transmission and comparable biological characteristics ^[6]. In 2012, there were an estimated 5 million to 10 million individuals worldwide who were infected with HTLV-1 ^[7]. Murphy et al. ^[8] estimated that the number of known cases of HTLV-2 infection is thought to be between 670,000 and 890,000 in 2015, a far smaller number than there are for HTLV-1. HTLV-1 mainly targets the CD4⁺ T cells and can cause two diseases, adult T-cell leukemia (ATL) and HTLV-1-associated myelopathy/tropical spastic paraparesis (HAM/TSP) ^[9]. In contrast, HTLV-2 mainly targets CD8⁺ T cells, also called cytotoxic T-lymphocytes (CTLs), which eliminate the cells that are infected with the virus ^[9]. HTLV-2 has been linked to peripheral neuropathy and may also be connected to tropical spastic paraparesis ^[9]. HTLV-1 and HTLV-2 depend on direct cell-to-cell contact for efficient transmission. Both viruses use the Envelope (Env) glycoproteins to facilitate cell attachment and entry into the host cells, enabling them to establish infection effectively. This mechanism plays a critical role in their persistence and ability to spread within the host ^[10]. Martinez et al. ^[10] conducted a comprehensive review comparing HTLV-1 and HTLV-2, focusing on key areas such as epidemiology, pathobiology, gene products, and genomic structure. Their work highlights the similarities and differences in how these viruses spread, their genetic makeup, and the diseases they cause, providing a deeper understanding of their biological characteristics and public health impact.

Co-infections between HIV-1 and HTLV-1/-2 are known to happen more often, because the viruses have the same pathways of acquisition and dissemination ^[11]. This is especially true in big cities where injection drug users (IDUs) and sexual activity are the major ways that HIV-1 and HTLV-1/-2 viruses spread ^[11]. IDUs may found in the US, Europe, Asia, South America, and many Native American Indian groups are endemic to HTLV-2 infection. It would seem that injectable drug users who are also HIV-1 infected are more likely to have HTLV-2 infection in several countries ^[6]. Since routine HTLV-1/-2 testing is not often done in outpatient clinics, HTLV-1/HIV-1 and HTLV-2 and HIV-1 coinfections likely occur more frequently than doctors realize ^[11]. HIV-1-positive people are thought to have rates of HTLV-1 or HTLV-2 coinfections that are at least 100–500 times higher than those in the general population. Five to ten percent of those living with HIV-1 infection may also have HTLV-1 or HTLV-2 co-infection in particular geographical areas ^[11]. Several publications have described cases of co-infection between HTLV-2 and HIV-1 (see the review articles ^[12,13,14]).

Our knowledge of viral dynamics has significantly increased thanks to rigorous mathematical modeling and analysis, which can help us come up with workable and efficient management plans to eradicate viral infections. One of the areas of mathematical immunology that is progressing the fastest is the formulation of mathematical models of the dynamics of HIV-1 infection. Three populations are included in the classic model of HIV-1 mono-infection ^[15]: Free HIV-1 particles, uninfected CD4⁺ T cells and infected cells. The model was expanded to incorporate the influence of CD8⁺ T cells in several publications (see e.g., ^{[15,16,17,18,19,20]}). B cells is another arm of the adaptive immune response, which produce antibodies to attack the viruses. Models with B-cell response have been investigated in many papers (see e.g., ^{[21,22,23,24,25,26]}). The HIV-1 mono-infection model under the impact of both B cells and CD8⁺ T cells can be written as ^[27]:

where $U = U(t),$ $Y = Y(t),$ $V = V(t),$ $E = E(t),$ and $W = W(t)$ are the concentrations of uninfected CD4⁺ T cells, HIV-1-infected CD4⁺ T cells, HIV-1 particles, uninfected CD8⁺ T cells and HIV-1-specific B cells at time $t$. Here, the proliferation rate of CD8⁺ T cells and B cells are represented, respectively, by $\Psi(Y, E)$ and $\Phi(V, W)$. The model has been extended in several works (see e.g., ^[28,29,30]). The literature took into consideration the following particular forms of $\Psi(Y, E)$ and $\Phi(V, W)$ as follows:

${\rm{SS}}\textbf{-(I):}$ Self-regulating immune response, $\Psi(Y, E) = \xi$ and $\Phi(V, W) = \varkappa$, where $\xi, \varkappa > 0$ ^[31],

${\rm{SS}}\textbf{-(II):}$ Linear immune response, $\Psi(Y, E) = \tilde{\pi}Y$ ^[32,33,34] and $\Phi (V, W) = \tilde{\varsigma}V$ ^[24,35], where $\tilde{\pi}, \tilde{\varsigma} > 0$,

${\rm{SS}}\textbf{-(III):}$ Predator-prey like immune response, $\Psi(Y, E) = \pi YE$ ^[15,20,31] and $\Phi (V, W) = \varsigma VW$ ^{[22,24,31,36]}, where $\pi, \varsigma > 0$

${\rm{SS}}\textbf{-(IV):}$ Combination of SS-(Ⅰ), SS-(Ⅱ) and SS-(Ⅲ), $\Psi(Y, E) = \xi+\tilde{\pi}Y+\pi YE$ ^[31,37] and $\Phi(V, W) = \varkappa+\tilde{\varsigma}V+\varsigma VW$ ^[31],

${\rm{SS}}\textbf{-(V):}$ Combination of predator-prey like immune and self-proliferation immune responses: $\Psi(Y, E) = \pi YE+qE\left(1-\frac {E}{E_{\max}}\right)$, where $q, E_{\max} > 0$ ^[17].

$S\textbf{S-(VI)}:$ Saturated immune response: $\Psi(Y, E) = \frac{\pi YE}{\vartheta+E}$ ^{[18,38,39,40]}, $\Phi(V, W) = \frac{\varsigma VW}{\vartheta+W}$ ^[41,42], where $\vartheta > 0$.

The infection rate of cells, denoted as $\beta_{1}UV$, is influenced by some biological factors, such as saturation and pyroptosis. Saturation is considered when the concentration of the viruses is high. In this case the infection rate is reduced and given by $\frac{\beta_{1} UV}{1+\nu V}$, where $\nu$ is the saturation constant ^[43]. Pyroptosis is a highly inflammatory type of programmed cell death triggered during incomplete HIV-1 infection, leads to the release of pro-inflammatory cytokines. These cytokines have the ability to attract more CD4⁺ T cells to the infection site, expanding the number of cells susceptible to HIV infection. This makes the deterioration of the immune system worse ^[44,45]. The impact of pyroptosis on HIV-1 dynamics was initially explored in a model presented in ^[46]. The infection rate was modeled by a bilinear incidence $\beta_{1}UV$, which is enhanced by the inflammatory cytokine ($C$) with a factor $\gamma$ as $\beta_{1}(1+\gamma C)UV$. This model was later extended to incorporate reaction-diffusion processes, as studied in subsequent works ^{[47,48,49,50]}. These extensions aimed to capture spatial effects and the spread of infection in tissues, providing deeper insights into the role of pyroptosis in HIV-1 infection.

The co-infection of HIV-1 and HTLV-1 has been modeled in a number of recent research (see e.g., ^{[43,51,52,53]}). The models presented in ^[43,51,52] were built on the premise that both HIV-1 and HTLV-1 compete for the same target cells, CD4⁺ T cells. The effect of CTL response and latently infected cells have been included in model presented in ^[51,52]. In ^[52], it was assumed that HIV spreads through two main pathways: Virus-to-cell transmission and direct cell-to-cell contact. In contrast, HTLV-1 is transmitted via two distinct mechanisms: (ⅰ) horizontally through direct cell-to-cell interactions, and (ⅱ) vertically during the mitotic division of Tax-expressing HTLV-1-infected cells. In ^[43], both uninfected and infected CD4⁺ T cells are modeled to proliferate according to a full logistic growth form. Additionally, the infection rate is modeled using a saturated incidence form. A stochastic model for the co-infection dynamics of HIV and HTLV-1, which also includes the effects of AIDS-related cancer cells, was explored in ^[53].

To the best of our knowledge, no earlier studies on modeling HTLV-2 and HIV-1 co-infection within a host have been conducted. In this study, we construct a new in vivo model of co-infection between HIV-1 and HTLV-2. Apart from the global stability of the equilibria, we investigate the fundamental characteristics of the solutions to the model. By constructing suitable Lyapunov functions and employing Lyapunov-LaSalle asymptotic stability theorem (L-LAST), the six equilibria's global stability is demonstrated. We conduct numerical simulations to demonstrate and validate the theoretical findings. We conclude by discussing the results.

Our proposed model and its analysis may provide valuable insights into the dynamics of co-infection between different human viruses. By capturing the interactions between multiple infections and the immune system's response to chronic viral co-infections, this model serves as a tool to explore how co-infection influences disease progression. Additionally, the framework has the potential to forecast new treatment approaches, offering predictions on optimal therapies that could address viral co-infections more effectively. This comprehensive analysis could contribute to developing strategies for improving patient outcomes.

2.   Model formulation

In this section, we propose a new model for the co-infection of HTLV-2 and HIV-1 in vivo. To formulate our model, we need the following hypothesis:

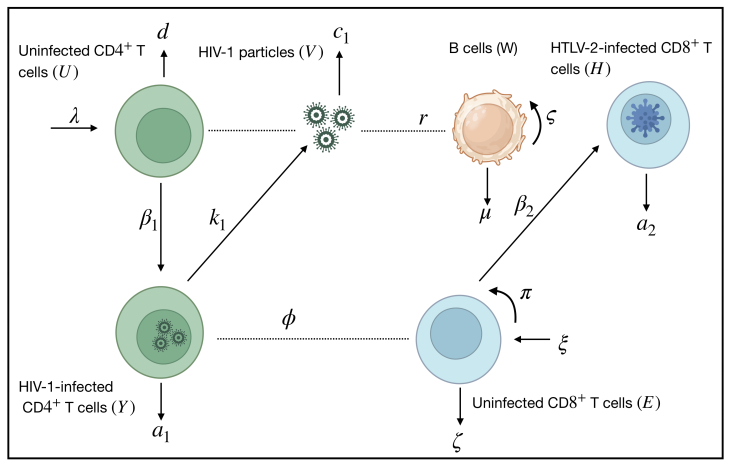
(H1) The key components of the model include the concentration of, uninfected CD4⁺ T cells ($U(t)$), HIV-1-infected CD4⁺ T cells ($Y(t)$), HIV-1 particles ($V(t)$), uninfected CD8⁺ T cells ($E(t)$), HTLV-2-infected CD8⁺ T cells ($H(t)$) and HIV-1-specific B cells ($W(t)$) at time $t$. The death (or clearance or decay) rates of compartments $U$, $Y$, $V$, $E$, $H$ and $W$ are denoted by $dU$, $a_1Y$, $c_1V$, $\zeta E$, $a_2H$ and $\mu W$, respectively. The HTLV-2 and HIV-1 co-dynamics is depicted in the schematic diagram in Figure 1.

(H2) HIV-1 primarily targets uninfected CD4⁺ T cells. Uninfected CD4⁺ T cells are produced at a constant rate $\lambda$ and become infected by HIV-1 particles through virus-to-cell transmission at a rate $\beta_1UV$ ^[15] (see Eq (2.1)).

(H3) HIV-1-infected CD4$^+$ T cells are generated at a rate of $\beta_1UV$ due to the interaction between uninfected CD4$^+$ T cells and free HIV-1 particles. These infected cells are subsequently eliminated by CD8$^+$ T cells at a rate of $\phi YE$ ^[15] (see Eq (2.2)).

(H4) Free HIV-1 particles are generated from HIV-1-infected CD4$^+$ T cells at the rate of $k_1Y$. These viral particles are then neutralized at a rate of $rVW$, where the neutralization is carried out by HIV-1-specific antibodies which are produced by the HIV-1-specific B cells ^[31] (see Eq (2.3)).

(H5) HTLV-2 mainly infects CD8 ⁺ T cells ^[9]. We assume that, in the absence of both HIV-1 and HTLV-2 infections, the baseline level of CD8$^+$ T cells is represented by $\xi/\zeta$, where $\xi$ signifies the source of CD8$^+$ T cells that are specific to HIV-1. Upon HIV-1 infection, the immune system is triggered, leading to an expansion of CD8$^+$ T cells at a rate $\pi YE$, which is influenced by the concentrations of CD4$^+$ T cells infected with HIV-1 and CD8$^+$ T cells ^[31]. Therefore, the production rate of uninfected CD8⁺ T cells results from a combination of self-regulation mechanisms ($\xi$) and immune responses similar to a predator-prey interaction ($\pi YE$), modeled by $\xi+\pi YE$. Uninfected CD8⁺ T cells become infected upon contact with HTLV-2-infected CD8⁺ T cells via cell-to-cell transmission, occurring at a rate $\beta_{2}EH$ ^[10] (see Eq (2.4)).

(H6) HTLV-2-infected CD8$^+$ T cells are generated at rate of $\beta_2EH$ due to the cell-to-cell interaction between uninfected CD8$^+$ T cells and HTLV-2-infected CD8$^+$ T cells ^[10] (see Eq (2.5)).

(H7) HIV-1-specific B cells are stimulated at rate $\varsigma VW$, which is influenced by the concentrations of free HIV-1 particles and HIV-1-specific B cells ^[22,31] (see Eq (2.6)).

Based on hypothesis H1-H7, our proposed HTLV-2 and HIV-1 co-infection model is given by:

The definition of variables and parameters are given in Table 1. The model's parameters are all positive. The initial condition is given by:

We emphasize that our proposed HTLV-2 and HIV-1 co-infection model (2.1)–(2.6) is different from the HTLV-1 and HIV-1 co-infection models presented in ^[43,51,52] in such away that both HTLV-1 and HIV-1 compete for the same target cells, CD4⁺ T cells (i.e., Eq (2.1) becomes $\dot{U} = \lambda-dU-\beta_{1}UV-\bar{\beta}_{1}UK$, where, $K$ denotes the HTLV-1-infected CD4⁺ T cells). A detailed analysis of the system described in model (2.1)–(2.6) will be addressed in next sections, where an in-depth examination of the model's dynamics will be carried out.

3.   Preliminaries

In this section, the fundamental qualitative characteristics of the system (2.1)–(2.6), such as non-negativity and boundedness of solutions, are examined. We find the model's equilibria and determine a set of threshold parameters which determine the existence of the model's equilibria.

3.1.   Non-negativity and boundedness

We demonstrate that the model (2.1)–(2.6) is well-posed by establishing the nonnegativity and boundedness of the solutions.

Lemma 1. Solution of the system (2.1)–(2.6) are non-negative and bounded.

Proof. From Eqs (2.1)–(2.6) We get

Therefore, in accordance with the Proposition B.7 of ^[61]

To demonstrate the solutions' boundedness, let define $\Gamma(t)$ as:

Next, we get

where $\varrho = \min\{d, a_{1}/2, c_{1}, \zeta, a_{2}, \mu\}$. Thus, $\Gamma \leq\frac{\lambda}{\varrho}+\frac{\xi\phi}{\pi\varrho} = \tau_{1}$, if$\; \Gamma(0)\leq\tau_{1}$. It follows that

if

where $\tau_{2} = \frac{2k_{1}}{a_{1}}\tau_{1}, \tau_{3} = \frac{\pi}{\phi}\tau _{1}\text{ and }\tau_{4} = \frac{2k_{1}\varsigma}{a_{1}r}\tau_{1}.$ □

3.2.   Equilibria and thresholds

Lemma 2. For model (2.1)–(2.6), there exist six equilibria besides seven threshold parameters ($R_{i},$ $i = 1, 2, \ldots, 7$) such that

(I) Infection-free equilibrium, $\Delta_{0}$, is always presented, where $\Delta_{0} = \left(U_{0}, 0, 0, E_{0}, 0, 0\right)$.

(II) If $R_{1} > 1$, then an HTLV-2 mono-infection equilibrium, $\Delta_{1}$, exists besides $\Delta_{0}$, where $\Delta_{1} = \left(U_{1}, 0, 0, E_{1}, H_{1}, 0\right)$.

(III) If $R_{2} > 1$, then an HIV-1 mono-infection equilibrium in the absence of HIV-1-specific B-cell response, $\Delta_{2}$, exists besides $\Delta_{0}$, where $\Delta_{2} = \left(U_{2}, Y_{2}, V_{2}, E_{2}, 0, 0\right)$.

(IV) If $R_{3} > 1$, then an HIV-1 mono-infection equilibrium with an active HIV-1-specific B-cell response, $\Delta_{3}$, exists besides $\Delta_{0}$, where $\Delta_{3} = \left(U_{3}, Y_{3}, V_{3}, E_{3}, 0, W_{3} \right)$.

(V) If $R_{7}\leq1 < R_{4}$ and $R_{5} > 1$, then an HTLV-2 and HIV-1 co-infection equilibrium in the absence of HIV-1-specific B-cell response, $\Delta_{4}$, exists besides $\Delta_{0}$, where $\Delta_{4} = \left(U_{4}, Y_{4}, V_{4}, E_{4}, H_{4}, 0\right)$.

(VI) If $R_{6} > 1$ and $R_{7} > 1$, then an HTLV-2 and HIV-1 co-infection equilibrium with an active HIV-1-specific B-cell response, $\Delta_{5}$, exists besides $\Delta_{0}$, where $\Delta_{5} = \left(U_{5}, Y_{5}, V_{5}, E_{5}, H_{5}, W_{5}\right)$.

Proof. Equilibria of (2.1)–(2.6) fulfill

We get that the provided model (2.1)–(2.6) has six equilibria:

1) Infection-free equilibrium, $\Delta_{0} = \left(U_{0}, 0, 0, E_{0}, 0, 0\right)$, where $U_{0} = \frac{\lambda}{d}$ and $E_{0} = \frac{\xi}{\zeta}.$

2) HTLV-2 mono-infection equilibrium, $\Delta_{1} = \left(U_{1}, 0, 0, E_{1}, H_{1}, 0\right)$, where

where

which stands for the HTLV-2 mono-infection basic reproduction ratio. The parameter $R_{1}$ plays a critical role in clinical settings, as it helps determine whether an HTLV-2 infection will persist chronically. It quantifies the average number of new HTLV-2-infected CD8⁺ T cells generated from the interaction between HTLV-2-infected CD8⁺ T cells and uninfected CD8⁺ T cells, indicating the potential for viral spread within the host.

3) HIV-1 mono-infection equilibrium in the absence of HIV-1-specific B-cell response, $\Delta_{2} = \left(U_{2}, Y_{2}, V_{2}, E_{2}, 0, 0\right)$, where

and $Y_{2}$ fulfills the following:

where

We define a function $G_{1}(Y)$ as:

Note that, $G_{1}$ is continuous on $\left(0, \frac{\zeta}{\pi}\right)$. We have

where

indicates HIV-1 mono-infection basic reproduction ratio, which determines whether or not an HIV-1 mono-infection can be established. $R_{2}$, refers to the average number of newly HIV-1-infected CD4⁺ T cells generated by a single infected cell in a situation where nearly all CD4⁺ T cells are uninfected. It provides a measure of how efficiently a virus can spread within the host at the early stages of infection, influencing whether the infection will proliferate or die out.

Since $G_{1}(0) > 0$ if $R_{2} > 1$ in addition to $\lim\limits_{Y\rightarrow \left({\frac{\zeta}{\pi}}\right) ^{-}}G_{1}(Y) = -\infty$, there exist $Y_{2}$ such that $0 < Y_{2} < \frac{\zeta}{\pi}$ and satisfies $G_{1}(Y_{2}) = 0$. Consequently, we get $U_{2} > 0, V_{2} > 0\text{ and }E_{2} > 0$.

4) HIV-1 mono-infection equilibrium with an active HIV-1-specific B-cell response, $\Delta_{3} = \left(U_{3}, Y_{3}, V_{3}, E_{3}, 0, W_{3}\right)$, where

and $Y_{3}$ fulfills the following:

where

We define a function $G_{2}(Y)$ as:

Note that $G_{2}$ is continuous on $\left(0, \frac{\zeta}{\pi}\right)$. We have $G_{2}(0) = \frac{\lambda\beta_{1}\zeta\mu}{\zeta} > 0$. Moreover, $\lim\limits_{Y\rightarrow \left({\frac{\zeta}{\pi}}\right) ^{-}} G_{2}(Y) = -\infty$, there is $Y_{3}$ such that $0 < Y_{3} < \frac{\zeta}{\pi}$ and satisfies $G_{2}(Y_{3}) = 0$. Consequently, we get

where

Here, $R_{3}$ is the activation number of HIV-1-specific B-cell response in the case of HIV-1 mono-infection. The parameter $R_{3}$ indicates whether the HIV-1-specific B-cell response will be activated in the absence of HTLV-2 infection. It serves as a threshold to assess the immune system's ability to respond to HIV-1 without the influence of co-infection, determining whether an effective immune response is triggered.

5) HTLV-2/HIV-I co-infection equilibrium in the absence of HIV-1-specific B-cell response, $\Delta_{4} = \left(U_{4}, Y_{4}, V_{4}, E_{4}, H_{4}, 0\right)$, where

where

Consequently, if $R_{4} > 1$ and $R_{5} > 1$, then the co-infection equilibrium in the absence of HIV-1-specific B-cell response, $\Delta_{4}$, exists. In this scenario, the threshold parameters $R_{4}$ and $R_{5}$ determine the likelihood of HIV-1 and HTLV-2 co-infection in the absence of an HIV-1-specific B-cell response. These values help assess whether conditions are favorable for the co-infection to establish and persist, particularly when the immune response to HIV-1 is not fully activated.

6) HTLV-2 and HIV-1 co-infection equilibrium with an active HIV-1-specific B-cell response, $\Delta_{5} = \left(U_{5}, Y_{5}, V_{5}, E_{5}, H_{5}, W_{5}\right)$, where

where

Thus, when $R_{6} > 1$ and $R_{7} > 1$, then the co-infection equilibrium with an active HIV-1-specific B-cell response, $\Delta_{5}$, exists. The parameter $R_{6}$ serves as an indicator of whether individuals infected with HIV-1 could also become co-infected with HTLV-2. It reflects the conditions under which co-infection may occur, based on the dynamics of the two viruses and the patient's immune response. In addition, $R_{7}$ indicates the activation number of HIV-1-specific B-cell response in the case HTLV-2/HIV-I co-infection. We note that

Hence, $R_{7} < R_{4}$.

□

4.   Global stability

In this section, we aim to examine the global asymptotic stability of the all model's equilibria (2.1)–(2.6) constructing Lyapunov functions ^[62] and applying Lyapunov-LaSalle asymptotic stability theorem (L-LAST) ^[63,64,65]. Define a function $S(x) = x-1-\ln x$ where $S(x)\geq0$ for all $x > 0$ and $S(1) = 0$. Furthermore, the arithmetic mean-geometric mean inequality presented below is employed to prove Theorems 1–6.

Consider the Lyapunov function candidate $L_{i}$ and define $\Lambda _{i}^{\prime}$ as the largest invariant set of

Theorem 1. The infection-free equilibrium $\Delta_{0}$ is globally asymptotically stable (GAS) if $R_{1}\leq1$ and $R_{2}\leq1$. In addition, if $R_{1} > 1$ and/or $R_{2} > 1$, then the $\Delta_{0}$ is unstable.

Proof. Define $L_{0}(U, Y, V, E, H, W)$ as:

Obviously, $L_{0}(U, Y, V, E, H, W) > 0\text{ for any }U, Y, V, E, H, W > 0\text{ and } L_{0}(U_{0}, 0, 0, E_{0}, 0, 0) = 0$. The derivative of $L_{0}$ along the solutions of system (2.1)–(2.6) can be calculated as:

By replacing the equations mentioned in model (2.1)–(2.6), we obtain

Collecting the terms and using $\lambda = dU_{0}$ and $\xi = \zeta E_{0}$, we obtain

Ultimately, we obtain

Hence, $\frac{dL_{0}}{dt}\leq0$ satisfies if $R_{1}\leq1\text{ and }R_{2}\leq1$. Moreover, $\frac{dL_{0}}{dt} = 0$ when $U = U_{0}$, $E = E_{0}$, $W = 0, \; \left(R_{2}-1\right) Y = 0\text{ and }\left(R_{1}-1\right) H = 0$. Solutions of the system tend to $\Lambda_{0}^{\prime}$ ^[66]. Any element in $\Lambda_{0}^{\prime}$ satisfies $U = U_{0}$, $E = E_{0}$, $W = 0,$

There are four cases:

(I) $R_{1} = 1$ and $R_{2} = 1$. Then from Eq (2.1) we get

From Eq (2.3) we have

Equation (2.4) suggests that

Hence $\Lambda_{0}^{\prime} = \{\Delta_{0}\}$.

(II) $R_{1} < 1$ and $R_{2} < 1$. Then from Eq (4.2) we have $Y = H = 0$ and Eq (4.3) indicates $V = 0$. Consequently, $\Lambda_{0}^{\prime } = \{\Delta_{0}\}$.

(III) $R_{1} = 1$ and $R_{2} < 1$. Then from Eq (4.2) we get $Y = 0$. Equations (4.3) and (4.5) imply $V = H = 0$. Thus $\Lambda_{0}^{\prime } = \{\Delta_{0}\}$.

(IV) $R_{1} < 1$ and $R_{2} = 1$. Equation (4.2) gives $H = 0$ while Eqs (4.3) and (4.4) give, $V = Y = 0$. Thus $\Lambda_{0}^{\prime} = \{\Delta _{0}\}$.

By L-LAST ^[63,64,65], $\Delta_{0}$ is GAS.

To establish the instability of $\Delta_{0}$ if $R_{1} > 1$ and/or $R_{2} > 1$, it is necessary to construct the Jacobian matrix $\mathcal{J} = \mathcal{J}(U, Y, V, E, H, W)$ of model (2.1)–(2.6) as:

Therefore, at $\Delta_{0}$, the characteristic equation is provided by

where $I$ is the identity matrix and $\sigma$ is the eigenvalue and

If $R_{1} > 1$ and/or $R_{2} > 1$, then $b_{0} < 0$ and/or $\tilde{b} _{0} < 0$, respectively. Hence, Eq (4.7) has positive root and then $\Delta_{0}$ is unstable. □

Theorem 2. HTLV-2 mono-infection equilibrium $\Delta_{1}$ is GAS if $R_{1} > 1$ and $R_{4}\leq1$. Moreover, if $R_{4} > 1$ then $\Delta_{1}$ is unstable.

Proof. construct $L_{1}(U, Y, V, E, H, W)$ as:

Clearly $L_{1}(U, Y, V, E, H, W) > 0\text{ for any }U, Y, V, E, H, W > 0\text{ and } L_{1}(U_{1}, 0, 0, E_{1}, H_{1}, 0) = 0$. Calculating $\frac{dL_{1}}{dt}$ as:

Collecting terms results to

By using the subsequent equilibrium conditions

we get

Thus,

Thus, if $R_{1} > 1$, $R_{4}\leq1$ and using inequality (4.1), we conclude that $\frac{dL_{1}}{dt}\leq0\text{ for any }U, Y, V, E, H, W > 0$. In addition, $\frac{dL_{1}}{dt} = 0$ if $U = U_{1}, E = E_{1}, W = 0\text{ and }\left(R_{4}-1\right) Y = 0$. $\Lambda_{1}^{\prime}$ is reached via the solutions of model (2.1)–(2.6). In $\Lambda_{1}^{\prime}$ we have $U = U_{1}, E = E_{1},$ $W = 0$ and

Two cases are at hand:

(I) $R_{4} = 1$, then from Eq (2.1)

From Eq (2.3) we have

Equation (2.4) implies that

The $\Lambda_{1}^{\prime} = \{\Delta_{1}\}$.

(II) $R_{4} < 1$, then Eq (4.8) implies that $Y = 0$ and Eqs (4.9) and (4.11) give $V = 0$ and $H = H_{1}$, respectively. Hence, $\Lambda_{1}^{\prime} = \{\Delta_{1}\}$.

Thus, by L-LAST, $\Delta_{1}$ is GAS. To determine whether $\Delta_{1}$ is unstable when $R_{4} > 1$, we compute the characteristic equation at $\Delta_{1}$ utilizing the Jacobian matrix provided in (4.6) as:

where

If $R_{4} > 1$, then $n_{0} < 0$, and hence, Eq (4.12) has a positive root. Consequently, $\Delta_{1}$ is unstable. □

Theorem 3. HIV-1 mono-infection equilibrium in the absence of HIV-1-specific B-cell response, $\Delta_{2}$ is GAS if $R_{2} > 1$, $R_{6}\leq1$ and $R_{7} \leq1$.

Proof. Define $L_{2}(U, Y, V, E, H, W)$ as:

Evidently, $L_{2}(U, Y, V, E, H, W) > 0\; \text{for any}\; U, Y, V, E, H, W > 0\; \text{and} \; L_{2}(U_{2}, Y_{2}, V_{2}, E_{2}, 0, 0) = 0$. Calculating $\frac{dL_{2}}{dt}$ as:

Collecting the above terms leads to

Utilizing the equilibrium conditions

we obtain

In case $R_{6}\leq1$ and $R_{7}\leq1$, then co-infection equilibrium with an active HIV-1-specific B-cell response $\Delta_{5}$ does not exist since $H_{5}\leq0$ and $W_{5}\leq0$. Thus,

This happens when $E_{2}\leq\frac{a_{2}}{\beta_{2}} = E_{5}$ and $V_{2}\leq \frac{\mu}{\varsigma} = V_{5}$. Then, using inequality (4.1), we obtain that $\frac{dL_{2}}{dt}\leq0$ for any $U$, $Y$, $V$, $E$, $H$, $W > 0$. Moreover, $\frac{dL_{2}}{dt} = 0$ if $U = U_{2}$, $Y = Y_{2}$, $V = V_{2}$, $E = E_{2}, \left(V_{2}-V_{5}\right) W = 0\text{ and }\left(E_{2} -E_{5}\right) H = 0$. $\Lambda_{2}^{\prime}$ is reached by the model's solutions. $\Lambda_{2}^{\prime}$ has elements with $U = U_{2}$, $Y = Y_{2}$, $V = V_{2}$, $E = E_{2}$,

We have four cases:

(I) $V_{2} = V_{5}\text{ and }E_{2} = E_{5}$. From Eq (2.4) we have

From Eq (2.3) implies that

Hence $\Lambda_{2}^{\prime} = \{\Delta_{2}\}$.

(II) $V_{2} < V_{5}\text{ and }E_{2} < E_{5}$. Then from Eq (4.13) we get $H = W = 0$. Thus $\Lambda_{2}^{\prime} = \{\Delta_{2}\}$.

(III) $V_{2} < V_{5}\text{ and }E_{2} = E_{5}$. Equation (4.13) leads to $W = 0$ while Eq (4.14) implies that $H = 0$. Thus, $\Lambda_{2}^{\prime } = \{\Delta_{2}\}$.

(IV) $V_{2} = V_{5}\text{ and }E_{2} < E_{5}$. Equations (4.13) and (4.15) imply that $H = W = 0$. Hence, $\Lambda_{2}^{\prime} = \{\Delta_{2}\}$.

Consequently, by L-LAST, $\Delta_{2}$ is GAS. □

Theorem 4. HIV-1 mono-infection equilibrium with an active HIV-1-specific B-cell response, $\Delta_{3}$ is GAS if $R_{3} > 1$, $R_{5}\leq1$.

Proof. Define $L_{3}(U, Y, V, E, H, W)$ as:

Evidently, $L_{3}(U, Y, V, E, H, W) > 0\; \text{for any}\; U, Y, V, E, H, W > 0\; \text{and} \; L_{3}(U_{3}, Y_{3}, V_{3}, E_{3}, 0, W_{3}) = 0$. Calculating $\frac{dL_{3}}{dt}$ as:

Collecting the above terms leads to

Utilizing the equilibrium conditions

We obtain

In case $R_{5}\leq1$, then $\Delta_{4}$ does not exist since $H_{4}\leq0$. Hence,

This occurs when $E_{3}\leq\frac{a_{2}}{\beta_{2}} = E_{4}$ and using inequality (4.1), we obtain that $\frac{dL_{3}}{dt}\leq0$ for any $U,$ $Y,$ $V,$ $E,$ $H,$ $W > 0$. Moreover, $\frac{dL_{3}}{dt} = 0$ if $U = U_{3}$, $Y = Y_{3}$, $V = V_{3}$, $E = E_{3}\text{ and }\left(E_{3}-E_{4}\right) H = 0$. The model's solutions converge to $\Lambda_{3}^{\prime}$ where $U = U_{3}$, $Y = Y_{3}$, $V = V_{3}$, $E = E_{3}$ and

We have two cases:

(I) $E_{3} = E_{4}$. From Eq (2.4) we have

From Eq (2.3) implies that

Hence $\Lambda_{3}^{\prime} = \{\Delta_{3}\}$.

(II) $E_{3} < E_{4}$. Then from Eq (4.16), we get $H = 0$ and from Eq (4.18), we obtain $W = W_{3}$. Thus $\Lambda_{3}^{\prime} = \{\Delta_{3}\}$.

Consequently, by L-LAST, $\Delta_{3}$ is GAS. □

Theorem 5. HTLV-2/HIV-I co-infection equilibrium in the absence of HIV-1-specific B-cell response, $\Delta_{4}$ is GAS if $R_{7}\leq1 < R_{4}$ and $R_{5} > 1$.

Proof. Define $L_{4}(U, Y, V, E, H, W)$ as:

Calculating $\frac{dL_{4}}{dt}$ as:

Then we get

Using the equilibrium conditions

we finally get

Thus, if $R_{7}\leq1 < R_{4}$ and $R_{5} > 1$ and using inequality (4.1), we conclude that $\frac{dL_{4}}{dt}\leq0\text{ for any }U, Y, V, E, H, W > 0$. In addition, $\frac{dL_{4}}{dt} = 0$ if $U = U_{4}, \; Y = Y_{4}, \; V = V_{4}, \; E = E_{4} \text{ and }\left(R_{7}-1\right) W = 0$. Solutions of model (2.1)–(2.6) converge to $\Lambda\mathcal{^{\prime}}_{4}$ where $U = U_{4}, \; Y = Y_{4}, \; V = V_{4}, \; E = E_{4}$ and

We have two cases:

(I) $R_{7} = 1$, hence from Eq (2.4)

and Eq (2.3) implies that

Hence, $\Lambda_{4}^{\prime} = \{\Delta_{4}\}$.

(II) $R_{7} < 1$, then from Eq (4.19) we get $W = 0$ and from Eq (4.20) we get $H = H_{4}$. Thus $\Lambda_{4}^{\prime} = \{\Delta_{4}\}$.

Thus, by L-LAST $\Lambda_{4}^{\prime} = \{\Delta_{4}\}$ and $\Delta _{4}$ is GAS. □

Theorem 6. HTLV-2 and HIV-1 co-infection equilibrium with an active HIV-1-specific B-cell response, $\Delta_{5}$ is GAS if $R_{6} > 1$ and $R_{7} > 1$.

Proof. Define $L_{5}(U, Y, V, E, H, W)$ as:

Evidently, $L_{5}(U, Y, V, E, H, W) > 0\text{ for any }U, Y, V, E, H, W > 0\; \text{and} \; L_{5}(U_{5}, Y_{5}, V_{5}, E_{5}, H_{5}, W_{5}) = 0$. Calculating $\frac{dL_{5} }{dt}$ as:

Collecting the above terms leads to

Utilizing the equilibrium conditions

We finally obtain

Therefore, if $R_{6} > 1$ and $R_{7} > 1$ then based on inequality (4.1), we deduce that $\frac{dL_{5}}{dt}\leq0\text{ for any }U, Y, V, E, H, W > 0$. In addition, $\frac{dL_{5}}{dt} = 0$ if $U = U_{5}, Y = Y_{5}, V = V_{5}, \text{ and }E = E_{5}$. Solutions of model (2.1)–(2.6) converge to $\Lambda_{5}^{\prime}$ where $U = U_{5}, Y = Y_{5}, V = V_{5}, E = E_{5}$ and from Eq (2.4), we get

Equation (2.3) implies that

Thus, using L-LAST, $\Lambda_{5}^{\prime} = \{\Delta_{5}\}$ and $\Delta_{5}$ is GAS. □

Table 2 provides an overview of the existence and global stability conditions for each equilibria of the model (2.1)–(2.6).

5.   Numerical simulations

In this section, we conduct numerical simulations to validate and expand on our theoretical findings, using specific parameter values to demonstrate the model's behavior under different conditions. We numerically investigate the stability of the model's equilibria, analyze the impact of HIV-1-specific B-cell response on the co-dynamics of HIV-1 and HTLV-2, and compare the proposed model with cases of HIV-1 and HTLV-2 mono-infections.

5.1.   Stability of equilibria

In this part, we solve system (2.1)–(2.6) numerically using the parameter values from Table 1. We present the numerical outcomes through graphical representations to clearly demonstrate the global stability findings outlined in Theorems 1–6. The numerical solutions of the system is performed using MATLAB solver ode45 which is widely recognized for its ability to solve ODEs efficiently. Its strengths lie in its accuracy, adaptability, robustness, and ease of use, making it highly suitable for various applications. These features make ode45 highly practical for general-purpose ODEs solving, particularly for problems where solutions are relatively smooth and do not exhibit stiff behavior.

We consider the following initial points:

We select various initial conditions just to demonstrate that, for any starting point within the feasible region, the system's solution will consistently converge to an equilibrium where the chosen parameter values meet the corresponding stability criteria.

The following circumstances result from the selection of values for the parameters $\beta_{1}$, $\beta_{2}$, $\varsigma$ and fixing $\pi = 0.0000005$:

Circumstance-1: $\beta_{1} = 0.0001$, $\beta_{2} = 0.0005$ and $\varsigma = 0.01$. Our results show that $R_{1} = 0.56 < 1$ and $R_{2} = 0.42 < 1$ for these parameter values. As seen in Figure 2, the trajectories that starting with the three different initials lead to the equilibrium $\Delta _{0} = (1000, 0, 0,333.33, 0, 0)$. This illustrates that $\Delta_{0}$ is GAS in accordance with Theorem 1. HIV-1 and HTLV-2 will be eliminated as a result of this.

Circumstance-2: $\beta_{1} = 0.0001$, $\beta_{2} = 0.002$ and $\varsigma = 0.01$. Hence, $R_{1} = 2.22 > 1$ and $R_{4} = 0.83 < 1$ are obtained. The results shown in Figure 3 show how the solutions go closer to the equilibrium $\Delta_{1} = (1000, 0, 0,150, 36.67, 0)$. As a result, Theorem 2 and the numerical results agree. This case demonstrates what occurs when an individual is infected with HTLV-2 but not HIV-1. While CD4⁺T cell concentrations are within normal limits, it is clear that HTLV-2 infection has almost led to a drop to the half in CD8⁺T cell counts.

Circumstance-3: $\beta_{1} = 0.0003$, $\beta_{2} = 0.0002$ and $\varsigma = 0.01$. Next, we compute $R_{2} = 1.27 > 1$, $R_{6} = 0.22 < 1$, and $R_{7} = 0.18 < 1$. It is clear that the standards stated in Table 2 are clearly met. Figure 4, which illustrates how the solutions converge to the equilibrium $\Delta_{2} = (785.97, 0.57, 9.08,333.34, 0, 0)$, and thus validates Theorem 3. This case demonstrates what occurs when an individual is infected only with HIV-1 in the absence of HIV-1-specific B-cell response. It is obvious that a reduction in CD4⁺T cell counts has been caused by HIV-1 infection.

Circumstance-4: $\beta_{1} = 0.0003$, $\beta_{2} = 0.0002$ and $\varsigma = 0.1$. Next, we compute $R_{3} = 1.19 > 1$ and $R_{5} = 0.22 < 1$. The conditions outlined in Table 2 are therefore evidently satisfied. As shown in Figure 5, the solutions converge to the equilibrium $\Delta_{3} = (932.84, 0.18, 2.4,333.33, 0, 4.48)$ and validates Theorem 4. This case illustrates what transpires when an individual infected only with HIV-1 and possesses an active HIV-1-specific B-cell response. Compared with circumstance-3, the concentration of uninfected CD4⁺ T cells is higher in patients with active HIV-1-specific B cells than in those who don't have it. Furthermore, the activation of HIV-1-specific B cells leads to a decrease in the concentrations of HIV-1-infected CD4⁺ T cells and HIV-1 particles. That means that HIV-1-specific B cells can control HIV-1 infection.

Circumstance-5: $\beta_{1} = 0.0005$, $\beta_{2} = 0.00093$ and $\varsigma = 0.01$. The parameters $R_{4} = 2.18 > 1$, $R_{5} = 1.03 > 1$ and $R_{7} = 0.99 < 1$ are provided by these data. As we have proven in Theorem 5, Figure 6 demonstrates that $\Delta_{4} = (458, 1.49, 23.67,322.58, 2.15, 0)$ exists and is GAS. Here, an individual has co-infections with HIV-1 and HTLV-2. Additionally, the patient may be experiencing a decline in their immune system, which could result in an increase in the symptoms of their condition. The patient might be more likely to die as a result of this.

Circumstance-6: $\beta_{1} = 0.0005$, $\beta_{2} = 0.00093$ and $\varsigma = 0.1$. The threshold parameters $R_{6} = 1.03 > 1$ and $R_{7} = 1.95 > 1$ are provided by these data. Figure 7 shows that $\Delta _{5} = (892.86, 0.3, 2.4,322.58, 2.15, 22.79)$ exists and is GAS, as we mentioned in Theorem 6. In this case, an individual has co-infections with HTLV-2 and HIV-1 with an active HIV-1-specific B-cell response. Compared to circumstance-5, the counts of uninfected CD4⁺T cells is higher, while the counts of HIV-1-infected CD4⁺ T cells and HIV-1 particles are lower. This result suggest that, even when there is HTLV-2 and HIV-1 co-infection, B cell activation is essential for infection control.

To provide additional verification, a comprehensive examination of the local stability of every given equilibrium is presented. The Jacobian matrix, denoted as $\mathcal{J} = \mathcal{J}(U, Y, V, E, H, W)$, is calculated with respect to the variables $U, Y, V, E, H$ and $W$ in the model (2.1)–(2.6) as described in (4.6). In the case of each equilibrium, the eigenvalues $\lambda_{i}, i = 1, \cdots, 6$ of $\mathcal{J}$ are computed. An equilibrium is considered to be locally stable if the eigenvalues of the system satisfy $\operatorname{Re}(\lambda_{i}) < 0$ for all $i = 1, 2, \cdots, 6$. By doing calculations for every nonnegative equilibrium points and utilizing the parameter values specified in Circumstance 1–6, we infer the eigenvalues associated with each equilibria. In Table 3, the positive equilibria and the real part of the eigenvalues are presented. These result support the global stability results provided in Theorem 1–6.

5.2.   Effect of HIV-1-specific B-cell response on the HTLV-2 and HIV-1 co-dynamics

This subsection examines the impact of stimulated rate constants of HIV-1-specific B-cell, denoted as $\varsigma$, on the system dynamics described by (2.1)–(2.6). To investigate the impact of HIV-1-specific B cells on the model's solutions, we hold the values of $\beta_{1} = 0.0007$, $\beta_{2} = 0.0009$, and $\pi = 0.0000005$ while varying the parameter $\varsigma$. By choosing the following initial points:

We can see from Figure 8 that as $\varsigma$ increases, the numbers of uninfected CD4⁺ T cells increase. In contrast, the numbers of HIV-1-infected CD4⁺T cells and free HIV-1 decrease. It is noteworthy to mention that an increase in the HIV-1-specific B cells does not have an effect on the numbers of uninfected CD8⁺T cells and HTLV-2-infected CD8⁺T cells. Consequently, HIV-1-specific B cells aid only in the controlling of HIV-1 infection. Due to the fact that $R_{1}$ and $R_{2}$ are independent of $\varsigma$, increasing $\varsigma$ does not result in the attainment of $\Delta_{0}$. As a result, HIV-1-specific B cells can't completely eradicate the HIV-1 infections; however, they are useful in suppressing HIV-1 progression.

5.3.   Comparison results

In this section, we present a comparison of the dynamics of HTLV-2 or HIV-1 mono-infection and HTLV-2 and HIV-1 co-infection. Our aim is to examine the influence of HTLV-2 or HIV-1 mono-infection on each other. In this part we will fix the value of $\pi = 0.2$ and $\varsigma = 0.1$.

5.3.1.   Comparison between HIV-1 mono-infection and HTLV-2 and HIV-1 co-infection

We compare the solutions of the HTLV-2 and HIV-1 co-infection model, represented by Eqs (2.1)–(2.6), with the solutions of the following HIV-1 mono-infection with HIV-1-specific B-cell response system (5.1)–(5.5):

We choose the values of the parameters $\beta_{1} = 0.001$ and $\beta_{2} = 0.002$, together with the given initial condition:

The solutions of two systems, denoted as (2.1)–(2.6) and (5.1)–(5.5), are presented in Figure 9. We can see from Figure 9 that, HIV-1-positive individuals who also have HTLV-2 infection had lower levels of free HIV-1 and uninfected CD8⁺ T cells and higher levels of HIV-1-specific B cells. We also observe from Figure 9 that after co-infection, the quantity of uninfected CD4⁺ T cells remains unchanged. Note that

Thus, $W_{5}$ is an increasing function of the HTLV-2 infection rate constant $\beta_{2}$. This suggests that the presence of HTLV-2 may activate B cells specific to HIV-1, which might lead to a drop in the HIV-1's level. These results are consistent with the findings of other studies (see e.g., ^[67,68]) showing that co-infection with HTLV-2 is linked to the ability to control HIV-1 replication, the higher chance of survival and the delayed onset of AIDS. HTLV-2 may work as a barrier against HIV-1 infection ^[69].

5.3.2.   Comparison between HTLV-2 mono-infection and HTLV-2 and HIV-1 co-infection

We compare the solutions of the HTLV-2 and HIV-1 co-infection model (2.1)–(2.6) with the solutions of the HTLV-2 mono-infection system.

We select the values $\beta_{1} = 0.007$ and $\beta_{2} = 0.003$ in addition to use the subsequent initial condition:

Solutions of the two systems (2.1)–(2.6) and (5.6)–(5.7) that are illustrated in Figure 10. It can be seen the numbers of uninfected CD8⁺T cells in both systems gradually tend to the same values. The numbers of HTLV-2-infected CD8⁺ T cells are more prevalent in HTLV-2 and HIV-1 co-infection patients than in HTLV-2 mono-infection patients. Nevertheless, in the context of HIV-1 infection, the emergence of malignant CD8⁺T-lymphoproliferative diseases appears to be feasible. It is anticipated that people who are co-infected with HTLV-2 and HIV-1 may experience a greater occurrence of HTLV-2-related T-cell malignant diseases ^[1]. This may be an explanation for why the number of HTLV-2-infected CD8⁺T cells is higher in patients with co-infection with HIV-1 compared to those without it as shown in Figure 10(b).

6.   Conclusions and discussion

HTLV-2 and HIV-1 are both retroviruses that target different immune cells–HTLV-2 infects CD8⁺ T cells, while HIV-1 primarily targets CD4⁺ T cells. Several studies have documented cases of patients co-infected with HTLV-2 and HIV-1. To optimize treatment strategies for such coinfections, mathematical models have been developed to better understand the interactions between these viruses and their effects on the immune system. These models help in predicting disease progression and evaluating potential therapeutic approaches. In this article, we propose a new mathematical model that describes the co-dynamics of HIV-1 and HTLV-2 in vivo. The model was given as a system of nonlinear ODEs, which describes the interactions between six compartments: uninfected CD4⁺ T cells, HIV-1-infected CD4⁺ T cells, HIV-1 particles, uninfected CD8⁺ T cells, HTLV-2-infected CD8⁺ T cells, and HIV-1-specific B cells. Initially, we demonstrated that the model's solutions are bounded and non-negative. Additionally, we identified six equilibrium points, with their existence and stability conditions described in terms of seven threshold parameters. A summary of all the equilibria presented in our model is given as follows:

● Infection-free equilibrium, $\Delta_{0}$, which usually exists. When $R_{1}\leq1$ and $R_{2}\leq1$, $\Delta_{0}$ is GAS. HTLV-2 and HIV-1 will be eradicated as a consequence of this. From a control perspective, making $R_{1}\leq1$ and $R_{2}\leq1$ would be an effective strategy. Controlling these parameters through the effectiveness of antiviral drugs. For physicians and researchers, curing patients of chronic viral co-infections such as HTLV2 and HIV-1 is a top priority. Effective antiviral medication can stop viruses from replicating and lower $R_{1}$ and $R_{2}$ to less than one. There is no specific antiviral treatment approved for HTLV-2. Unlike HIV-1, where antiretroviral therapy (ART) is well-established.

● HTLV-2 mono-infection equilibrium, $\Delta_{1}$, exists if $R_{1} > 1$ and is GAS if $R_{4}\leq1$. An individual who is infected with only HTLV-2 is the outcome illustrated in this case.

● HIV-1 mono-infection equilibrium in the absence of HIV-1-specific B-cell response, $\Delta_{2}$ is presented if $R_{2} > 1$ and is GAS if $R_{6}\leq1$ and $R_{7}\leq 1$. This case illustrates the consequences that ensue when an individual acquires only HIV-1 infection in the absence of HIV-1-specific B-cell response. This could be due to the body's low concentration of HIV-1 particles (i.e., $V\leq\mu/\varsigma$), which could not be sufficient to elicit an immune response.

● HIV-1 mono-infection equilibrium with an active HIV-1-specific B-cell response, $\Delta_{3}$ exists when $R_{3} > 1$ and is GAS when $R_{5}\leq1$. This case study the outcomes that occur when an individual is only infected with HIV-1 and exhibits an active HIV-1-specific B-cell response. The body contains enough free HIV-1 particles (i.e., $V > \mu/\varsigma$) in this case to activate the immune system.

● HTLV-2 and HIV-1 co-infection equilibrium in the absence of HIV-1-specific B-cell response, $\Delta_{4}$, exists when $R_{4} > 1$ and $R_{5} > 1$. Moreover, $\Delta_{4}$ is GAS if $R_{7}\leq1$. In this case, an individual is co-infected with HTLV-2 and HIV-1, but without HIV-1-specific B-cell response.

● HTLV-2 and HIV-1 co-infection equilibrium with an active HIV-1-specific B-cell response, $\Delta_{5}$ exists and is GAS if $R_{6} > 1$ and $R_{7} > 1$. A person in this instance is co-infected with HTLV-2 and HIV-1 and has an active HIV-1-specific B-cell response. This instance demonstrates that B-cell activation is a crucial factor in infection control.

The global asymptotic stability of all equilibria was established by constructing appropriate Lyapunov functions and utilizing the Lyapunov-LaSalle asymptotic stability theorem. We have provided numerical simulations to demonstrate the validity and robustness of our theoretical findings. We observed that the numerical and analytical results align closely, demonstrating consistency between the two approaches. The influence of HIV-1-specific B-cell response on the dynamics of HTLV-2 and HIV-1 co-infection was presented. We demonstrated that increasing the stimulation rate of the HIV-1-specific B-cell response in HTLV-2 and HIV-1 co-infection enhances the concentration of CD4⁺ T cells and reduces the level of free HIV-1 particles, thereby boosting the immune system's overall effectiveness. Therefore, HIV-1-specific B-cell response plays the role of controlling and suppressing HIV-1 progression. We compared between HIV-1 or HTLV-2 mono-infection with HTLV-2 and HIV-1 co-infection, separately. We observed that patients with HIV-1 who are also infected with HTLV-2 had larger levels of HIV-1-specific B cells and lower levels of uninfected CD8⁺ T cells and HIV-1. Furthermore, we note that following co-infection, the behavior dynamics of uninfected CD4⁺ T cells did not alter. These outcomes agree with prior research (see ^[70]), which indicates that co-infection with HTLV-2 is associated with the capacity to regulate HIV-1 replication, a greater likelihood of survival, and a postponed start of AIDS. However, co-infected patients with HTLV-2 and HIV-1 may experience a greater occurrence of HTLV-2-related T-cell malignant diseases.

When comparing HTLV-1 and HIV-1 co-infection and HTLV-2 and HIV-1 co-infection, studies such as ^[10] report that HTLV-1 co-infection can worsen the clinical course of HIV-1, accelerating progression to AIDS and complicating treatment. In contrast, HIV-1 and HTLV-2 co-infection appears to be more benign, showing a neutral or even protective association, with delayed AIDS progression, longer survival, and reduced mortality rates ^[71].

The main limitation of our study is the inability to estimate the model's parameter values using real data. This is due to several factors: Comprehensive data on HTLV-2 and HIV-1 co-infection is scarce, even though some data exists for patients with single HTLV-2 or HIV-1 infections. Moreover, comparing our results to a limited number of available studies may not yield reliable conclusions. Furthermore, obtaining real patient data for HTLV-2 and HIV-1 co-infection remains challenging.

This study could be extended by: (ⅰ) Employing real data to accurately estimate parameter values, (ⅱ) accounting for viral mutation, (ⅲ) developing the model using fractional differential equations to explore the effects of memory on viral co-dynamics, and (ⅳ) integrating reaction-diffusion dynamics and stochastic interactions. Additionally, the model can be treated as a nonlinear control system, where antiviral drug efficacy functions as the control input. Then, one can focus on designing optimal control strategies based on this framework. These research areas require further investigation, and we reserve them for future studies.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This Project was funded by the Deanship of Scientific Research (DSR) at King Abdulaziz University, Jeddah, Saudi Arabia, under grant No. (GPIP-283-130-2024). The authors, therefore, acknowledge with thanks DSR for technical and financial support.

Conflict of interest

The authors declare there is no conflicts of interest.