Non-fragile sampled-data control for synchronizing Markov jump Lur'e systems with time-variant delay

1.   Introduction

In the modern fields of scientific research and medical diagnostics ^[1,2,3], there is an increasing reliance on image restoration techniques ^[4,5,6,7], which are particularly prominent in the field of medical imaging. Ensuring image quality is paramount for the authenticity of data ^[8]. By processing X-ray projection data obtained from CT scans, we can reconstruct clear tomographic images with a resolution of $n\times n$ pixels. This technology encompasses two main schools: mathematical theoretical analysis ^[9] and iterative methods ^[10]. The former, like the filtered back projection method ^[11], is widely used in fields such as CT imaging, while the latter excels in dealing with noise interference and data loss. With technological advancements, image restoration is moving toward greater precision and efficiency.

To reconstruct images, we must solve a large-scale system of linear equations with multiple righthand sides, which is presented as follows:

In contemporary mathematics and engineering, solving systems of equations stands as a pivotal task, particularly in scientific research and industrial applications where efficiency and precision are of paramount importance. A variety of numerical methods have been widely adopted ^{[12,13,14,15]}, among which the Kaczmarz algorithm ^[16] is renowned for its iterative projection approach in approximating the true solution. The algorithm's simplicity has facilitated its application across various domains, including image reconstruction ^[12,17], medical imaging ^[11,18], and signal processing ^[19,20]. Advances in technology have given rise to multiple enhanced versions of the Kaczmarz algorithm ^{[21,22,23,24,25,26,27,28,29,30,31]}, improving performance in large-scale parallel computing and noisy data environments. Notably, with the development of free pseudo-inverse techniques, Du and Sun ^[24] further extended the randomized extended average block Kaczmar (REABK) method, proposing a class of pseudo-inverse-free stochastic block iterative methods for solving both consistent and inconsistent systems of linear equations, Free pseudo-inverse can accelerate convergence speed. Pseudo-inverse approximation is a specific case of generalized inverse techniques. For more theoretical analysis and applications, refer to literature ^[32]. Inspired by references ^[33,34], this paper introduces a faster lazy free greedy block Kaczmarz (LFGBK) method, exploring matrix sketching techniques as a key tool for accelerating matrix operations. This method employs sampling based on an approximate maximum distance criterion, excelling at selecting small, representative samples from large datasets for more efficient computation. The adaptive randomized block Kaczmarz (ARBK) ^[35] algorithm integrates adaptive and randomized block selection strategies. However, under certain specific matrix structures, ARBK may experience slow convergence or even fail to converge. Additionally, when dealing with large-scale sparse matrices, the ARBK algorithm incurs significant memory overhead. Our improved algorithm successfully overcomes these drawbacks, offering a more stable and efficient solution.

Additionally, it not only addresses single righthand side linear equations but also extends to multiple righthand side linear equations, solving the memory overflow issues that traditional algorithms face when dealing with image processing vectors. A comprehensive theoretical framework supports the convergence of these methods. Numerical experiments validate its effectiveness, demonstrating improved computational efficiency and laying a solid foundation for further optimization of matrix sketching techniques.

The structure of this paper is as follows: Section 2 introduces the necessary background knowledge. Section 3 presents the faster free pseudo-inverse GBK method for solving single righthand side linear equation systems. Section 4 proposes the leverage score sampling free pseudo-inverse GBK method for solving multiple righthand side linear equation systems. Section 5 details the numerical experiments, and Section 6 concludes the paper.

2.   Knowledge preparation

In this article, we adopt the same notation as in reference ^[27]. For example, ${A}_{\left(i\right)}, {A}^{T}, {A}^{†}, ||A||, {||A||}_{F},$ and $\left[n\right]$, respectively, represent the i-th row of the coefficient matrix A, transpose, generalized inverse, spectral norm, F-norm, and the set $\{\mathrm{1, 2}, \dots , n\}$.

Recently, Niu and Zheng combined greedy strategy with the block Kaczmarz method, proposing the GBK ^[29] method for solving large-scale consistent linear equation systems. See Algorithm 1 for the specific process.

Convergence analysis of the GBK method is described as follows:

Theorem 1 (^[29]) If the linear system of Eq (1) is consistent, then the iterative sequence ${\left\{{x}_{k}\right\}}_{k = 0}^{\infty }$ generated by algorithm 1 converges to the minimum norm solution ${x}_{*} = {A}^{†}b$ of the system of equations, and satisfies for any $k\ge 0$,

The formula for ${\gamma }_{k}\left(\eta \right)$ is defined as follows: ${\gamma }_{k}\left(\eta \right) = \eta \frac{{||A||}_{F}^{2}}{{||A||}_{F}^{2}-{||{A}_{{\mathcal{T}}_{k-1}}||}_{F}^{2}}\frac{{||{A}_{{\mathcal{T}}_{k}}||}_{F}^{2}}{{\sigma }_{max}^{2}\left({A}_{{\mathcal{T}}_{k}}\right)}$. Here, ${\gamma }_{0\left(\eta \right)}$ is defined as $\eta \frac{{||{A}_{{\mathcal{T}}_{0}}||}_{F}^{2}}{{\sigma }_{max}^{2}\left({A}_{{\mathcal{T}}_{0}}\right)}$, where $\eta$ is in the range $\left(\mathrm{0, 1}\right]$, and ${\sigma }_{min}\left(A\right)$ and ${\sigma }_{max}\left(A\right)$ represent the nonzero minimum singular value and maximum singular value of matrix $A$.

In the matrix sketching technique, as described in leverage score sampling ^[36,37], we select samples based on the leverage score of each row. Specifically, we will choose each row with a probability proportional to its leverage score. Therefore, rows with higher scores (i.e., rows with greater influence in the dataset) will have a greater chance of being selected.

The advantage of this sampling method lies in its ability to select a small, representative subset of samples from a large dataset, enabling more efficient computation. The resulting sample set $S\in {R}^{d\times m}$, where $d$ is the chosen number of samples, can be utilized to estimate various properties of the original matrix $A$, such as singular value decomposition, principal component analysis, and so on. The LFGBK algorithm is similar to the derivation process in reference ^[38].

Remark: In addition to the method proposed in this paper, there are other sampling techniques such as random Gaussian matrices, subsampled randomized Hadamard transform (SRHT), and uniform sampling. In previous experiments, we also tried other methods like random sparse sampling. Through comparison, we found that the method proposed in this paper excels in extracting the main features of matrices. Other methods not only have higher computational complexity but may also extract all-zero vectors during actual image processing, rendering calculations impossible. Our method effectively avoids these issues, which is why we chose to adopt it.

3.   Fast free pseudo-inverse GBK method for solving single righthand side linear equation systems

This chapter introduces an algorithm, namely, the leverage score sampling free pseudo-inverse GBK method for single righthand side, and provides a proof of the corresponding convergence theory for the algorithm.

First, each step follows the approximate maximum illustration principle.

Second, select the index set ${\mathcal{T}}_{k}$ for the block matrix ${A}_{{\mathcal{T}}_{k}}$; then, project the current estimate onto each row forming the block matrix ${A}_{{\mathcal{T}}_{k}}$; finally, calculate the average of the projections to determine the next iteration.

Before presenting the convergence theory for Algorithm 3, let us first introduce a lemma.

Lemma 1 (^[27]): If any vector $u$ belongs to the range of ${A}^{T}$, then

Theorem 2: The leverage score transformation S satisfies $d = O({n}^{2}/\mathrm{\delta }{\theta }^{2})$, and ${x}_{*} = {A}^{†}b$ is the minimum norm solution of the single righthand side linear equation systems, for any k ≥ 0.

The function ${\widetilde {\psi }}_{k}\left(\eta \right) = \eta t\left(\frac{2}{t}-\frac{1}{{t}^{2}}{\sigma }_{max}^{2}\left({\widehat{A}}_{{\mathcal{T}}_{k}}^{T}\right)\right){\sigma }_{min}^{2}, \eta \in \left(\mathrm{0, 1}\right],$ where $range\left(A\right), {\sigma }_{min}\left(A\right),$ and ${\sigma }_{max}\left(A\right)$ represent the range, nonzero minimum singular value, and maximum singular value of matrix $A$, respectively.

Proof. With algorithm 3 and ${\widetilde {r}}_{k} = \widetilde {b}-\widetilde {A}{x}_{k}$, we can obtain

Expand Eq (3) with the set $\left|{\mathcal{T}}_{k}\right| = t$ and ${\mathcal{T}}_{k} = \left\{{j}_{{k}_{1}}, \dots , {j}_{{k}_{t}}\right\}$.

Among them

and

Subtracting ${x}_{*}$ from Eq (4) simultaneously yields

Taking the spectral norm and squaring both sides of Eq (7), and for any positive semi-definite matrix Q, satisfying ${Q}^{2}\preccurlyeq {\lambda }_{max}\left(Q\right)Q$, we can obtain

Using Eq (5) and the inequality ${\left|{\widetilde {b}}_{{j}_{k}}-{\widetilde {A}}_{\left({j}_{k}\right)}{x}_{k}\right|}^{2}\ge {\widetilde {\varepsilon }}_{k}{||{\widetilde {A}}_{\left({j}_{k}\right)}||}_{2}^{2}$, a straightforward calculation yields.

Substituting ${\widetilde {\varepsilon }}_{k} = \eta \genfrac{}{}{0pt}{}{max}{1\le i\le d}\left\{\frac{{\left|{\widetilde {b}}_{i}-{\widetilde {A}}_{\left(i\right){x}_{k}}\right|}^{2}}{{||{\widetilde {A}}_{\left(i\right)}||}_{2}^{2}}\right\}$ into the above equation yields the following result:

Given ${x}_{0}\in range\left({A}^{T}\right)$ and ${x}_{*} = {A}^{†}b$, we have ${{x}_{k}-x}_{*}\in range\left({A}^{T}\right)$. Therefore, by Lemma 1, we can conclude that

$\ge {\lambda }_{min}^{2}\left({\widetilde {A}}^{T}\widetilde {A}\right){||{{x}_{k}-x}_{\mathrm{*}}||}_{2}^{2}$ Combining the above equation, we can obtain the following

From Eqs (8) and (12), we can obtain Eq (2), and the iterative sequence ${\left\{{x}_{k}\right\}}_{k = 0}^{\infty }$ converges to the minimum norm solution ${x}_{*} = {A}^{†}b$ of the system of equations. Hence, Theorem 2 is proved.

4.   Solving multiple righthand side linear systems with leverage score sampling free pseudo-inverse GBK method

In this chapter, we introduce an algorithm known as the multi-righthand-side leverage score sampling free pseudo-inverse GBK method, and we provide a proof for the corresponding convergence theory of the algorithm.

For most image reconstruction, the system of equations is formulated as follows:

In the context, $A\in {R}^{m\times n}, X = \left[{x}_{1}, {x}_{2}, \dots , {x}_{d}\right]\in {R}^{n\times d}, B = \left[{b}_{1}, {b}_{2}, \dots , {b}_{d}\right]\in {R}^{m\times d}, d > 1$. This paper addresses the solution of multiple righthand side linear equation systems and initially presents the index set for each iteration selection in the multiple righthand side linear equation systems.

Iterate through the following steps:

To solve systems of linear equations with multiple righthand sides, our approach involves working with the $j$ righthand side vector ${b}_{j}$ by selecting the working row ${\mathcal{T}}_{{k}_{j}}$ according to the criterion established in Eq (15).

The iterative formula corresponding to the solution at the $j$ right endpoint is as follows:

According to the criterion for selecting the index set in Eq (15), each term on the righthand side corresponds to the selection of a working row. For the system of linear equations with multiple righthand terms as in Eq (13), the Kaczmarz method can be extended to an iterative format that simultaneously solves for the righthand side system of linear equations.

In this context, ${X}^{(k+1)} = ({x}_{1}^{\left(k+1\right)}, {x}_{2}^{\left(k+1\right)}, \dots , {x}_{d}^{\left(k+1\right)})$ represents the approximate solution at the $k+1$ iteration.

To reduce computational effort, Algorithm 2 is employed to extract certain rows from matrix A corresponding to the index set ${\mathcal{T}}_{{k}_{j}}$. The sub-matrix formed by these rows is denoted as $\widetilde {A},$, while the sub-matrix of B corresponding to the index set ${\mathcal{T}}_{k}$ is denoted as $\widetilde {B}$. The specific configurations of $\widetilde {A}$ and $\widetilde {B}$ are as follows.

and

The transposed matrix ${B}_{{\mathcal{T}}_{{k}_{{j}_{i}}}}^{T}$ is represented as $\left({B}_{\left({\mathcal{T}}_{{k}_{{j}_{i}}}, 1\right)}, {B}_{\left({\mathcal{T}}_{{k}_{{j}_{i}}}, 2\right)}, \dots , {B}_{\left({\mathcal{T}}_{{k}_{{j}_{i}}}, d\right)}\right)$, where ${\mathcal{T}}_{{k}_{{j}_{i}}}$ is an element of the index set ${\mathcal{T}}_{{k}_{j}}$. Here, ${B}_{\left({\mathcal{T}}_{{k}_{{j}_{i}}}, t\right)}$ denotes the element in the $i$ row and $t$ column of the sub-matrix $\widetilde {B}$, and $\left|{\mathcal{T}}_{{k}_{j}}\right|$ denotes the number of row indices contained in the index set ${\mathcal{T}}_{{k}_{j}}$ with $\left|{\mathcal{T}}_{{k}_{j}}\right|$ equal to $t$.

The multi-righthand-side method proposed in this paper is a specialized block approach for solving large-scale righthand side linear equations using a leverage-based pseudo-inverse GBK method. We provide a detailed framework for this method, which involves simultaneous computation of multiple righthand sides, with each iteration involving a matrix $B\in {R}^{m\times t}$ containing $t$ righthand sides, resulting in the selection of $t$ row indices.

This article exclusively discusses the scenario where ${\alpha }_{k}$ equals $1$. The convergence theory for solving large-scale righthand side linear equation groups with the LFGBK method is presented below:

Theorem 3: Assume that the linear equation system (13) is consistent, and so are its extracted subsystems. The iterative sequence ${X}^{\left(k\right)}$ from $k = 0$ to infinity, generated by Algorithm 4 starting from the initial value ${x}_{0}$, converges to the least squares solution ${X}^{*} = {A}^{†}B$. The expected error for the iterative sequence solutions ${X}^{\left(k\right)}$ from $k = 0$ to infinity is:

The tilde-decorated $A$ and $B$, denoted as $\widetilde {A}$ and $\widetilde {B}$, respectively, represent the sub-matrices formed by the rows corresponding to the index set ${\mathcal{T}}_{{k}_{j}}$ within matrices $A$ and $B$.

Proof. According to Algorithm 4 and reference ^[39], we have

Since ${X}^{*} = {A}^{†}B$ is the least squares solution, we infer that ${x}_{j}^{*} = {A}^{†}{B}_{(:, j)}$ for $j = \mathrm{1, 2}, \dots , d$, where ${B}_{(:, j)}$ denotes the $j$ column of matrix $B$.

Further,

For $j = \mathrm{1, 2}, \dots , d$, it can be deduced that

Then

The specific details of the term $E{||{x}_{j}^{\left(k+1\right)}-{x}_{j}^{k}||}_{2}^{2}$ are elaborated in the proof of Theorem 3.2 in ^[39].

Due to

In this context, ${\widetilde {B}}_{\left(:, j\right)}$ denotes the $j$ column of the matrix $\widetilde {B}$.

Thus, by combining Eqs (20) and (22), we can derive inequality (19).

The proof of Theorem 3 reveals that the convergence rate of Algorithm 4 is related to the sub-matrix $\widetilde {A}$ sampled during each leveraged iteration.

5.   Numerical experiment

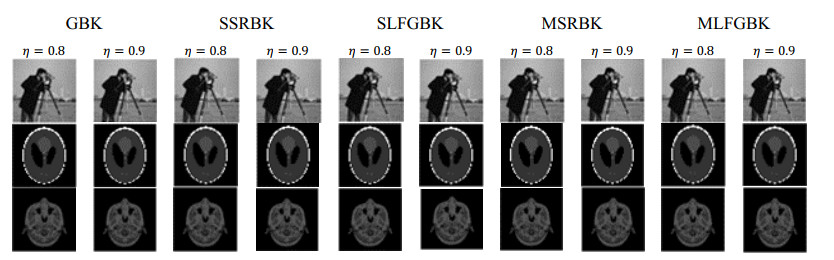
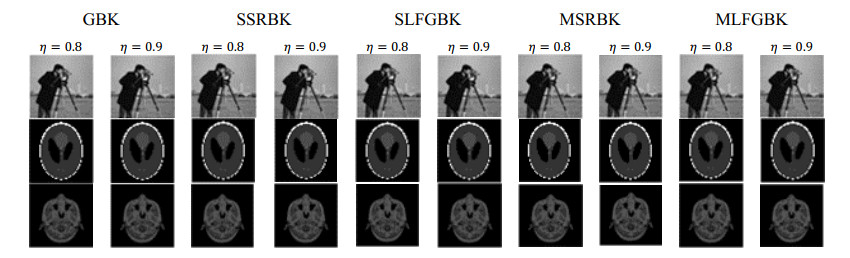
In this section, we evaluate the effectiveness of large-scale image restoration equations using several algorithms through comparative examples: the GBK method ^[29], the semi-stochastic block Kaczmarz method with simple random sampling for single righthand sides ^[40], the LFGBK method for single righthand sides, the semi-stochastic block Kaczmarz method with simple random sampling for multiple righthand sides ^[40], and the LFGBK method for multiple righthand sides. All experiments are implemented in MATLAB, with metrics such as peak signal-to-noise ratio (PSNR), structural similarity index (SSIM), mean squared error (MSE), and computational time (CPU in seconds) reported. Following the approach of ^[27], the PSNR, SSIM, MSE, and CPU metrics reflect the average iterations and computational time needed for 50 repeated calculations. During all computations, we initialize the matrix $x = zeros(n, m)$ and set the righthand side $B = AX$, where $X$ represents images from MATLAB's Cameraman, Phantom, and Mri datasets, each sized $100\times 100$. Matrix $A$ is constructed with elements corresponding to the product of the number of X-ray beams (4), the range of scanning angles t (0° to 179°), and the image pixels. The stopping criterion is set as $RSE = \frac{{||{X}_{k}-{X}_{*}||}_{2}^{2}}{{||{X}_{*}||}_{2}^{2}}\le {10}^{-6}$. In practice, the condition $O({n}^{2}/\delta {\theta }^{2})$ is quite stringent, but in many real-world computations, a sketching factor of $d = {n}^{2}$ yields satisfactory results. We consider matrices $A\in {\mathbb{R}}^{(4*180*n, m)}$ of two types: type a, generated by radon(), and type b, generated by randn().

Based on the numerical results from Tables 1 and 2, when variable A is generated using radon, we can draw the following conclusions: ⅰ) The GBK method, single righthand side SRBK (single RHS SRBK) method, single RHS LFGBK method, multiple righthand side SRBK (multiple RHS SRBK) method, and multiple RHS LFGBK method all demonstrate effectiveness in solving equation systems for image restoration. ⅱ) The GBK method, single RHS SRBK method, single RHS LFGBK method, multiple RHS SRBK method, and multiple RHS LFGBK method show similar restoration quality; however, the single RHS LFGBK and multiple RHS LFGBK methods significantly outperform the GBK, Single RHS SRBK, and Multiple RHS SRBK methods in terms of time efficiency. ⅲ) The LFGBK method exhibits superior acceleration effects at η = 0.9 compared to η = 0.8. ⅳ) The MLFGBK method displays more pronounced acceleration effects at η = 0.9 than at η = 0.8.

Based on the numerical results from Tables 3 and 4, when variable A is generated using randn, we can draw the following conclusions: ⅰ) The GBK method, single RHS SRBK method, single RHS LFGBK method, multiple RHS SRBK method, and multiple RHS LFGBK method all demonstrate effectiveness in solving equation systems for image restoration. ⅱ) The GBK method, single RHS SRBK method, single RHS LFGBK method, multiple RHS SRBK method, and multiple RHS LFGBK method show similar restoration quality; however, the Single RHS LFGBK and Multiple RHS LFGBK methods significantly outperform the GBK, single RHS SRBK, and multiple RHS SRBK methods in terms of time efficiency. ⅲ) The LFGBK method exhibits superior acceleration effects at η = 0.9 compared to η = 0.8. ⅳ) The MLFGBK method displays more pronounced acceleration effects at η = 0.9 than at η = 0.8.

6.   Conclusions

This study aims to explore a new image reconstruction algorithm, the LFGBK method, which utilizes a greedy strategy. The core of this method lies in transforming the image reconstruction problem into solving a linear system problem with multiple righthand sides. In traditional Kaczmarz algorithms, the iterative process of gradually approaching the solution is often inefficient and susceptible to the influence of initial value selection. However, the LFGBK method introduces leverage score sampling and extends from solving single righthand side linear equations to solving multiple righthand side linear equations, which is crucial for handling large-scale problems due to the time-consuming and resource-intensive nature of pseudo-inverse computation on large matrices. By avoiding pseudo-inverse calculation, the LFGBK method significantly improves the algorithm's computational efficiency. To validate the effectiveness of the proposed algorithm, this study conducts in-depth research through theoretical analysis and simulation experiments. The theoretical analysis confirms the convergence of the LFGBK method, ensuring the reliability and stability of the algorithm. The simulation experiments, compared with traditional Filtered Back Projection (FBP) methods, demonstrate the advantages of LFGBK in terms of image reconstruction quality. The experimental results show that the LFGBK method significantly preserves image details and reduces noise, proving its practicality and superiority in image reconstruction tasks.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Conflict of interest

The authors declare there is no conflict of interest.