Some identities of degenerate multi-poly-Changhee polynomials and numbers

Sang Jo Yun; Sangbeom Park; Jin-Woo Park; Jongkyum Kwon; Sang Jo Yun; Sangbeom Park; Jin-Woo Park; Jongkyum Kwon

doi:10.3934/era.2023367

Electronic Research Archive

2023, Volume 31, Issue 12: 7244-7255. doi: 10.3934/era.2023367

Previous Article Next Article

Research article Special Issues

Some identities of degenerate multi-poly-Changhee polynomials and numbers

1.
Department of Mathematics, Dong-A University, Busan 604-714, Korea
2.
Department of Mathematics, Kyungpook National University, Daegu 41566, Korea
3.
Department of Mathematics Education, Daegu University, Gyeongsan 38453, Korea
4.
Department of Mathematics Education, Gyeongsang National University, Jinju 52828, Korea
^† These authors contributed equally to this work

Received: 03 August 2023 Revised: 19 October 2023 Accepted: 05 November 2023 Published: 13 November 2023

Recently, many researchers studied the degenerate multi-special polynomials as degenerate versions of the multi-special polynomials and obtained some identities and properties of the those polynomials. The aim of this paper was to introduce the degenerate multi-poly-Changhee polynomials arising from multiple logarithms and investigate some interesting identities and properties of these polynomials that determine the relationship between multi-poly-Changhee polynomials, the Stirling numbers of the second kind, degenerate Stirling numbers of the first kind and falling factorial sequences. In addition, we investigated the phenomenon of scattering the zeros of these polynomials.

Keywords:

degenerate multi-poly-Changhee polynomials,
multiple logarithm,
the zeros of polynomials

Citation: Sang Jo Yun, Sangbeom Park, Jin-Woo Park, Jongkyum Kwon. Some identities of degenerate multi-poly-Changhee polynomials and numbers[J]. Electronic Research Archive, 2023, 31(12): 7244-7255. doi: 10.3934/era.2023367

Related Papers:

[1]	Dojin Kim, Sangbeom Park, Jongkyum Kwon . Some identities of degenerate higher-order Daehee polynomials based on $ \lambda $-umbral calculus. Electronic Research Archive, 2023, 31(6): 3064-3085. doi: 10.3934/era.2023155
[2]	Jian Cao, José Luis López-Bonilla, Feng Qi . Three identities and a determinantal formula for differences between Bernoulli polynomials and numbers. Electronic Research Archive, 2024, 32(1): 224-240. doi: 10.3934/era.2024011
[3]	Ibtissam Issa, Zayd Hajjej . Stabilization for a degenerate wave equation with drift and potential term with boundary fractional derivative control. Electronic Research Archive, 2024, 32(8): 4926-4953. doi: 10.3934/era.2024227
[4]	Qingjie Chai, Hanyu Wei . The binomial sums for four types of polynomials involving floor and ceiling functions. Electronic Research Archive, 2025, 33(3): 1384-1397. doi: 10.3934/era.2025064
[5]	Mohammad Kafini, Maher Noor . Delayed wave equation with logarithmic variable-exponent nonlinearity. Electronic Research Archive, 2023, 31(5): 2974-2993. doi: 10.3934/era.2023150
[6]	Licui Zheng, Dongmei Li, Jinwang Liu . Some improvements for the algorithm of Gröbner bases over dual valuation domain. Electronic Research Archive, 2023, 31(7): 3999-4010. doi: 10.3934/era.2023203
[7]	Tian-Xiao He, Peter J.-S. Shiue, Zihan Nie, Minghao Chen . Recursive sequences and girard-waring identities with applications in sequence transformation. Electronic Research Archive, 2020, 28(2): 1049-1062. doi: 10.3934/era.2020057
[8]	Tian-Xiao He, Peter J.-S. Shiue . Identities for linear recursive sequences of order $ 2 $. Electronic Research Archive, 2021, 29(5): 3489-3507. doi: 10.3934/era.2021049
[9]	Li Wang, Yuanyuan Meng . Generalized polynomial exponential sums and their fourth power mean. Electronic Research Archive, 2023, 31(7): 4313-4323. doi: 10.3934/era.2023220
[10]	Bin Han . Some multivariate polynomials for doubled permutations. Electronic Research Archive, 2021, 29(2): 1925-1944. doi: 10.3934/era.2020098

Abstract

1. Introduction

Carlitz ^[1] initiated a degenerate exponential function for the generalization of the Stirling numbers and attempted to generalize Bernoulli and Eulerian numbers using these functions in 1979. Since then, studies on degenerate versions of various special functions have been actively conducted by many researchers. For $r \in \mathbb{N}$ , Kim-Jang-Kwon studied the generalized degenerate Bernoulli polynomials, which are given by the generating function to be

$\begin{equation} \frac{t^r} {e_{\lambda}(t)-1} e_{\lambda}^{x} (t) = \sum\limits_{n = 0}^{\infty} {\mathcal{B}}_{n, \lambda}^{(r)}(x)\frac{t^{n}}{n!}\; {\text{ (see [2])}}. \end{equation}$

(1.1)

When $x = 0$ , ${\mathcal{B}}_{n, \lambda}^{(r)} = {\mathcal{B}}_{n, \lambda}^{(r)}(0)$ are called the generalized Bernoulli numbers. In particular, when $r = 1$ , then ${\mathcal{B}}_{n, \lambda}^{(1)}(x) = B_{n}(x)$ . Note that ${\mathcal{B}}_{0, \lambda}^{(r)}(x) = {\mathcal{B}}_{1, \lambda}^{(r)}(x) = \cdots = {\mathcal{B}}_{r-1, \lambda}^{(r)}(x) = 0$ .

For $\lambda(\ne 0)\in\mathbb{\mathbb C}$ , the degenerate exponential function is defined by

$\begin{equation} e_{\lambda}^{x}(t) = (1+\lambda t)^{\frac{x}{\lambda}} {\text{ (see [2–13])}}. \end{equation}$

(1.2)

We note that $\lim\limits_{\lambda\rightarrow 0}e_{\lambda}^{x}(t) = e^{xt}$ , $e_{\lambda}^{(1)}(t) = e_{\lambda}(t)$ and

$\begin{equation} e_{\lambda}^{x}(t) = \sum\limits_{n = 0}^{\infty}(x)_{n, \lambda}\frac{t^n}{n!}, \end{equation}$

(1.3)

where $(x)_{0, \lambda} = 1$ , $(x)_{n, \lambda} = x(x-\lambda)(x-2\lambda)\cdots(x-(n-1)\lambda), \; (n\ge 1).$

The Changhee polynomials $Ch_n(x)$ and the Changhee polynomials of order $k$ $Ch^{(k)}_{n}(x)$ are respectively given by the generating functions to be

$\begin{equation} \frac{2}{t+2} (1+t)^{x} = \sum\limits_{n = 0}^{\infty} Ch_{n} (x) \frac{t^n}{n!} {\text{ (see [14]}}. \end{equation}$

(1.4)

and

$\begin{equation} \bigg(\frac{2}{t+2} \bigg)^{k} (1+t)^{x} = \sum\limits_{n = 0}^{\infty} Ch^{(k)}_{n} (x)\frac{t^n}{n!} {\text{ (see [14])}}. \end{equation}$

(1.5)

The Stirling numbers of the first kind are defined as

$\begin{equation} (x)_n = \sum\limits_{l = 0}^{n}S_1 (n, l)x^l, \; (n\ge 0) {\text{ (see [6, 9])}}, \end{equation}$

(1.6)

where $(x)_0 = 1$ , $(x)_n = x(x-1)\cdots(x-n+1)$ , $(n \geq 1)$ , and the Stirling numbers of the second kind are given by

$\begin{equation} x^n = \sum\limits_{l = 0}^{n}S_2 (n, l)(x)_l, \; (n\ge 0) {\text{ (see [6, 9])}}. \end{equation}$

(1.7)

Let $\log_{\lambda}(t)$ be the compositional inverse function of $e_{\lambda}(t)$ such that $e_{\lambda}\left(\log_{\lambda} (t)\right) = \log_{\lambda}\left(e_{\lambda}(t)\right) = t$ . By Newton's binomial expansion, we see that

$\begin{equation} \log_\lambda(1+t) = \sum\limits_{n = 1}^{\infty}\frac{\lambda^{n-1}(1)_{n, 1/\lambda}}{n!}t^n \; {\text{ (see [6, 9, 10]}}), \end{equation}$

(1.8)

and by (1.8), we see that $\lim\limits_{\lambda\rightarrow 0}\log_{\lambda}(1+t) = \log(1+t)$ .

As the degenerate version of the Stirling numbers of the first and the second kind, Kim-Kim considered the degenerate Stirling numbers of the second kind $S_{2, \lambda}(n, k), \ (n, k\ge 0)$ , which are given by

$\begin{equation} (x)_{n, \lambda} = \sum\limits_{k = 0}^{n}S_{2, \lambda} (n, k)(x)_k, \quad (n\ge 0)\; {\text{ (see [6, 9, 10])}}, \end{equation}$

(1.9)

and, as the inversion formula of (1.9), the degenerate Stirling numbers of the first kind $S_{1, \lambda}(n, k)$ are given by

$\begin{equation} (x)_{n} = \sum\limits_{k = 0}^{n}S_{1, \lambda} (n, k)(x)_{k, \lambda}\quad(n\ge 0)\; {\text{ (see [6, 9, 10])}}. \end{equation}$

(1.10)

Since $\lim\limits_{\lambda \rightarrow 0} (x)_{n, \lambda} = x^n$ , we see that $\lim\limits_{\lambda \rightarrow 0} S_{1, \lambda}(n, k) = S_1(n, k)$ and $\lim\limits_{\lambda \rightarrow 0} S_{2, \lambda}(n, k) = S_2(n, k)$ .

In addition, by (1.9) and (1.10), it is easy to see that

$\begin{equation} \frac{1}{k!}(e_{\lambda}(t)-1)^k = \sum\limits_{n = k}^{\infty}S_{2, \lambda} (n, k)\frac{t^n}{n!}{\text{ and }}\frac{1}{k!}( \log_{\lambda}(1+t))^k = \sum\limits_{n = k}^{\infty}S_{1, \lambda} (n, k)\frac{t^n}{n!}\; {\text{ (see [6, 9, 10])}}. \end{equation}$

(1.11)

Special numbers and polynomials are interesting and important things in pure and applied mathematics, combinatorics and engineering (see ^[15]). In particular, authors gave two new identities involving the famous numbers of Fibonacci, Lucas, Pell and Pell-Lucas numbers in ^[16]. In ^[17], authors gave some new connection formulae between two generalized classes of Fibonacci and Lucas polynomials, and in ^[18], some celebrated orthogonal polynomials and other polynomials were given in terms of Bernoulli polynomials.

As one of the special functions, the Changhee numbers and polynomials were defined by Kim et al. in ^[14] and generalized these polynomials. In ^[19], authors defined the twisted Changhee polynomials and found some relationships between the Euler polynomials, the Stirling numbers of the first and the second kind and these polynomials. The $(r, s)$ -analogue of the Changhee polynomials was defined in ^[20], and in ^[21] the authors studied the degenerate version of Changhee polynomials. Jang et al. ^[22] investigated the zeros of twisted Changhee polynomials, and Park gave the degenerate version of twisted $q$ -Changhee polynomials of higher order in ^[23] and found some identities.

In 1998, Srivastava et al. ^[24] studied the generalized Bernoulli polynomials $B^{(\alpha)}_{n} (x)$ , and Kim et al. ^[13] introduced the generalized degenerate Bernoulli numbers $\beta^{(\alpha)}_{n, \lambda}$ by means of the Gauss hypergeometric function. Recently, Kim et al. ^[12] introduced the degenerate multi-poly-Bernoulli polynomials $\beta^{(k_1, k_2, \cdots, k_r)}_{n, \lambda}(x)$ by using the multiple polylogarithm. In ^[25], authors defined degenerate multi-poly-Euler polynomials by using degenerate multi-polyexponential functions and found some interesting identities of these polynomials and numbers. In ^[26], authors defined multi-poly-Genocchi polynomials with parameters $a, b$ and $c$ by using multiple polylogarithms and found some relationships between logarithm functions, poly-Bernoulli numbers and those polynomials. Kaneko et al. ^[27] defined the a zeta function that interpolates multi-poly-Bernoulli numbers, and showed that both these zeta functions and the $\xi$ -function defined by Arakawa and Kaneko are related closely to multiple zeta functions. Choi et al. introduced the Legendre-based poly-Euler polynomials and Legendre-based multi-poly-Euler polynomials and found some related identities and formulas in ^[28].

In this paper, we consider the degenerate multi-poly-Changhee polynomials and numbers and investigate some properties and identities of those polynomials. Furthermore, we find explicit examples of the degenerate multi-poly-Changhee polynomials and investigate the phenomenon of scattering the zeros of these polynomials.

2. The degenerate multi-poly Changhee numbers

For $k_1, k_2, \cdots, k_r \in \mathbb{Z}$ , the multiple logarithm is given by

$\begin{equation} Li_{k_1, \cdots, k_r}(x) = \sum\limits_{0 < n_{1} < n_{2} < \cdots < n_{r}}\frac{x^{n_r}}{n_{1}^{k_1}n_{2}^{k_2}\cdots n_{r}^{k_r}} \; {\text{ (see [12, 25–27])}}, \end{equation}$

(2.1)

where the sum is over all integers ${n_{1}, n_{2}, \cdots, n_{r}}$ satisfying $0 < n_{1} < n_{2} < \cdots < n_{r}$ .

From (2.1), Kim et al. ^[12] obtained the following results:

$\begin{equation} \frac{d}{dx}Li_{k_1, \cdots, k_r}(x) = \frac{1}{x}Li_{k_1, \cdots k_{r-1}, k_{r}-1}(x), \end{equation}$

(2.2)

$\begin{equation} Li_{\underbrace{1, \cdots , 1}_{r-\mathrm{times} } }(x) = \frac{1}{r!}(-\log (1-x))^{r}, \end{equation}$

(2.3)

and

$\begin{equation} S_{1}^{( \overbrace{1, \cdots , 1}^{r-\mathrm{times} } ) } (x) (n, r) = (-1)^{n-r}S_{1}(n, r) = \begin{bmatrix} n \\ r\end{bmatrix}, \end{equation}$

(2.4)

where the multi-Stirling number of the first kind is defined by

$\begin{equation} Li_{k_1, \cdots, k_r}(t) = \sum\limits_{n = r}^{\infty}S_{1}^{(k_{1}, \cdots , k_{r})}(n, r)\frac{t^n}{n!}. \end{equation}$

(2.5)

Now we consider the degenerate multi-poly-Changhee polynomials, which are given by the generating function to be

$\begin{equation} \frac{2^{r} {\mathrm{Li}}_{k_{1}, \cdots, k_{r}}(1-e^{-t})}{t^{r}(2+t)^{r}}e^{x}_{\lambda}(\log_{\lambda}(1+t)) = \sum\limits_{n = 0}^{\infty} {\mathrm{Ch}}_{n}^{(k_{1}, \cdots, k_{r})}(x)\frac{t^{n}}{n!}. \end{equation}$

(2.6)

Theorem 2.1. For $r \in \mathbb{Z}$ , $r\geq 1$ and $n\in\mathbb{N}\cup\{0\}$ , we have

${\mathrm{Ch}}_{n}^{(k_{1}, \cdots, k_{r})}(x) = \sum\limits_{l = 0}^{n}\sum\limits_{m = 0}^{l}\binom{n}{l}S_{1, \lambda}(l, m) {\mathrm{Ch}}_{n-l}^{(k_{1}, \cdots, k_{r})}(x)_{m, \lambda}.$

In particular, $k_{1} = \cdots = k_{r} = 1$ , ${\mathrm{Ch}}_{n}^{(\overbrace{1, \cdots, 1}^{r-\mathrm{times} })}(x) = \frac{1}{r!} {\mathrm{Ch}}_{n}^{(r)}(x)\; \; {and}\; (n\geq 0)$ .

Proof. From (2.6), we observe that

$\begin{equation} \begin{aligned} \sum\limits_{n = 0}^{\infty} {\mathrm{Ch}}_{n}^{(k_{1}, \cdots, k_{r})}(x)\frac{t^{n}}{n!}& = \frac{2^{r} {\mathrm{Li}}_{k_{1}, \cdots, k_{r}}(1-e^{-t})}{t^{r}(2+t)^{r}}e^{x}_{\lambda}(\log_{\lambda}(1+t))\\ & = \left(\sum\limits_{n = 0}^{\infty} {\mathrm{Ch}}_{n}^{(k_{1}, \cdots, k_{r})}\frac{t^{n}}{n!}\right) \left(\sum\limits_{n = 0}^{\infty} (x)_{n, \lambda}\frac{1}{n!}\left( \log_{\lambda}(1+t)\right)^{n}\right)\\ & = \sum\limits_{n = 0}^{\infty}\left(\sum\limits_{l = 0}^{n}\sum\limits_{m = 0}^{l}\binom{n}{l}S_{1, \lambda}(l, m) (x)_{m, \lambda} {\mathrm{Ch}}_{n-l}^{(k_{1}, \cdots, k_{r})}\right)\frac{t^{n}}{n!}. \end{aligned} \end{equation}$

(2.7)

Therefore, by comparing the coefficients on the both sides of (2.7), we proved the theorem. □

Theorem 2.2. For $r \in \mathbb{Z}$ , $r\geq 1$ and $n\in\mathbb{N}\cup\{0\}$ , we have

$\begin{aligned} & {\mathrm{Ch}}_{n}^{(k_{1}, \cdots, k_{r})}(x) = \sum\limits_{b = 0}^{n}\sum\limits_{l = 0}^{b}\sum\limits_{n_{r} = 1}^{l+1}\sum\limits_{m = 0}^{\infty} \binom{n}{b}\binom{b}{l}\binom{k_{r}+m-1}{m}n_{r}!\\ &\times \frac{(-1)^{l+1+n_{r}+m}S_{2}(l+1, n_{r})}{l+1}n_{r}^{-k_{r}-m} {\mathrm{Ch}}_{b-l}^{(k_{1}, \cdots, k_{r-1}-m)} {\mathrm{Ch}}_{n-b}(x). \end{aligned}$

Proof. From (2.6), we note that

$\begin{align} &\sum\limits_{n = 0}^{\infty} {\mathrm{Ch}}_{n}^{(k_{1}, \cdots, k_{r})}(x)\frac{t^{n}}{n!} = \frac{2^{r} {\mathrm{Li}}_{k_{1}, \cdots, k_{r}}(1-e^{-t})}{t^{r}(2+t)^{r}}e^{x}_{\lambda}(\log_{\lambda}(1+t)) \\ & = \frac{2^r}{t^r (2+t)^r} \sum\limits_{0 < n_{1} < \cdots < n_{r-1}} \frac{1}{n_{1}^{k_{1}}\cdots n_{r-1}^{k_{r-1}}} \sum\limits_{n_{r} = n_{r-1}+1}^{\infty} \frac{(1-e^{-t})^{n_{r}}}{n_{r}^{k_r}}e_{\lambda}^{x}(\log_{\lambda}(1+t)) \\ & = \frac{2^r}{t^r (2+t)^r} \sum\limits_{0 < n_{1} < \cdots < n_{r-1}} \frac{(1-e^{-t})^{n_{r-1}}}{n_{1}^{k_{1}}\cdots n_{r-1}^{k_{r-1}}} \sum\limits_{n_{r} = 1}^{\infty} \frac{(1-e^{-t})^{n_{r}}}{(n_{r}+n_{r-1})^{k_{r}}}e_{\lambda}^{x}(\log_{\lambda}(1+t)) \\ & = \frac{2^r}{t^r (2+t)^r} \sum\limits_{0 < n_{1} < \cdots < n_{r-1}} \frac{(1-e^{-t})^{n_{r-1}}}{n_{1}^{k_{1}}\cdots n_{r-1}^{k_{r-1}}} \\ &\times \sum\limits_{n_{r} = 1}^{\infty} n_{r}!\frac{1}{n_{r}!}(1-e^{-t})^{n_{r}}\frac{1}{(n_{r}+n_{r-1})^{k_{r}}}e_{\lambda}^{x}(\log_{\lambda}(1+t)) \\ & = \frac{2}{(2+t)}e^{x}_{\lambda}(\log_{\lambda}(1+t))\frac{1}{t}\frac{2^{r-1}}{t^{r-1}(2+t)^{r-1}} \\ &\times \sum\limits_{0 < n_{1} < \cdots < n_{r-1}} \frac{(1-e^{-t})^{n_{r-1}}}{n_{1}^{k_{1}}\cdots n_{r-1}^{k_{r-1}}}\frac{(1-e^{-t})^{n_{r-1}}}{n_{1}^{k_{1}}\cdots n_{r-1}^{k_{r-1}-m}}\sum\limits_{m = 0}^{\infty}(-1)^{m}\binom{k_{r}+m-1}{m} \\ & = \frac{2}{(2+t)}e^{x}_{\lambda}(\log_{\lambda}(1+t))\frac{2^{r-1}}{t^{r-1}(2+t)^{r-1}} \sum\limits_{0 < n_{1} < \cdots < n_{r-1}} \frac{(1-e^{-t})^{n_{r-1}}}{n_{1}^{k_{1}}\cdots n_{r-1}^{k_{r-1}-m}} \\ &\times \sum\limits_{l = 0}^{\infty}\left(\sum\limits_{n_{r} = 1}^{l+1}\sum\limits_{m = 0}^{\infty}(-1)^{m}\binom{k_{r}+m-1}{m} n_{r}!\frac{(-1)^{l+1-n_{r}}S_{2}(l+1, n_{r})}{l+1}n_{r}^{-k_{r}-m}\right)\frac{t^{l}}{l!} \\ & = \left(\sum\limits_{n = 0}^{\infty} {\mathrm{Ch}}_{n}(x)\frac{t^{n}}{n!}\right) \left(\sum\limits_{n = 0}^{\infty} {\mathrm{Ch}}_{n}^{(k_{1}, \cdots, k_{r-1}-m)}\frac{t^{n}}{n!}\right) \\ &\times \sum\limits_{l = 0}^{\infty}\left( \sum\limits_{n_{r} = 1}^{l+1}\sum\limits_{m = 0}^{\infty}(-1)^{m}\binom{k_{r}+m-1}{m}n_{r}! \frac{(-1)^{l+1-n_{r}}S_{2}(l+1, n_{r})}{l+1} n_{r}^{-k_{r}-m}\right) \frac{t^{l}}{l!} \\ & = \left(\sum\limits_{n = 0}^{\infty} {\mathrm{Ch}}_{n}(x)\frac{t^{n}}{n!}\right) \left(\sum\limits_{n = 0}^{\infty}\sum\limits_{l = 0}^{n}\sum\limits_{n_{r} = 1}^{l+1}\sum\limits_{m = 0}^{\infty} \binom{n}{l}(-1)^{m}\binom{k_{r}+m-1}{m}n_{r}! \right. \\ &\times \left.\frac{(-1)^{l+1-n_{r}}S_{2}(l+1, n_{r})}{l+1} n_{r}^{-k_{r}-m} {\mathrm{Ch}}_{n-l}^{(k_{1}, \cdots, k_{r-1}-m)}\right)\frac{t^{n}}{n!} \\ & = \sum\limits_{n = 0}^{\infty}\left(\sum\limits_{b = 0}^{n}\sum\limits_{l = 0}^{b}\sum\limits_{n_{r} = 1}^{l+1}\sum\limits_{m = 0}^{\infty} \binom{n}{b}\binom{b}{l}(-1)^{m}\binom{k_{r}+m-1}{m}n_{r}!\right. \\ &\left.\times \frac{(-1)^{l+1-n_{r}}S_{2}(l+1, n_{r})}{l+1}n_{r}^{-k_{r}-m} {\mathrm{Ch}}_{b-l}^{(k_{1}, \cdots, k_{r-1}-m)} {\mathrm{Ch}}_{n-b}(x)\right)\frac{t^{n}}{n!}. \end{align}$

(2.8)

Therefore, by comparing the coefficients on the both sides of (2.8), our proof is completed. □

Corollary 2.3. For $r \in \mathbb{Z}$ , $r\geq 1$ and $n\in\mathbb{N}\cup\{0\}$ , we have

$\begin{aligned} & {\mathrm{Ch}}_{n}^{(k_{1}, \cdots, -k_{r})}(x)\\ = &\sum\limits_{b = 0}^{n}\sum\limits_{l = 0}^{b}\sum\limits_{n_{r} = 1}^{l+1}\sum\limits_{m = 0}^{\infty} \binom{n}{b}\binom{b}{l}\binom{k_{r}}{m}n_{r}! \frac{(-1)^{l+1+n_{r}}S_{2}(l+1, n_{r})}{l+1}n_{r}^{-k_{r}-m} {\mathrm{Ch}}_{b-l}^{(k_{1}, \cdots, k_{r-1}-m)} {\mathrm{Ch}}_{n-b}(x). \end{aligned}$

Proof. Replacing $k_{r}$ by $-k_{r}$ , then

$\binom{-k_{r}+m-1}{m} = (-1)^{m}\binom{k_{r}}{m}$

and so our corollary is proved. □

From now on, we get the recurrence relation of the degenerate multi-poly-Changhee polynomials.

Theorem 2.4. For $r \in \mathbb{Z}$ , $r\geq 1$ and $n\in\mathbb{N}\cup\{0\}$ , we have

$\begin{aligned} & {\mathrm{Ch}}_{n}^{(k_{1}, \cdots, k_{r})}(x+1)- {\mathrm{Ch}}_{n}^{(k_{1}, \cdots, k_{r})}(x)\\ = &\sum\limits_{k = 1}^{n}\sum\limits_{a = 0}^{n-k}\sum\limits_{n_{r} = 1}^{k}\sum\limits_{m = 0}^{\infty} \binom{n}{k} \binom{n-k}{a}(-1)^{m+k-n_{r}}\binom{k_{r}+m-1}{m}n_{r}!n_{r}^{-k_{r}-m}\\ &\left.\times S_{2}(k, n_{r}) {\mathrm{Ch}}_{n-k, \lambda}^{(k_{1}, \cdots, k_{r-1})}(x) {\mathrm{Ch}}_{n-k-a}.\right.\; \; (n\geq 1). \end{aligned}$

Proof. Consider that

$\begin{equation} \begin{aligned} &\sum\limits_{n = 0}^{\infty}\left( {\mathrm{Ch}}_{n}^{(k_{1}, \cdots, k_{r})}(x+1)- {\mathrm{Ch}}_{n}^{(k_{1}, \cdots, k_{r})}(x)\right) \frac{t^{n}}{n!} = \frac{2^{r}e_{\lambda}^{x}(\log_{\lambda}(1+t))}{t^{r-1}(2+t)^{r}} {\mathrm{Li}}_{k_{1}, \cdots, k_{r}}(1-e^{-t})\\ & = \frac{2^{r}e^{x}_{\lambda}(\log_{\lambda}(1+t))}{t^{r-1}(2+t)^{r}} \sum\limits_{0 < n_{1} < \cdots < n_{r-1}}\frac{1}{n_{1}^{k_{1}}\cdots n_{r-1}^{k_{r-1}}}\sum\limits_{n_{r} = n_{r-1}+1}^{\infty}\frac{(1-e^{-t})^{n_{r}}}{n_{r}^{k_{r}}}\\ & = \frac{2^{r}e^{x}_{\lambda}(\log_{\lambda}(1+t))}{t^{r-1}(2+t)^{r}} \sum\limits_{0 < n_{1} < \cdots < n_{r-1}}\frac{(1-e^{-t})^{n_{r-1}}}{n_{1}^{k_{1}}\cdots n_{r-1}^{k_{r-1}}} \sum\limits_{n_{r} = 1}^{\infty}\frac{(1-e^{-t})^{n_{r}}}{(n_{r}+n_{r-1})^{k_{r}}}\frac{n_{r}!}{n_{r}!}\\ & = \frac{2}{2+t}\frac{2^{r-1}}{t^{r-1}(1+t)^{r-1}}e^{x}_{\lambda}(\log_{\lambda}(1+t)) \sum\limits_{0 < n_{1} < \cdots < n_{r-1}}\frac{(1-e^{-t})^{n_{r-1}}}{n_{1}^{k_{1}}\cdots n_{r-1}^{k_{r-1}-m}}\\ &\times \sum\limits_{n_{r} = 1}^{\infty}\sum\limits_{m = 0}^{\infty}(-1)^{m}\binom{k_{r}+m-1}{m}n_{r}!n_{r}^{-k_{r}-m} \sum\limits_{l = n_{r}}^{\infty}(-1)^{n_{r}+l}S_{2}(l, n_{r})\frac{t^{l}}{l!}\\ & = \left(\sum\limits_{n = 0}^{\infty} {\mathrm{Ch}}_{n}\frac{t^{n}}{n!}\right) \left(\sum\limits_{n = 0}^{\infty} {\mathrm{Ch}}_{n, \lambda}^{(k_{1}, \cdots, k_{r-1}}(x)\frac{t^{n}}{n!}\right)\\ &\times \left( \sum\limits_{k = 1}^{\infty}\sum\limits_{n_{r} = 1}^{k}\sum\limits_{m = 0}^{\infty}(-1)^{m+k-n_{r}}\binom{k_{r}+m-1}{m} n_{r}! n_{r}^{-k_{r}-m}S_{2}(k, n_{r})\frac{t^{k}}{k!}\right)\\ & = \sum\limits_{m = 0}^{\infty}\left(\sum\limits_{a = 0}^{m}\binom{m}{a} {\mathrm{Ch}}_{m, \lambda}^{(k_{1}, \cdots, k_{r-1})}(x) {\mathrm{Ch}}_{m-a}\frac{t^{m}}{m!}\right)\\ &\times \left( \sum\limits_{k = 1}^{\infty}\sum\limits_{n_{r} = 1}^{k}\sum\limits_{m = 0}^{\infty} (-1)^{m+k-n_{r}} \binom{k_{r}+m-1}{m} n_{r}! n_{r}^{-k_{r}-m}S_{2}(k, n_{r})\frac{t^{k}}{k!}\right)\\ & = \sum\limits_{n = 1}^{\infty}\left(\sum\limits_{k = 1}^{n}\sum\limits_{a = 0}^{n-k}\sum\limits_{n_{r} = 1}^{k}\sum\limits_{m = 0}^{\infty} \binom{n}{k} \binom{n-k}{a}(-1)^{m+k-n_{r}}\binom{k_{r}+m-1}{m}n_{r}!n_{r}^{-k_{r}-m}\right.\\ &\left.\times S_{2}(k, n_{r}) {\mathrm{Ch}}_{n-k, \lambda}^{(k_{1}, \cdots, k_{r-1})}(x) {\mathrm{Ch}}_{n-k-a}\right)\frac{t^{n}}{n!}. \end{aligned} \end{equation}$

(2.9)

Therefore, by comparing the coefficients on the both sides of (2.9), we proved our theorem. □

We will get another result of the recurrence relation as follows:

Theorem 2.5. For $r \in \mathbb{Z}$ , $r\geq 1$ and $n\in\mathbb{N}\cup\{0\}$ , we have

$\begin{aligned} & {\mathrm{Ch}}_{n, \lambda}^{(k_{1}, \cdots, k_{r})}(x+1)- {\mathrm{Ch}}_{n, \lambda}^{(k_{1}, \cdots, k_{r})}(x)\\ & = 2\sum\limits_{a = 0}^{n}\sum\limits_{n_{r} = 1}^{a+1}\sum\limits_{m = 0}^{\infty} \binom{n}{a}n_{r}! n_{r-1}^{-k_{r}-m} \frac{(-1)^{a+1-n_{r}+m}S_{2}(a+1, n_{r})}{a+1}. \end{aligned}$

Proof. Note that

(2.10)

Therefore, by comparing the coefficients on both sides of (2.10), our theorem is proved. □

Theorem 2.6. For $r \in \mathbb{Z}$ , $r\geq 1$ and $n\in\mathbb{N}\cup\{0\}$ , we have

${\mathrm{Ch}}_{n, \lambda}^{(k_{1}, \cdots, k_{r})}(x+y) = \sum\limits_{m = 0}^{n} {\mathrm{Ch}}_{n-m, \lambda}^{(k_{1}, \cdots, k_{r})}(x)(y)_{m}.$

Proof. From (2.6), we observe that

$\begin{equation} \begin{aligned} &\sum\limits_{n = 0}^{\infty} {\mathrm{Ch}}_{n, \lambda}^{(k_{1}, \cdots, k_{r})}(x+y)\frac{t^{n}}{n!}\\ & = \frac{2^{r}e^{x+y}_{\lambda}(\log_{\lambda}(1+t))}{t^{r}(2+t)^{r}} {\mathrm{Li}}_{k_{1}, \cdots, k_{r}}(1-e^{-t})\\ & = \frac{2^{r}}{t^{r}(2+t)^{r}} {\mathrm{Li}}_{k_{1}, \cdots, k_{r}}(1-e^{-t}) e^{x}_{\lambda}(\log_{\lambda}(1+t)) e^{y}_{\lambda}(\log_{\lambda}(1+t))\\ & = \left(\sum\limits_{n = 0}^{\infty} {\mathrm{Ch}}_{n, \lambda}^{(k_{1}, \cdots, k_{r})}(x)\frac{t^{n}}{n!}\right) \left(\sum\limits_{n = 0}^{\infty}(y)_{n}\frac{t^{n}}{n!}\right)\\ & = \sum\limits_{n = 0}^{\infty}\sum\limits_{m = 0}^{n} {\mathrm{Ch}}_{n-m, \lambda}^{(k_{1}, \cdots, k_{r})}(x)(y)_{m}\frac{t^{n}}{n!}. \end{aligned} \end{equation}$

(2.11)

Therefore, by comparing the coefficients on both sides of (2.10), we obtain our theorem. □

3. The zeros of degenerate multi-poly-Changhee polynomials

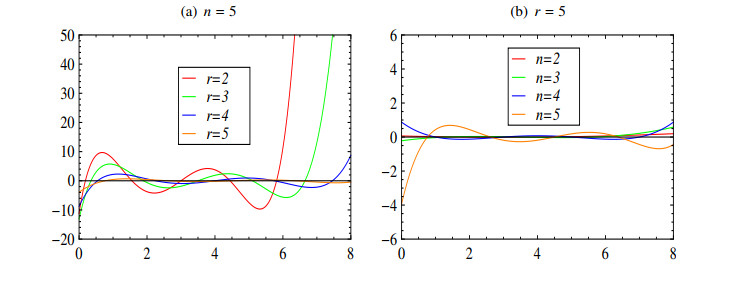
It is well known that finding the roots of polynomials is a very important task in applied mathematics. There is no formula for the roots of polynomials of degree five or higher, and there are formulas for the roots of polynomials of degree four or less, but their expressions are very complex. Hence, we want to investigate the numerical pattern of the roots of the polynomials ${\mathrm{Ch}}_{n}^{(k_{1}, \cdots, k_{r})}(x)$ . Before investigating the numerical pattern of the roots of the polynomials ${\mathrm{Ch}}_{n}^{(k_{1}, \cdots, k_{r})}(x)$ , we present the graphs of ${\mathrm{Ch}}_{n}^{(\overbrace{1, \cdots, 1}^{r-\mathrm{times} })}(x)$ with $n = 5$ for $r = 2, 3, 4, 5$ and of ${\mathrm{Ch}}_{n}^{(\overbrace{1, \cdots, 1}^{r-\mathrm{times} })}(x)$ with $r = 5$ for $n = 2, 3, 4, 5$ in Figure 1.

Figure 1. The graph of

${\mathrm{Ch}}_{n}^{(\overbrace{1, \cdots, 1}^{r-\mathrm{times} })}(x)$ .

DownLoad: Full-Size Img PowerPoint

The polynomial ${\mathrm{Ch}}_{n}^{(\overbrace{1, \cdots, 1}^{r-\mathrm{times} })}(x)$ can be explicitly expressed by using Mathematica. For example,

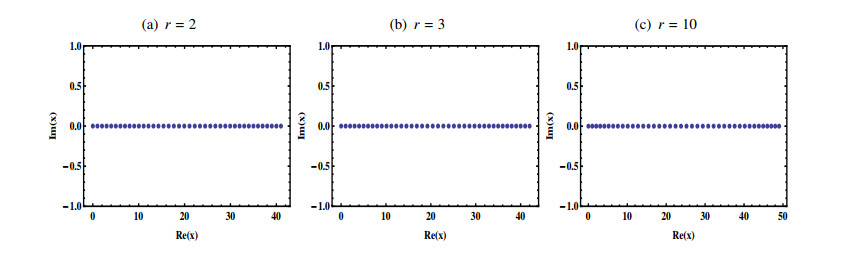
$\begin{aligned} {\mathrm{Ch}}_{1}^{(1, 1)}(x)& = \frac{1}{2}(-1+x), \\ {\mathrm{Ch}}_{2}^{(1, 1)}(x)& = \frac{1}{4}(3-6x+2x^2), \\ {\mathrm{Ch}}_{3}^{(1, 1)}(x)& = \frac{1}{4}(-6+19x-12x^2+2x^3), \\ {\mathrm{Ch}}_{1}^{(1, 1, 1)}(x)& = \frac{1}{12}(-3+2x), \\ {\mathrm{Ch}}_{2}^{(1, 1, 1)}(x)& = \frac{1}{6}(3-4x+x^2), \\ {\mathrm{Ch}}_{3}^{(1, 1, 1)}(x)& = \frac{1}{12}(-15+31x-15x^2+2x^3). \end{aligned}$

We want to observe the impact of the parameter $r$ on the distribution of the roots of the polynomials. For the aims, we set the degree of the polynomial as $n = 40$ . Using the Mathematical tool with 100 working precision, the roots of the polynomial ${\mathrm{Ch}}_{n}^{(\overbrace{1, \cdots, 1}^{r-\mathrm{times} })}(x)$ are computed. The absolute numerical error is bounded as the following:

$\sum\limits_{i = 1}^{40}| {\mathrm{Ch}}_{40}^{(\overbrace{1, \cdots, 1}^{r-\mathrm{times} })}(x_{i})| < 10^{-62},$

where $x_{i}$ denotes the roots of the polynomial. Hence, the numerical roots are reliable. We compute the numerical roots of ${\mathrm{Ch}}_{40}^{(\overbrace{1, \cdots, 1}^{r-\mathrm{times} })}(x)$ with $r = 2, 3, 10$ . The numerical results are plotted in Figure 2.

Figure 2. The computed roots of

${\mathrm{Ch}}_{40}^{(\overbrace{1, \cdots, 1}^{r-\mathrm{times} })}(x)$ .

DownLoad: Full-Size Img PowerPoint

4. Conclusions

Degenerate versions of some special polynomials and numbers were initiated by Carlitz, and many researchers have introduced many degenerate numbers and polynomials using Carlitz's degeneracy theory. Moreover, researchers also studied the identities and properties of these degenerate numbers and polynomials. Here, we would like to mention that the study of degenerate versions is not limited only to polynomials but can be extended also to transcendental functions like gamma functions, degenerate umbral calculus and degenerate probability density function.

In this paper, we considered the degenerate multi-poly-Changhee numbers and polynomials, which are defined by means of the multiple polylogarithms. We investigated some properties for those numbers and polynomials and also presented explicit examples of the polynomials by using the Mathematica tool. In order to better understanding the polynomials, the distribution of roots was presented.

In research following this paper, we plan to expand various special polynomials and numbers using multiple polylogarithm functions or multiple poly-exponential functions and find their properties.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Conflict of interest

The authors declare there is no conflicts of interest.

References

[1]	L. Carlitz, Degenerate stirling, bernoulli and eulerian numbers, Util. Math., 15 (1979), 51–88.
[2]	W. Kim, L. C. Jang, J. Kwon, Some properties of generalized degenerate Bernoulli polynomials and numbers, Adv. Stud. Cont. Math., 32 (2022), 479–486.
[3]	D. S. Kim, T. Kim, Representations by degenerate Bernoulli polynomials arising from Volkenborn integral, Math. Methods Appl. Sci., 45 (2022), 6615–6634. https://doi.org/10.1002/mma.8195 doi: 10.1002/mma.8195
[4]	T. Kim, D. S. Kim, Combinatorial identities involving degenerate harmonic and hyperharmonic numbers, Adv. Appl. Math., 148 (2023), 102535. https://doi.org/10.1016/j.aam.2023.102535 doi: 10.1016/j.aam.2023.102535
[5]	T. Kim, D. S. Kim, A new approach to fully degenerate Bernoulli numbers and polynomials, Filomat, 37 (2023), 2269–2278. https://doi.org/10.2298/FIL2307269K doi: 10.2298/FIL2307269K
[6]	T. Kim, D. S. Kim, Some identities involving degenerate Stirling numbers associated with several degenerate polynomials and numbers, Russ. J. Math. Phys., 30 (2023), 62–75. https://doi.org/10.1134/S1061920823010041 doi: 10.1134/S1061920823010041
[7]	T. Kim, D. S. Kim, Degenerate Whitney numbers of first and second kind of Dowling lattices, Russ. J. Math. Phys., 29 (2022), 358–377. https://doi.org/10.1134/S1061920822030050 doi: 10.1134/S1061920822030050
[8]	T. Kim, D. S. Kim, Degenerate r-Whitney numbers and degenerate r-Dowling polynomials via boson operators, Adv. Appl. Math., 140 (2022), 102394. https://doi.org/10.1016/j.aam.2022.102394 doi: 10.1016/j.aam.2022.102394
[9]	T. Kim, D. S. Kim, Some identities involving degenerate Stirling numbers associated with several degenerate polynomials and numbers, Russ. J. Math. Phys., 30 (2023), 62–75. https://doi.org/10.1134/S1061920823010041 doi: 10.1134/S1061920823010041
[10]	T. Kim, D. S. Kim, Some identities on degenerate r-Stirling numbers via boson operators, Russ. J. Math. Phys., 29 (2022), 508–517. https://doi.org/10.1134/S1061920822040094 doi: 10.1134/S1061920822040094
[11]	T. Kim, D. S. Kim, H. K. Kim, On generalized degenerate Euler–Genocchi polynomials, Appl. Math. Sci. Eng., 31 (2022), 2159958. https://doi.org/10.1080/27690911.2022.2159958 doi: 10.1080/27690911.2022.2159958
[12]	T. Kim, D. S. Kim, A note on degenerate multi-poly-Bernoulli numbers and polynomials, Appl. Anal. Disc. Math., 17 (2023).
[13]	T. Kim, D. S. Kim, L. C. Jang, H. Lee, H. Kim, Generalized degenerate Bernoulli numbers and polynomials arising from Gauss hypergeometric function, Adv. Differ. Equation, 2021 (2021), 175. https://doi.org/10.1186/s13662-021-03337-5 doi: 10.1186/s13662-021-03337-5
[14]	D. S. Kim, T. Kim, J. Seo, A note on Changhee polynomials and numbers, Adv. Studies Theor. Phys., 7 (2013), 993–1003.
[15]	G. E. Andrew, R. Askey, R. Roy, Special functions, in Encyclopedia of Mathematics and its Applications, Cambridge University Press, Cambridge, 1999.
[16]	W. M. Abd-Elhameed, N. A. Zeyada, New identities involving generalized Fibonacci and generalized Lucas numbers, Indian J. Pure Appl. Math., 49 (2018), 527–537. https://doi.org/10.1007/s13226-018-0282-7 doi: 10.1007/s13226-018-0282-7
[17]	W. M. Abd-Elhameed, A. N. Philippou, N. A. Zeyada, An novel results for two generalized classes of Fibonacci and Lucas polynomials and their uses in the reduction of some radicals, Mathematics, 10 (2022), 2342. https://doi.org/10.3390/math10132342 doi: 10.3390/math10132342
[18]	W. M. Abd-Elhameed, A. K. Amin, Novel identities of Bernoulli polynomials involving closed forms for some definite integrals, Symmetry, 14 (2022), 2284. https://doi.org/10.3390/sym14112284 doi: 10.3390/sym14112284
[19]	S. H. Rim, J. W. Park, S. S. Pyo, J. Kwon, The $n$ -th twisted Changhee polynomials and numbers, Bull. Korean Math. Soc., 52 (2015), 741–749.
[20]	Y. K. Cho, T. Kim, T. Mansour, S. H. Rim, On a $(r, s)$ -analogue of Changhee and Daehee numbers and polynomials, Kyungpook Math. J., 55 (2015), 225–232. https://doi.org/10.5666/KMJ.2015.55.2.225 doi: 10.5666/KMJ.2015.55.2.225
[21]	H. I. Kwon, T. Kim, J. J. Seo, A note on degenerate Changhee numbers and polynomials, Proc. Jangjeon Math. Soc., 18 (2015), 295–305.
[22]	L. C. Jang, C. S. Ryoo, J. J. Seo, H. I. Kwon, Some properties of the twisted Changhee polynomials and their zeros, Appl. Math. Comput., 274 (2016), 169–177. https://doi.org/10.1016/j.amc.2015.10.052 doi: 10.1016/j.amc.2015.10.052
[23]	J. W. Park, On the twisted $q$ -Changhee polynomials of higher order, J. Comput. Anal. Appl., 20 (2016), 424–431.
[24]	H. M. Srivastava, P. G. Todorov, An explicit formula for the generalized Bernoulli polynomials, J. Math. Anal. and Appl., 130 (1988), 509–513. https://doi.org/10.1016/0022-247X(88)90326-5 doi: 10.1016/0022-247X(88)90326-5
[25]	W. A. Khan, M. Acikgoz, U. Duran, Note on the type $2$ degenerate multi-poly-Euler polynomials, Symmetry, 12 (2020), 1691. https://doi.org/10.3390/sym12101691 doi: 10.3390/sym12101691
[26]	R. B. Corcino, M. P. Laurente, M. Ann R. P. Vega, On multi poly-Genocchi polynomials with parameters $a, b$ and $c$ , Eur. J. Pure Appl. Math., 13 (2020), 444–458. https://doi.org/10.29020/nybg.ejpam.v13i3.3676 doi: 10.29020/nybg.ejpam.v13i3.3676
[27]	M. Kaneko, H. Tsumura, Multi-poly-Bernoulli numbers and related zeta functions, Nagoya Math. J., 232 (2018), 19–54. https://doi.org/10.1017/nmj.2017.16 doi: 10.1017/nmj.2017.16
[28]	J. Choi, N. Khan, T. Usman, A note on Legendre-based multi poly-Eule polynomials, Bull. Iran. Math. Soc., 44 (2018), 707–717. https://doi.org/10.1007/s41980-018-0045-6 doi: 10.1007/s41980-018-0045-6

Reader Comments

Your name:*

Email:*
© 2023 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)

通讯作者: 陈斌, bchen63@163.com

1.
沈阳化工大学材料科学与工程学院沈阳 110142

Electronic Research Archive

1 1.3

Metrics

Article views(1293) PDF downloads(41) Cited by(0)

Preview PDF

Download XML

Export Citation

Article outline

Show full outline

Electronic Research Archive

Some identities of degenerate multi-poly-Changhee polynomials and numbers

Related Papers:

Abstract

1. Introduction

2. The degenerate multi-poly Changhee numbers

3. The zeros of degenerate multi-poly-Changhee polynomials

4. Conclusions

Use of AI tools declaration

Conflict of interest

References

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Catalog

Abstract

1. Introduction

2. The degenerate multi-poly Changhee numbers

3. The zeros of degenerate multi-poly-Changhee polynomials

4. Conclusions

Use of AI tools declaration

Conflict of interest

References

Electronic Research Archive

Some identities of degenerate multi-poly-Changhee polynomials and numbers

Related Papers:

Abstract

1. Introduction

2. The degenerate multi-poly Changhee numbers

3. The zeros of degenerate multi-poly-Changhee polynomials

4. Conclusions

Use of AI tools declaration

Conflict of interest

References

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Related pages

Tools

Export File

Citation

Format

Content

Catalog

Abstract

1. Introduction

2. The degenerate multi-poly Changhee numbers

3. The zeros of degenerate multi-poly-Changhee polynomials

4. Conclusions

Use of AI tools declaration

Conflict of interest

References