1.
Introduction
Let n be a positive integer greater than 1. For a given set S={a1,a2,…,an} with each ai being a positive integer and gcd(S):=gcd(a1,a2,…,an)=1, define L(S) to be the set of integers represented as nonnegative integer linear forms of integers in S; that is,
where N represents the natural number set containing zero. It is well known that (see, for example, Theorem 1.16 in [1]) for any positive integer z if
then z belongs to L(S). It follows that there are finitely many nonnegative integers that are not in L(S). So, if Lc(S):=N∖L(S), then Lc(S) is a finite set. Define
where |⋅| denotes the size of a set. Perhaps Sylvester was the first person who asked to determine g(S) and n(S). He also proved that
During the early part of the twentieth century, Frobenius raised the same problem in his lectures (according to [2]). Frobenius was largely instrumental in giving this problem the early recognition, and it was after him that the problem was named. This problem of determining g(S) is called the Frobenius problem and g(S) is the Frobenius number. The Frobenius problem has a rich and long history, with several applications, extensions and connections to several areas of research. A comprehensive survey covering all aspects of the problem was given by Ramíres-Alfonsín [3].
Exact determination of the g(S) and n(S) is a difficult problem in general. There are only a few cases where the g(S) and n(S) have been exactly determined for any n variables. Table 1 shows some of the results in the case of S being special progressions, which were obtained by researchers over the past few decades.
Here, √ means that the responding result was obtained. The results in the table show that scholars were gradually attacking the Frobenius problem for more general sets. For some very recent development aspects of this field, one can refer to [11,12,13].
For any nonnegative integer c, let
where k,a,b,d and h are positive integers with gcd(a,d)=1. It is natural to consider the Frobenius problem for Sc. In the paper, we present formulas for g(Sc) and n(Sc) for all sufficiently large values of d in the condition that c is a multiple of a or a multiple of d.
In order to state our theorem well, let us first define some notations. Let b,k and u be nonnegative integers with b≥2 and k≥1. For any positive integer x, define two sequences of nonnegative integers, denoted by {qi(x)}ki=0 and {ri(x)}ki=0, as follows:
where 0≤ri(x)≤bi+ui−1 for each 1≤i≤k and r0(x)=0. From Euclidean division, we know that {qi(x)}ki=0 and {ri(x)}ki=0 are uniquely determined by x, so they are well defined. It is immediate that
and
i.e., 0≤qi(x)≤b for any 1≤i≤k−1. In particular, when u=0, we use {¯qi(x)}ki=0 and {¯ri(x)}ki=0 to replace {qi(x)}ki=0 and {ri(x)}ki=0, respectively. Thus,
and
is the b-adic representation of ¯rm(x). Let
where v is a nonnegative integer.
Now, we can report the main theorem as follows.
Theorem 1.1. Let k,a,b,d and h be positive integers with gcd(a,d)=1 and b≥2. For any nonnegative integer c, let Sc:={a,ha+d,ha+c+bd,ha+2c+b2d,…,ha+kc+bkd}. The following statements are true.
(a) If c=ud for a nonnegative integer u and d≥ah(k(b−1)+u), then
and
(b) If c=va for a nonnegative integer v with v≤b−1 and d≥12akh(b−1)(2+(k−1)v), then
and
where Mi=12bi⌊a−1bi⌋(⌊a−1bi⌋−1)+⌊a−1bi⌋(a−bi⌊a−1bi⌋).
Here, 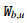 and
and 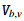 are defined as (1.3).
are defined as (1.3).
Clearly, Theorem 1.1 extends a result of Tripathi [10]. The paper is organized as follows. First, in Section 2, two key lemmas are given. Second, in Section 3, we present the proof of Theorem 1.1. Finally, in Section 4, another possible direction of the generalizations of S for the Frobenius problem is introduced, which can be served as a future research for the interested.
2.
Lemmas
Let S be any given finite set of positive integers with gcd(S)=1. Let a be a positive integer of S. For any integer x with 1≤x≤a−1, denote ⟨x⟩ to be the residue class of integers congruent to x modulo a. Let m(S,x) represent the least positive integer in L(S)∩⟨x⟩. Brauer and Shockley [14] obtained the following results, which give g(S) and n(S) from m(S,x).
Lemma 2.1. Let S be any finite set of positive integers with gcd(S)=1. For any a∈S,
The second lemma presents results of min(L(S)∩⟨x⟩).
Lemma 2.2. Let c be a fixed nonnegative integer, k,a,b,d and h be positive integers with gcd(a,d)=1 and b≥2. Let Sc={a,ha+d,ha+c+bd,ha+2c+b2d,…,ha+kc+bkd}. For any integer x with 1≤x≤a−1, let m(x):=min(L(Sc)∩⟨dx⟩), where ⟨dx⟩ denotes the residue class of integers congruent to dx modulo a. The following results are derived.
(a) if c=ud for a nonnegative integer u, then for any positive integer x with x≤a−1 we have
In particular, if d≥h(k(b−1)+u−⌊abk+uk⌋) with gcd(a,d)=1, then
(b) if c=va for a nonnegative integer v with v≤b−1, then for any positive integer x with x≤a−1 we have
Moreover, if d≥12kh(b−1)(2+(k−1)v)−h(1+kv)⌊abk⌋, then
Here, 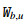 and
and 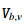 are defined as (1.3).
are defined as (1.3).
Proof. Let x be a positive integer with x≤a−1. For any N∈L(Sc)∩⟨dx⟩, one writes
with each xi being a nonnegative integer.
First, let c=ud for a nonnegative integer u. Rewrite
Since N∈⟨dx⟩, then (2.1) implies that
Let ∑ki=0(bi+ui)xi=at+x for some nonnegative integer t. On the one hand, we can regard as N a function of the variables t,x−1,x0,x1,…,xk and write N=N(t;x−1,x0,x1,…,xk). It then follows that
On the other hand, for any fixed t, one readily finds that
where Wb,u is defined in (1.3). Therefore,
Let F(t):=ah(⌊at+xbk+uk⌋+Wb,u(at+x))+d(at+x), and consider F(t+1)−F(t), which equals
Note that
and
By (2.2), one then has that F(t+1)≥F(t) for any nonnegative integer t if d≥h(k(b−1)+u−⌊abk+uk⌋). Thus
whenever d≥h(k(b−1)+u−⌊abk+uk⌋), as desired. Item (a) is proved.
Next, let c=va for an integer v with 0≤v≤b−1, then
Note that N≡dx(moda), then by (2.3) one may let ∑ki=0bixi=as+x for some nonnegative integer s. For any fixed nonnegative integer s, let
be a function of the variables x0,…,xk subject to ∑ki=0bixi=as+x, then one claims that
where each ¯qi is defined as (1.1). Now, let us prove the claim by mathematical induction on k as follows.
∙ Let k=1. Let as+x=x0+bx1=g1. Write g1=¯q1(g1)b+¯r1(g1) with 0≤¯r1(g1)≤b−1 and let ¯q0(g1)=¯r1(g1). Note that x1≤⌊g1b⌋=¯q1(g1), then we have
where the inequality in the third line holds because v≤b−1. It follows that
This is to say that the claim of (2.5) is true for k=1.
∙ Assume that the claim of (2.5) holds for k−1 with k≥2. Let gk:=∑ki=0bixi=as+x and ˜f(x0,x1,…,xk−1):=∑k−1i=0(1+vi)xi. By (2.4), one then deduces that
By the inductive hypothesis we have
where
and
for j=k−2,k−3,…,0. For gk=as+x, let {¯qi(gk)}ki=0 be the sequence defined as (1.1). It is observed that gk−xkbk(modbk−1) is independent on xk. One then finds that
for any 0≤j≤k−2. This together with (2.6) implies that
that is,
Hence, we arrive at
which means that (2.5) is true for k, so the claim of (2.5) is proved. It then follows from (2.3)–(2.5) that
Let G(s):=ah∑ki=0(1+vi)¯qi(as+x)+d(as+x). It is direct to check that G(s+1)−G(s)=ah(1+kv)(⌊as+x+abk⌋−⌊as+xbk⌋)+ah∑k−1i=0(1+iv)(¯qi(as+x+a)−¯qi(as+x)). Note that
and
for any 0≤i≤k−1. It infers that
so G(s+1)−G(s)≥0 for any nonnegative integer s whenever
Therefore,
for these values of d≥12kh(b−1)(2+(k−1)v)−h(1+kv)⌊abk⌋. The proof of Item (b) is finished.
This completes the proof of Lemma 2.2. □
3.
Proof of Theorem 1.1
In this section, we use Lemmas 2.1 and 2.2 to prove Theorem 1.1.
Proof of Theorem 1.1. First, let c=ud for a nonnegative integer and d≥ah(k(b−1)+u). Note that gcd(a,d)=1, then by Lemmas 2.1 and 2.2 we have that
Let H(x):=ah(⌊xbk+uk⌋+Wb,u(x))+dx, then
for any positive integer x. It follows from (3.1) that
Next, applying Lemmas 2.1 and 2.2 to computing n(Sc), one has that
Write a−1=q(bk+ku)+r with 0≤r≤bk−1, then
Putting (3.3) into (3.2), we derive that
as desired. Item (a) is proved.
Now, we let c=va for a nonnegative integer v with v≤b−1 and d≥12akh(b−1)(2+(k−1)v). To be similar as the proof of Item (a), we also can obtain that
Next, let us compute n(Sc) in the following. First, by employing Lemmas 2.1 and 2.2 we have that
Second, we compute ∑a−1x=1⌊xbk⌋ and ∑a−1x=1Vb,v(x). For the purpose, define two sequences {qi}ki=1 and {ri}ki=1 by
Then, for any 0≤i≤k, one deduces that
which is denoted by Mi for brevity. Recall that ¯qi(x) is defined as (1.1), and it is checked that
for any 0≤i≤k−1. It then follows that
Finally, putting (3.6) and (3.7) into (3.4) we arrive at
where Mi=12biqi(qi−1)+qi(ri+1), qi and ri are defined as (3.5). Thus, the proof of Item (b) is done.
The proof of Theorem 1.1 is completed. □
4.
Conclusions
Let S={a1,a2,…,an} be a set of positive integers with gcd(a1,a2,…,an)=1. The celebrated Frobenius problem is to find g(S) and n(S), which is the largest natural number that is not representable as a nonnegative integer combination of a1,a2,…,an and the number of natural numbers that are not nonnegative integer combinations of a1,a2,…,an, respectively. In this paper, we determined g(Sc) and n(Sc) for Sc={a,ha+d,ha+c+db,ha+2c+db2,…,ha+kc+dbk} in the case of that c is divided by one of a and d. In fact, we presented a formula for m(Sc,x) by determining the minimum value of certain functions with multi variables, where m(Sc,x) is the least positive integer in L(S)∩⟨x⟩ (see Lemma 2.2). By employing Lemmas 2.1 and 2.2 and with some technical calculations on some complex sums, we finally derived the explicit expressions of g(Sc) and n(Sc), so the paper extended a result of Tripathi in 2016. However, in this paper we do not say anything about this problem when a∤ and . Maybe it needs more new ideas to settle the problem for that case. In addition, the following generalization direction for the Frobenius problem is attractive as well.
Problem 4.1. Let and be positive integers with . Let be distinct positive integers. For
find and .
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
The authors would like to thank the anonymous referees for their helpful comments which improved the presentation of this paper. This work was supported partially by the NSF of China (No. 12226335).
Conflict of interest
The authors declare there is no conflicts of interest.









 DownLoad:
DownLoad:
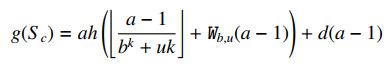
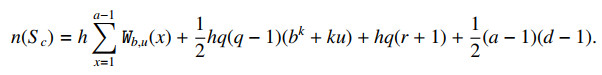
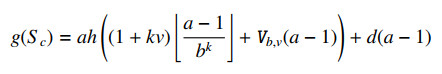
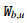 and
and 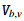 are defined as (1.3).
are defined as (1.3).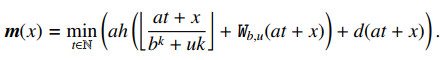
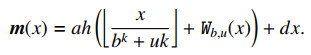
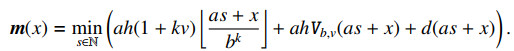
 and
and  are defined as (1.3).
are defined as (1.3).

