Topological optimization algorithm for mechanical-electrical coupling of periodic composite materials

1.   Introduction

Structural optimization of piezoelectric composites is one of the hot issues in structural design of materials. Piezoelectric composites are widely used in aircraft structure, electronic information technology and semiconductor materials ^[1,2]. Composite materials generally have some small periodicity, which makes it difficult to solve the differential equations that describe piezoelectric problems theoretically. For piezoelectric phenomena of composite structures, a simple and effective algorithm is developed based on the idea of homogenization^[3,4]. In ^[5], the homogenization method is used to establish a numerical algorithm for calculating the optimal design of composite structures. In ^[6], mainly presented a multi-scale and multi-material topology optimization algorithm for designing cellular structure. The reference ^[7] proposed a topology optimization method for structural heat transfer and load carrying capabilities. The optimal structure and microstructure topology optimization methods of materials are presented in ^[8]. In ^[9], a piezoelectric plate energy harvester of in-plane harmonic energy is studied, and proposed a topology optimization algorithm of two-dimensional piezoelectric material model, which minimizes the numerical instability. A topology optimization algorithm is proposed based on probabilistic reliability for piezoelectric uncertainty, and established a nested double-loop optimization algorithm to satisfy the displacement performance in ^[10]. For multi-scale structural topology optimization, in ^[11], mainly studies a two-scale concurrent topology optimization design of multi-micro heterogeneous materials. The two-scale design optimization problem of minimizing structural compliance under the constraints of seepage flow rate and material void is studied in ^[12]. In ^[13], a hierarchical topology optimization design method applied to single scale microstructure of mechanical materials is proposed. The finite element method is introduced through the homogenization method of composite materials, and the homogenization constant of composite materials is realized by the program ^[14,15,16]. A structure-material design two-scale optimization methods in the framework of level set method presented in ^[17]. In reference ^[18,19] proposed a topology optimization design method for solids and fluids periodicity and microstructure of porous materials. In ^[20], based on the multi-material topology optimization, some materials with fully combined bi-functions are developed and proposed a method for selecting reasonable parameters. A topology optimization algorithm to improve the alternating active phase and object of multiple materials and a new formula to overcome convergent oscillations are presented in ^[21]. A two-scale parallel optimization method is proposed and applied to the macroscopic and microscopic structures, finally, compared the optimized gradient and uniform graded lattice structures in ^[22]. In ^[23], mainly proposed a multi-material topology optimization algorithm and candidate material selection criteria, and applied the topology optimization algorithm to the compliance minimization problem. In ^[24], this paper mainly studies the bending behavior of three-dimensional periodic composite plates and designs a two-scale computing method, which is used to solve the effective parameters and displacement strains of the composite plates. A method of constructing a higher order scheme for numerical solutions of the fractional ordinary differential equations is proposed in ^[25]. The high-order numerical scheme of caputo time fractional differential equation with uniform accuracy is constructed by constructing high-order finite difference method and local truncation error in ^[26]. An effective topology optimization method for macrostructure and their corresponding parameterized microstructure is presented in ^[27]. In ^[28], a topology optimization algorithm based on level set composites is proposed, and the algorithm is applied to the compliance minimization of linear elastic problems. It established a two-scale coupling relationship between potential and displacement and analyzed some improved asymptotic error estimates in ^[29]. The structure optimization algorithm of piezoelectric material plate is established by moving asymptote method, and the program experiment is given by Matlab in ^[30]. For more practical applications, see ^[31,32].

According to the current literature research, there are few mechanical-electrical coupling topology optimization algorithms for piezoelectric composites. This paper constructs a structural optimization algorithm for the electro-mechanical coupling problem of composite materials based on the two-scale asymptotic expansion method. The algorithm is used to calculate the optimization problem of cantilever beam structure. This paper is arranged as follows: construction and analysis of topological optimization method for electro-mechanical coupling problems of periodic composite materials in Section 2. In Section 3, establish a topological optimization algorithm for the electro-mechanical coupling problem of periodic composite materials, and the topology optimization structure of fine mesh and homogenized solution were compared. Finally, some conclusions are given in Section 4.

 

2.   Construction and analysis of topological optimization method for mechanical-electrical coupling problems of periodic composite materials

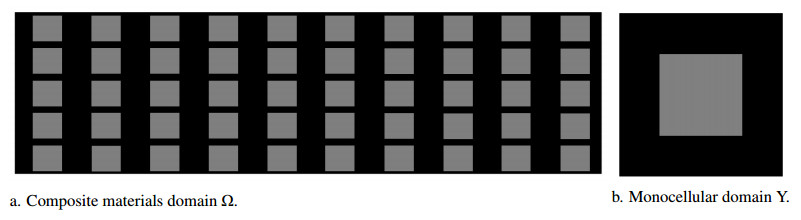
Suppose a cantilever beams with length $W$ and width $L$ were considered in the simulations. As shown in Figure 1, let $\Omega$ be a bounded domain with Lipschitz boundary. In what follows, Latin indices take numbers in 1, 2, 3, while Greek ones only run over 1, 2. In addition, we shall constantly use the Einstein summation convention.

The famous material interpolation schemes is the density-based method. For non-isotropic piezoelectric material, the interpolation function is the extension of solid isotropic microstructure with penalization (SIMP) scheme which can be written as follows:

It is noted that the parameter $\theta(x)$ is a design variable. Similarly, the Lame parameters describing the mechanical properties of a solid can be expressed as follows:

Consider the following minimization of mechanical-electrical coupling problem for two-dimensional periodic composite materials, the objective function is described as:

subject to

where $f_{i}(x)$ is the body force, $\rho(x)$ is the density of charge, $\vartheta$ is volume constraint, $\bf{n}$ is a normal vector, $u_{k}^{\varepsilon}(x)$ is the displacement vector, $\Phi^{\varepsilon}(x)$ is the scalar electric potential field, $t_{i}(x)$ is surface traction force, $q(x)$ denotes the electric body charge, and the boundary $\partial \Omega$ of $\Omega$ is composed of the traction boundary $B_{t}$ and the displacement boundary $B_{u}$ with $B_{u}\cap B_{t} = 0$ and $B_{u}\cup B_{t} = \partial \Omega$. Similarly, the electrical boundary $\Omega$ is divided into two parts, the electric potential boundary $B_{\phi}$ and the electric loads boundary $B_{q}$ with $B_{\phi}\cap B_{q} = 0$ and $B_{\phi}\cup B_{q} = \partial \Omega$.

Assume that all coefficients satisfy the following conditions

(I) $C_{ijhk}^{\theta, \varepsilon}(x) = C_{ijhk}^{\theta}(\xi), e_{ijk}^{\theta, \varepsilon}(x) = e_{ijk}^{\theta}(\xi), b_{ij}^{\theta, \varepsilon}(x) = b_{ij}^{\theta}(\xi)$ is periodic Y and $\xi = x \big/ {\varepsilon}$;

(II) $C_{ijhk}^{\theta, \varepsilon}(x)$ satisfies the following coercive condition $\Xi (k_{1}, k_{2})$, s.t.,

where $\{\zeta_{ih}\}$ is real elements with arbitrary symmetric matrix, $k_{1}$ and $k_{2}$ are positive constants independent of $\varepsilon$;

(III) $b_{ij}^{\theta, \varepsilon}(x)$ satisfies the following positive definite condition:

where $\{\zeta_{i}\}$ is an arbitrary vector with real element, $\tau_{1}$ and $\tau_{2}$ are constants greater than zero independent of $\varepsilon$;

(IV) For tensor $e_{ijk}^{\theta, \varepsilon}(x)$, we assume that $e_{ijk}^{\theta, \varepsilon}(x) = e_{ikj}^{\theta, \varepsilon}(x)$.

Theorem 2.1. Assume that the homogenization coefficients $\hat C_{ijhk}^{\theta}, \hat e_{ijk}^{\theta}$ and $\hat b_{ij}^{\theta}$ satisfy the conditions (I)–(IV), then the homogenization problem of Eq $(2.3)$ is as follows:

and satisfy the following equations

Let's define the coefficients of homogenization $\hat C_{ijhk}^{\theta}, \hat e_{ijk}^{\theta}$ and $\hat b_{ij}^{\theta}$ as follows:

where $H(\xi), G(\xi), M(\xi), N(\xi)$ are $Y$-periodic in $\xi$ and defined by as follows

and

Proof. For a detailed proof, see Appendix A.

The sensitivity analysis is derived by the Lagrange multiplier $L$, for the optimization problem of mechanical-electrical coupling of the discussed composite materials, the Lagrange multiplier can be defined as:

where $(\bar{u}^{0}(x), {\bar{\chi}}(x))\in U$ is a vector-valued function, ${\bar{\chi}}(x)$ is the Lagrange multiplier of the governing equation and the Neumann boundary condition on $B_{t}$, $(\bar{\Phi}^{0}(x), {\bar{\phi}}(x))\in Z$ is a quantity-valued function, ${\bar{\phi}}(x)$ is the Lagrange multiplier of the governing equation and the Neumann boundary condition on $B_{\phi}$. The dual spaces of $U$ and $Z$ are $U'$ and $Z'$, respectively.

Theorem 2.2. Suppose $\bar{u}_{k}^{0}(x)\in U$ and $\bar{\Phi}^{0}(x)\in Z$ are locally optimal solutions of $(2.5)$, then there are $\chi_{k}(x)\in U'$ and $\phi(x)\in Z'$, both of which satisfied the following conditions:

Proof. The partial derivative of Eq $(2.11)$ with respect to $\bar{u}_{k}^{0}(x)$ in the direction $\delta\bar{u}_{k}^{0}(x)$ at a stationary point $({u}_{k}^{0}(x), \chi_{k}(x))\in U$ leads to

Similarly, taking the derivative of Eq $(2.11)$ with respect to $\bar{\Phi}^{0}(x)$ in the direction $\delta\bar{\Phi}^{0}(x)$ at a stationary point $({\Phi}^{0}(x), \phi(x))\in Z$ leads to

In the third term on the right hand side of $(2.13)$ and $(2.14)$, $\delta \bar{u}_{k}^{0}(x)$ can commute with $\chi_{k}(x)$ and $\delta\bar\Phi^{0}$ commute with $\phi(x)$ due to the symmetric property of the bilinear form, i.e.,

Substituting $(2.15)$ into $(2.13)$ and $(2.16)$ into $(2.14)$ and taking integration by parts lead to the following equation

and

For arbitrarily function $\bar{u}_{k}^{0}(x)\in U$ and $\bar{\Phi}^{0}(x)\in Z$ are locally optimal solutions of $(2.5)$. Theorem $2.2$ has been proved.

The finite element method is used to solve the adjoint Eq $(2.12)$ to obtain $\chi_{k}(x)$ and $\phi(x)$, which are substituted into $J(\theta)$. The sensitivity of the objective function is obtained by taking the derivative of

With take the derivative of the design variable $\theta$:

Then the objective function of the sensitivity analysis is following as:

In order to ensure that checkerboard patterns are avoided in the solution of topology optimization problems, some design constraints must be limited. This situation can be eliminated by smoothing sensitivity of objective function $J(\theta)$ and material volume $V$ is given by the following equation:

where $G_{r}$ and $G$ are the smoothed and original densities, respectively. $\delta G_{r}$ is the variation of $G_{r}$, $\gamma_{i}$ is a positive constant. Considering only the volume constraint, the structural optimization problem of Eq $(2.19)$ can be expressed as:

For the constraint conditions of Eq $(2.22)$, the necessary condition for $\theta$ to be optimal is satisfying that a subset of the stability condition of the Lagrange function, so we use the Lagrange multiplier $\Lambda, \lambda_{1}$ and $\lambda_{2}$. Then, we have:

Similar references ^[33], to solve the optimization problem, the Optimality Criteria algorithm is used here which can be written as:

and $\beta = -\frac{\partial J}{\partial \theta}\bigg(\bar{\lambda} \frac{\partial V}{\partial \theta}\bigg)^{-1},$ where $\theta^{m+1}$ represents the value of the density variable in the iterative step $m = 1, 2, ..., n$, $move$ parameter is the maximum amount of density change, the value of $move$ is considered to be 0.2, $b$ is a damping coefficient and takes the value 0.3, $\bar{\lambda}$ is the Lagrange multiplier to augment the volume constrain.

Next, we introduce the optimization algorithm for the mechanical-electrical coupling problem of periodic composites as follows:

$1).$ The geometric structure $Y = [0, 1]^{2}$ and homogenization domain $\Omega$ of the reference cell and the material parameters of each material were determined, the two domains are divided into finite element spaces $K^{h_{1}}(Y)$ and $K^{h_{0}}(Y)$, where $h_{1}$ and $h_{2}$ represent the mesh size of the monocellular domain and finite element respectively;

$2).$ Equations $(2.9)$ and $(2.10)$ of first-order unicellular functions are solved on the finite element domain $K^{h_{1}}(Y)$, and obtain the first order monocellular solutions $M_{\alpha_{1}}(\xi), H_{\alpha_{1}}(\xi), N_{\alpha_{1}m}(\xi)$ and $G_{\alpha_{1} m}(\xi)$, and the coefficients of homogenization $\hat C_{ijhk}^{\theta}, \hat e_{ijk}^{\theta}$ and $\hat b_{ij}^{\theta}$. Interpolation is performed using the calculated homogenization coefficients at these mesh points, finally, we can obtain the homogenization coefficients of domain $K^{h_{0}}(\Omega)$;

$3).$ Substituting the homogenization coefficients $\hat C_{ijhk}^{\theta}, \hat e_{ijk}^{\theta}$ and $\hat b_{ij}^{\theta}$ into Eq $(2.5)$ to find $\Phi^{0}(x)$ and $u_{k}^{0}(x)$;

$4).$ By solving the adjoint Eq $(2.12)$ of mechanical-electric coupling by finite element method, we can obtain $\chi_{k}(x)$ and $\phi(x)$;

$5).$ Substituting $\Phi^{0}(x)$, $u^{0}(x)$, $\chi_(x)$ and $\phi(x)$ into $J(\theta)$ and take the derivative of $\theta$ to obtain the sensitivity analysis $(2.20)$;

$6).$ In order to eliminate checkerboard and other problems, smoothing sensitivity $(2.21)$ is used;

$7).$ In order to obtain the optimal solution of the structure, it is necessary to continuously iterate and update the element density value, modify design variables using update scheme $(2.23)$, here we use dichotomy to update the intermediate variable:

(a) Calculate the Lagrange multiplier $\Lambda = (\Lambda_{min}+\Lambda_{max})/2$, where $\Lambda_{min}$ and $\Lambda_{max}$ represent the upper limit and lower limit of the initial Kuhn-Tucker condition respectively, and substitute into $(2.24)$ to update the design variable $\theta$;

(b) The structural volume ${\int_{\Omega}}\theta^{m+1}dx$ is calculated, if ${\int_{\Omega}}\theta^{m+1}dx- {\int_{\Omega}}\vartheta dx > 0$, output $\Lambda = \Lambda_{min}$, otherwise print $\Lambda = \Lambda_{max}$;

(c) Repeat (a) and (b) until $\Lambda_{max} > 10^{-40}$ and $\left({\Lambda_{max}-\Lambda_{min}}\right)/(\Lambda_{min}+\Lambda_{max}) > 10^{-40}$, if true, output $\theta^{m+1} = \theta$, otherwise, go back to step (a).

8). Equations $(2.1)$ and $(2.2)$ were used to update the design variables for each material and calculate the average compliance and volume fraction as well as the variation of the variables;

9). Optimization convergence $\left|{\theta^{m+1}-\theta^{m}}\right| < 10^{-3}$, whether the number of iterations is greater than or equal to the maximum number of iterations, if so, output the result, otherwise return step (b).

3.   Numerical results

In this section, we give some numerical results show that the proposed algorithm is effective to calculate the optimal structure of the periodic composite cantilever beam under the influence of the electromechanical coupling. Suppose a cantilever beams $\Omega$ with length $W = 2(m)$ and width $L = 0.5(m)$ were considered in the simulations. As shown in Figure 1, let $\Omega$ be a bounded domain with Lipschitz boundary. The boundary $\partial \Omega$ of $\Omega$ is composed of the traction boundary $B_{t} = \{x = -0.96*l+1.04, y = 0.625, l\in(0, 1)\}$ and the displacement boundary $B_{u} = \{x = 0.04*l+1.96, y = 0, l\in(0, 1)\}$, which do not overlap each other so that $B_{u}\cap B_{t} = 0$ and $B_{u}\cup B_{t} = \partial \Omega$, a surface traction force $t_{i}(x) = -10^{7}(N)$ is applied to the border of $B_{t}$. Also consider the electrical boundary $\Omega$ is divided into two parts, the electric potential boundary $B_{\phi} = \{x = 0.08*l+0.96, y = 0, l\in(0, 1)\}$ and the electric loads boundary $B_{q}$, there are $B_{\phi}\cap B_{q} = 0$ and $B_{\phi}\cup B_{q} = \partial \Omega$. $q(x) = 10^{-2}(C)$ denotes the electric body charge applied to the border $B_{\phi}$ of the design domain. Assume that $\gamma_{i} = 0.002, \lambda = 0.4, r = 0.1, \theta_{min} = 0.001, \Lambda_{min} = 0, \Lambda_{max} = 100,000, \vartheta = 0.4(m^{3})$, the maximum number of iterations $n = 300$. And the Table 1 shows two different periodic composite material parameters.

In order to illustrate the effectiveness of topology optimization algorithms using solid isotropic material penalization method and homogenization method, some numerical results of periodic composite topology optimization are presented. In other words, the comparison of the mechanical-electrical coupling topology optimization between the composite cantilever in fine mesh which is the reference solution of this problem and the homogeneous cantilever in coarse mesh is shown in Figure 2. It can be seen from a3 and a4 in Figure 2 that the topology optimization results of composite structures are almost unchanged after $200$ and $300$ iterations. Similarly, it can also be seen from b3 and b4 in Figure 2 that the topology optimization results of homogeneous cantilever are almost unchanged after $200$ and $300$ iterations. Therefore, this shows that the topology optimization algorithm of material structure is convergent after $300$ iterations. It can be seen from a4 and b4 in Figure 2 that the topology optimization result of composite cantilever is consistent with the topology optimization result of homogeneous cantilever. Therefore, it is concluded that the homogeneity method can effectively obtain the topological optimization of the composite.

In the following Figure 3, it shows the convergence curve of the objective function. It can be seen from the curve change that the objective function value is decreasing fast in the first $100$ iterations and almost unchanged after $200$ iterations. In this paper, we take the topology optimization result of the structure at $300$ iterations as the final result of the material structure design. This is consistent with the conclusion in Figure 2.

Table 2 shows the grid information of composite material and homogenization structure respectively. It can be seen from the table 2 that the number of triangles or vertices of the composite material is much greater than that of the homogenization structure. So it can be known that the calculation cost of the fine mesh method is much higher than that of the homogenization method. Therefore the topology optimization algorithm of piezoelectric composite structure based on homogenization theory is very effective.

4.   Conclusions

In this paper, the topological optimization algorithm and numerical simulation for electro-mechanical coupling problems of composites are discussed. Using the two scale asymptotic method, we prove the homogenization problem of topological optimization electro-mechanical coupling problems of composites. By solving the homogenization problem of the topology optimization problem of the piezoelectric composite structure, we obtained the topology optimization algorithm of the topology optimization problem of the piezoelectric composite structure. The numerical results of the paper show that the results of equivalent homogenized materials are close to the results of calculating composite materials in fine mesh. Therefore the topology optimization algorithm of piezoelectric composite structure based on homogenization theory is effective. The structural optimization of piezoelectric materials has a broad application prospect, which can be used in intelligent sensors, intelligent control, intelligent robots, intelligent home, intelligent transportation and other fields. In addition, structural optimization of piezoelectric materials can also be used to improve the performance, reliability and energy efficiency of electronic components.

In the future work, we will use the topological optimization algorithm to establish the topology optimization algorithm of structural optimization of composite plates of electro-mechanical coupling problems.

Acknowledgments

Ziqiang Wang was supported by National Natural Science Foundation of China (Grant No. 11961009). Junying Cao was supported by National Natural Science Foundation of China (Grant No. 11901135), Foundation of Guizhou Science and Technology Department, China (Grant No. [2020]1Y015). Ziqiang Wang and Junying Cao were supported by Natural Science Research Project of Department of Education of Guizhou Province (Grant Nos. QJJ2022015 and QJJ2022047).

Conflict of interest

The authors declare there is no conflicts of interest.

Appendix

Appendix A: the proof of Theorem 2.1.

Proof. The asymptotic expansion of $\Phi^{\varepsilon}(x)$ and $u_{k}^{\varepsilon}(x)$ is as follows:

in which $x$ and $\xi$ are two independent variables, and the partial derivative operation is:

Suppose $\Phi^{j}(x, \xi)$ and $u^{j}(x, \xi)(j = 0, 1, 2), x \in \Omega, \xi\in Y$ are $Y$-periodic with respect to $\xi$. Define the operators $H_{\varepsilon}, F_{\varepsilon}, A_{\varepsilon}$ and $W_{\varepsilon}$ as follows:

Form $(2.4)$, the mechanical-electrical coupling equations can be written as:

where

By comparing the $\varepsilon$ power coefficients at both ends of Eqs $(A.4)$ and $(A.5)$, $(A.1)$ and $(A.2)$, we can obtain the following equations:

For Eq $(A.7)$, we can be further expressed is:

According to the theory of partial differential equation, both $\Phi^{0}(x, \xi)$ and $u_{k}^{0}(x, \xi)$ are independent of microscopic variable $\xi$, i.e.,

Substituting $(A.12)$ into $(A.8)$ yields:

By the linear property of $(A.12)$, the operators $H_{0}, F_{0}, W_{0}$ and $A_{0}$ refer only to the variable $\xi$, and the partial derivative operations ${\frac{\partial \Phi^{0}}{\partial x_{j}}}$ and ${\frac{\partial u_{k}^{0}}{\partial x_{j}}}$ are independent of $\xi$, so it can be solved in the following form

Substituting $(A.14)$ into $(A.13)$, which leads to

and

Suppose these three the homogenization coefficients $\hat C_{ijhk}^{\theta}$, $\hat e_{ijk}^{\theta}$ and $\hat b_{ij}^{\theta}$ satisfy conditions (I)-(IV), $\Phi^{\varepsilon}(x)\in Z = \{\Phi(x)\in H^{1}\left({\Omega}\right)\mid\Phi(x) = 0$ on $B_{t}\}$, $u_{k}^{\varepsilon}(x)\in U = \{u_{k}(x)\in [H^{1}(\Omega)]^{2}|u_{k}(x) = 0$ on $B_{u}\}$, so the monocellular problems $(A.15)$ and $(A.16)$ have unique solutions $M_{\alpha_{1}}(\xi), H_{\alpha_{1}}(\xi), N_{\alpha_{1}m}(\xi)$ and $G_{\alpha_{1}m}(\xi)\in W_{per}(Y)$, where $W_{per}(Y) = \{\theta(\xi)\mid\theta(\xi)\in H^{1}(\Omega)\}$, and $\theta(\xi)$ is periodic $Y$.

All operators of formula $(A.9)$ are expanded as follows:

For Eqs $(A.17)$ and $(A.18)$, you average the integral over $Y$, according to the definition $(A.14)$ of $\Phi^{1}(x)$ and $u_{k}^{1}(x)$, and the $Y$ periodicity of $\Phi^{2}(x)$ and $u_{k}^{2}(x)$ on $\xi$, Eqs $(A.17)$ and $(A.18)$ can still be written as:

Therefore, the homogenization equations are defined as:

where $\hat C_{ijkl}^{\theta}, \hat e_{kij}^{\theta}$ and $\hat b_{ij}^{\theta}$ are homogenization coefficients, which can be expressed as:

Substituting $(A.1)$ and $(A.2)$ into $(2.3)$ of the objective function, the minimization of mechanical-electrical coupling problem $(2.3)$ can be rewritten as:

Assume that $\varepsilon\rightarrow0$, because of $u_{k}^{0}(x, \xi)$ and $\Phi^{0}(x, \xi)$ are independent of $\xi$, the objective function of homogenization can be defined as:

The homogenization solution of $\Phi^{0}(x)$ and $u_{k}^{0}(x)$ satisfies the homogenization problem $(2.5)$, so Theorem $2.1$ is proved.