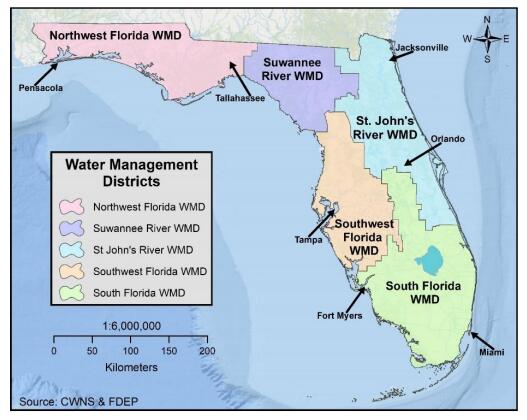
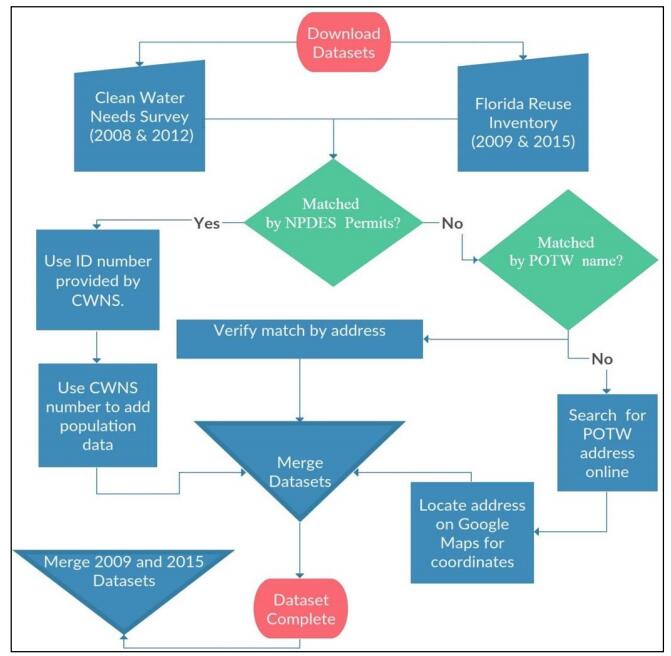
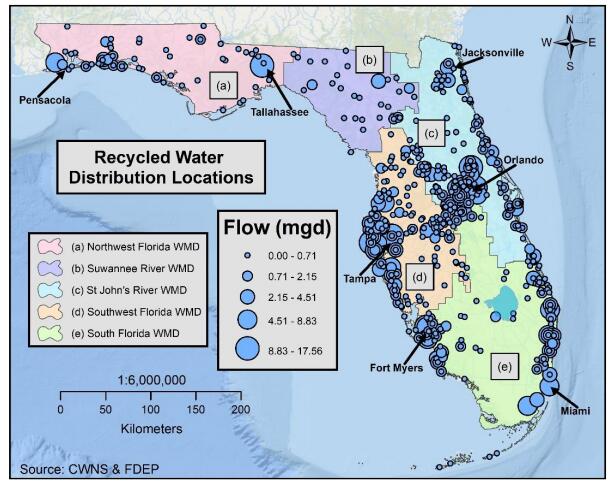
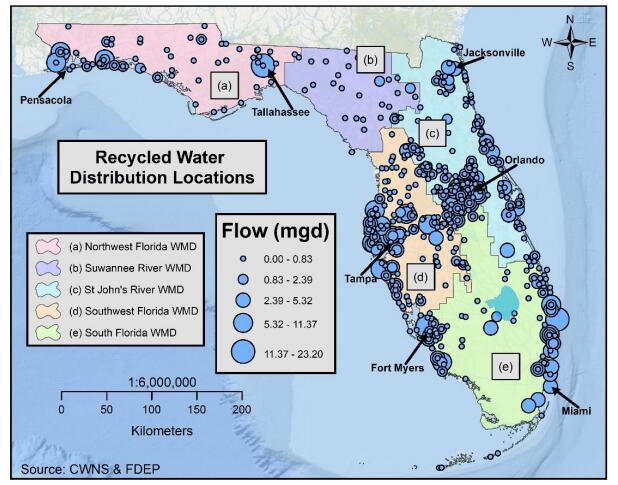
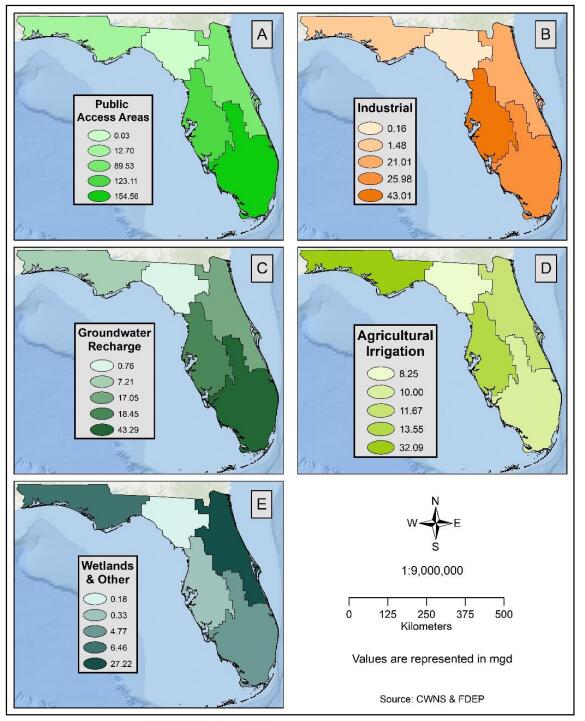
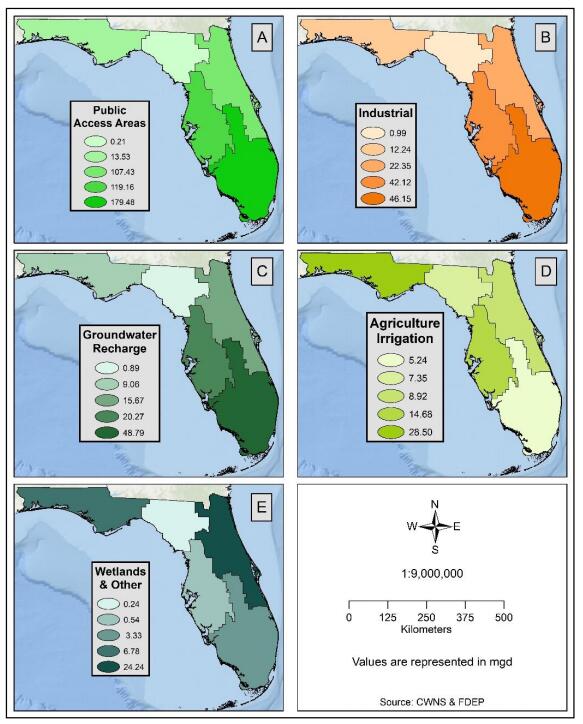
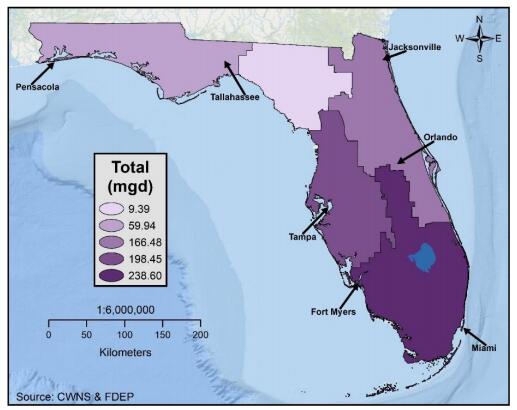
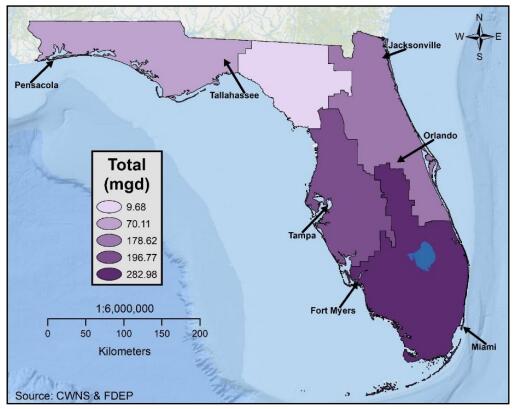
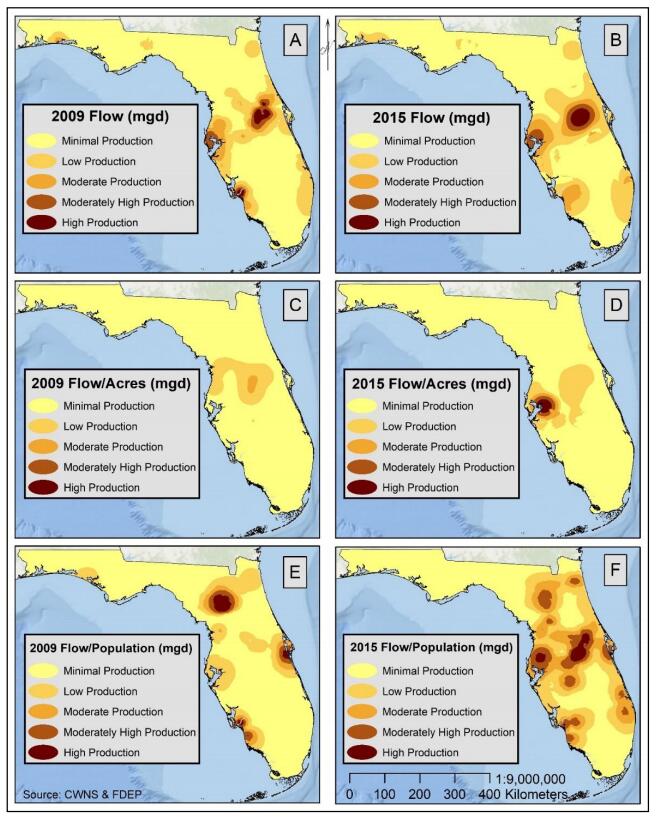
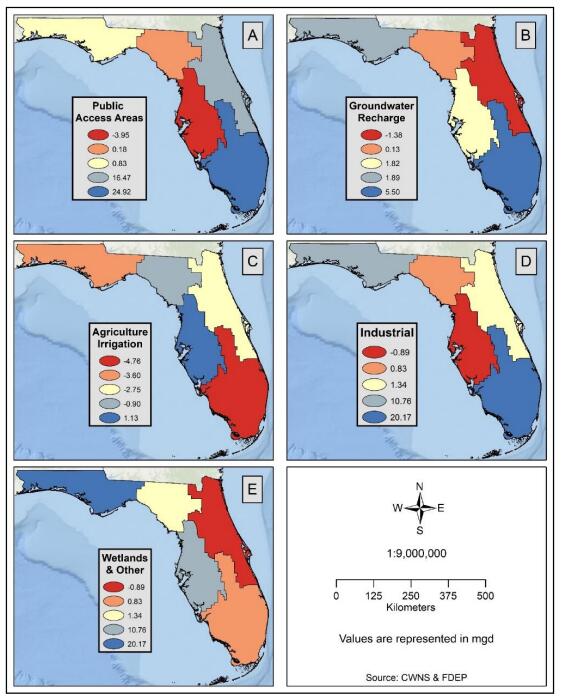
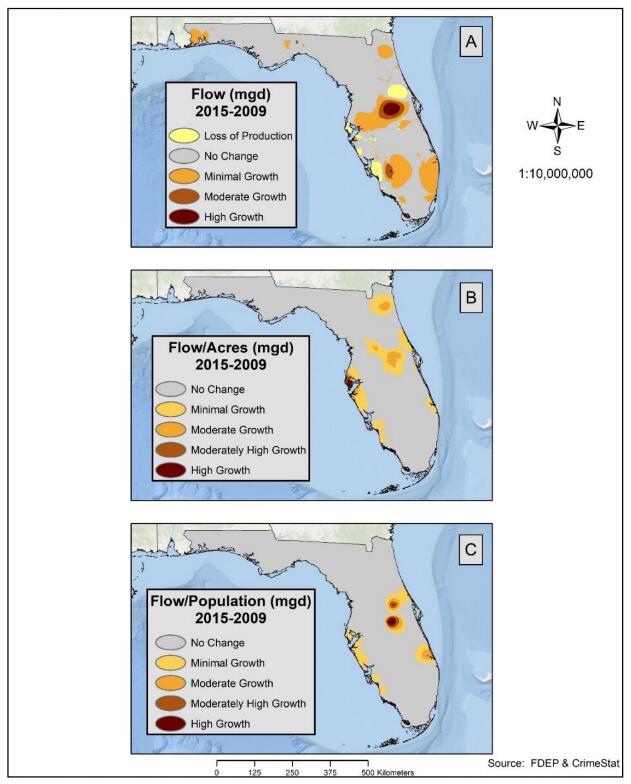
Water shortages resulting from increased demand or reduced supply may be addressed, in part, by redirecting recycled water for irrigation, industrial reuse, groundwater recharge, and as effluent discharge returned to streams. Recycled water is an essential component of integrated water management and broader adoption of recycled water will increase water conservation in water-stressed coastal communities. This study examined spatial patterns of recycled water use in Florida in 2009 and 2015 to detect gaps in distribution, quantify temporal change, and identify potential areas for expansion. Databases of recycled water products and distribution centers for Florida in 2009 and 2015 were developed by combining the 2008 and 2012 Clean Water Needs Survey databases with Florida’s 2009 and 2015 Reuse Inventory databases, respectively. Florida increased recycled water production from 674.85 mgd in 2009 to 738.15 mgd in 2015, an increase of 63.30 mgd. The increase was primarily allocated to use in public access areas, groundwater recharge, and industrial reuse, all within the South Florida Water Management District (WMD). In particular, Miami was identified in 2009 as an area of opportunity for recycled water development, and by 2015 it had increased production and reduced the production gap. Overall, South Florida WMD had the largest increase in production of 44.38 mgd (69%), while Southwest Florida WMD decreased production of recycled water by 1.68 mgd, or 3%. Overall increase in use of recycled water may be related to higher demand due to increased population coupled with public programs and policy changes that promote recycled water use at both the municipal and individual level.
1.
Introduction and Preliminaries
Let G be a finite, simple and connected graph. A family of subetaaphs H1,H2,…,Ht is called an edge-covering if every edge from E(G) belongs to at least one of the subetaaphs Hi, i=1,2,…,t. When Hi,i=1,2,…,t is isomorphic to a given graph H, then graph G admits an H-covering. G is called an (α,d)-H-antimagic if there exists a total labeling ϕ:V(G)∪E(G)→{1,2,…,v+e} with the H-weights,
forming an arithmetic progression α,α+d,α+2d,…,α+(t−1)d, where α>0 and d≥0 are two integers and t is the number of all subetaaphs of G isomorphic to H. Moreover, G is said to be super (α,d)-H-antimagic if ϕ(V(G))={1,2,3,…,|V(G)|}.
The H-supermagic graph was first introduced by Gutiérrez and Lladó in [3]. Some other results can be seen from [4,7,8,9,10,11]. An (a,d)-H-antimagic labeling was introduced by Inayah et al. [5]. The further results on antimagic labeling are discussed in [2,6,16]. In [12], authors discussed the supermagic and super (α,1)-C4-antimagic labeling of book graph and its disjoint union. The super (a,d)-C3-antimagicness of a corona graph for differences d∈{0,1,…,5} is discussed in [1]. M. A. Umar [14] study the existence of the super cycle-antimagic labeling of ladder graphs for differences d∈{0,1,…,15}. M.A.Umar et al. [13] gives the super (α,d)-C4-antimagic labeling of book graphs for differences d=1,2,…,13.
In this research manuscript, we investigated the existence of super (α,1)-C4-antimagic labeling of stacked book graphs SB(p,q) that can be thought of as generalization of a book graph and super (α,1)-C4(r+1)-antimagic labeling of its r subdivided graph SB(p,q)(r).
2.
Cycle-antimagic labeling of stacked book graphs
A Cartesian product of two graphs G1 and G2, denoted by G1◻G2, is the graph with vertex set V(G1)◻V(G2), where two vertices (u,u′) and (v,v′) are adjacent if and only if u=v and u′v′∈E(G2) or u′=v′ and uv∈E(G1).
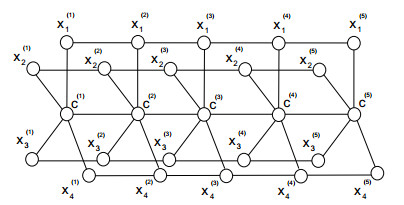
A stacked book graph denoted by SB(p,q) is defined as the cartesian product of a star graph Sp on p+1 vertices with a path Pq on q vertices. i.e., SB(p,q)≅Sp+1◻Pq, where the symbol ◻ used to denote the cartesian product of two graphs. The stacked book graph SB(p,q) contains q(p+1) vertices and q(2p+1)−(p+1) edges.
The vertex set V(SB(p,q)) have the elements {c(j),x(j)i:1≤i≤p,1≤j≤q} and the edge set E(SB(p,q)) have the elements
A typical picture of stacked book graph SB(p,q) is given in Figure 1:
Clearly stacked book graph SB(p,q) admits C4-covering. It will be worth noting for p=1, the stacked book graph SB(1,q) is a ladder graph P2◻Pq, for p=2, the stacked book graph SB(2,q) is a grid graph P2◻Pq and for q=2, the stacked book graph SB(p,2) is a book graph Pp◻P2. Ming-Ju Lee et al. describe the super (α,1)-cycle-antimagic labeling of grid graph Pp◻Pq in [15]. M. A. Umar et al. [12] give the supermagic and super (α,1)-C4-antimagic labeling of book graph and its disjoint union while [13] describes the super (α,d)-C4-antimagic labeling of book graphs for differences d=1,2,…,13. Therefore we consider p,q≥3 in this paper.
Let Ci,j4 be the (i,j)th cycle for 1≤i≤p,1≤j≤q−1 in SB(p,q). Each (i,j)th-cycle Ci,j4 in SB(p,q) has the vertex set {c(j),c(j+1),x(j)i,x(j+1)i} and the edge set {c(j)c(j+1),x(j)ix(j+1)i,c(j)x(j)i,c(j+1)x(j+1)i}.
The corresponding Ci,j4-weight under a total labeling ϕ would be:
For our convenience, throughout this paper by i=¯1,p, we mean i=1,2,…,p and vice versa.
Theorem 1. Let p,q≥3 be positive integers and Sp be a star on p+1 vertices. Then stacked book graph SB(p,q) admits a super (α,1)-C4-antimagic labeling.
Proof. The total labeling ϕ0 have the form:
Evidently,
and therefore,
Equations (2.1) and (2.2) gives:
For convenience, define wtϕ0(partial)=8q(p+1)+2+⌈q2⌉.
Therefore the Ci,j4-weights are:
which makes the total labeling ϕ0 a super (α,1)-C4-antimagic labeling and the proof is complete.
3.
Cycle-antimagic labeling of r-subdivided stacked book graph
Let G be a graph and r≥1 be a positive integer. By G(r), we define r-subdivided graph of G constructed by inserting r new vertices into every edge of G.
In this way, SB(p,q)(r) is the r-subdivided graph of stacked book graph with the vertex set {c(j),x(j)i,u(i,j)r:1≤i≤p,1≤j≤q}∪{ϵ(j)r,δ(i,j)r:1≤i≤p,1≤j≤q−1} and the edge set
where u(i,j)r, ϵ(j)r, δ(i,j)r are r new vertices inserted into the edges c(j)x(j)i, c(j)c(j+1) and x(j)ix(j+1)i respectively. Clearly r-subdivided stacked book graph SB(p,q)(r) admits C4(r+1)-covering.
Let Ci,j4(r+1) be the (i,j)th-cycle for 1≤i≤p,1≤j≤q−1 in SB(p,q)(r). Each (i,j)th-cycle Ci,j4(r+1) in SB(p,q)(r) has the vertex set
and the edge set {u(i,j)ku(i,j)k+1,u(i,j+1)ku(i,j+1)k+1,ϵ(j)kϵ(j)k+1,δ(i,j)kδ(i,j)k+1:1≤k≤r−1}∪
Ci,j4(r+1)-weight under a total labeling ϕ would be:
where
Theorem 2. Let p,q≥3 and r≥1 be positive integers and SB(p,q)(r) be r-subdivided stacked book graph then SB(p,q)(r) admits a super (β,1)-C4(r+1)-antimagic labeling.
Proof. The total labeling ϕ have the form:
Using expressions (3.2), (3.3) and (3.4), we have:
where SPartial3=r(r+1)(q−1)(2p+3)+q(2pr2+5pr+2p+2r+1)+r
One can observe here that the Partial1+2Partial2+SPartial3 are independent of i and j. Equation (3.8) clearly shows that wtϕ(Ci,j4(r+1)) only depends on i and j. Equation (3.8) with equation (2.4) proves that SB(p,q)(r) admits a super (β,1)-C4(r+1)-antimagic labeling which completes the proof.
4.
Conclusion
In this manuscript, we prove results related to super (α,1)-C4-antimagic labeling of stacked book graphs SB(p,q) and super (α,1)-C4(r+1)-antimagic labeling of its r subdivided graph SB(p,q)(r). One can extend these results for other differences d and for disjoint union of stacked book graphs. One can also prove results about applications of graph labeling in data science and communication networks.
Acknowledgments
The study was supported by the Key Industrial Technology Development Project of Chongqing Development and Reform Commission, China (Grant No. 2018148208), Key Technological Innovation and Application Development Project of Chongqing, China (Grant No. cstc2019jscx-fxydX0094), Innovation and Entrepreneurship Demonstration Team of Yingcai Program of Chongqing, China (Grant No. CQYC201903167), Science and Technology Innovation Project of Yongchuan District (Ycstc,2020cc0501).
The research was supported by the National Natural Science Foundation of China (Grant Nos. 11971142, 11871202, 61673169, 11701176, 11626101, 11601485).
The authors are grateful to the anonymous reviewers of this journal who helped to improve the paper.
Conflict of interests
The authors declare that there is no conflict of interests.









 DownLoad:
DownLoad: