Distance antimagic labeling of circulant graphs

1.   Introduction

Let $G = G(V, E)$ be a finite, simple, undirected graph. The notion of {distance magic labeling} of a graph $G$ was introduced in the Ph.D. thesis of Kamalappan ^[20] as a bijection $f:V(G) \rightarrow \{1, 2, \ldots, |V(G)|\}$ with the property that there is a magic constant ${\sf k}$ such that at any vertex $x$, the weight of vertex $x$, $\omega(x) = \sum_{y\in N(x)} f(y) = {\sf k}$, where $N(x)$ is the open neighborhood of $x$, i.e., the set of vertices adjacent to $x$. It has been proven that the magic constant of a distance magic graph is unique ^[2,14] and that many classes of graphs admit distance magic labeling (see ^[1] and ^[5]). However, the necessary and sufficient conditions for a graph to be distance magic are still unknown.

In the case of distinct vertex weights, we have distance antimagic labeling, formally defined as follows ^[7]. A bijection $f : V(G) \rightarrow \{1, 2, ..., |V(G)|\}$ is called a {distance antimagic labeling} of graph $G$ if $\omega(x) \ne \omega(y)$, for two distinct vertices $x$ and $y$. A graph that admits distance antimagic labeling is called a {distance antimagic graph}. It is clear that if a graph contains two vertices with the same open neighborhood, then it does not admit a distance antimagic labeling. Kamatchi and Arumugam ^[7] then conjectured that the converse of the previous statement is also true and proposed the following:

Conjecture A. ^[7] A graph $G$ is distance antimagic if and only if $G$ does not have two distinct vertices with the same open neighborhood.

Some families of graphs are distance antimagic, among others the path $P_n$, the cycle $C_n$ ($n \neq 4$), the wheel $W_n$ ($n \neq 4$) ^[7], and the hypercube $Q_n$ ($n \geq 3$) ^[8]. In 2016, Llado and Miller ^[10] utilized combinatorial nullstellensatz to prove that a tree with $l$ leaves and $2l$ vertices is distance antimagic. Recently, some product graphs have been shown to be distance antimagic ^[19,21].

In this paper, we consider distance antimagic circulant graphs. Let $n$ be a positive integer, and $S = \{s_1, s_2, \ldots, s_k\}$ be a set of integers such that $1\le s_1 < s_2 < \ldots < s_k < n$. A circulant graph $C(n; S)$ is a graph with a vertex-set $V = \{v_0, v_1, \ldots, v_{n-1}\}$ and an edge-set $E = \{(v_iv_{(i+s_j)(\bmod{n})} \ | \ 0\le i\le n-1, 1\le j\le k\}$. In other words, a circulant graph $C(n; S)$ is a Cayley graph whose adjacency matrix is circulant, where $S$ is the generating set. For each $s_i \in S$ coprime to $n$, including $s_1 = 1$, there exists a Hamiltonian cycle in $C(n; S)$. In ^[3], it is shown that the circulant graph $C(n; S)$ is connected if and only if $\gcd(s_1, s_2, \ldots, s_k, n) = 1$.

It is clear that the circulant graph $C(n; S)$ is isomorphic to $C(n; S')$, where $S' = \{n-s_1, n-s_2, \ldots, n-s_k\}$, and so throughout the paper we consider a generating set $S = \{s_1, s_2, \ldots, s_k\}$, where $1\le s_1 < s_2 < \ldots < s_k\le \lfloor\frac{n}{2}\rfloor$. In this case, the circulant graph $C(n; S)$ is regular of degree $2k$ if $s_k \neq n/2$, and $2k-1$ if $s_k = n/2$.

In recent years, researchers have taken interest in the study of both distance magic and antimagic labeling of circulant graphs. This is due to the fact that the circulant graphs are Cayley and so vertex transitive. Cichacz and Froncek ^[4] completely characterized distance magic $C(n; \{1, p\})$ for odd $p$ and gave some sufficient conditions for even $p$. Miklavic and Šparl later settled the characterization problem for even $p$ ^[12] in 2021. Miklavic and Šparl then provided a partial classification of distance magic $C(n; \{a, b, c\})$ ^[13]. For more generators, Godinho and Singh ^[6] gave necessary and sufficient conditions for distance magic $C(n; \{1, 2, \ldots r\})$, for $\gcd(n, r)$ is even.

In 2019, Patel and Vasava ^[15] proved that the circulant graph $C(2n;\{1, n\})$ is distance antimagic for even $n$, and later in 2021, Shrimali and Rathod ^[17] proved the case for odd $n$. Another result for distance antimagic circulant graphs is in ^[16], where it is proved that the circulant graph $C(2m;\{2, \ldots, m-2, m\})$ is distance antimagic.

We start our study by characterizing distance antimagic circulant graphs with one generator in Section 2. We then circulant graphs with two generators in Section 3, where we characterize distance antimagic $C(n; {1, k})$ with odd $n$. We also provide an alternative unified construction of distance antimagic labeling for the circulant graph $C(2n;\{1, n\})$, $n\neq 3$, as opposed to the two different labeling constructions in ^[15] and ^[17]. Section 4 provides sufficient conditions for distance antimagic circulant graphs with arbitrary generating sets. We conclude by summarizing and proposing an open problem in Section 5.

2.   Distance antimagic circulant graphs with one generator

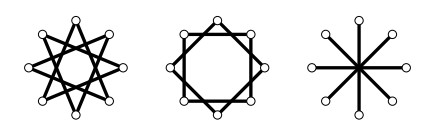
Let $n$ and $k$ be positive integers, where $k\le\lfloor \frac{n}{2}\rfloor$. The circulant graph $C(n; \{k\})$ can be categorized based on $n$ and $k$ as follows:

● If $gcd(n, k) = 1$, then the circulant graph $C(n; \{k\})$ is a cycle on $n$ vertices, $C_n$.

● If $gcd(n, k) = s \ne 1$ and $n \ne 2k$, then $C(n; \{k\})$ is isomorphic to $s C_{\frac{n}{s}}$.

● If $n = 2k$, then $C(n; \{k\})$ is isomorphic to $kP_2$.

Examples of the three types of $C(n; \{k\})$ can be found in Figure 1.

Figure 1.  The circulant graphs (a) $C(8;3)$, (b) $C(8;2)$, and (c) $C(8;4)$.

DownLoad: Full-Size Img PowerPoint

We are ready to show that Conjecture A is true for circulant graphs with one generator, $C(n; \{k\})$.

Theorem 2.1. Let $n$ and $k$ be positive integers, where $k\le\lfloor \frac{n}{2}\rfloor$. The circulant graph $C(n; \{k\})$ is distance antimagic if and only if $n \ne 4k$.

Proof. It is clear that the vertices with the same open neighborhoods belong to $C_4$ and $C(n; \{k\})$ admits $C_4$ as a component when $n = 4k$. Thus, the proof is completed by considering the following results:

$(1)$ For $n\neq 4$, the disjoint copies of $C_n$ are distance antimagic ^[7,18].

$(2)$ The disjoint copies of $P_2$ are distance antimagic.

3.   Distance antimagic circulant graphs with two generators

We begin by considering the circulant graph $C(n; \{1, k\})$, where $1 < k < \frac{n}{2}$. In the following lemma, we provide sufficient conditions for such circulant graphs with even $n$ to admit distance antimagic labeling.

Lemma 3.1. Let $n$ be an even integer. For $1 < k < \frac{n}{2}$, the circulant graph $C(n; \{1, k\})$ contains two vertices with the same open neighborhood if and only if $k = \frac{n}{2}-1$.

Proof. Since $k\le \frac{n}{2}$, the circulant graph $C(n; \{1, k\})$ is a $4-$regular graph. Let $k = \frac{n}{2}-1$ and consider two vertices, $v_0$ and $v_{\frac{n}{2}}$. Obviously, $v_0$ is adjacent to $v_1$, and $v_{\frac{n}{2}-1}$. Also, $v_{n-1}$ is adjacent to $v_{((n-1)+1)(\text{mod}\; n)} = v_0$ and $v_{\frac{n}{2}+1}$ is adjacent to $v_{((\frac{n}{2}+1)+\frac{n}{2}-1)(\text{mod}\; n)} = v_0$. Thus, $N(v_0) = \{v_1, v_{\frac{n}{2}-1}, v_{\frac{n}{2}+1}, v_{n-1}\}$. On the other hand, $v_{\frac{n}{2}}$ is adjacent to $v_{\frac{n}{2}+1}$ and $v_{n-1}$. Also, $v_1$ and $v_{\frac{n}{2}-1}$ are adjacent to $v_{\frac{n}{2}}$. This leads to $N(v_{\frac{n}{2}}) = \{v_{\frac{n}{2}+1}, v_{n-1}, v_1, v_{\frac{n}{2}-1}\}$.

For necessity, suppose that $k \neq \frac{n}{2}-1$, then all vertices have distinct open neighborhoods.

Now, we are ready to construct distance antimagic labeling for the circulant graph $C(n; \{1, k\})$, $1 < k < \frac{n}{2}$, with odd $n$.

Theorem 3.1. Let $n$ be an odd integer. For $1 < k < \frac{n}{2}$, the circulant graph $C(n; \{1, k\})$ is distance antimagic.

Proof. Define a labeling $f$ for $C(n; \{1, k\})$ such that $f(v_i) = i+1$, for $i = 0, 1, \ldots, n-1$. Thus, the distinct weights of the vertices are

Figure 2 illustrates an example of the labeling.

Figure 2.  A distance antimagic labeling for $C(11, \{1, 4\})$.

DownLoad: Full-Size Img PowerPoint

For even $n$, we characterize the distance antimagic $C(n; \{1, 2\})$ and $C(n; \{1, 3\})$ in the following theorems.

Theorem 3.2. Let $n > 3$ be an even integer. The circulant graph $C(n; \{1, 2\})$ is distance antimagic if and only if $n \ne 6$.

Proof. For $n = 4$, the circulant graph $C(4;\{1, 2\})$ is the complete graph $K_4$, which clearly is distance antimagic. By Lemma 3.1, the circulant graph $C(6;\{1, 2\})$ is not distance antimagic. For $n > 6$, we consider two cases based on the remainder modulo 4.

Case 1. Let $n\equiv 2(\text{mod}\; 4)$. Define a labeling $g_1:V\rightarrow \{1, 2, \ldots, n\}$ by

and so we obtain the following distinct vertex weights:

Case 2. Let $n\equiv 0(\text{mod}\; 4)$. Consider the following two sub-cases:

Subcase 2.1. Let $n = 12$ or $n > 16$. Define a labeling $g_2:V\rightarrow \{1, 2, \ldots, n\}$ by

and so we obtain the distinct vertex weights as follows:

Subcase 2.2. Let $n = 8, 16$. Define a labeling $g_3:V\rightarrow \{1, 2, \ldots, n\}$ by

For $n = 8$, the distinct vertex weights are

And for $n = 16$, the distinct vertex weights are

Figure 3 illustrates an example of the labeling for the case of $n \equiv 2(\text{mod}\; 4)$.

Figure 3.  A distance antimagic labeling for circulant graph $C(10;\{1, 2\})$.

DownLoad: Full-Size Img PowerPoint

Theorem 3.3. Let $n$ be an even integer. The circulant graph $C(n; \{1, 3\})$ is distance antimagic if and only if $n > 8$.

Proof. The circulant graph $C(6;\{1, 3\})$ has two vertices with the same open neighborhood, so it is not distance antimagic. According to Lemma 3.1, the circulant graph $C(8;\{1, 3\})$ is not distance antimagic. For $n > 8$, consider the following two cases:

Case 1. Let $n\ne 18$. Define a labeling $h_1:V\rightarrow \{1, 2, \ldots, n\}$ by

and so that we obtain the following distinct vertex weights:

Case 2. Let $n = 18$. Define a labeling $h_2:V\rightarrow \{1, 2, \ldots, n\}$ by

Thus, we obtain the following distinct vertex weights:

Figure 4 illustrates examples of the labelings for both cases of $n\neq 18$ and $n = 18$.

Figure 4.  Distance antimagic labelings for $C(14;\{1, 3\})$ and $C(18;\{1, 3\})$.

DownLoad: Full-Size Img PowerPoint

For even $n$, we could only prove the distance antimagicness of the circulant graph $C(n; \{1, k\})$ with $k = 2, 3$ (Theorems 3.2 and 3.3). For the sake of completeness, we propose the following:

Conjecture 3.1. For even $n$ and $3 < k < \frac{n}{2}-1$, the circulant graph $C(n; \{1, k\})$ is distance antimagic.

The remaining case for the circulant graph $C(n; \{1, k\})$ is for $k = \frac{n}{2}$, which implicitly requires $n$ to be even. Patel and Vasava ^[15] proved that the circulant graph $C(2n;\{1, n\})$ is distance antimagic for even $n$. Subsequently, Shrimali and Rathod ^[17] proved that the circulant graph $C(2n;\{1, n\})$ is distance antimagic for odd $n$. Both results utilized different labeling constructions, and here we prove Theorem 3.4 by an alternative unified construction of distance antimagic labeling for circulant graph $C(2n;\{1, n\})$, $n\neq 3$. The following observation is useful, and the proof is left to the readers.

Observation 1. The circulant graph $C(2n;\{1, n\})$ contains two vertices with the same open neighborhood if and only if $n = 3$.

Theorem 3.4. The circulant graph $C(2n;\{1, n\})$ is distance antimagic if and only if $n\neq 3$.

Proof. For $n = 1$ or $2$, the circulant graphs $C(2n;\{1, n\})$ are complete graphs, which are obviously distance antimagic.

For $n\geq 4$, define a labeling $o:V\rightarrow \{1, 2, \ldots, 2n\}$ by

Thus, the following distinct vertex weights are obtained:

Figure 5 illustrates an example of the labeling.

Figure 5.  A distance antimagic labeling for $C(8;\{1, 4\})$.

DownLoad: Full-Size Img PowerPoint

We conclude this section by providing a sufficient condition such that the circulant graph $C(2n;\{a_1, a_2\})$ is not distance antimagic and, subsequently, labeling for the circulant graph $C(n; \{a_1, a_2\})$, for odd $n$ and $1 < a_1 < a_2 < \frac{n}{2}$.

Theorem 3.5. Let $n, a_1, a_2$ be positive integers with $a_1 < a_2 < n$. If $a_1+a_2 = n$, then the circulant graph $C(2n;\{a_1, a_2\})$ is not distance antimagic.

Proof. It is clear that $v_0$ and $v_n$ are not adjacent. However, $v_0$ is adjacent to $v_{a_1}$ and $v_{2n-a_1}$, and $v_n$ is adjacent to $v_{n-a_1}$ and $v_{n+a_1}$. Since $a_2 = n-a_1$, $v_0$ is adjacent to $v_{n-a_1}$ and $v_{n+a_1}$, and $v_n$ is adjacent to $v_{a_1}$ and $v_{2n-a_1}$. Therefore, $N(v_0) = N(v_n)$.

Theorem 3.6. Let $n$ be odd. If $a_1, a_2$ are positive integers, where $1 < a_1 < a_2 < \frac{n}{2}$, then the circulant graph $C(n; \{a_1, a_2\})$ is distance antimagic.

Proof. Define a labeling $q:V\rightarrow \{1, 2, \ldots, n\}$ by $q(v_i) = i+1$, for $i = 0, 1, \ldots, n-1$. Thus, the following distinct vertex weights are obtained:

Figure 6 illustrates an example of the labeling.

Figure 6.  A distance antimagic labeling for $C(15;\{4, 7\})$.

DownLoad: Full-Size Img PowerPoint

4.   Circulant graphs with arbitrary generating set

In ^[16], Semeniuta proved that the circulant graph $C(2m;\{2, \ldots, m-2, m\})$ is distance antimagic. Here, we provide some sufficient conditions for the distance antimagicness of circulant graphs with arbitrary generating sets. We start by using similar reasoning as in the proof of Theorem 3.5, which results in the following theorem.

Theorem 4.1. Let $k$ be an even integer and $a_1, a_2, \ldots, a_{k-1}, a_k, n$ be positive integers with $a_1 < a_2 < \ldots < a_{k-1} < a_k < n$. If $a_i+a_{k-i+1} = n$, $1 \le i \le \frac{k}{2}$, then:

(1) The circulant graph $C(2n;\{a_1, a_2, \ldots, a_{k-1}, a_k\})$ is not distance antimagic,

(2) The circulant graph $C(2n;\{1, 2, \ldots, n-2, n-1)$ is not distance antimagic, and

(3) For even $n$, the circulant graph $C(2n;\{a_1, a_2, \ldots, a_{\frac{k}{2}}, \frac{n}{2}, a_{\frac{k}{2}+1}, \ldots, a_{k-1}, a_k\})$ is not distance antimagic.

Theorem 4.2. Let $m$ be an odd integer, $m \geq 3$, and $n$ be a positive integer. If $k$ is a positive integer, with $k < \frac{n}{2}$, then the circulant graph $C(mn; \{k, n-k, n+k, 2n-k, 2n+k, \ldots, \lfloor \frac{m}{2}\rfloor n-k, \lfloor \frac{m}{2}\rfloor n+k\})$ is not distance antimagic.

Proof. Since $k < \frac{n}{2}$, then $k < n-k < n+k < 2n-k < 2n+k < \ldots < \lfloor \frac{m}{2}\rfloor n-k < \lfloor \frac{m}{2}\rfloor n+k$. And since $m$ is odd, then $\lfloor \frac{m}{2} \rfloor = \frac{m-1}{2}$. Consider $v_0$ and $v_n$.

● $v_0$ is adjacent to $v_i$ and $v_{mn-i}$, $i\in\{k, n-k, n+k, 2n-k, 2n+k, ...\lfloor \frac{m}{2}\rfloor n-k, \lfloor \frac{m}{2}\rfloor n+k\}$, and

● $v_n$ is adjacent to $v_{n+j}$ and $v_{mn+n-j(\text{mod}\; mn)}$, $j\in\{k, n-k, n+k, 2n-k, 2n+k, ..., \lfloor \frac{m}{2}\rfloor n-k, \lfloor \frac{m}{2}\rfloor n+k\}$.

Thus, $N(v_0) = N(v_n)$.

Two examples of circulant graphs that are not distance antimagic can be found in Figure 7.

Figure 7.  The circulant graphs $C(16;\{3, 4, 5\})$ and $C(15;\{1, 4, 6\})$ that are not distance antimagic.

DownLoad: Full-Size Img PowerPoint

Similarly, we can prove the following:

Theorem 4.3. Let $m$ be an odd integer, $m \geq 3$, and $n$ be a positive integer. If $b_1, b_2, \ldots, b_k$ are positive integers, where $b_1 < b_2 < \ldots < b_k < \frac{n}{2}$, then the circulant graph $C(mn; \{b_1, \ldots, b_k, \ldots, \lfloor \frac{m}{2}\rfloor n-b_k, \ldots, \lfloor \frac{m}{2}\rfloor n-b_1, \lfloor \frac{m}{2}\rfloor n+b_1, \ldots, \lfloor \frac{m}{2}\rfloor n+b_k\})$ is not distance antimagic.

5.   Summary and an open problem

This article completely characterizes distance antimagic circulant graphs with one generator. For circulant graphs with two generators, we completely characterized distance antimagic $C(n; \{1, k\})$ for odd $n$. For even $n$, we managed to only show the distance antimagicness of $C(n; \{1, k\})$ for $k = 2, 3$. Due to the many isomorphism properties within circulant graphs, for instance, $C(n; \{s_1, \ldots, s_i, \ldots, s_k\}) \simeq C(n; \{s_1, \ldots, n-s_i, \ldots, s_k\})$ and $C(n; \{s_1, \ldots, s_k\}) \simeq C(n; \{ts_1, \ldots, ts_k\})$, when $\gcd(n, t) = 1$, we automatically obtain some distance antimagic $C(n; \{a_1, a_2\})$, with $a_1\neq 1$. For more details on the isomorphism within circulant graphs, refer to ^[9,11].

In general, the distance antimagicness of circulant graphs with more than two generators is still largely unknown. Therefore, we propose the following:

Open problem 1. Determine all $n$ and $S$ such that a circulant graph $C(n; S)$ is distance antimagic.

Author contributions

Rinovia Simanjuntak: Conceptualization; Rinovia Simanjuntak and Tamaro Nadeak: Methodology, Formal analysis, Writing-original draft; Syafrizal Sy, Rinovia Simanjuntak, Tamaro Nadeak, Kiki Ariyanti Sugeng and Tulus Tulus: Writing-review & editing; Syafrizal Sy: Supervision; Syafrizal Sy, Kiki Ariyanti Sugeng and Tulus Tulus: Funding acquisition. All authors have read and approved the final version of the manuscript for publication.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This research was supported by Riset Kolaborasi Indonesia (RKI) Skema A (Host) No. 7/UN16.19/PT.01.03/IS-RKI Skema A (Host)/2023.

Conflict of interest

The authors declare no conflicts of interest.