Toxicity associated with gadolinium-based contrast-enhanced examinations

Silvia Maria Lattanzio; Silvia Maria Lattanzio

doi:10.3934/biophy.2021015

AIMS Biophysics

2021, Volume 8, Issue 2: 198-220. doi: 10.3934/biophy.2021015

Previous Article Next Article

Review Special Issues

Toxicity associated with gadolinium-based contrast-enhanced examinations

Silvia Maria Lattanzio ^,

Department of Biomedical Sciences, University of Padua, Padua, Italy.

Received: 20 February 2021 Accepted: 26 April 2021 Published: 08 May 2021

This article reports known and emerging adverse health effects associated with the administration of gadolinium-based contrast agents. It focuses on the issue of the incomplete excretion of these drugs leading to the deposition of gadolinium in the tissues of the patients. The evidence of deposition is reviewed. The analysis presents gaps in our knowledge but also suggests neglected or still poorly considered parameters to possibly explain discrepancies among studies (e.g. off-label use; rate of administration; gadolinium concentration in the pharmaceutical formulation, cumulative metal toxicity). The article also presents a critical assessment of some aspects reported in the literature as well as future needs. Potential biases in the investigation and evaluation of the health/clinical implications associated with gadolinium deposition are pointed out. The analysis emphasizes that the vast majority of the clinical studies conducted up to date on gadolinium-based contrast agents were designed to assess acute toxicity and diagnostic efficacy of the agents, not to identify long-term health effects.

Keywords:

Citation: Silvia Maria Lattanzio. Toxicity associated with gadolinium-based contrast-enhanced examinations[J]. AIMS Biophysics, 2021, 8(2): 198-220. doi: 10.3934/biophy.2021015

Related Papers:

[1]	Walid Emam, Khalaf S. Sultan . Bayesian and maximum likelihood estimations of the Dagum parameters under combined-unified hybrid censoring. Mathematical Biosciences and Engineering, 2021, 18(3): 2930-2951. doi: 10.3934/mbe.2021148
[2]	Manal M. Yousef, Rehab Alsultan, Said G. Nassr . Parametric inference on partially accelerated life testing for the inverted Kumaraswamy distribution based on Type-II progressive censoring data. Mathematical Biosciences and Engineering, 2023, 20(2): 1674-1694. doi: 10.3934/mbe.2023076
[3]	Said G. Nassr, Amal S. Hassan, Rehab Alsultan, Ahmed R. El-Saeed . Acceptance sampling plans for the three-parameter inverted Topp–Leone model. Mathematical Biosciences and Engineering, 2022, 19(12): 13628-13659. doi: 10.3934/mbe.2022636
[4]	Wael S. Abu El Azm, Ramy Aldallal, Hassan M. Aljohani, Said G. Nassr . Estimations of competing lifetime data from inverse Weibull distribution under adaptive progressively hybrid censored. Mathematical Biosciences and Engineering, 2022, 19(6): 6252-6275. doi: 10.3934/mbe.2022292
[5]	M. G. M. Ghazal, H. M. M. Radwan . A reduced distribution of the modified Weibull distribution and its applications to medical and engineering data. Mathematical Biosciences and Engineering, 2022, 19(12): 13193-13213. doi: 10.3934/mbe.2022617
[6]	M. Nagy, M. H. Abu-Moussa, Adel Fahad Alrasheedi, A. Rabie . Expected Bayesian estimation for exponential model based on simple step stress with Type-I hybrid censored data. Mathematical Biosciences and Engineering, 2022, 19(10): 9773-9791. doi: 10.3934/mbe.2022455
[7]	Lernik Asserian, Susan E. Luczak, I. G. Rosen . Computation of nonparametric, mixed effects, maximum likelihood, biosensor data based-estimators for the distributions of random parameters in an abstract parabolic model for the transdermal transport of alcohol. Mathematical Biosciences and Engineering, 2023, 20(11): 20345-20377. doi: 10.3934/mbe.2023900
[8]	M. Nagy, Adel Fahad Alrasheedi . The lifetime analysis of the Weibull model based on Generalized Type-I progressive hybrid censoring schemes. Mathematical Biosciences and Engineering, 2022, 19(3): 2330-2354. doi: 10.3934/mbe.2022108
[9]	Ibrahim Alkhairy . Classical and Bayesian inference for the discrete Poisson Ramos-Louzada distribution with application to COVID-19 data. Mathematical Biosciences and Engineering, 2023, 20(8): 14061-14080. doi: 10.3934/mbe.2023628
[10]	Amal S. Hassan, Najwan Alsadat, Christophe Chesneau, Ahmed W. Shawki . A novel weighted family of probability distributions with applications to world natural gas, oil, and gold reserves. Mathematical Biosciences and Engineering, 2023, 20(11): 19871-19911. doi: 10.3934/mbe.2023880

Abstract

1. Introduction

Recently, the promising attention of statisticians towards the construction of new generalized distributions has been increased to explore and develop more flexible models from the baseline models. These generalized distributions open new horizons to study real-world problems and to provide more flexibility to model the asymmetric and complex random phenomena. Therefore, several models have been developed in the literature. One of the most handy and simplest lifetime distributions induced in the statistical literature is the exponential (Ex) distribution. It has been extensively adopted for analyzing lifetime data due to its simplicity and its lack of memory property.

On the other hand, the Ex distribution with only a constant hazard rate (HR) shape is not suitable for fitting data with different HR shapes as decreasing, unimodal (upside down bathtub), increasing or bathtub shaped hazard rates which are common in reliability and engineering, among other areas. This limitation has motivated the researchers to develop more flexible extensions of the Ex model.

For more details about other methods, the interested reader can see ^{[1,2,3,4,5,6,7,8,9,10,11,12,13,14,15]}.

In the present article, we are motivated to develop a new flexible version of the Ex model called the weighted-exponential (WDEx) distribution, which can provide greater flexibility in fitting insurance data. Additionally, the aim of the article is three-fold: the first is devoted to studying a new form of the Ex distribution based on the weighted-G (WD-G) family ^[16], called the WDEx distribution. Basic distributional properties of the WDEx model are explored. The WDEx model has some desirable characteristics. It can accommodate upside-down bathtub, decreasing, decreasing-constant, increasing, and increasing-constant HR shapes. Its probability density function (PDF) possesses unimodal, right-skewed, reversed-J shape, left-skewed. The tail of the WDEx distribution is heavier than the EEx and Ex distributions as shown in Section 4 based on computational values of risk measures. The WDEx distribution can be used to model insurance data. It provides an adequate fit than other fourteen competing Ex distributions as illustrated in Section 7 for this insurance data set.

The second objective of this paper is devoted to exploring five important actuarial or risk measures, called the value at risk (VaR), tail value at risk (TVaR), tail-variance (TV), tail-variance premium (TVP), and expected shortfall (ES), for the WDEx distribution. These measures play an important role in portfolio optimization under uncertainty.

The third objective is to study the estimation of the WDEx parameters by classical and Bayesian methods. Hence, nine estimation approaches are adopted for this purpose. We explore and rank the performance of these estimators based on empirical simulation results to develop a guideline for choosing the best estimation approach for estimating the WDEx parameters.

The paper is organized in eight Sections. In Section 2, we define the WDEx model. Its basic properties are explored in Section 3. Five actuarial indicators are studies in Section 4. The model parameters are estimated using classical and Bayesian estimation in Section 5. Simulation results are provided in Section 6. Section 7 is devoted to analyzing a real-life data. Finally, some remarks are given to conclude the paper in Section 8.

2. The WDEx distribution

In this section, we define the two-parameter WDEx distribution based on the WD-G family of ^[16]. The cumulative distribution function (CDF) and PDF of the WDEx distribution has the forms

$\begin{equation} F(x) = \frac{\log \left[\left(1-e^{- \lambda x}~~\right)^{\alpha }+1\right]}{\log (2)} \end{equation}$

(2.1)

and

$\begin{equation} f(x) = \frac{\alpha \lambda e^{- \lambda x} \left(1-e^{- \lambda x}~~\right)^{\alpha -1}}{\log (2) \left[\left(1-e^{- \lambda x}~~\right)^{\alpha }+1\right]}. \end{equation}$

(2.2)

The survival function (SF), HR function (HRF) and the reversed-HRF (RHRF) are, respectively, given by

$\begin{equation} S(x) = 1-\frac{\log \left[\left(1-e^{- \lambda x}~~\right)^{\alpha }+1\right]}{\log (2)}, \end{equation}$

(2.3)

$\begin{equation} h(x) = \frac{\alpha \lambda \left(1-e^{- \lambda x}~~\right)^{\alpha }}{\left(e^{\lambda x}-1\right) \left[\left(1-e^{- \lambda x}~~\right)^{\alpha }+1\right] \left\{\log (2)-\log \left[\left(1-e^{- \lambda x}~~\right)^{\alpha }+1\right]\right\}} \end{equation}$

(2.4)

and

$\begin{equation} r(x) = \frac{\alpha \lambda e^{- \lambda x} \left(1-e^{- \lambda x}~~\right)^{\alpha -1}}{\left(\left(1-e^{- \lambda x}~~\right)^{\alpha }+1\right) \log \left(\left(1-e^{- \lambda x}~~\right)^{\alpha }+1\right)}. \end{equation}$

(2.5)

The limiting behaviors of the PDF (2.2) and HRF (2.4) are given by

$\begin{equation*} \lim\limits_{x\to0}f(x) = \begin{cases} \infty, \alpha < 1\\ 0, \; \; \alpha \geq1 \end{cases} , \lim\limits_{x\to\infty}f(x) = 0. \end{equation*}$

and

$\begin{equation*} \lim\limits_{x\to0}h(x) = \begin{cases} \infty, \alpha < 1\\ 0, \; \; \alpha \geq1 \end{cases} , \lim\limits_{x\to\infty}h(x) = \lambda. \end{equation*}$

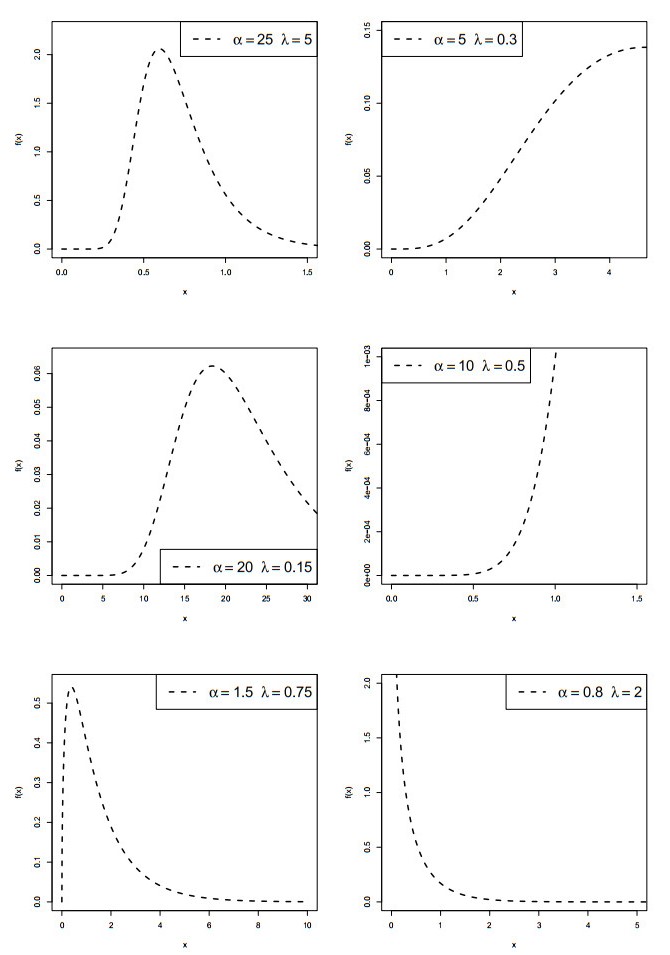
Plots of the PDF and HRF of the WDEx distribution are illustrated in Figures 1 and 2, respectively. These graphs show that the WDEx model possesses decreasing-constant, upside-down bathtub, increasing, decreasing, and increasing-constant HR functions along with sudden spikes at the end of upside-down bathtub shape, which manages the model to analyze a non-stationary real-life data.

Figure 1. Plots of the PDF of the WDEx distribution with various parametic values.

DownLoad: Full-Size Img PowerPoint

Figure 2. Plots of the HRF of the WDEx distribution with various parametric values.

DownLoad: Full-Size Img PowerPoint

The quantile function (QF) of the WDEx distribution is given by

$\begin{equation} Q(u) = -\frac{\log \left[1-\left(2^u-1\right)^{1/\alpha }\right]}{\lambda }, \end{equation}$

(2.6)

we can determine first, second and third quartile of the WDEx distribution by setting $u = 0.25, 0.5, 0.75$ , respectively. Also, by using Eq (2.6), we can determine Bowley's skewness and Moor's kurtosis for the WDEx distribution. The WDEx skewness and kurtosis graphs for the different parametric values of $\alpha$ and $\lambda$ are shown in Figure 3.

Figure 3. Plots of the skewness and kurtosis of the WDEx model.

DownLoad: Full-Size Img PowerPoint

3. Probabilistic and statistical properties

In this section, we provide some mathematical properties of the WDEx distribution.

3.1. Linear representation

A useful linear representations of the CDF and PDF of the WDEx model are introduced in this subsection. For $-1 < x\leq1$ , we have

$\begin{equation} \log(1+x) = \sum\limits_{k = 1}^{\infty}(-1)^{k+1}\frac{x^k}{k}. \end{equation}$

(3.1)

By applying the power series (3.1) to (2.1), the CDF and PDF of the WDEx distribution can be expressed as

$\begin{align*} \label{CDF G family linear} F(x;\alpha, \lambda)& = \sum\limits_{k = 1}^{\infty} \Phi_k G_k(x)\\ \end{align*}$

and

$\begin{align*} f(x;\alpha, \lambda)& = \sum\limits_{k = 1}^{\infty} \Phi_k g_k(x), \end{align*}$

where $\Phi_k = \frac{(-1)^{k+1}}{k \log(2)}$ , $G_k(x) = \left(1-e^{- \lambda x}\right)^{\alpha k}$ and $g_k(x) = \alpha k \lambda e^{- \lambda x} \left(1-e^{- \lambda x}\right)^{\alpha k -1}$ are the CDF and PDF of the exponentiated-exponential (EEx) distribution with parameters $\lambda$ and $\alpha k$ .

3.2. Moments and generating function

The $r\text{th}$ moments of the WDEx distribution takes the form

$\begin{eqnarray*} \mu^\prime_r = E(X^r)& = &\int_{0}^{\infty} x^r f(x)dx = \sum\limits_{k = 1}^{\infty} \sum\limits_{i = 0}^{\infty} \Phi_k \frac{\alpha k \Gamma(r+1)}{\lambda^r} (-1)^i \frac{D(\alpha k-1, i)}{(i+1)^{k+1}}, \end{eqnarray*}$

where $D(a-1, b) = \frac{(a-1)\ldots(a-b)}{b!}$ . Replacing $r = 1, 2, 3$ , and $4$ in the last formula, we obtain the first four moments for the WDEx distribution.

The $n\text{th}$ moment residual life of the WDEx distribution, $E(X^n|X > x)$ , has the form

$\begin{align*} E(X^n|X > x)& = \int_{x}^{\infty} y^n f(y)dy = \sum\limits_{k = 1}^{\infty} \Phi_k \frac{\alpha \lambda k}{1-\left(1-e^{- \lambda x}\right)^{\alpha k}}\int_{x}^{\infty} y^n \exp(-\lambda y) \left(1-\exp(-\lambda y)\right)^{\alpha k-1} dy\\ & = \sum\limits_{k = 1}^{\infty} \Phi_k \frac{\alpha (-1)^n}{\lambda^n \left[1-\left(1-e^{- \lambda x}\right)^{\alpha k}\right]} \int_{0}^{\exp(-\lambda x)} (\log z)^n (1-z)^{\alpha k -1} dz, \end{align*}$

where $z = \exp(-\lambda y)$ and the mean residual life function of the proposed model is $E(X|X > x)-1$ .

the moment generating function (MGF) of the WDEx distribution is

$\begin{equation*} M(t) = \int_{0}^{\infty} e^{tx} f(x)dx = \sum\limits_{k = 1}^{\infty} \Phi_k\alpha k \beta\left(1-\frac{t}{\lambda}, \alpha k\right), \end{equation*}$

where $\beta(a, b)$ is beta function. The characteristic function of the WDEx model is

$\begin{equation*} \phi(t) = \int_{0}^{\infty} e^{itx} f(x)dx = \sum\limits_{k = 1}^{\infty} \Phi_k \alpha k \beta\left(1-\frac{it}{\lambda}, \alpha k\right). \end{equation*}$

3.3. Mean deviation, bonferroni and Lorenz curves

The mean deviation about the mean of the WDEx model reduces to

$\begin{align*} \psi_1& = \int_{0}^{\infty} |x-\mu|f(x)dx = 2\mu F(\mu)-2\mu+2\int_{\mu}^{\infty}xf(x)dx\\ & = 2\mu F(\mu)-2\mu+2\sum\limits_{k = 1}^{\infty} \Phi_k \int_{\mu}^{\infty} x g_k(x) dx = 2\mu F(\mu)-2\mu\\ &+\frac{2\alpha k}{\lambda} \sum\limits_{k = 1}^{\infty} \sum\limits_{i = 0}^{\infty} \Phi_k \frac{(-1)^i}{(i+1)^2} \binom{\alpha k -1}{i} \left[1+\mu \lambda (i+1)\right] \exp(-\mu \lambda (i+1)). \end{align*}$

The mean deviation about the median of the WDEx distribution takes the form

$\begin{align*} \psi_2& = \int_{0}^{\infty} |x-M|f(x)dx = 2\int_{M}^{\infty}xf(x) dx-\mu = 2 \sum\limits_{k = 1}^{\infty} \Phi_k \int_{M}^{\infty}x g_k(x) dx -\mu\\ & = \frac{2\alpha k}{\lambda} \sum\limits_{k = 1}^{\infty} \sum\limits_{i = 0}^{\infty} \Phi_k \frac{(-1)^i}{(i+1)^2} \binom{\alpha k -1}{i} \left[1+M \lambda (i+1)\right] \exp(-M \lambda (i+1))-\mu. \end{align*}$

The Bonferroni and Lorenz curves for a positive random variable $X$ are defined the following formulae

$\begin{align*} B(F(x))& = \frac{E(X|X\leq x)}{\mu}\\ \text{and} L(F(x))& = \frac{E(X|X\leq x) F(x)}{\mu}, \end{align*}$

where the quantity $E(X|X\leq x)$ has the form

$\begin{align*} E(X|X\leq x) = \frac{\alpha k}{\lambda F(x)} \sum\limits_{k = 1}^{\infty} \sum\limits_{i = 0}^{\infty} \Phi_k \frac{(-1)^i}{(i+1)^2} \binom{\alpha k -1}{i} \left\{1-\left[1+ \lambda (i+1)x\right] \exp(- \lambda (i+1)x)\right\}. \end{align*}$

Hence,

$\begin{align*} B(p)& = \frac{\alpha k}{\lambda p \mu} \sum\limits_{k = 1}^{\infty} \sum\limits_{i = 0}^{\infty} \Phi_k \frac{(-1)^i}{(i+1)^2} \binom{\alpha k -1}{i} \left\{1-\left[1+ \lambda (i+1)x_p\right] \exp(- \lambda (i+1)x_p)\right\} \end{align*}$

and

$\begin{align*} L(p)& = \frac{\alpha k}{\lambda \mu} \sum\limits_{k = 1}^{\infty} \sum\limits_{i = 0}^{\infty} \Phi_k \frac{(-1)^i}{(i+1)^2} \binom{\alpha k -1}{i} \left\{1-\left[1+ \lambda (i+1)x_p\right] \exp(- \lambda (i+1)x_p)\right\}, \end{align*}$

where $x_p = -\frac{\log \left[1-\left(2^p-1\right)^{1/\alpha }\right]}{\lambda }$ is the QF of the WDEx model.

3.4. Order statistics

The PDF and CDF of the $i\text{th}$ order statistic for the WDEx distribution are given by

$\begin{eqnarray*} f_{i:n}(x) & = &\frac{f(x)}{B(i, n-i+1)} \sum\limits_{h = 0}^{\infty}(-1)^h \binom{n-i}{h}F^{h+i-1}(x)\\ & = &\frac{\alpha \lambda n! \log ^{-i}(2) \left(1-e^{\lambda (-x)}\right)^{\alpha } \log ^{i-1}\left(\left(1-e^{\lambda (-x)}\right)^{\alpha }+1\right) \left(1-\frac{\log \left(\left(1-e^{\lambda (-x)}\right)^{\alpha }+1\right)}{\log (2)}\right)^{n-i}}{\Gamma (i) \left(e^{\lambda x}-1\right) \Gamma (-i+n+1) \left(\left(1-e^{\lambda (-x)}\right)^{\alpha }+1\right)} \end{eqnarray*}$

and

$\begin{eqnarray*} F_{i:n}(x) & = &\sum\limits_{r = i}^{n} (^n_r) (F(x))^r (1-F(x))^{n-r}\\ & = &\log ^{-i}(2) \binom{n}{i} \log ^i\left(\left(1-e^{\lambda (-x)}\right)^{\alpha }+1\right) \left(1-\frac{\log \left(\left(1-e^{\lambda (-x)}\right)^{\alpha }+1\right)}{\log (2)}\right)^{n-i}\\ &\times& \, _2F_1\left(1, i-n;i+1;-\frac{\log \left(\left(1-e^{-x \lambda }\right)^{\alpha }+1\right)}{\log \left(\frac{2}{\left(1-e^{-x \lambda }\right)^{\alpha }+1}\right)}\right), \end{eqnarray*}$

where $\, _2F_1\left(1, i-n; i+1;-\frac{\log \left(\left(1-e^{-x \lambda }\right)^{\alpha }+1\right)}{\log \left(\frac{2}{\left(1-e^{-x \lambda }\right)^{\alpha }+1}\right)}\right)$ is a hyper geometric function.

4. Actuarial measures

Five risk measures are explored for the WDEx distribution in this section. Some actuarial measures such as VaR, TVaR, TV, TVP, and ES are calculated. A brief simulation study for these measures is provided. Finally, an application to the insurance loss data set is analyzed. For more information we refer to refs ^{[17,18,19,20,21]}.

4.1. VaR measure

The VaR is often referred to as the quantile risk measure or the concept of quantile premium, and it is defined with a certain amount of confidence, say q (typically $90$ , $95$ , or $99\%$ ). In comparison, VaR is a quantitative sum of accumulated loss distribution. Risk management are also interested in the "chance of an unfavorable outcome" and can be represented at a specific likelihood level using the VaR. The VaR of a random variable $X$ is the $q\text{th}$ quantile of its CDF, denoted by $VaR_q$ , and it is defined by $VaR_q = Q(q)$ (see Artzner ^[22]).

The VaR measure of the WDEx distribution is expressed by

$\begin{equation*} {VaR_q = }-\frac{\log \left[1-\left(2^q-1\right)^{1/\alpha }\right]}{\lambda }. \end{equation*}$

4.2. TVaR measure

The TVaR, which is now being assigned many names, including conditional tail-expectation and conditional VaR, is another significant indicator. The TVaR is used to measure the potential value of the loss provided that there has been an occurrence outside of a provided probability level. The TVaR of a random variable $X$ is represented by

$\begin{equation*} { TVaR_q = \frac{1}{(1-q)}\int_{VaR_q}^{\infty} x\, \, f(x)dx.} \end{equation*}$

The TVaR of the WDEx distribution is

$\begin{eqnarray} TVaR_q& = &\frac{\alpha}{(1-q)\; \lambda\; \log(2)}\sum\limits_{k = 1}^{\infty}\sum\limits_{m = 1}^{\infty} \frac{(-1)^{k+1}\left[1-\left(-1+2^q\right)^{k+\frac{m}{\alpha}}\right]}{m\; k\; (m+\alpha\; k)}. \end{eqnarray}$

(4.1)

4.3. TV measure

Landsman ^[23] presented the TV risk that is described by the variance of the loss distribution beyond some critical value. The TV of the WDEx distribution is described as

$\begin{equation} TV_q(X) = E(X^2|X > x_q)-(TVaR_q)^2{ = \frac{1}{(1-q)}\int_{VaR_q}^{\infty}x^2f(x)dx-(TVaR_q)^2}, \end{equation}$

(4.2)

where

$\begin{eqnarray} E(X^2|X > x_q)& = &\frac{2\alpha}{(1-q)\; \lambda^2\; \log(2)}\sum\limits_{k = 1}^{\infty}\sum\limits_{m = 1}^{\infty}\sum\limits_{n = 1}^{k} \frac{(-1)^{k+1}\left[1-\left(-1+2^q\right)^{k+\frac{m+1}{\alpha}}\right]}{k\; n\; (m+1)\; (m+\alpha\; k+1)}, \end{eqnarray}$

(4.3)

by using Eqs (4.1)–(4.3), we get the TV of the WDEx distribution.

4.4. TVP measure

The TVP is also another effective criterion in the insurance fields. The TVP of the WDEx distribution has the form

$\begin{equation} TVP_q(x) = TVaR_q + q\; TV_q, \end{equation}$

(4.4)

where $0 < q < 1$ . The TVP of the WDEx distribution follows by replacing Eqs (4.1) and (4.2) in (4.4).

4.5. ES measure

Artzner ^[22] developed the expected shortfall (ES) as a common indicator in financial risk. In some definitions, if the underlying distribution of $X$ is continuous then the ES coincides with the Conditional tail expectation and the TVaR. The ES of the WDEx distribution takes the form

$\begin{equation} ES_q(x) = \frac{1}{q}\int_{0}^{q} VaR_t\; dt = \sum\limits_{m = 1}^{\infty}\frac{1}{q\; m\; \lambda}\int_{0}^{q}(2^t-1)^{\frac{m}{\alpha}}dt. \end{equation}$

(4.5)

4.6. Numerical simulations for risk measures

In this sub-section, we discuss some empirical results for the five aforemention risk measures for the WDEx, EEx, and Ex distributions for some parametric values. The findings are obtained through to the followings steps:

(1) Random sample of size $n = 100$ is produced from the WDEx, EEx, and Ex distributions, and their parameters are calculated via the maximum likelihood (ML) approach.

(2) 1000 Replications are designed to determine the mean of the VaR, TVaR, TV, TVP as well as ES for the three distributions.

Simulation results of the average VaR, TVaR, TV, TVP and ES for the WDEx, EEx, and Ex distributions are provided in Tables 1 and 2 and displayed graphically in Figures 4 and 5.

Table 1. Simulation results of the five measures of risk for the WDEx, EEx, and Ex distributions.

Distribution	parameter	Significance level	VaR	TVaR	TV	TVP	ES
WDEx	$\alpha=3, \, \lambda=0.5$	0.60	3.24353	5.32312	4.07298	7.83746	1.89911
		0.65	3.53435	5.59982	4.08566	8.30964	2.01350
		0.70	3.86421	5.91721	4.09951	8.82180	2.13364
		0.75	4.24850	6.29046	4.11464	9.38883	2.26146
		0.80	4.71278	6.74496	4.13115	10.03667	2.39965
		0.85	5.30475	7.32825	4.14941	10.81284	2.55232
		0.90	6.13120	8.14701	4.16895	11.82411	2.72668
		0.95	7.53258	9.54158	4.19058	13.41092	2.93856
EEx	$\alpha=3, \, \lambda=0.5$	0.60	0.49017	2.04260	3.25950	3.99830	0.11832
		0.65	0.64444	2.25379	3.35743	4.43611	0.15262
		0.70	0.84081	2.50632	3.45651	4.92587	0.19448
		0.75	1.09436	2.81518	3.55661	5.48264	0.24565
		0.80	1.43025	3.20549	3.65760	6.13157	0.30867
		0.85	1.89560	3.72427	3.75935	6.91972	0.38752
		0.90	2.59602	4.47711	3.86176	7.95269	0.48924
		0.95	3.86842	5.80090	3.96470	9.56736	0.62946
Ex	$\lambda=0.5$	0.60	1.83505	3.83774	4.05243	6.26920	0.77933
		0.65	2.10247	4.10516	4.05243	6.73924	0.87059
		0.70	2.41119	4.41388	4.05243	7.25058	0.96933
		0.75	2.77632	4.77901	4.05243	7.81833	1.07725
		0.80	3.22321	5.22590	4.05243	8.46784	1.19689
		0.85	3.79935	5.80204	4.05243	9.24660	1.33222
		0.90	4.61137	6.61406	4.05243	10.26125	1.49032
		0.95	5.99953	8.00222	4.05243	11.85203	1.68693

| Show Table

DownLoad: CSV

Table 2. Simulation results of the five measures of risk for the WDEx, EEx, and Ex distributions.

Distribution	Parameter	Significance level	VaR	TVaR	TV	TVP	ES
WDEx	$\alpha=2, \, \lambda=0.75$	0.60	1.68889	3.03197	1.78964	4.11200	0.89027
		0.65	1.87191	3.21103	1.78988	4.37915	0.95860
		0.70	2.08127	3.41720	1.79047	4.67351	1.03113
		0.75	2.32712	3.66052	1.79145	5.00516	1.10910
		0.80	2.62636	3.95782	1.79286	5.39098	1.19423
		0.85	3.01058	4.34064	1.79474	5.86253	1.28924
		0.90	3.55059	4.87971	1.79711	6.49060	1.39887
		0.95	4.47215	5.80076	1.80005	7.50092	1.53359
EEx	$\alpha=2, \, \lambda=0.75$	0.60	0.59547	1.76160	1.59250	2.71710	0.18354
		0.65	0.73107	1.91880	1.61759	2.97024	0.22029
		0.70	0.89504	2.10354	1.64237	3.25320	0.26243
		0.75	1.09725	2.32577	1.66681	3.57588	0.31110
		0.80	1.35434	2.60215	1.69096	3.95491	0.36792
		0.85	1.69752	2.96394	1.71477	4.42150	0.43550
		0.90	2.19695	3.48134	1.73829	5.04581	0.51848
		0.95	3.07660	4.37836	1.76151	6.05179	0.62721
Ex	$\lambda=0.75$	0.60	1.13884	2.38172	1.56099	3.31832	0.48365
		0.65	1.30481	2.54769	1.56099	3.56233	0.54029
		0.70	1.49640	2.73928	1.56100	3.83198	0.60157
		0.75	1.72300	2.96588	1.56099	4.13662	0.66855
		0.80	2.00034	3.24322	1.56099	4.49202	0.74280
		0.85	2.35790	3.60078	1.56099	4.92762	0.82678
		0.90	2.86184	4.10472	1.56099	5.50962	0.92490
		0.95	3.72334	4.96623	1.56099	6.44917	1.04692

| Show Table

DownLoad: CSV

Figure 4. The above figure displays the graphs of the VaR, TVaR, TV, TVP, and ES using the values in Table 1.

DownLoad: Full-Size Img PowerPoint

Figure 5. The above figure displays the graphs of the VaR, TVaR, TV, TVP, and ES using the values in Table 2.

DownLoad: Full-Size Img PowerPoint

The model with highest value of VaR, TVaR, TV, TVP and ES metrics does also have a heavier tail than other competitor models. The results illustrate that the WDEx model has improved quantities of the five risk factors than the EEx, and Ex distributions. Thus, the WDEx model with these parameter values has a heavier-tail than other distributions and could be used efficiently to model heavy-tailed insurance data.

5. Classical and Bayesian estimation

This section is devoted to address the estimation of the WDEx parameters by various estimation methods including eight classical estimation approaches, such as the MLE, Anderson–Darling (ADE) and right-tail Anderson–Darling (RTADE), Cramér–von Mises (CVME), least-squares (LSE), weighted least-squares (WLSE), maximum product of spacings (MPS) and percentile estimation (PCE), and Bayesian approach under three loss functions namely, square error (SE), linear exponential (LINEX), and the general entropy (GE).

Consider the random sample of size $n$ , say $x_1, x_2, \ldots, x_n$ , from the PDF (2.2), and let $x_{1:n}, x_{2:n}, \ldots, x_{2:n}$ be their associated order statistics.

5.1. Maximum likelihood

The log-likelihood function of the WDEx distribution has the form

$\begin{equation} L = (\alpha -1) \sum\limits _{i = 1}^n \log \left((1-e)^{-\lambda x_i}\right)-\sum\limits _{i = 1}^n \log \left(\left(1-e^{-\lambda x_i}\right){}^{\alpha }+1\right)-\lambda \sum\limits _{i = 1}^n x_i+n \log \left(\frac{\alpha \lambda }{\log (2)}\right). \end{equation}$

(5.1)

Hence, the MLEs of $\alpha$ and $\lambda$ are determined by maximizing Eq (5.1) with respect to $\alpha$ and $\lambda$ , as the solutions of the following equations

$\begin{equation*} \frac{\partial L}{\partial \alpha} = -\sum \limits_{i = 1}^n \frac{\left(1-e^{-\lambda x_i}\right){}^{\alpha } \log \left(1-e^{-\lambda x_i}\right)}{\left(1-e^{-\lambda x_i}\right){}^{\alpha }+1}+\sum \limits_{i = 1}^n \log \left((1-e)^{-\lambda x_i}\right)+\frac{n}{\alpha } = 0 \end{equation*}$

and

$\begin{align*} \frac{\partial L}{\partial \lambda}& = (\alpha -1) \sum _{i = 1}^n \frac{x_i e^{-\lambda x_i}}{1-e^{-\lambda x_i}}-\sum _{i = 1}^n \frac{\alpha x_i e^{-\lambda x_i} \left(1-e^{-\lambda x_i}\right){}^{\alpha -1}}{\left(1-e^{-\lambda x_i}\right){}^{\alpha }+1}-\sum _{i = 1}^n x_i+\frac{n}{\lambda } = 0. \end{align*}$

Furthermore, solving the above two equations mathematically is complicated, hence the equations can be solved by the numerical methods to obtain the MLE of $\alpha$ and $\lambda$ .

5.2. Ordinary and weighted least-squares

The LSE of the WDEx parameters come from minimizing

$\begin{equation*} O = \sum\limits_{i = 1}^{n}\left[F(x_{i:n})-\frac{i}{n+1}\right]^2 = \sum\limits_{i = 1}^{n}\left[\frac{\log \left[\left(1-e^{- \lambda x_{i:n}}\right)^{\alpha }+1\right]}{\log (2)}-\frac{i}{n+1}\right]^2. \end{equation*}$

The LSE of the WDEx parameters are also obtained by solving the following equations

$\begin{equation*} \sum\limits_{i = 1}^{n}\left\{\frac{\log \left[\left(1-e^{- \lambda x_{i:n}}\right)^{\alpha }+1\right]}{\log (2)}-\frac{i}{n+1}\right\}\varDelta_s (x_{i:n}) = 0, \quad s = 1, 2, \end{equation*}$

where

$\begin{eqnarray} \varDelta_1 (x_{i:n})& = & \frac{\partial}{\partial \alpha}F(x_{i:n}) = \frac{\left(1-e^{-\lambda x_i}\right){}^{\alpha } \log \left(1-e^{-\lambda x_i}\right)}{\log (2) \left(\left(1-e^{-\lambda x_i}\right){}^{\alpha }+1\right)}, \end{eqnarray}$

(5.2)

$\begin{eqnarray} \varDelta_2 (x_{i:n})& = &\frac{\partial}{\partial \lambda}F(x_{i:n}) = \frac{\alpha x_i e^{-\lambda x_i} \left(1-e^{-\lambda x_i}\right){}^{\alpha -1}}{\log (2) \left(\left(1-e^{-\lambda x_i}\right){}^{\alpha }+1\right)}. \end{eqnarray}$

(5.3)

The WLSE of the WDEx parameters can be calculated by minimizing

$\begin{equation*} W = \sum\limits_{i = 1}^{n}\frac{(n+1)^2(n+2)}{i(n-i+1)}\left[F(x_{i:n})-\frac{i}{n+1}\right]^2 = \sum\limits_{i = 1}^{n}\frac{(n+1)^2(n+2)}{i(n-i+1)}\left[\frac{\log \left[\left(1-e^{- \lambda x_{i:n}}\right)^{\alpha }+1\right]}{\log (2)}-\frac{i}{n+1}\right]^2. \end{equation*}$

Furthermore, the WLSE of the WDEx parameters are obtained by solving the following equations

$\begin{equation*} \sum\limits_{i = 1}^{n}\frac{(n+1)^2(n+2)}{i(n-i+1)}\left[\frac{\log \left[\left(1-e^{- \lambda x_{i:n}}\right)^{\alpha }+1\right]}{\log (2)}-\frac{i}{n+1}\right] \varDelta_s (x_{i:n}) = 0, \end{equation*}$

where $\varDelta_s (x_{i:n}), s = 1, 2, 3$ are given by Eqs (5.2) and (5.3).

5.3. Anderson-Darling and right-tail Anderson-Darling

The ADE of the WDEx parameters are obtained by minimizing

$\begin{equation*} A = -n-\frac{1}{n}\sum\limits_{i = 1}^{n}(2i-1)[\log F(x_{i:n})+\log S(x_{i:n})]. \end{equation*}$

The ADE are also calculated by solving the following equations

$\begin{equation*} \sum\limits_{i = 1}^{n}(2i-1)\left[\frac{\varDelta_s (x_{i:n})}{F(x_{i:n})}-\frac{\varDelta_s (x_{n+1-i:n})}{S(x_{n+1-i:n})}\right] = 0, \end{equation*}$

where $\varDelta_s (x_{i:n}), s = 1, 2, 3$ were defined in (5.2) and (5.3), respectively.

The RTADE of the WDEx parameters can be calculated by minimizing

$\begin{equation*} R = \frac{n}{2}-2\sum\limits_{i = 1}^{n}F(x_{i:n})-\frac{1}{n}\sum\limits_{i = 1}^{n}(2i-1)\log S(x_{i:n}). \end{equation*}$

The RADE can also be follow by solving the non-linear equations

$\begin{equation*} -2\sum\limits_{i = 1}^{n}\varDelta_s (x_{n+1-i:n}) +\frac{1}{ n}\sum\limits_{i = 1}^{n}\frac{\varDelta_s (x_{n+1-i:n})}{S(x_{n+1-i:n})} = 0, \end{equation*}$

where $\varDelta_s (x_{i:n}), s = 1, 2, 3$ are defined in (5.2) and (5.3).

5.4. Maximum product of spacings

As an alternative to the ML method, the maximum product spacing (MPS) approach is adopted to estimate the parameters of continuous univariate distributions. The uniform spacings, say $D_i$ , of a random sample of size $n$ from the WDEx distribution are defined by

$\begin{equation*} D_i = F(x_{i})-F(x_{i-1}), \, \, i = 1, 2, ..., n. \end{equation*}$

where $F(x_0) = 0$ , $F(x_{n+1} = 1)$ and $\sum_{i = 1}^{n+1} D_i = 1$ . Then, the MPSE of the WDEx parameters can be obtained by maximizing

$\begin{equation*} G = \frac{1}{n+1} \sum\limits_{i = 1}^{n+1} \log(D_i), \end{equation*}$

with respect to $\alpha$ and $\lambda$ . Further, the MPSE of the WDEx parameters are also obtained by solving

$\begin{equation*} \frac{1}{n+1} \sum\limits_{i = 1}^{n+1} \frac{1}{D_i} [\varDelta_s (x_{i:n})-\varDelta_s (x_{i-1:n})] = 0, \end{equation*}$

where $\varDelta_s (x_{i:n}), s = 1, 2, 3$ are presented in (5.2) and (5.3).

5.5. Percentile estimation

Let $p_i = \frac{i}{n+1}$ be an estimate of $F(x_{i:n})$ . Hence, the PCE of the WDEx parameters are obtained by minimizing

$\begin{equation*} PCE = \sum\limits_{i = 1}^{n}[x_{i:n}-Q(p_i)]^2 = \sum\limits_{i = 1}^{n}\left[x_{i:n}-\frac{\log \left[1-\left(2^{p_i}-1\right)^{1/\alpha }\right]}{\lambda }\right]^2. \end{equation*}$

The PCE are calculated by solving the following equations

$\begin{equation*} \sum\limits_{i = 1}^{n}\left(x_{i:n}-\frac{\log \left[1-\left(2^{p_i}-1\right)^{1/\alpha }\right]}{\lambda }\right)\varPhi_s(x_{i:n}) = 0, \quad s = 1, 2, \end{equation*}$

where

$\begin{eqnarray*} \varPhi_1 (x_{i:n})& = & \frac{\partial}{\partial \alpha}Q(p_i) = \frac{\left(2^{p_i}-1\right){}^{1/\alpha } \log \left(2^{p_i}-1\right)}{\alpha ^2 \lambda \left(\left(2^{p_i}-1\right){}^{1/\alpha }-1\right)}, \\ \varPhi_2 (x_{i:n})& = & \frac{\partial}{\partial \lambda}Q(p_i) = \frac{\log \left(1-\left(2^{p_i}-1\right){}^{1/\alpha }\right)}{\lambda ^2}. \end{eqnarray*}$

5.6. Cramér–von mises

The CVME of the WDEx parameters are obtained by minimizing

$\begin{equation*} CV = \frac{1}{12n}+\sum\limits_{i = 1}^{n}\left[F(x_{i:n})-\frac{2i-1}{2n}\right]^2 = \frac{1}{12n}+\sum\limits_{i = 1}^{n}\left[\frac{\log \left[\left(1-e^{- \lambda x_{i:n}}\right)^{\alpha }+1\right]}{\log (2)}-\frac{2i-1}{2n}\right]^2, \end{equation*}$

They also are obtained by solving the following equations

$\begin{equation*} \sum\limits_{i = 1}^{n}\left\{\frac{\log \left[\left(1-e^{- \lambda x_{i:n}}\right)^{\alpha }+1\right]}{\log (2)}-\frac{2i-1}{2n}\right\} \varDelta_s (x_{i:n}) = 0, \end{equation*}$

where $\varDelta_s (x_{i:n}), s = 1, 2, 3$ are given in (5.2) and (5.3).

5.7. Bayesian estimation

The Bayesian estimation (BE) for the distribution parameters under different loss functions such as the SE, LINEX, and GE loss functions is studied. The parameters are assumed to have gamma priors. Thus,

$\pi_{1}(\alpha) \propto \alpha^{\mu_{1}-1}e^{\frac{-\alpha}{\lambda_{1}}}, \;\;\;\; \alpha > 0, \;\mu_{1}, \lambda_{1} > 0$

and

$\pi_{2}(\lambda) \propto \lambda^{\mu_{2}-1}e^{\frac{-\lambda}{\lambda_{2}}}, \;\;\;\; \lambda > 0\;\mu_{2}, \lambda_{2} > 0$

Suppose that the parameters are independent, therefore the joint PDF of the prior distribution has the form

$\begin{equation} \pi(\alpha, \lambda)\propto \lambda^{\mu_{2}-1}\alpha^{\mu_{1}-1}e^{-(\frac{\alpha}{\lambda_{1}}+\frac{\lambda}{\lambda_2})}. \end{equation}$

(5.4)

The posterior density function of the parameters $\alpha$ and $\lambda$ can be obtained from (5.1) and (5.4), as follows

$\begin{equation} \begin{split} \pi^{*}(\Theta|{t}) = \pi^{*}(\alpha, \lambda|{t}) & \propto L(\alpha, \lambda )\;\pi(\alpha, \lambda).\\ \end{split} \end{equation}$

(5.5)

The BE of the function of parameters $U = U(\Theta)$ , $\Theta = (\gamma, \alpha, \theta_{1}, b)$ under the SE loss function (LF) is given by

$\begin{equation} \hat{U}_{SE} = \underset{\Theta}{\int} U \;\pi^{*}(\Theta|{t}) \;d\Theta. \end{equation}$

(5.6)

Under the LINEX LF, the BE of $U = U(\Theta)$ reduces to

$\begin{equation} \hat{U}_{LINEX} = -\frac{1}{c}\log \left[\underset{\Theta}{\int} e^{-c U} \;\pi^{*}(\Theta|{t}) \;d\Theta\right], \end{equation}$

(5.7)

where $c\neq 0$ is the shape parameter of the LINEX LF.

Based on the GE LF, the BE of $U$ takes the form

$\begin{equation} \hat{U}_{GE} = \left(\underset{\Theta}{\int} U^{-q} \pi^{*}(\Theta|{t}) d\Theta \right)^{-1/q}, \end{equation}$

(5.8)

where $q \neq 0$ .

It is obvious that the integrals in Eqs (5.6)–(5.8) are complicated. Consequently, the important sampling method and the MCMC method are applied to obtain an approximation for these integrals. The Metropolis Hasting (MH) algorithm produces a series of draws from the WDEx distribution as follows:

Algorithm 1 The MCMC for BE

1. First we will start with initial values for the two parameters

$\alpha^{(0)}=\hat{\alpha}_{MLE},$

$\lambda^{(0)}=\hat{\lambda}_{MLE},$

2. Start the first iteration with counter

$i=1.$

3. Now we will generate a random value for

$\alpha^{*}$ from proposal distribution

$\textbf{N}(\alpha^{(i-1)}, var(\alpha^{(i-1)}))$ ., where

$var(\alpha^{(i-1)})$ is the variance of the parameter

$\alpha$

4. We will use the following equation

$A(\alpha^{(i-1)}|\alpha^{*})=\min\left[1, \frac{\pi^{*}(\alpha^{*}|\lambda^{(i-1)})} {\pi^{*}(\alpha^{(i-1)}|\lambda^{(i-1)})}\right]$ , the value of this equation donates the acceptance probability.

5. Now we will generate a random value that follows the uniform distribution

$U\thicksim U(0, 1)$ that ranges from 0 to 1.

6. If

$U\leq A(\alpha^{(i-1)}|\alpha^{*}),$ put

$\alpha^{(i)}=\alpha^{*}$ , else put

$\alpha^{(i)}=\alpha^{(i-1)}$ .

7. In order to evaluate the other parameter

$\lambda$ we will repeat the steps from ((2)–(6)) for

$\lambda$ .

8. Now increase the counter by one such that

$i=i+1$ .

9. To avoid any correlation between the initial values and the estimated values we will repeat the steps from ((3)–(8)),

$N=10, 000$ times to obtain

$(\alpha^{(1)}, \lambda^{(1)})$ , ...,

$(\alpha^{(N)}, \beta^{(N)})$ .

Then, the BEs of

$u(\alpha, \beta)$ using the MCMC under the three LFs are, respectively, given by

$\tilde{u}_{SE}=\frac{1}{N-M}\sum\limits_{i=M+1}^{N}u(\alpha^{(i)}, \lambda^{(i)}),$

$\tilde{u}_{LINEX}=-\frac{1}{c}\log\left[\frac{1}{N-M}\sum\limits_{i=M+1}^{N}\exp\{-c\; u(\alpha^{(i)}, \lambda^{(i)})\}\right]$

and

$\tilde{u}_{GE}=\left[\frac{1}{N-M}\sum\limits_{i=M+1}^{N}(u(\alpha^{(i)}, \lambda^{(i)}))^{-q}\right]^{-1/q},$

where

$M=2000$ is the burn-in period.

| Show Table

DownLoad: CSV

5.8. TK-approximation for Bayesian estimates

One of the most computationally efficient methods, for estimating the distribution parameter is the Tierney and Kadane ^[24] (TK) method. They developed an easily calculable integration approximation approach for evaluating the distribution parameters. The advantage of the TK approach is that it provides an easy and fast approximation method, however some methods are very hard to find the values of integration and takes a lot of time and effort.

Throughout this segment, we use the TK approximation method for calculating the Bayesian estimates (BEs) of the parameters that are focused on the SE, Linex, and GE LFs. TK method ^[24] is among the techniques to obtain the estimated value of the ratio of the two integrals as given in the following equation

$\begin{equation} \hat{U}(\Theta) = \frac{\underset{\Theta}{\int} U(\Theta) \;e^{\left[ l(\Theta|{t})+\rho(\Theta|{t})\right]} ~~\;d\Theta}{\underset{\Theta}{\int} e^{\left[ l(\Theta|{t})+\rho(\Theta|{t})\right]}~~ \;d\Theta}, \end{equation}$

(5.9)

where $U(\Theta)$ is any function of the parameters $(\alpha, \lambda)$ , $l(\Theta|{t})$ is defined in (5.1), and $\rho(\Theta|{t})$ is the logarithm joint prior distribution which is defined by

$\begin{eqnarray} \rho(\alpha, \lambda|{t})& = &(\mu_1-1) ln(\alpha)+(\mu_2-1) ln\lambda \\ &-&\left(\frac{\alpha}{\lambda_1}+\frac{\lambda}{\lambda_2}\right). \end{eqnarray}$

(5.10)

To obtain an explicit expression for $\hat{U}_{SE}(\Theta)$ using TK approximation, we consider the following functions

$\begin{equation} \delta(\Theta) = \frac{l(\Theta|{t})+\rho(\Theta|{t})}{n} \end{equation}$

(5.11)

and

$\begin{equation} \delta^*(\Theta) = \delta(\Theta)+\frac{ln U(\Theta)}{n}. \end{equation}$

(5.12)

Now, assume that the following groups of values $(\hat{\alpha}_{\delta}, \hat{\lambda}_{\delta})$ and $(\hat{\alpha}_{\delta^*}, \hat{\lambda}_{\delta^*})$ maximize the functions $\delta(\alpha, \lambda)$ and $\delta^*(\alpha, \lambda)$ , respectively.

Hence, we can evaluate the approximation of $\hat{U}(\Theta)$ by

$\begin{equation} \hat{U}_{TK}(\Theta) = \sqrt{\frac{|\Delta^*|}{|\Delta|}} \exp{\left[n \left\{\delta(\hat{\alpha}_{\delta}, \hat{\lambda}_{\delta})-\delta(\hat{\alpha}_{\delta^*}, \hat{\lambda}_{\delta^*})\right\}\right]}, \end{equation}$

(5.13)

where $|\Delta|$ and $|\Delta^*|$ refers to the determinants of negative inverse hessian of $\delta(\alpha, \lambda)$ and $\delta^*(\alpha, \lambda)$ , respectively.

6. Simulation results

Now, we asses the performance of the above estimation techniques in estimating the WDEx parameters using simulation results. Different sample sizes, $n = \{15, 30, 70, 100, 200, 350\}$ , and some initial values are assigned. We generated $5000$ random samples from the WDEx distribution to calculate the average absolute biases (ABBs), mean square errors (MSEs), and mean relative errors of estimates (MREs) using the R program©.

The following respective mathematical formulae are used to evaluate the ABBs, MSEs, and MREs (for $\pmb \theta = (\alpha, \lambda)^{'}$ )

$\begin{equation*} ABs = \frac{1}{N}\sum\limits_{i = 1}^{N}|\widehat{\pmb \theta}-\pmb \theta|, \, \, \, \, MSEs = \frac{1}{N}\sum\limits_{i = 1}^{N}(\widehat{\pmb \theta}-\pmb \theta)^2, \, \, \, \, MREs = \frac{1}{N}\sum\limits_{i = 1}^{N}|\widehat{\pmb \theta}-\pmb \theta|/\pmb \theta. \end{equation*}$

Table 3 reports the simulation results including the ABBs, MSEs, and MREs of the WDEx parameters using the nine estimation approaches. One can note that all methods provide small ABBs, MSEs and MREs in all parametric values. The nine estimators are consistent, i.e., the MSEs decrease as the sample size increases, for all studied cases.

Table 3. Simulation results of the WDEx distribution using different estimators for (

$\alpha = 0.75, \; \lambda = 0.75$ ).

n	Est.	Est. Par.	Classical
n	Est.	Est. Par.	MLE	ADE	CVME	MPS	LSE	PCE	RTADE	WLSE
15	BIAS	$\hat{\alpha}$	$0.25192877 ^{\{ 5 \}\{ 11 \}}$	$0.22405917 ^{\{ 2 \}\{ 8 \}}$	$0.30164256 ^{\{ 7 \}\{ 13 \}}$	$0.19839734 ^{\{ 1 \}\{ 7 \}}$	$0.24557181 ^{\{ 4 \}\{ 10 \}}$	$0.32687545 ^{\{ 8 \}\{ 14 \}}$	$0.29638657 ^{\{ 6 \}\{ 12 \}}$	$0.24157906 ^{\{ 3 \}\{ 9 \}}$
		$\hat{\lambda}$	$0.32093518 ^{\{ 5 \}\{ 11 \}}$	$0.30428638 ^{\{ 2 \}\{ 8 \}}$	$0.39524432 ^{\{ 8 \}\{ 14 \}}$	$0.26371696 ^{\{ 1 \}\{ 7 \}}$	$0.31652453 ^{\{ 4 \}\{ 10 \}}$	$0.34677645 ^{\{ 7 \}\{ 13 \}}$	$0.32593945 ^{\{ 6 \}\{ 12 \}}$	$0.31219147 ^{\{ 3 \}\{ 9 \}}$
	MSE	$\hat{\alpha}$	$0.16122813 ^{\{ 3 \}\{ 9 \}}$	$0.11215242 ^{\{ 2 \}\{ 8 \}}$	$0.26608275 ^{\{ 8 \}\{ 14 \}}$	$0.06560425 ^{\{ 1 \}\{ 7 \}}$	$0.1682729 ^{\{ 4 \}\{ 10 \}}$	$0.19013447 ^{\{ 6 \}\{ 12 \}}$	$0.22921014 ^{\{ 7 \}\{ 13 \}}$	$0.18043259 ^{\{ 5 \}\{ 11 \}}$
		$\hat{\lambda}$	$0.21915477 ^{\{ 4 \}\{ 10 \}}$	$0.20639267 ^{\{ 2 \}\{ 8 \}}$	$0.34394628 ^{\{ 8 \}\{ 14 \}}$	$0.11724707 ^{\{ 1 \}\{ 7 \}}$	$0.2237624 ^{\{ 5 \}\{ 11 \}}$	$0.2148123 ^{\{ 3 \}\{ 9 \}}$	$0.23978318 ^{\{ 7 \}\{ 13 \}}$	$0.23922943 ^{\{ 6 \}\{ 12 \}}$
	MRE	$\hat{\alpha}$	$0.33590503 ^{\{ 5 \}\{ 11 \}}$	$0.29874556 ^{\{ 2 \}\{ 8 \}}$	$0.40219008 ^{\{ 7 \}\{ 13 \}}$	$0.26452979 ^{\{ 1 \}\{ 7 \}}$	$0.32742908 ^{\{ 4 \}\{ 10 \}}$	$0.43583393 ^{\{ 8 \}\{ 14 \}}$	$0.3951821 ^{\{ 6 \}\{ 12 \}}$	$0.32210541 ^{\{ 3 \}\{ 9 \}}$
		$\hat{\lambda}$	$0.42791357 ^{\{ 5 \}\{ 11 \}}$	$0.40571517 ^{\{ 2 \}\{ 8 \}}$	$0.52699243 ^{\{ 8 \}\{ 14 \}}$	$0.35162261 ^{\{ 1 \}\{ 7 \}}$	$0.42203271 ^{\{ 4 \}\{ 10 \}}$	$0.4623686 ^{\{ 7 \}\{ 13 \}}$	$0.43458594 ^{\{ 6 \}\{ 12 \}}$	$0.4162553 ^{\{ 3 \}\{ 9 \}}$
	$\sum CRanks$		$27 ^{\{ 5 \}}$	$12 ^{\{ 2 \}}$	$46 ^{\{ 8 \}}$	$6 ^{\{ 1 \}}$	$25 ^{\{ 4 \}}$	$39 ^{\{ 7 \}}$	$38 ^{\{ 6 \}}$	$23 ^{\{ 3 \}}$
	$\sum C\&BRanks$		$63 ^{\{ 11 \}}$	$48 ^{\{ 8 \}}$	$82 ^{\{ 14 \}}$	$42 ^{\{ 7 \}}$	$61 ^{\{ 10 \}}$	$75 ^{\{ 13 \}}$	$74 ^{\{ 12 \}}$	$59 ^{\{ 9 \}}$
30	BIAS	$\hat{\alpha}$	$0.14405974 ^{\{ 3 \}\{ 9 \}}$	$0.13901101 ^{\{ 2 \}\{ 8 \}}$	$0.17725422 ^{\{ 7 \}\{ 13 \}}$	$0.13213658 ^{\{ 1 \}\{ 7 \}}$	$0.16209531 ^{\{ 5 \}\{ 11 \}}$	$0.25820992 ^{\{ 8 \}\{ 14 \}}$	$0.16964029 ^{\{ 6 \}\{ 12 \}}$	$0.14580412 ^{\{ 4 \}\{ 10 \}}$
		$\hat{\lambda}$	$0.18969311 ^{\{ 2 \}\{ 8 \}}$	$0.19141061 ^{\{ 3 \}\{ 9 \}}$	$0.23350009 ^{\{ 7 \}\{ 13 \}}$	$0.18115544 ^{\{ 1 \}\{ 7 \}}$	$0.22786428 ^{\{ 6 \}\{ 12 \}}$	$0.24136118 ^{\{ 8 \}\{ 14 \}}$	$0.20026589 ^{\{ 4 \}\{ 10 \}}$	$0.20766574 ^{\{ 5 \}\{ 11 \}}$
	MSE	$\hat{\alpha}$	$0.03746839 ^{\{ 3 \}\{ 9 \}}$	$0.03635968 ^{\{ 2 \}\{ 8 \}}$	$0.06052504 ^{\{ 7 \}\{ 13 \}}$	$0.02548745 ^{\{ 1 \}\{ 7 \}}$	$0.05095711 ^{\{ 5 \}\{ 11 \}}$	$0.10729773 ^{\{ 8 \}\{ 14 \}}$	$0.05828137 ^{\{ 6 \}\{ 12 \}}$	$0.04260275 ^{\{ 4 \}\{ 10 \}}$
		$\hat{\lambda}$	$0.06746508 ^{\{ 3 \}\{ 9 \}}$	$0.06525692 ^{\{ 2 \}\{ 8 \}}$	$0.09980727 ^{\{ 8 \}\{ 14 \}}$	$0.04907736 ^{\{ 1 \}\{ 7 \}}$	$0.09345408 ^{\{ 7 \}\{ 13 \}}$	$0.09161708 ^{\{ 6 \}\{ 12 \}}$	$0.07713619 ^{\{ 4 \}\{ 10 \}}$	$0.0814058 ^{\{ 5 \}\{ 11 \}}$
	MRE	$\hat{\alpha}$	$0.19207965 ^{\{ 3 \}\{ 9 \}}$	$0.18534802 ^{\{ 2 \}\{ 8 \}}$	$0.23633896 ^{\{ 7 \}\{ 13 \}}$	$0.1761821 ^{\{ 1 \}\{ 7 \}}$	$0.21612709 ^{\{ 5 \}\{ 11 \}}$	$0.34427989 ^{\{ 8 \}\{ 14 \}}$	$0.22618705 ^{\{ 6 \}\{ 12 \}}$	$0.19440549 ^{\{ 4 \}\{ 10 \}}$
		$\hat{\lambda}$	$0.25292415 ^{\{ 2 \}\{ 8 \}}$	$0.25521415 ^{\{ 3 \}\{ 9 \}}$	$0.31133346 ^{\{ 7 \}\{ 13 \}}$	$0.24154058 ^{\{ 1 \}\{ 7 \}}$	$0.30381904 ^{\{ 6 \}\{ 12 \}}$	$0.32181491 ^{\{ 8 \}\{ 14 \}}$	$0.26702119 ^{\{ 4 \}\{ 10 \}}$	$0.27688765 ^{\{ 5 \}\{ 11 \}}$
	$\sum CRanks$		$16 ^{\{ 3 \}}$	$14 ^{\{ 2 \}}$	$43 ^{\{ 7 \}}$	$6 ^{\{ 1 \}}$	$34 ^{\{ 6 \}}$	$46 ^{\{ 8 \}}$	$30 ^{\{ 5 \}}$	$27 ^{\{ 4 \}}$
	$\sum C\&BRanks$		$52 ^{\{ 9 \}}$	$50 ^{\{ 8 \}}$	$79 ^{\{ 13 \}}$	$42 ^{\{ 7 \}}$	$70 ^{\{ 12 \}}$	$82 ^{\{ 14 \}}$	$66 ^{\{ 11 \}}$	$63 ^{\{ 10 \}}$
70	BIAS	$\hat{\alpha}$	$0.08792199 ^{\{ 3 \}\{ 9 \}}$	$0.08650543 ^{\{ 2 \}\{ 8 \}}$	$0.10310607 ^{\{ 6 \}\{ 12 \}}$	$0.08281633 ^{\{ 1 \}\{ 7 \}}$	$0.10074083 ^{\{ 5 \}\{ 11 \}}$	$0.1753952 ^{\{ 8 \}\{ 14 \}}$	$0.10421227 ^{\{ 7 \}\{ 13 \}}$	$0.08803723 ^{\{ 4 \}\{ 10 \}}$
		$\hat{\lambda}$	$0.11408442 ^{\{ 1 \}\{ 7 \}}$	$0.12445549 ^{\{ 3 \}\{ 9 \}}$	$0.14143312 ^{\{ 7 \}\{ 13 \}}$	$0.1164039 ^{\{ 2 \}\{ 8 \}}$	$0.13839689 ^{\{ 6 \}\{ 12 \}}$	$0.16478766 ^{\{ 8 \}\{ 14 \}}$	$0.12896275 ^{\{ 5 \}\{ 11 \}}$	$0.12549479 ^{\{ 4 \}\{ 10 \}}$
	MSE	$\hat{\alpha}$	$0.01336042 ^{\{ 3 \}\{ 9 \}}$	$0.01302739 ^{\{ 2 \}\{ 8 \}}$	$0.01826087 ^{\{ 6 \}\{ 12 \}}$	$0.01051127 ^{\{ 1 \}\{ 7 \}}$	$0.01740773 ^{\{ 5 \}\{ 11 \}}$	$0.04721909 ^{\{ 8 \}\{ 14 \}}$	$0.01897672 ^{\{ 7 \}\{ 13 \}}$	$0.01339529 ^{\{ 4 \}\{ 10 \}}$
		$\hat{\lambda}$	$0.02286488 ^{\{ 2 \}\{ 8 \}}$	$0.02612201 ^{\{ 3 \}\{ 9 \}}$	$0.03569504 ^{\{ 7 \}\{ 13 \}}$	$0.02027791 ^{\{ 1 \}\{ 7 \}}$	$0.03209949 ^{\{ 6 \}\{ 12 \}}$	$0.04224291 ^{\{ 8 \}\{ 14 \}}$	$0.02824455 ^{\{ 5 \}\{ 11 \}}$	$0.02671826 ^{\{ 4 \}\{ 10 \}}$
	MRE	$\hat{\alpha}$	$0.11722932 ^{\{ 3 \}\{ 9 \}}$	$0.11534057 ^{\{ 2 \}\{ 8 \}}$	$0.13747476 ^{\{ 6 \}\{ 12 \}}$	$0.11042178 ^{\{ 1 \}\{ 7 \}}$	$0.13432111 ^{\{ 5 \}\{ 11 \}}$	$0.23386027 ^{\{ 8 \}\{ 14 \}}$	$0.13894969 ^{\{ 7 \}\{ 13 \}}$	$0.11738297 ^{\{ 4 \}\{ 10 \}}$
		$\hat{\lambda}$	$0.15211257 ^{\{ 1 \}\{ 7 \}}$	$0.16594066 ^{\{ 3 \}\{ 9 \}}$	$0.18857749 ^{\{ 7 \}\{ 13 \}}$	$0.1552052 ^{\{ 2 \}\{ 8 \}}$	$0.18452919 ^{\{ 6 \}\{ 12 \}}$	$0.21971689 ^{\{ 8 \}\{ 14 \}}$	$0.17195033 ^{\{ 5 \}\{ 11 \}}$	$0.16732638 ^{\{ 4 \}\{ 10 \}}$
	$\sum CRanks$		$13 ^{\{ 2 \}}$	$15 ^{\{ 3 \}}$	$39 ^{\{ 7 \}}$	$8 ^{\{ 1 \}}$	$33 ^{\{ 5 \}}$	$48 ^{\{ 8 \}}$	$36 ^{\{ 6 \}}$	$24 ^{\{ 4 \}}$
	$\sum C\&BRanks$		$49 ^{\{ 8 \}}$	$51 ^{\{ 9 \}}$	$75 ^{\{ 13 \}}$	$44 ^{\{ 7 \}}$	$69 ^{\{ 11 \}}$	$84 ^{\{ 14 \}}$	$72 ^{\{ 12 \}}$	$60 ^{\{ 10 \}}$
100	BIAS	$\hat{\alpha}$	$0.0711708 ^{\{ 2 \}\{ 8 \}}$	$0.07361175 ^{\{ 3 \}\{ 9 \}}$	$0.08687172 ^{\{ 6 \}\{ 12 \}}$	$0.06877471 ^{\{ 1 \}\{ 7 \}}$	$0.07956296 ^{\{ 5 \}\{ 11 \}}$	$0.15707028 ^{\{ 8 \}\{ 14 \}}$	$0.0891824 ^{\{ 7 \}\{ 13 \}}$	$0.07485017 ^{\{ 4 \}\{ 10 \}}$
		$\hat{\lambda}$	$0.10091505 ^{\{ 4 \}\{ 10 \}}$	$0.09963177 ^{\{ 2 \}\{ 8 \}}$	$0.11507711 ^{\{ 6 \}\{ 12 \}}$	$0.0956997 ^{\{ 1 \}\{ 7 \}}$	$0.11614478 ^{\{ 7 \}\{ 13 \}}$	$0.14353138 ^{\{ 8 \}\{ 14 \}}$	$0.10220272 ^{\{ 5 \}\{ 11 \}}$	$0.10079129 ^{\{ 3 \}\{ 9 \}}$
	MSE	$\hat{\alpha}$	$0.00836564 ^{\{ 2 \}\{ 8 \}}$	$0.00880658 ^{\{ 3 \}\{ 9 \}}$	$0.01255586 ^{\{ 7 \}\{ 13 \}}$	$0.0070432 ^{\{ 1 \}\{ 7 \}}$	$0.01016903 ^{\{ 5 \}\{ 11 \}}$	$0.03872841 ^{\{ 8 \}\{ 14 \}}$	$0.01247087 ^{\{ 6 \}\{ 12 \}}$	$0.0095693 ^{\{ 4 \}\{ 10 \}}$
		$\hat{\lambda}$	$0.01716988 ^{\{ 4 \}\{ 10 \}}$	$0.01679548 ^{\{ 2 \}\{ 8 \}}$	$0.02177566 ^{\{ 6 \}\{ 12 \}}$	$0.01380793 ^{\{ 1 \}\{ 7 \}}$	$0.02250852 ^{\{ 7 \}\{ 13 \}}$	$0.03103759 ^{\{ 8 \}\{ 14 \}}$	$0.01734026 ^{\{ 5 \}\{ 11 \}}$	$0.01694889 ^{\{ 3 \}\{ 9 \}}$
	MRE	$\hat{\alpha}$	$0.09489439 ^{\{ 2 \}\{ 8 \}}$	$0.098149 ^{\{ 3 \}\{ 9 \}}$	$0.11582897 ^{\{ 6 \}\{ 12 \}}$	$0.09169961 ^{\{ 1 \}\{ 7 \}}$	$0.10608395 ^{\{ 5 \}\{ 11 \}}$	$0.20942704 ^{\{ 8 \}\{ 14 \}}$	$0.11890987 ^{\{ 7 \}\{ 13 \}}$	$0.09980023 ^{\{ 4 \}\{ 10 \}}$
		$\hat{\lambda}$	$0.13455341 ^{\{ 4 \}\{ 10 \}}$	$0.13284236 ^{\{ 2 \}\{ 8 \}}$	$0.15343615 ^{\{ 6 \}\{ 12 \}}$	$0.1275996 ^{\{ 1 \}\{ 7 \}}$	$0.15485971 ^{\{ 7 \}\{ 13 \}}$	$0.19137517 ^{\{ 8 \}\{ 14 \}}$	$0.1362703 ^{\{ 5 \}\{ 11 \}}$	$0.13438838 ^{\{ 3 \}\{ 9 \}}$
	$\sum CRanks$		$18 ^{\{ 3 \}}$	$15 ^{\{ 2 \}}$	$37 ^{\{ 7 \}}$	$6 ^{\{ 1 \}}$	$36 ^{\{ 6 \}}$	$48 ^{\{ 8 \}}$	$35 ^{\{ 5 \}}$	$21 ^{\{ 4 \}}$
	$\sum C\&BRanks$		$54 ^{\{ 9 \}}$	$51 ^{\{ 8 \}}$	$73 ^{\{ 13 \}}$	$42 ^{\{ 7 \}}$	$72 ^{\{ 12 \}}$	$84 ^{\{ 14 \}}$	$71 ^{\{ 11 \}}$	$57 ^{\{ 10 \}}$
200	BIAS	$\hat{\alpha}$	$0.04897082 ^{\{ 1 \}\{ 7 \}}$	$0.05135288 ^{\{ 3 \}\{ 9 \}}$	$0.05580712 ^{\{ 5 \}\{ 11 \}}$	$0.05042855 ^{\{ 2 \}\{ 8 \}}$	$0.05620865 ^{\{ 6 \}\{ 12 \}}$	$0.11786812 ^{\{ 8 \}\{ 14 \}}$	$0.05902749 ^{\{ 7 \}\{ 13 \}}$	$0.0514394 ^{\{ 4 \}\{ 10 \}}$
		$\hat{\lambda}$	$0.0680904 ^{\{ 1 \}\{ 7 \}}$	$0.07177274 ^{\{ 3 \}\{ 9 \}}$	$0.08001323 ^{\{ 7 \}\{ 13 \}}$	$0.06943586 ^{\{ 2 \}\{ 8 \}}$	$0.07996607 ^{\{ 6 \}\{ 12 \}}$	$0.10198027 ^{\{ 8 \}\{ 14 \}}$	$0.07187114 ^{\{ 4 \}\{ 10 \}}$	$0.07208482 ^{\{ 5 \}\{ 11 \}}$
	MSE	$\hat{\alpha}$	$0.00376579 ^{\{ 1 \}\{ 7 \}}$	$0.00414776 ^{\{ 3 \}\{ 9 \}}$	$0.00504929 ^{\{ 5 \}\{ 11 \}}$	$0.00389309 ^{\{ 2 \}\{ 8 \}}$	$0.00516812 ^{\{ 6 \}\{ 12 \}}$	$0.02119878 ^{\{ 8 \}\{ 14 \}}$	$0.0057458 ^{\{ 7 \}\{ 13 \}}$	$0.00430278 ^{\{ 4 \}\{ 10 \}}$
		$\hat{\lambda}$	$0.00722093 ^{\{ 1 \}\{ 7 \}}$	$0.00838347 ^{\{ 3 \}\{ 9 \}}$	$0.01096736 ^{\{ 7 \}\{ 13 \}}$	$0.00726195 ^{\{ 2 \}\{ 8 \}}$	$0.01032872 ^{\{ 6 \}\{ 12 \}}$	$0.01585112 ^{\{ 8 \}\{ 14 \}}$	$0.0084817 ^{\{ 4 \}\{ 10 \}}$	$0.00865163 ^{\{ 5 \}\{ 11 \}}$
	MRE	$\hat{\alpha}$	$0.06529443 ^{\{ 1 \}\{ 7 \}}$	$0.06847051 ^{\{ 3 \}\{ 9 \}}$	$0.07440949 ^{\{ 5 \}\{ 11 \}}$	$0.06723806 ^{\{ 2 \}\{ 8 \}}$	$0.07494487 ^{\{ 6 \}\{ 12 \}}$	$0.15715749 ^{\{ 8 \}\{ 14 \}}$	$0.07870332 ^{\{ 7 \}\{ 13 \}}$	$0.06858586 ^{\{ 4 \}\{ 10 \}}$
		$\hat{\lambda}$	$0.09078719 ^{\{ 1 \}\{ 7 \}}$	$0.09569698 ^{\{ 3 \}\{ 9 \}}$	$0.10668431 ^{\{ 7 \}\{ 13 \}}$	$0.09258115 ^{\{ 2 \}\{ 8 \}}$	$0.10662142 ^{\{ 6 \}\{ 12 \}}$	$0.1359737 ^{\{ 8 \}\{ 14 \}}$	$0.09582819 ^{\{ 4 \}\{ 10 \}}$	$0.09611309 ^{\{ 5 \}\{ 11 \}}$
	$\sum CRanks$		$6 ^{\{ 1 \}}$	$18 ^{\{ 3 \}}$	$36 ^{\{ 6.5 \}}$	$12 ^{\{ 2 \}}$	$36 ^{\{ 6.5 \}}$	$48 ^{\{ 8 \}}$	$33 ^{\{ 5 \}}$	$27 ^{\{ 4 \}}$
	$\sum C&BRanks$		$42 ^{\{ 7 \}}$	$54 ^{\{ 9 \}}$	$72 ^{\{ 12.5 \}}$	$48 ^{\{ 8 \}}$	$72 ^{\{ 12.5 \}}$	$84 ^{\{ 14 \}}$	$69 ^{\{ 11 \}}$	$63 ^{\{ 10 \}}$
300	BIAS	$\hat{\alpha}$	$0.03667764 ^{\{ 1 \}\{ 6 \}}$	$0.03990136 ^{\{ 3 \}\{ 9 \}}$	$0.04288476 ^{\{ 5 \}\{ 11 \}}$	$0.03760933 ^{\{ 2 \}\{ 7 \}}$	$0.04356189 ^{\{ 6 \}\{ 12 \}}$	$0.0934606 ^{\{ 8 \}\{ 14 \}}$	$0.04654803 ^{\{ 7 \}\{ 13 \}}$	$0.040086 ^{\{ 4 \}\{ 10 \}}$
		$\hat{\lambda}$	$0.04795812 ^{\{ 1 \}\{ 6 \}}$	$0.05338798 ^{\{ 3 \}\{ 9 \}}$	$0.05993014 ^{\{ 6 \}\{ 12 \}}$	$0.05257793 ^{\{ 2 \}\{ 7 \}}$	$0.06112134 ^{\{ 7 \}\{ 13 \}}$	$0.07718156 ^{\{ 8 \}\{ 14 \}}$	$0.05407786 ^{\{ 5 \}\{ 11 \}}$	$0.05393484 ^{\{ 4 \}\{ 10 \}}$
	MSE	$\hat{\alpha}$	$0.00215764 ^{\{ 1 \}\{ 6 \}}$	$0.00250001 ^{\{ 3 \}\{ 8 \}}$	$0.00296309 ^{\{ 6 \}\{ 12 \}}$	$0.00221696 ^{\{ 2 \}\{ 7 \}}$	$0.00293099 ^{\{ 5 \}\{ 11 \}}$	$0.01343653 ^{\{ 8 \}\{ 14 \}}$	$0.00346372 ^{\{ 7 \}\{ 13 \}}$	$0.0025318 ^{\{ 4 \}\{ 10 \}}$
		$\hat{\lambda}$	$0.00376997 ^{\{ 1 \}\{ 6 \}}$	$0.00453163 ^{\{ 3 \}\{ 8 \}}$	$0.00573555 ^{\{ 6 \}\{ 12 \}}$	$0.00421602 ^{\{ 2 \}\{ 7 \}}$	$0.00580597 ^{\{ 7 \}\{ 13 \}}$	$0.0091151 ^{\{ 8 \}\{ 14 \}}$	$0.00478321 ^{\{ 5 \}\{ 10 \}}$	$0.00471786 ^{\{ 4 \}\{ 9 \}}$
	MRE	$\hat{\alpha}$	$0.04890353 ^{\{ 1 \}\{ 6 \}}$	$0.05320181 ^{\{ 3 \}\{ 9 \}}$	$0.05717968 ^{\{ 5 \}\{ 11 \}}$	$0.05014577 ^{\{ 2 \}\{ 7 \}}$	$0.05808252 ^{\{ 6 \}\{ 12 \}}$	$0.12461413 ^{\{ 8 \}\{ 14 \}}$	$0.06206403 ^{\{ 7 \}\{ 13 \}}$	$0.053448 ^{\{ 4 \}\{ 10 \}}$
		$\hat{\lambda}$	$0.06394416 ^{\{ 1 \}\{ 6 \}}$	$0.07118398 ^{\{ 3 \}\{ 9 \}}$	$0.07990685 ^{\{ 6 \}\{ 12 \}}$	$0.07010391 ^{\{ 2 \}\{ 7 \}}$	$0.08149512 ^{\{ 7 \}\{ 13 \}}$	$0.10290874 ^{\{ 8 \}\{ 14 \}}$	$0.07210381 ^{\{ 5 \}\{ 11 \}}$	$0.07191312 ^{\{ 4 \}\{ 10 \}}$
	$\sum CRanks$		$6 ^{\{ 1 \}}$	$18 ^{\{ 3 \}}$	$34 ^{\{ 5 \}}$	$12 ^{\{ 2 \}}$	$38 ^{\{ 7 \}}$	$48 ^{\{ 8 \}}$	$36 ^{\{ 6 \}}$	$24 ^{\{ 4 \}}$
	$\sum C\& BRanks$		$36 ^{\{ 6 \}}$	$52 ^{\{ 8.5 \}}$	$70 ^{\{ 11 \}}$	$42 ^{\{ 7 \}}$	$74 ^{\{ 13 \}}$	$84 ^{\{ 14 \}}$	$71 ^{\{ 12 \}}$	$59 ^{\{ 10 \}}$
15	BIAS	$\hat{\alpha}$	$0.07080639 ^{\{ 2 \}\{ 2 \}}$	$0.07080648 ^{\{ 3 \}\{ 3 \}}$	$0.07079734 ^{\{ 1 \}\{ 1 \}}$	$0.10887156 ^{\{ 6 \}\{ 6 \}}$	$0.078971 ^{\{ 5 \}\{ 5 \}}$	$0.07215014 ^{\{ 4 \}\{ 4 \}}$
		$\hat{\lambda}$	$0.07334416 ^{\{ 2 \}\{ 2 \}}$	$0.07334414 ^{\{ 1 \}\{ 1 \}}$	$0.07335074 ^{\{ 3 \}\{ 3 \}}$	$0.13371233 ^{\{ 6 \}\{ 6 \}}$	$0.12036804 ^{\{ 5 \}\{ 5 \}}$	$0.11400132 ^{\{ 4 \}\{ 4 \}}$
	MSE	$\hat{\alpha}$	$0.00700589 ^{\{ 4 \}\{ 4 \}}$	$0.0070059 ^{\{ 5 \}\{ 5 \}}$	$0.00700451 ^{\{ 3 \}\{ 3 \}}$	$0.01710565 ^{\{ 6 \}\{ 6 \}}$	$0.00623642 ^{\{ 2 \}\{ 2 \}}$	$0.00520564 ^{\{ 1 \}\{ 1 \}}$
		$\hat{\lambda}$	$0.00734358 ^{\{ 2 \}\{ 2 \}}$	$0.00734357 ^{\{ 1 \}\{ 1 \}}$	$0.00734515 ^{\{ 3 \}\{ 3 \}}$	$0.02521906 ^{\{ 6 \}\{ 6 \}}$	$0.01448847 ^{\{ 5 \}\{ 5 \}}$	$0.0129963 ^{\{ 4 \}\{ 4 \}}$
	MRE	$\hat{\alpha}$	$0.09440852 ^{\{ 2 \}\{ 2 \}}$	$0.09440864 ^{\{ 3 \}\{ 3 \}}$	$0.09439646 ^{\{ 1 \}\{ 1 \}}$	$0.14516208 ^{\{ 6 \}\{ 6 \}}$	$0.10529467 ^{\{ 5 \}\{ 5 \}}$	$0.09620019 ^{\{ 4 \}\{ 4 \}}$
		$\hat{\lambda}$	$0.09779221 ^{\{ 2 \}\{ 2 \}}$	$0.09779219 ^{\{ 1 \}\{ 1 \}}$	$0.09780098 ^{\{ 3 \}\{ 3 \}}$	$0.17828311 ^{\{ 6 \}\{ 6 \}}$	$0.16049072 ^{\{ 5 \}\{ 5 \}}$	$0.15200176 ^{\{ 4 \}\{ 4 \}}$
	$\sum BRanks$		$14 ^{\{ 2 \}}$	$14 ^{\{ 2 \}}$	$14 ^{\{ 2 \}}$	$36 ^{\{ 6 \}}$	$27 ^{\{ 5 \}}$	$21 ^{\{ 4 \}}$
	$\sum C \&BRanks$		$14 ^{\{ 2 \}}$	$14 ^{\{ 2 \}}$	$14 ^{\{ 2 \}}$	$36 ^{\{ 6 \}}$	$27 ^{\{ 5 \}}$	$21 ^{\{ 4 \}}$
30	BIAS	$\hat{\alpha}$	$0.06707577 ^{\{ 4 \}\{ 4 \}}$	$0.06707579 ^{\{ 5 \}\{ 5 \}}$	$0.06707479 ^{\{ 3 \}\{ 3 \}}$	$0.08818954 ^{\{ 6 \}\{ 6 \}}$	$0.05398142 ^{\{ 2 \}\{ 2 \}}$	$0.0484456 ^{\{ 1 \}\{ 1 \}}$
		$\hat{\lambda}$	$0.07063728 ^{\{ 2 \}\{ 2 \}}$	$0.07063729 ^{\{ 3 \}\{ 3 \}}$	$0.07063836 ^{\{ 4 \}\{ 4 \}}$	$0.09669995 ^{\{ 6 \}\{ 6 \}}$	$0.07140666 ^{\{ 5 \}\{ 5 \}}$	$0.06590862 ^{\{ 1 \}\{ 1 \}}$
	MSE	$\hat{\alpha}$	$0.00638449 ^{\{ 4.5 \}\{ 4.5 \}}$	$0.00638449 ^{\{ 4.5 \}\{ 4.5 \}}$	$0.00638429 ^{\{ 3 \}\{ 3 \}}$	$0.01167204 ^{\{ 6 \}\{ 6 \}}$	$0.00291399 ^{\{ 2 \}\{ 2 \}}$	$0.00234698 ^{\{ 1 \}\{ 1 \}}$
		$\hat{\lambda}$	$0.00685741 ^{\{ 4.5 \}\{ 4.5 \}}$	$0.00685741 ^{\{ 4.5 \}\{ 4.5 \}}$	$0.00685694 ^{\{ 3 \}\{ 3 \}}$	$0.01388726 ^{\{ 6 \}\{ 6 \}}$	$0.00509891 ^{\{ 2 \}\{ 2 \}}$	$0.00434395 ^{\{ 1 \}\{ 1 \}}$
	MRE	$\hat{\alpha}$	$0.08943436 ^{\{ 4 \}\{ 4 \}}$	$0.08943439 ^{\{ 5 \}\{ 5 \}}$	$0.08943306 ^{\{ 3 \}\{ 3 \}}$	$0.11758605 ^{\{ 6 \}\{ 6 \}}$	$0.07197522 ^{\{ 2 \}\{ 2 \}}$	$0.06459413 ^{\{ 1 \}\{ 1 \}}$
		$\hat{\lambda}$	$0.09418304 ^{\{ 2 \}\{ 2 \}}$	$0.09418306 ^{\{ 3 \}\{ 3 \}}$	$0.09418448 ^{\{ 4 \}\{ 4 \}}$	$0.12893327 ^{\{ 6 \}\{ 6 \}}$	$0.09520888 ^{\{ 5 \}\{ 5 \}}$	$0.08787816 ^{\{ 1 \}\{ 1 \}}$
	$\sum BRanks$		$21 ^{\{ 4 \}}$	$25 ^{\{ 5 \}}$	$20 ^{\{ 3 \}}$	$36 ^{\{ 6 \}}$	$18 ^{\{ 2 \}}$	$6 ^{\{ 1 \}}$
	$\sum C \&BRanks$		$21 ^{\{ 4 \}}$	$25 ^{\{ 5 \}}$	$20 ^{\{ 3 \}}$	$36 ^{\{ 6 \}}$	$18 ^{\{ 2 \}}$	$6 ^{\{ 1 \}}$
70	BIAS	$\hat{\alpha}$	$0.0628967 ^{\{ 4 \}\{ 4 \}}$	$0.06289672 ^{\{ 5 \}\{ 5 \}}$	$0.06289578 ^{\{ 3 \}\{ 3 \}}$	$0.06988905 ^{\{ 6 \}\{ 6 \}}$	$0.03512338 ^{\{ 2 \}\{ 2 \}}$	$0.03097589 ^{\{ 1 \}\{ 1 \}}$
		$\hat{\lambda}$	$0.06382592 ^{\{ 3 \}\{ 3 \}}$	$0.06382593 ^{\{ 4 \}\{ 4 \}}$	$0.06382623 ^{\{ 5 \}\{ 5 \}}$	$0.08500664 ^{\{ 6 \}\{ 6 \}}$	$0.04706336 ^{\{ 2 \}\{ 2 \}}$	$0.04163393 ^{\{ 1 \}\{ 1 \}}$
	MSE	$\hat{\alpha}$	$0.00529453 ^{\{ 4.5 \}\{ 4.5 \}}$	$0.00529453 ^{\{ 4.5 \}\{ 4.5 \}}$	$0.00529439 ^{\{ 3 \}\{ 3 \}}$	$0.00766215 ^{\{ 6 \}\{ 6 \}}$	$0.00123365 ^{\{ 2 \}\{ 2 \}}$	$0.00095951 ^{\{ 1 \}\{ 1 \}}$
		$\hat{\lambda}$	$0.00577517 ^{\{ 3.5 \}\{ 3.5 \}}$	$0.00577517 ^{\{ 3.5 \}\{ 3.5 \}}$	$0.00577528 ^{\{ 5 \}\{ 5 \}}$	$0.01076173 ^{\{ 6 \}\{ 6 \}}$	$0.00221496 ^{\{ 2 \}\{ 2 \}}$	$0.00173338 ^{\{ 1 \}\{ 1 \}}$
	MRE	$\hat{\alpha}$	$0.08386227 ^{\{ 4 \}\{ 4 \}}$	$0.08386229 ^{\{ 5 \}\{ 5 \}}$	$0.08386104 ^{\{ 3 \}\{ 3 \}}$	$0.0931854 ^{\{ 6 \}\{ 6 \}}$	$0.04683117 ^{\{ 2 \}\{ 2 \}}$	$0.04130118 ^{\{ 1 \}\{ 1 \}}$
		$\hat{\lambda}$	$0.08510123 ^{\{ 3.5 \}\{ 3.5 \}}$	$0.08510123 ^{\{ 3.5 \}\{ 3.5 \}}$	$0.08510164 ^{\{ 5 \}\{ 5 \}}$	$0.11334219 ^{\{ 6 \}\{ 6 \}}$	$0.06275115 ^{\{ 2 \}\{ 2 \}}$	$0.0555119 ^{\{ 1 \}\{ 1 \}}$
	$\sum BRanks$		$22.5 ^{\{ 3 \}}$	$25.5 ^{\{ 5 \}}$	$24 ^{\{ 4 \}}$	$36 ^{\{ 6 \}}$	$12 ^{\{ 2 \}}$	$6 ^{\{ 1 \}}$
	$\sum C \&BRanks$		$22.5 ^{\{ 3 \}}$	$25.5 ^{\{ 5 \}}$	$24 ^{\{ 4 \}}$	$36 ^{\{ 6 \}}$	$12 ^{\{ 2 \}}$	$6 ^{\{ 1 \}}$
100	BIAS	$\hat{\alpha}$	$0.05470376 ^{\{ 4 \}\{ 4 \}}$	$0.05470375 ^{\{ 3 \}\{ 3 \}}$	$0.05470411 ^{\{ 5 \}\{ 5 \}}$	$0.06296533 ^{\{ 6 \}\{ 6 \}}$	$0.02807831 ^{\{ 2 \}\{ 2 \}}$	$0.02458989 ^{\{ 1 \}\{ 1 \}}$
		$\hat{\lambda}$	$0.06312911 ^{\{ 3.5 \}\{ 3.5 \}}$	$0.06312911 ^{\{ 3.5 \}\{ 3.5 \}}$	$0.0631295 ^{\{ 5 \}\{ 5 \}}$	$0.07802856 ^{\{ 6 \}\{ 6 \}}$	$0.04616373 ^{\{ 2 \}\{ 2 \}}$	$0.04172589 ^{\{ 1 \}\{ 1 \}}$
	MSE	$\hat{\alpha}$	$0.00439471 ^{\{ 3.5 \}\{ 3.5 \}}$	$0.00439471 ^{\{ 3.5 \}\{ 3.5 \}}$	$0.00439478 ^{\{ 5 \}\{ 5 \}}$	$0.00608088 ^{\{ 6 \}\{ 6 \}}$	$0.00078839 ^{\{ 2 \}\{ 2 \}}$	$0.00060466 ^{\{ 1 \}\{ 1 \}}$
		$\hat{\lambda}$	$0.00567389 ^{\{ 4.5 \}\{ 4.5 \}}$	$0.00567389 ^{\{ 4.5 \}\{ 4.5 \}}$	$0.00567383 ^{\{ 3 \}\{ 3 \}}$	$0.00900842 ^{\{ 6 \}\{ 6 \}}$	$0.00213109 ^{\{ 2 \}\{ 2 \}}$	$0.00174105 ^{\{ 1 \}\{ 1 \}}$
	MRE	$\hat{\alpha}$	$0.07293834 ^{\{ 3.5 \}\{ 3.5 \}}$	$0.07293834 ^{\{ 3.5 \}\{ 3.5 \}}$	$0.07293881 ^{\{ 5 \}\{ 5 \}}$	$0.08395377 ^{\{ 6 \}\{ 6 \}}$	$0.03743775 ^{\{ 2 \}\{ 2 \}}$	$0.03278652 ^{\{ 1 \}\{ 1 \}}$
		$\hat{\lambda}$	$0.08417215 ^{\{ 3.5 \}\{ 3.5 \}}$	$0.08417215 ^{\{ 3.5 \}\{ 3.5 \}}$	$0.08417267 ^{\{ 5 \}\{ 5 \}}$	$0.10403808 ^{\{ 6 \}\{ 6 \}}$	$0.06155164 ^{\{ 2 \}\{ 2 \}}$	$0.05563452 ^{\{ 1 \}\{ 1 \}}$
	$\sum BRanks$		$22.5 ^{\{ 4 \}}$	$21.5 ^{\{ 3 \}}$	$28 ^{\{ 5 \}}$	$36 ^{\{ 6 \}}$	$12 ^{\{ 2 \}}$	$6 ^{\{ 1 \}}$
	$\sum C \&BRanks$		$22.5 ^{\{ 4 \}}$	$21.5 ^{\{ 3 \}}$	$28 ^{\{ 5 \}}$	$36 ^{\{ 6 \}}$	$12 ^{\{ 2 \}}$	$6 ^{\{ 1 \}}$
200	BIAS	$\hat{\alpha}$	$0.04001852 ^{\{ 4.5 \}\{ 4.5 \}}$	$0.04001852 ^{\{ 4.5 \}\{ 4.5 \}}$	$0.04001848 ^{\{ 3 \}\{ 3 \}}$	$0.04705698 ^{\{ 6 \}\{ 6 \}}$	$0.01733801 ^{\{ 2 \}\{ 2 \}}$	$0.01516892 ^{\{ 1 \}\{ 1 \}}$
		$\hat{\lambda}$	$0.05856409 ^{\{ 4 \}\{ 4 \}}$	$0.0585641 ^{\{ 5 \}\{ 5 \}}$	$0.05856347 ^{\{ 3 \}\{ 3 \}}$	$0.06345567 ^{\{ 6 \}\{ 6 \}}$	$0.02796569 ^{\{ 2 \}\{ 2 \}}$	$0.02441503 ^{\{ 1 \}\{ 1 \}}$
	MSE	$\hat{\alpha}$	$0.00253077 ^{\{ 4.5 \}\{ 4.5 \}}$	$0.00253077 ^{\{ 4.5 \}\{ 4.5 \}}$	$0.00253076 ^{\{ 3 \}\{ 3 \}}$	$0.00362108 ^{\{ 6 \}\{ 6 \}}$	$0.00030061 ^{\{ 2 \}\{ 2 \}}$	$0.0002301 ^{\{ 1 \}\{ 1 \}}$
		$\hat{\lambda}$	$0.00476338 ^{\{ 4.5 \}\{ 4.5 \}}$	$0.00476338 ^{\{ 4.5 \}\{ 4.5 \}}$	$0.0047633 ^{\{ 3 \}\{ 3 \}}$	$0.00626275 ^{\{ 6 \}\{ 6 \}}$	$0.00078208 ^{\{ 2 \}\{ 2 \}}$	$0.00059609 ^{\{ 1 \}\{ 1 \}}$
	MRE	$\hat{\alpha}$	$0.05335802 ^{\{ 4.5 \}\{ 4.5 \}}$	$0.05335802 ^{\{ 4.5 \}\{ 4.5 \}}$	$0.05335798 ^{\{ 3 \}\{ 3 \}}$	$0.06274264 ^{\{ 6 \}\{ 6 \}}$	$0.02311735 ^{\{ 2 \}\{ 2 \}}$	$0.02022522 ^{\{ 1 \}\{ 1 \}}$
		$\hat{\lambda}$	$0.07808545 ^{\{ 4 \}\{ 4 \}}$	$0.07808546 ^{\{ 5 \}\{ 5 \}}$	$0.07808462 ^{\{ 3 \}\{ 3 \}}$	$0.08460756 ^{\{ 6 \}\{ 6 \}}$	$0.03728759 ^{\{ 2 \}\{ 2 \}}$	$0.03255338 ^{\{ 1 \}\{ 1 \}}$
	$\sum BRanks$		$26 ^{\{ 4 \}}$	$28 ^{\{ 5 \}}$	$18 ^{\{ 3 \}}$	$36 ^{\{ 6 \}}$	$12 ^{\{ 2 \}}$	$6 ^{\{ 1 \}}$
	$\sum C\&BRanks$		$26 ^{\{ 4 \}}$	$28 ^{\{ 5 \}}$	$18 ^{\{ 3 \}}$	$36 ^{\{ 6 \}}$	$12 ^{\{ 2 \}}$	$6 ^{\{ 1 \}}$
300	BIAS	$\hat{\alpha}$	$0.03245976 ^{\{ 4.5 \}\{ 4.5 \}}$	$0.03245976 ^{\{ 4.5 \}\{ 4.5 \}}$	$0.03245972 ^{\{ 3 \}\{ 3 \}}$	$0.03938224 ^{\{ 6 \}\{ 8 \}}$	$0.01407489 ^{\{ 2 \}\{ 2 \}}$	$0.01252037 ^{\{ 1 \}\{ 1 \}}$
		$\hat{\lambda}$	$0.04732128 ^{\{ 3.5 \}\{ 3.5 \}}$	$0.04732128 ^{\{ 3.5 \}\{ 3.5 \}}$	$0.0473218 ^{\{ 5 \}\{ 5 \}}$	$0.05290774 ^{\{ 6 \}\{ 8 \}}$	$0.02365826 ^{\{ 2 \}\{ 2 \}}$	$0.02092282 ^{\{ 1 \}\{ 1 \}}$
	MSE	$\hat{\alpha}$	$0.00166778 ^{\{ 4 \}\{ 4 \}}$	$0.00166778 ^{\{ 4 \}\{ 4 \}}$	$0.00166778 ^{\{ 4 \}\{ 4 \}}$	$0.00252766 ^{\{ 6 \}\{ 9 \}}$	$0.0001981 ^{\{ 2 \}\{ 2 \}}$	$0.00015676 ^{\{ 1 \}\{ 1 \}}$
		$\hat{\lambda}$	$0.00341064 ^{\{ 3.5 \}\{ 3.5 \}}$	$0.00341064 ^{\{ 3.5 \}\{ 3.5 \}}$	$0.00341069 ^{\{ 5 \}\{ 5 \}}$	$0.00482747 ^{\{ 6 \}\{ 11 \}}$	$0.00055971 ^{\{ 2 \}\{ 2 \}}$	$0.00043776 ^{\{ 1 \}\{ 1 \}}$
	MRE	$\hat{\alpha}$	$0.04327968 ^{\{ 4.5 \}\{ 4.5 \}}$	$0.04327968 ^{\{ 4.5 \}\{ 4.5 \}}$	$0.04327963 ^{\{ 3 \}\{ 3 \}}$	$0.05250965 ^{\{ 6 \}\{ 8 \}}$	$0.01876651 ^{\{ 2 \}\{ 2 \}}$	$0.01669383 ^{\{ 1 \}\{ 1 \}}$
		$\hat{\lambda}$	$0.06309505 ^{\{ 4 \}\{ 4 \}}$	$0.06309504 ^{\{ 3 \}\{ 3 \}}$	$0.06309574 ^{\{ 5 \}\{ 5 \}}$	$0.07054365 ^{\{ 6 \}\{ 8 \}}$	$0.03154434 ^{\{ 2 \}\{ 2 \}}$	$0.02789709 ^{\{ 1 \}\{ 1 \}}$
	$\sum BRanks$		$24 ^{\{ 4 \}}$	$23 ^{\{ 3 \}}$	$25 ^{\{ 5 \}}$	$36 ^{\{ 6 \}}$	$12 ^{\{ 2 \}}$	$6 ^{\{ 1 \}}$
	$\sum C\&BRanks$		$24 ^{\{ 4 \}}$	$23 ^{\{ 3 \}}$	$25 ^{\{ 5 \}}$	$52 ^{\{ 8.5 \}}$	$12 ^{\{ 2 \}}$	$6 ^{\{ 1 \}}$

| Show Table

DownLoad: CSV

Table 4. The CI length for different parametric values of all estimation methods.

n	Est. Par.	MLE		ADE		CVME		MPS		LSE		PCE		RTADE		WLSE		Bayesian
n	Est. Par.	L. BP	L. BT	L. BP	L. BT	L. BP	L. BT	L. BP	L. BT	L. BP	L. BT	L. BP	L. BT	L. BP	L. BT	L. BP	L. BT	L. CR
15	$\hat{\alpha}$	$1.76864 ^{\{ 14 \}}$	$1.01231 ^{\{ 5 \}}$	$1.23169 ^{\{ 7 \}}$	$0.9917 ^{\{ 4 \}}$	$2.44613 ^{\{ 16 \}}$	$1.42478 ^{\{ 11 \}}$	$0.75104 ^{\{ 1 \}}$	$0.85626 ^{\{ 3 \}}$	$1.37582 ^{\{ 10 \}}$	$1.2964 ^{\{ 9 \}}$	$1.73329 ^{\{ 13 \}}$	$4.52643 ^{\{ 17 \}}$	$2.21266 ^{\{ 15 \}}$	$1.4343 ^{\{ 12 \}}$	$1.26902 ^{\{ 8 \}}$	$1.09219 ^{\{ 6 \}}$	$0.79185 ^{\{ 2 \}}$
	$\hat{\lambda}$	$1.8179 ^{\{ 13 \}}$	$1.21276 ^{\{ 3 \}}$	$1.61918 ^{\{ 9 \}}$	$1.35754 ^{\{ 6 \}}$	$2.45476 ^{\{ 16 \}}$	$1.76051 ^{\{ 12 \}}$	$1.08184 ^{\{ 2 \}}$	$1.21353 ^{\{ 4 \}}$	$1.82447 ^{\{ 14 \}}$	$1.7064 ^{\{ 10 \}}$	$1.51256 ^{\{ 7 \}}$	$2.71437 ^{\{ 17 \}}$	$1.85662 ^{\{ 15 \}}$	$1.32039 ^{\{ 5 \}}$	$1.73185 ^{\{ 11 \}}$	$1.56473 ^{\{ 8 \}}$	$1.02613 ^{\{ 1 \}}$
30	$\hat{\alpha}$	$0.76771 ^{\{ 10 \}}$	$0.61941 ^{\{ 3 \}}$	$0.69962 ^{\{ 6 \}}$	$0.63344 ^{\{ 5 \}}$	$0.93483 ^{\{ 14 \}}$	$0.73927 ^{\{ 8 \}}$	$0.54674 ^{\{ 1 \}}$	$0.62416 ^{\{ 4 \}}$	$0.8346 ^{\{ 13 \}}$	$0.82046 ^{\{ 12 \}}$	$1.17514 ^{\{ 16 \}}$	$2.60316 ^{\{ 17 \}}$	$0.96934 ^{\{ 15 \}}$	$0.81431 ^{\{ 11 \}}$	$0.75708 ^{\{ 9 \}}$	$0.73181 ^{\{ 7 \}}$	$0.56731 ^{\{ 2 \}}$
	$\hat{\lambda}$	$1.01832 ^{\{ 9 \}}$	$0.85197 ^{\{ 4 \}}$	$0.95639 ^{\{ 7 \}}$	$0.87947 ^{\{ 6 \}}$	$1.2636 ^{\{ 16 \}}$	$1.08914 ^{\{ 13 \}}$	$0.74985 ^{\{ 2 \}}$	$0.85211 ^{\{ 5 \}}$	$1.15014 ^{\{ 15 \}}$	$1.14232 ^{\{ 14 \}}$	$1.0211 ^{\{ 10 \}}$	$1.58731 ^{\{ 17 \}}$	$1.04276 ^{\{ 12 \}}$	$0.81825 ^{\{ 3 \}}$	$1.03151 ^{\{ 11 \}}$	$1.00314 ^{\{ 8 \}}$	$0.73465 ^{\{ 1 \}}$
70	$\hat{\alpha}$	$0.44252 ^{\{ 9 \}}$	$0.40638 ^{\{ 3 \}}$	$0.43855 ^{\{ 8 \}}$	$0.4246 ^{\{ 5 \}}$	$0.52287 ^{\{ 15 \}}$	$0.47767 ^{\{ 11 \}}$	$0.363 ^{\{ 1 \}}$	$0.4131 ^{\{ 4 \}}$	$0.47865 ^{\{ 12 \}}$	$0.47271 ^{\{ 10 \}}$	$0.82108 ^{\{ 16 \}}$	$1.36637 ^{\{ 17 \}}$	$0.51984 ^{\{ 14 \}}$	$0.47879 ^{\{ 13 \}}$	$0.43536 ^{\{ 6 \}}$	$0.43582 ^{\{ 7 \}}$	$0.37696 ^{\{ 2 \}}$
	$\hat{\lambda}$	$0.59365 ^{\{ 6 \}}$	$0.54695 ^{\{ 4 \}}$	$0.61226 ^{\{ 10 \}}$	$0.59699 ^{\{ 7 \}}$	$0.75869 ^{\{ 16 \}}$	$0.69736 ^{\{ 14 \}}$	$0.487 ^{\{ 1 \}}$	$0.54884 ^{\{ 5 \}}$	$0.65062 ^{\{ 12 \}}$	$0.6587 ^{\{ 13 \}}$	$0.70313 ^{\{ 15 \}}$	$0.80559 ^{\{ 17 \}}$	$0.60571 ^{\{ 8 \}}$	$0.50151 ^{\{ 3 \}}$	$0.60658 ^{\{ 9 \}}$	$0.61611 ^{\{ 11 \}}$	$0.49915 ^{\{ 2 \}}$
100	$\hat{\alpha}$	$0.33944 ^{\{ 5 \}}$	$0.31992 ^{\{ 3 \}}$	$0.34198 ^{\{ 6 \}}$	$0.33375 ^{\{ 4 \}}$	$0.42215 ^{\{ 14 \}}$	$0.38962 ^{\{ 10 \}}$	$0.30229 ^{\{ 1 \}}$	$0.34622 ^{\{ 7 \}}$	$0.39767 ^{\{ 11 \}}$	$0.39816 ^{\{ 12 \}}$	$0.68273 ^{\{ 16 \}}$	$1.05362 ^{\{ 17 \}}$	$0.4355 ^{\{ 15 \}}$	$0.41384 ^{\{ 13 \}}$	$0.3649 ^{\{ 9 \}}$	$0.35835 ^{\{ 8 \}}$	$0.31696 ^{\{ 2 \}}$
	$\hat{\lambda}$	$0.47339 ^{\{ 6 \}}$	$0.43589 ^{\{ 4 \}}$	$0.47704 ^{\{ 7 \}}$	$0.47049 ^{\{ 5 \}}$	$0.56073 ^{\{ 15 \}}$	$0.52885 ^{\{ 12 \}}$	$0.40649 ^{\{ 1 \}}$	$0.4866 ^{\{ 8 \}}$	$0.54784 ^{\{ 13 \}}$	$0.55029 ^{\{ 14 \}}$	$0.59234 ^{\{ 16 \}}$	$0.62163 ^{\{ 17 \}}$	$0.52259 ^{\{ 11 \}}$	$0.43411 ^{\{ 3 \}}$	$0.51049 ^{\{ 10 \}}$	$0.5069 ^{\{ 9 \}}$	$0.42203 ^{\{ 2 \}}$
200	$\hat{\alpha}$	$0.2389 ^{\{ 4 \}}$	$0.23142 ^{\{ 3 \}}$	$0.2516 ^{\{ 9 \}}$	$0.2482 ^{\{ 8 \}}$	$0.27946 ^{\{ 13 \}}$	$0.27005 ^{\{ 10 \}}$	$0.22294 ^{\{ 1 \}}$	$0.24721 ^{\{ 7 \}}$	$0.27286 ^{\{ 12 \}}$	$0.27282 ^{\{ 11 \}}$	$0.52575 ^{\{ 16 \}}$	$0.70941 ^{\{ 17 \}}$	$0.29224 ^{\{ 15 \}}$	$0.2862 ^{\{ 14 \}}$	$0.24663 ^{\{ 6 \}}$	$0.2461 ^{\{ 5 \}}$	$0.2278 ^{\{ 2 \}}$
	$\hat{\lambda}$	$0.32208 ^{\{ 5 \}}$	$0.31305 ^{\{ 4 \}}$	$0.35705 ^{\{ 11 \}}$	$0.3489 ^{\{ 9 \}}$	$0.3895 ^{\{ 15 \}}$	$0.37969 ^{\{ 12 \}}$	$0.30621 ^{\{ 2 \}}$	$0.34766 ^{\{ 8 \}}$	$0.38153 ^{\{ 14 \}}$	$0.3812 ^{\{ 13 \}}$	$0.43553 ^{\{ 17 \}}$	$0.39775 ^{\{ 16 \}}$	$0.35301 ^{\{ 10 \}}$	$0.30882 ^{\{ 3 \}}$	$0.33943 ^{\{ 6 \}}$	$0.34042 ^{\{ 7 \}}$	$0.3042 ^{\{ 1 \}}$
350	$\hat{\alpha}$	$0.17441 ^{\{ 4 \}}$	$0.17146 ^{\{ 2 \}}$	$0.1858 ^{\{ 6 \}}$	$0.18336 ^{\{ 5 \}}$	$0.20941 ^{\{ 13 \}}$	$0.20323 ^{\{ 9 \}}$	$0.17002 ^{\{ 1 \}}$	$0.21806 ^{\{ 15 \}}$	$0.20592 ^{\{ 10 \}}$	$0.20694 ^{\{ 11 \}}$	$0.40697 ^{\{ 16 \}}$	$0.49775 ^{\{ 17 \}}$	$0.21169 ^{\{ 14 \}}$	$0.20828 ^{\{ 12 \}}$	$0.19022 ^{\{ 7 \}}$	$0.19045 ^{\{ 8 \}}$	$0.17249 ^{\{ 3 \}}$
	$\hat{\lambda}$	$0.24024 ^{\{ 5 \}}$	$0.23525 ^{\{ 4 \}}$	$0.25748 ^{\{ 8 \}}$	$0.2569 ^{\{ 7 \}}$	$0.29707 ^{\{ 15 \}}$	$0.28529 ^{\{ 12 \}}$	$0.23099 ^{\{ 2 \}}$	$0.30366 ^{\{ 16 \}}$	$0.28776 ^{\{ 13 \}}$	$0.29495 ^{\{ 14 \}}$	$0.34137 ^{\{ 17 \}}$	$0.27981 ^{\{ 11 \}}$	$0.25913 ^{\{ 10 \}}$	$0.22713 ^{\{ 1 \}}$	$0.25778 ^{\{ 9 \}}$	$0.25635 ^{\{ 6 \}}$	$0.23339 ^{\{ 3 \}}$
$\sum Ranks$		$90 ^{\{ 6.5 \}}$	$42 ^{\{ 3 \}}$	$94 ^{\{ 9 \}}$	$71 ^{\{ 4 \}}$	$178 ^{\{ 16 \}}$	$134 ^{\{ 11 \}}$	$16 ^{\{ 1 \}}$	$86 ^{\{ 5 \}}$	$149 ^{\{ 13 \}}$	$143 ^{\{ 12 \}}$	$175 ^{\{ 15 \}}$	$197 ^{\{ 17 \}}$	$154 ^{\{ 14 \}}$	$93 ^{\{ 8 \}}$	$101 ^{\{ 10 \}}$	$90 ^{\{ 6.5 \}}$	$23 ^{\{ 2 \}}$

| Show Table

DownLoad: CSV

Table 5. Overage probabilities for all estimation methods.

n	Est. Par.	MLE		ADE		CVME		MPS		LSE		PCE		RTADE		WLSE		Bayesian
n	Est. Par.	CV. BP	CV. BT	CV. BP	CV. BT	CV. BP	CV. BT	CV. BP	CV. BT	CV. BP	CV. BT	CV. BP	CV. BT	CV. BP	CV. BT	CV. BP	CV. BT	CV. CR
15	$\hat{\alpha}$	$0.8 ^{\{ 1 \}}$	$0.85 ^{\{ 3 \}}$	$0.93 ^{\{ 10.5 \}}$	$0.95 ^{\{ 16 \}}$	$0.84 ^{\{ 2 \}}$	$0.9 ^{\{ 6 \}}$	$0.91 ^{\{ 8 \}}$	$0.94 ^{\{ 13.5 \}}$	$0.94 ^{\{ 13.5 \}}$	$0.93 ^{\{ 10.5 \}}$	$0.92 ^{\{ 9 \}}$	$0.86 ^{\{ 4 \}}$	$0.9 ^{\{ 6 \}}$	$0.9 ^{\{ 6 \}}$	$0.94 ^{\{ 13.5 \}}$	$0.94 ^{\{ 13.5 \}}$	$1 ^{\{ 17 \}}$
	$\hat{\lambda}$	$0.82 ^{\{ 1.5 \}}$	$0.89 ^{\{ 7 \}}$	$0.94 ^{\{ 14.5 \}}$	$0.91 ^{\{ 9 \}}$	$0.85 ^{\{ 4 \}}$	$0.88 ^{\{ 6 \}}$	$0.93 ^{\{ 11.5 \}}$	$0.97 ^{\{ 16 \}}$	$0.94 ^{\{ 14.5 \}}$	$0.9 ^{\{ 8 \}}$	$0.93 ^{\{ 11.5 \}}$	$0.84 ^{\{ 3 \}}$	$0.93 ^{\{ 11.5 \}}$	$0.82 ^{\{ 1.5 \}}$	$0.93 ^{\{ 11.5 \}}$	$0.87 ^{\{ 5 \}}$	$1 ^{\{ 17 \}}$
30	$\hat{\alpha}$	$0.88 ^{\{ 4 \}}$	$0.92 ^{\{ 11 \}}$	$0.94 ^{\{ 13.5 \}}$	$0.88 ^{\{ 4 \}}$	$0.92 ^{\{ 11 \}}$	$0.91 ^{\{ 8.5 \}}$	$0.85 ^{\{ 1 \}}$	$0.88 ^{\{ 4 \}}$	$0.89 ^{\{ 6 \}}$	$0.91 ^{\{ 8.5 \}}$	$0.86 ^{\{ 2 \}}$	$0.9 ^{\{ 7 \}}$	$0.97 ^{\{ 16 \}}$	$0.94 ^{\{ 13.5 \}}$	$0.95 ^{\{ 15 \}}$	$0.92 ^{\{ 11 \}}$	$1 ^{\{ 17 \}}$
	$\hat{\lambda}$	$0.89 ^{\{ 4 \}}$	$0.92 ^{\{ 8.5 \}}$	$0.98 ^{\{ 16 \}}$	$0.91 ^{\{ 6 \}}$	$0.93 ^{\{ 11 \}}$	$0.92 ^{\{ 8.5 \}}$	$0.91 ^{\{ 6 \}}$	$0.94 ^{\{ 13 \}}$	$0.95 ^{\{ 14.5 \}}$	$0.93 ^{\{ 11 \}}$	$0.87 ^{\{ 3 \}}$	$0.86 ^{\{ 2 \}}$	$0.91 ^{\{ 6 \}}$	$0.81 ^{\{ 1 \}}$	$0.95 ^{\{ 14.5 \}}$	$0.93 ^{\{ 11 \}}$	$1 ^{\{ 17 \}}$
70	$\hat{\alpha}$	$0.94 ^{\{ 9 \}}$	$0.97 ^{\{ 16 \}}$	$0.91 ^{\{ 4.5 \}}$	$0.95 ^{\{ 12.5 \}}$	$0.89 ^{\{ 2.5 \}}$	$0.89 ^{\{ 2.5 \}}$	$0.84 ^{\{ 1 \}}$	$0.94 ^{\{ 9 \}}$	$0.93 ^{\{ 6.5 \}}$	$0.95 ^{\{ 12.5 \}}$	$0.93 ^{\{ 6.5 \}}$	$0.95 ^{\{ 12.5 \}}$	$0.95 ^{\{ 12.5 \}}$	$0.91 ^{\{ 4.5 \}}$	$0.94 ^{\{ 9 \}}$	$0.96 ^{\{ 15 \}}$	$0.978 ^{\{ 17 \}}$
	$\hat{\lambda}$	$0.87 ^{\{ 2.5 \}}$	$0.93 ^{\{ 12 \}}$	$0.93 ^{\{ 12 \}}$	$0.92 ^{\{ 10 \}}$	$0.91 ^{\{ 8.5 \}}$	$0.87 ^{\{ 2.5 \}}$	$0.88 ^{\{ 4.5 \}}$	$0.88 ^{\{ 4.5 \}}$	$0.91 ^{\{ 8.5 \}}$	$0.9 ^{\{ 6.5 \}}$	$0.94 ^{\{ 14 \}}$	$0.9 ^{\{ 6.5 \}}$	$0.93 ^{\{ 12 \}}$	$0.83 ^{\{ 1 \}}$	$0.95 ^{\{ 15.5 \}}$	$0.95 ^{\{ 15.5 \}}$	$0.993 ^{\{ 17 \}}$
100	$\hat{\alpha}$	$0.94 ^{\{ 10.5 \}}$	$0.96 ^{\{ 13 \}}$	$0.94 ^{\{ 10.5 \}}$	$0.92 ^{\{ 5.5 \}}$	$0.9 ^{\{ 3 \}}$	$0.96 ^{\{ 13 \}}$	$0.82 ^{\{ 1 \}}$	$0.93 ^{\{ 8 \}}$	$0.96 ^{\{ 13 \}}$	$0.97 ^{\{ 16.5 \}}$	$0.89 ^{\{ 2 \}}$	$0.92 ^{\{ 5.5 \}}$	$0.97 ^{\{ 16.5 \}}$	$0.93 ^{\{ 8 \}}$	$0.93 ^{\{ 8 \}}$	$0.91 ^{\{ 4 \}}$	$0.967 ^{\{ 15 \}}$
	$\hat{\lambda}$	$0.93 ^{\{ 12 \}}$	$0.91 ^{\{ 8.5 \}}$	$0.9 ^{\{ 6 \}}$	$0.96 ^{\{ 16 \}}$	$0.93 ^{\{ 12 \}}$	$0.93 ^{\{ 12 \}}$	$0.86 ^{\{ 2 \}}$	$0.9 ^{\{ 6 \}}$	$0.95 ^{\{ 15 \}}$	$0.91 ^{\{ 8.5 \}}$	$0.88 ^{\{ 3.5 \}}$	$0.85 ^{\{ 1 \}}$	$0.93 ^{\{ 12 \}}$	$0.88 ^{\{ 3.5 \}}$	$0.93 ^{\{ 12 \}}$	$0.9 ^{\{ 6 \}}$	$0.984 ^{\{ 17 \}}$
200	$\hat{\alpha}$	$0.93 ^{\{ 9.5 \}}$	$0.95 ^{\{ 15 \}}$	$0.95 ^{\{ 15 \}}$	$0.91 ^{\{ 6.5 \}}$	$0.94 ^{\{ 12.5 \}}$	$0.93 ^{\{ 9.5 \}}$	$0.93 ^{\{ 9.5 \}}$	$0.9 ^{\{ 4.5 \}}$	$0.9 ^{\{ 4.5 \}}$	$0.91 ^{\{ 6.5 \}}$	$0.85 ^{\{ 1 \}}$	$0.95 ^{\{ 15 \}}$	$0.94 ^{\{ 12.5 \}}$	$0.93 ^{\{ 9.5 \}}$	$0.88 ^{\{ 3 \}}$	$0.86 ^{\{ 2 \}}$	$0.972 ^{\{ 17 \}}$
	$\hat{\lambda}$	$0.9 ^{\{ 6 \}}$	$0.88 ^{\{ 5 \}}$	$0.95 ^{\{ 14 \}}$	$0.93 ^{\{ 11.5 \}}$	$0.96 ^{\{ 15 \}}$	$0.97 ^{\{ 16 \}}$	$0.87 ^{\{ 3.5 \}}$	$0.91 ^{\{ 7.5 \}}$	$0.93 ^{\{ 11.5 \}}$	$0.91 ^{\{ 7.5 \}}$	$0.86 ^{\{ 2 \}}$	$0.81 ^{\{ 1 \}}$	$0.92 ^{\{ 9.5 \}}$	$0.87 ^{\{ 3.5 \}}$	$0.98 ^{\{ 17 \}}$	$0.92 ^{\{ 9.5 \}}$	$0.949 ^{\{ 13 \}}$
350	$\hat{\alpha}$	$0.92 ^{\{ 9 \}}$	$0.91 ^{\{ 7 \}}$	$0.89 ^{\{ 4.5 \}}$	$0.89 ^{\{ 4.5 \}}$	$0.94 ^{\{ 13 \}}$	$0.91 ^{\{ 7 \}}$	$0.93 ^{\{ 11 \}}$	$0.93 ^{\{ 11 \}}$	$0.98 ^{\{ 17 \}}$	$0.97 ^{\{ 16 \}}$	$0.87 ^{\{ 1 \}}$	$0.96 ^{\{ 14 \}}$	$0.88 ^{\{ 2.5 \}}$	$0.88 ^{\{ 2.5 \}}$	$0.93 ^{\{ 11 \}}$	$0.91 ^{\{ 7 \}}$	$0.962 ^{\{ 15 \}}$
	$\hat{\lambda}$	$0.95 ^{\{ 15 \}}$	$0.97 ^{\{ 17 \}}$	$0.92 ^{\{ 5 \}}$	$0.94 ^{\{ 11 \}}$	$0.94 ^{\{ 11 \}}$	$0.94 ^{\{ 11 \}}$	$0.91 ^{\{ 3 \}}$	$0.92 ^{\{ 5 \}}$	$0.94 ^{\{ 11 \}}$	$0.95 ^{\{ 15 \}}$	$0.92 ^{\{ 5 \}}$	$0.83 ^{\{ 1 \}}$	$0.93 ^{\{ 7 \}}$	$0.88 ^{\{ 2 \}}$	$0.94 ^{\{ 11 \}}$	$0.95 ^{\{ 15 \}}$	$0.936 ^{\{ 8 \}}$
$\sum Ranks$		$84 ^{\{ 5 \}}$	$123 ^{\{ 11 \}}$	$126 ^{\{ 13 \}}$	$112.5 ^{\{ 9 \}}$	$105.5 ^{\{ 8 \}}$	$102.5 ^{\{ 7 \}}$	$62 ^{\{ 3 \}}$	$102 ^{\{ 6 \}}$	$135.5 ^{\{ 15 \}}$	$127 ^{\{ 14 \}}$	$60.5 ^{\{ 2 \}}$	$72.5 ^{\{ 4 \}}$	$124 ^{\{ 12 \}}$	$56.5 ^{\{ 1 \}}$	$141 ^{\{ 16 \}}$	$114.5 ^{\{ 10 \}}$	$187 ^{\{ 17 \}}$

| Show Table

DownLoad: CSV

7. Modeling an insurance data

Here, we analyze a data set from the insurance sector to illustrate the utility of the WDEx distribution. This data set reflects the monthly unemployment insurance metrics from July 2008 to April 2013, and it includes 58 observations as recorded by the department of labor, state of Maryland, USA. The data frame consists of 21 variables and the variable number 9 is fitted using the WDEx model. Data is listed below and it can be found at: https://catalog.data.gov/dataset/unemployment-insurance-data-from-July-2008-to-April-2013.

48.2	48.2	55.6	49.4	54.7	84.4	85.6	92.1	115.7	92.7
87.4	104.1	86.6	96.7	74.1	70.4	84	80.3	86.5	86.9
104.7	74.3	66.7	79.1	65.7	78.6	59.9	59	72.6	66.6
89.9	75.2	72.1	63.2	70.3	58.9	59.7	72.6	55.3	62.6
55.5	60.4	84.2	68.9	65.2	70	56.6	56.3	71.9	60.3
54	65.2	56.3	69.6	68.8	66	63.5	64.9

| Show Table

DownLoad: CSV

We compare the WDEx distribution with some well-known competing distributions including the beta exponential (BEx) ^[25], gamma (G), exponentiated Weibull (EW) ^[26], Harris extend exponential (HEEx) ^[27], alpha power exponentiated-exponential (APEEx) ^[28], Frechet–Weibull mixture exponential (FWMEx) ^[29], Marshall–Olkin alpha-power exponential (MOAPEx) ^[30], Marshall Olkin exponential (MOEx) ^[31], Frechet–Weibull (FW) ^[32], Weibull (W), alpha-power exponential (APEx) ^[33], transmuted exponential (TEx) ^[34], EEx, and Ex distributions. The competing models are compared by using some discrimination measures such as Anderson–Darling (AD), Cramér–von Mises (CM), and Kolmogorov–Smirnov (KS) with its $p$ -value (KS $p$ -value).

The MLEs and the statistical metrics are calculated using the R software©. Table 6 provides analytical metrics along with the MLEs and their standard errors (SEs). The findings in Table 6 suggest that the WDEx offers better fits than other competitive models and it can be selected as an appropriate model to evaluate the analyzed insurance data.

Table 6. The analytical measures and the MLEs of the WDEx distribution and other competing models.

Model	AD	CM	KS	KS $p$ -value	Estimates (SEs)
WDEx	0.22888	0.03088	0.05815	0.98949	$\hat{\alpha}=132.362\ (56.1205)$
WDEx					$\hat{\lambda}=0.07249\ (0.00691)$
FW	0.38156	0.04884	0.06949	0.94209	$\hat{\alpha}=4.46474\ (66.2443)$
					$\hat{\beta}=3.17550\ (115.269)$
					$\hat{\lambda}=25.3428\ (579.785)$
					$\hat{k}=1.25626\ (18.6392)$
BEx	0.27609	0.04162	0.07932	0.85886	$\hat{a}=75.9965\ (84.8089)$
					$\hat{b}=1.91398\ (1.80320)$
					$\hat{\lambda}=0.05573\ (0.03166)$
EEx	0.23791	0.03101	0.08120	0.83898	$\hat{\alpha}=232.474\ (126.888)$
EEx					$\hat{\lambda}=0.08431\ (0.00884)$
G	0.45378	0.07394	0.08162	0.83451	$\hat{a}=24.6226\ (4.54042)$
G					$\hat{b}=0.34427\ (0.06413)$
EW	0.23348	0.03278	0.08179	0.83263	$\hat{\beta}=1.15364\ (0.11836)$
					$\hat{\lambda}=0.03802\ (0.02282)$
					$\hat{\theta}=106.742\ (69.8959)$
HEEx	0.31048	0.04283	0.08205	0.82975	$\hat{\alpha}=3.80452\ (0.75598)$
					$\hat{\lambda}=0.00662\ (0.00113)$
					$\hat{\theta}=2115870\ (11864.4)$
APEEx	0.22899	0.03147	0.08234	0.82653	$\hat{\alpha}=1.22817\ (1.95307)$
					$\hat{a}=0.08631\ (0.01593)$
					$\hat{c}=248.897\ (168.117)$
FWMEx	0.43428	0.06586	0.09245	0.70449	$\hat{a}=0.01001\ (0.01317)$
					$\hat{\alpha}=18.1993\ (114.082)$
					$\hat{\lambda}=40.6229\ (6.75603)$
					$\hat{k}=0.47024\ (2.94764)$
MOAPEx	0.77269	0.12783	0.09341	0.69217	$\hat{\alpha}=413.107\ (876.070)$
					$\hat{\lambda}=0.11824\ (0.01269)$
					$\hat{\theta}=674.591\ (637.159)$
MOEx	0.77594	0.12836	0.09397	0.68499	$\hat{\alpha}=4174.02\ (3747.42)$
MOEx					$\hat{\lambda}=0.11858\ (0.01261)$
W	1.19149	0.18595	0.12496	0.32540	$\hat{a}=4.88793\ (0.46156)$
W					$\hat{b}=77.6595\ (2.21593)$
APEx	0.42964	0.06957	0.28502	0.00016	$\hat{\alpha}=1432.64\ (802.869)$
APEx					$\hat{\lambda}=0.00352\ (0.00233)$
TEx	0.43477	0.07062	0.39111	$#60;0.00001$	$\hat{\lambda}=$ -1.00000 $\ (0.51995)$
TEx					$\hat{\theta}=0.02028\ (0.00262)$
Ex	0.45213	0.07366	0.49029	$#60;0.00001$	$\hat{\lambda}=0.01398\ (0.00183)$

| Show Table

DownLoad: CSV

The fitted PDF, CDF, SF, and probability-probability (P-P) graphs of the WDEx model are displayed in Figure 6, whereas the total time on test (TTT) and WDEx HRF plots for the analyzed data are depicted in Figure 7. The TTT plots confirms that the data has an increasing HRF. We conclude that the WDEx distribution is suitable for modeling the insurance data.

Figure 6. The fitted WDEx PDF, CDF, SF, and P-P plots for insurance data.

DownLoad: Full-Size Img PowerPoint

Figure 7. The HRF plot of the WDEx model and TTT plot for insurance data set.

DownLoad: Full-Size Img PowerPoint

Moreover, the nine estimation approaches mentioned before in Section 5 are adopted to estimate the WDEx parameters. Table 7 records the calculations of the WDEx parameters using such estimation techniques and the empirical values for insurance data.

Table 7. Different estimates of the WDEx parameters using several estimators along with goodness-of-fit measures for insurance data.

Method	$\hat{\alpha}$	$\hat{\lambda}$	AD	CM	KS	KS $p$ -value
MLE	132.36153	0.07249	0.22888	0.03088	0.05815	0.98949
WLSE	132.36153	0.07269	0.22855	0.03084	0.06117	0.98173
CVME	132.36173	0.07270	0.22853	0.03083	0.06138	0.98107
OLSE	132.36145	0.07273	0.22849	0.03083	0.06173	0.97992
PCE	132.36153	0.07295	0.22812	0.03078	0.06516	0.96630
ADE	155.92600	0.07513	0.22928	0.03068	0.06857	0.94795
MPS	130.36158	0.07244	0.22857	0.03086	0.06015	0.98469
RTADE	157.11897	0.07521	0.22939	0.03068	0.06846	0.94860
BMC	194.1689	0.07856	0.23413	0.03148	0.08025	0.84907
BTK	160.4825	0.07402	0.49763	0.07956	0.08157	0.83500

| Show Table

DownLoad: CSV

The P-P graphs and histogram of insurance data with the fitted WDEx density for different estimation techniques are shown in Figure 8. Figure 9 shows the histogram of the data with the fitted WDEx PDF for different estimators.

Figure 8. The P-P plots of the WDEx model using different estimators for insurance data.

DownLoad: Full-Size Img PowerPoint

Figure 9. The histogram of insurance data with the fitted WDEx densities using different estimators.

DownLoad: Full-Size Img PowerPoint

8. Conclusions

In this paper, we studied a new extension of the exponential model that exhibits upside-down bathtub, decreasing, decreasing-constant, increasing, and increasing-constant hazard rates. The studied model is called the weighted-exponential (WDEx) distribution. Some basic distributional characteristics are derived. Five risk measures are calculated for the WDEx distribution. Eight classical estimation methods along with the Bayesian estimation are utilized to estimate the WDEx parameters. The simulation results show that the proposed estimators provide good performance. Moreover, the practical applicability of the WDEx distribution is addressed using a real-life insurance data set, showing its superiority fit over fourteen competing exponential models.

Acknowledgments

The authors thanks the respected editors for supporting us in the review process.

Conflict of interest

The authors declare there is no conflict of interest.

Conflict of interest

The authors declare no conflict of interest.

References

[1]	Tamburrini O, Aprile I, Falcone C, et al. (2011) Off-label use of intravascular iodinated organic and MR contrast media. Radiol Med 116: 1-14. doi: 10.1007/s11547-010-0601-5
[2]	Meloni MM, Barton S, Xu L, et al. (2017) Contrast agents for cardiovascular magnetic resonance imaging: an overview. J Mater Chem B 5: 5714-5725. doi: 10.1039/C7TB01241A
[3]	Lauffer RB (1987) Paramagnetic metal complexes as water proton relaxation agents for NMR imaging: theory and design. Chem Rev 87: 901-927. doi: 10.1021/cr00081a003
[4]	Schörner W, Kazner E, Laniado M, et al. (1984) Magnetic resonance tomography (MRT) of intracranial tumours: Initial experience with the use of the contrast medium gadolinium-DTPA. Neurosurg Rev 7: 303-312. doi: 10.1007/BF01892910
[5]	Essig M, Anzalone N, Combs SE, et al. (2012) MR imaging of neoplastic central nervous system lesions: review and recommendations for current practice. Am J Neuroradiol 33: 803-817. doi: 10.3174/ajnr.A2640
[6]	Anzalone N, Gerevini S, Scotti R, et al. (2009) Detection of cerebral metastases on magnetic resonance imaging: intraindividual comparison of gadobutrol with gadopentetate dimeglumine. Acta Radiol 50: 933-940. doi: 10.1080/02841850903095385
[7]	Malayeri AA, Brooks KM, Bryant LH, et al. (2016) National Institutes of health perspective on reports of gadolinium deposition in the brain. J Am Coll Radiol 13: 237-241. doi: 10.1016/j.jacr.2015.11.009
[8]	Weinmann HJ, Brasch RC, Press WR, et al. (1984) Characteristics of gadolinium-DTPA complex: a potential NMR contrast agent. Am J Roentgenol 142: 619-624. doi: 10.2214/ajr.142.3.619
[9]	Lin SP, Brown JJ (2007) MR contrast agents: Physical and pharmacologic basics. J Magn Reson Imaging 25: 884-899. doi: 10.1002/jmri.20955
[10]	Ersoy H, Rybicki FJ (2007) Biochemical safety profiles of gadolinium-based extracellular contrast agents and nephrogenic systemic fibrosis. J Magn Reson Imaging 26: 1190-1197. doi: 10.1002/jmri.21135
[11]	Bellin MF, Van Der Molen AJ (2008) Extracellular gadolinium-based contrast media: an overview. Eur J Radiol 66: 160-167. doi: 10.1016/j.ejrad.2008.01.023
[12]	Evans CH (1990) Biochemistry of the Lanthanides New York: Plenum Press. doi: 10.1007/978-1-4684-8748-0
[13]	De León-Rodríguez LM, Martins AF, Pinho MC, et al. (2015) Basic MR relaxation mechanisms and contrast agent design. J Magn Reson Imaging 42: 545-565. doi: 10.1002/jmri.24787
[14]	Levine D, McDonald RJ, Kressel HY (2018) Gadolinium retention after contrast-enhanced MRI. JAMA 320: 1853-1854. doi: 10.1001/jama.2018.13362
[15]	Shepherd M, Lata S, Mani S, et al. (2009) Anaphylaxis to gadolinium radiocontrast: a case report and review of the literature. J La State Med Soc 161: 282-284.
[16]	Raisch DW, Garg V, Arabyat R, et al. (2014) Anaphylaxis associated with gadolinium-based contrast agents: Data from the food and drug administration's adverse event reporting system and review of case reports in the literature. Expert Opin Drug Saf 13: 15-23. doi: 10.1517/14740338.2013.832752
[17]	Franckenberg S, Berger F, Schaerli S, et al. (2018) Fatal anaphylactic reaction to intravenous gadobutrol, a gadolinium-based MRI contrast agent. Radiol Case Rep 13: 299-301. doi: 10.1016/j.radcr.2017.09.012
[18]	Jung JW, Kangand HR, Kim MH, et al. (2012) Immediate hypersensitivity reaction to gadolinium-based MR contrast media. Radiology 264: 414-422. doi: 10.1148/radiol.12112025
[19]	Morzycki A, Bhatia A, Murphy KJ (2017) Adverse reactions to contrast material: a Canadian update. Can Assoc Radiol J 68: 187-193. doi: 10.1016/j.carj.2016.05.006
[20]	Behzadi AH, Farooq Z, Newhouse JH, et al. (2018) MRI and CT contrast media extravasation a systematic review. Medicine 97: e0055. doi: 10.1097/MD.0000000000010055
[21]	Varela DC, Sepulveda P, Prieto J, et al. (2015) Extravasation of intravenous contrast media: What every radiologist should know. Rev Chil Radiol 21: 151-157. doi: 10.4067/S0717-93082015000400006
[22]	Blasco-Perrin H, Glaser B, Pienkowski M, et al. (2013) Gadolinium induced recurrent acute pancreatitis. Pancreatology 13: 88-89. doi: 10.1016/j.pan.2012.12.002
[23]	Unal O, Arslan H (1999) Cardiac arrest caused by IV gadopentetate dimeglumine. Am J Roentgenol 172: 1141. doi: 10.2214/ajr.172.4.10587169
[24]	US Food and Drug AdministrationMedical Imaging Drugs Advisory Committee Meeting, FDA briefing document: Gadolinium retention after gadolinium based contrast magnetic resonance imaging in patients with normal renal function. (2017) .
[25]	Maramattom BV, Manno EM, Wijdicks EFM, et al. (2005) Gadolinium encephalopathy in a patient with renal failure. Neurology 64: 1276-1278. doi: 10.1212/01.WNL.0000156805.45547.6E
[26]	Hui FK, Mullins M (2009) Persistence of gadolinium contrast enhancement in CSF: A possible harbinger of gadolinium neurotoxicity? Am J Neuroradiol 30: e1. doi: 10.3174/ajnr.A1205
[27]	Kim SH, Jo EJ, Kim MY, et al. (2013) Clinical value of radiocontrast media skin tests as a prescreening and diagnostic tool in hypersensitivity reactions. Ann Allergy Asthma Immunol 110: 258-262. doi: 10.1016/j.anai.2013.01.004
[28]	Shellock FG, Kanal E (1999) Safety of magnetic resonance imaging contrast agents. J Magn Res Im 10: 477-484. doi: 10.1002/(SICI)1522-2586(199909)10:3<477::AID-JMRI33>3.0.CO;2-E
[29]	Grobner T (2006) Gadolinium-a specific trigger for the development of nephrogenic fibrosing dermopathy and nephrogenic systemic fibrosis? Nephrol Dial Transpl 21: 1104-1108. doi: 10.1093/ndt/gfk062
[30]	Thomson LK, Thomson PC, Kingsmore DB, et al. (2015) Diagnosing nephrogenic systemic fibrosis in the post-FDA restriction era. J Magn Reson Imaging 41: 1268-1271. doi: 10.1002/jmri.24664
[31]	Larson KN, Gagnon AL, Darling MD, et al. (2015) Nephrogenic systemic fibrosis manifesting a decade after exposure to gadolinium. JAMA Dermatol 151: 1117-1120. doi: 10.1001/jamadermatol.2015.0976
[32]	Bernstein EJ, Schmidt-Lauber C, Kay J (2012) Nephrogenic systemic fibrosis: a systemic fibrosing disease resulting from gadolinium exposure. Best Pract Res Cl Rheumatol 26: 489-503. doi: 10.1016/j.berh.2012.07.008
[33]	Sanyal S, Marckmann P, Scherer S, et al. (2011) Multiorgan gadolinium (Gd) deposition and fibrosis ina patient with nephrogenic systemic fibrosis-an autopsy-based review. Nephrol Dial Transplant 26: 3616-3626. doi: 10.1093/ndt/gfr085
[34]	Kay J, Bazari H, Avery LL, et al. (2008) Case 6-2008: a 46-year-old woman with renal failure and stiffness of the joints and skin. New Engl J Med 358: 827-838. doi: 10.1056/NEJMcpc0708697
[35]	Bhave G, Lewis JB, Chang SS (2008) Association of gadolinium based magnetic resonance imaging contrast agents and nephrogenic systemic fibrosis. J Urol 180: 830-835. doi: 10.1016/j.juro.2008.05.005
[36]	Cowper SE, Su LD, Bhawan J, et al. (2001) Nephrogenic fibrosing dermopathy. Am J Dermatopath 23: 383-393. doi: 10.1097/00000372-200110000-00001
[37]	Cowper SE, Robin HS, Steinberg SM, et al. (2000) Scleromyxedema-like cutaneous disease in renal dialysis patients. Lancet 356: 1000-1001. doi: 10.1016/S0140-6736(00)02694-5
[38]	Weigle JP, Broome DR (2008) Nephrogenic systemic fibrosis: chronic imaging findings and review of the medical literature. Skeletal Radiol 37: 457-464. doi: 10.1007/s00256-008-0464-1
[39]	Zou Z, Zhang HL, Roditi GH, et al. (2011) Nephrogenic systemic fibrosis: review of 370 biopsy-confirmed cases. JACC: Cardiovasc Imag 4: 1206-1216. doi: 10.1016/j.jcmg.2011.08.013
[40]	Morris MF, Zhang Y, Zhang H, et al. (2009) Features of nephrogenic systemic fibrosis on radiology examinations. Am J Roentgenol 193: 61-69. doi: 10.2214/AJR.08.1352
[41]	Tsushima Y, Kanal E, Thomsen HS (2010) Nephrogenic systemic fibrosis: risk factors suggested from Japanese published cases. Brit J Radiol 83: 590-595. doi: 10.1259/bjr/17689538
[42]	Thomsen HS, Morcos SK, Almén T, et al. (2013) Nephrogenic systemic fibrosis and gadolinium-based contrast media: updated ESUR contrast medium safety committee guidelines. Eur Radiol 23: 307-318. doi: 10.1007/s00330-012-2597-9
[43]	Mazhar SM, Shiehmorteza M, Kohl CA, et al. (2009) Nephrogenic systemic fibrosis in liver disease: a systematic review. J Magn Reson Imaging 30: 1313-1322. doi: 10.1002/jmri.21983
[44]	Elmholdt TR, Jørgensen B, Ramsing M, et al. (2010) Two cases of nephrogenic systemic fibrosis after exposure to the macrocyclic compound gadobutrol. NDT Plus 3: 285-287.
[45]	Kay J (2008) Gadolinium and nephrogenic systemic fibrosis: The evidence of things not seen. Clev Clin J Med 75: 112. doi: 10.3949/ccjm.75.2.112
[46]	Todd DJ, Kay J (2008) Nephrogenic systemic fibrosis: an epidemic of gadolinium toxicity. Curr Rheumatol Rep 10: 195-204. doi: 10.1007/s11926-008-0033-6
[47]	Sieber MA, Lengsfeld P, Frenzel T, et al. (2008) Preclinical investigation to compare different gadolinium-based contrast agents regarding their propensity to release gadolinium in vivo and to trigger nephrogenic systemic fibrosis-like lesions. Eur Radiol 18: 2164-2173. doi: 10.1007/s00330-008-0977-y
[48]	Semelka RC, Prybylskib JP, Ramalho M (2019) Influence of excess ligand on nephrogenic systemic fibrosis associated with nonionic, linear gadolinium-based contrast agents. Magn Res Imaging 58: 174-178. doi: 10.1016/j.mri.2018.11.015
[49]	US Food and Drug Administration FDA request boxes warning for contrast agents used to improve MRI images (2007) .Available from: http://wayback.archive-it.org/7993/20170112033008/http://www.fda.gov/NewsEvents/Newsroom/PressAnnouncements/2007/ucm108919.htm.
[50]	Khawaja AZ, Cassidy DB, Al Shakarchi J, et al. (2015) Revisiting the risks of MRI with Gadolinium based contrast agents: review of literature and guidelines. Insights Imaging 6: 553-558. doi: 10.1007/s13244-015-0420-2
[51]	Canga A, Kislikova M, Martínez-Gálvez M, et al. (2014) Renal function, nephrogenic systemic fibrosis and other adverse reactions associated with gadolinium-based contrast media. Nefrologia 34: 428-438.
[52]	Martin DR, Krishnamoorthy SK, Kalb B, et al. (2010) Decreased incidence of NSF in patients on dialysis after changing gadolinium contrast-enhanced MRI protocols. J Magn Reson Imaging 31: 440-446. doi: 10.1002/jmri.22024
[53]	Altun E, Martin DR, Wertman R, et al. (2009) Nephrogenic systemic fibrosis: Change in incidence following a switch in gadolinium agents and adoption of a gadolinium policy—report from two US universities. Radiology 253: 689-696. doi: 10.1148/radiol.2533090649
[54]	Xia D, Davis RL, Crawford JA, et al. (2010) Gadolinium released from MR contrast agents is deposited in brain tumors: in situ demonstration using scanning electron microscopy with energy dispersive X-ray spectroscopy. Acta Radiol 51: 1126-1136. doi: 10.3109/02841851.2010.515614
[55]	Kanda T, Ishii K, Kawaguchi H, et al. (2014) High signal intensity in the dentate nucleus and globus pallidus on unenhanced T1-weighted MR images: Relationship with increasing cumulative dose of a gadolinium based contrast material. Radiology 270: 834-841. doi: 10.1148/radiol.13131669
[56]	McDonald RJ, McDonald JS, Kallmes DF, et al. (2015) Intracranial gadolinium deposition after contrast-enhanced MR imaging. Radiology 275: 772-782. doi: 10.1148/radiol.15150025
[57]	Olchowy C, Cebulski K, Łasecki M, et al. (2017) The presence of the gadolinium-based contrast agent depositions in the brain and symptoms of gadolinium neurotoxicity-a systematic review. PLoS One 12: e0171704. doi: 10.1371/journal.pone.0171704
[58]	Pullicino R, Radon M, Biswas S, et al. (2018) A review of the current evidence on gadolinium deposition in the brain. Clin Neuroradiol 28: 159-169. doi: 10.1007/s00062-018-0678-0
[59]	Gianolio E, Gregorio ED, Aime S (2019) Chemical insights into the issues of Gd retention in the brain andother tissues upon the administration of Gd-containing MRI contrast agents. Eur J Inorg Chem 2019: 137-151. doi: 10.1002/ejic.201801220
[60]	Kanda T, Osawa M, Oba H, et al. (2015) High signal intensity in dentate nucleus on unenhanced T1-weightedMR images: association with linear versus macrocyclic gadolinium chelate administration. Radiology 275: 803-809. doi: 10.1148/radiol.14140364
[61]	Weberling LD, Kieslich PJ, Kickingereder P, et al. (2015) Increased signal intensity in the dentate nucleus on unenhanced T1-weighted images after gadobenate dimeglumine administration. Invest Radiol 50: 743-748. doi: 10.1097/RLI.0000000000000206
[62]	Errante Y, Cirimele V, Mallio CA, et al. (2014) Progressive increase of T1 signal intensity of the dentate nucleus on unenhanced magnetic resonance images is associated with cumulative doses of intravenously administered gadodiamide in patients with normal renal function, suggesting dechelation. Invest Radiol 49: 685-690. doi: 10.1097/RLI.0000000000000072
[63]	Zhang Y, Cao Y, Shih GL, et al. (2017) Extent of signal hyperintensity on unenhanced T1-weighted brain MR images after more than 35 administrations of linear gadolinium-based contrast agents. Radiology 282: 516-525. doi: 10.1148/radiol.2016152864
[64]	Radbruch A, Weberling LD, Kieslich PJ, et al. (2015) Gadolinium retention in the dentate nucleus and globus pallidus is dependent on the class of contrast agent. Radiology 275: 783-791. doi: 10.1148/radiol.2015150337
[65]	Malhotra A, LeSar B, Wu X, et al. (2018) Progressive T1 shortening of the dentate nucleus in patients with multiple sclerosis: Result of multiple administrations of linear gadolinium contrast agents versus intrinsic disease. Am J Roentgenol 211: 1099-1105. doi: 10.2214/AJR.17.19155
[66]	Flood TF, Stence NV, Maloney JA, et al. (2017) Pediatric brain: Repeated exposure to linear gadolinium-based contrast material is associated with increased signal intensity at unenhanced T1-weighted MR imaging. Radiology 282: 222-228. doi: 10.1148/radiol.2016160356
[67]	Adin ME, Kleinberg L, Vaidya D, et al. (2015) Hyperintense dentate nuclei on T1-weighted MRI: relation to repeat gadolinium administration. Am J Neuroradiol 36: 1859-1865. doi: 10.3174/ajnr.A4378
[68]	Miller JH, Hu HH, Pokorney A, et al. (2015) MRI brain signal intensity changes of a child during the course of 35 gadolinium contrast examinations. Pediatrics 136: e1637-e1640. doi: 10.1542/peds.2015-2222
[69]	Hu HH, Pokorney A, Towbin RB, et al. (2016) Increased signal intensities in the dentate nucleus and globus pallidus on unenhanced T1-weighted images: evidence in children undergoing multiple gadolinium MRI exams. Pediatr Radiol 46: 1590-1598. doi: 10.1007/s00247-016-3646-3
[70]	Bae S, Lee H, Han K, et al. (2017) Gadolinium deposition in the brain: association with various GBCAs using a generalized additive model. Eur Radiol 27: 3353-3361. doi: 10.1007/s00330-016-4724-5
[71]	Quattrocchi CC, Mallio CA, Errante Y, et al. (2015) Gadodiamide and dentate nucleus T1 hyperintensity in patients with meningioma evaluated by multiple follow-up contrast-enhanced magnetic resonance examinations with no systemic interval therapy. Invest Radiol 50: 470-472. doi: 10.1097/RLI.0000000000000154
[72]	McDonald JS, McDonald RJ, Jentoft ME, et al. (2017) Intracranial gadolinium deposition following gadodiamide-enhanced magnetic resonance imaging in pediatric patients: a case-control study. JAMA Pediatr 171: 705-707. doi: 10.1001/jamapediatrics.2017.0264
[73]	Mallio CA, Vullo GL, Messina L, et al. (2020) Increased T1 signal intensity of the anterior pituitary gland on unenhanced magnetic resonance images after chronic exposure to gadodiamide. Invest Radiol 55: 25-29. doi: 10.1097/RLI.0000000000000604
[74]	Gianolio E, Bardini P, Arena F, et al. (2017) Gadolinium retention in the rat brain: Assessment of the amounts of insoluble gadolinium-containing species and intact gadolinium complexes after repeated administration of gadolinium-based contrast agents. Radiology 285: 839-849. doi: 10.1148/radiol.2017162857
[75]	Rasschaert M, Schroeder JA, Wu TD, et al. (2018) Multimodal imaging study of gadolinium presence in rat cerebellum: differences between Gd chelates, presence in the Virchow-Robin space, association with lipofuscin, and hypotheses about distribution pathway. Invest Radiol 53: 518. doi: 10.1097/RLI.0000000000000490
[76]	Radbruch A, Richter H, Fingerhu S, et al. (2019) Gadolinium deposition in the brain in a large animal model. Comparison of linear and macrocyclic gadolinium-based contrast agents. Invest Radiol 54: 531-536. doi: 10.1097/RLI.0000000000000575
[77]	Boyken J, Frenzel T, Lohrke J, et al. (2018) Gadolinium accumulation in the deep cerebellar nuclei and globus pallidus after exposure to linear but not macrocyclic gadolinium-based contrast agents in a retrospective pig study with high similarity to clinical conditions. Invest Radiol 53: 278-285. doi: 10.1097/RLI.0000000000000440
[78]	Robert P, Violas X, Grand S, et al. (2016) Linear gadolinium-based contrast agents are associated with brain gadolinium retention in healthy rats. Invest Radiol 51: 73-82. doi: 10.1097/RLI.0000000000000241
[79]	Strzeminska I, Factor C, Robert P, et al. (2020) Long-term evaluation of gadolinium retention in rat brain after single injection of a clinically relevant dose of gadolinium-based contrast agents. Invest Radiol 55: 138-143. doi: 10.1097/RLI.0000000000000623
[80]	Radbruch A, Haase R, Kieslich PJ, et al. (2017) No signal intensity increase in the dentate nucleus on unenhanced T1-weighted MR images after more than 20 serial injections of macrocyclic gadolinium-based contrast agents. Radiology 282: 699-707. doi: 10.1148/radiol.2016162241
[81]	Radbruch A, Haase R, Kickingereder P, et al. (2017) Pediatric brain: no increased signal intensity in the dentate nucleus on unenhanced T1-weighted MR images after consecutive exposure to a macrocyclic gadolinium-based contrast agent. Radiology 283: 828-836. doi: 10.1148/radiol.2017162980
[82]	Tibussek D, Rademacher C, Caspers J, et al. (2007) Gadolinium brain deposition after macrocyclic gadolinium administration: a pediatric case-control study. Radiology 285: 223-230. doi: 10.1148/radiol.2017161151
[83]	Schneider GK, Stroeder J, Roditi G, et al. (2017) T1 signal measurements in pediatric brain: findings after multiple exposures to gadobenate dimeglumine for imaging of non neurologic disease. Am J Neuroradiol 38: 1799-1806. doi: 10.3174/ajnr.A5270
[84]	Conte G, Preda L, Cocorocchio E, et al. (2017) Signal intensity change on unenhanced T1-weighted images in dentate nucleus and globus pallidus after multiple administrations of gadoxetate disodium: an intraindividual comparative study. Eur Radiol 27: 4372-4378. doi: 10.1007/s00330-017-4810-3
[85]	Ryu YJ, Choi YH, Cheon J, et al. (2018) Pediatric brain: Gadolinium deposition in dentate nucleus and globus pallidus on unenhanced T1-weighted images is dependent on the type of contrast agent. Invest Radiol 53: 246-255. doi: 10.1097/RLI.0000000000000436
[86]	Stanescu AL, Shaw DW, Murata N, et al. (2020) Brain tissue gadolinium retention in pediatric patients after contrast-enhanced magnetic resonance exams: pathological confirmation. Pediatr Radiol 50: 388-396. doi: 10.1007/s00247-019-04535-w
[87]	Bjørnerud A, Vatnehol SAS, Larsson C, et al. (2017) Signal enhancement of the dentate nucleus at unenhanced MR imaging after very high cumulative doses of the macrocyclic gadolinium-based contrast agent gadobutrol: an observational study. Radiology 285: 434-444. doi: 10.1148/radiol.2017170391
[88]	Splendiani A, Perri M, Marsecano C, et al. (2018) Effects of serial macrocyclic based contrast materials gadoterate meglumine and gadobutrol administrations on gadolinium related dentate nuclei signal increases in unenhanced t1-weighted brain: a retrospective study in 158 multiple sclerosis (MS) patients. Radiol Med 123: 125-134. doi: 10.1007/s11547-017-0816-9
[89]	Stojanov DA, Aracki-Trenkic A, Vojinovic S, et al. (2016) Increasing signal intensity within the dentate nucleus and globus pallidus on unenhanced T1W magnetic resonance images in patients with relapsing remitting multiple sclerosis: Correlation with cumulative dose of a macrocyclic gadolinium-based contrast agent, gadobutrol. Eur Radiol 26: 807-815. doi: 10.1007/s00330-015-3879-9
[90]	Tedeschi E, Palma G, Canna A, et al. (2016) In vivo dentate nucleus MRI relaxometry correlates with previous administration of gadolinium-based contrast agents. Eur Radiol 26: 4577-4584. doi: 10.1007/s00330-016-4245-2
[91]	Lattanzio SM, Imbesi F (2020) Fibromyalgia associated with repeated gadolinium contrast-enhanced MRI examinations. Radiol Case Rep 15: 534-541. doi: 10.1016/j.radcr.2020.02.002
[92]	Roberts DR, Welsh CA, LeBel DP, et al. (2017) Distribution map of gadolinium deposition within the cerebellum following GBCA administration. Neurology 88: 1206-1208. doi: 10.1212/WNL.0000000000003735
[93]	Gibby WA, Gibby KA, Gibby WA (2004) Comparison of Gd-DTPA-BMA (Omniscan) versus Gd-HPDO3A (ProHance) retention in human bone tissue by inductively coupled plasma atomic emission spectroscopy. Invest Radiol 39: 138-142. doi: 10.1097/01.rli.0000112789.57341.01
[94]	White GW, Gibby WA, Tweedle MF (2006) Comparison of Gd(DTPA-BMA)(Omniscan) versus Gd(HPDO3A)(ProHance) relative to gadolinium retention in human bone tissue by inductively coupled mass spectroscopy. Invest Radiol 41: 272-278. doi: 10.1097/01.rli.0000186569.32408.95
[95]	Darrah TH, Prutsman-Pfeiffer JJ, Poreda RJ, et al. (2009) Incorporation of excess gadolinium into human bone from medical contrast agents. Metallomics 1: 479-488. doi: 10.1039/b905145g
[96]	Murata N, Gonzalez-Cuyar LF, Murata K, et al. (2016) Macrocyclic and other non–group 1 gadolinium contrast agents deposit low levels of gadolinium in brain and bone tissue: Preliminary results from 9 patients with normal renal function. Invest Radiol 51: 447-53. doi: 10.1097/RLI.0000000000000252
[97]	Lord ML, Chettle DR, Gräfe JL, et al. (2018) Observed deposition of gadolinium in bone using a new noninvasive in vivo biomedical device: Results of a small pilot feasibility study. Radiology 287: 96-103. doi: 10.1148/radiol.2017171161
[98]	Turyanskaya A, Rauwol M, Pichler V, et al. (2020) Detection and imaging of gadolinium accumulation inhuman bone tissue by micro- and submicro-XRF. Sci Rep 10: 6301. doi: 10.1038/s41598-020-63325-9
[99]	Vidaud C, Bourgeois D, Meyer D (2012) Bone as target organ for metals: the case of f-elements. Chem Res Toxicol 25: 1161-1175. doi: 10.1021/tx300064m
[100]	Gräfe JL, McNeill FE (2018) Measurement of gadolinium retention: current status and review from an applied radiation physics perspective. Physiol Meas 39: 06TR01. doi: 10.1088/1361-6579/aacc16
[101]	Hasegawa M, Duncan BR, Marshall DA, et al. (2020) Human hair as a possible surrogate marker of retained tissue gadolinium. A pilot autopsy study correlating gadolinium concentrations in hair with brain and other tissues among decedents who received gadolinium-based contrast agents. Invest Radiol 55: 636-642. doi: 10.1097/RLI.0000000000000681
[102]	Saussereau E, Lacroix C, Cattaneo A, et al. (2008) Hair and fingernail gadolinium ICP-MS contents in an overdose case associated with nephrogenic systemic fibrosis. Forensic Sci Int 176: 54-57. doi: 10.1016/j.forsciint.2007.06.026
[103]	US Food and Drug Administration, 5-18, 2015 Available from: https://www.fda.gov/drugs/drug-safety-and-availability/fda-drug-safety-communication-fda-evaluating-risk-brain-deposits-repeated-use-gadolinium-based.
[104]	EMA/625317/2017. EMA's final opinion confirms restrictions on use of linear gadolinium agents in body scans Available at: http://www.ema.europa.eu/docs/en _ GB/document _ library/ Referrals _ document/gadolinium _ contrast _ agents _ 31/ European _ Commission _ final _ decision/WC500240575.pdf.
[105]	Lancelot E, Desché P (2020) Gadolinium retention as a safety signal: experience of a manufacturer. Invest Radiol 55: 20-24. doi: 10.1097/RLI.0000000000000605
[106]	PMDA, Revision of Precautions, Gadodiamide hydrate Meglumine gadopentetate, 2017 Available from: http://www.pmda.go.jp/files/000221377.pdf.
[107]	PMDA, Revision of Precautions, Gadoxetate sodium, Gadoteridol, Meglumine gadoterate, Gadobutrol, 2017 Available from: http://www.pmda.go.jp/files/000221376.pdf.
[108]	Kanda T, Nakai Y, Hagiwara A, et al. (2017) Distribution and chemical forms of gadolinium in the brain: a review. Br J Radiol 90: 20170115. doi: 10.1259/bjr.20170115
[109]	Bracco Diagnostics Bayer, Guerbet GE Healthcare Important drug warning for all gadolinium-based contrast agents [dear health care provider letter] (2018) .Available from: https://www.guerbet.com/media/uh4h4kon/dhcp-letter-05-02-2018-signed.pdf.
[110]	Harvey HB, Gowda V, Cheng G (2019) Gadolinium deposition disease: a new risk management threat. J Am Coll Radiol 17: 546-550. doi: 10.1016/j.jacr.2019.11.009
[111]	Semelka RC, Commander CW, Jay M, et al. (2016) Presumed gadolinium toxicity in subjects with normal renal function a report of 4 cases. Invest Radiol 51: 661-665. doi: 10.1097/RLI.0000000000000318
[112]	Semelka RC, Ramalho M, Jay M (2016) Summary of special issue on gadolinium bioeffects and toxicity with a look to the future. Magn Reson Imaging 34: 1399-1401. doi: 10.1016/j.mri.2016.09.002
[113]	US Food and Drug AdministrationMedical Imaging Drugs Advisory Committee Meeting, FDA briefing document: Gadolinium retention after gadolinium-based contrast magnetic resonance imaging in patients with normal renal function, 27–28. (2017) .
[114]	Burke LMB, Ramalho M, AlObaidy M, et al. (2016) Self-reported gadolinium toxicity: A survey of patients with chronic symptoms. Magn Reson Imaging 34: 1078-1080. doi: 10.1016/j.mri.2016.05.005
[115]	Semelka RC, Ramalho J, Vakharia A, et al. (2016) Gadolinium deposition disease: initial description of adisease that has been around for a while: a family of disorders. Magn Res Imaging 34: 1383-1390. doi: 10.1016/j.mri.2016.07.016
[116]	Roberts DR, Lindhorst SM, Welsh CT, et al. (2016) High levels of gadolinium deposition in the skin of a patient with normal renal function. Invest Radiol 51: 280-289. doi: 10.1097/RLI.0000000000000266
[117]	Barbieri S, Schroeder C, Froehlich JM, et al. (2016) High signal intensity in dentate nucleus and globus pallidus on unenhanced T1-weighted MR images in three patients with impaired renal function and vascular calcification. Contrast Media Mol Imaging 11: 245-250. doi: 10.1002/cmmi.1683
[118]	Swaminathan S (2016) Gadolinium toxicity: iron and ferroportin as central targets. Magnet Reson Imaging 34: 1373-1376. doi: 10.1016/j.mri.2016.08.016
[119]	Di Gregorio ED, Furlan C, Atlante S, et al. (2020) Gadolinium retention in erithrocytes and leukocytes from human and murine blood upon treatment with gadolinium-based contrast agents for magnetic resonance imaging. Invest Radiol 55: 30-37. doi: 10.1097/RLI.0000000000000608
[120]	Di Gregorio E, Ferrauto G, Furlan C, et al. (2018) The issue of gadolinium retained in tissue. Invest Radiol 53: 167-172. doi: 10.1097/RLI.0000000000000423
[121]	Kartamihardja AAP, Hanaoka H, Andriana P, et al. (2019) Quantitative analysis of Gd in the protein content of the brain following single injection of gadolinium-based contrast agents (GBCAs) by size exclusion chromatography. Br J Radiol 92: 20190062. doi: 10.1259/bjr.20190062
[122]	Newton BB, Jimenez SA (2009) Mechanism of NSF: New evidence challenging the prevailing theory. J Magn Reson Imaging 30: 1277-1283. doi: 10.1002/jmri.21980
[123]	Taoka T, Jost G, Frenzel T, et al. (2018) Impact of the glymphatic system on the kinetic and distribution of gadodiamide in rat brain. Invest Radiol 53: 529-534. doi: 10.1097/RLI.0000000000000473
[124]	Nehra AK, McDonald RJ, Bluhm AM, et al. (2018) Accumulation of gadolinium in human cerebrospinal fluid after gadobutrol-enhanced MR imaging: a prospective observational cohort study. Radiology 288: 416-423. doi: 10.1148/radiol.2018171105
[125]	McDonald RJ, Levine D, Weinreb J, et al. (2018) Gadolinium retention: A research roadmap from the 2018 NIH/ACR/RSNA workshop on gadolinium chelates. Radiology 289: 517-534. doi: 10.1148/radiol.2018181151
[126]	Le Fur M, Caravan P (2019) The biological fate of gadolinium-based MRI contrast agents: a call to action for bioinorganic chemists. Metallomics 11: 240-254. doi: 10.1039/C8MT00302E
[127]	Tweedle MF (2016) Gadolinium deposition: Is it chelated or dissociated gadolinium? How can we tell? Magn Res Imaging 34: 1377-1382. doi: 10.1016/j.mri.2016.09.003
[128]	Kiviniemi A, Gardberg M, Ek P, et al. (2019) Gadolinium retention in gliomas and adjacent normal brain tissue: association with tumor contrast enhancement and linear/macrocyclic agents. Neuroradiology 61: 535-544. doi: 10.1007/s00234-019-02172-6
[129]	Kanda T, Fukusato T, Matsuda M, et al. (2015) Gadolinium-based contrast agent accumulates in the brain even in subjects without severe renal dysfunction: evaluation of autopsy brain specimens with inductively coupled plasma mass spectroscopy. Radiology 276: 228-232. doi: 10.1148/radiol.2015142690
[130]	Herculano-Houzel S (2009) The human brain in numbers: a linearly scaled-up primate brain. Front Hum Neurosci 3: 31. doi: 10.3389/neuro.09.031.2009
[131]	Popescu BFG, Robinson CA, Rajput A, et al. (2009) Iron, copper, and zinc distribution of the cerebellum. Cerebellum 8: 74-79. doi: 10.1007/s12311-008-0091-3
[132]	Kromrey ML, Liedtke KR, Ittermann T, et al. (2017) Intravenous injection of gadobutrol in an epidemiological study group did not lead to a difference in relative signal intensities of certain brain structures after 5years. Eur Radiol 27: 772-777. doi: 10.1007/s00330-016-4418-z
[133]	Staks T, Schuhmann-Giampieri G, Frenzel T, et al. (1994) Pharmacokinetics, dose proportionality and tolerability of gadobutrol after single intravenous injection in healthy volunteers. Invest Radiol 29: 709-715. doi: 10.1097/00004424-199407000-00008
[134]	Gutierrez JE, Rosenberg M, Duhaney M, et al. (2015) Phase 3 efficacy and safety trial of gadobutrol, a 1.0 molar macrocyclic MR imaging contrast agent, in patients referred for contrast-enhanced MR imagingof the central nervous system. J Magn Reson Imaging 41: 788-796. doi: 10.1002/jmri.24583
[135]	Kuwatsuru R, Takahashi S, Umeoka S, et al. (2015) A multicenter, randomized, controlled, single-blind comparison phase III study to determine the efficacy and safety of gadobutrol 1.0 M versus gadopentetate dimeglumine following single injection in patients referred for contrast-enhanced MRI of the body regions or extremities. J Magn Reson Imaging 41: 404-413. doi: 10.1002/jmri.24566
[136]	Liang Z, Ma L, Wang D, et al. (2012) Efficacy and safety of gadobutrol (1.0 M) versus gadopentetate dimeglumine (0.5 M) for enhanced MRI of CNS lesions: A phase III, multicenter, single-blind, randomized study in Chinese patients. Mag Res Insights 5: MRI-S9348.
[137]	Naito S, Tazaki H, Okamoto T, et al. (2017) Comparison of nephrotoxicity between two gadolinium-contrasts, gadodiamide and gadopentetate in patients with mildly diminished renal failure. J Toxicol Sci 42: 379-384. doi: 10.2131/jts.42.379
[138]	Semelka RC, Hernandes MA, Stallings CG, et al. (2013) Objective evaluation of acute adverse events andimage quality of gadolinium-based contrast agents (gadobutrol and gadobenate dimeglumine) by blinded evaluation. Pilot study. Magn Reson Imaging 31: 96-101. doi: 10.1016/j.mri.2012.06.025
[139]	Tanaka A, Masumoto T, Yamada H, et al. (2016) A Japanese, multicenter, open-label, phase 3 study to investigate the safety and efficacy of gadobutrol for contrast-enhanced MR imaging of the central nervous system. Magn Reson Med Sci 15: 227-236. doi: 10.2463/mrms.mp.2015-0083
[140]	Zech CJ, Schwenke C, Endrikat J (2019) Diagnostic efficacy and safety of gadoxetate disodium vs gadobenate dimeglumine in patients with known or suspected focal liver lesions: Results of a clinical phase III study. Magn Reson Insight 12: 1178623X19827976.
[141]	Tweedle MF, Wedeking P, Kumar K (1995) Biodistribution of radiolabeled, formulated gadopentetate, gadoteridol, gadoterate, and gadodiamide in mice and rats. Invest Radiol 30: 372-380. doi: 10.1097/00004424-199506000-00008
[142]	Rocklage SM, Worah D, Kim SH (1991) Metal ion release from paramagnetic chelates: what is tolerable? Magn Reson Med 22: 216-221. doi: 10.1002/mrm.1910220211
[143]	Khairinisa MA, Takatsuru Y, Amano I, et al. (2018) The effect of perinatal gadolinium-based contrast agents. Invest Radiol 53: 110-118. doi: 10.1097/RLI.0000000000000417
[144]	Ray JG, Vermeulen MJ, Bharatha A, et al. (2016) Association between MRI exposure during pregnancy and fetal and childhood outcomes. JAMA 316: 952-961. doi: 10.1001/jama.2016.12126
[145]	Runge VM, Kuehl TJ, Jackson CB, et al. (2005) Subchronic toxicity of the gadolinium chelates. Acad Radiol 12: S6-S9. doi: 10.1016/j.acra.2005.02.015
[146]	Alkhunizi SM, Fakhoury M, Abou-Kheir W, et al. (2020) Gadolinium retention in the central and peripheral nervous system: implications for pain, cognition, and neurogenesis. Radiology 297: 407-416. doi: 10.1148/radiol.2020192645
[147]	Wang S, Hesse B, Roman M, et al. (2019) Increased retention of gadolinium in the inflamed brain after repeated administration of gadopentetate dimeglumine. Invest Radiol 54: 617-626. doi: 10.1097/RLI.0000000000000571
[148]	Reimer P, Vosshenrich R (2008) Off-label use of contrast agents. Eur Radiol 18: 1096-1101. doi: 10.1007/s00330-008-0886-0
[149]	Essig M, Shiroishi MS, Nguyen TB, et al. (2013) Perfusion MRI: The five most frequently asked technical questions. Am J Roentgenol 200: 24-34. doi: 10.2214/AJR.12.9543
[150]	Wolansky LJ, Cadavid D, Punia V, et al. (2015) Hypophosphatemia is associated with the serial administration of triple-dose gadolinium to patients for brain MRI. J Neuroimaging 25: 379-383. doi: 10.1111/jon.12241
[151]	Essig M, Giesel E, Le-Huu M, et al. (2004) Perfusion MRI in CNS disease: current concepts. Neuroradiology 46: S201-S207. doi: 10.1007/s00234-004-1331-y
[152]	Lee JY, Park JE, Kim HS, et al. (2017) Up to 52 administrations of macrocyclic ionic MR contrast agent are not associated with intracranial gadolinium deposition: multifactorial analysis in 385 patients. PloS One 12: e0183916. doi: 10.1371/journal.pone.0183916
[153]	Ng KH, Ahmad AC, Nizam M, et al.Magnetic resonance imaging: Health effects and safety, Proceedings of the international conference on non-ionizing radiation at UNITEN, Electromagnetic Fields and our Health. (2003) .
[154]	Cho S, Lee Y, Choi YJ, et al. (2014) Enhanced cytotoxic and genotoxic effects of gadolinium following ELF-EMF irradiation in human lymphocytes. Drug Chem Toxicol 37: 440-447. doi: 10.3109/01480545.2013.879662
[155]	Sadiq S, Ghazala Z, Chowdhury A, et al. (2012) Metal toxicity at the synapse: presynaptic, postsynaptic, and long-term effects. J Toxicol 2012: 132671. doi: 10.1155/2012/132671
[156]	Food U S, Drug Administration, Safety Announcement 2017 Available from: https://www.fda.gov/media/109825/download.
[157]	Veiga M, Mattiazzi P, de Goisc JS, et al. (2020) Presence of other rare earth metals in gadolinium-based contrast agents. Talanta 216: 120940. doi: 10.1016/j.talanta.2020.120940
[158]	Parfrey P (2005) The clinical epidemiology of contrast-induced nephropathy. Cardiovasc Intervent Radiol 28: S3-S11. doi: 10.1007/s00270-005-0196-8
[159]	Karcaaltincaba M, Oguz B, Haliloglu M (2009) Current status of contrast-induced nephropathy and nephrogenic systemic fibrosis in children. Pediatr Radiol 39: S382-S384. doi: 10.1007/s00247-009-1236-3
[160]	Kulaksiz S, Bau M (2011) Anthropogenic gadolinium as a micro-contaminant in tap water used as drinking water in urban areas and megacities. Appl Geochem 26: 1877-1885. doi: 10.1016/j.apgeochem.2011.06.011
[161]	Hatje V, Bruland KW, Flegal AR (2016) Increases in anthropogenic gadolinium anomalies and rare earth element concentrations in San Francisco bay over a 20 year record. Environ Sci Technol 50: 4159-4168. doi: 10.1021/acs.est.5b04322
[162]	Rabiet M, Brissaud F, Seidel JL, et al. (2009) Positive gadolinium anomalies in wastewater treatment plant effluents and aquatic environment in the Hérault watershed (South France). Chemosphere 75: 1057-1064. doi: 10.1016/j.chemosphere.2009.01.036
[163]	Chen Y, Cao XD, Lu Y, et al. (2000) Effects of rare earth metal ions and their EDTA complexes on antioxidant enzymes of fish liver. B Environ Contam Tox 65: 357-365. doi: 10.1007/s001280000136
[164]	Henriques B, Coppola F, Monteiro R, et al. (2019) Toxicological assessment of anthropogenic gadolinium in seawater: Biochemical effects in mussels mytilus galloprovincialis. Sci Total Environ 664: 626-634. doi: 10.1016/j.scitotenv.2019.01.341
[165]	Hanana H, Turcotte P, André C, et al. (2017) Comparative study of the effects of gadolinium chloride and gadolinium-based magnetic resonance imaging contrast agent on freshwater mussel, dreissena polymorpha. Chemosphere 181: 197-207. doi: 10.1016/j.chemosphere.2017.04.073
[166]	Martino C, Costa C, Roccheria MC, et al. (2018) Gadolinium perturbs expression of skeletogenic genes, calcium uptake and larval development in phylogenetically distant sea urchin species. Aquat Toxicol 194: 57-66. doi: 10.1016/j.aquatox.2017.11.004
[167]	Schmidt K, Bau M, Merschel G, et al. (2019) Anthropogenic gadolinium in tap water and in tap-based beverages from fast-food franchises in six major cities in Germany. Sci Total Environ 687: 1401-1408. doi: 10.1016/j.scitotenv.2019.07.075

This article has been cited by:

1.	Muqrin A. Almuqrin, Ahmed M. Gemeay, M. M. Abd El-Raouf, Mutua Kilai, Ramy Aldallal, Eslam Hussam, Fathalla A. Rihan, A Flexible Extension of Reduced Kies Distribution: Properties, Inference, and Applications in Biology, 2022, 2022, 1099-0526, 1, 10.1155/2022/6078567
2.	Huda M. Alshanbari, Omalsad Hamood Odhah, Ehab M. Almetwally, Eslam Hussam, Mutua Kilai, Abdal-Aziz H. El-Bagoury, Sania Qureshi, Novel Type I Half Logistic Burr-Weibull Distribution: Application to COVID-19 Data, 2022, 2022, 1748-6718, 1, 10.1155/2022/1444859
3.	Muqrin A. Almuqrin, A new flexible distribution with applications to engineering data, 2023, 69, 11100168, 371, 10.1016/j.aej.2023.01.046
4.	M. E. Bakr, Abdulhakim A. Al-Babtain, Zafar Mahmood, R. A. Aldallal, Saima Khan Khosa, M. M. Abd El-Raouf, Eslam Hussam, Ahmed M. Gemeay, Statistical modelling for a new family of generalized distributions with real data applications, 2022, 19, 1551-0018, 8705, 10.3934/mbe.2022404
5.	Yinghui Zhou, Zubair Ahmad, Zahra Almaspoor, Faridoon Khan, Elsayed tag-Eldin, Zahoor Iqbal, Mahmoud El-Morshedy, On the implementation of a new version of the Weibull distribution and machine learning approach to model the COVID-19 data, 2022, 20, 1551-0018, 337, 10.3934/mbe.2023016
6.	Mahdi Rasekhi, Mohammad Mehdi Saber, G. G Hamedani, M. M.Abd El-Raouf, Ramy Aldallal, Ahmed M. Gemeay, Melike Kaplan, Approximate Maximum Likelihood Estimations for the Parameters of the Generalized Gudermannian Distribution and Its Characterizations, 2022, 2022, 2314-4785, 1, 10.1155/2022/4092576
7.	Najwan Alsadat, A new modified model with application to engineering data sets, 2023, 72, 11100168, 1, 10.1016/j.aej.2023.03.050
8.	Marwa M. Mohie El-Din, M.A. Meraou, Najwan Alsadat, Anoop Kumar, M.M. Abd El-Raouf, Mahmoud Mohamed Bahloul, Modeling insurance loss data using novel approach of moment exponential model: Inference, actuarial measures and application, 2024, 106, 11100168, 544, 10.1016/j.aej.2024.08.060
9.	M.M. Abd El-Raouf, Mohammed AbaOud, A novel extension of generalized Rayleigh model with engineering applications, 2023, 73, 11100168, 269, 10.1016/j.aej.2023.04.063
10.	Eslam Hussam, Mohamed A. Sabry, M. M. Abd El-Raouf, Ehab M. Almetwally, Fuzzy vs. Traditional Reliability Model for Inverse Weibull Distribution, 2023, 12, 2075-1680, 582, 10.3390/axioms12060582
11.	Muqrin A. Almuqrin, Bayesian and non-Bayesian inference for the compound Poisson log-normal model with application in finance, 2024, 90, 11100168, 24, 10.1016/j.aej.2024.01.031
12.	Hassan M. Aljohani, Statistical inference for a novel distribution using ranked set sampling with applications, 2024, 10, 24058440, e26893, 10.1016/j.heliyon.2024.e26893
13.	Mohammed AbaOud, Muqrin A. Almuqrin, The weighted inverse Weibull distribution: Heavy-tailed characteristics, Monte Carlo simulation with medical application, 2024, 102, 11100168, 99, 10.1016/j.aej.2024.05.056
14.	Aijaz Ahmad, Najwan Alsadat, Mintodê Nicodème Atchadé, S. Qurat ul Ain, Ahmed M. Gemeay, Mohammed Amine Meraou, Ehab M. Almetwally, Md. Moyazzem Hossain, Eslam Hussam, New hyperbolic sine-generator with an example of Rayleigh distribution: Simulation and data analysis in industry, 2023, 73, 11100168, 415, 10.1016/j.aej.2023.04.048
15.	Aijaz Ahmad, Fatimah M. Alghamdi, Afaq Ahmad, Olayan Albalawi, Abdullah A. Zaagan, Mohammed Zakarya, Ehab M. Almetwally, Getachew Tekle Mekiso, New Arctan-generator family of distributions with an example of Frechet distribution: Simulation and analysis to strength of glass and carbon fiber data, 2024, 100, 11100168, 42, 10.1016/j.aej.2024.05.021
16.	Ibrahim Alkhairy, A new approach of generalized Rayleigh distribution with analysis of asymmetric data sets, 2024, 100, 11100168, 1, 10.1016/j.aej.2024.04.070
17.	Mohd Irfan, A. K. Sharma, 2024, Chapter 22, 978-3-031-54546-7, 284, 10.1007/978-3-031-54547-4_22
18.	Meshayil M. Alsolmi, Fatimah A. Almulhim, Meraou Mohammed Amine, Hassan M. Aljohani, Amani Alrumayh, Fateh Belouadah, Statistical Analysis and Several Estimation Methods of New Alpha Power-Transformed Pareto Model with Applications in Insurance, 2024, 16, 2073-8994, 1367, 10.3390/sym16101367

Reader Comments

Your name:*

Email:*
© 2021 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)

通讯作者: 陈斌, bchen63@163.com

1.
沈阳化工大学材料科学与工程学院沈阳 110142

AIMS Biophysics

1.1 2.4

Metrics

Article views(9995) PDF downloads(483) Cited by(7)

Preview PDF

Download XML

Export Citation

Article outline

Show full outline

AIMS Biophysics

Toxicity associated with gadolinium-based contrast-enhanced examinations

Related Papers:

Abstract

1. Introduction

2. The WDEx distribution

3. Probabilistic and statistical properties

3.1. Linear representation

3.2. Moments and generating function

3.3. Mean deviation, bonferroni and Lorenz curves

3.4. Order statistics

4. Actuarial measures

4.1. VaR measure

4.2. TVaR measure

4.3. TV measure

4.4. TVP measure

4.5. ES measure

4.6. Numerical simulations for risk measures

5. Classical and Bayesian estimation

5.1. Maximum likelihood

5.2. Ordinary and weighted least-squares

5.3. Anderson-Darling and right-tail Anderson-Darling

5.4. Maximum product of spacings

5.5. Percentile estimation

5.6. Cramér–von mises

5.7. Bayesian estimation

5.8. TK-approximation for Bayesian estimates

6. Simulation results

7. Modeling an insurance data

8. Conclusions

Acknowledgments

Conflict of interest

References

This article has been cited by:

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Related pages

Tools

Export File

Citation

Format

Content

Catalog

Abstract

1. Introduction

2. The WDEx distribution

3. Probabilistic and statistical properties

3.1. Linear representation

3.2. Moments and generating function

3.3. Mean deviation, bonferroni and Lorenz curves

3.4. Order statistics

4. Actuarial measures

4.1. VaR measure

4.2. TVaR measure

4.3. TV measure

4.4. TVP measure

4.5. ES measure

4.6. Numerical simulations for risk measures

5. Classical and Bayesian estimation

5.1. Maximum likelihood

5.2. Ordinary and weighted least-squares

5.3. Anderson-Darling and right-tail Anderson-Darling

5.4. Maximum product of spacings

5.5. Percentile estimation

5.6. Cramér–von mises

5.7. Bayesian estimation

5.8. TK-approximation for Bayesian estimates

6. Simulation results

7. Modeling an insurance data

8. Conclusions

Acknowledgments

Conflict of interest

References