1.
Introduction
Bone, a complex tissue composed of different cell types, is fundamental for a lifelong maintenance of vital skeleton functions, being important as muscles support and protection of vital organs (i.e. brain), besides acting as a metabolic organ with major reserves of phosphate and calcium [1]. Bone tissue is continuously repairing and renewing in a process known as bone remodeling [2]. This mechanism is characterized by a continuous process of osteoclasts-mediated resorption and bone formation mediated by osteoblasts [3]. Osteoblasts and osteoclasts are key players in various processes, such as bone repair after fracture, bone formation in postnatal, and in the prevention of osteoporosis [4]–[6]. It is well-known that in the mentioned processes pro-inflammatory cytokines cause the activation of nitric oxide synthase (NOS) enzymes, evidencing the involvement of nitric oxide (NO) in this role [4].
NO is an endogenous signaling molecule that plays pivotal roles in biological medium. In 1992, NO was considered the molecule of the year by Science and, in 1998, the Nobel Prize of Medicine and Physiology was awarded to Robert F. Furchgott, Louis J. Ignarro and Ferid Murad for their path-breaking discoveries regarding the effects of NO on the cardiovascular system [7],[8]. NO is involved in the maintenance of blood pressure, in the host immune responses, and it is a key molecule in the central nervous system [9]. In bone, at low concentrations (pico-nano molar range), NO is able to promote proliferation, survival and differentiation of osteoblasts, whereas at high concentrations (micromolar range), NO can inhibit bone resorption/formation. Moreover, the administration of exogenous NO (NO donors) might find important applications regarding bone pathway.
Thus, this review presents the mechanisms of action of NO in bone tissue, and the potential benefits of the administration of NO donors for bone remodeling, fracture healing, and postmenstrual woman. Furthermore, a critical discussion is provided in order to highlight many unexplored roles of NO in bone tissue, which can represent important advances in the medical field.
2.
Nitric Oxide: synthesis and regulation
The free radical NO is a diatomic molecule found in mammalian cells. Due to its lipophilic behavior and small size, NO can easily diffuse in various cell membranes and tissues performing important roles in various biological processes, such as angiogenesis, vasodilation, cell communication, antioxidant, antitumor, and antimicrobial actions, in addition to tissue repair and regeneration, including skin, cartilage and bone tissues [10]–[14]. The in vivo NO formation occurs via the action of NOS, which catalyzes the oxidation of L-arginine to L-citrulline. This reaction can be inhibited by arginine substituted derivatives such as L-NG-monomethyl arginine (L-NMMA), L-arginine-methyl ester (L-NAME), and aminoguanidine [15],[16]. There are three NOS isoforms: neuronal nitric oxide synthase (nNOS or NOS-1), inducible nitric oxide synthase (iNOS or NOS-2), and endothelial nitric oxide synthase (eNOS or NOS-3) [15]–[17]. nNOS and eNOS are constitutive isoforms that produce low concentrations of NO for longer periods, whereas iNOS produces high NO concentrations for a short time [18],[19]. Besides, iNOS is activated by endotoxin and/or pro-inflammatory cytokines (ILs, TNF, and IFN-γ) [15].
The biological effects of NO are related to its concentration and local of production/generation. The minimum concentration of NO formation related to muscle relaxation is 10 nM [20] and, in general, low concentrations are related to cytoprotective effects [12],[21]. In contrast, high NO concentrations, 10–100 times higher, are related to toxic effects [12],[22],[23]. At high concentrations, NO reacts with superoxide anion (O2•−) leading to the formation of the harmful peroxynitrite (ONOO−). ONOO− is involved with cell death and apoptosis through several cellular mechanisms, including cell membrane rupture and inhibition of the generation of adenosine triphosphate [23],[24]. Many of NO physiological actions are driven by the activation of soluble guanylate cyclase (sGC). The binding of NO to the heme group of this enzyme causes a conformational change that increases its activity resulting in the formation of cyclic guanosine-3′,5′-monophosphate (GMPc) [15],[25].
2.1. NO donors
As a free radical in a biological environment, NO can be rapidly deactivated through reactions with oxygen and heme groups of proteins [26]. Different low molecular weight molecules act as NO donors/generators in the biological system, preserving NO bioactivity [27]–[30]. Depending on their chemical structure, NO donors can release NO through different types of mechanisms. S-nitrosothiols (RSNOs) act as spontaneous thermal and photochemical NO donors through the homolytic S-N bond cleavage and free NO release [22],[31],[32]. In addition, NO can be released by chemical reactions with acid, alkali, metal and thiol groups by organic nitrates, nitrites and syndnonimines [28]. For therapeutic uses, NO donors might have selectivity, allowing a sustained NO release at sub-toxic levels. The most commonly used NO donors are organic nitrates, diazeniodiolates (NONOates) and S-nitrosothiols (RSNOs) [27]–[29],[31]. Among them, RSNOs can mimic the endogenous generation of NO. Thiols (RSHs) are easily nitrosated in the presence of N2O3 or NO2− in acidic medium, generating RSNOs, which are significantly more stable than NO itself [31],[33]. Several important works have demonstrated the importance of using NO donors, including RSNOs, in different biomedical applications including the promotion and acceleration of wound healing and as a potent antibacterial agent [14],[34]. In this direction, the uses of NO donors might find important applications to reduce implant-associated infections and in the promotion of tissue regeneration in the orthopedic area, as described in the next sections.
3.
NO in homeostasis and pathologies of bone tissue
3.1. NO and bone tissue
In recent years, it has become evident that NO has a key role as a molecular messenger in bone tissue homeostasis and during bone pathologies [5],[15],[35],[36]. Bone tissue is mainly composed of osteoblast, osteoclast and osteocytes. These cell types have different morphologies and functions [15]. Osteoblast secretes extracellular matrix protein, allowing its differentiation into osteocyte [15],[36]. Osteocytes are long-lived and highly active cells that are embedded in the mineralized matrix of mature bone [15]. In contrast, osteoclasts are resorbed in the mineralized matrix in order to allow osteoblasts to create new bone matrix [15],[36].
All NOS isoforms have been identified in bone tissue and in isolated bone cells (osteoblast and osteoclast) by PCR (Polymerase Chain Reaction) and immunohistochemistry analyses [37]–[42]. Several studies show that eNOS is the predominantly expressed isoform in bone on constitutive bases. It is widely found in bone marrow mesenchymal cells (MSCs), osteoblasts, osteocytes and osteoclasts [40],[43]. nNOS mRNA expression has been detected in bone [37],[38], and investigations using bone cell cultures from mice with inactivation of the nNOS gene suggest that nNOS participates in the regulation of bone mass and bone turnover [44]. iNOS expression has been shown in fetal bone, however, it does not appear to be constitutively expressed in normal adult bone. iNOS expression may be induced by proinflammatory cytokines and/or endotoxins in osteoblasts, bone marrow cells, and in osteoclasts and preosteoclastic cells [2]. In this direction, the effects of NO on the physiology and pathophysiology of bone tissue are described below.
3.2. Effects of NO on bone formation and resorption
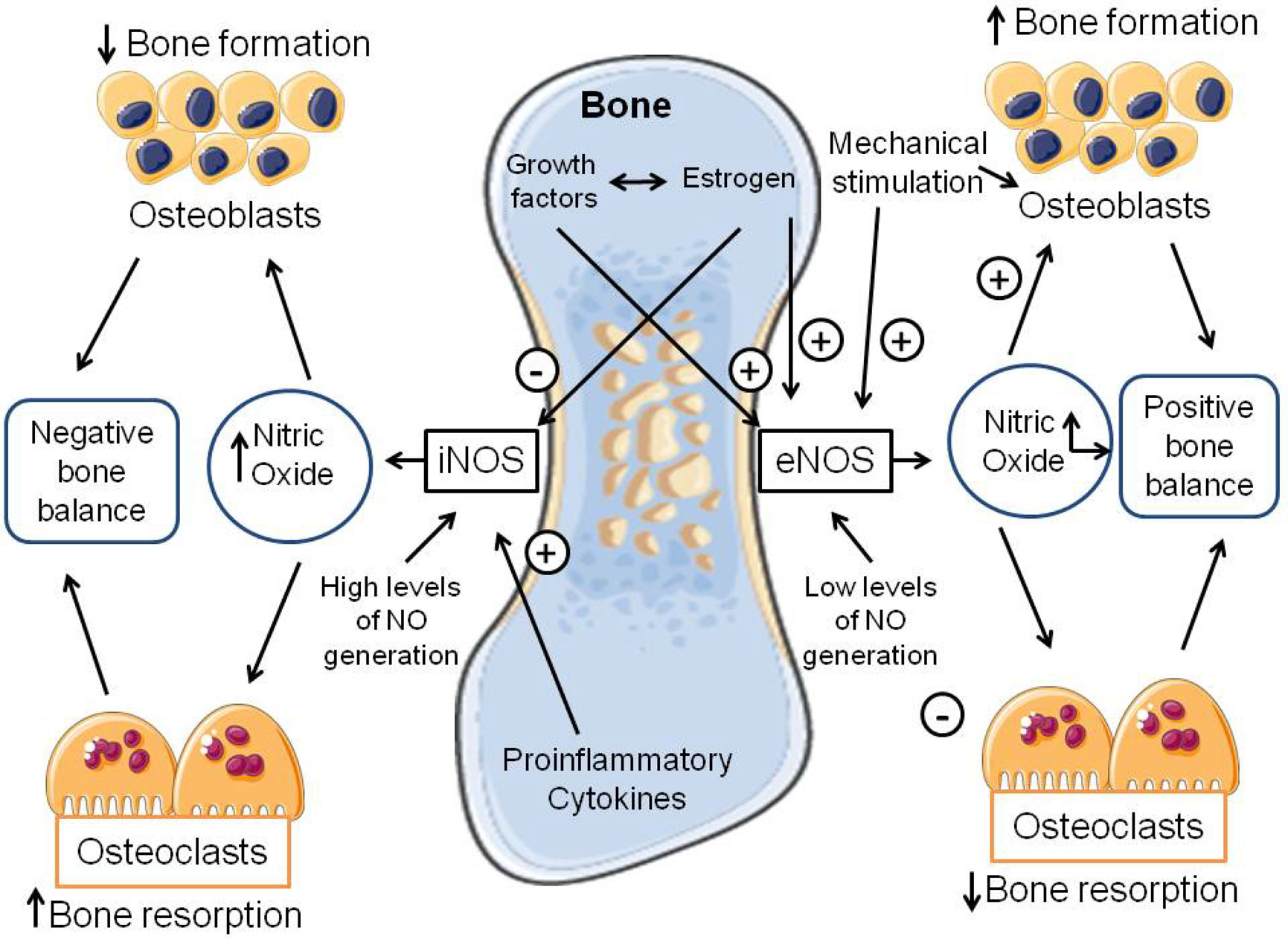
NO appears to be a potent regulator of bone metabolism [45]–[48]. Indeed, bone cells produce NO in response to various stimuli including proinflammatory cytokines, mechanical stimulation, estrogen, thyroid hormone and ageing [5],[15],[49]. Figure 1 illustrates the interactions of different factors and NO in bone homeostasis and metabolism. Under inflammatory conditions, iNOS activity is assigned as the main source of NO within the bone. NO derived from this pathway potentiates cytokine and inflammation inducing bone loss [2]. In contrast, eNOS appears to be the isoform primarily expressed in the basal state and plays a key role in regulating bone formation [47].
Constitutive NO production in osteoclasts seems to be essential for their normal function, since NOS inhibitors inhibit the activity and mobility of isolated osteoclasts, thus hindering the natural process of bone remodeling [2],[47]. However, strong evidence suggests that NO has a biphasic effect on osteoclastic activity. At low concentrations, NO potentiates IL-1-induced osteoclastic bone resorption, whereas at high concentrations, NO inhibits osteoclastic formation and activity, causing apoptosis of osteoclastic progenitors [2]. Observations from several in vitro studies show that high NO concentrations may be responsible for the inhibitory effect of IFNγ on bone resorption stimulated by IL-1, IL-6 and TNFα [50],[51] and that these pro-resorptive cytokines act by producing large amounts of prostaglandins E2 (PGE2), which is the mediator of this effect. Given these facts, it has been proposed that NO and PGE2 modulate cytokine-induced bone resorption. This modulation depends on the balance between the amount of NO and PGE2 produced by inducing different combinations of proinflammatory cytokines [51].
NO seems to have a biphasic effect on osteoblastic activity. In vitro studies have shown that a small amount of NO constitutively produced by osteoblasts, or slowly released by NO donors, can act as a stimulator of osteoblast growth and differentiation [53]. While high NO concentration has a potent inhibitory effect on osteoblastic growth and differentiation, which may be partly due to a pro-apoptotic effect of NO [54]. Investigations into the role of NO as a modulator of human osteoblast metabolism in vitro have shown that NO released by 3-morpholine sidnonimine (SIN-1) has a dose-dependent inhibitory effect on osteoblast proliferation. In addition, inhibition of NOS by N-Nitro-L-arginine (L-NNA) in these cell cultures increased osteoblastic proliferation [47].
In addition to NO concentration, production pathways might play important effects on bone cell function. Studies using mice with inactivation of the NOS gene show that NO synthesized via eNOS is important for normal osteoblastic function, anabolic bone response to exogenous estrogen, and bone response to mechanical loads and shear stress (Figure 1) [47],[55],[56]. In the presence of estrogen, only the eNOS isoform is expressed by bone cells. In contrast, NO produced via iNOS appears to regulate the effects of proinflammatory cytokines on bone and is essential for their stimulatory effects on bone resorption both in vitro and in vivo [2],[48],[57],[58]. In vitro, estrogen blocks NO synthesis via iNOS and stimulates increased mRNA levels and eNOS activity. Moreover, in ovariectomized mice with inactivation of the iNOS gene, a significant decrease in bone loss and bone turnover induced by estrogen deficiency is observed [47],[59]. The effects of NO produced via nNOS on bone metabolism appear to be of some importance, however, it requires further investigations [44].
Some studies have shown that the NO synthesized in response to mechanical stimulation, or treatment with estrogen and thyroid hormones, stimulates cGMP synthesis, resulting in cGMP-dependent protein kinases (PKGs) activation. PKG, in turn, regulates all stages of osteoblastic cells, promoting proliferation and differentiation, and inhibiting apoptosis [15],[54]. Although it was initially believed that the inhibitory effect of NO on osteoclastic bone resorption was mediated by an independent mechanism of GMPc, recent evidence suggests that GMPc dependent pathways may be involved [15],[54]. Other studies also show that a soluble factor named osteoprotegerin (OPG) and a member of the TNF-α receptor family named RANK and its ligand (RANKL), produced by stromal cells osteogenic lesions, play a fundamental role in the osteoclastogenesis regulation mechanism. RANKL is involved in the differentiation and function of osteoclast precursor cells, while OPG acts as a bait receptor to block the interaction of RANKL with its functional receptor RANK, thereby inhibiting osteoclastogenesis [2],[15],[59],[60].
Bone marrow mesenchymal stem cells (MSCs) have the capacity to differentiate into multiple cell lineages and are a major source of osteoblast precursors, which can be recruited during the normal course of bone remodeling or injury [61]. MSCs possess two fundamental characteristics: the ability to proliferate and the capacity to differentiate. The reported effects of NO in MCSs functions also depend on its concentrations [62]. Picomolar to nanomolar NO concentrations usually have beneficial effects on MSCs, such as the increase of cell survival and proliferation [62]–[64]. NO donors and eNOS can be sources of lower NO levels, which downstream cytoplasmatic, mitochondrial, and nuclear signaling. On the other hand, micromolar NO levels produced by iNOS, NO donors or NOS transfection can lead to opposite effects, i.e. the promotion of the interruption of the cell cycle, apoptosis and senescence [65]. An investigation of osteogenic differentiation of MSCs in the presence and absence of NOS inhibitor was performed in osteopenic female rats subjected to physical activity [63]. It was demonstrated that NOS inhibition by L-NAME reduces the osteogenic differentiation of MSCs from normal rats, indicating that NO is an important factor in the induction of mesenchymal stem cell differentiation into osteoprogenitor cells [63].
3.3. The role of NO in bone disease
As NO is a key mediator of bone healing, its unbalance is related to bone diseases. NO stimulates several molecules (cGMP, PKG, among others) promoting cell differentiation, proliferation and inhibition of apoptosis. Therefore, NO has a great potential as a therapeutic target for the treatment of bone diseases [15].
Menopause, hypothyroidism and ageing are related to bone formation issues, for instance, women in menopause have high risk for prevalence of osteoporosis [66]. Patients with hypothyroidism show low bone turnover that might impair bone formation [15]. Aging is strongly associated with sarcopenia (muscle mass loss) and osteoporosis [5]. All these conditions are also associated with low concentration of NO metabolites [15]. In human studies, plasma concentration of NO metabolites (nitrite and nitrate) positively correlated with estrogen levels in women [15]. Their levels are decreased in post-menopaused women and increased after estrogen supplementation [49].
Osteoporosis is attributed to an imbalance between bone formation and resorption, followed by bone mass loss and microarchitectural deterioration, leading to increased bone fragility and fracture risk [66],[67]. Several studies have shown that NOS inhibitors have abolished the protective effect of estrogen on bone ovariectomized rats, whereas treatments with NO donors were almost effective as estrogen in prevention of ovariectomy-induced bone loss [47],[57],[68],[69]. The treatment with thyroid hormone in patients with hypothyroidism induces NO synthesis by increasing calcium, which is a cofactor of NO synthesis in vivo [15]. Pandya et al. demonstrated that arginase activity was significantly higher in aged mice compared to new ones. This increase of arginase may alter L-arginine mechanism of NO synthesis via NOS. The aged mice also show decreased cell survival and increased apoptosis [5]. In a similar approach, it has been suggested that the control of the levels of L-arginine may be a new effective strategy for osteoporosis prevention. In this sense, Visser et al. showed that supplementation with this amino acid increases the basal release of NO by endothelial cells and may inhibit bone resorption and stimulate bone formation by activation of the GH- IGF-I axis [70]. Fiore et al. suggest that the administration of L-arginine prevents bone loss caused by cyclosporin A (a drug implicated in the pathogenesis of post-transplant bone diseases) [71]. Taken together, these results indicate that both anabolic effects of estrogen and anti-bone resorption may be partly mediated by NO.
Therefore, NO is involved in several phases of bone healing and growth. It is virtually produced by all cells in bone tissue with significant relevance for its homeostasis. The decrease in the production of NO correlates with several pathologies, such as osteoporosis. In the cases of impairment of endogenous NO production, the administration of exogenous NO donors/generators able to release therapeutic amounts of NO has promising potential in bone tissue applications, as described in the next sections.
3.4. The importance of NO in bone tissue regeneration
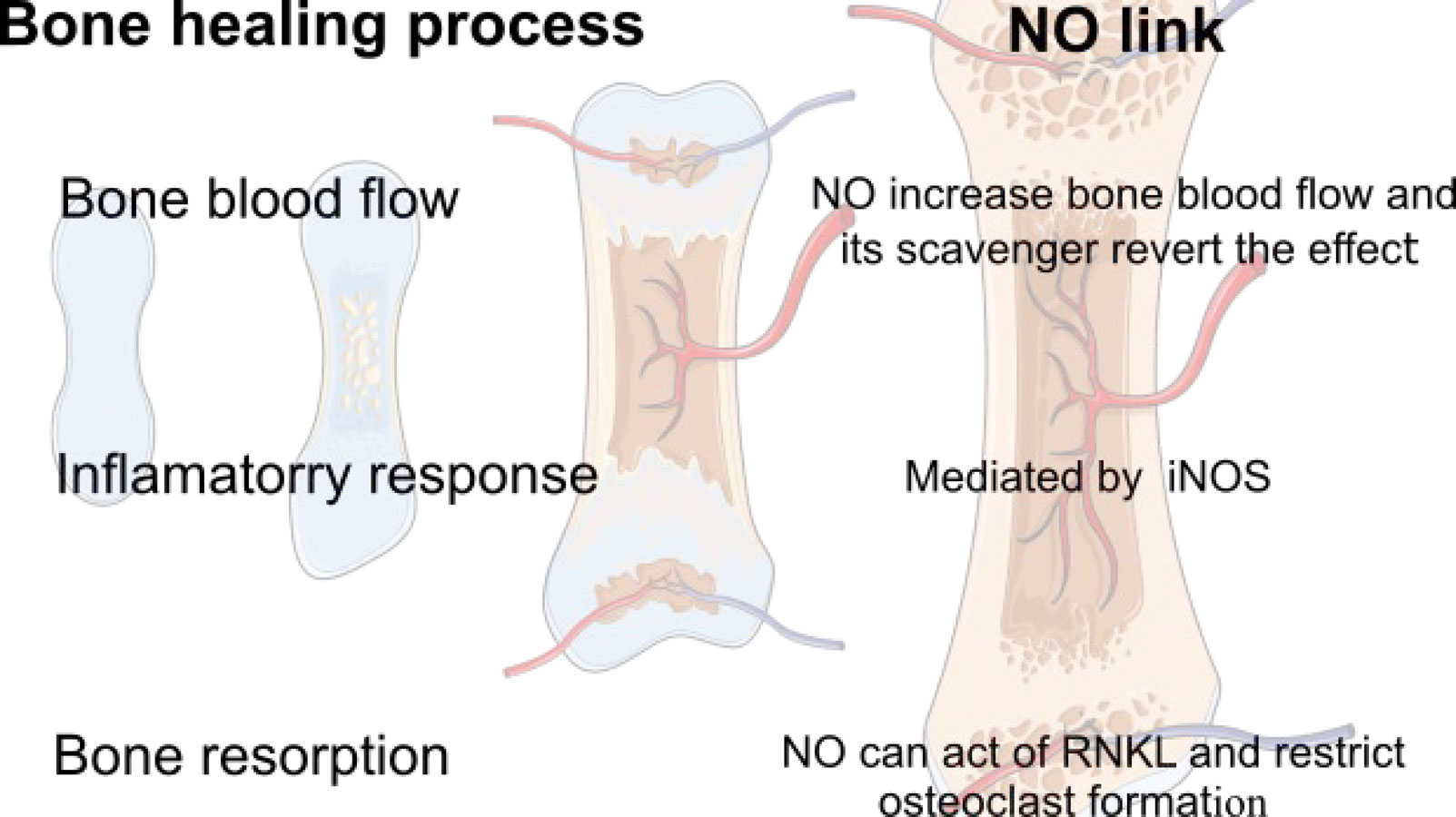
The first step of bone healing is the increase of bone blood flow (BBF) immediately after bone injurie or mechanical stimuli for growth [36]. BBF supplies nutrients and oxygen to bone tissues according to their metabolic and mechanical needs. The BBF mechanism and regulation are still not completed elucidated, however human and animal experiments suggest that NO is an important player [34]. Heinonem et al. measured blood flow in healthy volunteers in rest and exercising with NOS scavenger (provided by L-NMMA administration). At rest, the BBF was reduced to 0.7 ± 0.3 mL 100 g−1 min−1 in the group treated with NO scavenger in comparison with 1.1 ± 0.4 mL 100 g−1 min−1 for the control group. With the volunteer's groups submitted to exercise, the BBF also reduced to 5.5 ± 1.4 mL g−1 min−1 for the group treated with NO scavenger in comparison with BBF levels of 6.3 ± 1.5 mL mL g−1 min−1 for control group. Thus, as expected, BBF is higher for volunteers under exercise compared with rest condition, and the NO scavenger decreased BBF levels for volunteers under exercise and rest conditions [34]. With the increase of BBF, there is an inflammatory process with several mediators such as IL-1, IL-6, TNF-α and iNOS (Figure 2) [39],[72]. This inflammation pathway is also related to the suppression of bone formation causing osteoblast apoptosis. Therefore, this inflammatory process cannot be prolonged, due to the risk of osteoporosis development. Indeed, NO has been used as a biomarker of bone remodeling and osteoblast activities [73],[74].
Following the increase of BBF, the next phase of bone tissue regeneration consists in the recruitment of mesenchymal stem cells associated with myostatin gene GDF-8 and with the removal and re-absorption of soft and hard tissue debris by macrophage and osteoclast [5]. In endochondral ossification, the recruited mesenchymal stem cells are differentiate to chondrocytes (by chondrogenesis process) and this process is triggered by ischemia and other molecular messengers (IGF-I, PTHrP, IHH and HIF-Iα). The chondrogenesis process produces cartilaginous matrix that is substituted by osteoblasts producing mineralized matrix that will replace the bone (Figure 2) [15].
Overall, the healing process greatly depends on an optimum balance between bone resorption and osteoblasts formation. An unbalance of higher bone resorption can decrease bone formation causing osteoporosis and increasing the risk of bone injuries. Osteoclast formation is regulated by RANKL, in which NOS can restrict its formation (Figure 2). Therefore, new therapeutic approaches capable to increase NO independence of pro-inflammatory cytokines can be a promising approach in the treatment of bone diseases.
4.
Selected examples of NO releasing/generating systems on bone tissue regeneration
As stated before, NO plays key roles in bone physiology and pathophysiology. In this context, the delivery of NO to bone in a controlled and targeted manner may result in new and effective treatments for fracture repair and conditions caused by imbalances in bone turnover. Different classes of NO donors have been used for bone tissue regeneration [75], in addition to scaffolds that release NO, including bioactive glass and rubber [76]–[78]. This section presents and discusses relevant publications based on the progress in the design of NO-releasing/generating approaches for bone tissue therapy, as summarized in Table 1.
4.1. Effects of NO in inflammatory periodontal disease
Inflammatory periodontal disease represents the most important cause of tooth loss in adults [79]–[83]. The periodontal ligament (PDL) is a soft connective tissue located between the cementum that covers the root of the tooth and the bone that forms the alveolar wall. It consists of cells and an extracellular compartment of fibers and amorphous fundamental substance. The PDL cells include osteoblasts, osteoclasts, fibroblasts, undifferentiated mesenchymal cells and cementoblasts [81]. It is a fabric particularly well-suited connective system for its primary function, which is to support the tooth at the same time as allowing it to withstand the considerable forces of chew. PDL still acts as an indispensable sensory receptor for proper positioning of the maxilla and mandible during normal function. The PDL thickness progressively decreases with age. PDL cells have demonstrated stem cell properties in multi tissue differentiation potential [81]. Recent studies have reported an increased NO production during osteogenic differentiation in human PDL cells. Lee et al. investigated the osteogenic potential of the NO donor sodium nitroprusside (SNP) in human PDL cells. In addition, the authors examined the heme oxygenase isoform 1 pathways (HO-1) involved in the expression of osteogenic differentiation markers as alkaline phosphatase (ALP), osteonectin (ON), osteocalcin (OC) and bone sialoprotein (BSP). In vitro results showed that the release of NO by SNP decreased cell proliferation and promoted osteoblastic differentiation in PDL cells as demonstrated by MTT assay measurements, ALP activity and Western Blot Analysis [80].
Similarly, the effect of NO donor (isosorbide) was reported in an experimental periodontitis model in rats [79]. The histopathological assays performed in this study showed that a localized administration of exogenous NO reduced the inflammatory cell infiltration, cementum resorption, and alveolar bone loss in an in vivo periodontitis model. Martins et al. and Menezes et al. presented similar results in an approach that involved local application of S-nitrosoglutathione (GSNO) coupled with hydroxypropylmethylcellulose (HPMC) [83] or polyvinylpyrrolidone (PVP) [82] in an experimental periodontal disease (EDP) model. The treatment with HPMC/GSNO and PVP/GSNO reduced alveolar bone loss, oxidative stress and the levels of pro-inflammatory cytokine (TNF-α and IL-1β) and elevated bone ALP, inducing bone neoformation [82],[83].
4.2. NO and bone remodeling
As NO is known as a mediator of cytokine effect regarding bone tissue remodeling, it is essential to investigate the effects resultant of the stimulation of endogenous NO release, and the effects from the administration of NO-donors [84]. It has been reported that NO-release from both primary fetal osteoblast-like cells and osteosarcoma cells is only stimulated with the combination of three pro-inflammatory cytokines (IL-1β, TNF-α, IFN-γ), indicating an important role of NO in the process of bone remodeling [84]. Interesting results were also obtained for exogenous NO donor, administrated via SNP. SNP showed positive effects at low concentrations (3–30 µmol L−1), increasing more than twice the number of osteoclast cells, although, at high concentrations (100 µmol L−1) the opposite effect was observed, evidencing a dose-dependent characteristic of NO in bone remodeling [84]. Sugiatno et al. evaluated the effects of osteoblast cell lines treated with S-nitroso acetyl penicillamine (SNAP)/Hydroxyapatite (HA) biomaterial, as S-nitrosothiol molecule that spontaneously releases NO. The results showed an increase of osteoblast cell line after treatment with SNAP at 1 mmol L−1. This effect was abolished by using 2-(4-carboxyphenyl)-4,4,5,5-tetramethylimidazoline-1-oxyl-3-oxide), known as carboxy PTIO, a NO scavenger. Thus, these results showed that NO released from SNAP/HA platform can increase osteoblast formation at low concentrations [75].
The effects of diethylenetriamine diazeniumdiolate (NONOate) donors at various concentrations on the differentiation and proliferation of osteoblast-like cells (MC3T3-E1 cells) were studied in vitro [85]. NONOate treatment at low concentrations (10–50 µM) significantly increased cell proliferation and ALP activity, while at higher concentrations (50–100 µM), NONOate induced a decrease in cell number and differentiation [85]. In a similar approach, human osteoblasts treated with high NO concentration (SNP at 2 mM) significantly decreased cell viability, ALP activity and induced cell apoptosis. While cell pretreatment with low NO concentration (SNP at 0.3 mM) significantly lowered the high NO-induced effects [86].
The influence of exogenous NO administration was also evaluated regarding the induction of bone formation using animal models, focusing on rat tail vertebrae [56]. When compared to controls, NO-treated mice demonstrated 8-fold improvement in the bone formation rate in mechanically stimulated vertebrae. In this scenario, NO was revealed as a fundamental component for bone formation, corroborating to previously reported results [56].
The effects of NO on bone cell function, in addition to being influenced by concentration, also appear to be dependent on the rate at which NO is released from the donor species. Mancini et al. tested the effects of two NO-donors SNP and 2,29-(hydroxynitrosohydrazino)bis-ethanamine (NOC-18) with different kinetics of NO-release on primary rat osteoblasts. In this approach, the slow release of NO through NOC-18 mimicked the release of NO from eNOS, while iNOS release was more accurately modeled by SNP, which promotes a faster NO release. The NOC-18 donor, at low and moderate concentrations (10 and 50 µM), contributed to cell growth and proliferation, increasing ALP activity of primary rat osteoblasts. While the NO-donor SNP has the opposite effect when used at concentrations of 50 to 100 µM. A rapid NO release at high concentrations inhibited proliferation and induced apoptosis of primary rat osteoblasts [54]. Thus, this result reinforces the biphasic effect of NO.
4.3. NO is involved in fracture healing
An important study was developed in order to better understand the role of NO in fracture and bone healing [4]. Diwan et al. showed for the first time that the activity of the three NOS isoforms is increased after fracture in humans and rats. This approach comprised the investigation of three distinct phases: (i) the presence or absence of NOS in rat during femoral fracture repair; (ii) the presence or absence of NOS in human fractures healing; and (iii) the effect of NO supplementation and NOS deficiency influence in rat fracture repair. All NOS isoforms were expressed during fracture healing, although each isoform was expressed in a different stage. iNOS levels were expressed on day 4 and showed a maximum level on the day 15 after fracture, proceeded by a delayed increase in eNOS and nNOS expressions. The NOS systemic inhibition led to an evident reduction in the fracture healing, while the healing could be reestablished via the localized administration of exogenous NO supplementation using carboxybutyl chitosan NONOate [4]. These results showed an important potential clinical significance and reinforced the promising use of NO in bone-healing procedures. The use of NO in bone formation and repair was also evaluated in combination with bone morphogenic protein 2 (BMP2), an important growth factor which has significant functions in bone treatments [87]. BMP2 has positives effects, although it is required at high amounts, leading to low cost effectiveness. Interestingly, a co-therapy using NONOate as NO donor enhanced the activity of the BMP2, as NO improved signaling via protein kinase A. This result indicates an improvement in the use of BMP2, which might be administrated in near future. Although, more studies are required to better investigate the effects of the proposed combined treatment [87].
Besides being of fundamental importance in fracture repair, NOS isoforms are also involved in the regulation of bone formation in postnatal [6]. Aguirre et al. developed a study carried with mice that presented eNOS gene deficiency, as the hypothesis relayed on the major role played by the endothelial form of the enzyme. It was confirmed that this abnormality led to the reduction of bone ratio formation, as well as the bone volume (up to 45%). Similar pattern was observed in osteoblast and osteoclast cell lineages, as the cells proliferation and differentiation were decreased. The delay was overcome with the administration of exogenous NO donor, indicating the beneficial therapeutic effects for bone formation [6]. As previously described, eNOS plays a pivotal role in bone formation and repair. In this sense, Bandara and coworkers evaluated the osteogenic differentiation of equine adipose derived stem cells (eASCs) through the control of NO synthesis, recreating the interaction between eNOS and the membrane protein caveolin-1 [88]. The cell differentiation was promoted in a cellular environment and with optimum levels of NO (5.5 µM), indicating that the modification in cells may possibly result in a cell-based treatment, using modified cells through transplantation. Treatment with exogenous NO donor (NONOate: 5 µM to 15 µM) also promoted and confirmed the direct role of NO levels on eASC osteogenesis [88].
Several investigations have studied the effect of exogenous NO on bone marrow MSCs proliferation, migration and differentiation. Abnosi and Pari studied the impact of the NO donor (SNP) in rat bone marrow MSCs. Cytotoxicity, concentration of calcium and the activity of the enzymes alanine transaminase (ALT), aspartate transaminase (AST), alkaline phosphatase (ALP), and lactate dehydrogenase (LDH) were evaluated. The results indicated that at high concentration (1000 µM), SNP reduced the viability of the cells, but no toxicity was observed at a low concentration (100 µM) during 20 days of treatment. SNP also reduced the differentiation time of MSCs to osteoblasts and increased matrix mineralization via the activation of ALP activity and metabolic changes. Overall, SNP presented promising application in bone repair [62]. Other approaches have studied the effect of the NO donor SNP on bone marrow cells and have found that the treatment of MSCs progenitor cells with 500 to 2000 µM of SNP for 48 hours can significantly reduce cell proliferation. However, low NO concentration (100 µM) regulated pluripotency and differentiation of MSCs via cGMP-independent mechanism [89]. The concentrations of 10 and 25 µM of SNP activated respiratory activity to some extent. Conversely, the treatment with SNP at 100-500 µM reduced the respiratory activity of MSC to approximately 80% [90]. These studies demonstrated that NO also has a biphasic effect on bone marrow MSCs functions.
4.4. Estrogen and NO connection
Despite NO functions in bone formation, NO is a potential therapeutic agent with important effects in osteoporosis in postmenstrual women. A randomized double-blind trial was conducted with 144 healthy postmenopausal women [91]. The participants received placebo or daily oral administration of the organic nitrate isosorbide mononitrate (ISMO: 20 mg) for 12 weeks. This clinical study evidenced not only an increase in bone formation observed for women treated with NO donors, but also the prevention of bone loss. These results reinforce the important role played by NO in bone formation and open venues for studies and development of NO delivery platforms to prevent and treat postmenstrual osteoporosis [92]. Jamal and coworkers strengthen the importance of developing more efficient medicines to prevent and to treat osteoporosis, mostly because actual treatments are not completely effective, since they do not prevent cortical bone fractures. Moreover, osteoporosis is an increasing problem, due to world populations aging [92]. In this sense, biphosphates have been used as a drug vehicle for targeting bone [93]. This class of compound has the ability to chelate calcium ions, and highly interacts with bone mineral surface. Although, biphosphates are not biodegradable, leading to an accumulation in the skeleton for life. Different modifications have been developed in biphosphates, including modifications to improve biodegradability or to confer different functions. NO-donor biphosphate was developed by Lazzarato and coworkers, as NO inhibits the osteoclast-mediated resorption, being a potential option in age-related bone diseases. It was confirmed that the NO-releasing biphosphates had a preferable accumulation in bone, when compared to blood and muscles, and inhibited osteoclasts differentiation in a dose-dependent manner. Still, further investigations are required to improve the effects of NO-releasing biphosphates for future human applications [93]. Another NO donor was developed focusing in osteoporosis treatment for postmenstrual women [94]. Usually, nitrates are employed to deliver NO for this kind of treatment, and despite presenting promisor effects, nitrates induce oxidative stress, which may increase cardiovascular mortality, and their long-term use causes tolerance. Thus, a direct and inedited NO-releasing nitrosyl-cobinamide, a molecule derived from the vitamin B12 precursor, was studied in vitro and in osteoporosis mouse model. Firstly, in vitro, the developed NO donor promoted intracellular signaling, proliferation and protected murine primary osteoblasts from apoptosis. In vivo, the treatment promoted bone formation, increased in osteoblastic gene expression, and prevented osteoclasts differentiation [94]. Thus, this NO donor presented promisor results, overcoming issues found in other NO donor species, such as nitrates.
Lin et al. incorporated the NO donor (NONOate) into micellar depots composed by capric acid and octadecane microparticles (CA/OD MPs). The therapeutic efficacy of the micellar depots was evaluated in a in vivo ovariectomized (OVX) rat model. Bone qualities of the femur and spine were evaluated by Micro-CT scanning before and after the treatments. The control (untreated) and free NONOate groups showed architectural bone deterioration, while NO treatment with MPs appears to reduce bone loss by inhibiting bone turnover. Free NONOate had a short half-life so frequent administrations were required to achieve the same effect observed in the treatment with MPs. These results suggest that the sustained NO release from the micellar systems was more effective to reverse OVX-induced osteoporosis [85].
Several studies using nitroglycerin (NG) as NO donor have shown to be effective for preventing glucocorticoid-induced bone loss in Wistar rats [95], attenuating bone loss [57] and restoring lost bone mass due to ovariectomy in Sprague-Dawley rats [68]. In addition, treatment with this NO donor in clinical research has been shown to be as effective as estrogen in preventing estrogen-deficient bone loss in ovariectomized women. NG administration was found to be more advantageous than estrogen administration, since NG long-term treatment (over one year) did not result in tachyphylaxis and the required NG dose was very low, 3 or 4 times lower than the dose generally used to maintain cardiovascular homeostasis [69].
5.
Conclusion: perspectives and challenges
From the revised literature, a robust evidence suggests that NO is important signaling molecule involved in the physiology and pathophysiology of bone tissue. As NO can have opposite effects in biological system, depending on its concentration and cell redox, the completely understand of the NO roles in bone tissue need to be further explored. Several in vitro and in vivo studies demonstrated that NO (endogenous synthesized or exogenous administrated) has a biphasic effect on bone resorption and osteoclast activity. At low concentrations, NO promotes osteoblasts proliferation, differentiation and survival, which are important stages for bone regeneration. However, at high concentrations, NO can impair bone resorption and formation. Therefore, in clinical settings, it is of fundamental importance to control the rates/amount of NO release from biomaterials to achieve the desired effect. In this sense, versatile biomaterials, including nano/micro materials, have been extensively prepared allowing a sustained NO release directly to the bone tissue. The complete characterization of the NO release profile from these biomaterials needs to be addressed. The measurement of NO release/generation from a donor/biomaterial in vivo, direct in the bone tissue, is the major challenge for the complete characterization of the NO release profile. Different classes of NO donors/generators can be directly applied or combined with biomaterials for bone tissue regeneration. These NO donors can release NO by different mechanisms and different rates, therefore, in each approach, the measurement of NO release should carefully evaluate.
It should be noted that the combination of NO donors/generators with biomaterials have been extensively employed in different biomedical applications, including cancer treatment, for antimicrobial activities and for soft tissue regeneration [13]. However, its application in bone tissue is still in the infancy. This is a promising approach that needs to be further investigated, considering that non-invasive treatment of bone trauma and injuries is a current and major health problem, especially with the aging of the population. The delivery of exogenous NO to bone using NO donors allied to biomaterials in the sustained and localized NO release has also been shown to increase osteogenesis with a relevant impact on dental and orthopedist areas. We hope that this review open new avenues in the topic.









 DownLoad:
DownLoad: