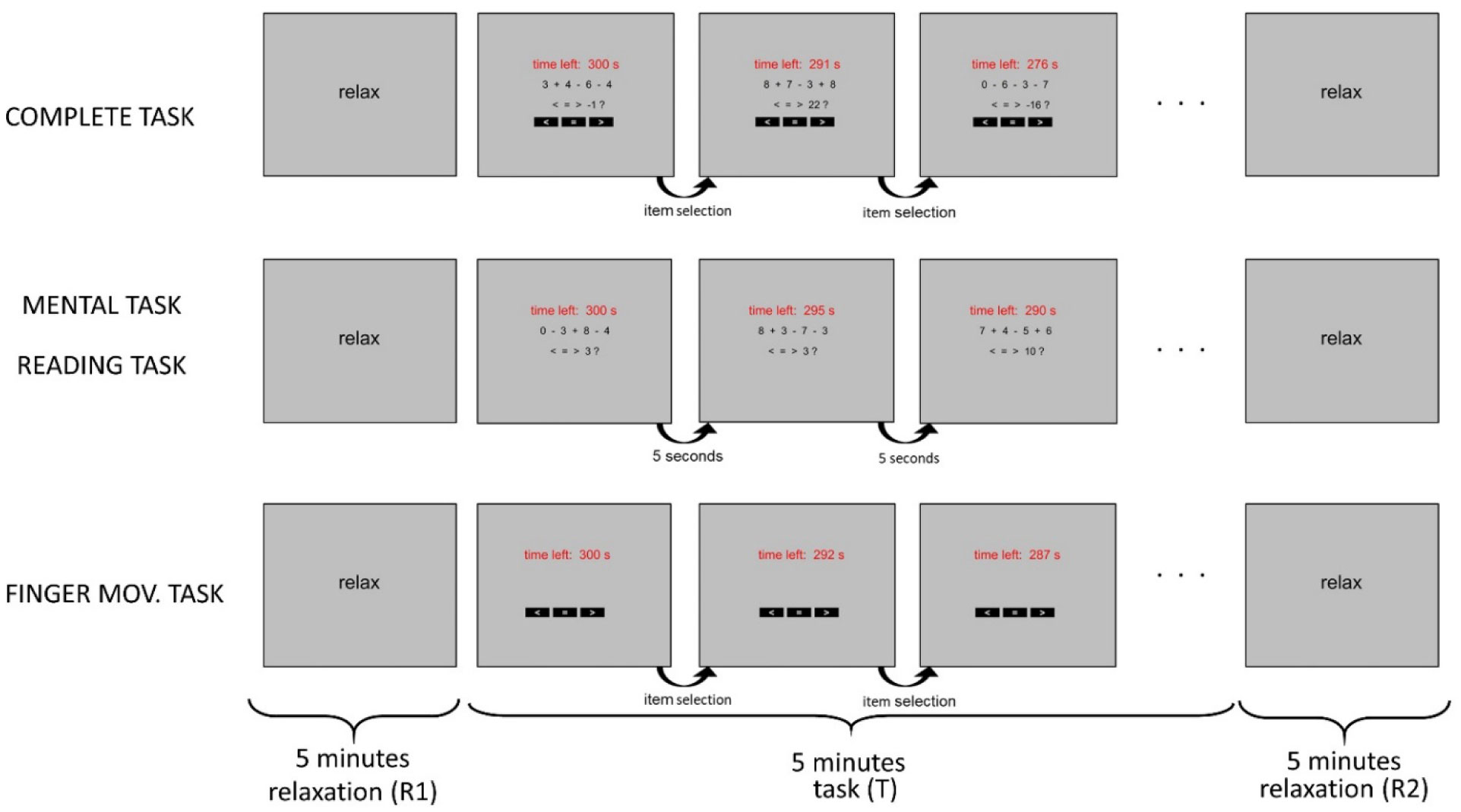
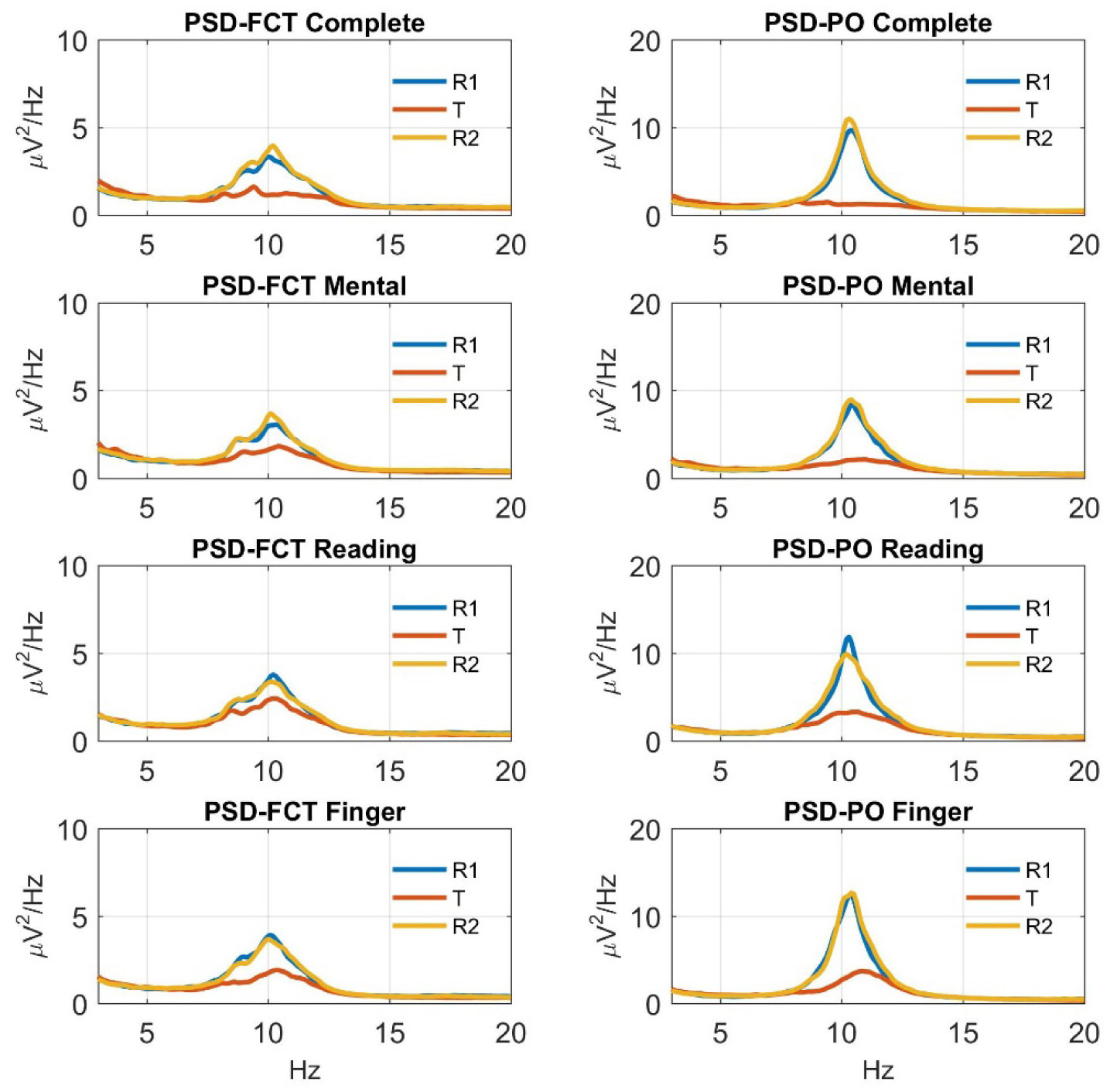
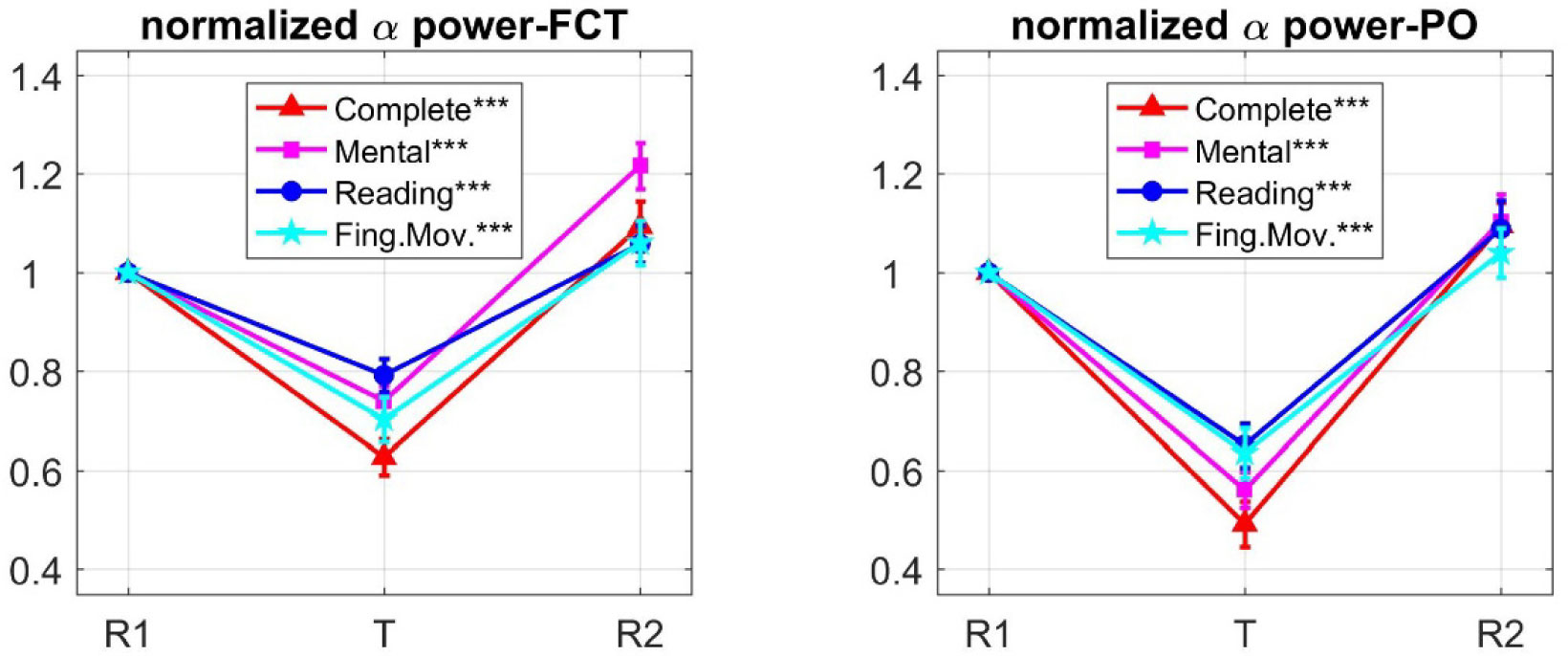
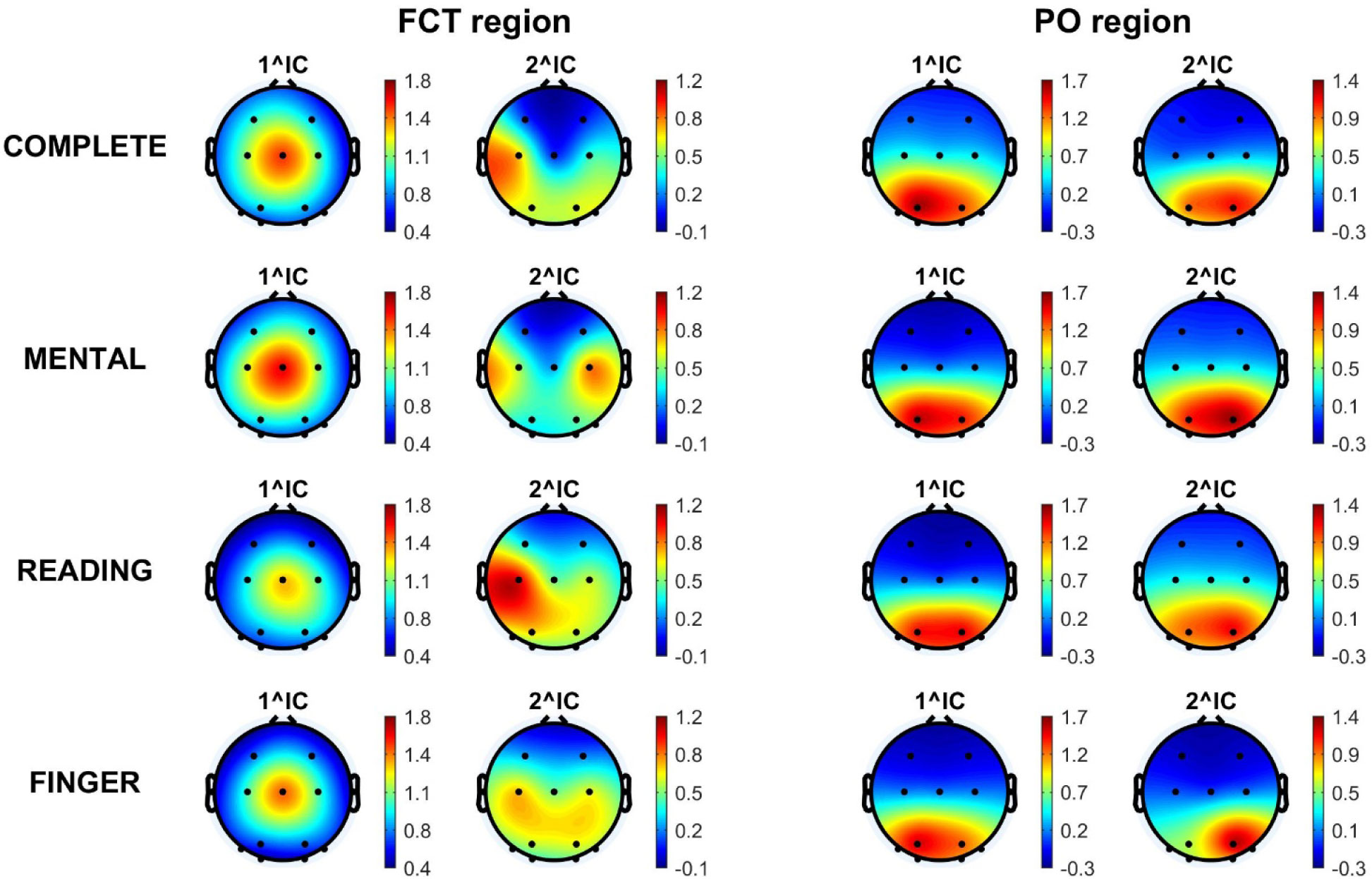
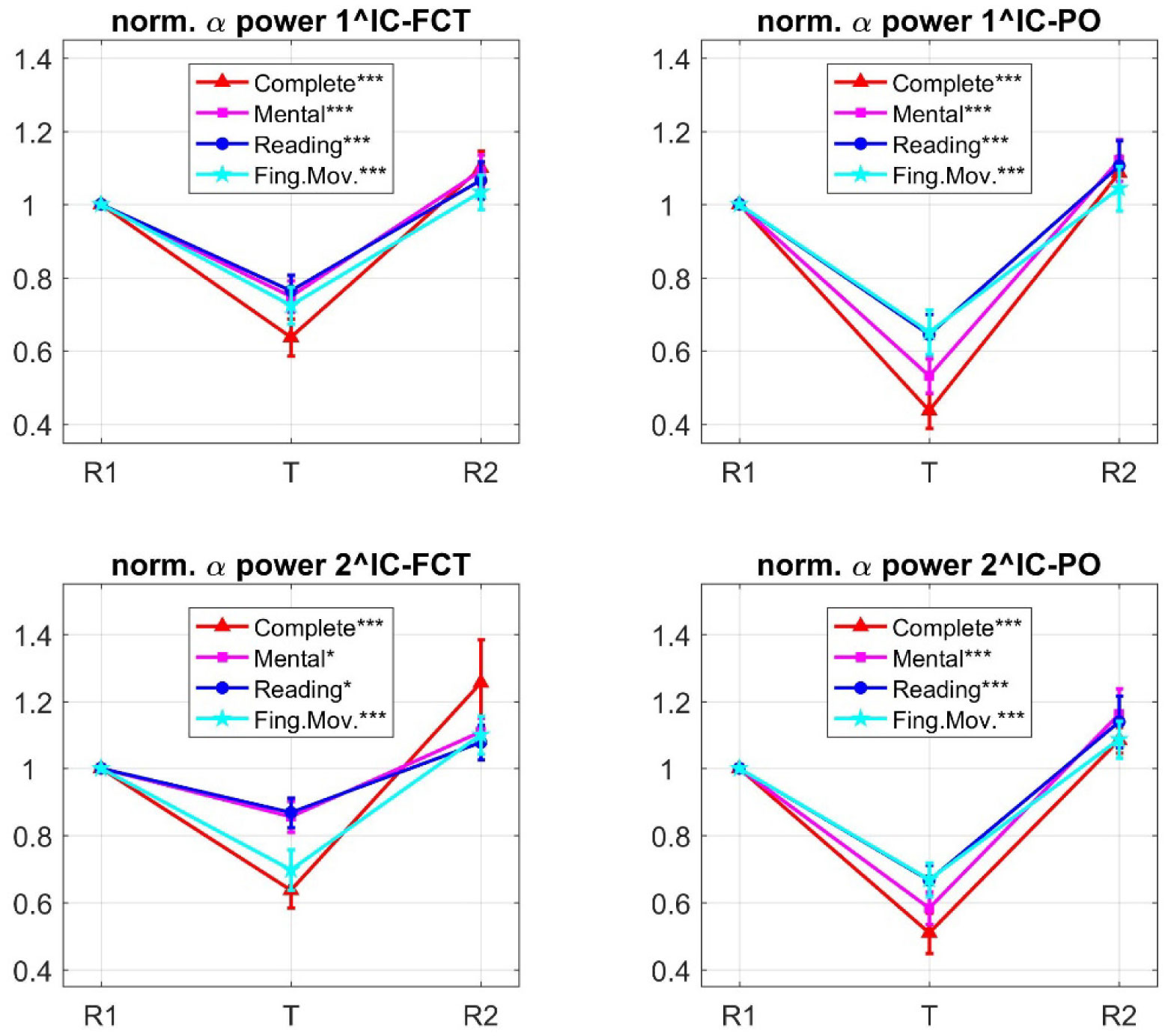
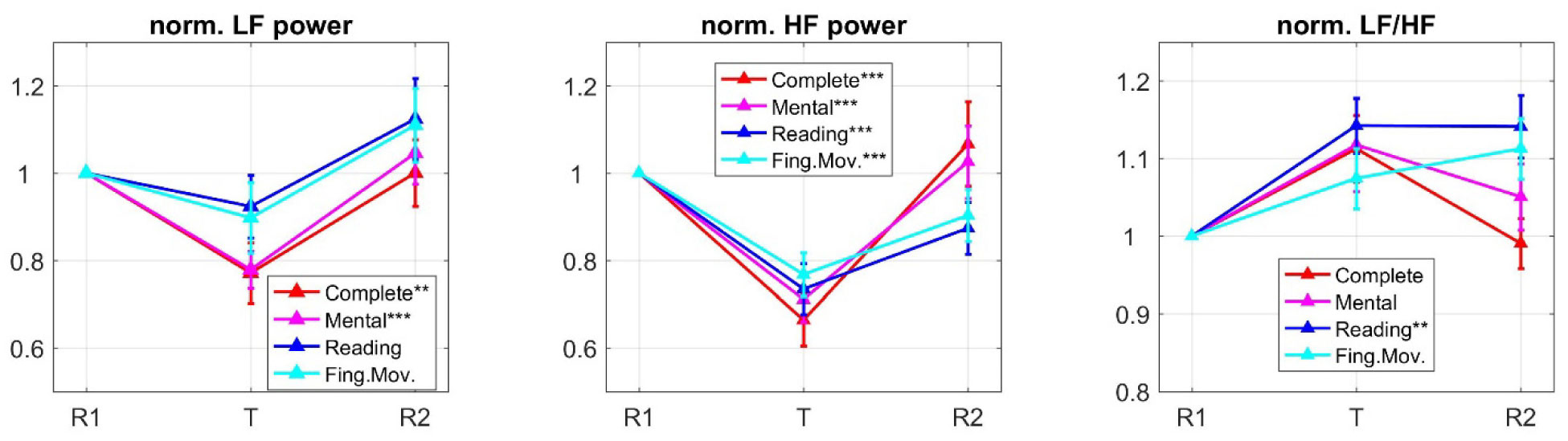
According to recent evidence, oscillations in the alpha-band (8–14 Hz) play an active role in attention via allocation of cortical resources: decrease in alpha activity enhances neural processes in task-relevant regions, while increase in alpha activity reduces processing in task-irrelevant regions. Here, we analyzed changes in alpha-band power of 13-channel electroencephalogram (EEG) acquired from 30 subjects while performing four tasks that differently engaged visual, computational and motor attentional components. The complete (visual + computational + motor) task required to read and solve an arithmetical operation and provide a motor response; three simplified tasks involved a subset of these components (visual + computational task, visual task, motor task). Task-related changes in alpha power were quantified by aggregating electrodes into two main regions (fronto-central and parieto-occipital), to test regional specificity of alpha modulation depending on the involved attentional aspects. Independent Component Analysis (ICA) was applied to discover the main independent processes accounting for alpha power over the two scalp regions. Furthermore, we performed analysis of Heart Rate Variability (HRV) from one electrocardiogram signal acquired simultaneously with EEG, to test autonomic reaction to attentional loads. Results showed that alpha power modulation over the two scalp regions not only reflected the number of involved attentional components (the larger their number the larger the alpha power suppression) but was also fine-tuned by the nature of the recruited mechanisms (visual, computational, motor) relative to the functional specification of the regions. ICA revealed topologically dissimilar and differently attention-regulated processes of alpha power over the two regions. HRV indexes were less sensitive to different attentional aspects compared to alpha power, with vagal activity index presenting larger changes. This study contributes to improve our understanding of the electroencephalographic and autonomic correlates of attention and may have practical implications in neurofeedback, brain-computer interfaces, neuroergonomics as well as in clinical practice and neuroscience research exploring attention-deficit disorders.
1.
Introduction
L. Carlitz ([1]) introduced analogues of Bernoulli numbers for the rational function (finite) field $ K = \mathbb F_r(T) $, which are called Bernoulli-Carlitz numbers now. Bernoulli-Carlitz numbers have been studied since then (e.g., see [2,3,4,5,6]). According to the notations by Goss [7], Bernoulli-Carlitz numbers $ BC_n $ are defined by
Here, $ e_C(x) $ is the Carlitz exponential defined by
where $ D_i = [i][i-1]^r\cdots [1]^{r^{i-1}} $ ($ i\ge 1 $) with $ D_0 = 1 $, and $ [i] = T^{r^i}-T $. The Carlitz factorial $ \Pi(i) $ is defined by
for a non-negative integer $ i $ with $ r $-ary expansion:
As analogues of the classical Cauchy numbers $ c_n $, Cauchy-Carlitz numbers $ CC_n $ ([8]) are introduced as
Here, $ \log_C(x) $ is the Carlitz logarithm defined by
where $ L_i = [i][i-1]\cdots [1] $ ($ i\ge 1 $) with $ L_0 = 1 $.
In [8], Bernoulli-Carlitz numbers and Cauchy-Carlitz numbers are expressed explicitly by using the Stirling-Carlitz numbers of the second kind and of the first kind, respectively. These properties are the extensions that Bernoulli numbers and Cauchy numbers are expressed explicitly by using the Stirling numbers of the second kind and of the first kind, respectively.
On the other hand, for $ N\ge 1 $, hypergeometric Bernoulli numbers $ B_{N, n} $ ([9,10,11,12]) are defined by the generating function
where
is the confluent hypergeometric function with $ (x)^{(n)} = x(x+1)\cdots(x+n-1) $ ($ n\ge 1 $) and $ (x)^{(0)} = 1 $. When $ N = 1 $, $ B_n = B_{1, n} $ are classical Bernoulli numbers defined by
In addition, hypergeometric Cauchy numbers $ c_{N, n} $ (see [13]) are defined by
where
is the Gauss hypergeometric function. When $ N = 1 $, $ c_n = c_{1, n} $ are classical Cauchy numbers defined by
In [14], for $ N\ge 0 $, the truncated Bernoulli-Carlitz numbers $ BC_{N, n} $ and the truncated Cauchy-Carlitz numbers $ CC_{N, n} $ are defined by
and
respectively. When $ N = 0 $, $ BC_n = BC_{0, n} $ and $ CC_n = CC_{0, n} $ are the original Bernoulli-Carlitz numbers and Cauchy-Carlitz numbers, respectively. These numbers $ BC_{N, n} $ and $ CC_{N, n} $ in (1.9) and (1.10) in function fields are analogues of hypergeometric Bernoulli numbers in (1.7) and hypergeometric Cauchy numbers in (1.8) in complex numbers, respectively. In [15], the truncated Euler polynomials are introduced and studied in complex numbers.
It is known that any real number $ \alpha $ can be expressed uniquely as the simple continued fraction expansion:
where $ a_0 $ is an integer and $ a_1, a_2, \dots $ are positive integers. Though the expression is not unique, there exist general continued fraction expansions for real or complex numbers, and in general, analytic functions $ f(x) $:
where $ a_0(x), a_1(x), \dots $ and $ b_1(x), b_2(x), \dots $ are polynomials in $ x $. In [16,17] several continued fraction expansions for non-exponential Bernoulli numbers are given. For example,
More general continued fractions expansions for analytic functions are recorded, for example, in [18]. In this paper, we shall give expressions for truncated Bernoulli-Carlitz numbers and truncated Cauchy-Carlitz numbers.
In [19], the hypergeometric Bernoulli numbers $ B_{N, n} $ ($ N\ge 1 $, $ n\ge 1 $) can be expressed as
When $ N = 1 $, we have a determinant expression of Bernoulli numbers ([20,p.53]). In addition, relations between $ B_{N, n} $ and $ B_{N-1, n} $ are shown in [19].
In [21,22], the hypergeometric Cauchy numbers $ c_{N, n} $ ($ N\ge 1 $, $ n\ge 1 $) can be expressed as
When $ N = 1 $, we have a determinant expression of Cauchy numbers ([20,p.50]).
Recently, in ([23]) the truncated Euler-Carlitz numbers $ EC_{N, n} $ ($ N\ge 0 $), introduced as
are shown to have some determinant expressions. When $ N = 0 $, $ EC_n = EC_{0, n} $ are the Euler-Carlitz numbers, denoted by
where
is the Carlitz hyperbolic cosine. This reminds us that the hypergeometric Euler numbers $ E_{N, n} $ ([24]), defined by
have a determinant expression [25,Theorem 2.3] for $ N\ge 0 $ and $ n\ge 1 $,
When $ N = 0 $, we have a determinant expression of Euler numbers (cf. [20,p.52]). More general cases are studied in [26].
In this paper, we also give similar determinant expressions of truncated Bernoulli-Carlitz numbers and truncated Cauchy-Carlitz numbers as natural extensions of those of hypergeometric numbers.
2.
Continued fraction expansions of truncated Bernoulli-Carlitz and Cauchy-Carlitz numbers
Let the $ n $-th convergent of the continued fraction expansion of (1.12) be
There exist the fundamental recurrence formulas:
with $ P_{-1}(x) = 1 $, $ Q_{-1}(x) = 0 $, $ P_0(x) = a_0(x) $ and $ Q_0(x) = 1 $.
From the definition in (1.9), truncated Bernoulli-Carlitz numbers satisfy the relation
Thus,
yield that
Notice that the $ n $-th convergent $ p_n/q_n $ of the simple continued fraction (1.11) of a real number $ \alpha $ yields the approximation property
Now,
and $ P_n(x) $ and $ Q_n(x) $ ($ n\ge 2 $) satisfy the recurrence relations
(They are proved by induction). Since by (2.2) for $ n\ge 2 $
we have the following continued fraction expansion.
Theorem 1.
Put $ N = 0 $ in Theorem 1 to illustrate a simpler case. Then, we have a continued fraction expansion concerning the original Bernoulli-Carlitz numbers.
Corollary 1.
From the definition in (1.10), truncated Cauchy-Carlitz numbers satisfy the relation
Thus,
yield that
Now,
and $ P_n(x) $ and $ Q_n(x) $ ($ n\ge 2 $) satisfy the recurrence relations
Since by (2.2) for $ n\ge 2 $
we have the following continued fraction expansion.
Theorem 2.
3.
A determinant expression of truncated Cauchy-Carlitz numbers
In [14], some expressions of truncated Cauchy-Carlitz numbers have been shown. One of them is for integers $ N\ge 0 $ and $ n\ge 1 $,
[14,Theorem 2].
Now, we give a determinant expression of truncated Cauchy-Carlitz numbers.
Theorem 3. For integers $ N\ge 0 $ and $ n\ge 1 $,
where
with
We need the following Lemma in [27] in order to prove Theorem 3.
Lemma 1. Let $ \{\alpha_n\}_{n\ge 0} $ be a sequence with $ \alpha_0 = 1 $, and $ R(j) $ be a function independent of $ n $. Then
if and only if
with $ \alpha_0 = 1 $.
Proof of Theorem 3. By the definition (1.10) with (1.6), we have
Thus, for $ n\ge 1 $, we get
By Lemma 1, we have
Examples. When $ n = r^{N+1}-r^N $,
Let $ n = r^{N+2}-r^N $. For simplicity, put
Then by expanding at the first column, we have
The second term is equal to
The first term is
Therefore,
From this procedure, it is also clear that $ CC_{N, n} = 0 $ if $ r^{N+1}-r^N\nmid n $, since all the elements of one column (or row) become zero.
4.
A determinant expression of truncated Bernoulli-Carlitz numbers
In [14], some expressions of truncated Bernoulli-Carlitz numbers have been shown. One of them is for integers $ N\ge 0 $ and $ n\ge 1 $,
[14,Theorem 1].
Now, we give a determinant expression of truncated Bernoulli-Carlitz numbers.
Theorem 4. For integers $ N\ge 0 $ and $ n\ge 1 $,
where
with $ \delta_l^\ast $ as in (3.2).
Proof. The proof is similar to that of Theorem 3, using (1.9) and (1.2).
Example. Let $ n = 2(r^{N+1}-r^N) $. For convenience, put
Then, we have
It is also clear that $ BC_{N, n} = 0 $ if $ r^{N+1}-r^N\nmid n $.
5.
Applications by the Trudi's formula
We shall use Trudi's formula to obtain different explicit expressions and inversion relations for the numbers $ CC_{N, n} $ and $ BC_{N, n} $.
Lemma 2. For a positive integer $ n $, we have
where $ \binom{t_1+\cdots + t_n}{t_1, \dots, t_n} = \frac{(t_1+\cdots + t_n)!}{t_1!\cdots t_n!} $ are the multinomial coefficients.
This relation is known as Trudi's formula [28,Vol.3,p.214], [29] and the case $ a_0 = 1 $ of this formula is known as Brioschi's formula [30], [28,Vol.3,pp.208–209].
In addition, there exists the following inversion formula (see, e.g. [27]), which is based upon the relation
Lemma 3. If $ \{\alpha_n\}_{n\geq 0} $ is a sequence defined by $ \alpha_0 = 1 $ and
From Trudi's formula, it is possible to give the combinatorial expression
By applying these lemmata to Theorem 3 and Theorem 4, we obtain an explicit expression for the truncated Cauchy-Carlitz numbers and the truncated Bernoulli-Carlitz numbers.
Theorem 5. For integers $ N\ge 0 $ and $ n\ge 1 $, we have
where $ a_n $ are given in Theorem 3.
Theorem 6. For integers $ N\ge 0 $ and $ n\ge 1 $, we have
where $ d_n $ are given in Theorem 4.
By applying the inversion relation in Lemma 3 to Theorem 3 and Theorem 4, we have the following.
Theorem 7. For integers $ N\ge 0 $ and $ n\ge 1 $, we have
where $ a_n $ is given in Theorem 3.
Theorem 8. For integers $ N\ge 0 $ and $ n\ge 1 $, we have
where $ d_n $ is given in Theorem 4.
Acknowledgments
We would like to thank the referees for their valuable comments.
Conflict of interest
The authors declare no conflict of interest.













 DownLoad:
DownLoad: