Quantitative generation of microfluidic flow by using optically driven microspheres

Nomenclature: $a$: Radius of the microsphere; ${\bf{q}}$: Position of the microsphere; ${\bf{c}}$: Controller; ${{\bf{q}}^d}$: Desired position of the microsphere; ${\bf{e}}$: Position error of the microsphere; $r$: Distance from sphere center to target location; ${F_{drag}}$: Drag force; ${r_0}$: Critical value; ${F_{trapping}}$: Trapping force; $U$: Velocity magnitude of the microsphere; $k$: Stiffness of the optical trap; ${\bf{V}}$: Fluid flow velocity; ${K_i}$: Integrating gain; $x$: Offset of the cell from the trap; ${K_p}$: Proportional gain; $\beta$: Drag coefficient of the liquid; ${\bf{l}}$: Position of the optical trap; $\zeta$: Time variable.

1.   Introduction

Microfluidic systems are miniatured factories that can manipulate fluids in micro- and nano-metric scales ^[1]. In comparison with conventional macroscopic systems, microfluidic systems have attracted increasing attention for their advantages, including enhancing processing accuracy, reducing material consumption, and saving cost. In biomedical engineering, the ability to handle small volumes of biological samples and reagents enables many innovative assays, especially when a sample is precious and rare. Microfluidic systems have shown great potential for applications in rapid diagnosis ^[2,3], disease screening, drug delivery ^[4,5], cell biology ^[6,7], and synthetic biology ^[8,9].

Fluid flow actuation in micro- and nano-liter volumes is an essential step in microfluidic systems ^[10]. Considerable efforts have been devoted to generating precisely controllable fluid flow. One of the most popular methods used to control the movement of fluid flow is using a syringe pump to inject a small volume of liquid into a customized microfluidic chip fabricated by soft lithography techniques and poly-dimethylsiloxane ^[11,12,13]. This method is low cost and has been widely used to generate, mix, and cease fluid flow. However, it is mainly used to control liquid flow in the entire microfluid channel and has a relatively large time constant. Another type of actuation mechanism, involves the use of indirect micromanipulation techniques, such as electric fields ^[14], acoustic wave ^[15], magnetic fields ^[16,17,18], and optical fields ^[19], to control microfluidic flow. These physical fields drive microobjects to move in liquid and hence generate localized microfluidic flows surrounding these microobjects.

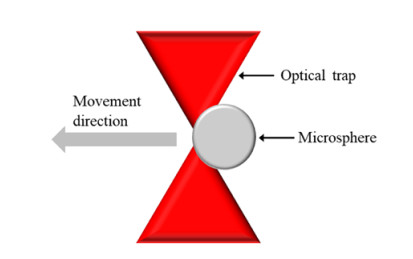
Among microtechniques, an optical field method, also named "optical tweezers" or "optical trap" ^[20], is a popular tool because of its high flexibility and precision. An optical trap can be used to trap and move microobjects ranging from tens of nanometers to tens of micrometers through radiation pressure from a focused laser beam (Figure 1). Optical force in the orders of a few piconewtons has been widely used to manipulate organelles, macromolecules, and cells in biology and medicine ^[21]. Optical traps have been used as an ideal small force gauge because the optical trapping force on a trapped microsphere as a particular laser power is linearly proportional to the deviation of the microsphere from the trap focus ^[22]. Many meaningful applications, including DNA stretching, cell deformability, and kinesin motion, have been explored.

Figure 1.  Schematic of moving a microsphere with an optical trap.

DownLoad: Full-Size Img PowerPoint

In microfluidic systems, optical traps have also been applied because of the perfect size matching between trapped microobjects and typical microfluidic chips and the force matching between the optical sensing force and the force involved in many microfluidic systems ^[23]. Marr et al. ^[24] created pumps and valves by using colloidal microspheres and via laser-initiated photopolymerization; they controlled the fluid flow within customized channels. Neale et al. ^[25] fabricated microgears, which can be rotated with an optical trap and function as micropumps to drive liquid, on the basis of the form birefringence principle. Maruo et al. ^[26] developed a lobed micropump by direct laser writing with a femtosecond laser beam. Two built-in rotors were cooperatively driven by the time-divided laser scanning and moved liquids. Recently, Būtaitė et al. ^[27] demonstrated a versatile hydrodynamic manipulation platform that utilizes multiple optically actuated microrotors. These innovative microtools have enabled the microfluidic control and exhibited good development and application perspective in micro-total-analysis systems. However, customized designs and fabrications, which are often expensive and time consuming, are necessary in the microtool-based methods. In addition, the usage of sophisticated microtools complicates the quantitative calculation and control of the generated fluid flows. Several microbeads-based methods have been reported as alternative techniques for addressing these issues. Leach et al. ^[28] rotated two birefringent vaterite particles with optical traps and generated flow to transport microbeads in a microfluidic channel. Wu et al. ^[29] generated localized microfluidic flow by rotating birefringent beads, which can control the direction of growth of individual nerve fibers. Both methods are based on the rotation of birefringent beads and only liquids at short distances can be driven. Furthermore, ensuring the precision and robustness of flow control is difficult because open-loop strategy is used in these demonstrations.

In this study, a new approach is proposed to quantitatively generate a localized microfluidic flow by automatically driving a microsphere to move in liquid. A closed-loop control strategy with visual servoing feedback is introduced to achieve high precision and robustness. This method does not require any special microfabrication facility, and the microfluidic flow can be quantitively adjusted by controlling the direction, speed, and distance of the microsphere from target locations. To the best of our knowledge, this work is the first demonstration of optically driving liquids through translational movement of microspheres with closed-loop control. This work will contribute to the applications that need precise and adjustable tiny flows. Examples of such examples include exploring the behavior and function of single cell under fluid flows ^{[29,30,31,32]} and transporting materials in microfluidic systems.

The remainder of this paper is organized as follows. Section 2 presents the materials and methods. Section 3 reports experimental results to demonstrate the proposed approach. Section 4 provides the summary and conclusions of this study.

2.   Materials and methods

2.1.   Automated movement of microsphere

2.1.1.   Experimental setup

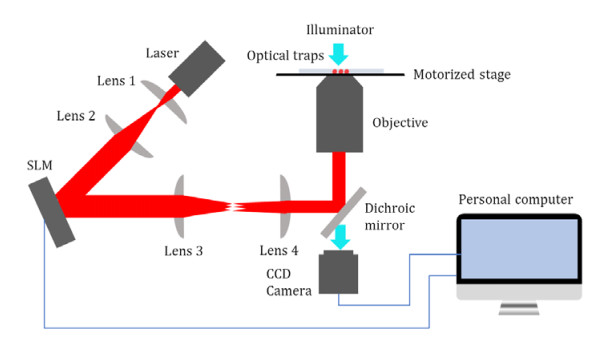
As described in our previous reports ^[33,34], a manipulation system of holographic optical tweezers (HOTs) is established on the basis of a motorized xyz stage and an inverted microscope (Ti-U, Nikon) with an objective (Plan Apo 60X/1.20 WI, Nikon) (Figure 2). A trapping beam is provided with a continuous laser beam with a maximum output of 3W at a wavelength of 1064 nm (V-I06C-3000 OEM J-series, Spectra Physics). The laser beam is first magnified by a telescope (Lens 1 and Lens 2) to match the beam width to the size of a spatial light modulator (SLM). Another telescope (Lens 3 and Lens 4) is then used to image the SLM plane onto the back focal plane of the microscope objective. In the process, the laser beam is split into multiple beams by the computer-generated hologram combined with the SLM, and each beam is focused into an individually controllable optical trap. A charge-coupled device (CCD) camera (Plan Apo 60X/1.20 WI, Nikon) is used to obtain the images of the workspace and enable the visual servo control by providing feedback of the microsphere. All the mechanical components are supported by an antivibration table in a clean room. The system software is developed using C++ language.

Figure 2.  Schematic of the manipulation system of HOTs.

DownLoad: Full-Size Img PowerPoint

2.1.2.   Generation of microfluidic flow

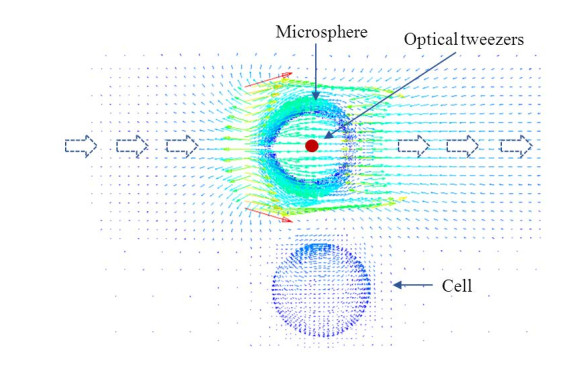
Figure 3 shows the schematic of generating microfluidic flow via the movement of a microsphere and provides a typical case of a cell next to a microsphere as an example. When a microsphere is moved in liquid by using optical tweezers, the microsphere "pulls" the surrounding liquid to flow with it, and the cell is subjected to microfluidic flow. The direction of the fluid flow can be adjusted by changing the direction of the movement of the microsphere, and the velocity of the flow can be regulated by controlling the movement speed and distance of the microsphere from the cell. A closed-loop control strategy with visual servoing feedback is introduced to automatically move the microsphere and to achieve high precision of the generated microfluidic flow.

Figure 3.  Generation of microfluidic flow by moving a microsphere with optical tweezers.

DownLoad: Full-Size Img PowerPoint

2.1.3.   Closed-loop control for optically moving a microsphere

Various control algorithms have been developed to transport microspheres with optical tweezers ^{[35,36,37,38]}. We introduce a feedforward plus PI-type controller in this study ^[33]. The dynamic equation of the trapped microsphere can be expressed as

where $k$ is the stiffness of the optical trap, $\beta$ is the drag coefficient of the liquid, and ${\bf{l}}$ and ${\bf{q}}$ are the position of the optical trap and the microspheres, respectively.

On the basis of the dynamic equation (1), we introduce a controller as follows:

where ${r_0}$ is a critical value introduced to prevent the escape of the microsphere from the optical trap in the movement; and ${\bf{c}}$ is a feedforward plus PI-type controller described as follows:

where ${K_p}$ and ${K_i}$ are positive feedback control gains, $\zeta$ is a time variable from 0 to $t$, and ${\bf{e}}$ is the position error between the desired cell position ${{\bf{q}}^d}$ and the actual cell position ${\bf{q}}$, expressed by

2.2.   Theoretical solution of the generated microfluidic flow

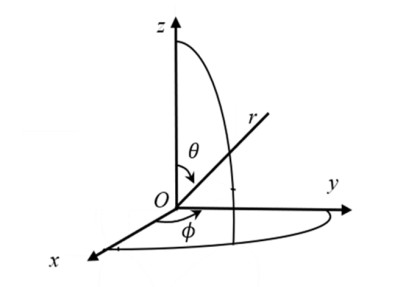
A sphere of radius $a$ is considered to be moving in a viscous incompressible liquid with a constant velocity magnitude $U$ along the Z axis, and the influence of the vessel wall is disregarded. Adopting the spherical coordinates as shown in Figure 4 and according to the Stokes equations ^[39], we can obtain the generated fluid flow velocity ${\bf{V}}$ as

Figure 4.  Schematic of spherical coordinates.

DownLoad: Full-Size Img PowerPoint

where $r$ is the distance from the sphere center to the target location.

3.   Experiments

3.1.   Experimental principle

A drag force-based method is introduced to characterize the velocity of the generated microfluidic flow. According to Stokes law, the drag force ${F_{drag}}$ applied to a sphere by a fluid flow can be calculated as

where $\beta$ is the drag coefficient and can be obtained experimentally. Therefore, if we obtain ${F_{drag}}$, we can determine the fluid flow velocity ${\bf{V}}$.

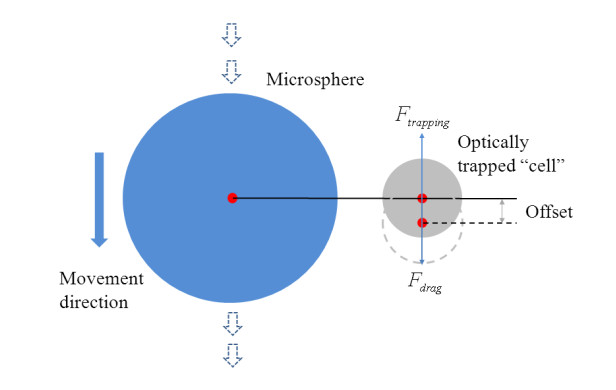
The schematic of characterizing ${F_{drag}}$ is shown in Figure 5. A large microsphere and a small microsphere are trapped in liquid without other substances around them. For description simplicity, the small microsphere is called "cell" in this paper. The large microsphere is then moved in a straight line next to the cell, generating a microfluidic flow. Therefore, the cell is subjected to ${F_{drag}}$ from the fluid flow and deviate from its original position. The cell stops in a new balanced position under ${F_{drag}}$ and the trapping force from the optical trap, ${F_{trapping}}$. We can have

Figure 5.  Schematic of characterizing the microfluidic flow.

DownLoad: Full-Size Img PowerPoint

where $k$ is the stiffness of the optical trap, and $x$ is the offset of the cell from the trap. We can obtain the stiffness $k$ by conducting an experimental calibration ^[33] and determine the offset $x$ by recording the positions of the cell through image processing. ${F_{drag}}$ can be calculated according to equation (7).

3.2.   Experimental results

Experiments were performed to compare the actual and theoretical microfluidic flow velocity. A microsphere with a radius of 12.0 µm and a cell with a radius of 4.0 µm were used, and the distance between the microsphere center and the cell center was 22.5 µm, indicating that the minimum distance between the surface of the microsphere and the cell was 18.5 µm and that the maximum distance was 26.5 µm. The relative velocity between the microsphere and the cell was set to 40.0 µm/s. According to equation (5), we could calculate the velocity of the microfluids flowing through the cell, ranging from 25.1 to 33.5 µm/s.

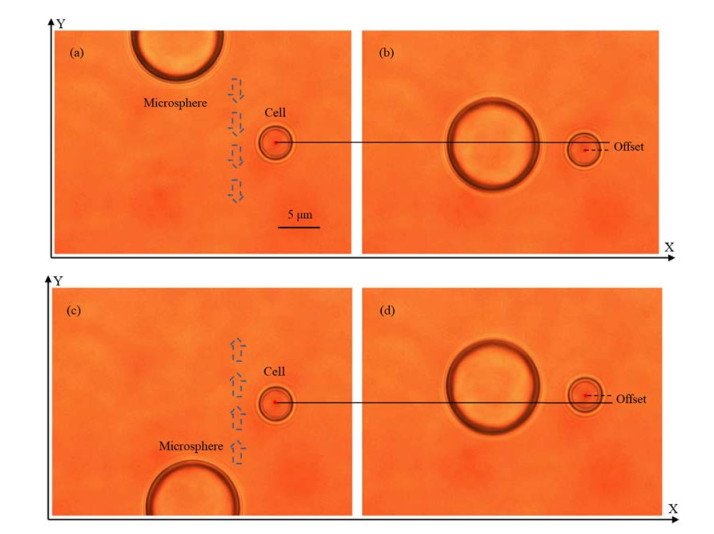
The laser power on the cell was set to 0.2 W, and $k/\beta$ obtained by calibration was 10.1 ${S^{ - 1}}$. Figure 6 illustrates the process of the quantitative measurement of microfluidic flow velocity. As shown in Figures 6 (a) and (b), the microsphere moved in the negative direction along the y-axis. When the microsphere passed near the cell, the cell moved with the microsphere under ${F_{drag}}$ from the generated fluid flow and ${F_{trapping}}$ from the optical trap. Figures 6 (c) and (d) show a similar measurement process of the microsphere moving in the positive direction along the y-axis. Figures 6 (b) and (d) illustrate that the cell was clearly moved and offsets were visible, implying that the microfluidic flow was successfully generated by the moved microsphere.

Figure 6.  Quantitative measurement of microfluidic flow velocity.

DownLoad: Full-Size Img PowerPoint

Figure 7 depicts a typical example of the offsets of the cell from the optical trap under the generated microfluidic flow. In each cycle, the maximum offset was reached when the y-axis coordinates of the microsphere and the cell were identical. In Figure 7, the maximum offsets in each cycle were closed, indicating that our method used to move the microsphere achieved a high precision. When processing data, we used the absolute value of the five largest values in each cycle and then obtained the average as the result of each experiment. Ten experiments were repeated, and the mean of the absolute offset was 2.7 µm. According to equations (6) and (7), we determined the microfluidic flow velocity of 27.3 µm/s, which was between 25.1 and 33.5 µm/s and the same as that of the theoretical value.

Figure 7.  Offsets of the cell under the generated microfluidic flow.

DownLoad: Full-Size Img PowerPoint

4.   Summary and conclusions

This study can be summarized as follows: (1) a novel approach is proposed to generate microfluidic flow quantitatively by automatically moving a microsphere in liquid via a manipulation system of HOTs. (2) A closed-loop control strategy is introduced to achieve high movement precision and robustness. (3) The theoretical solution of the generated microfluid is obtained on the basis of Stokes equations. (4) An experimental method is proposed to characterize the microfluidic flow. Experiments are performed and the experimental results are consistent with the theoretical findings, verifying the effectiveness of our approach.

This method does not impose any dedicated fabrication of microtool, and the microfluidic flow is dexterously adjustable by controlling the direction, speed, and distance of microspheres from a target location. However, our approach is limited by the relatively smaller generated fluid than those obtained using conventional methods with a syringe pump. In addition, our approach is unsuitable for applications wherein target locations are susceptible to light interference. The proposed approach shows potential for applications involving microfluidic flow actuation, investigations on cell behavior under microfluidic stimulation, and material transport in microfluidic systems.

Acknowledgments

The authors acknowledge the support from the National Natural Science Foundation of China (No. 61803270 and 61701442), and Natural Science Foundation of Guangdong Province (No. 2015A030310268).

Conflict of interest

All authors declare no conflicts of interest in this paper.