Bifurcation analysis in a singular Beddington-DeAngelis predator-prey model with two delays and nonlinear predator harvesting

1.   Introduction

In recent decades, an increasing number of scholars have paid attention to population dynamics of prey-predator ecosystem ^[1,2,3]. During investigating such biological phenomena, dynamical behavior of biological and mathematical models are affected by many factors, such as the function response. All kinds of predator-prey models with Holling type, Crowley-Martin type and Leslie-Gower type, etc. have been investigated extensively by the researchers ^{[4,5,6,7,8,9]}. However, a few of literatures have studied the predator-prey systems with Beddington-DeAngelis type functional response ^{[10,11,12,13,14,15,16,17]}.

The Beddington et al. ^[18,19] gave the follows functional response

Here, $l_{1}$ represents that per predator population per time can eat the maximum number of prey population, $l$ is a positive constant and denotes the effect of handling time for predators, and $l_{2}$ is positive and measures the magnitude of interference among predators, $d$ represents the prey density where the attack rate is half-saturated. It is obvious that two cases are possible as following. One case is that, if $l = 1$, $l_{2} = 0$ and $d > 0$, then it reduces to a Holling Ⅱ functional response (or Michaelis-Menten functional response) ^[20]. The other case is that, if $l = 0$, $l_{2} = 0$ and $d > 0$, then it reduces to a linear mass-action functional response (or Holling Ⅰ functional response) ^[21].

Conforto et al. ^[16] considered a three-dimensional reaction-diffusion system incorporating the dynamics of handling and searching predators, and showed that its solutions converge when a small parameter tends to 0 towards the solutions of a reaction-cross diffusion system of predator-prey type involving a Holling-type Ⅱ or Beddington-DeAngelis functional response. Employing the upper and lower solution method and comparison theory, Li et al. ^[12] got the sufficient conditions of the upper ultimate boundedness and permanence of this system which implies that impulse always changes the situation of survival for species, and obtained the conditions for the existence of unique globally stable positive periodic solution.

Generally speaking, the introduction of time lag in the mathematical models ^{[22,23,24,25,26,27,28,29,30,31,32]} tends to reflect the interaction and coexistence mechanism of population in the past. System with two delays is discussed by using the equivalent system with a single time delay in reference ^[30]. Liu et al. ^[33] used a Markovian switching process to model the telephone noise in the environment, proposed a stochastic regime-switching predator-prey model with harvesting and distributed delays, obtained the sufficient and necessary conditions for the existence of an optimal harvesting policy, and gave the explicit forms of the optimal harvesting effort and the maximum of sustainable yield.

Biological resources in the predator-prey system tend to be harvested and sold in order to obtain economic profit. In general, three types of harvesting function have been studied in the literatures ^{[32,34,35,36,37]}.

(Ⅰ) Constant harvesting function is

where $C$ is a suitable constant.

(Ⅱ) Proportionate harvesting function is

where $q$ is the catchability coefficient.

(Ⅲ) Nonlinear harvesting function is

where $m_{1}, m_{2}$ are suitable positive constants.

It is easy to find that there are several unrealistic features in the proportional harvesting, such as stochastic search for prey and unbounded linear harvesting. However, the nonlinear harvesting function (Ⅲ) eliminates the above unrealistic features and satisfies

that is to say, the nonlinear harvesting function shows saturation effects in terms of harvest effort and inventory abundance ^[38].

As we known that the harvested prey-predator systems have been focused by both theoretical and mathematical biologists ^[15,39,40]. Chakraborty et al. ^[40] studied the global dynamics and bifurcation of the predator-prey with constant harvesting. Liu et al. ^[15] investigated Hopf bifurcation and center stability for a predator-prey biological economic model with linear prey harvesting. Liu et al. ^[39] discussed bifurcation in a prey-predator model with nonlinear predator harvesting, and obtained the conditions for Turing and Hopf bifurcation. However, little work has been done on dynamic effects of economic interest on prey-predator system with nonlinear predator harvesting and Beddington-DeAngelis functional response.

In 1954, the common-property resource economic theory was proposed by Gordon in ^[41], which investigated the dynamic effects of harvesting efforts on the ecosystem from an economic point of view. Thus, in order to study the economic interest of commercial harvesting, an equation is proposed:

Recently, a number of delay differential algebraic systems were proposed to investigate the impact of commercial harvesting on prey-predator model ^[42,43]. Liu et al. ^[44] investigated a delayed differential-algebraic system with double time delays, Holling type Ⅱ functional response and linear commercial harvesting effort on predator population. By jointly using the normal form of differential algebraic system and the bifurcation theory, Li et al. ^[45] discussed the stability and bifurcations, and obtained richer dynamics of the bioeconomic differential algebraic predator-prey model with nonlinear prey harvesting.

Due to the above analysis and discussion, we will extend the work in ^[44,45] by considering nonlinear predator harvesting, double delays and Beddington-DeAngelis functional response function into our bioeconomic differential algebraic predator-prey system in this paper. The aim of our work is to reveal the dynamical behavior of Beddington-DeAngelis predator-prey model with two delays and nonlinear predator harvesting, to obtain a reasonable profit and provide some guidance for the harvest of biological economy system.

The rest of the paper is organized as follows. In Section 2, a differential algebraic predator-prey model including two delays, Beddington-DeAngelis functional response and nonlinear predator harvesting is proposed. In Section 3, positive solutions are analyzed when $m = 0$ and $m > 0$, respectively. In Section 4, in the absence of time delay, the singularity induced bifurcation is discussed by using differential-algebraic system theory, what's more, state feedback controllers are designed to remove singular induced bifurcation. In the presence of time delay, by analyzing the corresponding characteristic transcendental equation, the local stability around the interior equilibrium are studied. Furthermore, the existence of Hopf bifurcation is investigated. Directions of Hopf bifurcation and stability of the bifurcating periodic solutions are also discussed by using normal form theory and center manifold theorem. Numerical simulations illustrate the effectiveness of the mathematical conclusions in Section 5. Discussions and conclusions are included in the last section.

2.   Model formation

Leslie and Gower ^[46] proposed the classical predator-prey system, which is as follows

Here, $X(T)$, $Y(T)$ indicate prey and predator population at time $T$ respectively, $s_{1}$, $s_{2}$ and $K$ are intrinsic growth rate of prey, intrinsic growth rate of predator and carrying capacity. $l_{1}$ is the maximum number of prey each predator can eat each time and $l_{2}$ is a semi saturation constant, and the predation rate is $\frac{l_{2}}{2}$. The carrying capacity of predator is proportional to the size of prey population. $l_{3}$ is the amount of prey needed to support a predator population in equilibrium.

Based on the fact that Beddington-DeAngelis functional response is more authentic ^[47], we introduce it in system (2.1). Thus, the new system is

Considering nonlinear predator harvesting, system (2.2) is constructed as follows

By using following transformations

system (2.3) is non-dimensionalized as follows

where $a, b, \alpha, \beta, r, q, p, c, m_{1}$ and $m_{2}$ are all positive constants.

Simultaneously, an algebraic equation is also included due to the economic profit of harvesting. Based on Eq (1.2), we have

here $p$ is the price per unit harvested biomass, $c$ is the cost per unit harvest, while $m$ means the net economic revenue.

In general, the delay differential equation model can produce more efficient and accurate dynamics than the ordinary differential equation model as capturing oscillation dynamics.

Therefore, by combining the above biological economic algebraic equation and time delay, a differential-algebraic system with two time delays is given as follows

where $\tau_{1}$ is maturation time for prey population, $\tau_{2}$ is gestation delay for predator population. The initial conditions of system (2.6) take the following form:

System (2.6) can be transformed into matrix form as follows

where

Remark 1. Compared with system proposed in ^[44], nonlinear predator harvesting and Beddington-DeAngelis functional response are considered in system (2.6).

Remark 2. Compared with system proposed in ^[45], system (2.6) contains two delays and Beddington-DeAngelis functional response, and focuses on economic interest of commercial harvest effort on predator.

3.   The existence of equilibria

For system (2.6), there is a bioeconomic equilibrium state when $m = 0$. First, we give the following assumptions:

(H1): $c > rx_{0}\; \; \; \text{and}\; \; \; px_{0}(\beta r-1) > \beta c,$

(H2): $c < rx_{0}\; \; \; \text{and}\; \; \; px_{0}(\beta r-1) < \beta c,$

(H3): $\frac{bc}{p}+1-\frac{c}{p} > 0.$

Therefore, if one of the assumptions $(H_{1})$ and $(H_{2})$ holds, then the interior equilibrium $P_{0} = (x_{0}, y_{0}, E_{0}) = (x_{0}, \frac{c}{p}, \frac{pac\beta(c-rx_{0})}{px_{0}(\beta r-1)-\beta c})$ exists. Here $x_{0}$ satisfies the following equation

Obviously, a simple sufficient condition that Eq (3.1) has at least one positive root is that $(H_{1})$ and $(H_{3})$ or $(H_{2})$ and $(H_{3})$ hold.

In the case of $m > 0$, we suppose

(H4): $pq(1+ax^{*}-x^{*}-ax^{*2}) > (qc+mm_{1})(1+bx^{*}-b) > 0$,

(H5): $pq(1+ax^{*}-x^{*}-ax^{*2}) < (1+bx^{*}-b)(qc+mm_{1}) < 0.$

If one of the assumptions $(H_{4})$ and $(H_{5})$ holds, then the interior equilibrium $P^{*} = (x^{*}, y^{*}, E^{*})$ exists, here $E^{*} = \frac{mm_{2}(1+ax^{*}-x^{*}-ax^{*2})}{pq(1+ax^{*}-x^{*}-ax^{*2})-(qc+mm_{1})(1+bx^{*}-b)}, y^{*} = \frac{1+ax^{*}-x^{*}-ax^{*2}}{1+bx^{*}-b}$ and $x^{*}$ satisfies the following equation

here

Based on Routh-Hurwitz criterion ^[1], Eq (3.2) has at least one positive root when $1 < b$ and $\alpha m_{1} < m_{2}$. Suppose $(\tau_{1}, \tau_{2}, m)\in \Omega_{1}$, here

4.   Bifurcation analysis of positive equilibria

4.1.   System without delays

Here, we are interested in the stability of system (2.6) at the interior equilibrium ${P_{0}}$.

When $\tau_{1} = 0, \tau_{2} = 0$, system (2.6) takes the following form

Lemma 4.1. (Singularity induced bifurcation theorem ^[49,50]). If the differential-algebraic equations satisfy the following conditions at the singular equilibrium:

(I) ${D}_{y}\, f_{3}$ has a simple zero eigenvalue and

(II)

is nonsingular,

(III)

is also nonsingular, here $\Delta = {D}_{E}f_{3}$, then the singularity induced bifurcation occurs at the singular equilibrium.

Theorem 4.2. A singularity induced bifurcation takes place at the interior equilibrium ${P_{0}}$ of the differential algebraic system (4.1). When the bifurcation parameter $m$ increases through zero, system (4.1) is unstable at ${P_{0}}$.

Proof. We can obtain that the Jacobin matrix of system (4.1) around $P_{0}$ is

where $J_{11} = 1-2\, x_{0}-(b+\frac{x_{0}}{y_{0}})(1-x_{0})^{2}, J_{12} = \frac {-x_{0}\, \left(1-x_{0} \right) ^{2} \left(ax_{0}+1 \right) }{{y_{0}}^{2}}, J_{22} = -{\frac {{E_{0}}^{2}}{ \left(\alpha\, y_{0}+E_{0} \right) ^{2}}}+\beta\, r-2\, {\frac {\beta\, y_{0}}{x_{0}}}$.

Let $m$ be bifurcation parameter, $\text{D}$ be differential operator. We can obtain the following results.

(Ⅰ)

(Ⅱ) If $J_{11}\neq0$ holds, then it can be obtained that

(Ⅲ) Defining $\Delta = \text{D}_{E}f_{3} = \frac{qm_{2}y(py-c)}{(m_{1}E+m_{2}y)^2}$, it follows from simple computations that

Hence a singularity induced bifurcation occurs around $P_{0}$ of system (4.1) and the bifurcation value is $m = 0$.

On the other hand,

where $P_{1} = \left(\begin{array}{ccc} \text{D}_{x}\, f_{1} & \text{D}_{y}\, f_{1} & \text{D}_{E}\, f_{1}\\ \text{D}_{x}\, f_{2} & \text{D}_{y}\, f_{2} & \text{D}_{E}\, f_{2}\\ \text{D}_{x}\, f_{3} & \text{D}_{y}\, f_{3} & \text{D}_{E}\, f_{3} \end{array} \right).$

According to Lemma 4.1 and Theorem 3 in ^[49], when $m$ increases through $0$, one eigenvalue of system (4.1) moves from $\mathbb{C}^{-}$ to $\mathbb{C}^{+}$ along real axis by diverging through $\infty$. Hence, the Theorem 4.2 is proved.

By using the similar proof of Theorem 4.2, it is easy to show system (4.1) is unstable around $P^{*}$, what's more, state feedback controllers are designed to remove singularity induced bifurcation and stabilize system (4.1) around $P_{0}$ and $P^{*}$, respectively.

In the case of $m = 0$, according to the leading matrix $\bar{A}$ in (4.1) and $J_{P_{0}}$, we can obtain rank $(J_{P_{0}}, \bar{A}J_{P_{0}}, \bar{A}^{2}J_{P_{0}}) = 3$. It is not hard to find that system (4.1) is locally controllable around $P_{0}$ based on Theorem 2-2.1 in ^[48]. Therefore, a feedback controller can be used to stabilize system (4.1) around $P_{0}$. By using Theorem 3-1.2 in ^[48], a feedback controller is as follows

where $\hat{k}$ is a feedback gain.

Applying the controller into system (4.1), we can obtain that a controlled system is

Theorem 4.3. If the feedback gain $\hat{k} > {max}\left\{Q_{1}, Q_{2}, Q_{3}\right\}$, here

then system (4.2) is stable around $P_{0}$.

Proof. At first, the Jacobin matrix of system (4.2) around $P_{0}$ is

The characteristic equation of system (4.2) around $P_{0}$ is $\det \big(\lambda\, \bar{A} -\hat{J}_{P_{0}}\big) = 0$ based on $\bar{A}$ in system (4.2) and $\hat{J}_{P_{0}}$, which can be written as follows

where

By simple computation, if $\hat{k} > \text{max}\left\{Q_{1}, Q_{2}, Q_{3}\right\}$, then system (4.2) is stable around $P_{0}$.

Similarly, in the case of $m > 0$, a controlled system is

where $\tilde{k}$ is a feedback gain.

By using the similar analysis in Theorem 4.3, we can obtain the following result.

Theorem 4.4. If controller feedback gain $\tilde{k} > {max}\left\{\tilde{Q}_{1}, \tilde{Q}_{2}\right\}$, where

then system (4.3) is stable around $P^{*}$.

Remark 3. According to design of feedback controller, we can make interior equilibria be stable, which shows that prey-predator ecosystem can be kept sustainable and economic interest can be kept ideal by controlling commercial harvest effort on predator.

4.2.   System with delays

4.2.1.   Case Ⅰ: $\tau_{1} > 0, \tau_{2}=0$

By analyzing system (2.6), a characteristic equation of around $P^{*}$ is

When $\tau_{1} > 0,$ and $\tau_{2} = 0$, Eq (4.4) takes the following form

By simple computation, we can obtain that $\lambda = 0$ is not a root of Eq (4.5). We suppose that $\lambda = i\beta_{1}$ ($\beta_{1}$ is a positive real number) is a root of Eq (4.5). By separating real and imaginary parts, we can obtain the following two transcendental equations

By computing two equations in Eq (4.6), it gives that

Theorem 4.5. If $\xi_{4}^{2}-(\xi_{2}+ \xi_{5})^{2} < 0$ holds,

(i) system (2.6) is locally asymptotically stable around $P^{*}$ when $(\tau_{1}, \tau_{2}, m) \in \Omega_{1}\cap \Omega_{2}$;

(ii) system (2.6) undergoes Hopf bifurcation around $P^{*}$ when $(\tau_{1}, \tau_{2}, m) \in \Omega_{1}\cap \Omega_{3}$. Here, $\Omega_{2}$ and $\Omega_{3}$ are defined as follows

where $N_{1} = (\xi_{1}^{2}+2\xi_{4})^{\frac{1}{2}}+\frac{E^{*}\alpha y^{*}}{(E+\alpha y^{*})^{2}}-\frac{\beta y^{*}}{x^{*}}$ and $(E^{*}+\alpha y^{*})^{2}N_{1} < E^{*2}$.

Proof. If $\xi_{4}^{2}-(\xi_{2}+ \xi_{5})^{2} < 0$, based on Routh-Hurwitz criterion ^[1], we can guarantee that Eq (4.7) has at least one positive root. Consequently, Eq (4.5) has a pair of purely imaginary roots $\lambda = \pm i\beta^{*}_{1}$.

Based on Eq (4.6), we can calculate $\tau_{1k}$ as follows

By using Butlers lemma ^[55], system (2.6) is locally asymptotically stable around $P^{*}$ when $(\tau_{1}, \tau_{2}, m) \in \Omega_{1}\cap \Omega_{2}$.

Next, we will determine

By differentiating Eq (4.5) with respect to $\tau_{1}$, we have

By virtue of Eq (4.6), we have

If $0 < m < \frac{-\alpha y^{*}pqE^{*}}{m_{2}(E^{*}+\alpha y^{*})^{2}N_{1}-m_{2}E^{*2}}$ and $(E^{*}+\alpha y^{*})^{2}N_{1} < E^{*2}$, then $(\xi_{0}+\xi_{3})^2-2\xi_{4}-\xi_{1}^{2} > 0$ holds, which implies that $\Theta > 0$. Hence, when $(\tau_{1}, \tau_{2}, m) \in \Omega_{1}\cap \Omega_{3}$, transversality condition holds and Hopf bifurcation occurs.

4.2.2.   Case Ⅱ: $\tau_{1}=0, \tau_{2} > 0$

When $\tau_{1} = 0$ and $\tau_{2} > 0$, Eq (4.4) can be written the following form

Similarly, it shows that $\lambda = 0$ is not a root of Eq (4.9). We suppose that $\lambda = i\beta_{2}$ ($\beta_{2} > 0$) is a root of Eq (4.9). We can obtain the following two transcendental equations

which gives that

Theorem 4.6. If $\xi_{2}^{2}-(\xi_{4}+ \xi_{5})^{2} < 0$ holds,

(i) system (2.6) is locally asymptotically stable around $P^{*}$ when $(\tau_{1}, \tau_{2}, m) \in \Omega_{1}\cap \Omega_{4}$;

(ii) system (2.6) undergoes Hopf bifurcation around $P^{*}$ when $(\tau_{1}, \tau_{2}, m) \in \Omega_{1}\cap \Omega_{5}$, where $\Omega_{4}$ and $\Omega_{5}$ are defined as follows

here, $\sqrt {m_{2} \left(-{\xi_{2}}^{2}+{\xi_{3}}^{2} \right) }\left(\alpha y^{*}+E^{*} \right) ^{2} > m_{2}E^{*}$.

By computing Eq (4.10), we can obtain $\tau_{2k}$ is

The proof of Theorem 4.6 is similar to that of Theorem 4.5. So, we omit it.

4.2.3.   Case Ⅲ: $\tau_{1} > 0, \tau_{2}=\hat{\tau}_{2}\in (0, \tau_{20}), \tau_{1}\neq \tau_{2}$

In this part, $\tau_{1}$ is considered as a parameter while $\tau_{2}$ is regarded as a fixed value $\hat{\tau}_{2}\in(0, \tau_{20})$, which is a stable interval calculated in Subsection 4.2.2. Here $\Omega_{6}$ is defined as follows

Let $\lambda = i\alpha_{1}$ ($\alpha_{1}$ is a positive real number) represent a purely imaginary root of Eq (4.4). By separating real and imaginary parts, we have the following two transcendental equations

Based on Eq (4.13), it derives that

where

Let

Due to its complicated form, it is not easy for us to analyze properties of roots of transcendental equation (4.15). Based on dynamical system theory ^[1], we know that if and only if every eigenvalue has negative real part, system (2.6) is locally asymptotically stable around $P^{*}$. What's more, by analyzing existence of Hopf bifurcation around the corresponding interior equilibrium $P^{*}$, the periodic oscillation of system (2.6) is investigated. Hale ^[51] proposed that when the corresponding eigenvalue has a pair of purely imaginary roots, system usually exhibits Hopf bifurcation. Obviously, if Eq (4.15) has finite positive and simple roots $0 < \alpha_{10} < \alpha_{11} < \cdots < \alpha_{1n}$, Eq (4.4) has a pair of purely imaginary roots.

Without loss of generality, we denote $\alpha_{1c} =$ max $\left\{ \alpha_{1k}\right\}, k = 0, 1, 2, \cdot\cdot\cdot n$ and regard $\tau_{1}$ as the bifurcation parameter, while we have the following corresponding critical value $\tau_{1c}$

here, $\omega_{1c} \in[0, 2\pi]$ satisfies the following equations

Furthermore, it is important to check transversal condition. The necessary condition for the existence of Hopf branches is that the eigenvalues passes through the imaginary axis with non-zero speed ^[51].

By differentiating $\lambda$ with respect to $\tau_{1}$ in Eq (4.4), it derives that

where

By virtue of Eq (4.18), it can be obtained that

where

It is obvious to show $\hat{\Theta} > 0$ when $B_{11}B_{13}+B_{12}B_{14} > 0$. Therefore, we have the following results on stability and bifurcation in system (2.6).

Theorem 4.7. For system (2.6), suppose that $B_{11}B_{13}+B_{12}B_{14} > 0$ holds and $(\tau_{1}, \tau_{2}, m) \in \Omega_{1}\cap \Omega_{6}$.

(i) If Eq (4.15) has no positive root, then system (2.6) is locally asymptotically stable around $P^{*}$ when $(\tau_{1}, \tau_{2}, m) \in \Omega_{1}\cap \Omega_{6}$.

(ii) If Eq (4.15) has at least one positive and simple root $\alpha_{1}^{*}$, there exists a critical delay $\tau_{1}^{*} = {min}\left\{\frac{\omega_{1}^{*}+2k\pi}{\alpha_{1}^{*}}\right\} > 0$ such that system (2.6) is locally asymptotically stable around $P^{*}$ when $(\tau_{1}, \tau_{2}, m) \in \Omega_{1}\cap \Omega_{6}\cap \Omega_{7},$ here

(iii) If Eq (4.15) has finite positive and simple roots $0 < \alpha_{10} < \alpha_{11} < \cdot\cdot\cdot < \alpha_{1n}$, there exists a critical delay $\tau_{1c}$ defined in (4.16) such that system (2.6) is locally asymptotically stable around $P^{*}$ when $(\tau_{1}, \tau_{2}, m) \in \Omega_{1}\cap \Omega_{6}\cap \Omega_{8}$, here

If $B_{11}B_{13}+B_{12}B_{14} > 0$, then system (2.6) undergoes a Hopf bifurcation around $P^{*}$ when $(\tau_{1}, \tau_{2}, m) \in \Omega_{1}\cap \Omega_{6}\cap \Omega_{9}$, here

4.2.4.   Case Ⅳ: $\tau_{1} \in (0, \tau_{10}), \tau_{2} > 0, \tau_{1}\neq \tau_{2}$

In this part, $\tau_{2}$ is seen as a parameter, while $\tau_{1}$ is regarded as a fixed value $\hat{\tau}_{1} \in(0, \tau_{10})$ that is a stable interval calculated in Subsection 4.2.1. $\Omega_{10}$ is defined as follows$:$

Let $\lambda = i\alpha_{2}$ ($\alpha_{2}$ is a positive real number) represent a purely imaginary root of Eq (4.4). We define

where,

Theorem 4.8. For system (2.6), suppose that $B_{21}B_{23}+B_{22}B_{24} > 0$ holds and $(\tau_{1}, \tau_{2}, m) \in \Omega_{1}\cap \Omega_{10}$.

(i) If Eq (4.20) has no positive root, then system (2.6) is locally asymptotically stable around $P^{*}$ when $(\tau_{1}, \tau_{2}, m) \in \Omega_{1}\cap \Omega_{10}$.

(ii) If Eq (4.20) has at least one positive and simple root $\alpha_{2}^{*}$, there exists a critical delay $\tau_{2}^{*} = {min}\left\{\frac{\omega_{2}^{*}+2k\pi}{\alpha_{2}^{*}}\right\} > 0$ such that system (2.6) is locally asymptotically stable around $P^{*}$ when $(\tau_{1}, \tau_{2}, m) \in \Omega_{1}\cap \Omega_{10}\cap \Omega_{11},$ here

(iii) If Eq (4.20) has finite positive and simple roots $0 < \alpha_{20} < \alpha_{21} < \cdot\cdot\cdot \alpha_{2n}$, there exists a critical delay $\tau_{2c}$ defined in (4.19) such that system (2.6) is locally asymptotically stable around $P^{*}$ when $(\tau_{1}, \tau_{2}, m) \in \Omega_{1}\cap \Omega_{10}\cap \Omega_{12}$, here

If $B_{21}B_{23}+B_{22}B_{24} > 0$ holds, then system (2.6) undergoes a Hopf bifurcation around $P^{*}$ when $(\tau_{1}, \tau_{2}, m) \in \Omega_{1}\cap \Omega_{10}\cap \Omega_{13}$, here

Where the corresponding critical value $\tau_{2c}$ satisfies

here $\omega_{2c} \in[0, 2\pi]$ satisfies

Similarly, by differentiating $\lambda$ with respect to $\tau_{2}$ in Eq (4.4) and computing Eq (4.13), we can obtain

here

4.3.   Properties of Hopf bifurcation

In this part, we shall study the direction of the Hopf bifurcation and the stability of bifurcating periodic solution of system (2.6) when $\tau_{1}$ is regarded as a parameter, $\tau_{2} = \hat{\tau}_{2}$ is a fixed value. Similarly, we can discuss other cases. The approach employed here is the normal form method and center manifold theorem introduced by Hassard et al.^[52] and Guckenheimer et al.^[53]. It follows from implicit function theorem ^[53] and the third equation of system (2.6) that $E(t) = \frac{mm_{2}y(t)}{q(py(t)-c)-mm_{1}}$. Hence, system (2.6) can be transformed as follows

Some transformations associated with $P^{*}(x^{*}, y^{*})$ are given as follows:

Here, we define $\bar{\tau}_{1} = \mu+\tau_{1c}$, then $\mu = 0$ is the Hopf bifurcation value of system (2.6).

By simplifying, system (2.6) can be transformed to the following functional differential equation that is in the Banach space of continuous functions mapping $C = C([-\tilde{\tau}, 0], \mathbb{R}^{2})(\tilde{\tau} = \text{max}\left\{\tau_{1c}, \hat{\tau}_{2}\right\})$, here $\tau_{1c}, \hat{\tau}_{2}$ are defined in (4.16) and (4.21), respectively,

here,

Based to Riesz representation theorem ^[54], there is a $2\times2$ matrix function $\eta(\theta, \mu)$, here, $\theta \in \left[-\tilde{\tau}, 0\right]$ and

where $\phi(\theta) = (\phi_{1}(\theta), \phi_{2}(\theta)\in C([-\tilde{\tau}, 0], \mathbb{R}^{2}),$ and

here, $\delta$ denotes the Dirac delta function.

Next, for $\phi \in C_{1}([-\tilde{\tau}, 0], \mathbb{R}^{2})$, we define the operator $A(\mu)$ as

where $F(\mu, \phi) = (F_{1}(\mu, \phi), F_{2}(\mu, \phi))^{T}$ and

then system (4.23) is equivalent to

For $\psi \in C^{1}([-\tilde{\tau}, 0], (\mathbb{R}^{2})^{*})$, we suppose that

and a bilinear inner product

where $\eta(\theta) = \eta(\theta, 0)$.

From the above analysis, we know that $A$ and $A^{*}$ are adjoint operators. According to discussion in Subsection 4.2, $\pm i \alpha_{1c}$ are eigenvalues of both $A$ and $A^{*}$.

Suppose $q(\theta) = (1, \chi)^{T}e^{i\alpha_{1c}\tau_{1c}\theta}, \theta$ is eigenvector of $A$ corresponding to $i\alpha_{1c}$, which gives that $Aq (\theta) = i\alpha_{1c} q (\theta)$. Based on definition of $A$, (4.24), (4.25) and (4.26), we have

Hence, we can obtain $\chi = \frac{i\chi_{1c}-a_{11}e^{-i\alpha_{1c}\tau_{1c}}}{a_{12}}$.

Similarly, By simple computation, we can obtain eigenvector of $A^{*}$ corresponding to $i\alpha_{1c}$, i.e., $q^{*}(s) = D(1, \chi^{*})^{T}e^{i\alpha_{1c}\tau_{1c}s}$, here $\chi^{*} = \frac{i\alpha_{1c} -a_{11} e^{-i\alpha_{1c}\tau_{1c}}}{a_{23}}$.

In order to assume $\left\langle q ^{*}(s), q (\theta) \right\rangle = 1$, we can determine the value of $D$. Based on (4.28), we have

Hence, we can choose $\bar{D} = \frac{1}{1+\chi\bar{\chi^{*}}+a_{11}\tau_{1c}e^{-i\alpha_{1c}\tau_{1c}}}.$

Next, let $u_{t}$ be the solution of Eq (4.27) when $\mu = 0$, and

On the center manifold $C_{0}$, it gives that

$z$ and $\tilde{z}$ are local coordinates for $C_{0}$ in the direction of $q^{*}$ and $\bar{q}^{*}$.

For solution $u_{t}\in C_{0}$ of Eq (4.27), when $\mu = 0$, we have

Where,

It follows from Eq (4.29) and (4.30) that

By virtue of (4.30), (4.31) and (4.32), we have

where

According to comparing (4.31) with (4.33), we can obtain

By virtue of (4.30) and (4.32), we have

Here,

By comparing coefficient and computing, we can obtain

We know that

Based on (4.35) and (4.37), it derives that

Based on (4.36) and (4.38), we can obtain

Based on $q(\theta) = (1, \chi)^{T}e^{i\alpha_{1c}\tau_{1c}\theta}$, we have

where $E_{1} = (E^{1}_{1}, E^{2}_{1})$ is a constant vector.

Similarly, based on (4.36) and (4.39), we have

here, $E_{2} = (E^{1}_{2}, E^{2}_{2})$ is a constant vector.

By above definitions and conditions, we have

where $G_{1} = 2i\alpha_{1c}(2i\alpha_{1c}-a_{21}-a_{22})-a_{12}a_{23}$, $G_{2} = a_{11}(a_{21}+a_{22})-a_{12}a_{23}$.

By above analyses and the results of Kuang^[54], the following results can be given:

By computing Eq (4.40), we have the following theorem.

Theorem 4.9. In Eq (4.40), the following results are true.

(i) The sign of $\mu_{2}$ determines the direction of the Hopf bifurcation: if $\mu_{2} > 0 (\mu_{2} < 0)$, then Hopf bifurcation is supercritical (subcritical) and the bifurcating periodic solutions exist for $\tau > \tau_{1c} (\tau < \tau_{1c})$.

(ii) The sign of $\varepsilon_{2}$ determines the stability of the bifurcating periodic solution: the bifurcating periodic solutions are stable (unstable) if $\varepsilon_{2} < 0 (\varepsilon_{2} > 0)$.

(iii) The sign of $T_{2}$ determines the period of the bifurcating periodic solutions: the period increases (decreases) if $T_{2} > 0 (T_{2} < 0)$.

5.   Numerical simulation

In this section, some numerical simulation are presented for supporting the analytic results obtained.

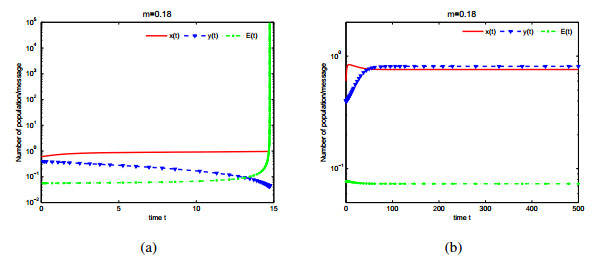
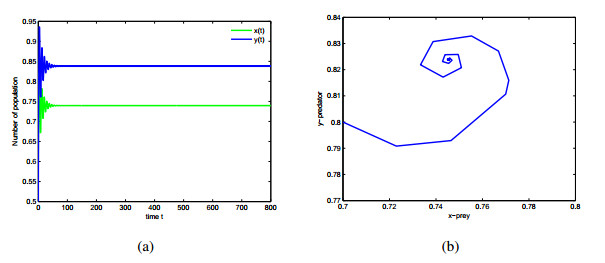
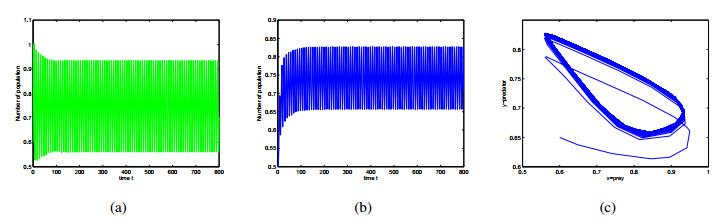
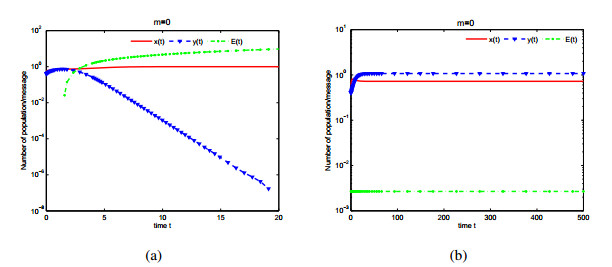
First, in order to verify some results of singularity induced bifurcations, the values of some parameters of system (2.6) are given: $a = 1, b = 2, c = 0.01, m_{1} = 0.8, \alpha = 2, \beta = 0.1, m_{2} = 1, p = 4,$ $q = 0.5, r = 0.15.$ When $\tau_{1} = \tau_{2} = 0$, singularity induced bifurcation occurs as $m = 0$ (see Figure 1) and $m = 0.18$ (see Figure 2) respectively. According to Theorem 4.3, we obtain that the feedback gain satisfies $\hat{k} = 1 > 0.19$. Thus state feedback controller $u(t) = (E(t)-0.008)$ is designed to stabilize system (4.1) as $m = 0$ (see Figure 1.(b)). According to Theorem 4.4, state feedback controller $\tilde{u}(t) = (E(t)-0.01)$ is designed to stabilize system (4.1) as $m = 0.18$ (see Figure 2.(b)).

Next, in order to show the phenomenon of Hopf bifurcation, the values of some parameters of system (2.6) are given: $a = 2, b = 1.02, c = 1.86, m_{1} = 0.3, \alpha = 0.5, \beta = 0.5, m_{2} = 1, p = 15.2, q = 0.05, r = 2.85$. When $m = 0.9 > 0$, if $(H_{4})$ or $(H_{5})$ holds, then $x^{*} = 0.745$ is obtained by solving Eq (3.2), that is, the interior equilibrium is $P^{*} = (0.745, 0.835, 2.760)$.

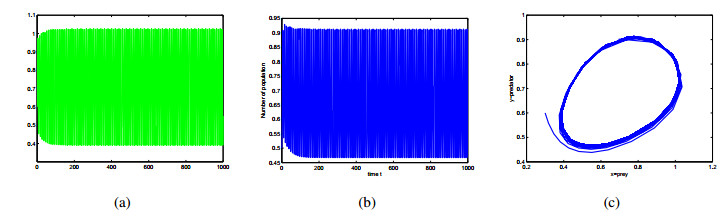
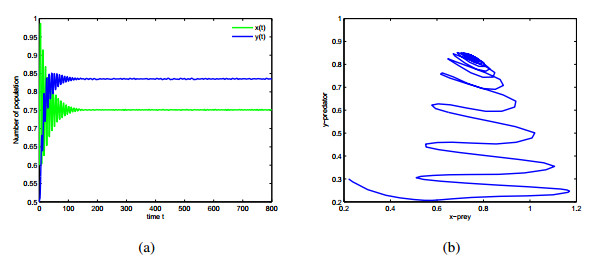
Based on Theorem 4.5, by computing $\xi_{4}^{2}-(\xi_{2}+ \xi_{5})^{2} = -0.609 < 0$, we have that system (2.6) is locally asymptotically stable around $P^{*}$ when $(\tau_{1}, \tau_{2}, m) \in \Omega_{1}\cap \Omega_{2} = \{(\tau_{1}, \tau_{2}, m)|0 < \tau_{1} = 1.5 < \tau_{10} = 2.4, \tau_{2} = 0, 0 < m < 22.4\}$. However, system (2.6) undergoes Hopf bifurcation around $P^{*}$ when $(\tau_{1}, \tau_{2}, m) \in \Omega_{1}\cap \Omega_{3} = \{(\tau_{1}, \tau_{2}, m)|\tau_{1} = 2.5 > \tau_{10} = 2.4, \tau_{2} = 0, 0 < m < 22.4\}$ (see Figures 3 and 4).

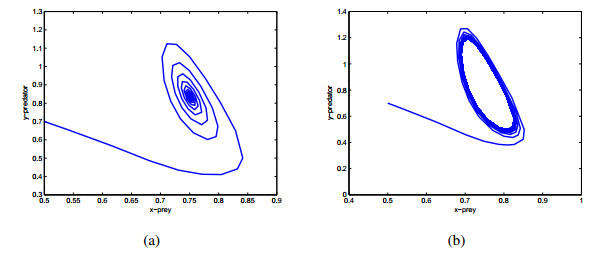
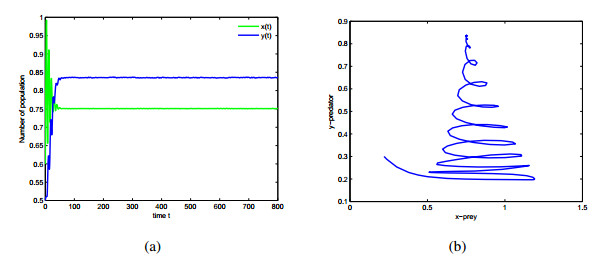
Similarly, system (2.6) is locally asymptotically stable around $P^{*}$ when $(\tau_{1}, \tau_{2}, m)\in \Omega_{1}\cap$ $\Omega_{4} = \left\{(\tau_{1}, \tau_{2}, m)|\tau_{1} = 0, \tau_{2} = 1.6 < \tau_{20} = 1.65, 0 < m < 22.4\right\}$. However, system (2.6) undergoes Hopf bifurcation around $P^{*}$ when $(\tau_{1}, \tau_{2}, m) \in \Omega_{1}\cap \Omega_{5} = \{(\tau_{1}, \tau_{2}, m)|\tau_{1} = 0$, $\tau_{2} = 1.8 > \tau_{20} = 1.65,$ $0 < m < 22.4\}$ (see Figure 5).

When we consider $\tau_{1}$ as a parameter and $\tau_{2} = 2.3$ as a fixed value based on Theorem 4.7, we know that Eq (4.15) has finite positive roots, and obtain the critical value of delay is $\tau_{1c} = 2.12$. Therefore, system (2.6) is locally asymptotically stable around $P^{*}$ when $(\tau_{1}, \tau_{2}, m) \in \Omega_{1}\cap \Omega_{6}\cap \Omega_{8} = \{(\tau_{1}, \tau_{2}, m)|0 < \tau_{1} = 2 < \tau_{1c} = 2.12, \tau_{2} = \hat{\tau}_{2} = 2.3$, $0 < m < 22.4\}$ (see Figure 6). However, when $(\tau_{1}, \tau_{2}, m) \in \Omega_{1}\cap \Omega_{6}\cap \Omega_{9} = \{(\tau_{1}$, $\tau_{2}, m)|\tau_{1} = 2.2 > \tau_{1c} = 2.12, \tau_{2} = \hat{\tau}_{2} = 2.3, 0 < m < 22.4\}$, system (2.6) undergoes Hopf bifurcation around $P^{*}$ (see Figure 7).

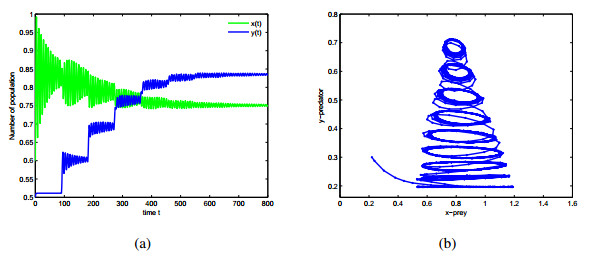
Similarly, we regard $\tau_{2}$ as a parameter and $\tau_{1} = 2$ as a fixed value. When $(\tau_{1}, \tau_{2}, m)\in\Omega_{1}\cap\Omega_{10}\cap\Omega_{12} = \left\{(\tau_{1}, \tau_{2}, m)|\tau_{1} = \hat{\tau}_{1} = 2, 0 < \tau_{2} = 6 < \tau_{2c}, 0 < m < 22.4\right\}$, system (2.6) is locally asymptotically stable around $P^{*}$ (see Figure 8). However, when $(\tau_{1}, \tau_{2}, m)\in\Omega_{1}\cap \Omega_{10}\cap \Omega_{13} = \{(\tau_{1}, \tau_{2}, m)|\tau_{1} = \hat{\tau}_{1} = 2, \tau_{2} = 90 > \tau_{2c}, 0 < m < 22.4\}$, system (2.6) undergoes Hopf bifurcation (see Figure 9).

Based on Theorem 4.9, we can obtain $\mu_{2} = -0.06 < 0, \varepsilon_{2} = -30.57 < 0$ and $T_{2} = -146020 < 0$. Thus, Hopf bifurcation is subcritical and the bifurcating periodic solutions exist for $\tau_{1} < \tau_{1c}$, bifurcating periodic solutions are stable and the period decreases because of $\varepsilon_{2} < 0, T_{2} < 0$.

6.   Conclusions

It is well known that commercial harvesting and economic benefits have a strong impact on the dynamical behavior. Liu et al. ^[44] investigated a differential-algebraic prey-predator system with linear harvesting on predator and Holling-II. Li et al. ^[45] analyzed a differential-algebraic prey-predator system without time delay. However, nonlinear harvesting and Beddington-DeAngelis functional response more realistic. Therefore, this paper proposed a singular Beddington-DeAngelis predator-prey model with two delays and nonlinear predator harvesting by extending the work of references ^[44] and ^[45], and obtained some results. The existence of equilibria was analyzed. Without considering time delay, the existence of singularity induced bifurcation by regarding economic interest as bifurcation parameter was discussed. In order to remove singularity induced bifurcation and stabilize system (4.1), state feedback controllers $u(t) = (E(t)-0.008)$ (see Figure 1b) and $\tilde{u}(t) = (E(t)-0.01)$ (see Figure 2b) were designed, which shows that the system can be kept in a stable state with benefits by capturing predators. While considering time delay, stability of system were discussed by analyzing the corresponding characteristic transcendental equation. When $\tau_{2} = 0$, the critical value of time delay is $\tau_{10} = 2.4$; when $\tau_{1} = 0$, the critical value of time delay is $\tau_{20} = 1.65$; when $\tau_{1}$ is regarded as a parameter and $\tau_{2}$ as a fixed value, the critical value of time delay is $\tau_{1c} = 2.12$. At the same time, when $\tau_{2}$ is regarded as a parameter and $\tau_{1}$ as a fixed value, the critical value of time delay is $\tau_{2c} = 81$. It was obvious that system lost local stability around it's corresponding interior equilibrium when time delays crossed corresponding the critical values, and Hopf bifurcations occurred (see Figures 4, 5b, 7, and 9). Finally, by using normal form theory and center manifold theorem, Hopf bifurcation is subcritical and the bifurcating periodic solutions exist for $\tau_{1} < \tau_{1c}$, bifurcating periodic solutions are unstable and the period decreases because of $\varepsilon_{2} < 0, T_{2} < 0$, which could be found in Theorem 4.9.

In fact, the prey and predator may be captured simultaneously in real world. Thus, in order to make this model more practical, nonlinear predator harvesting and nonlinear prey harvesting can be introduced into our predator-prey system, which is

We leave this work in the future.

Acknowledgments

The authors are grateful to the anonymous reviewers for their constructive comments. This work is supported by the National Natural Science Foundation of China (Grant Nos. 11661050 and 11861044), and the HongLiu first-class disciplines Development Program of Lanzhou University of Technology.

Conflict of interest

All authors declare no conflicts of interest in this paper.