Effect of edge and vertex addition on Albertson and Bell indices

Sadik Delen; Ismail Naci Cangul; Sadik Delen; Ismail Naci Cangul

doi:10.3934/math.2021055

AIMS Mathematics

2021, Volume 6, Issue 1: 925-937. doi: 10.3934/math.2021055

Previous Article Next Article

Research article

Effect of edge and vertex addition on Albertson and Bell indices

Sadik Delen ,
Ismail Naci Cangul ^,

Bursa Uludag University, Mathematics Dept., Gorukle 16059 Bursa-Turkey

Received: 25 August 2020 Accepted: 29 October 2020 Published: 05 November 2020
MSC : 05C07, 05C10, 05C30

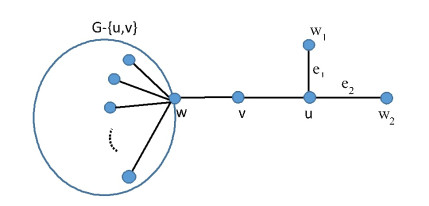
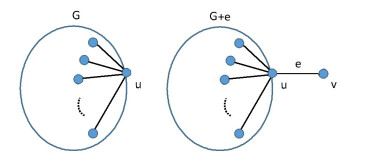
Topological graph indices have been of great interest in the research of several properties of chemical substances as it is possible to obtain these properties only by using mathematical calculations. The irregularity indices are the ones to determine the degree of irregularity of a graph. Albertson and Bell indices are two of them. Edge and vertex deletion and addition are important and useful methods in calculating several properties of a given graph. In this paper, the effects of adding a new edge or a new vertex to a graph on the Albertson and Bell indices are determined.

Keywords:

Citation: Sadik Delen, Ismail Naci Cangul. Effect of edge and vertex addition on Albertson and Bell indices[J]. AIMS Mathematics, 2021, 6(1): 925-937. doi: 10.3934/math.2021055

Related Papers:

[1]	Xuemin Fan, Wenjie Zhang, Lu Xu . Global dynamics of a predator-prey model with prey-taxis and hunting cooperation. Electronic Research Archive, 2025, 33(3): 1610-1632. doi: 10.3934/era.2025076
[2]	Érika Diz-Pita . Global dynamics of a predator-prey system with immigration in both species. Electronic Research Archive, 2024, 32(2): 762-778. doi: 10.3934/era.2024036
[3]	Yuan Tian, Hua Guo, Wenyu Shen, Xinrui Yan, Jie Zheng, Kaibiao Sun . Dynamic analysis and validation of a prey-predator model based on fish harvesting and discontinuous prey refuge effect in uncertain environments. Electronic Research Archive, 2025, 33(2): 973-994. doi: 10.3934/era.2025044
[4]	Jialu Tian, Ping Liu . Global dynamics of a modified Leslie-Gower predator-prey model with Beddington-DeAngelis functional response and prey-taxis. Electronic Research Archive, 2022, 30(3): 929-942. doi: 10.3934/era.2022048
[5]	Miao Peng, Rui Lin, Zhengdi Zhang, Lei Huang . The dynamics of a delayed predator-prey model with square root functional response and stage structure. Electronic Research Archive, 2024, 32(5): 3275-3298. doi: 10.3934/era.2024150
[6]	Xiaowen Zhang, Wufei Huang, Jiaxin Ma, Ruizhi Yang . Hopf bifurcation analysis in a delayed diffusive predator-prey system with nonlocal competition and schooling behavior. Electronic Research Archive, 2022, 30(7): 2510-2523. doi: 10.3934/era.2022128
[7]	Yujia Xiang, Yuqi Jiao, Xin Wang, Ruizhi Yang . Dynamics of a delayed diffusive predator-prey model with Allee effect and nonlocal competition in prey and hunting cooperation in predator. Electronic Research Archive, 2023, 31(4): 2120-2138. doi: 10.3934/era.2023109
[8]	Yichao Shao, Hengguo Yu, Chenglei Jin, Jingzhe Fang, Min Zhao . Dynamics analysis of a predator-prey model with Allee effect and harvesting effort. Electronic Research Archive, 2024, 32(10): 5682-5716. doi: 10.3934/era.2024263
[9]	Ailing Xiang, Liangchen Wang . Boundedness of a predator-prey model with density-dependent motilities and stage structure for the predator. Electronic Research Archive, 2022, 30(5): 1954-1972. doi: 10.3934/era.2022099
[10]	Ruizhi Yang, Dan Jin . Dynamics in a predator-prey model with memory effect in predator and fear effect in prey. Electronic Research Archive, 2022, 30(4): 1322-1339. doi: 10.3934/era.2022069

Abstract

1. Introduction

Dealing with optimization problems is maximizing or minimizing objective functions by selecting optimal parameters and schemes under given constraints. From the perspective of objective function, there are two branches of optimization problems, multi-objective problems and single-objective problems. The single-objective problems have a unique objective function and the result is an undisputed optimal solution. Multi-objective problems usually have multiple objective functions, and the result is usually a pareto optimal solution set, which usually requires trade-offs to select the relatively better solution.

From the perspective of decision variables, optimization problems are classified into continuous problems and discrete problems. In continuous problems, the decision variables belong to the field of real numbers. The range of continuum problems is vast, and the literature is rich, covering such hot fields as engineering, medical science, and machine learning ^[1,2,3]. However, the decision variables are often the elements of an integer set in discrete problems. There are many practical optimization problems in the field of discrete optimization, e.g., the Traveling Salesman Problem (TSP) ^[4,5,6], Graph Coloring Problem (GCP) ^[5] and DNA Sequence Design Problem (DSDP) ^[7]. TSP is classified as an Np problem because its time complexity is O (N!) ^[8]. Although the solution of TSP is very time-consuming ^[9], it still has many practical applications in many areas, e.g., DNA Fragment Assembly Problem (DFAP) ^[10], Job Shop Scheduling Problem (JSP) ^[11,12] and Vehicle Routing Problem (VRP) ^[13].

The methods for solving TSP are roughly classified into two categories in literature: deterministic algorithms and nondeterministic algorithms. The deterministic algorithms include, Branch and bound (BnB) ^[14], Dynamic Programming (DP) ^[15] and Lagrangian Dual (LD) ^[16], etc. However, as the size of TSP increases, the performance of such algorithms declines significantly ^[17]. nondeterministic algorithms are generally referring to approximation algorithms and meta-heuristic algorithms, where meta-heuristic algorithms can solve TSP well in controllable time cost. Numerous meta-heuristic algorithms for solving TSP were put forward in the existing literature. These algorithms usually use discrete operators to reconstruct the original algorithms. For example, Karuna Panwar reconstructed the Gray Wolf Optimizer (GWO) by 2-optimization (2-opt) and hamming distance to solve TSP ^[6]. Mesut Gunduz proposed a Discrete JAYA algorithm (DJAYA) to solve TSP. In DJAYA, roulette is used to control the behavior of the transformation operator, and two search trend parameters ST1 and ST2 are added to enhance comprehensive optimization ability ^[18]. Huang et al. put forward a nearest neighbor heuristic information mechanism and obtained Discrete Shuffled Frog-leaping Algorithm (DSFLA). In DSFLA, population diversity is maintained by adopting a reverse roulette strategy, and exploration ability is enhanced by utilizing a separate elite set mechanism ^[19]. Akhand et al. realized the discreteness of the Discrete Spider Monkey Optimizer (DSMO) by utilizing two new cross operators ^[20]. To deal with TSP, Cinar et al. put forward Discrete Tree Seed Algorithm (DTSA). In DTSA, a combination of multiple transformation operators is introduced to increase exploration ability, and the final solution is improved by 2-opt ^[21]. Yongquan Zhou et al combined 3-Opt and 2-Opt to propose a discrete invasive weed optimization algorithm (DIWO) to solve the TSP problem ^[22], and the team also proposed discrete flower pollination algorithms based on the order-based crossover, pollen discarding behavior and partial behaviors ^[23]. Although these algorithms have good performance, they still have room for improvement in robustness and time cost. In particular, The TSP is a practical problem with more stringent requirements for robustness and time cost. We hope to propose a new discrete algorithm with stable performance and fast running speed to solve TSP.

We put forward a Discrete Salp Swarm Algorithm (DSSA) for solving TSP. Salp Swarm Algorithm (SSA) is a swarm-based algorithm ^[24]. It was originally used to solve benchmark and real problems of continuous optimization, and SSA also has satisfactory performance in solving engineering design problems. There are two main reasons for proposing a discrete version of SSA to solve the TSP problem:

(1) There are few pieces of literature on the discretization of SSA, especially on TSP.

(2) The exploration mode of the SSA algorithm is that the leader leads the follower to move, which makes the approach of the whole population towards the optimal solution gradually, which is similar to the common neighborhood search idea in the TSP problem.

Therefore, this paper proposes an improved DSSA based on the properties of TSP, and compares it with many advanced meta-heuristic algorithms on 23 benchmark instances. Experimental results reflect DSSA the effectiveness and robustness in solving TSP. In addition, the application results of DSSA on TSP also illustrate the application prospect of this algorithm in solving discrete optimization problems. The rest is arranged as follows: In Section 2, TSP and the corresponding mathematical model are briefly described. The original SSA is briefly described in Section 3. In section 4, the d-opt operator, TPALS operator and DSSA are introduced. Section 5 proves that DSSA has good performance and robustness in solving TSP through several experiments. Finally, in Section 6, the conclusion is presented.

2. Traveling Salesman Problem (TSP)

We can describe TSP as follows, a salesman should pass multiple cities and towns to sell goods. The salesman starts in one city, passes through all the planned cities along the way, and ends his trip in the starting city. And to cut down time costs, the salesman should choose the shortest travel path as far as possible. The main difficulty of the TSP is that there are too many potential travel routes: for symmetric TSP of n cities, there is a total of (n-1)/2! Possible paths. The distance from the ith city to the jth city is calculated using Euclidean distance, as shown in Formula Eq (1) ^[6]:

${d}_{i, j} = \sqrt{{\left({x}_{i}-{x}_{j}\right)}^{2}+{\left({y}_{i}-{y}_{j}\right)}^{2}}$

(1)

The distance from the ith city to the jth city is defined di, j. xi and yi are x coordinate and y coordinate of the ith city, xj and yj are x coordinate and y coordinate of the jth city. To calculate the length of the travel path, we use the f function in Eq (2) ^[6]:

$\mathit{min}\left(f\right) = {d}_{n, 1}+{\sum }_{k = 1}^{n-1}{d}_{k, k+1}$

(2)

Where n is city numbers. If dj, i and di, j are equivalent(i = 1, 2, …, n), then it is called symmetric TSP. We need to find a least cost Hamiltonian path on a weighted graph in TSP ^[6].

3. Salps Swarm Algorithm (SSA)

SSA is a very efficient algorithm which is put forward by Seyedali Mirjalili in 2017, which is inspired by the phenomenon that salps move in a chain when foraging. There is one leader and many followers in salps, where the leader leads swarm to the food position, while followers directly or indirectly follow the leader ^[24].

The leader position is renew using Formula Eq (3):

${x}_{1, j} = \left\{\begin{array}{c}{F}_{j}+{c}_{1}\left(\left(u{b}_{j}-l{b}_{j}\right){c}_{2}+l{b}_{j}\right)\quad{c}_{3} > 0.5\\ {F}_{j}-{c}_{1}\left(\left(u{b}_{j}-l{b}_{j}\right){c}_{2}+l{b}_{j}\right)\quad{c}_{3}\le 0.5\end{array}\right.$

(3)

Where x1, j represent the jth dimension leader position and Fj represents the jth dimension food position. ubj represents the jth dimension upper bound, lbj represents the jth dimension lower bound. c2 and c3 are random numbers in [0, 1]. c1 is the key coefficient used to balance exploration and exploitation, its calculation formula is shown in Eq (4):

${c}_{1} = 2{e}^{-\left(\frac{4t}{T}\right)}$

(4)

Where T is maximum iterations and t is current iteration. The followers position is renewed using formula Eq (5):

${x}_{i, j} = \frac{1}{2}\left({x}_{i, j}+{x}_{i-1, j}\right)\quad i\ge 2$

(5)

Where xi, j represents the jth dimension position of follower i. See 1 for pseudocode about SSA.

Algorithm 1 The Classical SSA

Initialize the salp population x_i (i = 1, 2, ..., n) considering ub and lb
while (end condition is not satisfied)
  calculate the fitness of each salp
  F = the best salp
  update c₁ by (4)
  for each salp (x_i)
     if (i = = 1)
      update the position of the leading salp by (3)
     else
      update the position of the follower salp by (5)
     end if
  end for
  amend the salps based on the upper and lower bounds of variables
end while
return F

4. Discrete Salps Swarm Algorithm (DSSA)

4.1. d-opt

To cut down the time cost of 2-optimization (2-opt), we improved it to obtain a d-optimization (d-opt). 2-opt is a local search algorithm proposed by Croes ^[25] which is broad applied by researchers to deal with various discrete problems. The core idea of 2-opt is to select i and j, and then reverse the subsequence from i to j. If the path cost becomes smaller, perform this operation; otherwise, keep the original solution. For example, the original solution is A−D−C−B−E. If i = 2 and j = 5 are selected, the original solution is converted to A−E−B−C−D. The algorithm continuously improves the solution by repeating these steps.

The time cost of 2-opt is high for two main reasons: 1) 2-opt traverses all possible i and j (i ≠ j), 2) and calculates the total length of the path in each iteration. d-opt improves the above two disadvantages respectively. Firstly, parameter d is introduced to reduce the traversal scale. Where d represents the minimum distance from i to j selected, only subsequences with a length greater than d are selected to attempt inversion. Secondly, d-opt only calculates the change of path length after inversion, not the total path length. See Algorithm 2 and Algorithm 3 for pseudocode about d-opt.

4.2. TPALS

In order to better integrate the Problem Aware Local Search (PALS) algorithm into DSSA to solve TSP. We improve it to obtain Tsp Problem Aware Local Search (TPALS). PALS is a heuristic algorithm proposed by Alba and Luque in 2007 to solve DNA Fragment Assembly Problem (DFAP) ^[26]. The solutions of PALS are defined as sequences of ordinal numbers of DNA fragments and replaced the current solution with neighborhood information in each iteration. The neighborhood solution set is obtained by reversing the subsequence from given i to j in the current solution. Unlike 2-opt, the termination condition of PALS is that no better solution exists in the domain solution set.

Algorithm 2 d-opt (tour, d)
tour: Initial solution for i = 1: n-d for j = i+d:n deltaF ← CalculateDeltaF(tour, i, j) if (deltaF < 0) ApplyMovement (tour, I, j) end if end for end for return tour

Algorithm 3 CalculateDeltaF(tour, i, j)

calculate the path length len
if (i!= 1 and j!= len)
  deltaF ← d_{tour[i-1], tour[j]} – d_{tour[i-1], tour[i]} + d_{tour[i], tour[j+1]} – d_{tour[j], tour[j+1]}
else if (i == 1 and j!= len)
  deltaF ← d_{tour[i], tour[j+1]} – d_{tour[j], tour[j+1]} + d_{tour[len], tour[j]} – d_{tour[len], tour[i]}
else if (i!= 1 and j == len)
  deltaF ← d_{tour[i-1], tour[j]} – d_{tour[i-1], tour[i]} + d_{tour[i], tour^[1]} – d_{tour[j], tour^[1]}
else if (i == 1 and j == len)
  deltaF ← d_{tour[i], tour[j]} – d_{tour[j], tour[i]}
end if
return deltaF

Two problems need to be overcome in applying PALS to TSP. Firstly, the indicator for evaluating the neighborhood solution set in PALS is contig, so we delete the calculation about contig and take the solution with a shorter path length as the better solution among the neighborhood solutions. Secondly, there is no need to consider the overlap score between the last fragment and the first fragment in DFAP, so we add the calculation of the last path back to the starting point in TPALS. See Algorithm 4 for pseudocode about TPALS, where deltaF is also calculated with Algorithm 3.

4.3. The proposed Discrete Salps Swarm Algorithm (DSSA)

SSA was originally put forward to solve continuous problems, while TSP is discrete. Therefore, we use discrete operators to reconstruct the original SSA to solve the TSP. The discrete operators used are d-opt and TPALS mentioned above. To increase the exploration ability, we verify the effectiveness of five classical discrete crossover operators respectively, and introduced the operator with the best performance into DSSA. Each slap in the swarm represents a viable solution to TSP.

Algorithm 4 TPALS (tour)

tour: Initial solution
repeat
    L ← ∅
    for i = 1:n-1
      for j = i+1:n
        deltaF ← CalculateDeltaF(tour, i, j)
        if (deltaF < 0)
          L ← L ∪ (i, j, deltaF)
        end if
     end for
    end for
    if L ≠ ∅
       (i, j) ← SelectMovement (L)
       ApplyMovement(tour, i, j)
    end if
until no changes;
return tour

In the proposed method, d-opt is used to update leaders, and the update formula is shown in Eq (6):

$Tou{r}_{i} = d-opt\left(Tou{r}_{i}, d\right)$

(6)

Where Touri represents ith slap. d is a parameter used to control the search intensity of d-opt, and its updating formula is shown in Eq (7):

$d = [n\times (dMax- (dMax-dMin)\times \frac{t}{T}\left)\right]$

(7)

Where n is city numbers in TSP. The minimum and maximum value of d are defined as dMax and dMin. T is the maximum iterations and t is the current iteration. [.] is integer function.

We use TPALS and crossover operators to renew the followers position. There are 6 alternative crossover operators in this paper, and the best crossover operator is determined in Experiment 5.1. The update formula of followers is shown in Eq (8):

$Tou{r}_{i} = operator\left(Tou{r}_{i}, Tou{r}_{i-1}\right)$

(8)

Where operator is the best crossover operator determined in the experiment.

To enhance the exploration ability, DSSA introduced a mechanism named Second Leader Principle (SPL), whose core idea is that in each iteration, a second leader will appear among followers, and the second leader will also use TPALS to renew the position. The formula of second leader is shown in Eq (9):

$Tou{r}_{i} = TPALS\left(Tou{r}_{i}\right)$

(9)

The formula for calculating the probability of followers becoming the second leader is shown in Eq (10):

${p}_{i} = \frac{i}{N}\;i = 2, \dots , n$

(10)

Note that there is only one second leader in each iteration. In Algorithm 5, the pseudo code about DSSA can be obtained.

Algorithm 5 DSSA

Initialize the salp population Tour_i(i = 1, 2, ..., n)
while (end condition is not satisfied)
    calculate the fitness of each salp
    bestTour = the best salp
    update c₁ by (8)
    for each salp (Tour_i)
      if (i = = 1)
        update the position of the leading salp by (6)
      else
        update the position of the follower salp by (8) and (9)
      end if
    end for
end while
return bestTour

5. Experiments and results

We tested it on 23 benchmark instances of small, medium, and large symmetric TSP to verify the effectiveness of the DSSA ^[18]. Table 1 provides the relevant information of benchmark instances that appeared in the article. Where the number after the instance name represents the number of cities, for example, Oliver30 indicates that the benchmark instance has 30 cities. All the benchmark functions used in the paper are from TSPLIB.

Table 1. TSP instance used in the experiments.

Instance	Dimension size	Optimal
oliver30	30	420
att48	48	33522
eil51	51	426
berlin52	52	7542
st70	70	675
eil76	76	538
pr76	76	108159
kroA100	100	21282
kroB100	100	22141
kroC100	100	20749
kroD100	100	21294
kroE100	100	22068
eil101	101	629
lin105	105	14379
pr124	124	59030
pr136	136	96772
kroB150	150	26130
pr152	152	73682
u159	159	42080
pr226	226	80369
pr264	264	49135
pr299	299	48191
pr439	439	107217

| Show Table

DownLoad: CSV

All methods run 20 times for a comprehensive comparison. Each was run with the set parameters: population number $N$ = 50, iterations number $T = D+{\Sigma }_{i = 1}^{D}$ , where $D$ is the scale of the problem. The results were analyzed by Best, Avg, Standard deviation (Std) and Relative error (Re). The calculation formula of Re is shown in Eq (10) ^[18]:

${R}_{e} = \frac{Avg-optimal}{optimal}\times 100 \%$

(10)

Where Avg is the average value of the best path cost obtained by running the algorithm 20 times, and Optimal is the Optimal path cost of the benchmark instance. All experiments were carried out under the same experimental environment: Intel(R) Core (TM) I510500 3.10 GHz CPU and 16.00 GB RAM, and were programmed on MATLAB R2020b. The parameters of the algorithm used in this article are shown in Table 2.

Table 2. Parameter settings.

Algorithms	Parameters	Values
DSSA	Population size	50
	Crossover function	SEC
	C1	$\in$ [0.1, 0.9]
DGWO	Population size	50
DGWO	Crossover function	2-opt
ESA	Population size	50
	Successor functions	2-opt & insertion
	Temperature	−supΔf/ln(p)
	Cooling constant	0.95
GA	Population size	50
	Crossover function	OX
	Mutation functions	Insertion & 3-opt
	Cross. prob.	0.95
	Mut. prob	0.25
	Selection function	Binary tournament
	Survior function	Binary tournament
FDA	Population size	50
	Movement functions	2-opt & 3-opt
	Initial ${A}_{i}^{0}$	Random number in [0.7, 1.0]
	Initial ${r}_{i}^{0}$	Random number in [0.0, 0.4]
	α & γ	0.98
IDGA	Population size	50
	Crossover function	OB & OBX
	Mutation functions	Insertion & 3-opt
	Cross. prob.	[0.95, 0.9, 0.8, 0.75]
	Mut. prob	[0.05, 0.1, 0.2, 0.25]
	Selection function	Binary tournament
	Survior function	Binary tournament
	Migration strat.	Best–Replace–Worst

| Show Table

DownLoad: CSV

5.1. Experiment 1: Determine the best crossover operator

In order to determine the influence of crossover operators and parameter c1 on DSSA, this experiment studied five crossover operators and five parameter combinations on the 19 benchmark instances. The alternative Crossover operators are Partial-Mapped Crossover (PMX) ^[27], Order Crossover (OX) ^[28], position-based Crossover (PBX) ^[29], Order Based Crossover (OBX) ^[29] and Subtour Exchange Crossover (SEC) ^[30]. Table 3 shows the influence of different crossover operators on DSSA performance, in which bold numbers represent best results. From Table 3, When the SEC crossover operator is used, the Re of 19 instances is the smallest among all algorithms, and is less than one percent. In addition, see Table 4 for the Friedman test results of Best and Avg. From Table 4, the rank of DSSA-SEC is the smallest on both Best and Avg, and the p-value is much less than 0.05, which indicates that DSSA-SEC is obviously superior to other algorithms in performance and robustness. Therefore, SEC is regarded as the best crossover operator of DSSA.

Table 3. Performance analysis of crossover operators.

Instance	Algorithm	Best	Avg	Re	Time
oliver30	DSSA-PMX	420	420.1	0.02%	0.43
	DSSA-OX	420	420.75	0.18%	0.36
	DSSA-PBX	420	420.05	0.01%	0.47
	DSSA-OBX	420	421.1	0.26%	0.41
	DSSA-SEC	420	420	0.00%	0.46
att48	DSSA-PMX	33522	33738.3	0.65%	1.63
	DSSA-OX	33522	33817.7	0.88%	1.41
	DSSA-PBX	33522	33706.65	0.55%	1.74
	DSSA-OBX	33522	33866.1	1.03%	1.64
	DSSA-SEC	33522	33564.7	0.13%	1.78
eil51	DSSA-PMX	426	430.65	1.09%	1.95
	DSSA-OX	426	431.8	1.36%	1.70
	DSSA-PBX	428	433.6	1.78%	2.08
	DSSA-OBX	428	435.4	2.21%	1.97
	DSSA-SEC	426	427.55	0.36%	2.04
berlin52	DSSA-PMX	7542	7566.5	0.32%	2.07
	DSSA-OX	7542	7708.3	2.20%	1.79
	DSSA-PBX	7542	7577.75	0.47%	2.27
	DSSA-OBX	7542	7646.8	1.39%	2.14
	DSSA-SEC	7542	7542	0.00%	2.14
st70	DSSA-PMX	675	679.5	0.67%	4.93
	DSSA-OX	675	684.35	1.39%	4.48
	DSSA-PBX	675	680.45	0.81%	5.29
	DSSA-OBX	675	684.85	1.46%	5.33
	DSSA-SEC	675	675.05	0.01%	5.29
eil76	DSSA-PMX	541	549	2.04%	6.45
	DSSA-OX	542	553.3	2.84%	5.82
	DSSA-PBX	545	554.05	2.98%	6.84
	DSSA-OBX	538	555.25	3.21%	6.91
	DSSA-SEC	538	540.5	0.46%	7.02
pr76	DSSA-PMX	108159	108479.2	0.30%	6.38
	DSSA-OX	108280	109228.9	0.99%	5.79
	DSSA-PBX	108159	109075.8	0.85%	6.77
	DSSA-OBX	108309	109317.6	1.07%	6.83
	DSSA-SEC	108159	108159	0.00%	6.71
kroA100	DSSA-PMX	21282	21334.5	0.25%	14.77
	DSSA-OX	21343	21714	2.03%	14.31
	DSSA-PBX	21378	21512.55	1.08%	16.31
	DSSA-OBX	21282	21581.35	1.41%	16.90
	DSSA-SEC	21282	21287.8	0.03%	16.08
kroB100	DSSA-PMX	22141	22252.2	0.50%	14.83
	DSSA-OX	22283	22629.25	2.21%	14.41
	DSSA-PBX	22141	22507.3	1.65%	16.17
	DSSA-OBX	22258	22543.7	1.82%	16.82
	DSSA-SEC	22141	22159	0.08%	15.91
kroC100	DSSA-PMX	20749	20835.95	0.42%	14.71
	DSSA-OX	20853	21179.15	2.07%	14.43
	DSSA-PBX	20749	20972.65	1.08%	16.89
	DSSA-OBX	20749	21084.1	1.62%	16.85
	DSSA-SEC	20749	20758	0.04%	15.76
kroD100	DSSA-PMX	21294	21378.1	0.39%	15.19
	DSSA-OX	21294	21742.25	2.11%	14.44
	DSSA-PBX	21309	21744.3	2.11%	16.12
	DSSA-OBX	21343	21684.8	1.84%	17.13
	DSSA-SEC	21294	21323.45	0.14%	15.45
kroE100	DSSA-PMX	22068	22192.5	0.56%	15.04
	DSSA-OX	22111	22438	1.68%	14.42
	DSSA-PBX	22117	22423.75	1.61%	16.09
	DSSA-OBX	22068	22452.7	1.74%	17.08
	DSSA-SEC	22068	22100.35	0.15%	15.97
eil101	DSSA-PMX	633	643.65	2.33%	15.55
	DSSA-OX	635	653.55	3.90%	14.89
	DSSA-PBX	645	654.95	4.13%	17.11
	DSSA-OBX	647	655.7	4.24%	17.47
	DSSA-SEC	629	633.95	0.79%	16.87
lin105	DSSA-PMX	14379	14430.4	0.36%	17.08
	DSSA-OX	14379	14539.95	1.12%	16.85
	DSSA-PBX	14379	14461.35	0.57%	19.24
	DSSA-OBX	14379	14531.85	1.06%	19.95
	DSSA-SEC	14379	14381.2	0.02%	17.90
pr124	DSSA-PMX	59030	59080.4	0.09%	28.45
	DSSA-OX	59030	59563.4	0.90%	29.50
	DSSA-PBX	59030	59399.75	0.63%	33.46
	DSSA-OBX	59030	59362.8	0.56%	34.25
	DSSA-SEC	59030	59042.15	0.02%	30.52
pr136	DSSA-PMX	96956	97529.15	0.78%	40.27
	DSSA-OX	97609	99776.55	3.10%	39.50
	DSSA-PBX	97270	98644.85	1.94%	44.66
	DSSA-OBX	97889	99695.8	3.02%	46.27
	DSSA-SEC	96772	97048.7	0.29%	44.97
kroB150	DSSA-PMX	26141	26285.75	0.60%	54.36
	DSSA-OX	26324	26905.75	2.97%	54.69
	DSSA-PBX	26246	26679.6	2.10%	60.04
	DSSA-OBX	26411	26732.1	2.30%	63.88
	DSSA-SEC	26130	26176.45	0.18%	59.66
pr152	DSSA-PMX	73682	73866.4	0.25%	54.95
	DSSA-OX	74373	74739.95	1.44%	57.20
	DSSA-PBX	73818	74193.55	0.69%	63.69
	DSSA-OBX	73888	74405	0.98%	64.94
	DSSA-SEC	73682	73763.6	0.11%	60.20
u159	DSSA-PMX	42080	42339.7	0.62%	62.77
	DSSA-OX	42535	43654.4	3.74%	66.44
	DSSA-PBX	42080	42998.9	2.18%	73.35
	DSSA-OBX	42080	43154.8	2.55%	75.62
	DSSA-SEC	42080	42132.8	0.13%	65.58

| Show Table

DownLoad: CSV

Table 4. Friedman test of DSSA with different crossover operators.

Rank & p	DSSA-PMX	DSSA-OX	DSSA-PBX	DSSA-OBX	DSSA-SEC
rank (Best)	2.39	3.63	3.34	3.47	2.16
p	5.999E-05
rank (Avg)	2.11	4.37	3.21	4.32	1.00
p	3.774E-13

| Show Table

DownLoad: CSV

5.2. Experiment 2: Comparisons with DSSA, ESA, GA, IBA and IDGA

In this experiment, DSSA was compared with several classical or advanced algorithms (DGWO, DFA, DICA, ESA, GA, IBA, IDGA), which have been taken from recently published work ^[6,31]. Table 5 shows the performance of eight algorithms on 23 benchmark instances, with the best results in bold. Where "\" indicates that the algorithm has not been tested on related problems in the original literature. As can be seen from Table 5, DSSA achieved the best results in all indicators. On the one hand, from the Best index, DSSA can get the theoretical optimal value in 23 instances, which shows that DSSA has satisfactory performance in solving TSP problems. According to the analysis, this may be due to the SEC operator and d-opt operator which gradually reduces the search range, which to some extent improves the accuracy of the optimal solution. On the other hand, from the Avg index, DSSA can win in all 23 instances, which shows that DSSA has satisfactory robustness in solving TSP problems. This shows that the combination of the TPALS operator and the SPL mechanism provides a certain degree of randomness to the algorithm and effectively avoids the algorithm falling into the local optimal solution. In addition, DSSA is superior to DGWO and slightly inferior to the other six algorithms in the Time index, this indicates that DSSA takes a little longer to solve the TSP problem, which may be due to the fact that both d-opt operator and TPALS operator contain the behavior of searching for the optimal solution of the neighborhood. But as a whole, the Re of these six algorithms is much larger than DSSA. If more than 1% of the instance of Re were considered as failures, 53.8% (7/13) of DGWO, 82.4% (14/17) of DFA, 88.2% (15/17) of DICA, 76.5% (13/17) of ESA, and 88.2% (15/17) of GA failed, 64.7% (11/17) of IBA and 88.2% (15/17) of IDGA failed. In all DSSA cases, the Re is less than 1%.

Table 5. Comparisons with DSSA, DGWO, DFA, DICA, ESA, GA, IBA and IDGA.

Fun	Alg	Avg	Best	Re (%)	Time	Fun	Alg	Avg	Best	Re (%)	Time
oliver 30	DSSA	420	420	0.00	0.5	eil 101	DSSA	633.95	629	0.79	16.87
	DGWO	\	\	\	\		DGWO	\	\	\	\
	DFA	420	420	0.00	0.4		DFA	659	643	4.77	13.3
	DICA	420	420	0.00	0.5		DICA	663.8	644	5.53	12
	ESA	420	420	0.00	0.7		ESA	658.4	650	4.67	16.3
	GA	422.8	420	0.67	0.2		GA	673.8	655	7.12	10.6
	IBA	420	420	0.00	0.4		IBA	646.4	634	2.77	13.1
	IDGA	421.5	420	0.36	0.2		IDGA	660.7	650	5.04	11.7
att 48	DSSA	33564.7	33522	0.13	1.8	lin 105	DSSA	14381.2	14379	0.02	17.90
	DGWO	33600	33523	0.23	3.0		DGWO	14520	14382	0.98	34.3
	DFA	\	\	\	\		DFA	\	\	\	\
	DICA	\	\	\	\		DICA	\	\	\	\
	ESA	\	\	\	\		ESA	\	\	\	\
	GA	\	\	\	\		GA	\	\	\	\
	IBA	\	\	\	\		IBA	\	\	\	\
	IDGA	\	\	\	\		IDGA	\	\	\	\
eil 51	DSSA	427.55	426	0.36	2.04	pr 124	DSSA	59042.15	59030	0.02	30.52
	DGWO	\	\	\	\		DGWO	59390.9	59030	0.61	44.4
	DFA	430.8	426	1.13	1.6		DFA	59404.3	59030	0.63	18.8
	DICA	432.3	426	1.48	1.8		DICA	59436.9	59030	0.69	19
	ESA	431.6	426	1.31	2.1		ESA	59593.6	59030	0.95	23.1
	GA	440.8	427	3.47	1.7		GA	59901	59030	1.48	17.3
	IBA	428.1	426	0.49	1.7		IBA	59412.1	59030	0.65	18.5
	IDGA	434.4	426	1.97	1.2		IDGA	59912.8	59072	1.50	17.8
berlin 52	DSSA	7542	7542	0.00	2.1	pr 136	DSSA	97048.7	96772	0.29	44.97
	DGWO	\	\	\	\		DGWO	99310.5	97826	2.62	74.3
	DFA	7542	7542	0.00	2.2		DFA	99683.7	97716	3.01	24.1
	DICA	7542	7542	0.00	2.5		DICA	99583.7	97736	2.91	24
	ESA	7542	7542	0.00	2.3		ESA	99858.3	98499	3.19	29.5
	GA	7542	7542	0.00	2.3		GA	100472.4	98432	3.82	23.8
	IBA	7542	7542	0.00	2.1		IBA	99351.2	97547	2.67	23.4
	IDGA	7542	7542	0.00	2.4		IDGA	99932.7	98532	3.27	23.7
st 70	DSSA	675.05	675	0.01	5.3	krob 150	DSSA	26176.45	26130	0.18	59.66
	DGWO	\	\	\	\		DGWO	26756.2	26320	2.39	125.2
	DFA	685.3	675	1.53	4.3		DFA	\	\	\	\
	DICA	684.7	675	1.44	4.1		DICA	\	\	\	\
	ESA	682.1	675	1.05	4.5		ESA	\	\	\	\
	GA	709.8	675	5.16	4.2		GA	\	\	\	\
	IBA	679.1	675	0.61	3.9		IBA	\	\	\	\
	IDGA	690.2	675	2.25	4.1		IDGA	\	\	\	\
eil 76	DSSA	540.5	538	0.46	7.0	pr 152	DSSA	73763.6	73682	0.11	60.20
	DGWO	\	\	\	\		DGWO	74230	73690	0.74	142.8
	DFA	556.8	543	3.49	5.3		DFA	74934.3	74033	1.70	32.1
	DICA	557.6	544	3.64	5.3		DICA	74886.7	74052	1.63	32
	ESA	553.7	546	2.92	5.8		ESA	74969.5	74172	1.75	39.5
	GA	565.4	545	5.09	5.6		GA	75658.3	74520	2.68	33.4
	IBA	548.1	539	1.88	5.1		IBA	74676.9	73921	1.35	31
	IDGA	557.7	545	3.66	5.1		IDGA	75126.7	74249	1.96	32
pr 76	DSSA	108159	108159	0.00	6.7	u159	DSSA	42132.8	42080	0.13	65.58
	DGWO	108900	108159	0.68	13.2		DGWO	42563.3	42142	1.14	142.8
	DFA	\	\	\	\		DFA	\	\	\	\
	DICA	\	\	\	\		DICA	\	\	\	\
	ESA	\	\	\	\		ESA	\	\	\	\
	GA	\	\	\	\		GA	\	\	\	\
	IBA	\	\	\	\		IBA	\	\	\	\
	IDGA	\	\	\	\		IDGA	\	\	\	\
kroA100	DSSA	21287.8	21282	0.03	16.1	pr 226	DSSA	80446.8	80369	0.10	248.4
	DGWO	\	\	\	\		DGWO	81153.7	80648	0.95	648.6
	DFA	21483.6	21282	0.95	10.3		DFA	\	\	\	\
	DICA	21500.3	21282	1.03	10.8		DICA	\	\	\	\
	ESA	21481.7	21282	0.94	14		ESA	\	\	\	\
	GA	21812.4	21350	2.49	9.9		GA	\	\	\	\
	IBA	21445.3	21282	0.77	10.6		IBA	\	\	\	\
	IDGA	21731.8	21345	2.11	10.7		IDGA	\	\	\	\
kroB100	DSSA	22159	22141	0.08	15.9	pr 264	DSSA	49166.15	49135	0.06	422.8
	DGWO	22444.6	22159	1.37	34.5		DGWO	\	\	\	\
	DFA	22604.8	22183	2.10	11.6		DFA	51837	50491	5.50	93
	DICA	22599.7	22180	2.08	11.3		DICA	51943.6	50553	5.72	94.1
	ESA	22602.2	22202	2.09	13.6		ESA	52198.5	51603	6.23	102.5
	GA	22687.4	22176	2.47	10.7		GA	52499.8	51712	6.85	92.1
	IBA	22506.4	22140	1.65	11.1		IBA	50908.3	49756	3.61	92.5
	IDGA	22712.6	22208	2.59	10.7		IDGA	52290	51653	6.42	94.5
kroC100	DSSA	20758	20749	0.04	15.8	pr 299	DSSA	48286.9	48191	0.20	633.7
	DGWO	21780	20749	1.58	34.4		DGWO	\	\	\	\
	DFA	21096.3	20756	1.67	12.8		DFA	49839.7	48579	3.42	149.1
	DICA	21103.9	20756	1.71	11.7		DICA	49880.3	48600	3.51	150.3
	ESA	21170.4	20749	2.03	15.4		ESA	50532.3	49242	4.86	158.7
	GA	21510.4	20861	3.67	10.2		GA	50817.1	49659	5.45	147.6
	IBA	21050	20749	1.45	12		IBA	49674.1	48310	3.08	147.2
	IDGA	21298.7	20830	2.65	11.2		IDGA	50513.3	49572	4.82	149.94
kroD100	DSSA	21323.5	21294	0.14	15.5	pr 439	DSSA	107562.3	107217	0.32	2261
	DGWO	\	\	\	\		DGWO	112850.3	110415	5.25	2811
	DFA	21683.8	21408	1.83	12.4		DFA	115558.2	111967	7.78	202.4
	DICA	21666.8	21399	1.75	12.6		DICA	115763.1	111983	7.97	203.7
	ESA	21726.5	21500	2.03	15.9		ESA	116706.9	113497	8.85	206.4
	GA	22184.6	21492	4.18	9.7		GA	116943.4	113576	9.07	208.4
	IBA	21593.4	21294	1.41	11.7		IBA	115256.4	11153	7.50	201.9
	IDGA	21696.9	21582	1.89	12.1		IDGA	116436.1	113207	8.60	205.7
kroE100	DSSA	22100.4	22068	0.15	16	\	\	\	\	\	\
	DGWO	22131	22410	1.54	34.3		\	\	\	\	\
	DFA	22413	22079	1.56	11.6		\	\	\	\	\
	DICA	22453.3	22083	1.75	11.7		\	\	\	\	\
	ESA	22499.7	22099	1.96	15		\	\	\	\	\
	GA	22741.3	22150	3.05	9.4		\	\	\	\	\
	IBA	22349.6	22068	1.28	11.4		\	\	\	\	\
	IDGA	22721.9	22110	2.96	12.6		\	\	\	\	\

| Show Table

DownLoad: CSV

5.3. Experiment 3: Convergence analysis

In this experiment, DSSA was compared with several classical or advanced algorithms (IBA, ESA and DFA), which have been taken from recently published work ^[6,31]. In Table 6, the average number (in thousands) of objective function evaluations required to reach the final solution for each instance is shown, with the best results in bold. From Table 6, on the one hand, the average evaluations number of DSSA is much smaller than the other algorithms, which indicates that DSSA shows better convergence in all 23 instances, on the other hand, the evaluations number of DSSA does not change significantly by orders of magnitude as the size of the problem rises, suggesting that DSSA has advantages in solving TSP on a larger scale. Finally, despite the longest single run time of the DSSA, the overall time cost of solving TSP can be reduced by determining the appropriate evaluations number. Therefore, the DSSA proposed in the paper is a promising approach to solving TSP.

Table 6. Convergence of DSSA, DFA, ESA nad IBA, expressed in thousands of objective function evaluations.

Instance / Algorithms	DSSA	DFA	ESA	IBA
oliver30	0.89	3.38	23.91	2.17
eil51	8.51	17.56	85.91	15.37
berlin52	1.99	23.68	128.26	20.07
st70	9.82	69.56	216.08	72.67
eil76	19.93	164.18	262.89	91.53
kroA100	19.24	812.56	784.84	739.86
kroB100	20.29	813.68	729.83	461.05
kroC100	14.81	835.79	726.35	872.51
KroD100	14.81	875.74	689.49	600.31
KroE100	20.89	843.72	791.76	602.94
3il101	32.86	617.83	598.11	512.73
pr124	16.92	1589.71	1446.91	1602.51
pr136	47.04	2763.8	2318.2	2866.6
pr152	23.19	4769.37	3853.91	4853.19
pr264	47.13	6686.39	6096.45	6375.46
pr299	113.26	7016.91	6731.23	6597.94
pr439	278.13	8736.28	8006.91	8346.85

| Show Table

DownLoad: CSV

6. Conclusion

As a swarm-based algorithm, SSA was put forward to deal with continuous optimization problems of single and multiple objectives. In this paper, we proposed a DSSA for solving TSP. Firstly, we improved 2-opt and PALS into d-opt and TPALS respectively, and added them into DSSA as discrete operators. Secondly, we made a comparative study of five crossover operators, and confirmed that SEC is the best crossover operator of DSSA and introduce it into DSSA. Finally, the proposed DSSA was compared with several advanced algorithms on 23 benchmark examples, and the results showed DSSA possesses satisfactory properties and robustness in solving TSP. In the process of experiment, we found that the SEC operator and d-opt operator which gradually reduced the search range could improve the exploitation ability of the algorithm and help to improve the accuracy of the optimal solution, and the combination of the TPALS operator and the second leader mechanism provided certain randomness to the algorithm, so that the algorithm could avoid falling into the local optimal solution. At the same time, DSSA also exposes the disadvantage of long running time. According to the analysis, it may be because the d-opt operator and TPALS operator both contain the behavior of searching for the optimal solution of the neighborhood. In the future, In the future, we plan to make improvements to address the long running time of DSSA, and we intend to put forward excellent and novel discrete operators for DSSA to deal with DNA fragment assembly problems.

Acknowledgement

This work is supported by 111 Project (No.D23006), by the National Natural Science Foundation of China (Nos. 62272079, 61972266), Liaoning Revitalization Talents Program (No. XLYC2008017), Natural Science Foundation of Liaoning Province (Nos. 2021-MS-344, 2021-KF-11-03, 2022-KF-12-14), the Postgraduate Education Reform Project of Liaoning Province (No. LNYJG2022493), the Dalian Outstanding Young Science and Technology Talent Support Program (No. 2022RJ08).

Conflict of interest

On behalf of all authors, the corresponding author states that there is no conflict of interest.

References

[1]	M. O. Albertson, The irregularity of a graph, Ars Combinatoria, 46 (1997), 219-225.
[2]	F. K. Bell, A note on the irregularity of graphs, Linear Algebra Appl., 161 (1992), 45-54. doi: 10.1016/0024-3795(92)90004-T
[3]	K. Das, N. Akgunes, M. Togan, A. Gunes, I. N. Cangul, A. Çevik, On the first Zagreb index and multiplicative Zagreb coindices of graphs, An. Sti. U. Ovid. Co-Mat., 24 (2016), 153-176.
[4]	K. Das, A. Yurttas, M. Togan, A. Çevik, I. N. Cangul, The multiplicative zagreb indices of graph operations, J. Inequal. Appl., 90 (2013), 1-9.
[5]	S. Delen, I. N. Cangul, A New Graph Invariant, Turkish Journal of Analysis and Number Theory, 6 (2018), 30-33.
[6]	S. Delen, I. N. Cangul, Extremal Problems on Components and Loops in Graphs, Acta Math. Sin., 35 (2019), 161-171. doi: 10.1007/s10114-018-8086-6
[7]	G. H. Fath-Tabar, I. Gutman, R. Nasiri, Extremely irregular trees, Bulletin (Académie serbe des sciences et des arts. Classe des sciences mathématiques et naturelles. Sciences mathématiques), 38 (2013), 1-8.
[8]	B. Furtula, Energy and Estrada Index of Phenylenes, Indian J. Chem. A, 47 (2008), 220-224.
[9]	B. Furtula, I. Gutman, Z. K. Vukićević, G. Lekishvili, G. Popivoda, On an old/new degree-based topological index, Bulletin Classe des sciences mathematiques et natturalles, 148 (2015), 19-31.
[10]	I. Gutman, B. Furtula, C. Elphick, Three New/Old Vertex-Degree-Based Topological Indices, MATCH Commun. Math. Co., 72 (2014), 617-632.
[11]	I. Gutman, N. Trinajstić, Graph theory and molecular orbitals III. Total π-electron energy of alternant hydrocarbons, Chem. Phys. Lett., 17 (1972), 535-538.
[12]	I. Gutman, M. Togan, A. Yurttas, A. S. Çevik, I. N. Cangul, Inverse problem for sigma index, MATCH Commun. Math. Co., 79 (2018), 491-508.
[13]	K. N. Prakasha, S. K. R. Polaepalli, I. N. Cangul, Minimum Covering Randic Energy of a Graph, Kyungpook Mathematical Journal, 57 (2017), 701-709.
[14]	P. S. Ranjini, V. Lokesha, I. N. Cangul, On the Zagreb indices of the line graphs of the subdivision graphs, Appl. Math. Comput., 218 (2011), 699-702.
[15]	P. S. Ranjini, M. A. Rajan, V. Lokesha, On Zagreb indices of the sub-division graphs, Int. J. Math. Eng. Appl., 4 (2010), 221-228.
[16]	M. Togan, A. Yurttas, I. N. Cangul, All versions of Zagreb indices and coindices of subdivision graphs of certain graph types, Advanced Studies in Contemporary Mathematics, 26 (2016), 227-236.
[17]	H. J. Wiener, Structural Determination of Paraffin Boiling Points, J. Am. Chem. Soc., 69 (1947), 17-20. doi: 10.1021/ja01193a005

This article has been cited by:

1.	Xiangwen Yin, Promoting peer learning in education: Exploring continuous action iterated dilemma and team leader rotation mechanism in peer-led instruction, 2023, 31, 2688-1594, 6552, 10.3934/era.2023331
2.	Xin Du, Quansheng Liu, Yuanhong Bi, Bifurcation analysis of a two–dimensional p53 gene regulatory network without and with time delay, 2023, 32, 2688-1594, 293, 10.3934/era.2024014

Reader Comments

Your name:*

Email:*
© 2021 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)