In dearth of parameterization, various uncertain-ordinary theories like the theory of fuzzy sets and the theory of probability, which failed to address the emergence of modern day sophisticated, complex, and unpredictable problems of various disciplines such as economics and engineering. We aim to provide an appropriate mathematical tool for resolving such complicated problems with the initiation and conceptualization of the notion of double-framed soft sets in hemirings. In the structural theory, h-ideals of hemirings play a key role, therefore, new types of h-ideals of a hemiring R known as double-framed soft h-interior ideals and double-framed soft h-ideals are determined. It is shown that every double-framed soft h-ideal of R is double-framed soft h-interior ideal but the converse is not true which is verified through suitable examples. Further, the conditions under which both these concepts coincide are provided. More precisely, if a hemiring R is h-hemiregular, (resp. h-intra-hemiregular, h-semisimple), then every double-framed soft h-interior ideal of R will be double-framed soft h-ideal. Several classes of hemirings such as h-hemiregular, h-intra-hemiregular, h-simple and h-semisimple are characterized by the notion of double-framed soft h-interior ideals.
1.
Introduction
Especially in reliability analysis and survival analysis, the scheme of progressive Type-Ⅱ censoring has been used most commonly. It is preferable than the classical Type-Ⅱ censoring scheme. In several real-life areas, progressive censorship is beneficial, including, industrial, life research and clinical settings applications. It permits the removal of the experimental units surviving until the test finishes. Assume an experiment of lifetime testing with n units are placed on the test and is not desirable to detect all failure times under the limitation of cost and time, so only part of failures of the units are observed, such sample is called censored sample. Only m(m<n) units of failure times can be observed in progressive censoring schemes. At the occurrence of the first failure, R1 of the n−1 surviving units are randomly selected and removed from the test and at the second observed failure, R2 of the n−R1−2 surviving units are randomly selected and removed and so on. Finally, at the time of mth failure, the experiment will stop, then the reset survived units Rm=n−R1−…−Rm−1−m are excluded from the test. The censoring sizes {Ri,i=1,..,m−1} are prefixed. We shall show the m ordered times of failure thus observed by X1:m:n,…,Xm:m:n. It is clear that n=m+m∑k=1Rk. These ordered failure times which are detected from this form of censoring are called progressively Type-Ⅱ censored order statistics. Various authors have researched the order statistics and progressive Type-Ⅱ censoring features of such a life test that is progressively censored. Some primary referred works are Balakrishnan and Aggarwala [1], Balakrishnan [2], Cramer and Iliopoulos [3], Raqab et al.[4], Mohie El-Din and Shafay [5], and Balakrishnan and Cohen [6].
The drawbacks of the progressive censorship scheme of Type-Ⅱ are that if the units are highly reliable, the experiment time can be very long. So, works of Kundu and Joarder [7] and Childs et al. [8] treat this problem by proposing a new type of censoring at which the stopping time of the experiment is min{Xm:m:n,T}, where T∈(0,∞) is pre-fixed beforehand. This type called progressive hybrid censoring scheme (PHCS). The total time of the experiment under PHCS will not exceed T. Several authors have studied the PHCS, see for instance the works Lin et al. in [9] and [10], Hemmati and Khorram in [11], and Moihe El-Din et al. [12].
The downside of the PHCS, on the other hand, is that it can not be implemented when so less failures can be detected before T. Due this cause, Cho et al. [13] proposed a general type of censoring called generalized PHCS in which the lower number of failures are pre-determined. The experiment of life-testing would save time and the expense of failures on the basis of this censoring scheme. Furthermore, due to further failures of experiment, statistical efficiency estimates are improved. The following section explains the comprehensive designation of the generalized PHCS and its advantages. One of the important special cases of the generalized PHCS is the adaptive progressive censoring. This type is the first special case of the generalized PHCS as will be shown later in Section 2. For recent work on this topic, see for example, Moihe El-Din et al. [14], Mohie El-Din et al. [15], Abu-Moussa et al. [16], Lee et al. in [17] and Parviz and Panahi in [18].
The contribution in this paper is that we consider the developing of the inference techniques for Burr Type-Ⅻ data based on the generalized PHCS, which is not considered in the literature. The Burr Type-Ⅻ distribution has the following density function (PDF) and distribution function (CDF), respectively given by
The survival and hazard functions are given, respectively, by
The Bayesian estimate ˆθBS relative to the squared error loss function is given by the mean of the posterior distribution
Assuming that the minimum loss exists at ˆθ=θ, it is possible to express the LINEX loss function as
The sign and magnitude of the υ shape parameter are the directions and degrees of asymmetry. It is easily seen that the (unique) Bayesian estimator of θ, denoted by ˆθredBL under the LINEX loss function, the value ˆθBL which minimizes Eθ|X_[LBL(ˆθ,θ)] is given by
given that the expectation involved Eθ|x_[exp(−υθ)] is finite. Calabria and Pulcini [19] have addressed the issue of selecting the value of the v parameter. The general entropy (GE) loss function is another widely used asymmetric loss function, it is given by
for κ>0, positive error has a more extreme impact than negative error, with negative errors being more severe than positive for κ<0. In this case, the Bayesian estimate ˆθBE relative to the GE loss function is given by
provided that the involved expectation Eθ|x_[θ]−κ is finite. It can be shown that, when κ=1, the Bayesian estimate in (1.8) coincides with the Bayesian estimate under the weighted squared error loss function. Similarly, when κ=−1, the Bayesian estimate in (1.8) coincides with the Bayesian estimate under the SE loss function.
The remainder of this paper is structured as follows: A summary of the model of generalized PHCS is provided in Section 2. Section 3 extracts the maximum likelihood (ML) estimates with their uniqueness property, while the Bayesian estimates for the unknown parameters, survival and hazard functions under three loss functions are derived in Section 4. Section 5 stems from the Bayesian single-sample prediction for all censoring stage failure times of all units withdrawn. While in Section 6 the Bayesian prediction for progressive order statistics from an unnoticed future sample of the same distribution. Simulation studies are conducted in section 7 for comparing the the efficiency of the proposed inferential techniques. In Section 8, data set is used for real life to demonstrate the theoretical findings. Finally, the paper is concluded in Section 9.
2.
The model explanation
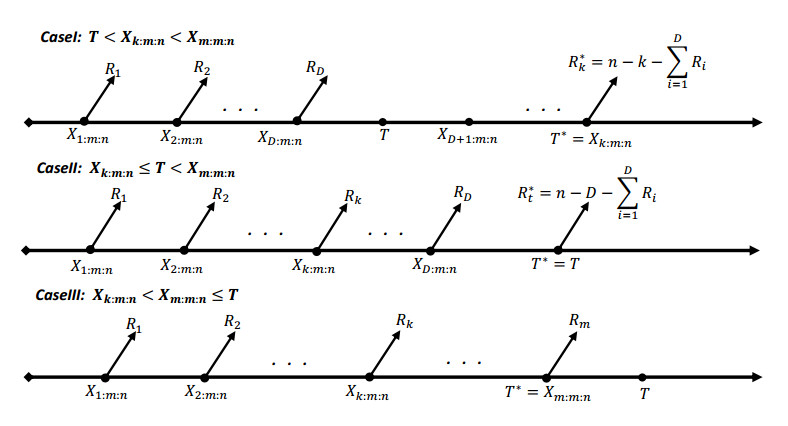
Consider a life study in which n equivalent units are tested. Let us denote to the lifetimes coming from a distribution with CDF, F(x|α,β) and PDF, f(x|α,β) by X1,X2,...,Xn. The generalized PHCS is as follows: Let T>0 and k,m∈{1,2,...,n} are pre-fixed integers in which k<m with the pre-determined censoring scheme R=(R1,R2,...,Rm) satisfying n=m+R1+…+Rm. At the occurrence of first failure, R1 of the remaining units are eliminated randomly. At the occurrence of the second failure R2, of the surviving units are eliminated from the experiment and so on until the termination time T∗=max{Xk:m:n,min{Xm:m:n,T}} is reached, at this moment the reset surviving units are eliminated from the test. The "generalized PHCS" changes PHCS by permitting the experiment to proceed beyond T, if only a few failures up to T are observed. Ideally, the experimenters would like to observe m failures within this system, but they will detect at least k failure. Let D indicate the number of failures observed up to T (see Figure 1).
As mentioned above, one of the following types of observations is given under the generalized PHCS:
1. Assume that the kth failure time is coming after T, then the termination of the experiment occurs at Xk:m:nand the observations are {X1:m:n<...<Xk:m:n}.
2. Assume that T is reached after the kth failure and before the mth failure. In this case, the termination time is T and we will observe {X1:m:n<...<Xk:m:n<Xk+1:m:n<...<XD:m:n}.
3. Assume that the mth failure detected after kth failure and before T, then the termination time is Xm:m:n and we will observe {X1:m:n<...<Xk:m:n<Xk+1:m:n<...<Xm:m:n}.
Now, the joint probability density function based on the generalized PHCS for all cases are given by:
where R∗j is the jth value of the vector R∗,
R∗τ is the number of units that are removed at T, given by
$$ and
The likelihood function of α,β under the generalized PHCS can be derived using (1.2) and (1.1) in (2.1), as
where W(β|x_)=D∗∑i=1(R∗i+1)ln(1+xβi)+R∗τln(1+Tβ) and xi=xi:D∗:n for simplicity of notation.
3.
Maximum likelihood estimation
The corresponding log-likelihood function is obtained from (2.6) as
equating the first derivatives of (3.1) with respect to β and α to zero, we get
ML estimates of the parameters α and β, ˆαML and ˆβML respectively, can be obtained by solving these two likelihood Eqs (3.2) and (3.3). We have employed the Newton-Raphson iteration method to evaluate ˆαMLand ˆβML. By using the invariance property the ML estimates of the corresponding survival and hazard functions are then given, respectively, by
3.1. Existence and uniqueness for MLEs
The MLE estimate for α can be obtained in an explicit form depending on ˆβML from (3.2) as follows,
Then, ^αML is exist and unique if ^βML exist and unique. Now, substituting by (3.6) in (3.3), we get
The MLE of β is obtained by solving the non-linear equation J(β)=0 in β. The question now, does the MLE of β is exist and unique? the answer of this question is related by the behavior of the function J(β). It is necessary to require at least two distinct observations xi≠xj for some i≠j in the sample, to can estimate the parameters α and β jointly. The following theorem shows the requirements that is necessary for the existence and uniqueness of ˆβML.
Theorem 3.1. Let x1≤x2≤...≤xD∗ be the data sample with at least two distinct values, then the MLE of ˆβ, and hence for ˆα, exist and unique if and only if xi<1 for some i(1≤i≤D∗).
Proof. The idea of the proof is to show that J(β) is a decreasing function with J(0)>0 and J(∞)<0, which mean that J(β) has a unique root in (0,∞), therefore ˆα also is exist and unique.
Now, after a straightforward algebraic manipulations, we can prove that
where
Its obvious that, J(∞)<0 if and only if xi<1 for some 1≤i≤D∗. Therefore, there exists at least one finite solution for the equation J(β)=0. Now, by showing that the function J(β) is monotone decreasing in β, by showing that its derivative J′(β) is less than zero, then it follows ˆβML is exist and unique.
For more details about the existence and uniqueness for the parameters of Burr Type-Ⅻ distribution in case of Type-Ⅱ censoring, see Wingo [20].
Example 1. In this example, a real data set represent the time to failure (in months) for electronic components on a test. These data was reported in Wingo [20]. Wing assumed that Burr Type-Ⅻ distribution is used to fit these lifetime data. The test performed using 30 units but its terminated after the failure of 20 units. The data is given as follows,
Here, we use these data to generate a generalized PHCS using the following steps, as follows
1. Case-Ⅰ Let T=1,k=15,m=20 and n=30, then (T<Xk<Xm) and the termination time is xk=1.8. The failure times are x={0.1,0.1,0.2,0.3,0.4,0.5,0.5,0.6,0.7,0.8,0.9,0.9,1.2,1.6,1.8} with censoring scheme R={0,1,0,0,2,0,0,0,3,0,0,0,0,0,9} and R∗T=0.
2. Case-Ⅱ Let T=2.55,k=15,m=20 and n=30, then (Xk<T<Xm) and the termination time is T. The failure times are x={0.1,0.1,0.2,0.3,0.4,0.5,0.5,0.6,0.7,0.8,0.9,0.9,1.2,1.6,1.8,2.3,2.5} with censoring scheme R={0,1,0,0,2,0,0,0,3,0,0,0,0,2,0,0,0} and R∗T=5.
3. Case-Ⅲ Let T=3.5,k=15,m=20 and n=30, then (Xk<Xm<T) and the termination time is Xm=3.1. The failure times are x={0.1,0.1,0.2,0.3,0.4,0.5,0.5,0.6,0.7,0.8,0.9,0.9,1.2,1.6,1.8,2.3,2.5,2.6,2.9,3.1}, with censoring scheme R={0,1,0,0,2,0,0,0,3,0,0,0,0,2,0,0,0,0,0,2} and R∗T=0.
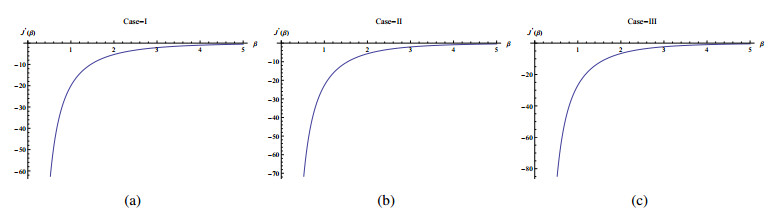
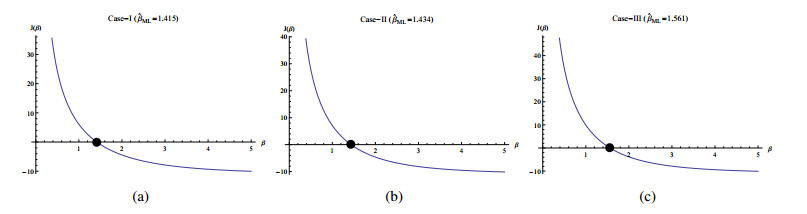
Figure 2 shows that the function J′(β) is a negative function in all cases, while Figure 3 shows that the function J(β) is a monotone decreasing function with only one root for J(β)=0.
This example shows that the MLE of β is exist and unique and hence α, where ˆαML equals 0.763076,0.774599 and 0.853238 for Case-Ⅰ, Case-Ⅱ and Case-Ⅲ, respectively.
3.2. Approximate confidence intervals for α and β
For large D∗, the observed Fisher information matrix of the parameters α and β is given by
where
and a 100(1−γ)% two-sided approximate confidence intervals for the parameters α and β are then
and
respectively, where V(ˆα) and V(ˆβ)are the estimated variances of ˆαML and ˆβML, which are given by the first and the second, diagonal element of I−1(ˆα,ˆβ), and zγ/2 is the upper (γ/2) percentile of standard normal distribution.
3.3. Approximate confidence intervals for R(t) and h(t)
Greene [21] used the delta method to construct the approximate confidence intervals for the survival and hazard functions depending in the MLEs. This method is used here in this subsection for calculating the linear approximation of that function, and then calculated the variance of the simpler linear function that can be used for large sample inference, see Greene [21] and Agresti [22].
where
and
Then, the approximate estimates of V(ˆR(t)) and V(ˆh(t))are given, respectively, by
where Gti is the tranpose of Gi, i=1,2. These results yields the approximate confidence intervals for R(t) and h(t) as:
and
4.
Bayesian estimations
Under the assumption that both parameters α and β are unknown, we may consider the joint prior density function of α and β which was suggested by Al-Hussaini and Jaheen [23] given by
where a, b, c, d are non-negative constants. If the hyper parameters a,b,c, and d are chosen to be equal zero, then the informative priors are reduced to the non-informative priors.
Upon combining (2.6) and (4.1), given the generalized PHCS, the posterior density function of α,β is obtained as
where
Hence, from (1.4), the Bayesian estimates of α and β under the squared error loss function are obtained, respectively, as
From (1.6), the Bayesian estimator of α and β under the LINEX loss function are obtained, respectively, as
From (1.8), the Bayesian estimator of α and β under the GE loss function are obtained, respectively, as
Since the integrals in (4.4), (4.5), (4.6), (4.7), (4.8) and (4.9) can't be computed analytically, so the Markov chain Monte Carlo (MCMC) method are used for evaluating these integrals. Now, depending on the posterior distribution in (4.2), the conditional posterior distributions π∗1(α|β;x_) and π∗2(β|α;x_) of the parameters α and β can be computed and written, respectively, as
and
Since, the conditional distribution of β in (4.11) is not a well-known distribution, the Metropolis-Hastings sampler is used to generate samples of β inside the MCMC algorithm; see Metropolis et al. [24]. MCMC algorithm (1) is used to generate samples of α and β from the conditional posterior distributions which will used for approximating the Bayes estimates of them.
Assume g(α,β) is any function in α and β, then the Bayesian estimates of g using the MCMC values, are obtained as follows:
based on SEL, the Bayesian estimate of g is given by,
Based on the LINEX loss function,
For the GEL function, the Bayesian estimate is given by,
The 100(1−γ)% Bayesian confidence intervals or credible intervals (L,U) for parameter θ (θ is α or β) if
Since the integration in (4.15) can't be solved analytically, so the 100(1−γ) MCMC approximate credible intervals for α and β using the (N−B) generated values after sorting it in an ascending order, (α(1),α(2),...,α(N−B)) and (β(1),β(2),...,β(N−B)), are given as follows,
and the lengths of the credible intervals are the absolute difference between the lower and the upper bounds.
5.
One-sample Bayesian prediction
For ρ=1,2,...,R∗j, let Xρ:R∗j denote the ρth order statistic out of R∗j removed units at stage j. Then, the conditional density function of Xρ:R∗j, given the observed generalized PHCS, is given, see Basak et al.[25], by
where
with xτ=T.
By using (1.2) and (1.1) in (5.1), given generalized PHCS, the conditional density function of Xρ:R∗j is then given as follows:
where Cq=(−1)q(ρ−1q)R∗j!(ρ−1)!(R∗j−ρ)! and ϖq=q+R∗j−ρ+1 for q=0,...,ρ−1.
Upon combining (4.2), (5.2) and using the MCMC technique, then the Bayesian predictive density function of Xρ:R∗j, given generalized PHCS, is obtained as
The Bayesian predictive survival function of Xρ:R∗j, given generalized PHCS, is given as
The Bayesian point predictor of Xρ:R∗j under the squared error loss function is the mean of the predictive density, given by
where f∗(x|x_) is given as in (5.3). The Bayesian predictive bounds of 100(1−γ)% two-sided equi-tailed (ET) interval for Xρ:R∗j can be obtained by solving the following two equations:
where ˉF∗(t|x_) is given as in (5.4), and LET and UET denote the lower and upper bounds, respectively. On the other hand, for the highest posterior density (HPD) method, the following two equations need to be solved:
and
where f∗(x|x_) is as in (5.3), and LHPD and UHPD denote the HPD lower and upper bounds, respectively.
6.
Two-sample Bayesian prediction
Let Y1:ℓ:N≤Y2:ℓ:N≤…≤Yℓ:ℓ:N be a future independent progressive Type-Ⅱ censored sample from the same population with censoring scheme S=(S1,...,Sℓ). In this section, we develop a general procedure for deriving the point and interval predictions for Ys:ℓ:N, 1≤s≤ℓ, based on the observed generalized PHCS. The marginal density function of Ys:ℓ:N is given by Balakrishnan et al. [26] as
where 1≤s≤ρ, c(N,s)=N(N−S1−1)...(N−S1...−Ss−1+1),Mq,s=N−S1−...−Ss−q−1−s+q+1,and cq,s−1=(−1)q{[q∏u=1s−q+u−1∑υ=s−q(Sυ+1)][s−q−1∏u=1s−q−1∑υ=u(Sυ+1)]}−1.
Upon substituting (1.2) and (1.1) in (6.1), the marginal density function of Ys:ℓ:N is then obtained as
Upon combining (4.2), (6.2) and using the MCMC method, given generalized PHCS, the Bayesian predictive density function of Ys:ℓ:N is obtained as
From (6.3), we simply obtain the predictive survival function of Ys:ℓ:N, given generalized PHCS, as
The Bayesian point predictor of Ys:ℓ:N, 1≤s≤m, under the squared error loss function is the mean of the predictive density, given by
where f∗Ys:ℓ:N(ys|x_) is given as in (6.3).
The Bayesian predictive bounds of 100(1−γ)% ET interval for Ys:ℓ:N, 1≤s≤m, can be obtained by solving the following two equations:
where ˉF∗Ys:ℓ:N(t|x_) is given as in (6.4), and LET and UET denote the lower and upper bounds, respectively. For the HPD method, the following two equations need to be solved:
and
where f∗Ys:ℓ:N(ys|x_) is as in (6.3), and LHPD and UHPD denote the HPD lower and upper bounds, respectively.
7.
Simulation study
Before progressing further, first we describe how we generate generalized PHCS data for a given set n, m, k, R1,R2,...,Rm and T. We use the transformation suggested in Balakrishnan and Aggarwala [1].
Thus, the generalized PHCS data can be easily generated as follows. If T<Xk:m:n<Xm:m:n, then we have Case Ⅰ and by using the transformation suggested in Ng et al. [27] and then the corresponding generalized PHCS is (X1:m:n,...,XD:m:n,XD+1:m:n...,Xk:m:n). If Xk:m:n<T<Xm:m:n, then we have Case Ⅱ and we find D such that XD:m:n<T<XD+1:m:n. The corresponding generalized PHCS is (X1:m:n,...,XD:m:n). If Xk:m:n<Xm:m:n<T, then we have Case Ⅲ and the corresponding generalized PHCS is (X1:m:n,...,Xm:m:n).
In this section, Monte Carlo simulation study is carried out to compare Performance under various ML and Bayesian estimates Schemes for sampling. Different values for n,m,k and T are used for generating 2000 generalized PHCS from the Burr Type-Ⅻ distribution (with α=2 and β=1). The values of T are chosen to ensure that the three cases of generalized PHCS are represented. So, T1 is chosen to be in the first quarter of data, while T2 is chosen around the mean. Finally, T3 is chosen to be within the third quarter. They chosen to be (T1,T2,T3)=(0.5,1.5,2.5). For the purpose of comparison, we computed the ML estimate and Bayesian estimates of α and β under the SE, LINEX (with υ = 0.5) and GE (with κ = 0.5) loss functions using informative priors (IP) and non-informative prior (NIP). Also, we have computed the mean square error (MSE) and the estimated expected bias (EB) for each estimate.
Different samples of size (n) are used for performing the simulation study with different effective samples sizes (m,k). While, the process of removing the survival units are executed using these censoring schemes
1. cheme 1: Ri=2(n−m)m if i is odd and Ri=0 if i is even.
2. Scheme 2: Ri=2(n−m)m if i is even and Ri=0 if i is odd.
3. Scheme 3: Ri=0 for i=1,2,...,D∗, Ri=n−D∗ for i=D∗.
All these cases adopted a cording to the case of generalized progressive censoring and all Bayesian results are computed based on two different choices of the hyper parameters (a,b,c,d), namely,
1. Informative prior (IP): a=80, b=20, c=20 and d=40 (by letting the mean of the marginal prior distribution of α is 2 and its variance is 0.05, and the mean of the marginal prior distribution of β is 1 and its variance is 0.05).
2. Non-informative prior (NIP): a=b=c=d=0.
The 90% and 95% asymptotic confidence intervals and Bayesian credible intervals for ˆα, ˆβ, ^R(t), and ^h(t) are constructed and its estimated average length (AL) is computed, also, the estimated coverage probabilities (CP) for these intervals were computed as the number of intervals that covered the true values divided by 2000. The credible intervals are obtained under informative and non-informative priors.
Tables 1–4 are present the values of MSE and EB of the ML and Bayesian estimates for α, β, S(x), and h(t) respectively based on different values of T under three different censoring schemes. While, Tables 5–8 are present the AL of 90% and 95% confidence intervals and corresponding CP for ˆα, ˆβ, ^R(t), and ^h(t), respectively.
From Tables 1–4 the computational results show that most cases, the Bayesian estimation based on the SE, Linex and GE loss functions is more precise than the ML estimation. Also, when n and m increase, the mean-squared error decreases. An exceptional case occurred when (n,m,k)=(50,20,15), it does not follow the pattern due to the effective number of failures is changed according to the occurred case. The effective sample size in this case may be 15, 20 or 15<D<20. Moreover, a comparison of the results for the informative priors with the corresponding ones, as we would expect. Finally, from the average length and coverage probabilities presented in Tables 5–8, we see that the estimates behave well in terms of the coverage probabilities and the Bayesian show better performance comparing with the ML estimates in terms of the average width.
8.
Data analysis
In order to show the performance of the inferential results established for the Burr Type-Ⅻ distribution bases on the generalized progressive hybrid censoring, we consider here the real data set that is used in Example 1, which is reported in Wingo [20]. Wing assumed that Burr Type-Ⅻ distribution is used to fit these lifetime data. The test performed using 30 units but its terminated after the failure of 20 units. We shall use these data to consider the following progressive censoring schemes: Suppose n=20,m=18and Ri=0 for i=1,...,16, R17=R18=1, then we would have the following progressive data: 0.1, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 0.9, 1.2, 1.6, 1.8, 2.3, 2.05, 2.6, and 2.9. We consider different k=16, and with different values of T, we have three different generalized PHCS, namely;
1. Scheme 1: Suppose T=2, since T<X16:18:20<X18:18:20, then the experiment would have terminated at X16:18:20, with R∗i=0 for i=1,...,15, R∗16=4, R∗τ=0, and we would have the following data: 0.1, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 0.9, 1.2, 1.6, 1.8, 2.3, and 2.05.
2. cheme 2: Suppose T=2.7, since X16:18:20<T<X18:18:20, then the experiment would have terminated at T=2, with R∗i=0 for i=1,...,16, R∗17=1, R∗τ=2, and we would have the following data: 0.1, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 0.9, 1.2, 1.6, 1.8, 2.3, 2.05, and 2.6.
3. Scheme 3: Suppose T=3.5, since X16:18:20<X18:18:20<T, then the experiment would have terminated at X18:18:20, with R∗=R, R∗τ=0, and we would have the following data: 0.1, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 0.9, 1.2, 1.6, 1.8, 2.3, 2.05, 2.6, and 2.9.
The ML and Bayesian estimates for the parameters, survival and hazard functions based on the generalized PHCS are obtained and presented in Table 9. The 90% and 95% asymptotic confidence interval and the credible intervals are constructed and presented in Table 10. Also, the point predictor and 95% equi-tailed and the HPD prediction intervals are computed for Ys:ℓ:N from the future progressively censored sample of size ℓ=5 from a sample of size N=10 with progressive censoring scheme S=(0,2,1,2,0) based on the generated generalized PHCS and two different choices of the hyper parameters as given in Section 7, these data are presented in Table 11.
The Bayesian results are computed based the joint prior density in (4.1) with two different choices of the hyper parameters (a,b,c,d), namely,
1. Informative prior (IP):a=24.2, b=29.2, c=18.432 and d=15.0685 (These values have obtained by letting the mean and variance for the marginal prior distribution of α equal ˆαML in case of complete data and 0.05, respectively. Also, the mean and variance for the marginal prior distribution of β equal ˆβML of the complete data and 0.05, respectively, then we solve the resulting two equations for each parameter).
2. Non-Informative prior (NIP):a=b=c=d=0.
Form Table 9, we noted that MLE is slightly larger than the Bayesian estimates based on NIP in the case of α and β. When it is compared with the Bayesian estimates based on the IP, we noted that its value is smaller than the Bayesian estimates of α and larger than the Bayesian estimates of β. From Table 10, in most cases, we noted the average length of the intervals is smaller in scheme 2 but not far from the other schemes. From Table 11, the the highest posterior density intervals of unobserved future sample gives accurate results than those of equi-tailed intervals, while the point predictor values are met our expectation compared with the original real data.
In general, we can conclude that the generalized PHCS is applicable when we are going to test the Burr Type-Ⅻ failure times of the electronic components. It is more suitable for saving the time and cost of the lifetime experiments.
9.
Conclusions
The ML and Bayesian estimates of the unknown parameters as well as the survival and hazard functions of the Burr Type-Ⅻ lifetime distribution are obtained when the observed sample is a generalized PHCS sample. The existence and uniqueness of the MLEs are investigated. In the Bayesian approach Squared error, Linex and general entropy loss functions based in informative and non-informative prior distributions are considered. The 90% and 95% asymptotic and credible confidence intervals are also constructed for the parameters as well as for the survival and hazard functions. The Bayesian point and interval prediction of future order statistics from the same sample were also developed for a progressive Type-Ⅱ of an unpredictable future sample. From the numerical results, we list the following concluding remarks:
1. The MLEs of the unknown parameters of the Burr Type-Ⅻ lifetime distribution based on the generalized PHCS sample are exist and unique if and only if there are some values below 1 in the sample.
2. In most cases, the Bayesian estimates depending on the informative priors perform better then the MLEs.
3. The results of ML estimates can be seen in Tables 1–4, as predicted, very similar to that of non-informational priors based on Bayesian estimators. Thus it is often easier to use the ML rather than the Bayesian estimators when we do not have preliminary knowledge about unknown parameters because the Bayesian estimators are computing more expensive.
4. In most cases, as n and m increase, the MSE decreases.
5. The average length of the confidence intervals is decreasing when the T increases. Further, the comparison of the results for the informative priors with those for non-informative priors indicates that the previous produces more accurate results, as we expect. In addition, when n and m increasing, the average length decreases.
6. The credible intervals perform well as compared with the asymptotic confidence intervals.
7. In all cases of confidence intervals, the 95% is wider than the 90% ones, as expected.
All in all, the proposed techniques depending on the generalized PHCS can be applied for testing the failure times of the products and electronic components which have Burr Type-Ⅻ failure times. Which will guarantee saving the testing time and decreasing the testing cost with a good efficiency of the analysis.
Acknowledgments
The authors are grateful to the anonymous referee for a careful checking of the details and for helpful comments that improved this paper. Also, The authors would like to thank the Deanship of Scientific Research at King Saud University for its funding this Research Group (RG-1435-056).
Conflict of interest
Authors declare there is no conflict of interest.









 DownLoad:
DownLoad: