The fractional-order unified chaotic system: A general cascade synchronization method and application

1.   Introduction

Since pioneering works of Pecora and Carroll's ^[1], chaos synchronization and control have turned a hot topic and received much attention in various research areas. A number of literatures shows that chaos synchronization can be widely used in physics, medicine, biology, quantum neuron and engineering science, particularly in secure communication and telecommunications ^[1,2,3]. In order to realize synchronization, experts have proposed lots of methods, including complete synchronization and $Q$-$S$ synchronization ^[4,5], adaptive synchronization ^[6], lag synchronization^[7,8], phase synchronization ^[9], observer-based synchronization ^[10], impulsive synchronization ^[11], generalized synchronization ^[12,13], lag projective synchronization ^[14,15], cascade synchronization et al ^{[16,17,18,19,20]}. Among them, the cascade synchronization method is a very effective algorithm, which is characterized by reproduction of signals in the original chaotic system to monitor the synchronized motions.

It is know that, because of the complexity of fractional differential equations, synchronization of fractional-order chaotic systems is more difficult but interesting than that of integer-order systems. Experts find that the key space can be enlarged by the regulating parameters in fractional-order chaotic systems, which enables the fractional-order chaotic system to be more suitable for the use of the encryption and control processing. Therefore, synchronization of fractional-order chaotic systems has gained increasing interests in recent decades ^{[21,22,23,24,25,26,27,28,29,30,31]}. It is noticed that most synchronization methods mentioned in ^{[4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20]} work for integer-order chaotic systems. Here, we shall extend to cascade synchronization for integer-order chaotic systems to a kind of general form, namely function cascade synchronization (FCS), which means that one chaotic system may be synchronized with another by sending a signal from one to the other wherein a scaling function is involved. The FCS is effective both for the fractional order and integer order chaotic systems. It constitutes a general method, which can be considered as a continuation and extension of earlier works of ^[13,16,19]. The nice feature of our method is that we introduce a scaling function for achieving synchronization of fractional-order chaotic systems, which can be chosen as a constant, trigonometric function, power function, logarithmic and exponential function, hyperbolic function and even combinations of them. Hence, our method is more general than some existing methods, such as the complete synchronization approach and anti-phase synchronization approach et al.

To sum up, in this paper, we would like to use the FCS approach proposed to study the synchronization of fractional-order chaotic systems. We begin our theoretical work with the Caputo fractional derivative. Then, we give the FCS of the fractional-order chaotic systems in theory. Subsequently, we take the fractional-order unified chaotic system as a concrete example to test the effectiveness of our method. Finally, we make a short conclusion.

2.   The method of FCS for fractional-order chaotic systems

As for the fractional derivative, there exists a lot of mathematical definitions ^[32,33]. Here, we shall only adopt the Caputo fractional calculus, which allows the traditional initial and boundary condition assumptions. The Caputo fractional calculus is described by

Here, we give the function cascade synchronization method to fractional-order chaotic systems. Take a fractional-order dynamical system:

as a drive system. In the above $x = (x_1, x_2, x_3)^T$ is the state vector, $f: R^3 \rightarrow R^3$ is a continuous function, $L x$ and $N(x)$ represent the linear and nonlinear part of $f(x)$, respectively.

Firstly, on copying any two equations of $(2.2)$, such as the first two, one will obtain a sub-response system:

with $y = (X_1, Z)^T$. In the above, $x_3$ is a signal provided by (2.2), while $\tilde{U} = (u_1, u_2)^T$ is a controller to be devised.

For the purpose of realizing the synchronization, we now define the error vector function via

where $\tilde{e} = (e_1, e_2)^T$, $\tilde{x} = (x_1, x_2)^T$ and $\tilde{Q}(\tilde{x}) = {\rm diag}({Q}_1(x_1), {Q}_2(x_2))$.

Definition 1. For the drive system (2.2) and response system (2.3), one can say that the synchronization is achieved with a scaling function matrix $\tilde{Q}(\tilde{x})$ if there exists a suitable controller $\tilde{U}$ such that

Remark 1. We would like to point out that one can have various different choices on the scaling function $\tilde{Q}(\tilde{x})$, such as constant, power function, trigonometric function, hyperbola function, logarithmic and exponential function, as well as limited quantities of combinations and composite of the above functions. Particularly, when $\tilde{Q}(\tilde{x}) = I$ and $-I$ ($I$ being a unit matrix), the problem is reducible to the complete synchronization and anti-phase synchronization of fractional-order chaotic systems, respectively. When $\tilde{Q}(\tilde{x}) = \alpha I$, it becomes to the project synchronization. And when $\tilde{Q}(\tilde{x})$ = ${\rm diag}(\alpha_1, \alpha_2)$, it turns to the modified projective synchronization. Hence, our method is more general than the existing methods in ^[4,13].

It is noticed from (2.5) that the system (2.3) will synchronize with (2.2) if and only if the error dynamical system (2.5) is stable at zero. For this purpose, an appropriate controller $\tilde{U}$ such that (2.5) is asymptotical convergent to zero is designed, which is described in the following theorem.

Theorem 1. For a scaling function matrix $\tilde{Q}(\tilde{x})$, the FCS will happen between (2.2) and (2.3) if the conditions:

(i) the controller $\tilde{U}$ is devised by

(ii) the matrix $\tilde{K}$ is a $2\times 2$ matrix such that

are satisfied simultaneously. In the above, $\tilde{P}(\tilde{x}) = {\rm {diag}}(\dot{Q}_1(x_1)\frac{ d^q x_1}{d t^q}, \dot{Q}_2(x_2)\frac{ d^q x_2}{d t^q})$, $\tilde{K}$ is a $2\times 2$ function matrix to be designed. While $\tilde{C} = (\tilde{C}_{ij})$ is a $2\times 2$ function matrix wherein

Remark 2. It needs to point out that the construction of the suitable controller $\tilde{U}$ plays an important role in realizing the synchronization between (2.2) and (2.3). Theorem 2 provides an effective way to design the controller. It is seen from the theorem that the controller $\tilde{U}$ is closely related to the matrix $\tilde{C}$. Once the condition $(2.8$) is satisfied, one will has many choices on the controller $\tilde{U}$.

Remark 3. Based on the fact that the fractional orders themselves are varying parameters and can be applied as secret keys when the synchronization algorithm is adopted in secure communications, it is believed that our method will be more suitable for some engineering applications, such as chaos-based encryption and secure communication.

Proof: Let's turn back to the error function given in (2.4). Differentiating this equation with respect to $t$ and on use of the first two equations of (2.2) and (2.3), one will obtain the following dynamical system

Assuming that $\lambda$ is an arbitrary eigenvalue of matrix $L_1+\tilde{K}$ and its eigenvector is recorded as $\eta$, i.e.

On multiplying (2.10) by $\eta^{\mathbf {H}}$ on the left, we obtain that

where ${\mathbf {H}}$ denotes conjugate transpose. Since $\bar{\lambda}$ is also an eigenvalue of $L_1+\tilde{K}$, we have that

On multiplying (2.12) by $\eta$ on the right, we derive that

From (2.11) and (2.13), one can easily get that

with $\Lambda = \tilde{C}+\tilde{C}^{\mathbf {H}}$. Since $\tilde{C}$ satisfy the condition (2.8), one can know that $\Lambda$ denotes a real positive diagonal matrix. Thus we have $\eta^{\mathbf {H}}\Lambda\eta > 0$. Accordingly, we can get

which shows

According to the stability theorem in Ref. ^[34], the error dynamical system (2.9) is asymptotically stable, i.e.

which implies that synchronization can be achieved between (2.2) and (2.3). The proof is completed.

Next, on copying the last two equations of (2.2), one will get another sub-response system:

where $X_1$ is a synchronized variable in (2.3), $z = (X_2, X_3)^T$ and $\bar{U} = (u_3, u_4)^T$ is the controller being designed.

Here, we make analysis analogous to the above. Now we define the error $\bar{e}$ via

where $\bar{e} = (e_3, e_4)^T$, $\bar{x} = (x_2, x_3)^T$ and $\bar{Q}(\bar{x}) = {\rm diag}({Q}_3(x_2), {Q}_4(x_3))$. If devising the the controller $\bar{U}$ as

and $L_2+\bar{K}$ satisfying

where $\bar{P}(\bar{x}) = {\rm {diag}}(\dot{Q}_3(x_2)\frac{ d^q x_2}{d t^q}, \dot{Q}_4(x_3)\frac{ d^q x_3}{d t^q})$, $\bar{C} = (\bar{C}_{ij})$ denotes a $2\times 2$ function matrix satisfying

then the error dynamical system (2.19) satisfies

Therefore, one achieve the synchronization between the system (2.2) and (2.18). Accordingly, from (2.5) and (2.23), one can obtain that

which indicates the FCS is achieved for the fractional order chaotic systems.

3.   Applications of FCS method to fractional-order unified chaotic system

In the sequel, we shall extend the applications of FCS approach to the fractional-order unified chaotic system to test the effectiveness.

The fractional-order unified chaotic system is described by:

where $x_i, (i = 1, 2, 3)$ are the state parameters and $a\in[0, 1]$ is the control parameter. It is know that when $0\leq a < 0.8$, the system (3.1) corresponds to the fractional-order Lorenz system ^[35]; when $a = 0.8$, it is the Lü system ^[36]; while when $0.8 < a < 1$, it turns to the Chen system ^[37].

According to the FCS method in section 2, we take (3.1) as the drive system. On copying the first two equation, we get a sub-response system of (3.1):

where $\tilde{U} = (u_1, u_2)^T$ is a controller to be determined. In the following, we need to devise the desired controller $\tilde{U}$ such that (3.1) can be synchronized with (3.2). For this purpose, we set the error function $\tilde{e} = (e_1, e_2)$ via :

On devising the controller $\tilde{U}$ as (2.6), one can get that the error dynamical system is

where

If choosing, for example, the matrix $\tilde{K}$ as

where $\lambda_1 > 0$ and $\lambda_2 > 0$, then one can obtain that

Therefore the dynamical system (3.4) becomes

According to Theorem 2, the synchronization is realized in the system (3.1) and (3.2).

Subsequently, on copying the last two equations of (3.1), we get another sub-response system:

where $\bar{U} = ({u_3, \ u_4})^T$ is the controller needed. When choosing the error function $\bar{e} = (e_3, e_4)$ as:

and the controller $\bar{U}$ as (2.20), where

and the matrix $\bar{K}$ is chosen by

where $\lambda_3 > 0$ and $\lambda_4 > 0$. Calculations show that the error dynamical system (2.19) becomes

which, according to the stability theorem, indicates that $\bar{e}$ will approach to zero with time evolutions. Therefore, the FCS is realized for the fractional-order unified chaotic system.

In the above, we have revealed that the FCS is achieved for the fractional-order unified chaotic system in theory. In the sequel, we shall show that the FCS is also effective in the numerical algorithm.

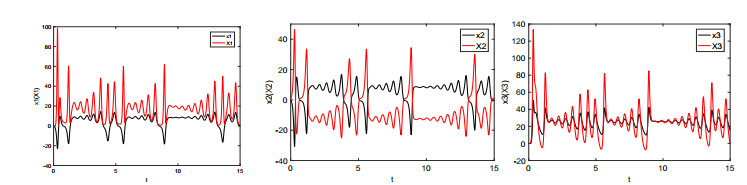
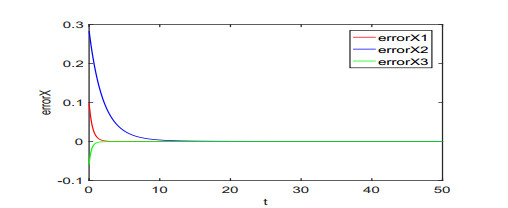
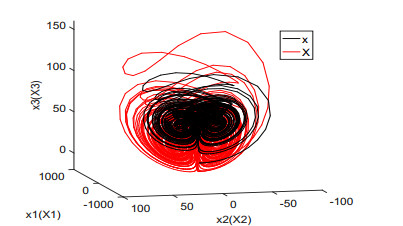
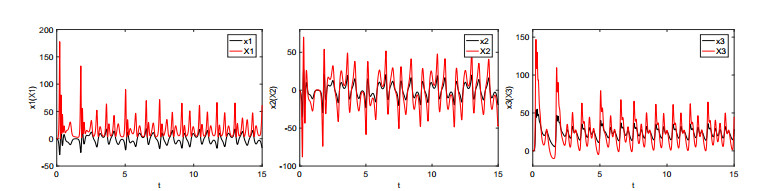
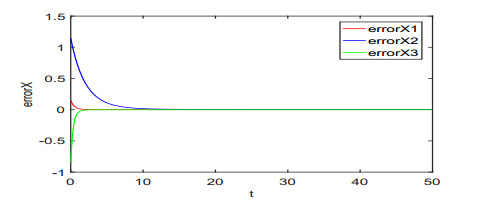
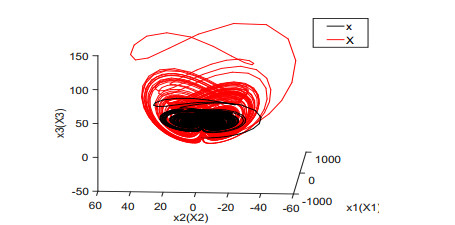
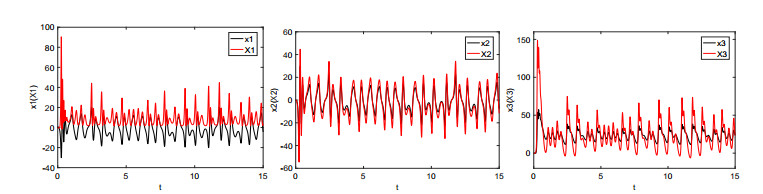
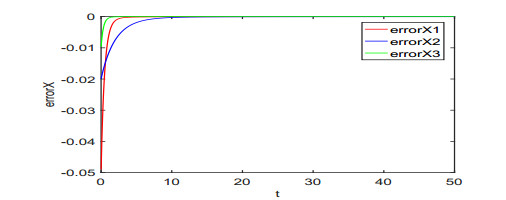
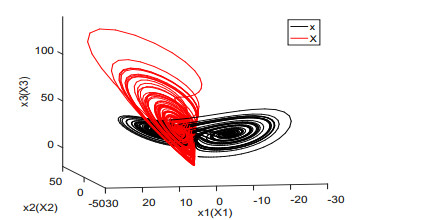
For illustration, we set the fractional order $q = 0.98$ and the parameters $\lambda_i (i = 1, \cdots, 4)$ as $(\lambda_1, \lambda_2, \lambda_3, \lambda_4) = (2, 3, 0.5, 0.3)$. It is noticed that when the value of $a\in[0, 1]$ is given, the system (3.1) will be reduced to a concrete system. For example, when $a = 0.2$, it corresponds to the fractional-order Lorenz system. The chaotic attractors are depicted in Figure 1. Time responses of states variables and synchronization errors of the Lorenz system are showed in Figures 2 and 3, respectively. When $a = 0.8$, it is the fractional-order Lü system. The chaotic attractors, time responses of state variables and synchronization errors are exhibited in Figures 4–6, respectively. When $a = 0.95$, it turns to the fractional-order Chen system. Numerical simulation results are depicted in Figures 7–9. From the chaotic attractors pictures marked by Figures 1, 4 and 5, one can easily see that the trajectories of the response system (colored red) display certain consistency to that of the drive system (colored black) because of the special scaling functions chosen. Meanwhile, one can also see the synchronization is realized from Figures 3, 6 and 9. Therefore, we conclude that the FCS is a very effective algorithm for achieving the synchronization of the fractional-order unified chaotic system.

4.   Conclusions

Chaos synchronization, because of the potential applications in telecommunications, control theory, secure communication et al, has attracted great attentions from various research fields. In the present work, via the stability theorem, we successfully extend the cascade synchronization of integer-order chaotic systems to a kind of general function cascade synchronization algorithm for fractional-order chaotic systems. Meanwhile, we apply the method to the fractional-order unified chaotic system for an illustrative test. Corresponding numerical simulations fully reveal that our method is not only accuracy, but also effective.

It is worthy of pointing out that the scaling function introduced makes the method more general than the complete synchronization, anti-phase synchronization, modified projective synchronization et al. Therefore, in this sense, our method is applicable and representative. However, the present work just study the fractional-order chaotic system without time-delay. It is known that in many cases the time delay is inevitably in the real engineering applications. Lag synchronization seems to be more practical and reasonable. Hence, it will be of importance and interest to study whether the FCS method can be used to realize the synchronization of fractional-order chaotic systems with time-delay. We shall considered it in our future work.

Acknowledgments

The authors would like to express their sincere thanks to the referees for their kind comments and valuable suggestions. This work is supported by the National Natural Science Foundation of China under grant No.11775116 and No.11301269.

Conflict of interest

We declare that we have no conflict of interests.