We provide a large deviation principle for jumps and stochastic diffusion processes, according to a viscosity coefficient (ε) and a small scaling parameter (δ) both going at the same rate. To do so we have to come up with estimates on the moment Lyapunov function trajectories.
1.
Introduction
In mathematical biology, predicting the time evolution of a biomass or a population over a spatial domain is a very important problem. Often, Lotka-Voterra-type equations are used to describe population dynamics, whether studying competition or predator-prey models. Such systems have been studied in many settings. Conditions under which two species can coexist have been treated theoretically. Numerical models have been developed that hope to mimic behavior of the system represented in the models. In the case that dispersion is occurring to each species, biomass or population studies over a domain ΩT=(0,T)×Ω for some Ω⊂Rd, generally with d=1,2, or 3 may take the general form
where L is a linear operator on Ω, distinct from the Laplacian, that can take various forms. If a1,a2>0 in system (1.1), then some degree of local diffusion of each species is modeled by the equations. The b1=b2=0 case has been considered by multiple authors, such as in [1,2,3,4] and in their accompanying references.
In real world settings, populations in competition may demonstrate diffusion, dispersion, or some degree of both local and nonlocal behaviors. Competition for common resources may not only follow in their immediate neighborhood, but also in the entire spatial domain. In addition, this competition is not necessarily occurring only between individuals at the same location, but also between individuals at different locations; see [5] and references therein for an excellent motivation for and summary of models of nonlocal dispersion operators. Following similar reasoning, when b1=b2=1, the operator L given by
has been motivated as an accurate reflection of dispersion between species for suitable J, and will be used here. The authors in [6] show the derivation of the nonlinear dispersion operator as J∗u−(J∗1)u, but then point out that it is unrealistic to use a convolution term to model biological species in bounded domains. Further, the restriction L in (1.2) of J∗u−(J∗1)u arises naturally in cases of hostile surroundings, a periodic environment, or under reflected boundary conditions. In [7], these assumptions are shown to be unnecessary, where the dispersion operator L in (1.2) is used to model nonlocal interaction. There, the authors show that for L, total internal energy is conserved and free energy decreases along trajectories so that L a suitable choice to reflect dispersion as a replacement for local dispersion modeled by the Laplacian for a symmetric interaction kernel J. Thus, operator L is also used both in nonlocal Allen-Cahn-type equations (c.f. [8]) or when describing population changes with nonlocal dispersion in biological systems (as in [9] and references therein).
Indeed, when restricted to ΩT⊂(0,T)×Rd, kernel function J in (1.2) becomes a measure of the probability that population members at all positions x affect those at y∈Rd, and vice-versa. Hence,
may be used to describe the rate at which members of a species are leaving x∈Ω at time t to travel to all other sites y∈Rd. Thus, for b1=b2=1, various forms of system (1.1) using L in (1.2) have also been studied in depth, including traveling wave solutions, spreading speed, stability of traveling waves, and of entire solutions as in [10,11,12], and references therein.
There has been a good deal of work on Lotka-Volterra models that include local diffusion, and more recently, nonlocal dispersion has been treated in such systems (see [1,2,3,4,13,14], along with references therein). In [15], an implicit approach to the numerical analysis of the system is introduced that mimics the dynamical properties of the true solution. In addition, it is proven that the scheme introduced there is uniquely solvable and unconditionally stable. The asymptotic behavior of the difference scheme is studied by constructing upper and lower solutions for the difference scheme. The convergence rate of the numerical solution to the true solution of the system is also given.
Following notation in (1.1) and (1.2) is
where Ω, ΩT, and L are defined previously. Here, u(t,x)≥0 and v(t,x)≥0 denote the population densities of the competing species for time t≥0 and x∈Ω⊂Rd for d=1,2. In addition, we assume that the system whose solutions describe the density of each species that began with (1.1) has been nondimensionalized, so that in (1.3), a,b,K1,K2>0 depend on the initial choice of constants in (1.1). To our knowledge, this system has not been analyzed with an unconditionally stable, nonstandard numerical method whose convergence rate can be given. This is the goal of this contribution.
As described previously, the system is used to model the two species competing with each other for the same prey, where both species are continuously distributed in time t throughout a region Ω, with each exhibiting free movement in the form of nonlocal dispersion. The method introduced to discretize (1.3) and the study of its properties will follow a similar development to the one used in [16], where properties of a single integro-differential equation that models an Ising spin system, with a convolution term that involves the Kac potential, are discussed in detail (see [17,18,19,20]).
In Section 2, we introduce the difference scheme used for the approximation of (1.3) over ΩT⊂(0,T)×R. We prove existence of the numerical solution to the scheme and that this solution is stable, independent of the choice of Δt and Δx. We give the convergence rate of the numerical scheme to the true solution. In Section 3, we present some results of numerical experiments that confirm the stability and convergence of the proposed difference scheme in one- and two-dimensional spatial domains Ω. In Section 4, we provide a summary of the results.
2.
A nonstandard numerical scheme
Analysis will be carried out over a domain Ω in one-dimensional space. All results carry over naturally to higher-dimensional space. For t>0 we introduce time step tk=kΔt for k=0,1,2,…, where Δt is of fixed size to be determined later. On the interval Ω=(−L,L)⊂R we define the partition
Using uki and vki to represent the numerical approximation to the true solutions u and v to (1.3) at (tk,xi), our choice of difference scheme for n=1 in (1.3) is nonstandard to invoke desirable properties that will be established later, namely
for k=0,1,2,… and for 0≤i≤N. Throughout, for convenience, the discretization of Lu as given in (1.2) for (2.1) will be denoted by
a similar expression is used for Lv. We also introduce the initial conditions in (1.3) as
for i=0,1,2,…,N, where for all i, u0(xi),v0(xi)≥0.
Solving (2.1) for uk+1i and vk+1i gives the iteration scheme for n=1 as
for k=0,1,2,… and i=0,1,2,…,N.
Although we present and prove theorems for n=1, it is useful for programming numerical models to show the method of approximating (1.3) for n=2 as well. In this case, we choose Ω=(−L,L)×(−W,W)⊂R2, and partitions
and
where △x=2L/M and △y=2W/N.
The difference scheme for (1.3) includes
together with
all for i=0,1,…,M and j=0,1,…,N, where in (2.4),
From (2.3) and (2.4), we arrive at the explicit finite difference scheme
for i=0,1,…,M, j=0,1,…,N, and k=0,1,2,….
Theorem 2.1. For n=1 and for the initial conditions in (1.3), let m1=maxu0(x), m2=maxv0(x), M1=max{K1,m1}, and M2=max{K2,m2}. Then for all k=0,1,2,… and for i=0,1,2,…,N,
Hence, the numerical scheme (2.2) is unconditionally nonnegative and unconditionally stable.
Proof. We proceed by induction. For k=0,
for i=0,1,2,…,N, so that (2.6) holds.
Assume now that (2.6) holds for some k∈N. Then for k+1,
Similarly, vk+1i≤M2, so the result holds for k+1 if it holds for k. Therefore, by mathematical induction, (2.6) is valid for all k=0,1,2… and for i=0,1,2,…,N. □
We now turn to the question of convergence of the difference equations (2.2) to the true solution of (1.3).
Theorem 2.2. If u,v∈C1,2([0,T]ׯΩ) are solutions to (1.3), then the solution of (2.2) converges to u and v as Δt,Δx→0, uniformly on [0,T], with rate O(Δt+Δx2).
Proof. Let (u(t,x),v(t,x)) represent the solution pair to (1.3), where u,v∈C1,2([0,T]ׯΩ). Set
We will prove the convergence claim based on u, then the same will follow for v by the symmetry of equations in (1.3). Let Δt=T/K, so that tk=kΔt for k=0,1,2,…,K. From (1.3) and (2.1) we have
where Ru is a function with Ru(Δt,Δx)=O(Δt+Δx2). Let
for k=0,1,2,…,K and i=0,1,2,…,N. Then X0i=0, Y0i=0, for i=0,1,2,…,N. Using (2.1) in conjunction with (2.7),
so that from (2.8),
We turn to upper bounds on each of the terms in (2.9). To accomplish this, for each k, k=0,1,2,…,K, we will use Wku=maxi|Uki−uki| and Wkv=maxi|Vki−vki|. Setting C1=maxi(J∗1)i,
and
Now, since |uki| and |vki| are uniformly bounded by M1 and M2, from (2.1),
where C(M1,M2,C1) is a constant that depends only on M1, M2, and C1. Hence there exists C2 such that
and
where K1 is that constant related to carrying capacity in (1.3), so that for some constants C3, C4, and C5,
and thus there exist constants C6, C7, and C8 with
Substituting (2.10) and (2.11) into (2.9), we obtain
for i=0,1,…,N, where C8 and C9 are constants independent of i and k, and where △t2-terms are absorbed into ΔtRu(Δt,Δx). Therefore, for each k, k=0,1,2,…,K,
Similarly, there exist C10 and C11 with
where, as with Ru, Rv is a function with Rv(Δt,Δx)=O(Δt+Δx2). Now setting Zk=Wku+Wkv, from (2.13) and (2.14), there exists a constant C0 with
for k=0,1,2,…,K. Set
Then since Z0=0, using (2.15) and (2.16) and iterating,
for k=0,1,2,…,K−1. Since ex≥1+x, it follows that eKx≥(1+x)K, so that for all k, k=0,1,2,…,K−1, and again using D from (2.16),
Thus, for k=0,1,2,…,K−1,
so that Zk→0 for k=0,1,2,…,K as Δt→0, Δx→0. This completes the proof. □
Remark. Similar results hold for n=2 in Theorems 2.1 and 2.2, and their proofs.
3.
Numerical results
In this section we finish by presenting some results of computational experiments that verify the stability and convergence of the proposed difference scheme, confirming that the numerical solutions preserve the properties of the theoretical solution as well as those guaranteed by Theorem 2.2. Since there is no exact solution to compare with the approximation generated by the difference scheme, we use fix △x and compute for various △t values, then vice-versa. We compare the results in tables. We also present graphical results for dimensions n=1 in (2.2) and n=2 in (2.5).
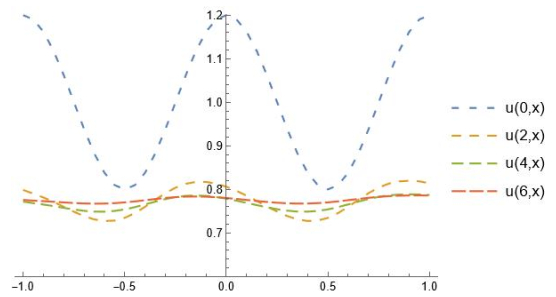
CASEI. For n=1, we test method (2.1) for Ω=(−1,1), ϵ=0.1, a=0.4, b=0.6, K1=K2=1, u0(x)=0.2cos(2πx)+1, and v0(x)=0.3sin(2πx)+1, where J(x)=(ϵ√π)−1exp(−x2/ϵ2). We call these approximations (u(t,x),v(t,x)). Their convergence to steady state solutions is demonstrated in Figures 1 and 2 for Δt=Δx=0.05, as an example, since convergence is independent of time and space steps and graphs look much the same for any reasonable choices of small Δt and Δx.
CASEIA: Hold △x=0.05. Let (u(t,x),v(t,x)) denote the numerical solution under the parameters as chosen above corresponding to △t, while (u1(t,x),v1(t,x)) corresponds to △t1. Table 1 shows the maximum absolute errors, max|u(t,x)−u1(t,x)| and max|v(t,x)−v1(t,x)|, at t=5 across Ω.
We note that the reduction of Δt by a factor of 0.5 reduces the error by O(Δt), as predicted by Theorem 2.2.
CASEIB: We fix △t=0.1 and vary △x. As before, we let (u(t,x),v(t,x)) represent the numerical solutions corresponding to △x, and let (u1(t,x),v1(t,x)) represent the numerical solutions corresponding to △x1. We compare the error differences max|u(t,x)−u1(t,x)| and max|v(t,x)−v1(t,x)| at t=5 across Ω.
We note that the reduction of Δx by a factor of 0.5 reduces the error by a factor of O(Δx2), or about 0.25, as stated in Theorem 2.2.
CASEII. For n=2, let Ω=(−1,1)×(−1,1), and let ϵ=0.1, a=0.4, b=0.6, u0(x,y)=0.4+0.2cos(2πx)cos(2πy), and v0(x,y)=0.5+0.3sin(2πx)sin(2πy), where Jϵ(x,y)=1ϵ2πexp(−x2+y2ϵ2).
We first show graphs of some approximate solutions generated by the two-dimensional method (2.5) for Δt=0.25, and Δx=Δy=0.2 in Figures 3 and 4. As in the one-dimensional case, since convergence is independent of time and space steps and graphs look much the same for any reasonable choices of small Δt and Δx, we have chosen these values as a representative of any such reasonable choice.
CASEIIA: We hold △x=△y=0.1 and compare accuracy for various △t-values in (2.5). Denote the numerical solution (u(t,x,y),v(t,x,y)) as the one generated by (2.5) corresponding to △t and (u1(t,x,y),v1(t,x,y)) corresponding to △t1. We compare the differences max|u(t,x,y)−u1(t,x,y)| and max|v(t,x,y)−v1(t,x,y)| at t=5 across Ω in Table 3.
CASEIIB: Finally, we carry out the same accuracy test for fixed Δt=0.25 and various Δx=Δy and Δx1=Δy1 values at time t=5. The results are displayed in Table 4.
All approximations in the tables show convergence at the rates predicted by Theorem 2.2.
4.
Conclusions
The foregoing results have motivated the use of a Lotka-Volterra-type equation with operator L that reflects intra-species dispersion, or nonlocal interaction, with competition between species whose populations are given by u and v. A nonstandard numerical scheme was introduced that is stable, independent of the choice of time step, and that yields biologically sensible (nonnegative) numerical approximations to populations u and v of this system. Moreover, this nonstandard scheme was shown to be convergent to the solution of the proposed system and the order of convergence given. Because its convergence was established, it is possible to state with confidence that accurate solutions to the system are shown in the numerical experiments that were offered to confirm the results.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
The authors would like to thank the reviewers for their help and insightful suggestions for improvement of this paper.
Conflict of interest
The authors declare there are no conflicts of interest.









 DownLoad:
DownLoad:





