Introduction
In the recent years, there has been a surge of interest in the investigation of problems defined by partial differential equations along the edges of a network (or graph), with particular transmission conditions at the nodes (or vertexes) of the graph (please see [12,14] for the usual terminology in graph theory). To cite only a few representative examples, see [26] for the case of an elliptic operator in a ramified domain, [30,31] for the Helmholtz equation in a network seen as a limit of a two-dimensional thin domain, or [1] for the resolution of the Hamilton-Jacobi equation. Respective problems are typically referred to as problems posed on quantum graphs, see [11].
The works that inspired the present article concern the modeling of the respiratory system [23]. To a first approximation, the human lung can be seen as a network of many small tubes (the bronchioli) inside which the air flows. In some models [23], the tubes are assumed to be thin enough so that the air pressure is constant in each cross-section: as a consequence, each tube can be represented by a (1D) edge of a graph. In addition, to take into account that the number of bronchioli is very large, the bronchioli network is modeled as an infinite tree with some fractal and self-similarity properties (as defined in the reference monograph [22]). Finally, one models the air flow by solving the Laplace equation in such a network (which includes implicitly nodal transmission conditions). The infinite nature of the tree is indeed the main source of difficulty from both mathematical and numerical points of view. In particular, to complete the model, one needs to impose some "boundary condition at infinity" whose precise meaning requires to work with the weak formulation of the problem and an adequate functional framework, as explained in more detail later in the paper.
Our motivation was to study the propagation of sound in such a structure. This is important in applications since sound propagation in the human lung can be used for the detection of some pathologies of the respiratory system [27,32]. Therefore, we have to study the wave equation (in short $ \partial_t^2 u + \mathcal{A} u = 0 $, where $ \mathcal{A} $ is a second order differential operator along the tree), instead of the Laplace equation. One of the particularities / difficulties of our model is that we need to consider a weighted wave equation, in order to account for the fact that the bronchioli have different thicknesses. This model can be justified by an asymptotic analysis with respect to the small transverse dimensions of the bronchiolar tubes (see [18,21]). From the physical point of view, such a model is somewhat unrealistic in the sense that it assumes that the boundaries of the bronchioli are rigid, neglecting the interaction with the parenchyma, which is the "elasto-acoustic" domain inside which the bronchioli network is embedded (see for instance [13] for the modelling of sound propagation inside the parenchyma, or [28] for the coupling issue, in the context of the air flow modelling). Thus, from the point of view of this particular application, studying this model has to be seen as a first step towards a more realistic modelling. Moreover, as we shall see in this paper, this "simple" model already raises exciting and challenging questions, from both mathematical and numerical points of view.
In particular, as far as numerical computations are concerned, the main source of difficulty is the infinite number of edges in the tree. Thus, we need to address the problem of truncating the computational domain to a finite subtree, which raises the question of the identification of the boundary condition [15] to be put at the artificial extremities of the truncated tree. This is the main motivation of this work. As we are going to see, we are able to give an answer to this question under the assumption that, after a certain generation, the subtrees are self-similar. It is worthwhile mentioning that the same type of questions was considered in a series of papers by Y. Achdou, N. Tchou and their collaborators: in these works, they do not study fractal trees but (particular) domains with a fractal boundary. In many papers they treat the Laplace operator [5,6,7], but also the time harmonic wave (Helmholtz) equation [3,2,4], for the solution of which they propose a particular iterative algorithm.
As a matter of fact, applying the Fourier-Laplace transform equation to the wave equation leads to study a family of Helmholtz equations parametrized by the frequency. This is the point of view that we shall adhere to for the construction of transparent boundary conditions. This approach emphasizes the close link between the properties of the solution of the wave equation and the spectral theory of the underlying elliptic operator $ \mathcal{A} $. Such a theory has been extensively studied in the literature when $ \mathcal{A} $ is the Laplace operator (see e.g. [36], [23]). However, those results concern only a special case of non-weighted Laplacians, and thus cannot be directly applied to our weighted "operator" $ \mathcal{A} $. On the other hand, an eigenvalue problem for the Laplacian with weights was considered in [24]; nonetheless, the problem setting is quite different from ours and does not seem easily adaptable to the problem we consider. For other related problems, in particular, properties of Sobolev and $ L^p $ spaces on trees please see [25,35,34]. Let us finally remark that some properties of weighted spaces on infinite graphs were studied in [16], however, in the context of the discrete Laplacian and respective energy norms.
The paper is organized as follows. In section 1, we provide a geometrical and functional framework for studying wave propagation problems defined on infinite trees. In particular, we define weighted Sobolev spaces on such trees, which allows to formulate rigorously the Dirichlet and Neumann problem on a tree, and to obtain the corresponding well-posedness result for the time-domain wave equation. Next, we discuss the question of the construction of transparent boundary conditions for truncating the computational domain to a finite tree. Such construction is based on a use of the Dirichlet-to-Neumann (DtN) operator. Finally, we recall some classical results about the well-posedness of the Helmholtz equation for complex frequencies, as well as the representation of the solution to the Helmholtz equation in the case when the resolvent of the Laplace operator is compact.
In section 2, we define a notion of a self-similar $ p- $adic weighted tree. In this short section we introduce specific notation, which we will use throughout the paper. Section 3 is dedicated to various properties of the Sobolev spaces defined on self-similar $ p $-adic weighted trees. Sections 3.1, 3.2 are devoted to a particular class of trees, for which prove the existence and continuity of a trace operator at infinity (section 3.1) and characterize its image and kernel (section 3.2). This operator is important for understanding the distinction between the Dirichlet and Neumann problems for this class of trees. This question is treated in complete detail in section 3.3. For the convenience of the reader, the summary of the results of sections 3.1-3.3 is given in section 3.4. Finally, in section 3.5, we study the crucial question of compactness of the embedding of Sobolev spaces, which governs the nature of the spectrum of the Laplacian and implies the meromorphicity of its resolvent.
Section 4 is dedicated to the analysis of the properties of the solutions of a family of Helmholtz equations parametrized by frequency. In particular, in section 4.1 we introduce the notion of quasi-self-similarity for functions depending on frequency, and show that on self-similar trees the solutions of the Helmholtz equation are quasi-self-similar. In section 4.2 we consider a particular case of the Lapace equation, for which the solutions are self-similar and can be obtained in explicit form.
Section 5 is devoted to various characterizations of transparent boundary conditions (the DtN operator) for the Helmholtz equation on self-similar trees. First of all, based on the results of the previous sections, we show the meromorphicity of the symbol of the DtN operator in section 5.1. In section 5.2 we demonstrate that it satisfies a certain non-linear equation. We prove in particular the uniqueness of the solution to this equation under appropriate conditions. Next, section 5.3 is dedicated to certain positivity properties of the symbol of the DtN, related to the stability of the transparent boundary conditions in the time domain. In section 5.4, we provide an algorithm for the evaluation of the symbol of the DtN for complex frequencies. The numerical results obtained with the help of this algorithm are given in section 5.5.
In section 6 we propose an approximation of the DtN operators that stems from the truncation of the Taylor series for their symbol. We thus obtain first- and second-order transparent boundary conditions, for which we prove the stability. Their efficiency is validated with the help of the numerical experiments.
Finally, section 7 is dedicated to the open questions and possible extensions of this work.
1.
Description of the problem
1.1. The wave equation in a graph
In this work we will conciliate the view of the graph as an algebraic structure with its vision as a geometric object, see [11]. A graph $ \mathbb{G} $ is defined by a set of vertices $ \boldsymbol{\mathcal{V}}: = \{M_v, \, v\in\mathcal{V}\} $, seen geometrically as a subset of $ \mathbb{R}^d $, $ d = 2, 3 $, and a set of edges $ {\boldsymbol{\mathcal{E}}}: = \{\Sigma_e, \, e\in\mathcal{E}\}\subset \boldsymbol{\mathcal{V}}\times \boldsymbol{\mathcal{V}} $, with $ \mathcal{V}, \, \mathcal{E} $ being countable sets. We consider an oriented graph, i.e. two vertices $ (M_v, M_{v'}) $ are connected by at most one edge $ \Sigma_e $ identified to the segment $ [M_v, \, M_{v'}]\subset \mathbb{R}^d $. This implies $ M_v\neq M_{v'} $. This edge is given an orientation via an abscissa $ s_e\in [a_e, \, b_e ] $. The origin $ M_v $ corresponds to $ s_e = a_e \in \mathbb{R} $, the end point $ M_{v'} $ corresponds to $ s_e = b_e: = a_e + |M_{v'}-M_v| $, and also
By definition, $ M_v $ is the origin, and $ M_{v'} $ is the end. This point of view allows to identify the algebraic object $ \mathbb{G} $ with the geometric structure
For any $ v \in \mathcal{V} $, we denote by $ { \mathcal{E}_v} $ the subset of $ \mathcal{E} $ corresponding to all edges adjacent to $ {M_v} $:
We assume in the following that $ { \mathcal{E}_v} $ is a finite set for all $ {v} $. We use the notation $ s $ for the collection of the $ s_i $'s, which can be seen as a generalized coordinate along $ \mathbb{G} $.
Let us finally remark that the dimension $ d $ does not play any role in the analysis of the problem considered in this article, but, as we will see in section 1.2, it occurs when interpreting the model studied in this work as a limit model defined in an open set in $ \mathbb{R}^d $.
Definition 1.1. (Weight). A weight is a function $ \mu : \mathbb{G} \to \mathbb{R}_*^+ $ such that, on each edge $ \Sigma_e $, $ \mu $ is constant and takes the value $ \mu_e $.
Remark 1.2. Choosing the weight function $ \mu $ constant along each edge is not essential but simplifies the presentation.
Remark 1.3. We will denote a graph $ \mathbb{G} $, to which the weight $ \mu $ is assigned, by $ ( \mathbb{G}, \mu) $.
Definition 1.4. [Wave equation] A solution of the weighted wave equation on $ \mathbb{G} $, with weight $ \mu $, is a function $ u(s, t) : { \mathbb{G}} \times \mathbb{R}^+ \rightarrow \mathbb{R} $ satisfying, with $ u_e = \left. u\right|_{\Sigma_e} $,
and at each node $ M_v $ of $ \, \mathbb{G} $, which is an intersection of at least two edges, i. e. $ \# \, \mathcal{E}_v \geqslant 2 $,
where $ \mu_e $ is given by definition 1.1, and $ \varepsilon_{v, e} $ depends of the orientation of $ \, \Sigma_e $:
Note that (3)$ (i) $ is nothing but the continuity of $ u $ at $ M_v $ while (3)$ (ii) $ is a generalized Kirchhoff condition.
Equations (2) and (3) can be collected in a single equation, using a (very intuitive) notion of distributional derivative along $ { \mathbb{G}} $, as follows
where $ \mu : { \mathbb{G}} \rightarrow \mathbb{R}^+_* $ is a piecewise constant function that takes the value $ \mu_e $ along $ \Sigma_e $. This will be made more precise in the next section in the case where $ \mathbb{G} $ is a tree.
1.2. A physical justification of the model (3).
One of the particularities of the model (3), at least with respect to more standard cases, is the presence of the weight function $ \mu $. As a matter of fact, this weight function occurs when considering the wave propagation in a 'thick' graph $ \mathbb{G}^{\delta} $, which we can define as follows based on a given finite graph $ \mathbb{G} $:
where $ \mathcal{E} $ is a finite set, and $ B(0, \delta) $ is the open ball of $ \mathbb{R}^d $ of center $ 0 $ and radius $ \delta $. One sees here that the coefficients $ \mu_i $ are characteristic of the geometry of the "thick graph" $ \mathbb{G}^\delta $. Then $ u $, which solves (2), can be seen as the limit of the solution $ u^\delta $ of the $ d- $dimensional acoustic wave equation (with velocity 1) in $ \mathbb{G}^\delta $ satisfying Neumann conditions on $ \partial \mathbb{G}^\delta $ (see [21,30,18] for various justifications):
In [18], it is explained how the conditions (3) can be improved to get a more accurate model with respect to $ \delta $.
1.3. Infinite trees
In the following, we consider a particular case where the graph $ \mathbb{G} $ is an infinite rooted oriented tree, as illustrated by figure 2. The notation and terminology that we use below may deviate from a classical notation/terminology used in the graph theory, but are better adapted for our purposes.
First of all, let us provide an auxiliary definition.
Definition 1.5. [Child/parent of an edge and of a vertex] Given two oriented edges $ \Sigma = [{M_\star}, \, M] $ and $ \Sigma' = [{M_\star}', \, M'] $, we will call $ \Sigma $ a parent of $ \Sigma' $ (or, equivalently, $ \Sigma' $ is a child of $ \Sigma $) if $ M\equiv {M_\star}' $. Accordingly, we shall say that the edge $ \Sigma $ is a parent of the vertex $ M $, and $ \Sigma' $ is a child of the vertex $ M $.
Definition 1.6. [Rooted graph and a root] We shall say that a graph $ \mathcal{T} $ is rooted if it has a unique edge that has no parents. This edge is called root and denoted $ \Sigma $.
Definition 1.7. [Tree] We will call a tree a rooted connected graph $ \mathcal{T} $ that has no cycles (i.e. every two vertices are connected by a single path).
The above definition is equivalent to saying that
● each edge (apart from the root) has only one parent;
● except from the origin of the root, each vertex has one parent.
Definition 1.8. [Generations of a tree] In a tree, we define a generation $ \mathcal{G}^n, \, n\in\mathbb{N}_0, $ as a union of edges of this tree as follows:
● the generation $ \mathcal{G}^0 = \{\Sigma\} $;
● the generation $ \mathcal{G}^k $ is a union of children of the edges belonging to $ \mathcal{G}^{k-1} $, $ k \geqslant 1 $.
Definition 1.9. [Infinite trees] If for all $ n \geqslant 0 $, $ \mathcal{G}^n \neq \emptyset $, such a tree is called infinite. Evidently, an infinite tree, as a geometric object, satisfies
and in such trees each vertex $ M_v, \, v \in \boldsymbol{\mathcal{V}} $ belongs to at most two successive generations. In what follows we will be using the notation $ \mathcal{G}^n(\mathcal{T}) $ instead of $ \mathcal{G}^n $, to indicate that we are looking at the $ n $-th generation of the graph $ \mathcal{T} $. A typical example of infinite trees in $ \mathbb{R}^2 $ is provided in figure 2.
With the above definition, we can introduce the following notation:
$ - $ we will denote by $ J(n)+1 $ the number of the edges of the $ n $-th generation $ \mathcal{G}^n( \mathcal{T}) $;
$ - $ $ \mathcal{E} $ has a natural numbering with two indexes $ e\equiv (n, j) $, with $ n \in \mathbb{N} $ describing the numbering of the generation and $ 0 \leqslant j \leqslant J(n) $ with $ j $ corresponding to the edge numbering inside $ \mathcal{G}^n( \mathcal{T}) $:
$ - $ for each $ n\in\mathbb{N} $, $ 0 \leqslant j \leqslant J(n) $, we shall write $ \Sigma_{n, j} = [M_{n, j}^*, \, M_{n, j}] $.
Let us define the set of children indices of a given vertex $ M_{n, j} $:
According to (8) and to the orientation of the tree, the Kirchhoff condition (3)$ (ii) $ at $ M_{n, j} $ can be rewritten, $ \mbox{with } u_{n, j} = u|_{\Sigma_{n, j}} $, as
where $ \mu_{n, j} $ is the weight associated to the edge $ \Sigma_{n, j} $.
For convenience, we denote the value of a continuous function $ u $ in a vertex $ M_{n, j} $ by
Definition 1.10. [Truncated tree] We denote by $ \mathcal{T}^n $ the truncated tree at generation $ n $, i. e. the union of the $ m $-th generations $ \mathcal{G}^m( \mathcal{T}) $, for $ m \leqslant n $ (see figure 2 for $ \mathcal{T}^1 $).
Definition 1.11. [Subtree] For any $ (n, j) \in \mathcal{I} $, we denote by $ \mathcal{T}_{n, j} $ a subtree with the root $ \Sigma_{n, j} $, that constitutes the largest connected subgraph of $ \mathcal{T} \setminus { \mathcal{T}^{n-1}} $ that contains $ M_{n, j} $ (and none of the $ M_{n, k} $, for $ k \not = j $).
For an illustration of the notion of the subtree see figure 2 for $ \mathcal{T}_{2, 4} $. It is not difficult to notice that $ \mathcal{T} \setminus { \mathcal{T}^{n-1}} $ is the union of the subtrees $ \mathcal{T}_{n, j} \, $ for $ \, 0 \leqslant j \leqslant J(n) $.
One of the goals of this work is to study the wave equation on such infinite trees. Of course, in this case the wave equation needs to be completed by a boundary condition at the root $ {M_\star} $ of the tree, for instance the Dirichlet entrance condition ($ f(t) $ represents the source term)
by the boundary conditions on the leaves of the tree (which we will discuss in a moment), by initial conditions, for instance homogeneous initial conditions
but also, in general, by a "boundary condition at infinity", which is trickier to define and will be made precise in Section 1.5.
In the following we shall very soon restrict our discussion to compact trees.
Definition 1.12. [Compact tree] Let $ \mathcal{T} $ be a tree. A path of $ \mathcal{T} $ is by definition a connected (possibly infinite) union of edges of $ \mathcal{T} $. By definition, the tree is compact if there exists a uniform bound for the lengths of all paths of $ \mathcal{T} $. This implies in particular that $ \mathcal{T} $ is included in a compact set of $ \mathbb{R}^d $, for some $ d \geqslant 1 $.
In what follows, we will study only the following subclass of infinite trees.
Assumption 1.13. A tree $ \mathcal{T} $ is compact and has no leaves.
1.4. Functional spaces on a weighted tree
Let us first consider a very degenerate case of an infinite tree. Given $ L > 0 $, $ \mu\equiv 1 $, $ \alpha \in {(0, 1)} $, let us set $ x_0 = 0 $ and
that form a strictly increasing sequence of real numbers $ x_n\rightarrow L $, as $ n\rightarrow \infty $ (see figure 3 for $ \alpha = 0.5 $). We can construct a corresponding "1D tree", defined as follows:
In this case, each generation $ \mathcal{G}^{n}( \mathcal{T}) $ is reduced to the segment $ [x_n, x_{n+1}] $, and we thus have
It is then easy to check that the wave equation (2, 3) on such a tree is nothing but the 1D wave equation along $ (0, L) $. Indeed, we need to equip it with proper boundary conditions, in the root vertex $ x_0 $, and at the 'infinite' boundary of the tree $ x = L $. The natural space in which, for each $ t \geqslant 0 $, finite energy solutions $ u(., t) $ of (5) live, is the Sobolev space $ {\rm H}^1(0, L) $. Our goal in this paragraph is to define the equivalent of such a space in a weighted infinite tree, as it was done in similar situations in [23]. In the following, when not explicitly mentioned, the functions we consider can be real- or complex-valued, depending on the context.
Definition 1.14. [Functional spaces] Let $ ( \mathcal{T}, \mu) $ be a weighted tree.
1. Lebesgue space of square-integrable functions. We denote by $ {\rm L}_\mu^2( \mathcal{T}) $ the set of functions $ u : \mathcal{T} \to \mathbb{C} $ having a finite $ {\rm L}_\mu^2( \mathcal{T}) $-norm, namely
2. Sobolev space. We denote by $ {\rm H}_\mu^1( \mathcal{T}) $ the space made of continuous $ {\rm L}_\mu^2( \mathcal{T}) $ functions $ u : \mathcal{T} \to \mathbb{C} $ having a finite $ {\rm H}_\mu^1( \mathcal{T}) $-semi-norm, namely
and the $ {\rm H}_\mu^1( \mathcal{T}) $-norm of $ u $ is defined by
All the above spaces are then obviously equipped with a Hilbert space structure and will provide an adequate framework for studying the wave equation on $ \mathcal{T} $.
Notation. In what follows, for any $ (u, v) \in {\rm L}_\mu^2( \mathcal{T}) $ we shall denote
1.5. Dirichlet and Neumann initial boundary value problems
We are now in position to provide a rigorous definition of the problems that we are interested in. Let us first explain our approach for the case when $ \mathcal{T} $ is the degenerate tree (13), i.e. $ \mathcal{T} \equiv [0, L) $. In this tree $ x = L $ would correspond to "the boundary at infinity" of the tree. As it is well-known, there are two standard homogeneous boundary conditions at $ x = L $ that can be associated with the 1D wave equation along $ (0, \, L) $, namely
These conditions are perfectly reflecting: in particular, they are energy preserving in the absence of the source term. We consider below the generalization of these boundary conditions for a general infinite tree $ \mathcal{T} $. For this, we shall pass through the notion of weak solution of the wave equation that reduces the distinction between Dirichlet and Neumann conditions to the distinction between the functional spaces in which the solution is searched and the test functions live. Since the Dirichlet condition is systematically considered at the entrance of the tree, see (11), the denomination Dirichlet or Neumann only refers to the condition at infinity. We begin with the Neumann condition.
The Neumann initial boundary value problem $ ({\mathcal{P}}_ \mathfrak{n}) $. Provided the Hilbert space
which is a closed subspace of $ {\rm H}_\mu^1( \mathcal{T}) $, the Neumann problem $ ({\mathcal{P}}_ \mathfrak{n}) $ reads
In the case of the degenerate tree (13), $ V_ \mathfrak{n} = \lbrace u \in {\rm H}^1(0, L) \; / \; u(0) = 0 \rbrace $. For the Dirichlet condition, one should replace in the weak formulation $ V_ \mathfrak{n} $ by $ V_ \mathfrak{d} = \lbrace u \in V_ \mathfrak{n} \; / \; u(L) = 0 \rbrace $, which is also characterized as the closure in $ V_ \mathfrak{n} $ of compactly supported in $ (0, L) $ functions of $ V_ \mathfrak{n} $. We shall adapt this approach to define the corresponding problems in the case of an infinite tree. We first define the subspace of $ {\rm H}_\mu^1( \mathcal{T}) $, which consists of functions that "vanish at infinity" in the following way.
Definition 1.15. Let $ ( \mathcal{T}, \mu) $ be a weighted tree.
1. $ {\rm H}_{\mu, \text{c}}^1( \mathcal{T}) $ is the subspace of $ {\rm H}_\mu^1( \mathcal{T}) $ of compactly supported functions, i.e.
2. $ {\rm H}_{\mu, \text{0}}^1( \mathcal{T}) $ the closure of $ \, {\rm H}_{\mu, \text{c}}^1( \mathcal{T}) $ in $ {\rm H}_\mu^1( \mathcal{T}) $:
Remark 1.16. As one can expect, in certain cases, the space $ {\rm H}_{\mu, \text{0}}^1( \mathcal{T}) $ can be related to the closed subspace of $ {\rm H}_\mu^1( \mathcal{T}) $, whose "trace at infinity" (defined in a certain way) vanishes. This will be made more precise in the case of a $ p $-adic self-similar tree in section 3.2.
The Dirichlet initial boundary value problem $ ({\mathcal{P}}_ \mathfrak{d}) $. Provided the Hilbert space
which is a closed subspace of $ {\rm H}_{\mu, \text{0}}^1( \mathcal{T}) $, the Dirichlet problem $ ({\mathcal{P}}_ \mathfrak{d}) $ reads
Let us state, without proof, a classical result about problems ($ \mathcal{P}_\mathfrak{n}$) and ($\mathcal{P}_\mathfrak{d} $).
Proposition 1.17. Let $ T \in \mathbb{R}_*^+ $, and let $ f \in C^2([0, T]) $, with $ f(0) = f'(0) = 0 $. Then, the problem ($ \mathcal{P}_\mathfrak{n}$) (resp. ($\mathcal{P}_\mathfrak{d} $)) admits a unique solution.
When one considers the problem of the numerical approximation of ($ \mathcal{P}_\mathfrak{n}$) and ($\mathcal{P}_\mathfrak{d} $), one immediately faces the question of truncating the tree after a finite number of generations and constructing corresponding transparent or absorbing boundary conditions, which is the main objective of the present paper.
1.6. About the construction of transparent boundary conditions
Numerically, a natural objective would be to restrict the computation to the solution $ u $ of ($ \mathcal{P}_\mathfrak{n}$) or ($\mathcal{P}_\mathfrak{d} $) to a truncated tree $ { \mathcal{T}^n} $ by imposing some (transparent) Dirichlet-to-Neumann (DtN) condition at each end point $ M_{n, j} $ of $ { \mathcal{T}^n} $. This can be made by combining the Kirchhoff condition (9) with the use of DtN operators $ \Lambda_{n+1, k} $ associated to each of the subtrees $ \big\{ \mathcal{T}_{n+1, k}, \, k \in \mathcal{C}_{n, j} \big\} $. More precisely, $ \varphi(t) \mapsto \Lambda_{n+1, k} \; \varphi(t) $ is the DtN operator
where $ \widetilde{u}^\varphi_{n+1, k}(\cdot, t) : \mathcal{T}_{n+1, k} \mapsto \mathbb{R} $ is defined on the subtree $ \mathcal{T}_{n+1, k} $ as the unique solution of the Dirichlet (or Neumann) problem (in the sense of section 1.5) of the wave equation, posed in the subtree $ \mathcal{T}_{n+1, k} $, with the Dirichlet condition at the root vertex of this tree $ M_{n, j} $ $ \widetilde{u}^\varphi_{n+1, k}( M_{n, j}, t) = \varphi(t) $.
The transparent condition at the end point $ M_{n, j} $ then relates $ u_{n, j}(M_{n, j}, .) $ to $\partial_s u_{n, j} $
$ (M_{n, j}, .) $ according to
where
Since the wave equation has constant coefficients in time, it is clear that $ \Lambda_{n+1, {k}} $ is a time convolution operator. More precisely, using the Fourier-Laplace transform in time
we get a relation of the form
The symbol $ \mathbf{\Lambda}_{n+1, {k}}(\omega) $ is given by
where $ \widehat{u}_{n+1, {k}}(\cdot, \omega) $ is the solution of the (Dirichlet or Neumann, we omit for simplicity the condition at infinity) Helmholtz problem
At this point, we have not advanced much, since the computation of the symbol $ \mathbf{\Lambda}_{n+1, k} $ requires solution of a subtree problem which is as difficult as the original problem! However, this problem can be simplified when the tree $ \mathcal{T} $ admits, starting from the $ n $-th generation, a certain structure. In particular, we shall investigate in this paper trees with such a structure, namely, fractal trees [22], for which, at least for $ n $ large enough, all subtrees $ ( \mathcal{T}_{n, j}, \mu) $ are self-similar weighted trees, as defined in section 2.
We finish this section by some results on the Helmholtz equation in general trees, in particular, the well-posedness and the meromorphicity of the solution with respect to the frequency for some particular classes of trees.
1.7. Helmholtz equation in general trees: Basic results
We consider the following problem on a weighted tree $ ( \mathcal{T}, \, \mu) $. Given a complex frequency $ \omega \in \mathbb{C} $, we look for the solution $ u: \mathcal{T}\rightarrow \mathbb{C} $ to the Helmholtz equation with non-homogeneous Dirichlet data at the entrance of the tree
completed, like the wave equation in section 1.5, by a homogeneous (Dirichlet or Neumann) condition at infinity. More rigorously, using the functional framework of section 1.4 and the Hilbert spaces $ V_ \mathfrak{n} $ and $ V_ \mathfrak{d} $ introduced in section 1.5 by (18) and (21), we can define the Dirichlet and Neumann (at infinity) problems as follows
1.7.1. Existence and uniqueness results
For these two problems, we can immediately state the well-posedness result for non-real frequencies.
Proposition 1.18. For each $ \omega \not\in \mathbb{R} $ , $(\mathcal{P}_{\mathfrak{n}, \omega }) $ (resp. $(\mathcal{P}_{\mathfrak{d}, \omega }) $ ) admits a unique solution
Proof. It is a simple application of the Lax-Milgram theorem left to the reader.
Since $ \mu $ is real-valued,
A complementary point of view consists in introducing the two unbounded positive self-adjoint operators in $ {\mathcal{H}} : = {\rm L}_\mu^2( \mathcal{T}) $, namely $ \mathcal{A}_ \mathfrak{d} $ and $ \mathcal{A}_ \mathfrak{n} $, associated to $(\mathcal{P}_{\mathfrak{d}, \omega }) $ and $(\mathcal{P}_{\mathfrak{n}, \omega }) $. Namely, given a sesquilinear form
we define these operators as follows:
It is easy to check that, defining
the domains of the operators $ \mathcal{A}_{ \mathfrak{d}} $, $ \mathcal{A}_{ \mathfrak{n}} $ are given by
and thus $ D( \mathcal{A}_ \mathfrak{d}) \subseteq D( \mathcal{A}_ \mathfrak{n}) $. These operators are positive definite since
The solutions to the problems ($ \mathcal{P}_ {\mathfrak{n}, \omega} $) and ($ \mathcal{P}_ {\mathfrak{d}, \omega} $) can be expressed via the resolvents of the operators defined above as follows. Let $ u_{r} $ be a function supported in $ \Sigma_{0, 0} $, $ u_{r} ({M_\star}) = 1 $ and $ u_{r} \in {\rm H}^2(\Sigma_{0, 0}) $. With
the functions $ u_{ \mathfrak{n}}(\cdot, \omega) $ and $ u_{ \mathfrak{d}}(\cdot, \omega) $ are given by
From standard properties of the resolvent of self-adjoint operators [19,29], we deduce the
Proposition 1.19. The functions $ \omega \mapsto u_{ \mathfrak{d}}(\cdot, \omega) $ and $ \omega \mapsto u_{ \mathfrak{n}}(\cdot, \omega) $ are analytic functions in $ \mathbb{C} \setminus \mathbb{R} $ with values in $ D( \mathcal{A}_ \mathfrak{d}) $ and $ D( \mathcal{A}_ \mathfrak{n}) $ (equipped with their graph norm) respectively.
1.7.2. The compact case : meromorphicity with respect to the frequency
Let us consider the case when one of the two following assumptions holds true:
Of course, (38)-$ \mathfrak{n} $ is stronger than (38)-$ \mathfrak{d} $. Both assumptions rely on properties of the tree and the weight function $ \mu $. For instance, in the case where $ \mu = 1 $, it is shown in [36] that the compactness of the tree (cf. definition 1.12) is a sufficient condition for (38)-$ \mathfrak{n} $ and (38)-$ \mathfrak{d} $ to hold. We shall investigate this question in more detail in the case of fractal trees in section 3.5.
The properties (38)-$ \mathfrak{n} $, (38)-$ \mathfrak{d} $ play an important role in this article. If (38)-$ \mathfrak{n} $ (resp. (38)-$ \mathfrak{d} $) holds, the operator $ \mathcal{A}_ \mathfrak{n} $ (resp. $ \mathcal{A}_ \mathfrak{d} $) has a compact resolvent, and thus its spectrum is a pure point spectrum with strictly positive eigenvalues (here repeated with their multiplicities):
Remark 1.20. Let us remark that $ \omega = 0 $ is not an eigenvalue of $ \mathcal{A}_ \mathfrak{n} $ and $ \mathcal{A}_{ \mathfrak{d}} $. This can be shown by contradiction. If $ \omega = 0 $ were an eigenvalue and $ u $ an associated eigenfunction, then this would imply, in particular, that $ a(u, u) = 0 $, and hence $ \partial_s u = 0 $. Since $ u({M_\star}) = 0 $, necessarily, $ u = 0 $.
The corresponding eigenfunctions, which form a Hilbert basis in $ {\rm L}_\mu^2( \mathcal{T}) $, are
In particular, under the assumption (38)-$ { \mathfrak{n}} $ (correspondingly, (38)-$ { \mathfrak{d}} $), the zero-frequency Neumann (Dirichlet) problem is well-posed. This result is classical (hence we provide no proof here) and relies on the Lax-Milgram theorem combined with the Poincaré inequality for $ V_{ \mathfrak{d}} $ ($ V_{ \mathfrak{n}} $), the latter valid because of the compactness assumption and the fact that $ \omega = 0 $ is not an eigenvalue of $ \mathcal{A}_{ \mathfrak{d}} $ ($ \mathcal{A}_{ \mathfrak{n}} $), see remark 1.20 (see e.g. [37,Theorem 2.6]).
Lemma 1.21 (Poincaré inequality). If (38)-$ \mathfrak{n} $ (resp. (38)-$ \mathfrak{d} $) holds, then
The well-posedness result then reads.
Lemma 1.22. If (38)-$ \mathfrak{n} $ (resp. (38)-$ \mathfrak{d} $) holds, the problem ($ \mathcal{P}_ {\mathfrak{n}, \omega} $) (resp. ($ \mathcal{P}_ {\mathfrak{d}, \omega} $)) for $ \omega = 0 $ admits a unique solution denoted by $ u_{ \mathfrak{n}}(., 0) $ (resp. $ u_{ \mathfrak{d}}(., 0) $).
We will use the above lemma and (37) to express the solution to the (Dirichlet or Neumann) Helmholtz problems in the basis of the corresponding eigenfunctions.
Proposition 1.23. If (38)-$ \mathfrak{n} $ holds, the function $ u_ \mathfrak{n}(\cdot, \omega): \mathbb{C}\ni \omega \rightarrow {\rm H}_\mu^1( \mathcal{T}) $ is an even meromorphic function in $ \mathbb{C} $ with poles $ \lbrace \pm \, \omega_ \mathfrak{n}^n, n \geqslant 1 \rbrace $. It is given by
Similarly, if (38)-$ \mathfrak{d} $ holds, $ u_ \mathfrak{d}(\cdot, \omega): \mathbb{C}\ni \omega \rightarrow {\rm H}_{\mu, \mathit{\text{0}}}^1( \mathcal{T}) $ is an even meromorphic function in $ \mathbb{C} $ with poles $ \lbrace \pm \, \omega_ \mathfrak{d}^n, n \geqslant 1 \rbrace $. It is given by
Proof. We will show the proof for $ u_{ \mathfrak{n}}(\cdot, \omega) $, with the proof for $ u_{ \mathfrak{d}}(\cdot, \omega) $ being verbatim the same. First, let us consider the function
Defining
we deduce that
Next, we expand $ u_{ \mathfrak{n}}(., 0) $ into a series of the eigenfunctions of $ \mathcal{A}_{ \mathfrak{n}} $. For this we remark that
where we use that $ \varphi_{ \mathfrak{n}}^n $ is an eigenfunction of $ \mathcal{A}_{ \mathfrak{n}} $. Thus, integrating the above by parts and using the fact that $ u_{ \mathfrak{n}}(., 0) $ satisfies ($ \mathcal{P}_ {\mathfrak{n}, \omega} $) with $ \omega = 0 $, we obtain
Thus, the desired result follows by inserting the expansion of $ u_{ \mathfrak{n}}(., 0) $ into (44).
Remark 1.24. The series (42) (resp. (43)) converges uniformly in $ \omega $ on any compact subset of $ \mathbb{C}\setminus \lbrace \pm \, \omega_ \mathfrak{n}^n, n \geqslant 1 \rbrace $ (resp. $ \mathbb{C}\setminus \lbrace \pm \, \omega_ \mathfrak{d}^n, n \geqslant 1 \rbrace $), in $ D(\mathcal{A}_{ \mathfrak{n}}) $-norm (resp. $ D(\mathcal{A}_{ \mathfrak{d}}) $-norm).
2.
Self-similar trees
In this section, we introduce a notion of a self-similar weighted $ p $-adic tree. We start with the definition of a non-weighted $ p $-adic tree.
Definition 2.1. [$ p $-adic tree] A tree $ \mathcal{T} $ is $ p $-adic if every edge of $ \mathcal{T} $ has precisely $ p $ children.
Remark 2.2. Any $ p $-adic tree is infinite. The number of edges in the $ n $-th generation of a $ p $-adic tree is $ p^n $, i.e. $ J(n) = p^n-1 $.
Later on, we will need to provide a numbering for edges and vertices of a $ p $-adic tree. For this we will use the $ p $-adic representation of integers. Let $ {\mathcal{I}}_p : = \lbrace0, \, 1, \ldots, p-1\rbrace $. Given $ (i_1, \, i_2, \ldots, \, i_n) \in {\mathcal{I}}^n_p $, one denotes by $ {(i_1 i_2 \cdots i_n)_p} $ an integer (see [20,pp. 22-25])
The map $ \Phi : (i_1, \, i_2, \ldots, \, i_n) \rightarrow {(i_1 i_2 \cdots i_n)_p} $ defines (for all $ n $) a bijection from $ {\mathcal{I}}^n_p $ into $ \lbrace0, \, 1, \, \ldots, p^n-1 \rbrace. $ The role of this notation and its meaning will become clear later. Now we have the ingredients necessary to define a self-similar $ p $-adic tree.
Definition 2.3. [Self-similar $ p $-adic tree] Let a root segment be $ \Sigma_{0, 0} = [{M_\star}, M_{0, 0}] $ (where without loss of generality we assume that $ {M_\star} $ is the origin). Let $ \lbrace \sigma_i , 0 \leqslant i \leqslant p-1 \rbrace $ in $ \mathbb{R}^d $ be affine direct similitudes, defined as
where
● $ \tau_i\equiv \tau $ is the translation (common to all similitudes) by a vector $ \overrightarrow{{M_\star} M_{0, 0}} $;
● $ h_i $ is a homothety with the center in the origin of the ratio $ \alpha_i $ (also called a ratio of the similitude): $ h_i(x) = \alpha_i x $, $ x\in\mathbb{R}^d $;
● $ {\Theta_i} $ is a rotation (all the rotations $ {\Theta_i} $ are assumed to be distinct).
Let additionally these similitudes satisfy the following assumption: for all $ \ell, k\in\mathbb{N} $, $ i_1, \ldots, $,
Then a tree $ \mathcal{T} $, defined as in (6), whose generations are given by
is called a self-similar $ p $-adic tree.
The assumption (46) ensures that the object constructed in the definition 2.3 defines a $ p $-adic tree (in particular, the absence of cycles in such a graph, and the fact that it is a connected object), see lemma 2.4.
By construction, for a self-similar tree as in definition 2.3, any $ edge $ of $ \mathcal{G}^n $ is the result of the product of $ n $ similitudes $ \lbrace \sigma_{i_k}, 1 \leqslant k \leqslant n\rbrace $ applied to the root edge $ \Sigma_{0, 0} $. In what follows, we chose to number the edges $ \lbrace\Sigma_{n, j}, 0 \leqslant j \leqslant p^n-1\rbrace $ in the following order (see also figure 4):
where
Obviously $ \sigma_{n, j} $ is a similitude. Moreover,
where $ \tau_{n, j} $ is a translation by vector $ [{M_\star}, M_{n, j}] $, $ {\Theta_{n, j}} $ is the rotation $ \Theta_{n, j} = \Theta_{j_1} \Theta_{j_2} \dots \Theta_{j_n} $ and $ h_{n, j} $ is the homothety $ h_{n, j} = h_{j_1} h_{j_2} \cdots h_{j_n} $. The ratio $ \alpha_{n, j} $ of $ \sigma_{n, j} $, which is also the ratio between the lengths of $ \Sigma_{n, j} $ and $ \Sigma_{0, 0} $, is thus
By construction, $ \Sigma_{n, j} = [ {M_{n, j}^\star} , M_{n, j}] $ oriented from $ M_{n, j}^\star = \sigma_{j_1} \, \sigma_{j_2} \cdots \sigma_{j_n}({M_\star}) $ towards $ M_{n, j} = \sigma_{j_1} \, \sigma_{j_2} \cdots \sigma_{j_n}(M_{0, 0}) $.
The fact that definition 2.3 does construct a connected $ p $-adic tree is a consequence of the following lemma.
Lemma 2.4. Let $ \mathcal{G}^n, \, n \geqslant 0, $ be defined in (47). Then $ \mathcal{T} = \bigcup\limits_{n\in\mathbb{N}}\mathcal{G}^n $ is a $ p $-adic tree.
Moreover, $ p $ edges of the generation $ \mathcal{G}^{n+1} $ that are connected to $ \Sigma_{n, j} $, namely
are numbered in a consecutive way, from $ pj $ to $ pj + p-1 $.
Proof. This proof is left to the reader. In particular, one can use the assumption (46) to show that the constructed graph has no loops. In order to show that it is connected, one can employ the numbering (48).
For the clarity of some proofs, we will need following notation:
● we shall distinguish an integer $ j $ in its $ p $-adic representation $ j = (j_1j_2\cdots j_n)_p $, and the corresponding sequence of integers $ j_1j_2\cdots j_n $ which we will denote by the bold letter $ \boldsymbol{j} = j_1j_2\cdots j_n $. The value of $ n $ in this representation is implicit and will be clear from the context each time it will be used.
● $ \Sigma_{\boldsymbol{j}} = \Sigma_{j_1j_2\cdots j_n}: = \Sigma_{n, j} $, $ u_{\boldsymbol{j}} = u_{j_1\cdots j_n}: = u_{n, j} $ and, similarly, the nodal values, cf. (10), $ \mathbf{u}_{ \boldsymbol{j}} = \mathbf{u}_{j_1\cdots j_n}: = \mathbf{u}_{n, j} $.
● with $ k_1, \, k_2, \ldots, k_m\in\{0, \, 1, \ldots, \, p-1\} $, defining $ \ell = (j_1j_2\cdots j_n k_1k_2\cdots k_m)_{p} $,
From the definition 1.11 of a subtree, it is clear that, a subtree $ \mathcal{T}_{1, i} $ of $ \mathcal{T} $ being defined by definition 2.3, can be identified with
and that, as a consequence,
In fact, the above property can be seen as an alternative to definition 2.3.
Definition 2.5. [Reference self-similar $ p $-adic tree] Given a self-similar tree $ \mathcal{T} $, constructed with the help of similitude transformations $ \{\sigma_i, \, i = 0, \ldots, p-1\} $ as in definition 2.3, we will call a reference tree a self-similar tree $ \mathcal{T}_r $, whose root $ \Sigma_{0, 0} $ is the segment $ [ {\mathbf 0}, {\mathbf 1}] $ with $ {\mathbf 1}: = (0, \cdots, 0, 1){\in\mathbb{R}^d} $, and which is constructed as in definition 2.3 based on the similitude transformations $ \{\sigma_i, \, i = 0, \ldots, p-1\} $.
For the reference tree, the length of $ \Sigma_{n, j} $ is $ \alpha_{n, j} $. Moreover, any tree obeying definition 2.3 is obviously obtained from the reference tree $ \mathcal{T}_r $ by applying a scaling of ratio $ \ell $ (the length of the root edge). This means that the most important geometric properties of any self-similar tree are encoded in the $ p- $uplet
When convenient, we shall denote $ \mathcal{T} \equiv \mathcal{T}_{\boldsymbol{\alpha}} $ to indicate that we consider a self-similar $ p $-adic tree whose geometry is associated to the $ p $-uplet $ \boldsymbol{\alpha} $.
Compact self-similar trees. The reader will easily remark that
Definition 2.6. [Self-similar weighted $ p $-adic tree] Let $ \mathcal{T} $ be a self-similar $ p $-adic tree, and let $ \mu $ be a weight function on $ \mathcal{T} $. Then $ ( \mathcal{T}, \mu) $ is a self-similar weighted $ p $-adic tree if there exist $ p $ positive numbers $ \lbrace \mu_i \rbrace_{0 \leqslant i < p} $ such that (with an obvious abuse of notation defining $ \sigma_i(s) $ as the abscissa of $ \sigma_i(\Sigma) $ if $ s $ is the abscissa of $ \Sigma $)
In particular, we have
A weighted self-similar tree is thus characterized by two $ p- $uplets $ ( \boldsymbol{\alpha}, \boldsymbol{\mu}) \in ( \mathbb{R}^+_*)^p\times ( \mathbb{R}^+_*)^p $, where $ \boldsymbol{\mu} = (\mu_0, \ldots, \mu_{p-1}) $. When necessary, we will denote the corresponding tree $ \mathcal{T}_{\boldsymbol{\alpha}, \boldsymbol{\mu}} $.
We shall often use in the sequel the following computational trick.
Proposition 2.7. Let $ ( \boldsymbol{\alpha}, \boldsymbol{\mu} ) \in ( \mathbb{R}^+_*)^p\times ( \mathbb{R}^+_*)^p $. For any $ {\zeta} \in \mathbb{R} $,
Proof. Taking all possible $ j $ in $ \lbrace 0, \dots, p^n-1 \rbrace $ is equivalent to taking all possible $ n $-uples $ (j_1, j_2, \dots, j_n) \in \lbrace 0, \dots, p-1 \rbrace^n $. Then, using (51) and (56), we have
The formula (57) follows then from the discrete version of Fubini's theorem.
Example : Regular and geometric trees. By definition, a self-similar $ p $-adic tree is called equilibrated or regular (according for instance to the terminology of Solomyak in [36]) if there exists $ \alpha \in (0, 1) $ such that
We illustrate in figure 4 all the notions and notations introduced above in the case of a symmetric regular dyadic tree, for which
and where $ {\Theta_1} $ and $ {\Theta_2} $ are the plane rotations of respective angles $ \pi/4 $ and $ -\pi/4 $. A tree is called $ d $-geometric when it is seen as the limit of a thick tree $ \mathcal{T}^\delta $ in $ \mathbb{R}^d $ (constructed as $ \mathbb{G}^\delta $ in Section 1.2), in which the ratio between the transverse and longitudinal dimensions of the edges are preserved along all generations. This corresponds to the relation $ \mu_i = \alpha_i^{d-1}, \forall \; 0 \leqslant i \leqslant p-1. $ A good illustration of a symmetric $ 3 $-geometric dyadic tree is the human lung, as modelled e.g. in [23].
3.
Sobolev spaces on compact self-similar trees
As discussed before, the principal goal of this work is to provide a theoretical and numerical basis for approximating the DtN operator, cf. section 1.6. For this we need to understand the following:
● whether the solutions to the problems ($ \mathcal{P}_ {\mathfrak{n}} $) and ($ \mathcal{P}_ {\mathfrak{d}} $) differ;
● whether (38)-$ \mathfrak{d} $ or (38)-$ \mathfrak{n} $ holds.
The goal of this section is to answer these questions in the case of self-similar trees. In all the derivations of this section, we will use the following simplifying assumption.
Assumption 3.1. A tree $ (\mathcal{T}, \mu) $ is a self-similar weighted reference compact tree (and thus $ |\boldsymbol{\alpha}|_{\infty}<1 $, see (54)), which we denote for brevity by $ \mathcal{T} $.
All the results of this section are valid for compact self-similar trees, and some of them hold for arbitrary, not necessarily compact, self-similar trees. This will be stated explicitly.
3.1. Trace operator
In this section, we will introduce a notion of the trace at infinity for functions in the Sobolev space $ {\rm H}_\mu^1( \mathcal{T}) $. On one hand, this allows to characterize the solution of the Dirichlet problem, defined in a variational way in ($ \mathcal{P}_ {\mathfrak{d}} $), by the Dirichlet condition at infinity. On the other hand, studying the trace will help us to answer other questions, e.g. whether the solutions of ($ \mathcal{P}_ {\mathfrak{d}} $) and ($ \mathcal{P}_ {\mathfrak{n}} $) differ.
Let us first define the "boundary at infinity" $ \Gamma_\infty $ of the tree $ \mathcal{T} $ as a segment $ [0, 1] $, i.e.
Next, we wish to define the trace at infinity of a function $ u \in {\rm H}_\mu^1( \mathcal{T}) $ as the limit of the trace of the same function at the boundary of the truncated tree $ \mathcal{T}^n $. It is constructed from the finite set of the values at each end point $ M_{n, j}, 0 \leqslant j \leqslant p^n-1 $, as a piecewise constant function on a very particular partition (mesh) of $ \Gamma_\infty $, namely:
To define intermediate values $ a_{n, j} $, let us introduce the following quantity (which, as we will see later, plays an important role in the analysis):
Then (the reason for the choice of this particular partition will be explained later),
First of all, notice that using (57) with $ \zeta = -1 $, we recover $ a_{n, p^n-1} = 1 $. Also, when $ \mu_j / \alpha_j $ is independent of $ j $, (62) defines a uniform mesh of a stepsize $ p^{-n}. $ We choose the partition like in (62), because, first of all, this choice ensures that the mesh $ \{ a_{n+1, j}, 0 \leqslant j \leqslant p^{n+1}-1 \} $ at the stage $ n+1 $ can be seen as a sub-mesh of the mesh $ \{ a_{n, j}, 0 \leqslant j \leqslant p^{n}-1 \} $ at the stage $ n $. In this case a segment of the coarser mesh is divided into $ p $ segments whose respective lengths are proportional to the ratio $ \mu_i/\alpha_i $. This particular choice of the ratio is motivated by the proof of the trace theorem 3.2. Moreover, it appears to be consistent with the existing works, cf. [23]. To see how we obtain the finer mesh from the coarser one, let us introduce
Then the passage from step $ n $ to $ n+1 $ is defined by the following (see also figure 5):
which leads, after some calculations, to (62).
Next, for any $ n \geqslant 0 $, we define the trace map at a generation $ n $, i. e. the end of the truncated tree $ \mathcal{T}^n $. More precisely, we define $ \tau_n u \in \mathbb{P}_0(\Gamma_n) \subset L^{\infty}(\Gamma_\infty) $ (here $ \mathbb{P}_0(\Gamma_n) $ is the space of functions that are piecewise constant with respect to the mesh $ \Gamma_n $), as follows:
Theorem 3.2. Assume that
Then, for any $ u $ in $ {\rm H}_\mu^1( \mathcal{T}) $, the following limit
and the application $ ~~ \tau _\infty $ defines a continuous trace operator from $ {\rm H}_\mu^1( \mathcal{T}) $ into $ L^2(\Gamma_\infty) $:
Moreover,
Proof. Let $ u \in {\rm H}_\mu^1( \mathcal{T}) $. To prove (67), we will show that $ \tau_{n+1}u - \tau_n u $, where $ \tau_n $ is defined by (65), is a convergent series in $ L^2(\Gamma_\infty) $.
The difference $ \tau_{n+1}u - \tau_n u $ is constant along each segment
where it takes the value $ {\mathbf u}_{n+1, pj+\ell} - {\mathbf u}_{n, j} $. As a consequence, using (62) (and (64)),
Recall that $ M_{n, j} $ is connected to each of the $ p $ points $ M_{n+1, pj+\ell}, 0 \leqslant \ell \leqslant p-1, $ via the corresponding edge $ \Sigma_{n+1, pj+\ell} $, cf. lemma 2.4. Hence,
Using the Cauchy-Schwarz inequality, we have
that is to say
After multiplication by $ ({\mu_{n, j}}/{\alpha_{n, j}}) \cdot ({\mu_{\ell}}/{\alpha_{\ell}}) $ (cf. the right hand side of (70)) and summation over $ \ell \in \{0, \ldots, p-1\} $ and $ j \in \{0, \ldots, p^n-1\} $, we get (this is where the coefficients $ \alpha_{\ell} $, $ \mu_{\ell} $, $ \alpha_{n, \ell} $, $ \mu_{n, \ell} $ disappear at the right hand side, justifying the choice of the mesh $ \Gamma_n $):
Thus, we deduce from (70) that
This proves, since $ \Big \langle \frac{\boldsymbol{\mu}}{\boldsymbol{\alpha}} \Big \rangle $ > 1, that the series $ \| \tau_{n+1}u - \tau_n u \|_{L^2(\Gamma_\infty)} $ converges. Finally,
To estimate $ \|\tau_0 u\|_{L^2(\Gamma_{\infty})} $, we apply the usual trace theorem in $ H^1(\Sigma_{0, 0}) \equiv H^1(0, 1) $:
For the embedding (69), note that if $ u $ is compactly supported in the sense of (19), for $ n $ large enough $ \tau_n u = 0 $ which implies $ \tau_\infty u = 0 $, in other words $ {\rm H}_{\mu, \text{c}}^1( \mathcal{T}) \subseteq \mbox{Ker } ~~ \tau _\infty $. Taking the closures in $ {\rm H}_\mu^1( \mathcal{T}) $, since $ \mbox{Ker } ~~ \tau _\infty $ is closed, we get (69) (see definition 1.15).
Remark 3.3. It is not difficult to see that (66) is a necessary condition for the existence of the trace, at least for compact regular trees with regular weights, i.e. when
Let the length of the root edge be $ 1-\alpha $. For any complex-valued function defined on such a tree, its restriction to the generation $ n $ can be identified to a collection of functions
A function $ u $ will be called symmetric if
Any symmetric function can be identified to a 1D function defined on an interval:
Let us introduce the space
According to the identification process $ u \equiv \hat u $, one easily checks that for $ u \in {\rm H}_{\mu, \text{s}}^1( \mathcal{T}) $, $ \hat u $ is continuous in $ I $, with $ H^1 $-regularity in each $ I_n $ and that
where the piecewise constant weight function $ w_d $ is defined by
Noticing that $ w_n = ( p \mu)^{\frac{\log (1-x_n)}{\log \alpha}} $, it is straightforward to check that the norm (73) is equivalent to the norm defined by
Since $ \alpha < 1 $, the condition (66) is not satisfied if and only if $ \beta \geqslant 1 $. On the other hand, the trace $ \tau_n u $ for $ u \in {\rm H}_{\mu, \text{s}}^1( \mathcal{T}) $ is a constant function (on $ \Gamma_\infty $) equal to $ \hat u(x_n) $. Thus to prove that the trace operator $ \tau_\infty $ is not defined for some $ u\in {\rm H}_{\mu, \text{s}}^1( \mathcal{T})\subset {\rm H}_\mu^1( \mathcal{T}) $, it suffices to find a function $ \hat{u} : [0, 1]\rightarrow\mathbb{C} $, such that $ \|\hat u\|^2_{1, w} $ is finite and $ |\hat u(x)| \rightarrow + \infty $ when $ x\rightarrow 1 $.
When $ \beta>1 $, one of such functions is $ \hat u(x) = \log (1-x) $. In particular,
For the limit case $ \beta = 1 $, the reader will easily check that
has a finite norm $ \|\hat{u}\|_{1, w} $, and yet $ \|\tau_{\infty}u\|_{L^2(\Gamma_{\infty})} = \infty $.
In what follows, we will use the notation $ \|\tau_n u\|: = \|\tau_n u\|_{ {\rm L}^2(\Gamma_{\infty})} $. Moreover, we will need the explicit expression for $ \|\tau_n u\|^2 $:
Remark 3.4. Theorem 3.2 holds both for compact and non-compact trees.
3.2. Kernel and image of the trace operator
We are now going to prove that, just like for the usual Sobolev spaces on the interval, the inclusion (69) is in fact an equality. This provides a useful characterization of $ {\rm H}_{\mu, \text{0}}^1( \mathcal{T}) $, as well as justifies the way to look at the solution $ u_ \mathfrak{d} $ of the Dirichlet problem for the wave equation as a limit when $ n $ goes to infinity of the solution $ u_{ \mathfrak{d}}^n $ to the wave equation in the truncated tree $ \mathcal{T}^n $ with homogeneous Dirichlet conditions at each end point $ M_{n, j} $ of $ \mathcal{T}^n $.
Theorem 3.5. Assume that (66) holds, so that the trace operator $ \tau_\infty $ is well-defined, then
The proof of this theorem is quite long. It will use the following lemma that provides a sufficient condition for a function in $ {\rm H}_\mu^1( \mathcal{T}) $ to belong to $ {\rm H}_{\mu, \text{0}}^1( \mathcal{T}) $. Let us emphasize the fact that this result is valid independently of whether the trace operator $ \tau_{\infty} $ is well-defined or not, i.e. it does not require (66).
Lemma 3.6. Let $ u\in {\rm H}_\mu^1( \mathcal{T}) $. If
then $ u\in {\rm H}_{\mu, \mathit{\text{0}}}^1( \mathcal{T}) $.
Proof. The proof relies on an approximation process adapted from [33]. Let $ u\in {\rm H}_\mu^1( \mathcal{T}) $, for which (77) holds true. Next, let a piecewise-linear function $ \varphi_{n} $ be defined as follows:
Notice that the support of $ \varphi'_n $ lies in $ \mathcal{T}^{2n} \setminus \mathcal{T}^n $. Also, for any $ \ell \leqslant n $
Our goal is to prove that $ u_n = \varphi_{n} u\in {\rm H}_{\mu, \text{c}}^1( \mathcal{T}) $ converges to $ u $ in $ {\rm H}_\mu^1( \mathcal{T}) $. For this it suffices to show that, as $ n\rightarrow \infty $, the sequences
By Lebesgue's dominated convergence theorem,
Therefore, it remains to show that $ \| \varphi_{n}'u\|_{L^2_{\mu}(\mathcal{T})}\rightarrow 0 $. Using $ \mbox{supp } \varphi_n \subset \mathcal{T}^{2n} \setminus \mathcal{T}^n $ and (78),
Since we want to bound the above using the traces $ \tau_m u $, we will bound $ \|u\|_{ {\rm L}_\mu^2(\Sigma_{m, j})}^2 $ by a quantity involving the value of $ u $ in the vertex $ M_{m, j} $ (and, eventually, its derivative $ \partial_s u $).
For this we will use the following 1D Poincaré inequality
Let us introduce a piecewise-constant interpolant $ \Pi u $ defined by
Then, thanks the the Poincaré inequality, applied to the function $ u - \Pi u $,
With the above and
we deduce the following upper bound on $ \|u\|_{ {\rm L}_\mu^2(\Sigma_{m, j})}^2 $:
Plugging in the above bound into (81), we end up with the following expression:
Obviously, the first term in the above tends to $ 0 $ as $ n\rightarrow +\infty $. So does the second term, thanks to the condition (77). Indeed, (77) can be rewritten as
Then the second term in the above bound can be estimated as follows:
Thus, $ \varphi_{n}'u\rightarrow 0 $ in $ {\rm L}_\mu^2( \mathcal{T}) $, and with (79, 80), $ \varphi_{n}u\rightarrow u $ in $ {\rm H}_\mu^1( \mathcal{T}) $.
To prove theorem 3.5, it remains to show that (77) holds for any $ u \in \mbox{Ker }\tau_\infty $. This proof relies on two technical lemmas that aim at connecting the norm of the traces at generations $ n $ and $ n+N $, namely $ \tau_{n} u $ and $ \tau_{n+N} u $. Our first result connects each nodal value $ {\mathbf u}_{n, j} = {\mathbf u_{ \boldsymbol{j}}} $ (recall that $ \boldsymbol{j} = j_1j_2\cdots j_n $, see the discussion after Lemma 2.4) with the values of $ u $ at all the end points of $ \mathcal{G}^{n+N} $ that are connected to $ M_{n, j} $, namely:
Lemma 3.7. Let $ u \in {\rm H}_\mu^1( \mathcal{T}) $. Let additionally $ \{q_{\ell}, \, 0 \leqslant \ell \leqslant p-1\} $ satisfy
Then the nodal value $ {\mathbf u}_{n, j} = {\mathbf u}_{ \boldsymbol{j}} $ is related to the nodal values (86) via
In the above $ P_{n, j}^N $ is a convex combination of point values at the end points of $ \mathcal{G}^{n+N} $ that are connected to $ M_{n, j} $, cf. (86), while each $ D_{n, j}^k $ is a convex combination of integrals of $ \partial_s u $ along the edges of the generation $ \mathcal{G}^{n+k} $ that are connected to $ M_{n, j} $.
Proof. The proof is done by induction. It consists essentially in playing with the basic identity (71) and in exploiting, in order to get an optimal result, all the paths that connect $ M_{n, j} $ to the possible end points of the generation $ \mathcal{G}^{n+N} $.
Let us first consider the case $ N = 1 $. According to (71),
To exploit all the possible paths between $ M_{ \boldsymbol{j}} $ and the $ M_{ \boldsymbol{j}\ell_1} $'s we make a convex linear combination of these equalities, using the coefficients $ q_{\ell_1} $, to obtain the identity
which is (87) for $ N = 1 $. Let us now assume that (87) holds and let us prove it for $ N+1 $. We use an analogue of (90) for $ {\mathbf u}_{\boldsymbol{j}\ell_1 \cdots \ell_N} $ instead of $ {\mathbf u}_{ \boldsymbol{j}} $ :
which we substitute into (87), using (88) and (89),
which is the desired result since the central term above is nothing but $ D_{n, j}^{N+1} $.
Remark 3.8. For the functions of the class $ {\rm H}_{\mu, \text{s}}^1(\mathcal{T}) $, when the tree and its weight is regular, cf. remark 3.3 for the definition and the notation, the above result is simply the fundamental theorem of calculus.
In order to prove theorem 3.5, we first need to relate the traces $ \tau_{n} u $ and $ \tau_{n+N} u $ in the norm. For this we will apply lemma 3.7 with $ q_{\ell} = \gamma_{\ell} $, where $ \{\gamma_{\ell}, \, 0 \leqslant \ell \leqslant p-1\} $ are defined in (63). Let us introduce a related quantity:
Lemma 3.9. For all $ u \in {\rm H}_\mu^1( \mathcal{T}) $, all $ n, \, N \geqslant 1 $,
Proof. By definition of $ \tau_n u $, we have, cf. (75),
Thus, using (87) with $ q_{\ell} = \gamma_{\ell} $, where $ \{\gamma_{\ell}, \, 0 \leqslant \ell \leqslant p-1\} $ are as in (63),
By convexity of $ x \rightarrow x^2 $, we deduce from (88) that
After multiplication by $ \mu_{n, j} / \alpha_{n, j} $ and summation over $ 0 \leqslant j \leqslant p^n-1 $, we get
or, alternatively, thanks to (93) for $ n+N $ instead of $ n $,
In the same way, by convexity again, we deduce from (89) that
Using the Cauchy-Schwarz inequality (like in (72))
Next, using the discrete Cauchy-Schwarz inequality and the definition of $ C_{{\boldsymbol \alpha}{\boldsymbol \mu}}^N $, we obtain
Multiplying the above by $ \frac{\mu_{n, j}}{\alpha_{n, j}} $ and using (98) results in the following inequality:
Since the sets $ \big \{ \Sigma_{\boldsymbol{j}\ell_1 \cdots \ell_k}, 0 \leqslant \ell_1, \ldots, \ell_k \leqslant p-1 \big\} $ form, when $ 0 \leqslant j \leqslant p^n-1 $, a partition of the generation $ \mathcal{G}^{n+k} $,
Thus, after summation of (100) over $ 0 \leqslant j \leqslant p^n-1 $, we get
Finally, the inequality (92) is obtained by gathering (94), (96) and (102).
Now we have all the ingredients necessary to prove theorem 3.5.
Proof of theorem 3.5. By theorem 3.2, see (69), it suffices to prove that $ \operatorname{Ker}\tau_{\infty}\subseteq {\rm H}_{\mu, \text{0}}^1( \mathcal{T}) $. In particular, we will show that following holds true:
By lemma 3.6 this will imply that $ \operatorname{Ker}\tau_{\infty}\subseteq {\rm H}_{\mu, \text{0}}^1( \mathcal{T}) $.
First, since (66) holds, we can define
From lemma 3.9 it follows that for all $ u \in {\rm H}_\mu^1( \mathcal{T}) $, $ n, \, N \geqslant 1 $,
Let us assume $ u \in \mbox{Ker } \tau_\infty $. Then, taking $ N \rightarrow + \infty $ in the above, we obtain
Since $ u\in {\rm H}_\mu^1( \mathcal{T}) $, the right-hand side of the above tends to zero as $ n\rightarrow \infty $, from where (103) follows, and hence $ u\in {\rm H}_{\mu, \text{0}}^1( \mathcal{T}) $.
It is natural to ask how big the image $ \mbox{Im } ~~ \tau _\infty $ of the map $ ~~ \tau _\infty $ is. The answer to this question involves another fundamental quantity, namely
Theorem 3.10. Assume that
Then, for any $ n \geqslant 1 $, $ \mathbb{P}_0(\Gamma_n) \subset \mathit{\mbox{Im}} ~~ \tau _\infty $. In particular, $ \mathit{\mbox{Im}} ~~ \tau _\infty $ is dense in $ L^2(\Gamma_\infty) $.
Proof. Let $ \mathbb{1}_{ \mathcal{T}} $ be a function that equals identically to $ 1 $ on $ \mathcal{T} $. It is easy to verify that
Let $ \varphi \in \mathbb{P}_0(\Gamma_n) $ and $ \boldsymbol{\varphi}_{n, j} $ be the value of $ \varphi $ in the interval $ [a_{n, j}, a_{n, j+1}] $. Let us construct $ u \in {\rm H}_\mu^1( \mathcal{T}) $ as follows
Remark that $ u \in {\rm L}_\mu^2( \mathcal{T}) $ is a consequence of (108). By construction, $ \tau_\infty u = \varphi $. Thus, $ \mathbb{P}_0(\Gamma_n)\subset \mbox{Im } ~~ \tau _\infty $. The density of $ \operatorname{Im}\tau_{\infty} $ follows from the approximation property of spaces $ \mathbb{P}_0(\Gamma_n) $.
Remark 3.11. Theorem 3.5, lemmas 3.6, 3.7, 3.9 and theorem 3.10 hold both for compact and non-compact trees.
Remark 3.12. The following result proves that $ ~~ \tau _\infty $ in not surjective: the traces posses some (weak) Sobolev regularity. In [33,Section 5.4], it was proven that
where the critical Sobolev regularity exponent $ \nu^* $ is defined as follows (see (63) for the definition of $ \gamma_i $):
When $ \big \langle \boldsymbol{\mu}\boldsymbol{\alpha} \big \rangle \geqslant 1 $, the situation is totally different: the image of $ ~~ \tau _\infty $ is reduced to $ 0 $, or, equivalently, $ {\rm H}_{\mu, \text{0}}^1( \mathcal{T}) = \mbox{Ker } ~~ \tau _\infty = {\rm H}_\mu^1( \mathcal{T}). $ This will be proven in section 3.3.
Theorem 3.13. Assume that $ \big \langle {\boldsymbol{\mu}}{\boldsymbol{\alpha}} \big \rangle \geqslant 1 $. Then
Proof. By theorem 3.18, see section 3.3, $ {\rm H}_{\mu, \text{0}}^1( \mathcal{T}) = {\rm H}_\mu^1( \mathcal{T}) $; the result follows from
3.3. On the distinction between $ {\rm H}_\mu^1( \mathcal{T}) $ and $ {\rm H}_{\mu, \text{0}}^1( \mathcal{T}) $
In this section we present the conditions on $ \boldsymbol{\alpha} $, $ \boldsymbol{\mu} $ that ensure that the spaces $ {\rm H}_{\mu, \text{0}}^1( \mathcal{T}) $ and $ {\rm H}_\mu^1( \mathcal{T}) $ coincide, or, in other words, when compactly supported functions (in the sense of (19)) are dense in $ {\rm H}_\mu^1( \mathcal{T}) $. Our first result in this direction is the following.
Theorem 3.14. If the condition (107) holds, then $ {\rm H}_{\mu, \mathit{\text{0}}}^1( \mathcal{T}) \subsetneq {\rm H}_\mu^1( \mathcal{T}) $.
Proof. The result is an immediate consequence of the trace theorem 3.10, since the equality $ {\rm H}_{\mu, \text{0}}^1( \mathcal{T}) = {\rm H}_\mu^1( \mathcal{T}) $, according to theorem 3.5, implies in particular that $ \mbox{Im } \tau_\infty = \{0\}. $
As we are going to see, when $ \big \langle \boldsymbol{\mu}\boldsymbol{\alpha} \big \rangle \geqslant 1 $ or $ \Big \langle \frac{\boldsymbol{\mu}}{\boldsymbol{\alpha}} \Big \rangle \leqslant 1 $, then $ {\rm H}_{\mu, \text{0}}^1( \mathcal{T}) \equiv {\rm H}_\mu^1( \mathcal{T}) $.
We shall state this result as two theorems, whose proofs are quite different:
● theorem 3.15 for $ \Big \langle \frac{\boldsymbol{\mu}}{\boldsymbol{\alpha}} \Big \rangle \leqslant 1 $ (and, consequently, $ \big \langle \boldsymbol{\mu}\boldsymbol{\alpha} \big \rangle<1 $).
● theorem 3.18 for $ \big \langle \boldsymbol{\mu}\boldsymbol{\alpha} \big \rangle \geqslant 1 $ (and, consequently, $ \Big \langle \frac{\boldsymbol{\mu}}{\boldsymbol{\alpha}} \Big \rangle>1 $).
Theorem 3.15. If $ \Big \langle \frac{\boldsymbol{\mu}}{\boldsymbol{\alpha}} \Big \rangle \leqslant 1 $, then $ {\rm H}_{\mu, \mathit{\text{0}}}^1( \mathcal{T}) = {\rm H}_\mu^1( \mathcal{T}) $.
To prove this result, we shall use the following technical lemma.
Lemma 3.16. Let $ (x_n), \, (\varepsilon_n), \, n\in\mathbb{N}, $ be two sequences of non-negative real numbers. Let one of the following hold true:
(i) $ x_{n+1} \leqslant \gamma \, x_{n}+\varepsilon_n $, where $ 0<\gamma<1 $ and $ \varepsilon_n\rightarrow 0 $ as $ n\rightarrow \infty $;
(ii) $ x_{n+1} \leqslant \gamma_n \, x_{n} +\varepsilon_n $, where $ \gamma_n = 1-\frac{a}{n+1} $, $ 0 < a < 1 $, and $ \sum\limits_{k = 0}^{\infty}\varepsilon_k < + \infty $.
Then the sequence $ x_n $ converges to $ 0 $ when $ n \rightarrow + \infty $.
Proof. See appendix A.
Proof of theorem 3.15. By lemma 3.6, it suffices to prove that (77) holds for any $ u \in {\rm H}_\mu^1( \mathcal{T}) $. To do so, we compare the norms of two successive partial traces of $ u $, cf. (75),
Because
we deduce, using the Young's inequality (with a parameter $ \eta_n>0 $, which we will choose later) and the Cauchy-Schwarz inequality for the integral, cf. (72),
Multiplying the above by $ \frac{\mu_{n, j}}{\alpha_{n, j}} \, \frac{\mu_{\ell}}{\alpha_{\ell}} $ and summing over $ 0 \leqslant j \leqslant p^n-1 $ and $ 0 \leqslant \ell \leqslant p-1 $ we obtain, with (110),
In the above the term $ \|\partial_s u\|_{ \mathcal{G}^{n+1}}^2 $ was obtained like in (101). Let us then consider separately, for the sake of clarity, the following two cases.
Case 1. $ \Big \langle \frac{\boldsymbol{\mu}}{\boldsymbol{\alpha}} \Big \rangle<1 $. We choose $ \eta_n = \eta $, independent of $ n $, so that
Then, by Lemma 3.16, case (ⅰ), we prove that $ t_n\rightarrow 0 $ as $ n\rightarrow +\infty $ which implies in particular (77).
Case 2. the limit case $ \Big \langle \frac{\boldsymbol{\mu}}{\boldsymbol{\alpha}} \Big \rangle = 1 $. Since $ \Big \langle \frac{\boldsymbol{\mu}}{\boldsymbol{\alpha}} \Big \rangle = 1 $, the previous approach will not work. To explain the choice of $ \eta_n $, let us define $ \widehat{t}_n : = n^{-1} \, t_n $, so that (111) becomes
We choose $ \eta_n $ so that
Then, as $ \varepsilon_n = (1+2n) \, (n+1)^{-1} \|\partial_s u\|^2_{\mathcal{G}^{n+1}} \leqslant 2\|\partial_s u\|^2_{\mathcal{G}^{n+1}} $ is summable, by Lemma 3.16, case (â…±) (with $ a = 1/2 $), we prove that that $ \widehat t_n\rightarrow 0 $, i. e. (77).
Remark 3.17. We have shown that when $ \Big \langle \frac{\boldsymbol{\mu}}{\boldsymbol{\alpha}} \Big \rangle<1 $, $ \Big \langle \frac{\boldsymbol{\mu}}{\boldsymbol{\alpha}} \Big \rangle^{n}\|\tau_nu\|^2\rightarrow 0 $ as $ n\rightarrow \infty $.
This does not hold when $ \Big \langle \frac{\boldsymbol{\mu}}{\boldsymbol{\alpha}} \Big \rangle = 1 $, with a counterexample provided by the identity function. Notice that
Nonetheless, in this case $ { \mathbb{1}_{ \mathcal{T}}}\in {\rm H}_{\mu, \text{0}}^1( \mathcal{T}) = {\rm H}_\mu^1( \mathcal{T}) $.
Finally, we consider the case when $ \big \langle \boldsymbol{\mu}\boldsymbol{\alpha} \big \rangle \geqslant 1 $, and, in particular, (66) holds.
Theorem 3.18. If $ \big \langle \boldsymbol{\mu}\boldsymbol{\alpha} \big \rangle \geqslant 1 $, then $ {\rm H}_{\mu, \mathit{\text{0}}}^1( \mathcal{T}) = {\rm H}_\mu^1( \mathcal{T}) $.
The proof of this result is, in its structure, quite similar to the proof of $ {\rm H}_{\mu, \text{0}}^1( \mathcal{T}) = \mbox{Ker } \tau_\infty $, i.e. theorem 3.5, where we use extensively lemma 3.7 and convexity or the Cauchy-Schwarz inequality based arguments. However, we need to proceed differently, because, unlike in theorem 3.5, we do not assume any longer that $ \|\tau_{n+N} u\| $ converges to $ 0 $. This prevents us from exploiting the inequality (92). The key trick will be to obtain an inequality similar to (92) where the quantity $ \|\tau_{n+N} u\| $ is replaced by a similar quantity, related to $ \tau_{n+N} u $, which tends to $ 0 $ when $ N\rightarrow \infty $ and resembles (in a certain sense which will be clear later) $ \|u\|^2_{L^2( \mathcal{G}^{n+N})} $. Instead of working directly with the the squared $ L^2 $-norm, we shall use the fact that, when $ n \rightarrow + \infty $, because the size of the edges of $ \mathcal{T} \setminus \mathcal{T}^n $ decreases drastically, $ u $ in $ {\rm H}_\mu^1( \mathcal{T}\setminus \mathcal{T}^n) $ can be accurately approximated by a piecewise-constant function, defined in (83), see the proof of lemma 3.6. This assertion is quantified by the following technical lemma.
Lemma 3.19. For all $ n \geqslant 1 $, $ u\in {\rm H}_\mu^1( \mathcal{T}) $,
In particular, for all $ u\in {\rm H}_\mu^1( \mathcal{T}), \quad \lim\limits_{n \rightarrow + \infty} \|\Pi u\|_{ {\rm L}_\mu^2( \mathcal{T}\setminus \mathcal{T}^{n})}^2 = 0 $.
Proof. The bounds (113) follow from
and the bound (84) for $ \|u -\Pi u\|^2_{ {\rm L}_\mu^2(\mathcal{T}\setminus\mathcal{T}^n)} $, rewritten in the form
The fact that $ \lim\limits_{n \rightarrow + \infty} \|\Pi u\|_{ {\rm L}_\mu^2( \mathcal{T}\setminus \mathcal{T}^{n})}^2 = 0 $ follows from the bound (114) and $ |\boldsymbol{\alpha}|_{\infty}<1 $.
The interest of working with $ \Pi u $ is that, inside $ \mathcal{G}^n $, $ \Pi u $ is defined by the same nodal values as $ \tau_n u $. As a consequence, it is easy to relate $ \tau_n u $ to $ \Pi u $ in $ \mathcal{G}^n $. This allows us to formulate an analogue of lemma 3.9, more precisely of the inequality (92). Let us first introduce
Lemma 3.20. For any $ u \in {\rm H}_\mu^1( \mathcal{T}) $, $ n, \, N \geqslant 1 $,
Proof. Let us first remark that
resembles $ \Big \langle \frac{\boldsymbol{\mu}}{\boldsymbol{\alpha}} \Big \rangle^n\|\tau_n u\|^2 $, cf. (75), with $ \mu_{n, j}\alpha_{n, j}^{-1} $ replaced by $ \mu_{n, j}\alpha_{n, j} $.
Thus, we will use the same idea as in the proof of lemma 3.9; we start with the inequality (94), however, we define $ P_{n, j}^N $ and $ D_{n, j}^k $ differently than in lemma 3.9. More precisely, we use lemma 3.7 with $ q_{\ell} = \mu_{\ell}\alpha_{\ell}{\big \langle \boldsymbol{\mu}\boldsymbol{\alpha} \big \rangle}^{-1} $, $ \ell = 0, \ldots, p-1 $.
As a consequence, proceeding as in the proof of lemma 3.9, we see that (94) is still valid but with different $ P_{n, j}^N $ and $ D_{n, j}^k $. In particular, the estimate (95) has to be replaced by
After multiplication by $ \mu_{n, j} / \alpha_{n, j} $ and summation over $ 0 \leqslant j \leqslant p^n-1 $, we obtain
Since $ \frac{\mu_{n, j}}{\alpha_{n, j}} = {\mu_{n, j}}{\alpha_{n, j}} \cdot \alpha_{n, j}^{-2} \leqslant {\mu_{n, j}}{\alpha_{n, j}} \, |\boldsymbol{\alpha}^{-1}|_{\infty}^{2n} $,
where the last equality follows from (117).
To obtain an upper bound for $ |D_{n, j}^k|^2 $, cf. (97), we use the convexity argument:
Using the Cauchy-Schwarz inequality, like in (72),
Using the discrete Cauchy-Schwartz inequality, introducing $ \nu: = \big \langle \boldsymbol{\mu}\boldsymbol{\alpha} \big \rangle^{-\frac{1}{2}} | \boldsymbol{\alpha}|_{\infty} $, we obtain
where we used the bound (120) and the definition (115) of $ \widehat{C}_{{\boldsymbol \alpha}{\boldsymbol \mu}}^N $. With (101),
The desired result is obtained by substituting (129) and (121) into (94).
Now we have all the components necessary to prove theorem 3.18.
Proof of theorem 3.18. We will use the characterization of the space $ {\rm H}_{\mu, \text{0}}^1( \mathcal{T}) $ of lemma 3.6, namely, we will show that (77) holds for all $ u\in {\rm H}_\mu^1( \mathcal{T}) $. For this we employ (116).
Since the tree is compact, i.e. $ |\boldsymbol{\alpha}_{\infty}|<1 $ and $ \big \langle \boldsymbol{\mu}\boldsymbol{\alpha} \big \rangle \geqslant1 $, the value $ \widehat{C}_{{\boldsymbol \alpha}{\boldsymbol \mu}}^N $ is bounded uniformly in $ N $ by
This allows us to take a limit $ N\rightarrow +\infty $ in (116). Together with lemma 3.19 (namely, using the fact that $ \lim\limits_{N\rightarrow \infty}\|\Pi u\|^2_{ {\rm L}_\mu^2( \mathcal{G}^{n+N})} = 0 $), we obtain the following inequality, valid for all $ u\in {\rm H}_\mu^1( \mathcal{T}) $,
This shows that $ \Big \langle \frac{\boldsymbol{\mu}}{\boldsymbol{\alpha}} \Big \rangle^n \|\tau_n u\|^2\rightarrow 0 $ as $ n\rightarrow \infty $, and, by lemma 3.6, $ u\in {\rm H}_{\mu, \text{0}}^1( \mathcal{T}) $.
Remark 3.21. Theorem 3.15 holds both for compact and non-compact trees. The proof of Theorem 3.18, however, uses the compactness of the tree.
3.4. Summary and different regions of parameters
In this section we will summarize the results of the previous sections about the trace operator and relationship between the spaces $ {\rm H}_{\mu, \text{0}}^1( \mathcal{T}) $ and $ {\rm H}_\mu^1( \mathcal{T}) $. Such a brief outline is provided in figure 6.
This difference between different values of $ \boldsymbol{\mu}, \, \boldsymbol{\alpha} $ will be expressed as well in the construction of transparent boundary conditions. Let us thus introduce the following space of parameters:
According to figure 6, we can partition it into the three regions:
Note that (this will be used later)
The choice of the notation with indices $ N $, $ ND $ and $ D $ will become clear later, when constructing transparent boundary conditions(cf. corollary 5.6 and remark 5.7).
3.5. Compact embedding of $ {\rm H}_\mu^1( \mathcal{T}) $ into $ {\rm L}_\mu^2( \mathcal{T}) $
It appears that independently of $ \boldsymbol{\mu} $, the embedding $ {\rm H}_\mu^1( \mathcal{T})\hookrightarrow {\rm L}_\mu^2( \mathcal{T}) $ is compact. The proof of this result is lengthy, and, moreover, uses somewhat different approaches depending whether the case $ \big \langle \boldsymbol{\mu}\boldsymbol{\alpha} \big \rangle \geqslant 1 $ or $ \big \langle \boldsymbol{\mu}\boldsymbol{\alpha} \big \rangle<1 $ is considered. Nonetheless, both approaches are based on the following characterization of the compactness, which follows from the works of F. Ali Mehmeti et S. Nicaise [8] and Y. Achdou et N. Tchou [6].
Lemma 3.22. Let $ V = {\rm H}_{\mu, \mathit{\text{0}}}^1( \mathcal{T}) $ or $ {\rm H}_\mu^1( \mathcal{T}) $. The injection of $ V $ in $ {\rm L}_\mu^2( \mathcal{T}) $ is compact if and only there exists a sequence $ (\gamma_n)_{n \in \mathbb{N}} $, s.t. $ \lim\limits_{n\rightarrow \infty}\gamma_n = 0 $ and
Proof. See appendix B.
Depending on the approach taken to prove the inequality (124), we split the compactness result into two theorems:
● the compactness of the embedding $ {\rm H}_\mu^1( \mathcal{T})\hookrightarrow {\rm L}_\mu^2( \mathcal{T}) $ when $ \big \langle \boldsymbol{\mu}\boldsymbol{\alpha} \big \rangle \geqslant 1 $ (i.e. in $ \mathbb{P}_{D} $) is the statement of theorem 3.23.
● the compactness of the embedding $ {\rm H}_\mu^1( \mathcal{T})\hookrightarrow {\rm L}_\mu^2( \mathcal{T}) $ when $ \big \langle \boldsymbol{\mu}\boldsymbol{\alpha} \big \rangle<1 $ (i.e. in $ \mathbb{P}_N\cup \mathbb{P}_{ND} $) is the principal result of theorem 3.24.
We start with the case $ \big \langle \boldsymbol{\mu}\boldsymbol{\alpha} \big \rangle \geqslant 1 $, as it uses inequalities used in the proof of lemma 3.9.
Theorem 3.23. If $ \big \langle \boldsymbol{\mu}\boldsymbol{\alpha} \big \rangle \geqslant 1 $, the embedding $ {\rm H}_\mu^1( \mathcal{T})\hookrightarrow {\rm L}_\mu^2( \mathcal{T}) $ is compact.
Proof. We use the criterion of lemma 3.22. Because of theorem 3.18, it suffices to demonstrate that (124) holds for any function from $ {\rm H}_{\mu, \text{0}}^1( \mathcal{T}) $. By lemma 3.19, in particular (113)-(â…±), we can just show that (124) holds with $ \|u\|_{ {\rm L}_\mu^2( \mathcal{T} \setminus \mathcal{T}^n)} $ replaced by $ \left\lVert {\Pi u} \right\rVert_{{ {\rm L}_\mu^2( \mathcal{T} \setminus \mathcal{T}^n)}} $.
Let us first assume that $ u\in {\rm H}_{\mu, \text{c}}^1( \mathcal{T}) $, i. e. $ \left. u\right|_{\mathcal{T}\setminus\mathcal{T}^{N}} = 0 $ for some $ N $. Thus, for all $ n < N $,
First, we apply lemma 3.7 with $ q_{\ell} = \gamma_{\ell} $, cf. (63), which gives, since $ P_{n, j}^N \equiv 0 $,
Together with (100), the above results in
With the bound $ C_{\boldsymbol{\alpha}\boldsymbol{\mu}}^{k}<C_{\boldsymbol{\alpha}\boldsymbol{\mu}} $, $ k\in\mathbb{N} $, see (104) (valid because $ \Big \langle \frac{\boldsymbol{\mu}}{\boldsymbol{\alpha}} \Big \rangle>\big \langle \boldsymbol{\mu}\boldsymbol{\alpha} \big \rangle \geqslant 1 $), and the observation (101), the above inequality yields:
Thus, for any $ u\in {\rm H}_{\mu, \text{c}}^1( \mathcal{T}) $, any $ n \geqslant 1 $, the above and (125) imply
With (113)-(ⅱ) and the density argument, a similar inequality holds for $ \|u\|_{ {\rm L}_\mu^2( \mathcal{T}\setminus \mathcal{T}^n)}^2 $ whenever $ u\in {\rm H}_{\mu, \text{0}}^1( \mathcal{T}) = {\rm H}_\mu^1( \mathcal{T}) $. We conclude with lemma 3.22.
The case $ \big \langle \boldsymbol{\mu}\boldsymbol{\alpha} \big \rangle<1 $ is slightly different, since we will show an inequality of the form
Compared with (127), $ \|\partial_s u\|^2_{ {\rm L}_\mu^2( \mathcal{T}^n)} $ is replaced by $ \|\partial_s u \|^2_{ {\rm L}_\mu^2( \mathcal{T}\setminus \mathcal{T}^n)} $.
The reason is that when $ \big \langle \boldsymbol{\mu}\boldsymbol{\alpha} \big \rangle<1 $, $ {\rm H}_{\mu, \text{c}}^1( \mathcal{T}) $ is not necessarily dense in $ {\rm H}_\mu^1( \mathcal{T}) $, cf. theorem 3.14, and thus the identity (126) is no longer valid.
Theorem 3.24. If $ \big \langle \boldsymbol{\mu}\boldsymbol{\alpha} \big \rangle<1 $, the embedding $ {\rm H}_\mu^1( \mathcal{T})\hookrightarrow {\rm L}_\mu^2( \mathcal{T}) $ is compact.
Proof. Like in the proof of theorem 3.23, it suffices to show that for all $ u\in {\rm H}_\mu^1( \mathcal{T}) $,
Without loss of generality, we may assume that $ u(M_{0, 0}) = 0 $. As discussed, we will show that $ \|\Pi u\|_{ {\rm L}_\mu^2(\mathcal{G}^n)} $ is controlled by $ \|\partial_s u\|_{ {\rm L}_\mu^2(\mathcal{T}^n)} $. For this, let us express $ \mathbf{u}_{n, j} $ as an integral of $ \partial_s u $ over the path that joins $ M_{0, 0} $ and $ M_{n, j} $:
Using discrete and continuous (cf. (72)) Cauchy-Schwarz inequalities, we have
After the multiplication by $ \alpha_{n, j} \mu_{n, j} \equiv \alpha_{j_1\cdots j_n}\mu_{j_1\cdots j_n} $, the above yields:
According to (117), by summation of the above over $ 0 \leqslant j \leqslant p^n-1, $ i. e. over $ 0 \leqslant j_1 \leqslant p-1, \cdots, 0 \leqslant j_n \leqslant p-1, $ we get
Setting $ A_{n, \ell} : = \sum\limits_{j_{\ell+1} = 0}^{p-1}\cdots\sum\limits_{j_n = 0}^{p-1}\alpha_{j_{\ell+1}}\mu_{j_{\ell+1}}\cdots \alpha_{j_n}\mu_{j_n} \equiv \big \langle \boldsymbol{\mu}\boldsymbol{\alpha} \big \rangle^{n-\ell} $ and writing
we get
A direct computation yields
Combining the above two expressions, we thus obtained (128) with
where $ C = C(\boldsymbol{\alpha}, \boldsymbol{\mu})>0 $ is a constant depending only on $ \big \langle \boldsymbol{\mu}\boldsymbol{\alpha} \big \rangle $ and $ |\boldsymbol{\alpha}|_{\infty} $. Using (113)-(â…±), we deduce that (124) holds for all $ u\in {\rm H}_\mu^1( \mathcal{T}) $ and conclude with lemma 3.22.
Remark 3.25. The statement of lemma 3.22 is valid both for compact and non-compact trees. The results of theorems 3.24, 3.23 do not hold for non-compact trees. It appears that the necessary [33,Theorem 6.1.7] (and, as we have shown, sufficient) condition for the compactness of the embedding $ {\rm H}_\mu^1( \mathcal{T})\hookrightarrow {\rm L}_\mu^2( \mathcal{T}) $ is $ |\boldsymbol{\alpha}|_{\infty}<1 $.
4.
Helmholtz equation on compact self-similar trees
As we will see later, in order to construct transparent boundary conditions, it will be necessary to understand the structure of the solutions to the Neumann ($ \mathcal{P}_ {\mathfrak{n}, \omega} $) and the Dirichlet ($ \mathcal{P}_ {\mathfrak{d}, \omega} $) problems for the Helmholtz equation. We address in this section the following questions:
● self-similarity (in a certain sense) of the solutions to ($ \mathcal{P}_ {\mathfrak{d}, \omega} $) and ($ \mathcal{P}_ {\mathfrak{n}, \omega} $);
● the continuity of the solutions to ($ \mathcal{P}_ {\mathfrak{d}, \omega} $) and ($ \mathcal{P}_ {\mathfrak{n}, \omega} $) in $ \omega = 0 $;
● the difference between the solutions to ($ \mathcal{P}_ {\mathfrak{d}, \omega} $) and ($ \mathcal{P}_ {\mathfrak{n}, \omega} $).
4.1. Helmholtz equation on compact self-similar trees
Let us introduce a notion of a quasi-self-similar function, which will play an important role in understanding of the structure of the solutions to the Helmholtz equation on self-similar trees.
Definition 4.1. [Quasi-self-similarity] A function $ u: \, \mathcal{T}\times \left( \mathbb{C}\setminus \mathbb{R}\right)\rightarrow \mathbb{C} $ is called quasi-self-similar if there exists a complex-valued function $ r : \mathbb{C} \setminus \mathbb{R} \rightarrow \mathbb{C} $ (quasi-self-similarity ratio) such that, for any $ 0 \leqslant i \leqslant p-1 $ and for any $ \omega \in \mathbb{C}\setminus \mathbb{R} $,
The above notion reduces to a classical notion of self-similarity in $ \omega = 0 $, namely
For any quasi-self-similar function $ u $, any $ j = (j_1\cdots j_n)_p $,
where $ \sigma_{n, j} $, $ \alpha_{n, j} $ are defined as in (49) and (51). It appears that solutions to the Dirichlet (Neumann) problems for the Helmholtz equation are quasi-self-similar.
Theorem 4.2. The function $ u_{ \mathfrak{d}}(s, \omega) $ (resp. $ u_{ \mathfrak{n}}(s, \omega) $), which solves (
$ \mathcal{P}_ {\mathfrak{d}, \omega} $) (resp. ($ \mathcal{P}_ {\mathfrak{n}, \omega} $)), is quasi-self-similar.
Proof. We provide the proof for $ u = u_{ \mathfrak{d}}(s, \omega) $, the one for $ u_{ \mathfrak{n}}(x, \omega) $ being verbatim the same. Let
Our goal is to show that $ u $ is quasi-self-similar of ratio $ r(\omega) $.
It is not difficult to notice that $ r(\omega)\neq 0 $ in $ \mathbb{C}\setminus \mathbb{R} $. Otherwise, by uniqueness of the solution of the Dirichlet Helmholtz problem in each subtree $ \mathcal{T}_{1, i} $, $ u(\cdot, \omega) $ would have vanished identically in each $ \mathcal{T}_{1, i} $, or, in other words $ u(\cdot, \omega) $ would have been supported in $ \Sigma_{0, 0} $. Using the Kirchhoff condition at the node $ M_{0, 0} $, we would have $ \partial_s u(M_{0, 0}, \omega) = 0 $. And, since $ u $ is solution of the Helmholtz equation along $ \Sigma_{0, 0} $ and satisfies $ u(M_{0, 0}, \omega) \equiv {r(\omega)} = 0 $, this would imply that $ \left. u \right|_{\Sigma_{0, 0}} = 0 $ (hence a contradiction to the boundary condition $ u({M_\star}, \omega) = 1 $).
Let us define the following quantity:
Notice that $ u_{i}({M_\star}, \omega) = 1 $. Also,
Choosing $ v_i \in V_{ \mathfrak{d}, i} = \{ v \in V_ \mathfrak{d} \; / \; \mbox{supp } v \subset \mathcal{T}_{1, i} \} $ in the weak formulation of ($ \mathcal{P}_ {\mathfrak{d}, \omega} $), we get (where $ s_i $ is the abscissa on $ \mathcal{T}_{1, i} $)
Performing in the above integrals the change of variables $ s_i = \sigma_i(s) $, where $ s $ is an abscissa on $ \mathcal{T} $, we obtain
for all $ v_i\in V_{ \mathfrak{d}, i} $. Notice that the above holds with $ v_i(\sigma_i(s))\in V_{ \mathfrak{d}, i} $ replaced by $ v(s)\in V_{ \mathfrak{d}} $ (since for any $ v_i\in V_{ \mathfrak{d}, i} $, there exists $ v\in V_{ \mathfrak{d}} $, s.t. $ v_i\circ \sigma_i = v $). Using (55), (134), the variational formulation (136) becomes
Since $ u_{i}({M_\star}, \omega) = 1 $, $ u_{i} $ is nothing but the solution of the Dirichlet Helmholtz problem associated to the frequency $ \alpha_i \, \omega $. Thus, with (133),
which concludes the proof.
4.2. Zero-frequency limit of the Helmholtz equation on compact self-similar trees
In this section we address the question of the well-posedness of the problems ($ \mathcal{P}_ {\mathfrak{d}, \omega} $) and ($ \mathcal{P}_ {\mathfrak{n}, \omega} $) when $ \omega = 0 $ (i.e. Laplace equation), as well as provide explicit solutions to these problems. With this analysis we aim at two goals. First, we would like to show that in the region of the parameters $ \mathbb{P}_{ND} $, cf. (122), the solutions of the problems ($ \mathcal{P}_ {\mathfrak{d}, \omega} $) and ($ \mathcal{P}_ {\mathfrak{n}, \omega} $), in general, differ. And second, we will use the knowledge of the explicit solution to the Laplace equation to distinguish between these problems when constructing transparent boundary conditions.
Let us now find explicitly the solutions to the Dirichlet/Neumann problem for the Laplace equation. This problem is well-posed, according to Lemma 1.22, in particular, because the compactness assumptions (38)-$ \mathfrak{n} $ and (38)-$ \mathfrak{d} $ hold true. First of all, let us formulate the following corollary of theorem 4.2 about the structure fo the solutions to the Laplace equation on a self-similar tree.
Theorem 4.3. The function $ u = u_{ \mathfrak{d}}(., 0) $, ($ u = u_{ \mathfrak{n}}(., 0) $), which solves ($ \mathcal{P}_ {\mathfrak{d}, \omega} $) (corresp. ($ \mathcal{P}_ {\mathfrak{n}, \omega} $)) with $ \omega = 0 $, is self-similar, i.e. it satisfies for some $ r_0 \in\mathbb{C} $ and all $ 0 \leqslant i \leqslant p-1 $,
Proof. The statement follows by extending the proof of theorem 4.2 to $ \omega = 0 $ (notice that the theorem is formulated for $ \omega\in\mathbb{C}\setminus\mathbb{R} $) and the definition of the quasi-self-similarity, cf. also (130) with $ r_0: = r(0) $.
In the following theorem we calculate explicitly the solutions to ($ \mathcal{P}_ {\mathfrak{d}, \omega} $) and ($ \mathcal{P}_ {\mathfrak{n}, \omega} $) for $ \omega = 0 $. In particular, we show that in the region $ \mathbb{P}_{ND} $, the functions that solve ($ \mathcal{P}_ {\mathfrak{d}, \omega} $) and ($ \mathcal{P}_ {\mathfrak{n}, \omega} $) for $ \omega = 0 $ are distinct.
Theorem 4.4. The solutions to ($ \mathcal{P}_ {\mathfrak{d}, \omega} $) and ($ \mathcal{P}_ {\mathfrak{n}, \omega} $) with $ \omega = 0 $ satisfy:
● if $ (\boldsymbol{\mu}, \, \boldsymbol{\alpha})\in \mathbb{P}_{N} $, then $ u_{ \mathfrak{n}}(., 0) = u_{ \mathfrak{d}}(., 0) = \mathbb{1}_{ \mathcal{T}} $.
● if $ (\boldsymbol{\mu}, \, \boldsymbol{\alpha})\in \mathbb{P}_{ND} $, then $ u_{ \mathfrak{n}}(., 0) = \mathbb{1}_{ \mathcal{T}} $, and $ u_{ \mathfrak{d}}(., 0) $ is a piecewise-linear function, which satisfies (138) with
● if $ (\boldsymbol{\mu}, \, \boldsymbol{\alpha})\in \mathbb{P}_D $, then $ u_{ \mathfrak{n}}(., 0) = u_{ \mathfrak{d}}(., 0) $ is a piecewise-linear function, which satisfies (138) with $ r_0 $ defined in (139).
Proof. Let us find a general form of the solution to ($ \mathcal{P}_ {\mathfrak{d}, \omega} $), ($ \mathcal{P}_ {\mathfrak{n}, \omega} $). First, the use of (132) results in the following identity:
Then the Kirchhoff condition (9) at the node $ M_{0, 0} = \sigma_i({M_\star}) $ reads:
Since $ \partial_s^2 u = 0 $ along $ \Sigma_{0, 0} $, $ \partial_s u({M_\star}) = \partial_s u(M_{0, 0}) $. There are two possible solutions:
● either $ \partial_s u({M_\star}) = 0 $, which, with $ u({M_\star}) = 1 $, implies that $ u = \mathbb{1}_{ \mathcal{T}} $.
● or $ \partial_s u({M_\star})\neq 0 $, then (140) implies that $ r_0 $ is as in (139). As $ \partial_s^2u = 0 $, $ u $ is linear on $ \Sigma_{0, 0} $. Due to self-similarity, $ u(M_{0, 0}) = r_0 $, and therefore
To summarize, $ u $ is a piecewise-linear and satisfies (132) with $ r_0 $ from (138). We will denote such a function by $ \mathbb{L}_{r_0} $.
Case 1. $ (\boldsymbol{\mu}, \, \boldsymbol{\alpha})\in \mathbb{P}_{N} $. The function $ \mathbb{1}_{ \mathcal{T}}\in {\rm H}_\mu^1( \mathcal{T}) = {\rm H}_{\mu, \text{0}}^1( \mathcal{T}) $, see (108) and theorem 3.15. Also, $ \mathbb{1}_{ \mathcal{T}} $ satisfies ($ \mathcal{P}_ {\mathfrak{d}, \omega} $) and ($ \mathcal{P}_ {\mathfrak{n}, \omega} $). Thus, by the uniqueness of the solution, cf. lemma 1.22, $ u_{ \mathfrak{d}}(., 0) = u_{ \mathfrak{n}}(., 0) = \mathbb{1}_{ \mathcal{T}} $.
Case 2. $ (\boldsymbol{\mu}, \, \boldsymbol{\alpha})\in \mathbb{P}_{ND}. $ Notice that the function $ \mathbb{1}_{ \mathcal{T}}\in {\rm H}_\mu^1( \mathcal{T}) $, see (108), and it solves ($ \mathcal{P}_ {\mathfrak{d}, \omega} $) with $ \omega = 0 $. By uniqueness, $ u_{ \mathfrak{n}}(., 0) = \mathbb{1}_{ \mathcal{T}} $.
The function $ \mathbb{1}_{ \mathcal{T}}\notin {\rm H}_{\mu, \text{0}}^1( \mathcal{T}) $, because $ \tau_{\infty} \mathbb{1}_{ \mathcal{T}} = 1 $, while $ {\rm H}_{\mu, \text{0}}^1( \mathcal{T}) = \operatorname{Ker}\tau_{\infty} $, see theorem 3.5. Hence, $ \mathbb{1}_{ \mathcal{T}} $ does not satisfy ($ \mathcal{P}_ {\mathfrak{d}, \omega} $), and thus $ u_{ \mathfrak{d}} = \mathbb{L}_{r_0} $.
Case 3.$ (\boldsymbol{\mu}, \, \boldsymbol{\alpha})\in \mathbb{P}_{D} $. In this case, $ {\rm H}_{\mu, \text{0}}^1( \mathcal{T}) = {\rm H}_\mu^1( \mathcal{T}) $ (theorem 3.18), hence $ u_{ \mathfrak{d}} = u_{ \mathfrak{n}} $.
Since in this case $ \mathbb{1}_{ \mathcal{T}}\notin {\rm L}_\mu^2( \mathcal{T}) $ (see (108)), we deduce that $ u_{ \mathfrak{n}} = u_{ \mathfrak{d}} = \mathbb{L}_{r_0} $.
Thus, we see that in the region $ \mathbb{P}_{ND} $, zero-frequency solutions to the Dirichlet and Neumann problems do not coincide. This result can be extended to $ \omega\in \mathbb{C}\setminus\mathbb{R} $, except, possibly, some isolated points. To see this, first notice that there exists $ R>0 $, such that for any sequence $ {(\omega_k)_{k\in\mathbb{N}}}\subset B(0, R) $, s.t. $ \omega_k\rightarrow 0 $ as $ k\rightarrow \infty $,
This is an immediate corollary of proposition 1.23 (notice that (38)-$ { \mathfrak{d}} $ and (38)-$ { \mathfrak{n}} $ hold) combined with remark 1.20. This implies the following result.
Corollary 4.5. The following holds true for the solutions of ($ \mathcal{P}_ {\mathfrak{d}, \omega} $) and ($ \mathcal{P}_ {\mathfrak{n}, \omega} $):
● if $ (\boldsymbol{\mu}, \boldsymbol{\alpha})\in\mathbb{P}_N\cup \mathbb{P}_D $, then $ u_{ \mathfrak{d}}(., \omega) = u_{ \mathfrak{n}}(., \omega) $ for all $ \omega\in\mathbb{C}\setminus\mathbb{R} $;
● if $ (\boldsymbol{\mu}, \boldsymbol{\alpha})\in\mathbb{P}_{ND} $, $ u_{ \mathfrak{d}}(., \omega)\neq u_{ \mathfrak{n}}(., \omega) $ except, possibly, in isolated points $ \omega $ of $ \mathbb{C}\setminus\mathbb{R} $.
Proof. The result in $ \mathbb{P}_N\cup \mathbb{P}_D $ follows from $ {\rm H}_{\mu, \text{0}}^1( \mathcal{T}) = {\rm H}_\mu^1( \mathcal{T}) $, cf. theorems 3.15, 3.18.
When $ (\boldsymbol{\mu}, \boldsymbol{\alpha})\in\mathbb{P}_{ND} $, we proceed by contradiction. First of all, remark that (38) holds, cf. theorem 3.24, and thus $ u_{ \mathfrak{d}}(., \omega) $ and $ u_{ \mathfrak{n}}(., \omega) $ are analytic $ {\rm H}_\mu^1( \mathcal{T}) $-valued functions of $ \omega\in\mathbb{C}\setminus\mathbb{R} $, see proposition 1.23. Let us now assume that there exists $ \omega_{\ell}\in\mathbb{C}\setminus\mathbb{R} $, s.t.
Then, by the uniqueness continuation theorem for holomorphic vector-valued functions, see [9,Proposition A.2,p.462], $ u_{ \mathfrak{d}}(., \omega) = u_{ \mathfrak{n}}(., \omega) $ in $ \mathbb{C}\setminus\mathbb{R} $. However, by (142), for $ \omega\rightarrow 0 $, the functions $ u_{ \mathfrak{d}}(., \omega) $, $ u_{ \mathfrak{n}}(., \omega) $ converge correspondingly to $ u_{ \mathfrak{d}}(., 0) $ and $ u_{ \mathfrak{n}}(., 0) $, and as $ u_{ \mathfrak{d}}(., 0)\neq u_{ \mathfrak{n}}(., 0) $, see theorem 4.4, we arrive at the contradiction.
The above property shows that the transparent boundary conditions, which we aim to construct, should take into account the fact that the solutions of the Dirichlet and of the Neumann problem differ when $ (\boldsymbol{\mu}, \, \boldsymbol{\alpha})\in\mathbb{P}_{ND} $.
5.
Construction of transparent boundary conditions for the Helmholtz equation
In this section, we investigate some properties of the DtN operator, as it was introduced in section 1.6, and more precisely the computation of its symbol as a function of the frequency $ \omega \in \mathbb{C} \setminus \mathbb{R} $. We consider the case of the reference $ p $-adic self-similar compact weighted tree with the weight $ \mu(s) = 1 $ on $ \Sigma_{0, 0} $, cf. assumption 3.1.
5.1. DtN operator for the Dirichlet and Neumann Helmholtz problems
Before entering into the details, let us remind that depending on the value $ (\boldsymbol{\mu}, \, \boldsymbol{\alpha}) $,
● if $ (\boldsymbol{\mu}, \, \boldsymbol{\alpha})\in\mathbb{P}_N\cup\mathbb{P}_D $, the solutions of the Neumann and the Dirichlet problem for the Helmholtz equation coincide.
● otherwise, if $ (\boldsymbol{\mu}, \, \boldsymbol{\alpha})\in\mathbb{P}_{ND} $, the solutions of the Neumann and the Dirichlet problem do not coincide, except, possibly, for isolated frequencies, cf. corollary 4.5.
Let us define the two Dirichlet and Neumann symbols as
According to proposition 1.23, the functions $ \omega \mapsto \mathbf{\Lambda}_ \mathfrak{d}(\omega) $ and $ \omega \mapsto \mathbf{\Lambda}_ \mathfrak{n}(\omega) $ are meromorphic in $ \mathbb{C} $ and analytic in the neighborhood of the origin, since $ \omega = 0 $ is not an eigenvalue of the operators $ \mathcal{A}_{ \mathfrak{n}} $, $ \mathcal{A}_{ \mathfrak{d}} $, cf. lemma 1.22. Moreover, using (42) and (43),
The convergence of the above series is uniform on the compact subsets of $ \mathbb{C} $ that do not contain $ \big\{ \pm \, \omega_ \mathfrak{d}^n\big\} $ (resp. $ \big\{ \pm \omega_ \mathfrak{n}^n \big\} \; $); this follows from Remark 1.24 and continuity of the trace $ u\rightarrow \partial_s u(M_{\star}) $ for functions from $ D(\mathcal{A}_{ \mathfrak{d}}) $ (resp. $ D(\mathcal{A}_{ \mathfrak{n}}) $).
Remark 5.1. The formulas (144) show that the set of poles of $ \mathbf{\Lambda}_{ \mathfrak{d}}(\omega) $ (resp. $ \mathbf{\Lambda}_{ \mathfrak{n}}(\omega) $) is a subset of $ \big\{ \pm \, \omega_ \mathfrak{d}^n\big\} $ (resp. $ \big\{ \pm \omega_ \mathfrak{n}^n \big\} \; $). We conjecture that these sets coincide.
Another property of the symbol of the DtN operator follows naturally from the explicit form of the zero-frequency solutions for the Helmholtz equation. It is formulated below.
Lemma 5.2. The symbols $ \mathbf{\Lambda}_{ \mathfrak{d}}(\omega) $, $ \mathbf{\Lambda}_{ \mathfrak{n}}(\omega) $ satisfy the following:
● in $ \mathbb{P}_N $,
● in $ \mathbb{P}_{ND} $,
● in $ \mathbb{P}_D $,
Proof. Let us consider $ \big \langle \boldsymbol{\mu}\boldsymbol{\alpha} \big \rangle \geqslant 1 $, the proof for the rest of the cases being almost identical. If $ \big \langle \boldsymbol{\mu}\boldsymbol{\alpha} \big \rangle \geqslant 1 $, $ {\rm H}_{\mu, \text{0}}^1( \mathcal{T}) = {\rm H}_\mu^1( \mathcal{T}) $, hence $ \mathbf{\Lambda}_{ \mathfrak{d}}(\omega) = \mathbf{\Lambda}_{ \mathfrak{n}}(\omega) $.
By theorem 4.4, and more precisely (141), $ u = u_{ \mathfrak{d}}(., 0) $ satisfies
Thus, $ \mathbf{\Lambda}_{ \mathfrak{d}}(0)\equiv\mathbf{\Lambda}_{ \mathfrak{n}}(0) = - \, \partial_s u_{0, 0}(0) = 1- \Big \langle \frac{\boldsymbol{\mu}}{\boldsymbol{\alpha}} \Big \rangle^{-1}. $
5.2. A functional equation for $ \mathbf{\Lambda}_{ \mathfrak{d}}(\omega) $ and $ \mathbf{\Lambda}_{ \mathfrak{n}}(\omega) $
In this section we will demonstrate how one can compute the symbols $ \mathbf{\Lambda}_{ \mathfrak{d}}(\omega) $ and $ \mathbf{\Lambda}_{ \mathfrak{n}}(\omega) $.
Lemma 5.3. Each function $ \mathbf{\Lambda}(\omega) = \mathbf{\Lambda}_{ \mathfrak{d}}(\omega) $ or $ \mathbf{\Lambda}_{ \mathfrak{n}}(\omega) $ satisfies the following quadratic functional equation
Proof. Let $ u(\cdot, \omega) = u_ \mathfrak{d}(\cdot, \omega) $ or $ u_ \mathfrak{n}(\cdot, \omega) $ and $ \mathbf{\Lambda}(\omega) = -\partial_s u({M_\star}, \omega) $. Along $ \Sigma_{0, 0} $ parametrized by $ s \in [0, 1] $, $ \left. u(., \omega)\right|_{\Sigma_{0, 0}} \equiv u_{0, 0}(., \omega) $ is the solution to the following Cauchy problem:
which leads to $ u_{0, 0}(s, \omega) = \cos \omega s - \mathbf{\Lambda}(\omega)\, \frac{\sin\omega s}{\omega} $. In particular,
Along $ \Sigma_{1, i} \equiv \sigma_i(\Sigma_{0, 0}) $, $ \left. u(., \omega)\right|_{\Sigma_{1, i}} \equiv u_{1, i}(., \omega) $. Thus, by quasi-self-similarity (129), and the definition of $ \mathbf{\Lambda}(\omega) $, we get
where the self-similarity ratio $ r(\omega) $ is given by, cf. (132),
One gets (145) by substituting (146), (147), (148) into the Kirchhoff equation (9) at $ M_{0, 0} $:
Remark 5.4. Depending on the values of $ \boldsymbol{\mu} $ and $ \boldsymbol{\alpha} $, the equation (145) encodes all the symbols of the DtN operators for all the self-similar trees (even non-compact). In particular, e.g., one can verify that the DtN symbol for the Helmholtz equation on the half-line ($ p = 1 $, $ \mu = \alpha = 1 $), namely, $ \pm i\omega $, solves (145).
Since this equation (145) is quadratic, one expects that it admits several (naively at least two) solutions. However, as we know, when $ (\boldsymbol{\mu}, \boldsymbol{\alpha})\in\mathbb{P}_N\cup \mathbb{P}_D $, the symbols $ \mathbf{\Lambda}_{ \mathfrak{d}}(\omega) $ and $ \mathbf{\Lambda}_{ \mathfrak{n}}(\omega) $ coincide, and hence only one of these solutions corresponds to the symbol of the DtN operator. We will show the following properties:
● when $ (\boldsymbol{\mu}, \boldsymbol{\alpha})\in\mathbb{P}_N\cup\mathbb{P}_D $, (145) admits a single even meromorphic solution that takes the value at the origin prescribed by lemma 5.2. This will allow us to select a physical solution (145) in the cases the symbols $ \mathbf{\Lambda}_{ \mathfrak{d}}(\omega) $ and $ \mathbf{\Lambda}_{ \mathfrak{n}}(\omega) $ coincide;
● when $ (\boldsymbol{\mu}, \boldsymbol{\alpha})\in\mathbb{P}_{ND} $, (145) admits two even meromorphic solutions, which take the values at the origin prescribed by lemma 5.2. They correspond to $ \mathbf{\Lambda}_{ \mathfrak{d}}(\omega) $ and $ \mathbf{\Lambda}_{ \mathfrak{n}}(\omega) $.
First of all, notice that because the symbol of the DtN operator satisfies (145) and is an even function, analytic in the origin, a priori one of the solutions of the equation (145) is even and analytic in the origin. Moreover, in the origin this solution satisfies lemma 5.2. A priori it is not obvious that such a solution is unique. However, the uniqueness can be shown, and the corresponding result is formulated in the following lemma.
Let us draw the attention of the reader to the fact that in the lemma below, we use $ N $ or $ D $ as indices instead of $ \mathfrak{n} $ or $ \mathfrak{d} $ because we refer to solutions of the characteristic equation (145) and not to the DtN symbols. However, the connection between $ \mathbf{\Lambda}_D(\omega), \mathbf{\Lambda}_N(\omega) $ and $ \mathbf{\Lambda}_ \mathfrak{d}(\omega), \mathbf{\Lambda}_ \mathfrak{n}(\omega) $ will be immediately clarified with corollary 5.6.
Lemma 5.5. Any solution of (145), continuous in the origin, satisfies
If $ (\boldsymbol{\mu}, \boldsymbol{\alpha})\in\mathbb{P}_N\cup\mathbb{P}_{ND} $, the equation (145) admits a unique even solution $ \mathbf{\Lambda}(\omega) = \mathbf{\Lambda}_N(\omega) $ analytic in the origin that satisfies $ \mathbf{\Lambda}_N(0) = 0 $. Moreover, as $ \omega\rightarrow 0 $,
If $ (\boldsymbol{\mu}, \boldsymbol{\alpha})\in\mathbb{P}_D\cup\mathbb{P}_{ND} $, the equation (145) admits a unique even solution $ \mathbf{\Lambda}(\omega) = \mathbf{\Lambda}_D(\omega) $ analytic in the origin that satisfies
Moreover, its Taylor expansion at the origin is given, as $ \omega\rightarrow 0 $, by
Proof. Please see the appendix C. Let us remark that it is possible to obtain a higher-order expansion of $ \mathbf{\Lambda}_D(\omega) $ and $ \mathbf{\Lambda}_N(\omega) $, and the corresponding formulas, since they are somewhat cumbersome, are omitted here; however, they can be found in appendix C, see, in particular, (188, 189).
Combining the above with lemma 5.2, we arrive at the following conclusion.
Corollary 5.6. Let $ \mathbf{\Lambda}_N(\omega) $ and $ \mathbf{\Lambda}_D(\omega) $ be defined in lemma 5.5. Then the following holds:
● if $ (\boldsymbol{\mu}, \boldsymbol{\alpha})\in\mathbb{P}_N $, then $ \mathbf{\Lambda}_{ \mathfrak{n}}(\omega) = \mathbf{\Lambda}_{ \mathfrak{d}}(\omega) = \mathbf{\Lambda}_N(\omega) $.
● if $ (\boldsymbol{\mu}, \boldsymbol{\alpha})\in\mathbb{P}_{ND} $, then $ \mathbf{\Lambda}_{ \mathfrak{n}}(\omega) = \mathbf{\Lambda}_N(\omega) $ and $ \mathbf{\Lambda}_{ \mathfrak{d}}(\omega) = \mathbf{\Lambda}_D(\omega) $.
● if $ (\boldsymbol{\mu}, \boldsymbol{\alpha})\in \mathbb{P}_D $, then $ \mathbf{\Lambda}_{ \mathfrak{n}}(\omega) = \mathbf{\Lambda}_{ \mathfrak{d}}(\omega) = \mathbf{\Lambda}_D(\omega) $.
Remark 5.7. The corollary clarifies the notation by explaining why, when $ (\boldsymbol{\mu}, \, \boldsymbol{\alpha})\in \mathbb{P}_D \cup \mathbb{P}_N $, even though Dirichlet and Neumann problems coincide, we have chosen to consider that we solve the Dirichlet problem when $ (\boldsymbol{\mu}, \, \boldsymbol{\alpha})\in \mathbb{P}_D $ and that we solve the Neumann problem when $ (\boldsymbol{\mu}, \, \boldsymbol{\alpha})\in \mathbb{P}_N $.
Remark 5.8. The uniqueness results of lemma 5.5 fail to be true if one looks for not necessarily smooth solutions $ \mathbf{\Lambda}(\omega) $. Let us give a counter-example in the case where all the $ \alpha_i $'s are rational numbers. Then the function $ \mathbf{\Lambda}(\omega) $ defined in $ \mathbb{C} \setminus \mathbb{R} $ by
is a solution of (145), different from $ \mathbf{\Lambda}_D(\omega) $ and satisfying $ \mathbf{\Lambda}(0) = \mathbf{\Lambda}_{D}(0) $. In the same way, the function $ \mathbf{\Lambda}(\omega) $ defined in $ \mathbb{C} \setminus \mathbb{R} $ by
is a solution of (145), different from $ \mathbf{\Lambda}_D(\omega) $ and satisfying $ \mathbf{\Lambda}(0) = \mathbf{\Lambda}_N(0) $.
5.3. Positivity properties of the DtN Operator
An important property of the DtN operator is its positivity, which is related to the energy conservation. This property will be crucial for obtaining an approximation of symbols $ \mathbf{\Lambda}_{ \mathfrak{d}} $, $ \mathbf{\Lambda}_{ \mathfrak{n}} $ that would lead to stable transparent boundary conditions. Let us introduce
Theorem 5.9. The symbol $ \mathbf{\Lambda}(\omega) = \mathbf{\Lambda}_{ \mathfrak{d}}(\omega) $ ($ \mathbf{\Lambda}(\omega) = \mathbf{\Lambda}_{ \mathfrak{n}}(\omega) $) satisfies the following:
In other words, $ \mathbf{f}(\omega) = - \, \omega^{-1}\mathbf{\Lambda}(\omega) $ is a Herglotz function [17].
Proof. This property can be shown directly, by examining the expressions (144); however, we provide a more general proof, which relies only on the properties of the underlying sesquilinear form. We show the result for $ \mathbf{\Lambda}(\omega) = \mathbf{\Lambda}_{ \mathfrak{d}}(\omega) $, with the proof for $ \mathbf{\Lambda}_{ \mathfrak{n}}(\omega) $ being verbatim the same. For this we test the Helmholtz equation with $ u_{ \mathfrak{d}}(., \omega) $ and use the Green's formula (cf. also (9) for the Kirchoff conditions), which gives
Dividing the above by $ \omega\neq 0 $, and using (143), we obtain the following identity:
It remains to notice that $ u_{ \mathfrak{d}}\neq 0 $ and thus the imaginary part of the above is strictly negative whenever $ \omega\in\mathbb{C}^+ $.
Remark 5.10. The above property will be employed to prove that the algorithm for the evaluation of the symbol of the DtN operator, which we present in the next section, is well-defined (i.e. no division by zero occurs in the course of this algorithm). But the meaning of this positivity property is much more important than this: it is fundamental for the stability of the boundary-value problems. This is implicitly used, in particular, in theorem 6.2.
Let us state the following two trivial properties of the Herglotz functions, useful further.
Lemma 5.11. Let $ f(\omega): \mathbb{C}\rightarrow \mathbb{C} $ be an even function analytic in the vicinity of the origin, which admits the expansion $ f(\omega) = f_0+f_2\omega^2+O(\omega^4) $ as $ \omega\rightarrow 0 $, with $ f_0, \, f_2\in\mathbb{R} $, and $ f_0\neq 0 $ or $ f_2\neq 0 $. Assume additionally that, for any $ \omega \in\mathbb{C}^+ $
Then if $ f_0\neq 0 $, then $ f_0>0 $, while, if $ f_0 = 0 $, then $ f_2<0 $.
Proof. For $ \omega\in\mathbb{C}^+ $ sufficiently small,
It is easy to conclude with (150).
Remark 5.12. The solutions $ \mathbf{\Lambda}_{ \mathfrak{n}}(\omega) $ and $ \mathbf{\Lambda}_{ \mathfrak{d}}(\omega) $ defined in corollary 5.6 via solutions $ \mathbf{\Lambda}_N(\omega) $ and $ \mathbf{\Lambda}_D(\omega) $ of (145), cf. lemma 5.5, satisfy (150). From the proof of lemma 5.5, it follows that under additional conditions on the parameters $ \boldsymbol{\mu} $ and $ \boldsymbol{\alpha} $, it is possible to extend the definitions of
as solutions of the equation (145). However, as already seen by verifying the conditions of lemma 5.11 for their expansions in the origin (cf. lemma 5.5), these functions no longer satisfy (150) in these regions (with an exception of a special case $ \Big \langle \frac{\boldsymbol{\mu}}{\boldsymbol{\alpha}} \Big \rangle\equiv 1 $, when $ \mathbf{\Lambda}_D(\omega)\equiv \mathbf{\Lambda}_N(\omega) $). Thus, they cannot be the symbols of a DtN operator. This is consistent with corollary 5.6.
5.4. Numerical approximation of the symbols $ \mathbf{\Lambda}_{ \mathfrak{n}}(\omega) $, $ \mathbf{\Lambda}_{ \mathfrak{d}}(\omega) $
Let us now provide an algorithm for the numerical approximation of $ \mathbf{\Lambda}_ \mathfrak{a}(\omega) $ by $ \mathbf{\Lambda}^a_ \mathfrak{a}(\omega) $, $ \mathfrak{a} = \mathfrak{d} $ or $ \mathfrak{n} $. The function $ \mathbf{\Lambda}^a_ \mathfrak{a}(\omega) $ will be constructed progressively inside an increasing sequence of balls $ \mathcal{B}_n $ that fill the whole complex plane as $ n\rightarrow \infty $. For this, we rewrite (145) in the form
This expression defines the values of the function $ \mathbf{\Lambda}(\omega) $ via the values of the same function in $ \omega_i = \alpha_i\omega $, $ |\omega_i|<|\omega| $, $ i = 0, \ldots, p-1 $. This property serves as the basis for an algorithm for evaluating the function $ \mathbf{\Lambda}_{ \mathfrak{a}}(\omega) $.
First of all, let us consider
where $ r_0 > 0 $, the radius of $ \mathcal{B}_0 $, is such that $ \mathcal{B}_0 $ does not contain any pole of $ \mathbf{\Lambda}_ \mathfrak{a}(\omega) $, i.e.
Then, at the continuous level, the iterative algorithm proceeds as follows.
● Initialization: given a truncation parameter $ N \in \mathbb{N} $, one approximates $ \mathbf{\Lambda}_ \mathfrak{a}(\omega) $ inside $ \mathcal{B}_0 $ by its truncated Taylor expansion (recall that $ \mathbf{\Lambda}_ \mathfrak{a}(\omega) $ is even), i. e.
where the (real) coefficients $ \lambda_{ \mathfrak{a}, n} $ are computed based on the formulas of appendix C. This is the step for which the cases $ \mathfrak{a} = \mathfrak{d} $ and $ \mathfrak{a} = \mathfrak{n} $ may differ.
● Induction: Supposing that $ \mathbf{\Lambda}^a_ \mathfrak{d}(\omega) $ has been computed inside $ \mathcal{B}_n $, one computes $ \mathbf{\Lambda}^a_ \mathfrak{d}(\omega) $ inside $ \mathcal{B}_{n+1} \setminus \mathcal{B}_n $ based on (151), i.e.
Note that the above expression completely defines $ \mathbf{\Lambda}^a_ \mathfrak{a}(\omega) $ inside $ \mathcal{B}_{n+1} \setminus \mathcal{B}_n $ since, by construction of $ \mathcal{B}_n $,
One could ask whether the above algorithm is well-defined, in the sense that a division by zero never occurs in (154). This is the case, provided a certain condition on (153); this fact is a corollary of the following two lemmas.
Lemma 5.13. Let $ f(\omega): \Omega \subset\mathbb{C}^+\rightarrow \mathbb{C} $ satisfy (150). Then
1. $ \omega\cos\omega+\sin\omega f(\omega)\neq 0 $ in $ \Omega $;
2. the function $ F(\omega) = - \, \omega \; \frac{\omega\sin\omega-f(\omega) \cos\omega }{\omega\cos\omega+f(\omega)\sin\omega } $ satisfies
Proof. Let us prove the first assertion. Notice that $ h(\omega) $ defined by
vanishes for some $ \omega\in\mathbb{C}^+ $ if and only if $ g(\omega) = 0 $. However, $ \operatorname{Im}{\cot\omega}<0 $ in $ \mathbb{C}^+ $, cf. [17,p.64], and thus, due to (150),
To prove 2., we compute $ \operatorname{Im}(\omega^{-1}F(\omega)) = - \operatorname{Im} \frac{1-\omega^{-1}f(\omega)\cot\omega}{\cot \omega +\omega^{-1}f(\omega)} $, which yields
The above is negative, for the same reasons as (155), and because $ \operatorname{Im}{\overline{z}} = - \operatorname{Im}{z} $.
The above result shows that if $ f^a_{\alpha, \mu}(\omega) $ defined in (154) satisfies (150), then no division by zero occurs in the expression (154). On the other hand, since for small $ |\omega| $ the value $ f^{a}_{\alpha, \mu}(\omega) $ is computed via the truncated Taylor expansion (153), it is natural to ask under which conditions this Taylor expansion will produce a function satisfying (150).
Lemma 5.14. Let $ f(\omega): \mathbb{C}\rightarrow \mathbb{C} $ be an even polynomial $ f(\omega) = \sum\limits_{\ell = 0}^nf_{2\ell} \, \omega^{2\ell}, $ $ f_{2\ell}\in \mathbb{R} $, $ 0 \leqslant \ell \leqslant n $.
If $ f $ satisfies (150), then, necessarily,
Otherwise, if either $ f_0>0 $ or $ f_0 = 0 $ and $ f_2<0 $, then (150) holds for $ |\omega| $ small enough.
Proof. The first part of the statement follows by contradiction, by taking $ \omega\in\mathbb{C}^+ $ large enough. The second part of the statement mimics the proof of lemma 5.11.
To formulate the principal result about the feasibility of the algorithm (153, 154), let us introduce an auxiliary quantity $ r_*(N) $, which satisfies
Then we can formulate the following lemma about the properties of the algorithm.
Lemma 5.15. Let $ N\in \mathbb{N}\setminus\{0\} $ and $ r_0 < r_*(N). $
Then the algorithm based on (153, 154) is well-defined. Moreover, the function computed by this algorithm satisfies
Proof. It is easy to see that it is sufficient to check that the stated result holds for the first step of the algorithm (i.e. the construction of $ \mathbf{\Lambda}_{ \mathfrak{a}}^a(\omega) $ in $ \mathcal{B}_1 $). Then one proceeds by induction, by employing lemma 5.13.
First of all, thanks to lemma 5.14 (in the case $ N = 1 $) or (156) (for $ N>1 $), the function computed by (153) satisfies
Next, using the definition of the function $ f_{\alpha, \mu} $, see (151), and the one of $ \mathcal{B}_1 $, see (152),
Then applying lemma 5.13, item 1, with
we deduce that
Thus, there is no problem to extend the function $ \mathbf{\Lambda}^a_ \mathfrak{a}(\omega) $ to $ \mathcal{B}_{1} \setminus \mathcal{B}_0 \cap \mathbb{C}^+ $ using the formula (154). Moreover, by the item 2 of lemma 5.13, the function $ \mathbf{\Lambda}^a_ \mathfrak{d}(\omega) $ satisfies
Remark 5.16. We did not investigate the (expected) convergence of our algorithm when $ N \rightarrow + \infty $ and / or $ r_0 \rightarrow 0 $ but verified it numerically. Note that by construction, $ \mathbf{\Lambda}^a_ \mathfrak{a}(\omega) $ is polynomial in $ \mathcal{B}_{0} $, rational in each $ \mathcal{B}_{n+1} \setminus \mathcal{B}_n $ and discontinuous across each $ \partial \mathcal{B}_n $.
In practice, we compute a discrete approximation of $ \mathbf{\Lambda}^a_ \mathfrak{a}(\omega) $ along the rays on the complex plane $ {\mathcal{A}}rg \, \omega = \operatorname{const}. $ First notice that if suffices to compute $ \mathbf{\Lambda}^a_ \mathfrak{d}(\omega) $ in the quarter plane $ {\mathcal{A}}rg \, \omega \in \; ]0, \pi/2] $ since, once this is done, one completes the construction of $ \mathbf{\Lambda}^a_ \mathfrak{d}(\omega) $ using $ \mathbf{\Lambda}^a_ \mathfrak{a}(\omega) $ = $ \mathbf{\Lambda}^a_ \mathfrak{a}(- \omega) $ = $ \mathbf{\Lambda}^a_ \mathfrak{d}(\overline{\omega}) $, which follows from (30).
Next, we consider the following polar mesh of the quarter plane $ {\mathcal{A}}rg \, \omega \in \; ]0, \pi/2] $: let $ N_\theta \in \mathbb{N} $ be the number of the discretization points in the polar angle and $ N_0\in \mathbb{N} $ that defines the number of the discretization points in the ball $ \mathcal{B}_0 $. Let us define
where $ \Delta r = \frac{r_0}{N_{0}} $ and $ \Delta \theta = \frac{\pi}{2N_{\theta}} $, cf. figure 7. The value $ N_0 $ is chosen so that
Then, for each fixed $ j $ one computes the $ \{ \omega_j^n , n \geqslant 1\} $ in the following way:
● As long as $ n \leqslant N_0 $, $ \mathbf{\Lambda}^a_ \mathfrak{d}( \omega_j^n) $ is computed via the initialization step.
● As soon as $ n > N_0 $, $ \mathbf{\Lambda}^a_ \mathfrak{d}( \omega_j^n) $ is computed using the induction step, with an additional approximation induced by a linear interpolation procedure. More precisely, thanks to (163), which appears as a necessary condition for the explicit nature of our algorithm, we deduce (the verification is left to the reader) that, for each $ 0 \leqslant i \leqslant p-1 $, there exists $ \ell < n $ and $ \eta \in [0, 1] $ such that
Remark that the condition (158) ensures that $ \alpha_i \omega_j^{n}<\omega_j^{n-1} $ for all $ n>N_0 $. Then, in formula (154) applied to $ \omega = \omega_j^n $, one makes the substitution
5.5. Numerical results for $ \mathbf{\Lambda}_{ \mathfrak{d}}(\omega) $ and $ \mathbf{\Lambda}_{ \mathfrak{n}}(\omega) $
We consider a dyadic symmetric tree (cf. figure 4) characterized by $ p = 2 $, $ \alpha_1 = \alpha_2 = \alpha $ and $ \mu_1 = \mu_2 = \mu $, and compute the symbols of the DtN operators $ \mathbf{\Lambda}_{ \mathfrak{d}} $ and $ \mathbf{\Lambda}_{ \mathfrak{n}} $ for different values of $ (\boldsymbol{\mu}, \boldsymbol{\alpha}) $.
The approximation of $ \boldsymbol{\Lambda}_{ \mathfrak{d}}(\omega) $ and $ \boldsymbol{\Lambda}_{ \mathfrak{n}}(\omega) $. First of all, let us take $ \alpha = \mu = 0.6 $. In this case $ (\boldsymbol{\mu}, \boldsymbol{\alpha})\in\mathbb{P}_{ND} $, and thus $ \mathbf{\Lambda}_{ \mathfrak{d}}(\omega)\neq \mathbf{\Lambda}_{ \mathfrak{n}}(\omega) $, see corollary 5.6. The plots of $ |\boldsymbol{\Lambda}_{ \mathfrak{d}}(\omega)| $ and $ |\boldsymbol{\Lambda}_{ \mathfrak{n}}(\omega)| $ are shown in figure 8 (for $ \omega\in\mathbb{C} $). These results indicate that the algorithm based on (153, 154) detects the location of the poles of the meromorphic functions $ \boldsymbol{\Lambda}_{ \mathfrak{d}}(\omega) $ and $ \boldsymbol{\Lambda}_{ \mathfrak{n}}(\omega) $, and allows to define the values of these functions for $ \omega\notin\mathbb{R} $.
The property (149) of $ \boldsymbol{\Lambda}_{ \mathfrak{d}}(\omega) $ and $ \boldsymbol{\Lambda}_{ \mathfrak{n}}(\omega) $. As shown in lemma 5.15, the property (154) is preserved by the algorithm (153, 154) (provided certain conditions on $ N $ and $ r_0 $ in (153)). In figure 9 we illustrate this fact.
Meromorphic solutions of (145) $ \boldsymbol{\Lambda}_D(\omega) $ and $ \boldsymbol{\Lambda}_N(\omega) $, which are not symbols of the DtN operator. Finally, let us demonstrate what happens to the functions $ \boldsymbol{\Lambda}_D(\omega) $ and $ \boldsymbol{\Lambda}_N(\omega) $ in the regions where they fail to be the symbols of the DtN operators, see corollary 5.6 and remark 5.12. For this we set $ \alpha = 0.6 $ and $ \mu = 0.2 $ (so that $ (\boldsymbol{\mu}, \boldsymbol{\alpha})\in\mathbb{P}_N $), and compute $ \boldsymbol{\Lambda}_D(\omega) $, and next set $ \alpha = 0.6 $ and $ \mu = 2 $ (so that $ (\boldsymbol{\mu}, \boldsymbol{\alpha})\in\mathbb{P}_D $) and evaluate $ \boldsymbol{\Lambda}_N(\omega) $. The absolute values of these functions are shown in figure 10. As one can see, the function $ \boldsymbol{\Lambda}_D(\omega) $ has a zero on the imaginary axis (two dark blue spots on the imaginary axis in the left plot in figure 10), and the function $ \boldsymbol{\Lambda}_N(\omega) $ has a pole in $ i\mathbb{R} $. These two behaviors are incompatible with (149).
6.
Local approximate transparent boundary conditions for a fractal tree
In this section, we present a stable low-order local approximation of the DtN operator, based on the expansions provided in lemma 5.5, see corollary 5.6.
6.1. Construction of conditions of order 1 and 2
First of all, in practice we are interested in arbitrary $ p $-adic self-similar trees rather than just reference ones; the corresponding DtN operators, however, can be easily expressed via the DtN operators of the reference trees by a simple scaling argument. Given a reference $ p $-adic self-similar tree $ \mathcal{T} $ and a corresponding $ p $-adic self-similar tree whose root edge has length $ \ell $, i.e. $ \mathcal{T}_{\ell} : = \ell \, \mathcal{T} $ (with $ (\boldsymbol{\mu}, \boldsymbol{\alpha}) $ remaining the same for both trees), the symbol of the (Neumann or Dirichet) DtN operator $ \mathbf{\Lambda}_{ \mathfrak{a}, \ell} $ for $ \mathcal{T}_{\ell} $ is related to the corresponding DtN operator for the reference tree $ \mathbf{\Lambda}_ \mathfrak{a}(\omega) $ via
Let us come back to the transparent conditions (23) of section 1.6. For simplicity, but without any loss of generality, let us consider the case where the tree is the self-similar tree $ { \mathcal{T}}(\ell) $ associated to ($ \boldsymbol{\mu}, \boldsymbol{\alpha} $) and that we want to solve the wave equation with a non-homogeneous Dirichlet condition at the entrance of the tree. Suppose that we wish to truncate the computational domain after the $ n^{th} $ generation, by prescribing the DtN condition at each of the end points $ M_{n, j}, 0 \leqslant j \leqslant p^n-1 $, which is thus nothing but (23) and (24), rewritten as
where we recall that $ \mathcal{C}_{n, j} $ is given in (8) and that $ \Lambda_{n+1, k} $ is the DtN operator associated to the subtree $ \mathcal{T}_{n+1, k} $, see (22). Because of the self-similarity properties and lemma 2.4
Moreover, as the length of the root edge of the tree of $ \mathcal{T}_{n+1, pj+i} $ is $ \alpha_i \, \ell_{n, j} $ with $ \ell_{n, j} = \alpha_{n, j} \, \ell $, we have
where we have used (159) for notation, with $ \mathfrak{a} = \mathfrak{d} $ or $ \mathfrak{n} $. Thus the transparent boundary condition at the point $ M_{n, j} $ rewrites
From the compactness property of the tree, one expects that, since $ \ell_{n, j} $ decays exponentially fast to $ 0 $ with $ n $, to get a good approximation of $ \Lambda_{ \mathfrak{a}, \alpha_i \ell_{n, j}} $, it suffices, according to the formula (159), to have a good approximation of $ \mathbf{\Lambda}_ \mathfrak{a}(\omega) $ for small values of $ |\omega| $. In this perspective, truncated Taylor expansions around the origin offer an attractive solution since they lead to local boundary conditions. Then, the only theoretical question is to know if the truncation process preserves the stability of the new boundary value problem. In what follows, we shall investigate this question by looking at second order Taylor expansions. More precisely, we propose the approximations
where according to lemma 5.5, we have for the Dirichlet problem (and $ \Big \langle \frac{\boldsymbol{\mu}}{\boldsymbol{\alpha}} \Big \rangle >1 $)
while for the Neumann case (which means that $ \big \langle \boldsymbol{\mu}\boldsymbol{\alpha} \big \rangle < 1 $)
Remark 6.1. We will refer to these approximations as to the second-order conditions, because they are constructed using the first three terms of the expansion of the symbol of the DtN in $ \omega $ (as $ \lambda_{ \mathfrak{a}, 1}\equiv 0 $). We could have taken only the first two terms in the expansion, and in this case these conditions will be referred to as having the order one.
Note that one has the following sign properties:
Then, (162) combined with (159), suggests the following approximation of the operators $ \Lambda_{ \mathfrak{a}, \alpha_i \ell_{n, j}} $ appearing in (161) by second order differential operators:
This leads to the following boundary value problem on the truncated tree $ \mathcal{T}^n $: find $ u_{ \mathfrak{a}, 2}^n : \mathcal{T} \times \mathbb{R}^+ \rightarrow \mathbb{R} $ (the approximate solution) such that
completed by initial conditions and the Dirichlet condition at the entrance of the tree. The weak formulation of the above problem reads
Remark that, contrary to the case of the exact problems, where the distinction between Neumann and Dirichlet problems occurred in the variational spaces, for the approximate problems, the difference appears in the bilinear forms, via the coefficients $ (\lambda_{ \mathfrak{a}, 0}, \lambda_{ \mathfrak{a}, 2}) $.
Our main theoretical result is the following stability result.
Theorem 6.2. Let $ \mathfrak{a} = \mathfrak{n} $ (resp. $ \mathfrak{a} = \mathfrak{d} $) and let $ u_ \mathfrak{a} $ be the solution of problem ($ \mathcal{P}_ {\mathfrak{a}, n} $) for $ \mathfrak{a} = \mathfrak{n} $ (resp. $ \mathfrak{a} = \mathfrak{d} $) with the source term $ f $. Moreover, let $ f $ be compactly supported in $ (0, T_0) $, with $ T_0 < T $. Then, the energy $ \mathcal{E}_{ \mathfrak{a}, 2}^n(t) $ defined by
is constant for $ t>T_0 $. As a consequence, the approximate boundary conditions are uniformly stable in the sense that the approximate solution is bounded in energy norm by a constant which is independent of the truncation order $ n $.
Proof. Again the existence and uniqueness result is a classical exercise on the theory of second order linear hyperbolic problems. The result about the energy is obtained in the usual way after multiplying the first equation of (167) by $ \partial_t $ and integrating the result over $ \mathcal{T}^n $. Finally, the stability result, i.e. that $ \mathcal{E}_{ \mathfrak{a}, 2}^n(t) $ defines an energy (is non-negative), follows from (165).
6.2. Numerical validation of conditions of order $ 1 $ and $ 2 $
In this section we validate the performance of our approximate conditions numerically on the example of the dyadic symmetric tree (cf. figure 4). Our goal is to check the influence of the order (1 or 2) of the absorbing boundary condition together with the influence of the truncation order $ n $ of the tree. For each experiment, this evaluation will be made by by comparing the corresponding approximate solution to a reference solution computed with a large tree $ \mathcal{T}^N $ made of the $ N $ first generations with $ N $ large (and the second order absorbing boundary condition).
6.2.1. Discretization
We shall not discuss in detail the method that we used for the discretization of the truncated problem since it is quite classical.
The spatial discretization is done on a uniform spatial mesh with step size $ h $ whose nodes include, in particular, the vertices of the tree. To eliminate the effect of the spatial discretization on the accuracy of experiments, we use very small values of $ h $, so that it is compatible with the large reference tree $ \mathcal{T}^N $: each edge of the last generation is divided into $ K $ segments. All computations are done on the same mesh: more precisely, for the computations made on $ \mathcal{T}^n $ with $ n\ll N $, we use the restriction to $ \mathcal{T}^n $ of the mesh of $ \mathcal{T}^N. $ We use standard mass-lumped 1D-Lagrange finite elements (with a trivial adaptation for the basis functions to ensure their continuity at the vertices of the tree). For brevity we will use the same notation for the semidiscretized in space and the continuous solution.
For the time discretization, we use an explicit scheme coupled with an implicit discretization of the boundary terms. In particular, given a time step $ \Delta t $, and $ t^k = k\Delta t $, we denote by $ u_{ \mathfrak{a}, 2}^{n, k}\approx {u_{ \mathfrak{a}, 2}^n(\cdot, t^k)} $. Then in ($ \mathcal{P}_ {\mathfrak{a}, n} $), all the second-derivatives (related to volumic and boundary terms) are discretized by
the volumic term in the stiffness bilinear form of ($ \mathcal{P}_ {\mathfrak{a}, n} $) is discretized explicitly, i.e.
and, finally, the boundary $ 0 $-order term is discretized implicitly:
As a consequence, the resulting numerical scheme is stable under the classical CFL condition $ \operatorname{CFL} = \frac{\Delta t}{\Delta x} \leqslant 1 $. Moreover, the resolution of the problem remains fully explicit.
6.2.2. Numerical Experiments
We present the numerical simulations for the scattering problem with the Dirichlet condition at infinity
on the dyadic tree with the parameters
with the length of the first branch $ \ell = 2 $. The source terms $ f(s), g(s) $ are supported and centered on the first branch and are given by
According to figure 8, the smallest positive pole of $ \Lambda_ \mathfrak{d}(\omega) $ is
Thus we cannot expect a good approximation of $ \Lambda_ \mathfrak{d}(\omega) $ by the truncated Taylor expansion for $ |\omega| \geqslant \omega_ \mathfrak{d}^0. $
Due to the choice of the source term, for time $ t $ small enough $ u(s, t) $ is given on the first branch by $ f(s-t) $. Let us then consider the Fourier transform of $ f $, given by
We observe in particular that for
We perform the simulations with this source. To truncate the tree (find $ n $), we need to examine how well $ \Lambda_ \mathfrak{d}(\ell\alpha^{n+1} \omega) $ is approximated for $ |\omega|<|\omega_{\text{cut}}| $, cf. (161). In particular, $ n $ should satisfy $ \left|\ell\alpha^{n+1} \omega_{\text{cut}}\right|<\omega_{ \mathfrak{d}}^0 $. This estimate provides a lower bound for the truncation order $ n $ to expect a reasonable accuracy of the absorbing boundary condition (162):
In what follows, we compare the reference solution, computed on the tree $ \mathcal{T}^N $, $ N = 22 $ (the solution of ($ \mathcal{P}_ {\mathfrak{a}, n} $) with $ \mathfrak{a} = \mathfrak{d} $), to
● the solution $ u_{ \mathfrak{d}, 0}^ n $ defined as the solution of (167) where the the absorbing condition is replaced by the Dirichlet condition, hereafter referred to as the $ 0 $ order condition,
● the solution $ u_{ \mathfrak{d}, 1}^n $ defined as the solution of (167) with $ \lambda_{ \mathfrak{a}, 0} = \lambda_{ \mathfrak{d}, 0} $ and $ \lambda_{ \mathfrak{a}, 2} = 0 $, hereafter referred to as the first order condition,
● the solution $ u_{ \mathfrak{d}, 2}^n $ defined as the solution of (167) with $ \lambda_{ \mathfrak{a}, 0} = \lambda_{ \mathfrak{d}, 0} $ and $ \lambda_{ \mathfrak{a}, 2} = \lambda_{ \mathfrak{d}, 2} $, hereafter referred to as the second order condition.
In figure 11 we plot these computed solutions at the middle of the root branch of the tree $ M $ as functions of time $ t \in [0, T], \; T = 20 $, for $ n = 7 $ and $ n = 9 $ (which is compatible with (169)). The reference solution is in red, the approximate solution is in blue. As we can observe, the solution obtained on the truncated tree becomes closer and closer to the reference solution as the number of generations or the order of the truncating operator increases.
These qualitative results are quantified by table 1 and figure 12 where we computed the $ L^2 $ in time error between the reference and the approximate solutions (both computed at the point $ M $). In table 1, we demonstrate in particular the improved accuracy of the absorbing boundary conditions (162) compared to taking $ n = 7 $ and the Dirichlet ($ 0 $-order) condition.
In figure 12 we demonstrate that the convergence of the absorbing boundary conditions with respect to $ n $ is close to exponential, and, as expected, the error decreases with the order of the absorbing boundary condition. Let us remark that in this work we do not address the error analysis of these conditions, postponing this question to future works.
7.
Conclusions and Prospectives
The contributions of this work are of both theoretical and numerical nature. First of all, from the theoretical point of view, we have presented an extensive analysis of the properties of a weighted wave equation in an infinite compact tree with self-similar endings. One particularly tricky question is the treatment of the boundary conditions (Neumann or Dirichlet) at 'infinity', the understanding of which requires a deep analysis of particular weighted Sobolev spaces on compact fractal $ p $-adic trees. From the computational point of view, based on this analysis, we have constructed transparent boundary conditions for truncating the computational domain for solving the weighted wave equation on such fractal trees. The key ingredient is the construction of a reference DtN operator associated to a $ p $-adic self-similar tree, which is a time convolution operator whose symbol (the Fourier transform of the convolution kernel) is characterized as a particular solution of a non-linear functional equation. This solution is a meromorphic function, analytic in the vicinity of the origin. The analysis of the equation allows us in particular to compute the second-order Taylor expansion of this symbol around the origin, which we use for constructing approximate local boundary conditions. We have proven that these conditions are stable and their use results in a satisfactorily accurate approximation of the solutions. However, because the range of frequencies for which this Taylor expansion provides a good approximation is limited (to the pole-free region around the origin), in practice the use of such low-order conditions is likely to become prohibitively expensive for high-frequency problems. That is why we intend in a future work to improve the approximations of the boundary conditions, by considering two different approaches. The first idea is to replace the polynomial approximation by a rational approximation, in the spirit of [15], which would take into account the most significant poles of the exact symbol. The second idea is to consider the exact boundary conditions. In this case the main difficulty lies in the time discretization, for which we intend to adapt the convolution quadrature method [10].
Acknowledgments
The authors are grateful to Konstantin Pankrashkin (University of Paris-Sud) for fruitful discussions.
Appendix A.
Proof of lemma 3.16
The first case of the lemma is obvious. First of all, it is not difficult to verify by induction that:
The first term in the rhs of (170) converges to zero because $ \gamma<1 $. For the second term, we split the sum into two parts that we estimate separately:
The second case is slightly trickier. First of all, we obtain by induction the equivalent of the inequality (170), that is:
or equivalently, setting $ \Gamma_n = \prod\limits_{\ell = 0}^n \gamma_{\ell} $,
The first term in the rhs of (171) converges to $ 0 $ because, since $ 1-ax \leqslant \mathit{\boldsymbol{e}}^{-ax} $ for $ x \geqslant 0 $,
On the other hand, for $ n \geqslant N+1 $ ($ N $ to be fixed later), the second term in the rhs of (171) satisfies, since $ \Gamma_{n-1} / \, \Gamma_{k} < 1 $,
Since $ \sum\limits_{n = 0}^{\infty}\varepsilon_{n}<\infty $, for any $ \varepsilon > 0 $, we can choose $ N = N_\varepsilon $ so that $ \sum\limits_{k = N+1}^{+\infty} \, \varepsilon_{k} < \frac{\varepsilon}{2} $:
Since $ \Gamma_n \rightarrow 0 $, for $ n $ large enough $ \Gamma_{n-1} \, S_\varepsilon < \frac{\varepsilon}{2} $ and the conclusion follows.
Appendix B.
Proof of lemma 3.22
Step 1: proof that (124) implies the compactness. Let $ \gamma_n\rightarrow 0, \, n\rightarrow \infty, $ be s.t. (129) holds. Let $ u_n $ be a bounded sequence in $ V $. Our goal is to show that it has a convergent in $ {\rm L}_\mu^2( \mathcal{T}) $ subsequence. First, up to the extraction of a first subsequence, we can assume that $ u_n $ converges weakly in $ V $ to some limit $ u $.
Let us consider the sequence $ \left. u_n\right|_{ \mathcal{T}^0} $, which is bounded in $ {\rm H}_\mu^1( \mathcal{T}^0) $. Since $ {\rm H}_\mu^1( \mathcal{T}^0) $ is compactly embedded into $ {\rm L}_\mu^2( \mathcal{T}^0) $, there exists a subsequence $ u_n^0 $ of $ u_n $, s.t.
Similarly, $ \left.u_n^0\right|_{ \mathcal{T}^1} $ is bounded in $ {\rm H}_\mu^1( \mathcal{T}^1) $ and we extract from $ u_n^0 $ a subsequence $ u_n^1 $, s.t.
By induction, we can thus build a double-indexed sequence $ \{ u_n^k, (n, k) \in \mathbb{N}^2 \} $ satisfying
Let us now define the diagonal subsequence of $ u^n $
for which
Indeed, for all $ k $, $ \{u_n^n, n \geqslant k\} $ is a subsequence of $ n \rightarrow u_n^k $ which converges to $ u $ in $ {\rm L}_\mu^2( \mathcal{T}^k) $ thanks to (173).
Next, let us demonstrate that $ \tilde{u}_n\rightarrow u $ in $ {\rm L}_\mu^2( \mathcal{T}) $. Notice that
It remains to apply (124) to $ v = \widetilde{u}_n - u $. Since $ \widetilde{u}_n - u $ is bounded in $ {\rm H}_\mu^1( \mathcal{T}) $, there exists $ C>0 $, s.t.
Let $ \varepsilon > 0 $. We first fix $ k $ large enough such that $ C \, \gamma_k^2 < \varepsilon /2 $. Next, exploiting (175), we choose $ n $ large enough $ (n \geqslant N_k( \varepsilon)) $ so that $ \left\lVert {\widetilde{u}_n-u} \right\rVert_{{ {\rm L}_\mu^2( \mathcal{T}^k)}}^2 < \varepsilon/2 $ and we conclude that
Thus, $ \widetilde{u}_n $ converges to $ u $ in $ {\rm L}_\mu^2( \mathcal{T}) $.
Step 2: proof that the compactness implies (124). Assume that the embedding of $ V $ in $ {\rm L}_\mu^2( \mathcal{T}) $ is compact. Let us introduce
Note that $ \mathcal{T}^n \subset \mathcal{T}^{n+1} $ implies that $ \gamma_n $ is a decreasing sequence. Let us find a subsequence of $ \gamma_n $ that converges to $ 0 $, which would prove that $ \gamma_n\rightarrow 0 $ as $ n\rightarrow \infty $, i.e. (124). By compactness of $ \mathcal{B} $, there exists $ u_n \in \mathcal{B} $ that realizes the supremum in (178), i.e.
Again, by compactness of $ \mathcal{B} $, $ u_n $ has a subsequence $ (u_{ \varphi(n)})_{n \in \mathbb{N}} $, such that
Writing $ u_{ \varphi(n)} = (u_{ \varphi(n)} - u) + u $ and using the triangular inequality, we get
This shows that $ \gamma_{ \varphi(n)} $ tends to 0. Thus, $ \gamma_n\rightarrow 0 $ as $ n\rightarrow \infty $.
Appendix C.
Proof of lemma 5.5
Let $ \boldsymbol{\Lambda} $ be continuous in the origin. Taking the limit $ \omega\rightarrow 0 $ in (145), we obtain the following equation :
The above equation has the following solutions:
● when $ \Big \langle \frac{\boldsymbol{\mu}}{\boldsymbol{\alpha}} \Big \rangle\neq 1 $, there are two solutions:
● when $ \Big \langle \frac{\boldsymbol{\mu}}{\boldsymbol{\alpha}} \Big \rangle = 1 $, there is a single solution $ \mathbf{\Lambda}(0) = 0 $.
Hence the first part of the lemma. To prove the rest of the lemma we will show that under the appropriate assumptions on $ \boldsymbol{\mu} $ and $ \boldsymbol{\alpha} $, the value in $ 0 $ defines in a unique way any even function, analytic in a neighborhood of the origin, satisfying (145) in this neighborhood. Thus, let $ \mathbf{\Lambda}(\omega) $ be an even function, analytic around the origin. Then for $ |\omega| $ small enough, we have
Inserting this expansion into (145), we obtain the following equation:
Next, we wish to identify the terms in $ \omega^{2m} $ of the left and right hand sides of (184). First of all, for $ m = 0 $, $ \lambda_0 = \mathbf{\Lambda}(0) $, defined in (182).
For $ m \geqslant 1 $, one notices that the coefficient in $ \omega^{2m} $ in the left hand side of (184) is
As for the right hand side, we next observe that
where we have set
The coefficient in $ \omega^{2m} $ in the right hand side of (184) is
where we defined
In other words, with (186),
Isolating the terms involving $ \lambda_m $, that correspond to $ k = m $ in the first sum, $ (k = 0, q = m) $ and $ (k = m, q = 0) $ in the second sum, we get
With $ L_{2m} = R_{2m} $ (see (185) and (187)), we obtain a linear equation for $ \lambda_{2m} $:
Thus, to prove the uniqueness of an even solution analytic in the origin, it is sufficient to fix $ \lambda_0 $ to either of the values (182), and show that $ A_m\neq0 $ for all $ m \geqslant 1 $. As we will see later, this is the only place where Dirichlet and Neumann problems can de distinguished.
Now it remains to consider the two cases of the statement of the lemma, see also (123):
● If $ (\boldsymbol{\mu}, \boldsymbol{\alpha})\in\mathbb{P}_N\cup\mathbb{P}_{ND} \Leftrightarrow \big \langle \boldsymbol{\mu}\boldsymbol{\alpha} \big \rangle<1 $. We are interested in the solution that satisfies
In this case, we get the following expression for (189):
Notice that $ \eta_{m+1}<\eta_m $ for all $ m \geqslant 0 $, and hence $ A_{m+1}>A_m $, for all $ m \geqslant 1 $. Thus
hence the uniqueness of the solution with $ \mathbf{\Lambda}(0) = 0 $. With (188), it is easy to compute the first two terms of the expansion in $ \omega^2 $ of the solution $ \mathbf{\Lambda} $ in the origin. In particular, $ \lambda_2 = -(1-\big \langle \boldsymbol{\mu}\boldsymbol{\alpha} \big \rangle)^{-1} $, hence the announced Taylor expansion.
● If $ (\boldsymbol{\mu}, \boldsymbol{\alpha})\in\mathbb{P}_D\cup\mathbb{P}_{ND} \Leftrightarrow \Big \langle \frac{\boldsymbol{\mu}}{\boldsymbol{\alpha}} \Big \rangle>1 $. We are interested in the solutions satisfying
In this case (189) becomes
Like before, it is easy to see that $ A_{m+1}>A_m $, for all $ m \geqslant 1 $. Moreover,
because $ \Big \langle \frac{\boldsymbol{\mu}}{\boldsymbol{\alpha}} \Big \rangle^2>\Big \langle \frac{\boldsymbol{\mu}}{\boldsymbol{\alpha}} \Big \rangle>\big \langle \boldsymbol{\mu}\boldsymbol{\alpha} \big \rangle $.
Hence $ A_m>0 $ for all $ m \geqslant 1 $, thus the uniqueness of the solution. With (188), it is then immediate to obtain the announced Taylor expansion.
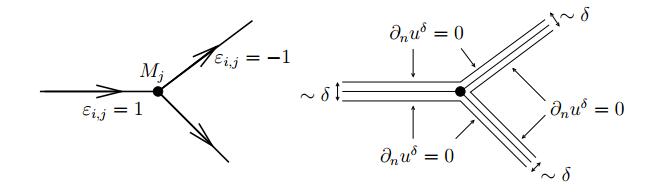









 DownLoad:
DownLoad:













