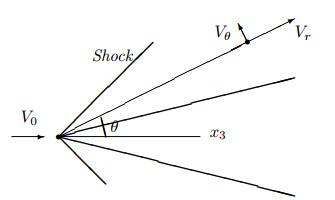
Spherical coordinate system
.We consider a conical body facing a supersonic stream of air at a uniform velocity. When the opening angle of the obstacle cone is small, the conical shock wave is attached to the vertex. Under the assumption of self-similarity for irrotational motions, the Euler system is transformed into the nonlinear ODE system. We reformulate the problem in a non-dimensional form and analyze the corresponding ODE system. The initial data is given on the obstacle cone and the solution is integrated until the Rankine-Hugoniot condition is satisfied on the shock cone. By applying the fundamental theory of ODE systems and technical estimates, we construct supersonic solutions and also show that no matter how small the opening angle is, a smooth transonic solution always exists as long as the speed of the incoming flow is suitably chosen for this given angle.
Citation: Wen-Ching Lien, Yu-Yu Liu, Chen-Chang Peng. Smooth Transonic Flows Around Cones[J]. Networks and Heterogeneous Media, 2022, 17(6): 827-845. doi: 10.3934/nhm.2022028
| [1] | Steinar Evje, Kenneth H. Karlsen . Hyperbolic-elliptic models for well-reservoir flow. Networks and Heterogeneous Media, 2006, 1(4): 639-673. doi: 10.3934/nhm.2006.1.639 |
| [2] | Frederike Kissling, Christian Rohde . The computation of nonclassical shock waves with a heterogeneous multiscale method. Networks and Heterogeneous Media, 2010, 5(3): 661-674. doi: 10.3934/nhm.2010.5.661 |
| [3] | Giuseppe Maria Coclite, Lorenzo di Ruvo, Jan Ernest, Siddhartha Mishra . Convergence of vanishing capillarity approximations for scalar conservation laws with discontinuous fluxes. Networks and Heterogeneous Media, 2013, 8(4): 969-984. doi: 10.3934/nhm.2013.8.969 |
| [4] | Xavier Litrico, Vincent Fromion . Modal decomposition of linearized open channel flow. Networks and Heterogeneous Media, 2009, 4(2): 325-357. doi: 10.3934/nhm.2009.4.325 |
| [5] | Mauro Garavello, Roberto Natalini, Benedetto Piccoli, Andrea Terracina . Conservation laws with discontinuous flux. Networks and Heterogeneous Media, 2007, 2(1): 159-179. doi: 10.3934/nhm.2007.2.159 |
| [6] | Tong Li, Sunčica Čanić . Critical thresholds in a quasilinear hyperbolic model of blood flow. Networks and Heterogeneous Media, 2009, 4(3): 527-536. doi: 10.3934/nhm.2009.4.527 |
| [7] | Wen Shen . Traveling wave profiles for a Follow-the-Leader model for traffic flow with rough road condition. Networks and Heterogeneous Media, 2018, 13(3): 449-478. doi: 10.3934/nhm.2018020 |
| [8] | Maya Briani, Emiliano Cristiani . An easy-to-use algorithm for simulating traffic flow on networks: Theoretical study. Networks and Heterogeneous Media, 2014, 9(3): 519-552. doi: 10.3934/nhm.2014.9.519 |
| [9] | Christophe Chalons, Paola Goatin, Nicolas Seguin . General constrained conservation laws. Application to pedestrian flow modeling. Networks and Heterogeneous Media, 2013, 8(2): 433-463. doi: 10.3934/nhm.2013.8.433 |
| [10] | Wen Shen . Traveling waves for conservation laws with nonlocal flux for traffic flow on rough roads. Networks and Heterogeneous Media, 2019, 14(4): 709-732. doi: 10.3934/nhm.2019028 |
We consider a conical body facing a supersonic stream of air at a uniform velocity. When the opening angle of the obstacle cone is small, the conical shock wave is attached to the vertex. Under the assumption of self-similarity for irrotational motions, the Euler system is transformed into the nonlinear ODE system. We reformulate the problem in a non-dimensional form and analyze the corresponding ODE system. The initial data is given on the obstacle cone and the solution is integrated until the Rankine-Hugoniot condition is satisfied on the shock cone. By applying the fundamental theory of ODE systems and technical estimates, we construct supersonic solutions and also show that no matter how small the opening angle is, a smooth transonic solution always exists as long as the speed of the incoming flow is suitably chosen for this given angle.
The supersonic flow over cones is a fundamental problem in fluid dynamics [1,8,14]. We consider a conical body facing a supersonic stream of air at a uniform velocity and the angle of attack is zero. Assume that the obstacle is an infinite cone with its vertex located at the origin. A shock wave is formed either as a bow shock, also called a detached shock away from the cone, or a conical shock attached to the vertex. We are interested in which case the opening angle of the conical obstacle is not too large and thus a conical shock wave with the same vertex is situated on the obstacle in three dimensional space.
The essential property of the conical flow is that all flow properties are constant along rays from a given vertex. We take the
| ∂∂x(ρu)+∂∂y(ρv)=−1y(ρv),∂∂x(ρu2+P)+∂∂y(ρuv)=−1y(ρuv),∂∂x(ρuv)+∂∂y(ρv2+P)=−1y(ρv2). | (1.1) |
And the pressure
| dvdσ+σdudσ=0,(1−u2c2)dudσ−2uvc2dvdσ−(1−v2c2)σdvdσ+v=0. | (1.2) |
The sound speed
Also, Maccoll and Taylor [13] discuss the problem in the spherical coordinate system. The numerical solution is constructed by a direct approach. Different from Busemann's method, the initial values are given at the surface of the obstacle cone. The complete solution is then worked out by numerical integration for three cones of semi-vertical angles
In this paper, we study steady Euler system in the spherical coordinates. Due to the self-similarity for conical flows, we obtain the following Taylor-Maccoll equation for
| {γ−12(V2m−V2r−V2θ)(2Vr+Vθcotθ+dVθdθ)−Vθ(VrdVrdθ+VθdVθdθ)=0.dVrdθ=Vθ. | (1.3) |
Here, the radial and normal components of the flow velocity
By applying the fundamental theory of ODE system, we show that no matter how small the opening angle
| Condition A:arctan(√1−μ2μ)≥arctan(μ)+θb. |
At present, our main concern is the existence of smooth transonic flows. The transition line between the subsonic and supersonic regions can be clearly indicated. Analogous to the problem [11], we might ask: Does there exist a transonic flow past the obstacle which coincides at infinity with the given undisturbed flow? This is a mixed type problem and should be investigated in the context of the partial differential equations. Steady transonic flow in multidimensional space has always been an important and challenging topic. We refer to the work of Chen and Fang [6] in which they also study the conical flow. They consider the transonic shock front behind which the flow is completely subsonic. They show that the self-similar transonic shock solution is conditionally stable with respect to the conical perturbation of the cone boundary. In two dimensional space, the problem of a flow past a straight wedge for a high subsonic free stream Mach number has been investigated by several authors. Cole [7] determined the singularity required to represent the flow near the point at infinity and showed how the condition at the stagnation point must be interpreted if one uses the transonic approximation which, in principle, does not permit stagnation point. His solution can be described as resulting from the assumption of a vertical sonic line. We also refer to [2] and [10] for more knowledge of transonic flows.
The paper is organized as follows. In Section 2, we describe the self-similar flow in the spherical coordinate system. The basic properties and equations are summarized in Section 2.1. Due to the self-similarity and the conservation laws, the Taylor-Maccoll equation is derived as a 2nd order ordinary differential equation. In Section 2.2, we introduce the non-dimensional physical quantities and rewrite the equation as a 1st order system for the self-similar solutions. In Section 3, we analyze the nonlinear ODE system. By the fundamental theory and some technical estimates, we construct the supersonic solutions. Further analysis using Gronwall's inequality reveals the phenomenon of the transition from the supersonic to subsonic region. Finally, the numerical simulations are presented in Section 4. In the Appendix, we derive the Rankine-Hugoniot condition and the equation of the shock polar in the spherical coordinates.
The essential property of the conical flow is that all flow properties are constant along rays from a given vertex. When the opening angle is not too large, an oblique shock wave
| x1=rsinθcosϕ,x2=rsinθsinϕ,x3=rcosθ, |
where
| Conservation of Mass:∂ρ∂r=−1Vr[ρ∂Vr∂r+2ρVrr+1rsinθ∂(ρVθsinθ)∂θ+1rsinθ∂(ρVϕ)∂ϕ] | (2.1) |
| Momentum in r direction:∂Vr∂r=−1Vr[Vθr∂Vr∂θ+Vϕrsinθ∂Vr∂ϕ−V2θ+V2ϕr+1ρ∂P∂r] | (2.2) |
| Momentum in θ direction:∂Vθ∂r=−1Vr[Vθr∂Vθ∂θ+Vϕrsinθ∂Vθ∂ϕ+VrVθr−V2ϕcotθr+1rρ∂P∂θ] | (2.3) |
| Momentum in ϕ direction:∂Vϕ∂r=−1Vr[Vθr∂Vϕ∂θ+Vϕrsinθ∂Vϕ∂ϕ+VrVϕr+VθVϕcotθr+1rρsinθ∂P∂ϕ] | (2.4) |
Here we consider the polytropic gases:
The PDE system (2.1)-(2.4) is complicated and thus we focus on the typical model with the self-similarity property [3,5]. We know that for the conical flow,
| 2ρVr+ρVθcotθ+ρ∂Vθ∂θ+Vθ∂ρ∂θ=0. | (2.5) |
Since the conical flow is irrotational:
| Vθ=∂Vr∂θ. | (2.6) |
From the conservation laws, Bernoulli's law for steady flow holds across a shock front:
| c2γ−1+V22=V2m2, | (2.7) |
where
The Bernoulli principle [1,Ch8.2] for irrotational flows can be expressed as follows.
| dP=−12ρd(V2). |
Hence,
| dP=−ρ(VrdVr+VθdVθ). | (2.8) |
Since
| dPdρ=c2, |
by (2.7) and (2.8), we obtain
| dρρ=−2γ−1(VrdVr+VθdVθV2m−V2r−V2θ). | (2.9) |
By (2.5), (2.6) and (2.9), we obtain the Taylor-Maccoll equation:
| γ−12[V2m−V2r−(dVrdθ)2][2Vr+dVrdθcotθ+d2Vrdθ2]−dVrdθ[VrdVrdθ+dVrdθd2Vrdθ2]=0. | (2.10) |
We note that
Because of (2.9), (2.5) can be written as a system of first order ODEs. Together with (2.6), we obtain the following system:
| {γ−12(V2m−V2r−V2θ)(2Vr+Vθcotθ+dVθdθ)−Vθ(VrdVrdθ+VθdVθdθ)=0.dVrdθ=Vθ. | (2.11) |
We introduce the non-dimensional physical quantities as follows.
| U≡VVm,Ur≡VrVm,Uθ≡VθVm. |
After direct calculations, we obtain
| {−UθUrdUrdθ+AdUθdθ=B,dUrdθ=Uθ, | (2.12) |
where
| {A=−U2θ+(γ−12)(1−U2r−U2θ)B=(1−γ2)(1−U2r−U2θ)(2Ur+Uθcotθ). |
Hence, we have the ODE system:
| {dUθdθ=U2θUr+BA,dUrdθ=Uθ. | (2.13) |
By direct calculations, we obtain the following lemma.
Lemma 2.1. Let
1.
| (γ+1γ−1)U2θ+U2r≤1. |
2. Let
| ddθ(U2)=1A[(1−γ)(1−U2)Uθ(Ur+cotθ⋅Uθ)]. |
Proof. (1) can be proved by direct calculations.
(2): Substituting (2.13) gives
| ddθ(U2)=dUθdθ⋅2Uθ+dUrdθ⋅2Ur=1A[2Uθ(1−γ2)(1−U2)(2Ur+cotθ⋅Uθ)+2UrUθ(γ−12)(1−U2)]=1A[(1−γ)(1−U2)Uθ(Ur+cotθ⋅Uθ)]. |
Remark 1. By (2.12), we have that
| A⋅dUθdθ=U2θUr+B,=Ur(−A)+(1−γ2)(1−U2r−U2θ)(Ur+Uθcotθ). |
If
Remark 2. Since
| 12V2+c2γ−1=12V2m, |
it follows that
| U22+U2(γ−1)(V/c)2=12. |
Here,
| |U|=[1+2(γ−1)M2]−1/2. | (2.14) |
In this section, we present the existence and stability of solutions of the system (2.13). Let the solution be denoted by
| U=(Uθ,Ur). |
We rewrite the system as follows:
| {dUθdθ=F(Uθ,Ur,θ)=U2θUr+BA,dUrdθ=G(Uθ,Ur,θ)=Uθ, | (3.1) |
where
| U(θb)=(0,ub). | (3.2) |
Here
The procedure of the construction is as follows.
Step 1. (Initial Condition)
The initial condition is chosen as
| U(θb)=(0,√γ−1γ+1). |
That is,
Step 2. (Boundary Condition)
The non-dimensional speed
Step 3. (The Shock Condition)
The angle the shock makes with the upstream flow is denoted by
| tanβ=√U20−U2rUr |
Here the 1-state
| θS=β |
for the given
We first focus on the region
| Ω={(Uθ,Ur):Ur∈(0,√γ−1γ+1],Uθ∈[−√γ−1γ+3,0]} |
According to (A.8) in the Appendix, the non-dimensional speed
| 1>U0>√γ−1γ+1. | (3.3) |
The intersection point of the shock polar with the
Lemma 3.1. Let
Proof. By direct calculations, we obtain
| A=12(γ−1)[1−U2r−γ+1γ−1U2θ]≥(γ−1)(5−γ2)2(γ+1)(γ+3)=a0(γ) |
for
Lemma 3.2. For any given opening angle of the obstacle cone
| |∂F∂Uθ|+|∂F∂Ur|+|∂G∂Uθ|+|∂G∂Ur|≤C1d+C2 |
for
Proof. We know that
| B=12(1−γ)(1−U2r−U2θ)(2Ur+Uθcotθ), |
we have
| |B|+|∂B∂Ur|+|∂B∂Uθ|≤c1d+c2. |
Here
Furthermore,
| ∂F∂Uθ=1A2[A(2UrUθ+∂B∂Uθ)−∂A∂Uθ(U2θUr+B)]∂F∂Ur=1A2[A(U2θ+∂B∂Ur)−∂A∂Ur(U2θUr+B)] |
It is easy to check by calculations and Lemma 3.1 that
| a0(γ)<A+|∂A∂Ur|+|∂A∂Uθ|≤ˆc, |
where
By Lemma 3.2, the functions
| U1(θ)=(Uθ(θ),Ur(θ)) |
and the corresponding
| A(θ)=−U2θ(θ)+(γ−12)(1−U2r(θ)−U2θ(θ)). |
We note that there exists
Lemma 3.3. Let
Proof. Due to the system (3.1) and direct calculations, we have
| g′(θ)=U′r+(−csc2θ)Uθ+cotθ⋅U′θ=−cot2θ⋅Uθ−cotθ⋅Ur−(cotθ⋅C(θ)g(θ))=−cotθ(1+C(θ))g(θ), |
where
| C(θ)=(γ−12)⋅(1−U2r−U2θ)A |
We note that
| g(θ)=(e∫θθb−cotτ(1+C(τ))dτ)g(θb). |
Since
Theorem 3.4. Let the non-dimensional speed
Proof. We first solve system (3.1) with (3.2) given by
| ddθ(U2)=1A[(1−γ)(1−U2)Uθ(Ur+cotθ⋅Uθ)]>0. |
| |U|=[1+2(γ−1)M2]−1/2. |
According to the ODE system,
| −Uθ=μ2(1−U2r)√U20−U2r |
and
In Section 3.1, we just show that the supersonic solution exists in the
| Condition A:arctan(√1−μ2μ)≥arctan(μ)+θb. | (3.4) |
Let
| ϕ(θ)=arctan(−Uθ(θ)Ur(θ)),θ∈[θb,ˉθ). |
Lemma 3.5.
Proof. Substituting
| ϕ(θb)=arctan(−Uθ(θb)Ur(θb))=arctan(0μ)=0. |
By direct calculations, we have
| ϕ′(θ)=(11+(UθUr)2)⋅(−U′θUr−(−Uθ)U′rU2r)=U2r+U2θ+UrC(θ)g(θ)U2r+U2θ, |
where
| C(θ)=(γ−12)⋅(1−U2r−U2θ)A>0 |
and by Lemma 3.3
| g(θ)=Ur(θ)+cotθ⋅Uθ(θ)>0. |
Since
To investigate the relation between
| tanβ(θ)=√U20−U2r(θ)Ur(θ), |
where
| U2θ(θ)=μ4(1−U2r(θ))2U20−U2r(θ). | (3.5) |
We then compare these functions
Lemma 3.6.
Proof. By (3.5), we have
| tanβ(θ)=√U20−U2rUr=1Ur|Uθ|γ−1γ+1(1−U2r). |
Since
| U2θ<(γ−1γ+1)(1−U2r). |
Hence,
| tanβ(θ)=1Ur|Uθ|γ−1γ+1(1−U2r)>U2θUr|Uθ|=|Uθ|Ur=tanϕ(θ). |
We thus obtain that
Remark 3. We also obtain that
Lemma 3.7.
Proof. It is clear that
| g(ˆθ)=Ur(ˆθ)+cot(ˆθ)Uθ(ˆθ)=0, |
which is a contradiction to Lemma 3.3.
When
| U2θ=μ4(1−U2r). | (3.6) |
Since
| U2θ(θ1)μ4+U2r(θ1)=1. |
Lemma 3.8. For the solution
| 1μ>tanβ(θ1)>√1−μ2μ |
Proof. We focus on the
| μ>Ur(θ1)>μ√1+μ2. |
Consider the function
| f(x)=√1−x2x,x∈(0,1). |
It is easy to check that
| f(μ)<f(Ur(θ1))<f(μ√1+μ2). |
That is,
| √1−μ2μ<tanβ(θ1)<1μ. |
Lemma 3.9.
Proof. We focus on the
| ϕ(θ1)<arctan(μ2√1+μ2μ√1+μ2)=arctan(μ). | (3.7) |
By mean value theorem, there exists
| ϕ(θ1)−ϕ(θb)=ϕ′(θc)(θ1−θb). |
By Lemma 3.4 and (3.7),
| arctan(μ)>ϕ(θ1)≥θ1−θb. |
Since we have that
| β(θ1)>arctan(√1−μ2μ)>θ1. |
Theorem 3.10. For the solution
Proof.
Remark 4. We note that
We now construct the transonic solution
| U∗(θb)=(0,√γ−1γ+1−ϵ∗). |
Thus,
The solution
| |U1(θ∗)−U∗(θ∗)|≤e(K|θ∗−θb|)|U1(θb)−U∗(θb)|. |
Since
Theorem 3.11. Let
Most importantly,
1. The solution
2. We can choose
In summary, we construct smooth transonic solutions when the opening angle of the conical obstacle is small and a conical shock wave is situated on the obstacle with the same vertex. Under the assumption of self-similarity for irrotational fluid, the Euler system (1.1) of steady flows is transformed into the nonlinear ODE system (3.1). We analyze the ODE system in Section 3 and present the numerical solutions in this section.
We choose
We briefly review the quantitative analysis of shock polars for polytropic gases. We refer the readers to Courant and Friedrichs [8,Ch4.C: Section 121] and the references therein for more details.
Consider a shock S in the
| N0=V0sinβ | (A.1) |
| L1=L0=V0cosβ(continuity of tangential component) | (A.2) |
Furthermore, Bernoulli's law for steady flows holds across a shock front:
| 12V20+c20γ−1=12V21+c21γ−1=12V2m. | (A.3) |
Also, we have the Prandtl relation for the polytropic gases.
| N0N1=c2p−μ2L20, | (A.4) |
where
By (A.1) and (A.2), the angle
| sinβ=1V0√V20−L21. |
It thus follows from (A.3) and (A.4) that
| N1=c2p−μ2L21V0sinβ=c2p−μ2L21√V20−L21. |
In the spherical coordinates, the radial and normal components of the flow velocity
| |Vθ|=c2p−μ2V2r√V20−V2r. |
By using the non-dimensional velocity,
| U2θ=μ4(1−U2r)2U20−U2r. | (A.5) |
Hence, for a given speed
| −Uθ=μ2(1−U2r)√U20−U2r. | (A.6) |
And for the 1-state
| tanβ=√U20−U2rUr. | (A.7) |
For the present problem, the incoming flow is supersonic with the given density
| N20=μ2(V2m−L20),V20=N20+L20. |
Hence at the
| U2θ=[1−U20]μ2/(1−μ2),U2r=[U20−μ2]/(1−μ2). |
And
Since
| 12V20+c20γ−1=12V2m, |
it follows that
| U202+U20(γ−1)(V0/c0)2=12. |
The relationship between the Mach number
| |U|=[1+2(γ−1)M2]−1/2. | (A.8) |
When
Remark 5. For the present problem,
Remark 6. At the shock angle
| U20>(γ−1γ+1)+U2r(2γ+1). | (A.9) |
The authors would like to thank Prof. M-H. Chen for his helpful discussions. Lien is supported in part by MOST Grant 107-2115-M-006-012. Liu is supported in part by MOST Grant 107-2115-M-006-017.
Spherical coordinate system
The shock cone
The
The fixed point
The numerical solution for
The numerical result for
List of the symbols
The simulations of shock polars