Input-output $L^2$-well-posedness, regularity and Lyapunov stability of string equations on networks

1.   Introduction and main results

Generally, the motion of elastic strings on network can be formulated by means of a graph ([12,15,24,25]). In this paper, we always suppose that $G = (V(G),E(G))$ is a connected planar metric graph with the vertex set $V(G) = \{p_1, p_2, \ldots , p_m\}$ and the edge set $E(G) = \{e_1, e_2, \ldots, e_n\}$. Thus, every edge $e_j$ with the length $\ell_j$ of $G$ can be parameterized by a continuous function $\pi_j$ with respective to its arc length. If every edge of $G$ is assigned to a direction that coincides with the arc length increasing, $G$ becomes a digraph. Denote by $\mathcal{I}_E(G) = \{1,2,\ldots,n\}$, $\mathcal{I}_V(G) = \{1,2,\ldots,m\}$ and $\mathcal{I}_{E}(p_j) = \mathcal{I}_{E}^{\,+}(p_j)\cup\mathcal{I}_{E}^{\,-}(p_j)$, where $\mathcal{I}_E^{\,+}(p_j)$ and $\mathcal{I}_{E}^{\,-}(p_j)$

and

Then, the number of elements in sets $\mathcal{I}_E(p_j)$, $\mathcal{I}^{+}_E(p_j)$ and $\mathcal{I}^{-}_E(p_j)$ are the degree ($\deg(p_j)$), out-degree ($\deg^{+}(p_j)$) and in-degree ($\deg^{-}(p_j)$) of the vertex $p_j$, respectively. The boundary and the interior of $G$ are defined respectively by

Denote the set $\left(\bigcup_{k = 1}^n e_k\right) \bigcup V(G)$ by $G$ for convenience, we thus can use a function $\mathbb{w}(z, t)$, from $G\times[0,+\infty)$ to $\mathbb{R}$, to describe the dynamic behavior of a one-dimensional (1-d) wave equations on network $G$, where $z$ stands for any point of the set $G$ and $t$ is the time. Especially, $\mathbb{w}(p,t)$ is the value of $\mathbb{w}(z,t)$ at the vertex $p \in V(G)$, which describes the dynamic behavior of the vertex $p$ with the time $t$. Let the restriction of $\mathbb{w}(z,t)$ to the $j$-th edge be parametrized by $w_j(x,t)$, that is, $w_j(x,t) = \mathbb{w}(z,t)|_{z\in e_j} = \mathbb{w}(\pi_j(x),t)$. Without loss of generality, we assume that every edge has the unit length. We fix a partition of the vertex set $V(G) = \mathfrak{D}\cup\partial G_N\cup(Int(G)\setminus\mathfrak{D})$, where $\partial G_N = \partial G\setminus\mathfrak{D}$. Thus, the string equations on a continuous type network $G$ can be formulated by (see also [8,13,15,16,22,24])

where $\rho_j(x)$ and $T_j(x)$ ($j = 1,\ldots,n$) are positive and bounded continuous functions, which are the mass density and the tension of the $j$-th string, respectively, $u(p,t)$ is the input signal at the vertex $p$. The input $u(p,t)$ may be zero, then $\mathfrak{F} = \{p \in V(G)|u(p,t)\equiv 0\}$ is called the free vertex set. That is, there no is input signal at the free vertex $p$. $p \in \mathfrak{D}$ is called a fixed vertex of $G$, since $\mathbb{w}(p,t) = 0$. Thus, the network $G$ is fixed on $\mathfrak{D}$, called the Dirichlet set. In this paper, we assume that $\mathfrak{D}$ is not empty and $V(G)\setminus\mathfrak{D} = \{p_{\jmath_1},p_{\jmath_2},\ldots,p_{\jmath_{m_0}}\}$, where $m_0$ is the number of vertices in the set $V(G)\setminus\mathfrak{D}$. The output of system (1) is

where $\mathbb{w}_t(p_{\jmath_k},t)$ is the derivative of $\mathbb{w}(p_{\jmath_k},t)$ with respective to time $t$.

One of the objective of this paper is to investigate the input-output well-posedness and regularity of 1-d wave equations on networks (1). Let the state space $\mathbb{X}$, the control space $\mathbb{U}$ and the observation space $\mathbb{Y}$ be Hilbert spaces, and $L_{loc}^2([0,+\infty), \mathbb{U})$ be the space of those functions on $[0,+\infty)$ whose restriction to $[0,\tau]$ is in $L^2([0,\tau], \mathbb{U})$, for every $\tau>0$. An infinite-dimensional linear system is input-output $L^2$-well-posed, if, for every $t \ge 0$, there exists $M_t > 0$, only depending on $t$, such that

where $X(t)$ is the state of system, $X_0$ is its initial state, $U(\cdot) \in L_{loc}^2([0,+\infty), \mathbb{U})$ is the input of system and $Y(\cdot)\in L_{loc}^2([0,+\infty), \mathbb{Y})$ is the output of system. Denote by ${\textbf{H}}(s)$ the input-output transfer function of the well-posed system. Thus, a well-posed system is called regular if $\lim\limits_{s\to +\infty} {\textbf{H}}(s)u = \mathcal{D}u, \forall u\in \mathbb{U}$, where $\mathcal{D}$ is a bounded operator from $\mathbb{U}$ to $\mathbb{Y}$. Refer to [7,20,21,23,26] and references therein for more details on the theory of input-output well-posedness and regularity. Since 1980s, it has been demonstrated that this class of systems is quite general, including many control systems described by partial differential equations with inputs and outputs on internal sub-domains, or on the (partial) boundary of the spatial region (see [4,5,6,10,11,14,18,30] and references therein). But the well-posedness and regularity of 1-d networks has received little attention in the literature. In [1], the well-posedness of a tree-shaped network of strings with feedback acting on the root of the tree was shown, based on the d'Alembert formula. One of main contributions of this paper is to prove the $L^2$-well-posedness and regularity of the general network system of strings (1) with outputs (2), by constructing suitable multipliers with graph theory and the asymptotical theory of fundamental solution. Here we state this result as Theorem 1.1 and its proof is deferred to Section 3.

Theorem 1.1. Assume that $\mathfrak{D}$ is not empty, $0<\rho_L\le\rho_k(x)\le \rho_U$, $0<T_L\le T_k(x)\le T_U$, and $\rho_k(\cdot),T_k(\cdot)\in C^1[0,1]$, $\forall k\in \mathcal{I}_E(G)$, and that the input $u(p,\cdot)\in L_{loc}^2([0,+\infty), \mathbb{R})$for every vertex $p\in V(G)\setminus (\mathfrak{D}\cup\mathfrak{F})$, andthe outputs are defined by (2). Then the system (1) is input-output $L^2$-well-posed and regular.

It is well-known that only tree-shaped networks with one fixed vertex can be exponential decay under appropriate velocity feedbacks; and when there exist more than two fixed vertices or closed cycles in networks of strings, under velocity feedbacks, the networks is at most polynomial decay or is not stable [13]. Based on the observability estimate, the polynomial decay of a planar tree-shaped network of strings under only one vertex being damped (one-node stabilization) were discussed in [1,2,8,24]. Riesz basis approach is used in [15,28,29] to prove that the spectrum-determined-growth (SDG) condition holds for the networks, so the stability of closed-loop systems can be determined by their spectral bound. The decay rate of the chain-shaped and star-shaped networks was estimated by choosing a suitable weighted energy functional in [27]. By means of the frequency domain method, the exponential stability of a tree-shaped network was confirmed in [16]. However, Lyapunov stability is more common and intuitive in engineering. So, in this paper, we use the Lyapunov method to study the stability on networks, e.g., the tree-shaped networks shown as Figure 1b and Figure 2. Thus, the second contribution of this paper is to provide a construction method of Lyapunov functional for general tree-shaped networks of strings with one fixed vertex.

For a connected tree $G = (V(G),E(G))$, a vertex is selected as its root, then, $G$ is said to be a rooted tree. A boundary vertex of the rooted tree is called a leaf vertex, or a leaf for short, if it is not the root. That is, $\partial G_N$ is consisted of all leaves of the rooted tree $G$. An edge incident with a leaf is called a leaf edge. For convenience, we give a hypothesis as follows (see [15,16]).

Hypotheses 1.2.

(1) The rooted tree-shaped networks $G$ with the fixed root $p_r$ hasno input signal at the internal vertex $p_k$ ($k\ne r$), i.e., $\mathfrak{D} = \{p_r\}$ and$u(p_k,t) = 0$, for $p_k\in Int(G)\setminus\mathfrak{D}$.

(2) $\deg(p_r) = \deg^{+}(p_r) = 1$, $\mathcal{I}_E^{+}(p_r) = \{r\}$.

(3) $\deg^{-}(p_k) = 1$ for all $k\in \mathcal{I}_V(G)$ with $k\ne r$.

Under Hypothesis 1.2, the motion of the tree-shaped network $G$ is described by

Thus, we have the following result.

Theorem 1.3. Assume that Hypothesis 1.2 holds and that$0<\rho_L\le\rho_k(x)\le \rho_U$, $0<T_L\le T_k(x)\le T_U$ on $[0,1]$ and $\rho_k(\cdot),T_k(\cdot)\in C^1[0,1]$, for every $k\in \mathcal{I}_E(G)$, then the tree-shaped network (3) is exponentially stable under the output feedback

where $\beta_k>0$.

Theorem 1.3 will be proven by constructing a suitable Lyapunov functional in Section 4.

Remark 1. Under Hypothesis 1.2 (3), a tree $G$ with the root $p_r$ is also called a branching with the root $p_r$ [3]. In fact, the root may be an internal vertex (i.e., (2) in Hypothesis 1.2 dose not hold). Hypothesis 1.2 only is for the sake of the proof of Theorem 1.3 and the construction of Lyapunov functional. If Hypothesis 1.2 (3) is not true, we can take a change of variable $x: = 1-x$, such that it is satisfied. Thus, we can also construct a Lyapunov functional such that the result of Theorem 1.3 also holds for all trees with one fixed root and all leaves controlled by velocity feedbacks, like (4). See the example in Subsection 4.2.2 below.

All in all, main contributions of this paper are:

(1): to prove the input-output $L^2$-well-posedness and regularity of the general network system of strings, by constructing suitable multipliers and the asymptotical theory of fundamental solution, respectively;

(2): to provide a construction method of Lyapunov functional for general tree-shaped networks of strings with one fixed root.

The choice of multipliers for the $L^2$-well-posedness and the Lyapunov functional, based on graph notions and theories, is the novelty of this paper, which is also the main difficulty of this paper. The paper is organized as follows. The matrix-vector form of network (1) is provided in light of graph theory in Section 2. Theorem 1.1 and Theorem 1.3 are proven in Section 3 and Section 4, respectively. Finally, the conclusions follow in Section 5.

2.   The matrix-vector form of system (1) in $\mathbb{R}^n$

To study the 1-d wave propagation on general networks, we need some fundamental notations, concepts of the graph theory and a proposition. See [3] and [9] for more details about the graph theory.

Definition 2.1. The matrices $\Upsilon^{+} = (\upsilon_{i,j}^{+})_{m\times n}$ and $\Upsilon^{-} = (\upsilon_{i,j}^{-})_{m\times n}$, given by

are called the outgoing incidence matrix and the incoming incidence matrix, respectively. The incidence matrix is defined by $\Upsilon = \Upsilon^{+}-\Upsilon^{-}$.

From the above definition, it follows that

where $\jmath_k^{+},\jmath_k^{-}\in\mathcal{I}_V(G)$, $k\in\mathcal{I}_E(G)$, $\epsilon_{\jmath_k^{+}}$ and $\epsilon_{\jmath_k^{-}}$ are the $\jmath_k^{+}$-th and the $\jmath_k^{-}$-th column vector of $I_m$, the identity matrix of order $m$, respectively. $\epsilon_{\jmath_k^{+}}$ shows that the $\jmath_k^{+}$-th vertex $p_{\jmath_k^{+}}$ is the starting point (tail) of the edge $e_k$, and $\epsilon_{\jmath_k^{-}}$ shows that the $\jmath_k^{-}$-th vertex $p_{\jmath_k^{-}}$ is the final point (head) of the edge $e_k$. We denote an $m_0\times m$ matrix by

where the vector $\epsilon_{\jmath_k}$ is the $\jmath_k$-th column of the identity matrix $I_m$. Then $P_{ \mathbb{D}}$ is an orthogonal projection from $\mathbb{R}^m$ to $\mathbb{R}^{m_0}$. Thus, $P_{ \mathbb{D}}W$ retains the $\jmath_1$-th row, the $\jmath_2$-th row, $\ldots$, the $\jmath_{m_0}$-th row of an $m$-row matrix $W$, and removes the other rows of $W$. Moreover,

where $I_{m_0}$ is the identity matrix of order $m_0$, $I_{\mathfrak{D}}$ is a diagonal matrix whose entries from the $\jmath_1$-th to the $\jmath_{m_0}$-th are one, others are zero.

Let

and call them the vectorization of $\mathbb{w}(z, t)$, where $\boldsymbol{p} = (p_1, p_2, \ldots, p_m)^{\top}$. Thus, the system (1) can be rewritten as

where $M(x) = {{{\rm{diag}}}}\left(\rho_1(x),\ldots,\rho_{n}(x)\right)$, $T(x) = {{{\rm{diag}}}}\left(T_1(x),\ldots,T_{n}(x)\right)$,

The output of system (2) can be read as

where $y_k(t)$ or $\mathbb{w}_t(p_{\jmath_k},t)$ is $0$ when $p_{\jmath_k}\in \mathfrak{F}$, which means that the system (1) has no output signal at free vertex $p_{\jmath_k}$.

Remark 2. Similar to the matrix $P_{ \mathbb{D}}$, we introduce matrices

and

where the vector $\epsilon_{\jmath_{k_i}}$ and $\epsilon_{\jmath_{\hat{k}_i}}$ are the $\jmath_{k_i}$-th and $\jmath_{\hat{k}_i}$-th column of the identity matrix $I_m$, respectively. Thus, the last boundary condition in (8) can be rewritten as

where $P_{u}P_{ \mathbb{D}}^{\top} \boldsymbol{u}(t)$ is the true (nonzero) input signal. According to (2), (7) and (9), the true (nonzero) output signal can be written as

The energy function of system (1) is defined as follows:

where $\langle \cdot,\,\cdot \rangle$ represents the Euclidean inner product in $\mathbb{R}^n$. Thus it can be derived from integration by parts and (8) that

which means that the output of system (1), i.e., $Y(t) = P_{\mathbb{D}} \boldsymbol{w}_t( \boldsymbol{p},t)$, is collocated.

In the end of this section, we introduce the following definition of edge adjacency matrix and its proposition which discloses relationship between this definition and Definition 2.1.

Definition 2.2. An edge in $G$ is said to be a loop, if its tail and head are the same. Let $G = (V(G),E(G))$ be a loopless digraph. The $n\times n$ matrix $B^{+}_G = (b^{+}_{i,j})_{n\times n}$, defined by

is called the outgoing edge adjacency matrix of $G$. The $n\times n$ matrix $B^{-}_G = (b^{-}_{i,j})_{n\times n}$, defined by

is called the incoming edge adjacency matrix of $G$. The $n\times n$ matrix $B^{t,h}_G = (b^{t,h}_{i,j})_{n\times n}$, defined by

is called the outgoing-incoming edge adjacency matrix $G$. The $n\times n$ matrix $B^{h,t}_G = (b^{h,t}_{i,j})_{n\times n}$, where

is called the incoming-outgoing edge adjacency matrix of $G$. Thus, the matrix $B_G = B_G^{+}+B_G^{-}+B^{t,h}_G+B^{h,t}_G$, is called the edge adjacency matrix of $G$.

Note that, in Definition 2.2, the diagonal entries of these matrices, $B_G$, $B_G^{+}$, $B_G^{-}$, $B^{t,h}_G$ and $B^{h,t}_G$, are all zeros, $B_G^{+}$ and $B_G^{-}$ are symmetrical and $B^{t,h}_G = (B^{h,t}_G)^{\top}$. In addition, the following proposition can be derived from Definition 2.1 and 2.2.

Proposition 1. Assume that $G$ is a loopless digraph, $\Upsilon^{+}$ and $\Upsilon^{-}$are its outgoing incidence matrix and incoming incidence matrix, respectively. Let

and $\Lambda^{\oplus} = {{{\rm{diag}}}}\left(\lambda_{\jmath^{+}_1}, \lambda_{\jmath^{+}_2},\ldots, \lambda_{\jmath^{+}_n} \right)$, where $\jmath^{+}_k$ and $\jmath^{-}_k$defined by (5). Then

(1): $(\Upsilon^{-})\Lambda(\Upsilon^{-})^{\top} = {{{\rm{diag}}}}\left(\sum\limits_{k\in \mathcal {I}_E^{-}(p_{1})}\lambda_k,\ldots, \sum\limits_{k\in \mathcal {I}_E^{-}(p_{i})}\lambda_k,\ldots, \sum\limits_{k\in \mathcal {I}_E^{-}(p_{m})}\lambda_k\right);$

(2): $(\Upsilon^{+})\Lambda(\Upsilon^{+})^{\top} = {{{\rm{diag}}}}\left(\sum\limits_{k\in \mathcal {I}_E^{+}(p_{1})}\lambda_k, \ldots, \sum\limits_{k\in \mathcal {I}_E^{+}(p_{i})}\lambda_k,\ldots, \sum\limits_{k\in \mathcal {I}_E^{+}(p_{m})}\lambda_k\right);$

(3): $(\Upsilon^{-})^{\top}\Lambda\Upsilon^{+} = [\Lambda^{\ominus}]B^{h,t}_G\; \hbox{ and } \;(\Upsilon^{+})^{\top}\Lambda\Upsilon^{-} = [\Lambda^{\oplus}]B^{t,h}_G = B^{t,h}_G[\Lambda^{\ominus}]$;

(4): $(\Upsilon^{-})^{\top}\Lambda\Upsilon^{-} = [\Lambda^{\ominus}](I+B_G^{-}) \; \hbox{ and } \;(\Upsilon^{+})^{\top}\Lambda\Upsilon^{+} = [\Lambda^{\oplus}](I+B_G^{+});$

where we agree that $\sum\limits_{s\in \emptyset}\lambda_k = 0$. Especially,

Remark 3. Assume that $m = n+1$, and $\widetilde{\Lambda} = {{{\rm{diag}}}}(\widetilde{\lambda}_0,\widetilde{\lambda}_1,\ldots,\widetilde{\lambda}_n)$. Denote by $\lambda_k = \widetilde{\lambda}_{k-1}$, for $k = 1,\ldots, n+1$, then $\widetilde{\Lambda} = {{{\rm{diag}}}}(\lambda_1,\lambda_2,\ldots,\lambda_{n+1})$,

and

3.   Proof of Theorem 1.1 and examples

The proof is divided into two parts: the input-output $L^2$-well-posedness and the regularity. We first prove the input-output $L^2$-well-posedness.

3.1.   Proof of input-output well-posedness

Proof. We choose bounded continuous and differentiable functions on $[0,1]$: $\xi_k(x)$, $k\in \mathcal{I}_E(G)$, such that

and

where $\Xi(x) = {{{\rm{diag}}}}\left(\xi_1(x),\ldots,\xi_{n}(x)\right)$ and $c_E>0$.

The first equation in (8) multiplied by $\Xi(x)w_{x}(x,t)$ on both sides, then integrated on $[0,1]$ with respect to $x$ and on $[0,t]$ with respect to $t$ leads to

Applying integration by parts, (9), the following equality

and boundary conditions in (8): $w(0,t) = (\Upsilon^{+})^{\top} \boldsymbol{w}( \boldsymbol{p},t)$, $w(1,t) = (\Upsilon^{-})^{\top} \boldsymbol{w}( \boldsymbol{p},t)$, to the left-hand side of (14) yields

Similarly, applying integration by parts to the right-hand side of (14) yields

Thus, it can be derived from (14) that

From the boundary condition $P_{ \mathbb{D}}\left[\Upsilon^{-}T(1)w_x(1,t)-\Upsilon^{+}T(0)w_x(0,t)\right] = \boldsymbol{u}(t)$ in (8), it is obtained that

It can be deduced from Definition 2.2 that

and

thus, it follows from (7), the equalities (4) in Proposition 1 and (13a) that

and

i.e., $\Xi(1)T(1)^{-1}-2(P_{ \mathbb{D}}\Upsilon^{-})^{\top}P_{ \mathbb{D}}\Upsilon^{-}$ and $-\Xi(0)T(0)^{-1}-2(P_{ \mathbb{D}}\Upsilon^{+})^{\top}P_{ \mathbb{D}}\Upsilon^{+}$ are symmetric positive definite matrices. Therefore,

Obviously, the equalities (1) and (2) in Proposition 1 and (13a) imply that

with

So, it yields that

where $c_{p} = \min\limits_{k = 1,\ldots, m_0}\{c_{p_{\jmath_k}}\}$. From the inequalities in (13b), it can be derived that

and

Thus, it follows from (15), (16), (17), (18) and (19) that

with $c_{0}^{-1} = \frac{1}{2c_E}\min\left\{1, c_{p}\right\}$. From (12) and (20), it can be deduced that

with $0<\gamma<\min\{1/2,1/c_0\}$. So, for $t\le \tau$,

Applying the Gronwall inequality to (21) leads to

and

From (20) and the above two inequalities, it follows that

Hence

which shows that $\forall \tau\ge 0$, there exists $M_{\tau}>0$ such that

Therefore, the system (1) is input-output $L^2$-well-posedness.

3.2.   Proof of regularity

Proof. Applying Laplace transform to the first equation in (1) leads to

We introduce a new independent variable for (22)

Obviously, $\theta(x)$ is strictly monotone function on $[0,1]$. Denote by $x(\theta)$ the inverse function of $\theta(x)$, $\theta\in[0,1]$, then

So, the following equalities can be easily calculated

and

Let $\widetilde{w}_{j}(\theta,s) = \widehat{w}_{j}(x(\theta),s)$ and

where the prime denotes the derivative with respect to $\theta$, then (22) can be reformulated by

So, Laplace transform of the system (1) can be written as follows:

where $\widetilde{T}(0) = \widetilde{A}^{-1}[M(0)T(0)]^{1/2}$, $\widetilde{T}(1) = \widetilde{A}^{-1}[M(1)T(1)]^{1/2}$,

Let $\widetilde{\eta}(\theta) = (\widetilde{w}(\theta,s),s^{-1} \widetilde{w}'(\theta,s))^{\top}$, then (23) shows that $\widetilde{\eta}(\theta)$ satisfies

According to the asymptotical theory of fundamental solution ([17,19]), the fundamental solution matrix of (24) has the form:

where $Q(\theta,s) = \left( \begin{array}{l} Q_{11}(\theta,s) & Q_{12}(\theta,s) \\ Q_{21}(\theta,s) & Q_{22}(\theta,s) \\ \end{array} \right)$, $\|Q(\theta,s)\|$ is uniformly bounded and

Thus,

where $\widetilde{\eta}(0) = (\widetilde{\eta}_{0,1},\widetilde{\eta}_{0,2})^{\top}$ and

Let $d(s) = P_{\mathbb{D}}\widehat{ \boldsymbol{w}}( \boldsymbol{p},s)$, then $\widehat{ \boldsymbol{w}}( \boldsymbol{p},s) = P_{\mathbb{D}}^{\top}d(s)$, $\widetilde{\eta}(0) = \left( \begin{array}{l} (P_{\mathbb{D}}\Upsilon^{+})^{\top}&0 \\ 0& I\\ \end{array} \right)\left( \begin{array}{l} d(s)\\ \widetilde{\eta}_{0,2}\\ \end{array} \right)$ and

Thus, it follows from (25) and the last boundary condition in (23) that $d(s)$ and $\widetilde{\eta}_{0,2}$ satisfy the linear system of equations:

where

Moreover, it can be deduced that

with

and

Thus, the linear system of equations (26) can be reformulated by

where $\widetilde{\eta}_d(s) = \frac{1}{2}\exp(s\widetilde{A})[\widetilde{\eta}_{0,2} +(P_{\mathbb{D}}\Upsilon^{+})^{\top} d(s)]$. Since

with

$\widetilde{D}_{C}$ is invertible for $\Re(s)>0$ large enough, and

where $o(D)$ stands for a matrix which tends to zero matrix with appropriate rows and columns as $s\to +\infty$. Thus, it follows from

(27) and (29) that

which implies that $\widehat{Y}(s) = sP_{\mathbb{D}}\widehat{ \boldsymbol{w}}( \boldsymbol{p},s) = sd(s) = [\widetilde{D}_{\Lambda}^{-1}+o(D)]\widehat{ \boldsymbol{u}}(s)$. So, it can be deduced from Remark 2, Proposition 1 and (28) that

i.e., the system (1) is regular.

3.3.   Examples

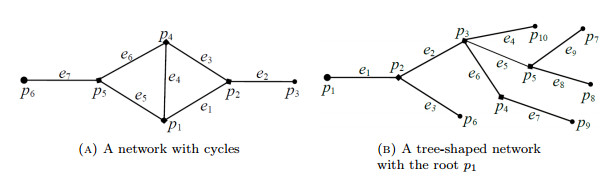
Here, we give two networks: one is a network with cycles, another is a tree-shaped network with the fixed root $p_1$, shown in Figure 1.

3.3.1.   A network with cycles

See Figure 1a, the motion of strings on the network $G$ is governed by

where $\mathfrak{D} = \{p_6\}$. The expressions $P_ \mathbb{D}$ and $P_{u}$ ((6) and (10)) lead to

where the vector $\epsilon_{k}$ is the $k$-th column of the identity matrix $I_{6}$. So, it follows from $\jmath_{k_1} = 1$, $\jmath_{k_2} = 3$, the definitions of $\mathcal{I}_E^{\,+}(p_j)$ and $\mathcal{I}_{E}^{\,-}(p_j)$, and (30) that

i.e., the system (31) is regular.

3.3.2.   A tree-shaped network with one fixed root

See Figure 1b, the motion of strings on the tree-shaped network $G$ is governed by

where $\mathfrak{D} = \{p_1\}$. The expressions $P_ \mathbb{D}$ and $P_{u}$ ((6) and (10)) lead to

where the vector $\epsilon_{k}$ is the $k$-th column of the identity matrix $I_{10}$. Thus, from (28) and (30), it can be derived that

i.e., the system (32) is regular.

4.   Proof of Theorem 1.3 and examples

For the tree-shaped network $G = (V(G),E(G))$, the number of vertices $m$ is equal to the number of edges plus one, i.e., $m = n+1$. Without loss of generality, let $\mathfrak{D} = \{p_1\}$, then, the number of vertices in the set $V(G)\setminus\mathfrak{D}$ is $m_0 = n$. It follows from Hypothesis 1.2 and (5) that $P_{ \mathbb{D}} = (0,I_n)_{n,n+1}$ and the index set $\{\jmath_1^{-}, \jmath_2^{-},\ldots, \jmath_n^{-}\} = \{2,3,\ldots,n+1\}$. Thus, it is derived from the system (8) and Proposition 1 that $(\Upsilon^{-})w(1,t) = D_G^{-} \boldsymbol{w}( \boldsymbol{p},t)$,

where

and $(D_G^{-})^{\ominus} = I_n$. Since $P_{ \mathbb{D}}\Upsilon^{-} \left[(\Upsilon^{-})^{\top}D_G^{-}P_{ \mathbb{D}}^{\top}\right] = I_n = \left[(\Upsilon^{-})^{\top}D_G^{-}P_{ \mathbb{D}}^{\top}\right] P_{ \mathbb{D}}\Upsilon^{-}$, it follows from the last boundary condition in the system (8) and Proposition 1 that

In the feedback control law (4), $\beta_k >0$ for $p_{\jmath_k}\in\partial G_N$. Now, we supplement $\beta_{k} = 0$ for $p_{\jmath_k}\in \mathfrak{F}$, and let $\beta = {{{\rm{diag}}}}(\beta_1,\ldots,\beta_{n})$, then (4) can be formulated by

In addition, it can be obtained from $B_G^{-} = 0$ and Proposition 1 that

Denote by $\beta^{\,-} = (\Upsilon^{-})^{\top}D_G^{-}P_{ \mathbb{D}}^{\top}\beta P_{ \mathbb{D}} D_G^{-}\Upsilon^{-} = (\Upsilon^{-})^{\top} \left( \begin{array}{l} 0 & 0 \\ 0 & \beta \\ \end{array} \right)\Upsilon^{-}$, then it is derived from (33), Proposition 1 and Remark 3 that

where $\jmath_k^{-}-1\in \{1,2,\ldots,n\}$, $k\in\mathcal{I}_E(G)$. Therefore, the closed-loop system (3)-(4) can be reformulated by (see also [15,28])

Remark 4. Since $p_{\jmath_k^{-}}$ is the final point (head) of the edge $e_k$ for $k\in\mathcal{I}_E(G)$, according to Definition 2.2, all entries in $k$-th row of $B_G^{h,t}$ are zeros for boundary vertex $p_{\jmath_k^{-}}\in \partial G_N$, i.e., $\deg(p_{\jmath_k^{-}}) = 1$. Moreover, for internal vertex $p_{\jmath_k^{-}}$, i.e., $\deg(p_{\jmath_k^{-}})>1$, $\beta_k^{-} = 0$. Hence, it can be followed from (34) that $\langle\,B_G^{h,t}z,\,\beta^{-}v\,\rangle_{ \mathbb{R}^n}\equiv 0$, for all $z,v\in \mathbb{R}^n$.

Let $\mathscr{V}_b(t) = \int_0^1 \langle\,b(x) w_x(x,t),\,M(x)w_t(x,t)\,\rangle_{ \mathbb{R}^n}dx$ with the diagonal matrix $b(x) = {{{\rm{diag}}}}\left(b_1(x),\ldots,b_n(x)\right)$ satisfying the following condition.

Condition 4.1.

(1) For every $k\in\mathcal{I}_E(G)$, $b_k(\cdot)\in C^{1}[0,1]$and there exist positive constants $c_{\rho\!L}$, $c_{\rho\!U}$, $c_{T\!L}$ and $c_{T\!U}$ such that$c_{\rho\!L}\le [b_k(x)\rho_k(x)]'\le c_{\rho\!U}$ and$c_{T\!L}\le[b_k(x)T_k^{-1}(x)]'\le c_{T\!U}$, for all $x\in[0,1]$.

(2) For every edge $e_k$, corresponding to the component $b_k(x)$,

where $c_b = \max_{x\in[0,1]}\{\|M(x)\|_2,\|b^2(x)T^{-1}(x)\|_2\}>0$ (see (36) below), the final point (head) of the edge $e_k$ is $p_{\jmath_k^{-}}$ and$\mathcal{I}_E^{-}(p_{\jmath_k^{-}}) = \{k\}$.

(3) For every edge $e_k$, corresponding to the component $b_k(x)$,

where the starting point (tail) of the edge $e_k$ is the vertex $p_{\jmath_k^{+}}$.

According to (1) and (2) in Condition 4.1, obviously, the following inequality

holds, and there exist $c_L>0$ and $c_U>0$ such that

Now, we construct a Lyapunov functional

where $0<c_bc_V <1$, then

In what follows, using this Lyapunov functional, we prove Theorem 1.3.

4.1.   Proof of Theorem 1.3

Proof. Using (35) and the following two equalities

and

we can get that

Moveover, it follows from (11) and (35) that

Thus, it can be obtained from Remark 4, (37), (39) and (40) that

where

and

Next, we prove that the symmetric matrices $C_{\beta}$ and $C_b$ are positive semi-definite. Denote by $\Lambda = {{{\rm{diag}}}}(\lambda_1,\lambda_2,\cdots,\lambda_{n+1})$, where

From Proposition 1, $B_G^{-} = 0$ and (34), it can be obtained that

where

Thus, (2) in Condition 4.1 and (34) lead to

i.e., $C_{\beta}$ is a positive semi-definite matrix. It follows from Proposition 1 that

The $k$-th row of $C_b$ matches the edge $e_k$, whose tail and head are the vertices $p_{\jmath_k^{+}}$ and $p_{\jmath_k^{-}}$, respectively. In light of Definition 2.2, the number of $1$ in the $k$-th row of $I+B_G^{+}$ is $\deg^{+}(p_{\jmath_k^{+}})$. Thus, when $\frac{b_{k}(0)}{T_{k}(0)}>\deg^{+}(p_{\jmath_k^{+}}) \sum_{i\in \mathcal{I}_E^{-}(p_{\jmath_k^{+}})}\frac{b_{i}(1)}{T_{i}(1)}$ for the internal vertex $p_{\jmath_k^{+}}$, the $k$-th row of $C_b$ is strictly (row) diagonally dominant. When $\frac{b_{k}(0)}{T_{k}(0)}>0$ for the root $p_{\jmath_k^{+}} = p_1$, the $k$-th row of $C_b$ has only one non-zero diagonal element $\frac{b_{k}(0)}{T_{k}(0)}$, since $\deg^{+}(p_1) = 1$ and $\deg^{-}(p_1) = 0$, according to Hypothesis 1.2; when $\frac{b_{k}(0)}{T_{k}(0)} = 0$ for the root $p_{\jmath_k^{+}} = p_1$, the entries in $k$-th row of $C_b$ are zeros. Hence, the matrix $C_b$ is positive semi-definite under (3) in Condition 4.1.

Thus, it follows from (38) and (41) that

which, together with (38), implies that the system (35), i.e., the closed-loop system (3)-(4), is exponential stable.

Remark 5. The construction of matrix multiplier $b(x)$ is crucial in the proof, here, we discuss its choice. A path in $G$ is a non-empty subgraph $P = (V_P,E_P)$ of the form $V_P = \{p_{\iota_0},p_{\iota_1}, \ldots, p_{\iota_{k}}\} \;\mbox{ and } \;E_P = \{e_{i_1},e_{i_2},\ldots, e_{i_{k}}\}$, where $p_{\iota_1}, \ldots, p_{\iota_{k}}$ and $e_{i_1},\ldots, e_{i_{k}}$ are all distinct vertices and edges, respectively, the edge $e_{i_j}$ is joined $p_{\iota_{j-1}}$ and $p_{\iota_{j}}$, $j = 1,\ldots, k$. The number of edges, $k$, is called the length of path, a path of length $k$ is called a $k$-path. The vertices $p_{\iota_0}$ and $p_{\iota_{k}}$, linked by $P$, are called its ends, so the path is also denoted by $P(p_{\iota_0},p_{\iota_{k}})$. If $p_{\iota_0}$ and $p_{\iota_{k}}$ are the same vertex, then $P(p_{\iota_0},p_{\iota_{k}})$ is called a cycle. For a connected tree $G = (V(G),E(G))$ with the root $p_r$, for every vertex $p\in V(G)\setminus\{p_r\}$, there is a unique path connecting $p$ and $p_r$, denoted by $P(p_r,p)$. The length of $P(p_r,p)$ is denoted by $m_p$ and let $d_P = \max_{p\in V(G)\setminus\{p_r\}} \{m_p\}$. We define sets: $V_0(G) = \{p_r\}$ and for $k\ge 1$, $V_k(G) = \{p\in V(G)| P(p_r,p) \;{\rm{ is \;a }}\; k-{\rm{path}}\}$ and

then $V(G) = \bigcup_{k = 0}^{d_P}V_k(G) \;\mbox{ and } \;E(G) = \bigcup_{k = 1}^{d_P}E_{k}(G)$, where $V_k(G)$s and $E_{k}(G)$s are mutual disjoint, respectively. Next, $b(x)$ on $[0,1]$ can be chosen via the following three steps.

Step 1: For every $p\in \partial G_N$, denote the path $P(p_r,p)$ by

where $p_{\iota_0} = p_{r}$ is the root and $p_{\iota_{m_p}} = p\in \partial G_N$. Let $b_{i_{m_p}}(0) = m_pT_{i_{m_p}}(0)$ and choose a value of $b_{i_{m_p}}(1)$ such that

Step 2: Beginning with the maximum $m_p$ (the longest path $P(p_r,p)$), for $j = m_p-1, \ldots,2,1$, corresponding to $e_{i_{k}}\in E_j(G)\cap E_P$, we calculate

and $b_{i_{k}}(0) = \frac{1}{2}\min\left\{\frac{\rho_{i_{k}}(1)}{\rho_{i_{k}}(0)}, e^{\frac{-c_{\rho}}{T_L\rho_L}}\frac{T_{i_{k}}(0)}{T_{i_{k}}(1)}\right\}b_{i_{k}}(1)$. Repeat the above procedure, till the least $m_p$ (the shortest path $P(p_r,p)$).

Step 3: For every edge $e_k\in E(G)$, by virtue of $b_k(0)$ and $b_k(1)$ given by above two steps, we choose $b_k(x)$ as follows:

and $c_{b}^{(k)} = \left(e^{\frac{c_{\rho}}{T_L\rho_L}}-1\right)^{-1} \left[\frac{b_k(1)}{T_k(1)} -e^{\frac{c_{\rho}}{T_L\rho_L}}\frac{b_k(0)}{T_k(0)}\right]>0$.

At last, after $b(x)$ is determined by above steps, it is easy to verify that

and

Thus, Condition 4.1 is always fulfilled. Note that the construction of $b(x)$ is not unique, the choice based on Step 1, 2 and 3 is just one way of constructing $b(x)$.

4.2.   Examples

To explain further how to choose the diagonal matrix-valued function $b(x)$ and construct the Lyapunov functional via steps in Remark 5, we provide two tree-shaped networks. The first one is shown in Figure 1b, the underlying tree is a branching with a fixed root $p_1$, i.e., $\mathfrak{D} = \{p_1\}\subset \partial G$ and Hypothesis 1.2 holds. The second one is shown in Figure 2 and $\mathfrak{D} = \{p_4\}\subset Int(G)$. Its underlying rooted tree is not a branching, i.e., (2) and (3) in Hypothesis 1.2 are not satisfied. A concrete Lyapunov functional will be constructed for the second example.

4.2.1.   A nine-string-tree with collocated velocity feedbacks

We reconsider the tree-shaped network governed by (32), shown in Figure 1b. The outgoing incidence matrix and the incoming incidence matrix of the underlying tree-shaped graph of system (32) are

and

respectively.

To choose $b(x)$ satisfying Condition 4.1, we first write down all paths from the root $p_1$ to leaves ($\partial G_N = \{p_6,p_7,p_8,p_9,p_{10}\}$) in the network (see Table 1).

Second, according to Remark 5, we choose the function $b_k(x)$ as follows.

Step 1: For the leaf $p_6$, the corresponding leaf edge is $e_3$, then $b_{3}(0) = 2T_{3}(0)$ and $b_{3}(1)\!>\!2e^{\frac{c_{\rho}}{T_L\rho_L}} \max\left\{\frac{T_{3}(0)\rho_{3}(0)}{\rho_{3}(1)},T_{3}(1)\right\}$. For the leaf $p_7$, the corresponding leaf edge is $e_9$, then $b_{9}(0) = 4T_{9}(0)$ and $b_{9}(1)\!>\!4e^{\frac{c_{\rho}}{T_L\rho_L}} \max\left\{ \frac{T_{9}(0)\rho_{9}(0)}{\rho_{9}(1)},T_{9}(1)\right\}$. For the leaf $p_8$, the corresponding leaf edge is $e_8$, then $b_{8}(0) = 4T_{8}(0)$ and $b_{8}(1)\!>\!4e^{\frac{c_{\rho}}{T_L\rho_L}} \max\left\{ \frac{T_{8}(0)\rho_{8}(0)}{\rho_{8}(1)},T_{8}(1)\right\}$. For the leaf $p_9$, the corresponding leaf edge is $e_7$, then $b_{7}(0) = 4T_{7}(0)$ and $b_{7}(1)\!>\!4e^{\frac{c_{\rho}}{T_L\rho_L}} \max\left\{ \frac{T_{7}(0)\rho_{7}(0)}{\rho_{7}(1)},T_{7}(1)\right\}$. For the leaf $p_{10}$, the corresponding leaf edge is $e_4$, then $b_{4}(0) = 3T_{4}(0)$ and $b_{4}(1)\!>\!3e^{\frac{c_{\rho}}{T_L\rho_L}} \max\left\{ \frac{T_{4}(0)\rho_{4}(0)}{\rho_{4}(1)},T_{4}(1)\right\}$.

Step 2: The maximum $m_p = 4$. For $e_{5} = e_{i_3}\in E_3(G)\cap E_{P(p_1,p_7)} = E_3(G)\cap E_{P(p_1,p_8)}$ and $p_{\iota_3} = p_5$, we choose $b_{5}(0) = \frac{1}{2}\min\left\{\frac{\rho_{5}(1)}{\rho_{5}(0)}, e^{\frac{-c_{\rho}}{T_L\rho_L}}\frac{T_{5}(0)}{T_{5}(1)}\right\}b_{5}(1)$ and

For $e_{6} = e_{i_3}\in E_3(G)\cap E_{P(p_1,p_9)}$ and $p_{\iota_3} = p_4$, we choose

and

For $e_{2} = e_{i_2}\in E_2(G)\cap E_{P(p_1,p_k)}$, $k = 7,8,9,10$, and $p_{i_2} = p_3$, we choose

and $b_{2}(0) = \frac{1}{2}\min\left\{\frac{\rho_{2}(1)}{\rho_{2}(0)}, e^{\frac{-c_{\rho}}{T_L\rho_L}}\frac{T_{2}(0)}{T_{2}(1)}\right\}b_{2}(1)$. For $e_{1}\! = \!e_{i_1}\in E_1(G)\cap E_{P(p_1,p_k)}$, $k\! = \!6,\ldots,10$, and $p_{\iota_1}\! = \!p_2$, we choose $b_{1}(0)\! = \! \frac{1}{2}\min\left\{\!\frac{\rho_{1}(1)}{\rho_{1}(0)}, e^{\frac{-c_{\rho}}{T_L\rho_L}}\frac{T_{1}(0)}{T_{1}(1)}\!\right\}b_{1}(1)$ and

Thus, $b(x)$ is constructed by Step 3 in Remark 5, and all assumptions in Theorem 1.3 are fulfilled. Finally, by use of (4), (34), (42), (43) and $\jmath_k = k+1$ for $k = 1,\ldots,9$, it is shown that the network (32), under velocity feedbacks

is exponentially stable.

4.2.2.   A six-string-tree with collocated velocity feedbacks

The tree-shaped network consisting of six strings with one fixed root is shown in Figure 2. The motion of the network can be formulated by

where $\rho_1(x) = \rho_2(x) = \rho_3(x) = 1$, $\rho_4(x) = 1.25-0.25x^2$, $\rho_5(x) = 2-x$, $\rho_{6}(x) = 1.25-(2\pi)^{-1}\sin(2\pi x)$, $T_1(x) = 1$, $T_2(x) = 1.5$, $T_3(x) = 2$, $T_4(x) = 1.25+(2\pi)^{-1}\sin(2\pi x)$, $T_5(x) = 1+x$ and $T_6(x) = 1+0.25x^2$. The outgoing incidence matrix and the incoming incidence matrix are

respectively. The Dirichlet set $\mathfrak{D} = \{p_4\}\subset Int(G)$, and $\deg^{-}(p_6) = 2$, which means that the rooted tree is not a branching and the system (44) is not the standard form of (3). $V(G)\setminus\mathfrak{D} = \{p_{\jmath_1},p_{\jmath_2},p_{\jmath_3}, p_{\jmath_4},p_{\jmath_5},p_{\jmath_6}\}$, where $p_{\jmath_k} = p_k$ for $k = 1,2,3$, $p_{\jmath_k} = p_{k+1}$ for $k = 4,5,6$, and $m_0 = 6$. $\mathfrak{F} = \{p_{\jmath_3},p_{\jmath_5}\} = \{p_3,p_6\}$. The set of leaves $\partial G_N = \partial G = \{p_1,p_2,p_5,p_7\}$. The system (44) is $L^2$-well-posedness and regular, according to Theorem 1.1.

Similar to (4), the collocated output feedback is read as

where $\beta_k>0$ and $p_{\jmath_k}\in\partial G_N$, $k = 1,2,4,6$. Hence, the closed-loop system (44) with (46) can be rewritten as

Notice that the closed-loop system (47) can not be written in the form of (35). Thus, the matrix-vector form of (47) can only be formulated by (8) with $\Upsilon^{-}$ and $\Upsilon^{+}$ being determined by (45), and

To construct a Lyapunov functional for (47), we do a change of variable $x: = 1-x$, for the edge $e_5$, and let $\widetilde{w}_5(x,t) = w_5(1-x,t)$, $\widetilde{\rho}_5(x) = 1+x$ and $\widetilde{T}_5(x) = 2-x$, and for $j\ne 5$, let $\widetilde{w}_{j}(x,t) = w_j(x,t)$, $\widetilde{\rho}_j(x) = \rho_j(x)$ and $\widetilde{T}_j(x) = T_j(x)$. Thus, (47) is reformulated by

Thus, (1) and (3) in Hypothesis 1.2 are satisfied and the underlying tree of system (49) is a branching with the root $p_4$, which is joined with two edges.

In the following, we determine the multiplier $\widetilde{b}(x)$ for (49) due to Remark 5. A simple calculation shows that $0<1 = \rho_L\le\widetilde{\rho}_k(x)\le \rho_U$, $0<1 = T_L\le \widetilde{T}_k(x)\le T_U$ and

All paths from the root $p_4$ to leaves ($\partial G_N = \{p_1,p_2,p_5,p_7\}$) in the tree-shaped network are filled in Table 2. Thus, using Step 1 in Remark 5, we choose $\widetilde{b}_{1}(0) = 2$ and $\widetilde{b}_{1}(1) = 2e^{\hat{c}_{\rho}}$ for the leaf edge $e_1$; $\widetilde{b}_{2}(0) = 3$ and $\widetilde{b}_{2}(1) = 3e^{\hat{c}_{\rho}}$ for the leaf edge $e_2$; $\widetilde{b}_{6}(0) = 2$ and $\widetilde{b}_{6}(1) = \frac{5}{2}e^{\hat{c}_{\rho}}$ for the leaf edge $e_6$; $\widetilde{b}_{5}(0) = 4$ and $\widetilde{b}_{5}(1) = 2e^{\hat{c}_{\rho}}$ for the leaf edge $e_5$. Using Step 2 in Remark 5, we choose $\widetilde{b}_{3}(1) = \frac{4}{3}$ and $\widetilde{b}_{3}(0) = \frac{2}{3}e^{-c_{\rho}}$ for the edge $e_3$; $\widetilde{b}_{4}(1) = \frac{2}{3}$ and $\widetilde{b}_{4}(0) = \frac{1}{3} e^{-c_{\rho}}$ for the edge $e_4$. According to Step 3 in Remark 5, we have

Hence, we obtain the matrix multiplier $b(x)$ for (47): $b_k(x) = \widetilde{b}_k(x)$ for $k\ne 5$ and $b_5(x) = -\widetilde{b}_5(1-x)$, that is,

Thus, the Lyapunov functional for the system (47) is

From (6), (8), (12), (45) and (48), it can be deduced that

Similar to (39), it follows from integration by parts, (6), (8), (44) and (45) that

where $O(\mathscr{E})$ satisfies (37),

and

Thus, it follows from (51), (52), (53) and (54) that

Let $c_V<\min\left\{\frac{\beta_1 e^{-\hat{c}_{\rho}}}{1+ \beta_1^2}, \frac{\beta_2e^{-\hat{c}_{\rho}} }{1.5+\beta_2^2}, \frac{\beta_4e^{-\hat{c}_{\rho}}}{\frac{25}{16}+\beta_4^2}, \frac{\beta_6e^{-\hat{c}_{\rho}}}{2+\beta_6^2},c_b^{-1}\right\}$, it can be derived that

Hence, the system (47) is exponentially stable.

5.   Conclusions

The multiplier method is applied to discuss the well-posedness and regularity of the open-loop system of strings network and the exponential stability of the closed-loop system in this paper. Especially, a Lyaponuv functional for tree-shaped networks of elastic strings is presented by constructing an appropriate multiplier. This construction method (see Remark 5) may be generalized to other types of networks, e.g., networks of beams etc, even for nonlinear networks, which will be discussed in other papers. In engineering, it is more meaningful work. Additionally, the issues of time-delay and anti-disturbance for networks governed by partial differential equations may also be investigated based on the same methods. These problems are worth exploring in future.

Acknowledgments

The authors would like to thank the editors and the anonymous reviewers whose valuable comments and suggestions were very helpful to the improvement of the manuscript.