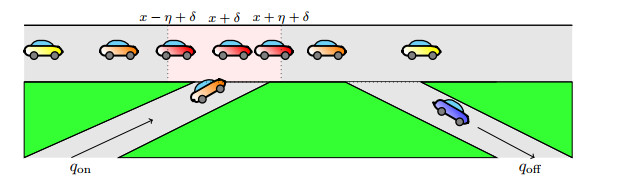
Illustration of the model setting
.We present a non-local version of a scalar balance law modeling traffic flow with on-ramps and off-ramps. The source term is used to describe the inflow and output flow over the on-ramp and off-ramps respectively. We approximate the problem using an upwind-type numerical scheme and we provide L∞ and BV estimates for the sequence of approximate solutions. Together with a discrete entropy inequality, we also show the well-posedness of the considered class of scalar balance laws. Some numerical simulations illustrate the behaviour of solutions in sample cases.
Citation: Felisia Angela Chiarello, Harold Deivi Contreras, Luis Miguel Villada. Nonlocal reaction traffic flow model with on-off ramps[J]. Networks and Heterogeneous Media, 2022, 17(2): 203-226. doi: 10.3934/nhm.2022003
| [1] | Helge Holden, Nils Henrik Risebro . Follow-the-Leader models can be viewed as a numerical approximation to the Lighthill-Whitham-Richards model for traffic flow. Networks and Heterogeneous Media, 2018, 13(3): 409-421. doi: 10.3934/nhm.2018018 |
| [2] | Michael Herty, J.-P. Lebacque, S. Moutari . A novel model for intersections of vehicular traffic flow. Networks and Heterogeneous Media, 2009, 4(4): 813-826. doi: 10.3934/nhm.2009.4.813 |
| [3] | Paola Goatin, Sheila Scialanga . Well-posedness and finite volume approximations of the LWR traffic flow model with non-local velocity. Networks and Heterogeneous Media, 2016, 11(1): 107-121. doi: 10.3934/nhm.2016.11.107 |
| [4] | Paola Goatin, Elena Rossi . Comparative study of macroscopic traffic flow models at road junctions. Networks and Heterogeneous Media, 2020, 15(2): 261-279. doi: 10.3934/nhm.2020012 |
| [5] | Mauro Garavello . A review of conservation laws on networks. Networks and Heterogeneous Media, 2010, 5(3): 565-581. doi: 10.3934/nhm.2010.5.565 |
| [6] | Ye Sun, Daniel B. Work . Error bounds for Kalman filters on traffic networks. Networks and Heterogeneous Media, 2018, 13(2): 261-295. doi: 10.3934/nhm.2018012 |
| [7] | Edward S. Canepa, Alexandre M. Bayen, Christian G. Claudel . Spoofing cyber attack detection in probe-based traffic monitoring systems using mixed integer linear programming. Networks and Heterogeneous Media, 2013, 8(3): 783-802. doi: 10.3934/nhm.2013.8.783 |
| [8] | Simone Göttlich, Ute Ziegler, Michael Herty . Numerical discretization of Hamilton--Jacobi equations on networks. Networks and Heterogeneous Media, 2013, 8(3): 685-705. doi: 10.3934/nhm.2013.8.685 |
| [9] | Abraham Sylla . Influence of a slow moving vehicle on traffic: Well-posedness and approximation for a mildly nonlocal model. Networks and Heterogeneous Media, 2021, 16(2): 221-256. doi: 10.3934/nhm.2021005 |
| [10] | Michael Herty, Lorenzo Pareschi, Mohammed Seaïd . Enskog-like discrete velocity models for vehicular traffic flow. Networks and Heterogeneous Media, 2007, 2(3): 481-496. doi: 10.3934/nhm.2007.2.481 |
We present a non-local version of a scalar balance law modeling traffic flow with on-ramps and off-ramps. The source term is used to describe the inflow and output flow over the on-ramp and off-ramps respectively. We approximate the problem using an upwind-type numerical scheme and we provide L∞ and BV estimates for the sequence of approximate solutions. Together with a discrete entropy inequality, we also show the well-posedness of the considered class of scalar balance laws. Some numerical simulations illustrate the behaviour of solutions in sample cases.
Models of conservation laws with nonlocal flux have been used to describe traffic flow dynamics in which drivers adapt their velocity with respect to what happens to the cars in front of them [3,5,9,11,18]. In this type of models, the flux function depends on a downstream convolution term between the density or the velocity of vehicles and a kernel function with support on the negative axis. However, the above models cannot be used to study the traffic flow on the highway with ramps since they did not include their presence. Indeed, ramps are an important element of traffic systems and develop some complex traffic phenomena, see [12,15,16,19,20,21,22].
In this work, we propose a new nonlocal traffic model which includes the effects of the inflow and output flow over the on- and off- ramps respectively. We start by considering a modified local reaction traffic model proposed in [16],
| ρt+(ρv(ρ))x=Son−Soff, | (1.1) |
where the non-negative functions
| Son(t,x,ρ)=1on(x)qon(t)(1−ρρmax), | (1.2) |
| Soff(t,x,ρ)=1off(x)qoff(t)ρρmax, | (1.3) |
where
| qon(t)=qrampon(t)Lon,qoff(t)=qrampoff(t)Loff, |
with
| 1on(x)={1x∈Ωon:=[x_on,¯xon],0otherwise,1off(x)={1x∈Ωoff:=[x_off,¯xoff],0otherwise. |
For simplicity we consider
In order to obtain a non-local version of the model (1.1), we first rewrite the flux function
| f(ρ)=ρv(ρ∗ωη),with(ρ∗ωη)(t,x)=∫x+ηxρ(t,y)ωη(y−x)dy. |
On the on-ramp the idea is that at position
| Son(t,x,ρ,ρ∗ωη,δ)=1on(x)qon(t)(1−ρ∗ωη,δρmax), | (1.4) |
where
| (ρ∗ωη,δ)(t,x)=∫x+η+δx−η+δρ(t,y)ωη,δ(y−x)dy, |
with
| Son(t,x,ρ,ρ∗ωη,δ)=1on(x)qon(t)(1−ρρmax)(1−ρ∗ωη,δρmax). | (1.5) |
Note that this term contains a product which differentiates it from the original model, this choice is also assumed in the multilane model studied in [8]. An alternative to avoid the double product in the previous equation (1.5) is the following
| Son(t,x,ρ,ρ∗ωη,δ)=1on(x)qon(t)(1−max{ρρmax;ρ∗ωη,δρmax}). | (1.6) |
{In both models with (1.5) and (1.6), if the main road is crowded only few vehicles can enter to the main road.}
The purpose of this work is the study of the well-posedness of a nonlocal reaction traffic flow model with source term given by (1.5) and (1.6).
In [2,3,4,5,6,9,11] the authors studied a nonlocal conservation law to model vehicular traffic flow in the case
Regarding to vehicular traffic flow models taking into account the presence of ramps, we can mention [16], where the authors study the (local) first order nonlinear conservation law (1.1). A (local) second order model is proposed in [21] to study the effects of on- and off-ramps on a main road during two rush periods. Likewise, other works about the study of effects of ramps in vehicular traffic flow models are referenced in [21]. In particular, in [7] the authors consider a Lighthill-Witham-Richards (LWR) traffic flow model on a junction composed by one mainline, an on-ramp and an off-ramp, which are connected by a node. Moreover, in [13] a non-local gas-kinetic traffic model including ramps is proposed, the model allows to simulate syncronized congested traffic and reproduces realistic phenomena of vehicular traffic by variations of the on-ramp flow. A new modeling methodology for merging and diverging flows is studied in [17], the methodology includes coupling effects between main and ramps flows and a new formulation for the modeling of traffic friction is also introduced.
This work is organized as follows. In Section 2 we present the proposed mathematical model with all the considered assumptions on it. Afterwards, we introduce an upwind-type scheme with two different source terms and derive important properties such as maximum principle,
The main goal of this work is to study the well-posedness of the non-local reaction traffic model
| ρt+(ρv(ρ∗ωη))x=Son(⋅,⋅,ρ,ρ∗ωη,δ)−Soff(⋅,⋅,ρ),x∈R, | (2.1) |
where
| ρ(x,0)=ρ0(x)∈(L1∩BV)(R,[0,ρmax]). | (2.2) |
From now on we call Model 0 the equations (2.1)-(1.4)-(2.2), Model 1 the equations (2.1)-(1.5)-(2.2), and Model 2 (2.1)-(1.6)-(2.2). Let us assume the following assumptions:
| qrampon∈L∞(R+;R+),qrampoff∈L∞(R+;R+).v∈C2([0,ρmax];R+), v′(ρ)≤0,ρ∈[0,ρmax].ωη∈C1([0,η];R+) with ω′η(x)≤0, ∫η0ωη(x)dx=1, ∀η>0.ωη,δ∈C1([δ−η,δ+η];R+) with ω′(x)η,δ≥0 for x∈[δ−η,0],ω′(x)η,δ≤0 for x∈[0,δ+η], and ∫δ+ηδ−ηωη,δ(x)dx=1, ∀η>0. | (H1) |
We recall the definition of weak entropy solution for (2.1).
Definition 2.1. Let
| ∫T0∫R(ρφt+ρVφx)dxdt+∫T0∫ΩonSonφdxdt−∫T0∫ΩoffSoffφdxdt+∫Rρ0(x)φ(0,x)dx=0, |
where
Definition 2.2. Let
| ∫T0∫R(|ρ−k|φt+|ρ−k|Vφx−sgn(ρ−k)kVxφ)dxdt+∫T0∫Ωonsgn(ρ−k)Sonφdxdt−∫T0∫Ωoffsgn(ρ−k)Soffφdxdt+∫R|ρ0−k|φ(0,x)dx≥0. |
Our main result is given by the following theorem, which states the well-posedness of problem (2.1) to (2.2) with source term given by (1.5) or (1.6). In order to simplify the computations we consider
Theorem 2.1. Let
| ‖ρ(t)‖L1(R)≤R1(t),0≤ρ(t,x)≤1,TV(ρ(t))≤etH(TV(ρ0)+tQT), |
where
| R1=‖ρ0‖L1(R)+‖qrampon(⋅)‖L1([0,t])−minx∈Ωon‖qrampon(⋅)ρ(⋅,x)‖L1([0,t])−minx∈Ωoff‖qrampoff(⋅)ρ(⋅,x)‖L1([0,t]), | (2.3) |
| QT=2(‖qon‖L∞([0,T])+‖qoff‖L∞([0,T])), | (2.4) |
| H=2‖qon‖L∞([0,T])+‖qoff‖L∞([0,T])+ωη(0)L, | (2.5) |
| L=(‖v‖L∞([0,1])+‖v′‖L∞([0,1])). | (2.6) |
We take a space step
| ρ0j=1Δx∫xj+1/2xj−1/2ρ0(x)dx. |
We define a piecewise constant approximate solution
| ρΔ(t,x)=ρnj, for {t∈[tn,tn+1[x∈]xj−1/2,xj+1/2],where n=0,…,NT−1,j∈Z. | (3.1) |
The
| Son(tn+1/2,xj,ρn+1/2j,Rn+1/2on,j)=1on,jqn+1/2on(1−ρn+1/2j)(1−Rn+1/2on,j), | (3.2) |
| Son(tn+1/2,xj,ρn+1/2j,Rn+1/2on,j)=1on,jqn+1/2on(1−max{ρn+1/2j,Rn+1/2on,j}). | (3.3) |
The
| Soff(tn+1/2,xj,ρn+1/2j)=1off,jqn+1/2offρn+1/2j, | (3.4) |
where we denote
| 1on,j={1Δx∫xj+1/2xj−1/21on(x)dx,x_on≤xj≤¯xon,0otherwise. |
| 1off,j={1Δx∫xj+1/2xj−1/21off(x)dx,x_off≤xj≤¯xoff,0otherwise. |
| qn+1/2on=1Δt∫tn+1tnqon(t)dt,qn+1/2off=1Δt∫tn+1tnqoff(t)dt. |
The approximate solution
Algorithm 3.1 (Upwind scheme).
● Input: approximate solution vector
● do
| ρn+1/2j←ρnj−λ(ρnjv(Rnj+1/2)−ρnj−1v(Rnj−1/2)) | (3.5) |
● enddo
● do
●
●
| ρn+1j←ρn+1/2j+ΔtSn+1/2on,j−ΔtSn+1/2off,j | (3.6) |
● enddo
● Output: approximate solution vector
The terms
| Rnj+1/2=⌊η/Δx⌋−1∑p=0γpρnj+p+1,Rn+1/2on,j=⌊δ+ηΔx⌋−1∑h=⌊δ−ηΔx⌋ˆγhρn+1/2j+h. |
Here we denote
Remark 3.1. If
| |Rn+1/2on,j|≤⌊δ+ηΔx⌋−1∑h=⌊δ−ηΔx⌋ˆγh|ρn+1/2j+h+1|≤⌊δ+ηΔx⌋−1∑h=⌊δ−ηΔx⌋ˆγh=1. |
Remark 3.2. The discrete convolution operator
| ∑j∈Z|Rn+1/2on,j+1−Rn+1/2on,j|≤∑j∈Z|ρn+1/2j+1−ρn+1/2j|. |
The proof of this property can be seen in [8] Lemma 3.2.
In order to prove the existence of solution of model (2.1)-(1.5), in the next lemmas we will show some properties of the approximate solutions constructed by the Algorithm 3.1.
Lemma 3.1 (Maximum principle). Let
| Δt≤min{Δx(γ0‖v′‖L∞([0,1])+‖v‖L∞([0,1])),1QT}, | (3.7) |
with
| 0≤ρΔ(t,x)≤1. |
Proof. The proof is made by induction. Let us assume that
Now focus on the remaining step, involving the source term.
| ρn+1j=ρn+1/2j+Δt(1on,jqn+1/2on(1−ρn+1/2j)(1−Rn+1/2on,j)−1off,jqn+1/2offρn+1/2j)≤ρn+1/2j+Δt1on,jqn+1/2on(1−ρn+1/2j)−Δt1off,jqn+1/2offρn+1/2j=(1−Δt(1on,jqn+1/2on+1off,jqn+1/2off))ρn+1/2j+Δt1on,jqn+1/2on. |
Because of CFL condition (3.7), the last right-hand side is a convex combination of
Lemma 3.2 (
| ‖ρΔ(T,⋅)‖L1(R)≤C1(T), |
with
| C1(t)=‖ρ0‖L1(R)+‖qrampon‖L1([0,t])−minx∈Ωon‖qrampon(⋅)ρΔ(⋅,x)‖L1([0,t])−minx∈Ωoff‖qrampoff(⋅)ρΔ(⋅,x)‖L1([0,t]). | (3.8) |
Proof. For the conservative form of the scheme (3.5), it is satisfied
| ‖ρn+1/2‖L1(R)=‖ρn‖L1(R). |
Now, we going to work
| |ρn+1j|≤|ρn+1/2j|+Δt1on,jqn+1/2on(1−|ρn+1/2j|)−Δt1off,jqn+1/2off|ρn+1/2j|, | (3.9) |
multiplying this inequality by
| ‖ρn+1‖L1(R)≤‖ρn+1/2‖L1(R)+Δtqn+1/2onΔx(∑j∈Ωkon1on,j−∑j∈Ωkon1on,j|ρn+1/2j|)−Δtqn+1/2offΔx∑j∈Ωkoff1off,j|ρn+1/2j|≤‖ρn‖L1(R)+ΔtLqn+1/2on(1−minj∈Ωkonρn+1/2j)−ΔtLqn+1/2offminj∈Ωkoffρn+1/2j=‖ρn‖L1(R)+ΔtLqn+1/2on−Δtminj∈ΩkonLqn+1/2onρn+1/2j−Δtminj∈ΩkoffLqn+1/2offρn+1/2j. |
Thus, by a standard iterative procedure we can deduce
| ‖ρn‖L1(R)≤‖ρ0‖L1(R)+‖qrampon‖L1([0,T])−minx∈Ωon‖qrampon(⋅)ρΔ(⋅,x)‖L1([0,T])−minx∈Ωoff‖qrampoff(⋅)ρΔ(⋅,x)‖L1([0,T]). |
We first prove the Lipschitz continuity of the source terms (3.2) in its second, third and fourth argument and of (3.4) in its second and third argument.
Lemma 3.3. The map
Proof. Let us start with term (3.2). We denote
| Son=Son(t,x,ρ,Ron)−Son(t,˜x,˜ρ,˜Ron), |
then
| |Son|≤|Son(t,x,ρ,Ron)−Son(t,x,˜ρ,Ron)|+|Son(t,x,˜ρ,Ron)−Son(t,x,˜ρ,˜Ron)|+|Son(t,x,˜ρ,˜Ron)−Son(t,˜x,˜ρ,˜Ron)|=|1onqon(1−Ron)(˜ρ−ρ)|+|1onqon(1−˜ρ)(˜Ron−Ron)|+|(1on−˜1on)qon(1−˜ρ)(1−˜Ron)|≤‖qon‖L∞([0,T])|˜ρ−ρ|+‖qon‖L∞([0,T])|˜Ron−Ron|+‖qon‖L∞([0,T])|1on−˜1on|≤‖qon‖L∞([0,T])(|˜ρ−ρ|+|˜Ron−Ron|+|1on−˜1on|). |
Now, we prove the Lipschitz continuity of
| |Soff|≤|Soff(t,x,ρ)−Soff(t,˜x,ρ,)|+|Soff(t,˜x,ρ)−Soff(t,˜x,˜ρ)|=|1offqoffρ−˜1offqoffρ|+|˜1offqoffρ−˜1offqoff˜ρ|≤‖qoff‖L∞([0,T])(|1off−˜1off|+|ρ−˜ρ|), |
Thus, we have completed the proof.
The Lipschitz continuity of the source term proved in Lemma 3.3 is one of the key ingredients in order to prove the following total variation bound on the numerical approximation.
Proposition 3.1 (
| ∑j∈Z|ρnj+1−ρnj|≤eTH(TV(ρ0)+TQT), |
with
Proof. Let us compute
| ρn+1j+1−ρn+1j=ρn+1/2j+1−ρn+1/2j+Δt[Sn+1/2on,j+1−Sn+1/2on,j]−Δt[Sn+1/2off,j+1−Sn+1/2off,j]. |
By the Lipschitz continuity of the source term proved in Lemma 3.3 and the property of the discrete convolution operator given in Remark 3.2, we get
| ∑j∈Z|ρn+1j+1−ρn+1j|≤(1+Δt‖qon‖L∞([0,T]))∑j∈Z|ρn+1/2j+1−ρn+1/2j|+Δt‖qon‖L∞([0,T])∑j∈Ωkon|1on,j+1−1on,j|+Δt‖qon‖L∞([0,T])∑j∈Z|Rn+1/2on,j+1−Rn+1/2on,j|+Δt‖qoff‖L∞([0,T])∑j∈Z|ρn+1/2j+1−ρn+1/2j|+Δt‖qoff‖L∞([0,T])∑j∈Ωoff|1off,j+1−1off,j|≤(1+Δt(2‖qon‖L∞([0,T])+‖qoff‖L∞([0,T])))∑j∈Z|ρn+1/2j+1−ρn+1/2j|+Δt‖qon‖L∞([0,T])∑j∈Ωkon|1on,j+1−1on,j|+Δt‖qoff‖L∞([0,T])∑j∈Ωoff|1off,j+1−1off,j|≤(1+Δt(2‖qon‖L∞([0,T])+‖qoff‖L∞([0,T])))∑j∈Z|ρn+1/2j+1−ρn+1/2j|+ΔtQT. | (3.10) |
Now, for convective part (3.5) we follow [9] and get
| |ρn+1/2j+1−ρn+1/2j|≤(1+Δtωη(0)L)∑j∈Z|ρnj+1−ρnj|, |
with
| ∑j∈Z|ρn+1j+1−ρn+1j|≤(1+Δt(2‖qon‖L∞([0,T])+‖qoff‖L∞([0,T])))×(1+Δtωη(0)L)∑j∈Z|ρnj+1−ρnj|+ΔtQT, |
which applied recursively yields
| ∑j∈Z|ρnj+1−ρnj|≤eTH(TV(ρ0)+TQT), | (3.11) |
with
Proposition 3.2 (
| TV(ρΔ;[0,T]×R)≤TCxt(T), |
with
| Cxt(T)=eTH((1+2L)(TV(ρ0)+TQT))+12QTC1(T)+‖qrampon‖L∞([0,T]). | (3.12) |
Proof.
| TV(ρΔ;[0,T]×R)=NT−1∑n=0∑j∈ZΔt|ρnj+1−ρnj|+(T−NTΔt)∑j∈Z|ρNTj+1−ρNTj|+NT−1∑n=0∑j∈ZΔx|ρn+1j−ρnj|. |
By
| NT−1∑n=0∑j∈ZΔt|ρnj+1−ρnj|+(T−NTΔt)∑j∈Z|ρNTj+1−ρNTj|≤TeTH(TV(ρ0)+TQT). | (3.13) |
On the other hand, observe that
| |ρn+1j−ρnj|≤|ρn+1j−ρn+1/2j|+|ρn+1/2j−ρnj|. | (3.14) |
We then estimate separately each term on the right hand side of the inequality (3.14).
By the definition of the relaxation step (3.6), for the first term on right hand side of (3.14) we have
| |ρn+1j−ρn+1/2j|≤Δt|Sn+1/2on,j−Sn+1/2off,j|≤Δt1on,jqn+1/2on(1−ρn+1/2j)(1−Rn+1/2on,j)+Δt1off,jqn+1/2offρn+1/2j≤Δtqn+1/2on(1on,j+1on,j|ρn+1/2j|)+Δt1off,jqn+1/2off|ρn+1/2j|, | (3.15) |
then multiplying by
| Δx∑j∈Z|ρn+1j−ρn+1/2j|≤Δtqn+1/2on(Δx∑j∈Ωkon1on,j+Δx∑j∈Ωkon1on,j|ρn+1/2j|)+Δtqn+1/2offΔx∑j∈Ωkoff1off,j|ρn+1/2j|≤Δtqn+1/2on(L+‖ρn+1/2‖L1(R))+Δtqn+1/2off‖ρn+1/2‖L1(R)=Δtqn+1/2on(L+‖ρn‖L1(R))+Δt‖qoff‖L∞([0,T])‖ρn‖L1(R)=12ΔtQT‖ρn‖L1(R)+Δt‖qrampon‖L∞([0,T]). | (3.16) |
Now we analyze the second term of the right hand side (3.14). Since the numerical flux defined in (3.5) is Lipschitz continuous in both arguments with Lipschitz constant
| |ρn+1/2j−ρnj|=λ|Fj+1/2(ρnj,Rnj+1/2)−Fj−1/2(ρnj−1,Rnj−1/2)|≤λL(|ρnj−ρnj−1|+|Rnj+1/2−Rnj−1/2|), |
multiplying by
| Δx∑j∈Z|ρn+1/2j−ρnj|≤2LΔt∑j∈Z|ρnj+1−ρnj|. | (3.17) |
Collecting together (3.16) and (3.17), and by using Lemma 3.2 and Proposition 3.1 we have,
| Δx∑j∈Z|ρn+1j−ρnj|≤12ΔtQT‖ρn‖L1(R)+Δt‖qrampon‖L∞([0,T])+2LΔt∑j∈Z|ρnj+1−ρnj|≤12ΔtQTC1(T)+Δt‖qrampon‖L∞([0,T])+2LΔteTH(TV(ρ0)+TQT). | (3.18) |
Then, collecting together (3.13) and (3.18) we get
| NT−1∑n=0∑j∈ZΔt|ρnj+1−ρnj|+(T−NTΔt)∑j∈Z|ρNTj+1−ρNTj|+NT−1∑n=0∑j∈ZΔx|ρn+1j−ρnj|≤TeTH((1+2L)(TV(ρ0)+TQT))+12TQTC1(T)+T‖qrampon‖L∞([0,T]). |
In order to define an entropy inequality we define, for
| Gj+1/2(u)=uv(Rj+1/2),Fκj+1/2(u)=Gj+1/2(u∨κ)−Gj+1/2(u∧κ), |
with
Lemma 3.4. Let
| |ρn+1j−κ|−|ρnj−κ|+λ(Fkj+1/2(ρnj)−Fkj+1/2(ρnj−1))−Δtsgn(ρn+1j−κ)(Son(tn+1/2,xj,ρn+1/2j,Rn+1/2on,j)−Soff(tn+1/2,xj,ρn+1/2j))+λsgn(ρn+1j−κ)κ(v(Rnj+1/2)−v(Rnj−1/2))≤0. |
Proof. We set
| Gj(u,w)=w−λ(Gj+1/2(w)−Gj−1/2(u))=w−λ(wv(Rj+1/2)−uv(Rj−1/2)). |
Clearly
The map
| ∂G∂w=1−λv(Rj+1/2)≥0,∂G∂u=λv(Rj−1/2). |
Moreover, we have the following identity
| Gj(ρnj−1∨κ,ρnj∨κ)−Gj(ρnj−1∧ κ,ρnj∧κ)=|ρnj−κ|−λ(Fkj+1/2(ρnj)−Fkj−1/2(ρnj−1)). |
Then, by monotonicity, the definition of scheme (3.5) and by using
| Gj(ρnj−1∨κ,ρnj∨κ)−Gj(ρnj−1∧ κ,ρnj∧κ)≥Gj(ρnj−1,ρnj)∨Gj(κ,κ)−Gj(ρnj−1,ρnj)∧Gj(κ,κ)=|Gj(ρnj−1,ρnj)−Gj(κ,κ)|=|ρn+1/2j−Gj(κ,κ)|=|ρn+1j−κ+λκ(v(Rnj+1/2)−v(Rnj−1/2))−Δt(Son(tn+1/2,xj,ρn+1/2j,Rn+1/2on,j)−Soff(tn+1/2,xj,ρn+1/2j))|≥|ρn+1j−κ|+λsgn(ρn+1j−κ)κ(v(Rnj+1/2)−v(Rnj−1/2))−Δtsgn(ρn+1j−κ)(Son(tn+1/2,xj,ρn+1/2j,Rn+1/2on,j)−Soff(tn+1/2,xj,ρn+1/2j)). |
The following Theorem states the
Theorem 3.1 (Uniqueness). Let
| ‖ρ(t)−˜ρ(t)‖L1(R)≤eCT(‖ρ0−˜ρ0‖L1(R)+L(‖qon−˜qon‖L1([0,t])+‖qoff−˜qoff‖L1([0,T]))). |
Proof. The proof follows closely Theorem 5.6 of [8].
By using Kružkov's doubling of variables technique we get
| ‖ρ(T,⋅)−˜ρ(T,⋅)‖L1(R)≤‖ρ0−˜ρ0‖L1(R)+∫T0∫Ωon|˜Son|dxdt+∫T0∫Ωoff|˜Soff|dxdt+∫T0∫R|V||∂xρ(t,x)|dxdt+∫T0∫R|Vx||ρ(t,x)|dxdt, |
where
| ˜Son=Son(t,x,qon,ρ,Ron)−Son(t,x,˜qon,˜ρ,˜Ron),˜Soff=Soff(t,x,qon,ρ)−Soff(t,x,˜qon,˜ρ),V=v(R)−v(P),Vx=∂xv(R)−∂xv(P). |
Let us now estimate all the terms appearing in the right hand side of the above inequality. We start bounding
| ∫T0∫Ωon|˜Son|dxdt=∫T0∫Ωon|Son(t,x,qon,ρ,Ron)−Son(t,x,˜qon,˜ρ,˜Ron)|dxdt≤∫T0∫Ωon(|˜S1on|+|˜S2on|+|˜S3on|)dxdt, |
where
| ˜S1on=Son(t,x,qon,ρ,Ron)−Son(t,x,qon,ρ,˜Ron),˜S2on=Son(t,x,qon,ρ,˜Ron)−Son(t,x,qon,˜ρ,˜Ron),˜S3on=Son(t,x,qon,˜ρ,˜Ron)−Son(t,x,˜qon,˜ρ,˜Ron). |
First we are going to bound
| |˜S1on|=|1onqon(1−ρ)((1−Ron)−(1−˜Ron))|≤‖qon‖L∞([0,T])|˜Ron−Ron|, |
thus
| ∫T0∫Ωon|˜S1on|dxdt≤‖qon‖L∞([0,T])∫T0∫Ωon|˜Ron−Ron|dxdt≤‖qon‖L∞([0,T])∫T0‖˜Ron−Ron‖L1(Ωon). |
Observe that
| ‖Ron−˜Ron‖L1(Ωon)≤‖ρ(t,⋅)−˜ρ(t,⋅)‖L1(Ωon), |
since
| ∫T0∫Ωon|˜S1on|dxdt≤‖qon‖L∞([0,T])∫T0‖ρ(t,⋅)−˜ρ(t,⋅)‖L1(Ωon)dt≤‖qon‖L∞([0,T])∫T0‖ρ(t,⋅)−˜ρ(t,⋅)‖L1(R)dt. |
Now we are going to bound
| |˜S2on|=|1onqon(1−˜Ron)(1−ρ)(˜ρ−ρ)|≤‖qon‖L∞([0,T])|ρ−˜ρ|. |
Integrating in time and space we have
| ∫T0∫Ωon|˜S2on|dxdt≤‖qon‖L∞([0,T])∫T0‖ρ(t,⋅)−˜ρ(t,⋅)‖L1(Ωon)dt≤‖qon‖L∞([0,T])∫T0‖ρ(t,⋅)−˜ρ(t,⋅)‖L1(R)dt. |
Bounding
| |˜S3on|=|1on(1−˜ρ)(1−˜Ron)(qon−˜qon)|≤|qon−˜qon|, |
thus
| ∫T0∫Ωon|˜S3on|dxdt≤∫T0∫Ωon|qon−˜qon|dxdt≤L‖qon−˜qon‖L1([0,T]). |
Therefore, we get the following estimate
| ∫T0∫Ωon|˜Son|dxdt≤2‖qon‖L∞([0,T])∫T0‖ρ(t,⋅)−˜ρ(t,⋅)‖L1(R)dt+L‖qon−˜qon‖L1([0,T]). | (3.19) |
Regarding
| |˜Soff|=|1offqoffρ−1off˜qoff˜ρ|≤|˜S1off|+|˜S2off|, |
where
| ˜S1off=Soff(t,x,qoff,ρ)−Soff(t,x,qoff,˜ρ),˜S2off=Soff(t,x,qoff,˜ρ)−Soff(t,x,˜qoff,˜ρ). |
Then,
| ∫T0∫Ωoff|˜S1off|dxdt≤‖qoff‖L∞([0,T])∫T0‖ρ(t,⋅)−˜ρ(t,⋅)‖L1(Ωoff)dt≤‖qoff‖L∞([0,T])∫T0‖ρ(t,⋅)−˜ρ(t,⋅)‖L1(R)dt, |
and
| ∫T0∫Ωoff|˜S2off|dxdt≤L‖qoff−˜qoff‖L1([0,T]). |
Thus, we get
| ∫T0∫Ωoff|Soff|dxdt≤‖qoff‖L∞([0,T])∫T0‖ρ(t,⋅)−˜ρ(t,⋅)‖L1(R)dt+L‖qoff−˜qoff‖L1([0,T]). | (3.20) |
{Next, focus on
| |V|≤ωη(0)‖v′‖L∞([0,1])‖ρ(t,⋅)−˜ρ(t,⋅)‖L1(R), |
we obtain}
| ∫T0∫R|V||∂xρ(t,x)|dxdt≤ωη(0)‖v′‖L∞([0,1])supt∈[0,T]‖ρ(t,⋅)‖TV(R)∫T0‖ρ(t,⋅)−˜ρ(t,⋅)‖L1(R)dt. | (3.21) |
Next, we pass to
| |Vx|≤(2(ωη(0))2‖v"‖L∞([0,1])+‖v′‖L∞([0,1])‖ω′η‖L∞([0,η]))‖ρ(t,⋅)−˜ρ(t,⋅)‖L1(R)+ωη(0)‖v′‖L∞([0,1])(|ρ−˜ρ|(t,x+η)+|ρ−˜ρ|(t,x)), |
thus
| ∫T0∫R|Vx||ρ(t,x)|dxdt≤W∫T0‖ρ(t,⋅)−˜ρ(t,⋅)‖L1(R)dt, | (3.22) |
where
| W=(2(ωη(0))2‖v"‖L∞([0,1])+‖v′‖L∞([0,1])‖ω′η‖L∞([0,η]))C1(t)+2ωη(0)‖v′‖L∞([0,1]). |
Collecting together (3.19), (3.20), (3.21) and (3.22) we get
| ‖ρ(T,⋅)−˜ρ(T,⋅)‖L1(R)≤‖ρ0−˜ρ0‖L1(R)+L(‖qon−˜qon‖L1([0,t])+‖qoff−˜qoff‖L1([0,t]))+C∫T0‖ρ(t,⋅)−˜ρ(t,⋅)‖L1(R)dt, | (3.23) |
where
| C=H+ωη(0)‖v′‖L∞([0,1])supt∈[0,T]‖ρ(t,⋅)‖TV(R)+W. | (3.24) |
An application of Gronwall Lemma to (3.23) completes the proof.
The convergence of the approximate solutions constructed by Algorithm 3.1 towards the unique weak entropy solution can be proven by applying Helly's compactness theorem. The latter can be applied due to Lemma 3.1 and Proposition 3.2 and states that there exists a sub-sequence of approximate solution
In this section we consider the problem (2.1) with the
| ρn+1j=ρn+1/2j+Δt1on,jqn+1/2on(1−max{ρn+1/2j,Rn+1/2on,j})−Δt1off,jqn+1/2offρn+1/2j. | (3.25) |
Lemma 3.5 (Maximum Principle). Let
| 0≤ρΔ(t,x)≤1. |
Proof. The proof is made by induction. We assume that
Now focus on the remaining step, involving the source term.
| ρn+1j=ρn+1/2j+Δt1on,jqn+1/2on(1−max{ρn+1/2j,Rn+1/2on,j})−Δt1off,jqn+1/2offρn+1/2j=ρn+1/2j+Δt1on,jqn+1/2on(1−ρn+1/2j+Rn+1/2on,j+|ρn+1/2j−Rn+1/2on,j|2)−Δt1off,jqn+1/2offρn+1/2j=ρn+1/2j+Δt(1on,jqn+1/2on−121on,jqn+1/2onρn+1/2j−121on,jqn+1/2onRn+1/2on,j−121on,jqn+1/2on|ρn+1/2j−Rn+1/2on,j|−1off,jqn+1/2offρn+1/2j)≤ρn+1/2j+Δt(1on,jqn+1/2on−121on,jqn+1/2onρn+1/2j−121on,jqn+1/2onRn+1/2on,j+121on,jqn+1/2on|Rn+1/2on,j|−121on,jqn+1/2on|ρn+1/2j|−1off,jqn+1/2offρn+1/2j)=ρn+1/2j+Δt(1on,jqn+1/2on−1on,jqn+1/2onρn+1/2j−1off,jqn+1/2offρn+1/2j)=(1−Δt(1on,jqn+1/2on+1off,jqn+1/2off))ρn+1/2j+Δt1on,jqn+1/2on, |
now we can proceed as in Lemma 3.1.
Lemma 3.6. Let
| ‖ρΔ(t)‖L1(R)≤C1(t), |
where
Proof. By (3.26) and CFL condition (3.7) we have
| |ρn+1j|≤|ρn+1/2j|+Δt1on,jqn+1/2on(1−|ρn+1/2j|)−Δt1off,jqn+1/2off|ρn+1/2j|, |
this cases reduce to (3.9) and we can proceed as in Lemma 3.2.
Lemma 3.7. The map
Proof.
| |Son(t,x,ρ,Ron)−Son(t,˜x,˜ρ,˜Ron)|≤S1+S2+S3, |
where
| S1=|Son(t,x,ρ,Ron)−Son(t,x,˜ρ,Ron)|S2=|Son(t,x,˜ρ,Ron)−Son(t,x,˜ρ,˜Ron)|S3=|Son(t,x,˜ρ,˜Ron)−Son(t,˜x,˜ρ,˜Ron)|. |
by the definition of
| |max(a1,b)−max(a2,b)|≤|a1−a2|, |
we have
| S1≤‖qon‖L∞([0,T])|1−max{ρ,Ron}−(1−max{˜ρ,Ron})|=‖qon‖L∞([0,T])|max{˜ρ,Ron}−max{ρ,Ron}|≤‖qon‖L∞([0,T])|˜ρ−ρ|. |
Pass now to
| S2≤‖qon‖L∞([0,T])|max{˜ρ,˜Ron}−max{˜ρ,Ron}|≤‖qon‖L∞([0,T])|Ron−˜Ron|. |
Next, we analyze the
| S3=|1onqon(1−max{˜ρ,˜Ron})−˜1onqon(1−max{˜ρ,˜Ron})|≤‖qon‖L∞([0,T])|1on−˜1on||1−max{˜ρ,˜Ron}|≤‖qon‖L∞([0,T])|1on−˜1on|. |
Proposition 3.3 (
| ∑j∈Z|ρnj+1−ρnj|≤eTH(TV(ρ0)+TQT), |
with
Proof. Due to the results obtained in Lemma 3.7, the proof is analogous to that one of Proposition 3.1.
Proposition 3.4 (
| TV(ρΔ;[0,T]×R)≤TCxt(T), |
with
Proof. For this proof we need to compute the following estimate,
| |ρn+1j−ρn+1/2j|≤Δt|Sn+1/2on,j−Sn+1/2off,j|=Δt|1on,jqon(1−max{ρn+1/2j,Rn+1/2on,j})−1off,jqoffρn+1/2j|.≤Δt1on,j‖qon‖L∞([0,T])|1−max{ρn+1/2j,Rn+1/2on,j}|+Δt1off,j‖qoff‖L∞([0,T])|ρn+1/2j|. |
Here we need to consider two cases, which are described below:
| |ρn+1j−ρn+1/2j|≤Δt1on,j‖qon‖L∞([0,T])|1−ρn+1/2j|+Δt1off,j‖qoff‖L∞([0,T])|ρn+1/2j|≤Δt1on,j‖qon‖L∞([0,T])(1+|ρn+1/2j|)+Δt1off,j‖qoff‖L∞([0,T])|ρn+1/2j|≤Δt‖qon‖L∞([0,T])(1on,j+1on,j|ρn+1/2j|)+Δt‖qoff‖L∞([0,T])1off,j|ρn+1/2j|. |
| |ρn+1j−ρn+1/2j|≤Δt1on,j‖qon‖L∞([0,T])|1−Rn+1/2on,j|+Δt1off,j‖qoff‖L∞([0,T])|ρn+1/2j|≤Δt‖qon‖L∞([0,T])(1on,j+1on,j|ρn+1/2j|)+Δt‖qoff‖L∞([0,T])1off,j|ρn+1/2j|. |
Note that both cases reduces to (3.15) and therefore the rest of the proof is analogous to Proposition 3.2.
In this section we present some numerical examples to describe the effects that the ramps have on a road. We solve Model 1 and Model 2 by means Algorithm 3.1 with the term
| ωη(x):=2η−xη2χ[0,η](x),ωη,δ(x):=1η6165π(η2−(x−δ)2)5/2χ[−η+δ,η+δ](x), |
for convective and reactive terms respectively, with
Dynamic of Model 1 vs. Model 2.
In this example we show numerically the behavior of the density of vehicles in a main road with the presence of one on-ramp and one off-ramp. We solve (2.1) numerically in the interval
In Fig. 2 we can see that when vehicles enter the ramp, the density of vehicles on the main road increases and a shock wave with negative speed is formed, after that, a rarefaction wave appears and when some vehicles leave the main road through off-ramp a shock wave with positive speed is formed. In particular we can observe a difference between the maximum density that is reached in each model, which may be due to the presence of the term
limit
In this example we take a look at the limit case
Example 2.
| 0.1 | 0.05 | 0.01 | 0.004 | |
| 2.8e-1 | 1.6e-1 | 3.6e-2 | 1.1e-2 |
Maximum principle.
In this example we verify that the Algorithm 3.1 with the terms
| ρ0(x)={0.1ifx≤1.11.0ifx>1.1, |
Free main road.
In this example we consider a free main road, i.e, we consider a initial condition
In this paper we introduced a nonlocal balance law to model vehicular traffic flow including on- and off-ramps. We presented three different models called Model 0, Model 1 and Model 2 and we proved existence and uniqueness of solutions for Model 1 and Model 2. We approximated the problem through a upwind-type numerical scheme, providing a Maximum principle,
FAC is member of GNFM (Gruppo Nazionale per la Fisica Matematica) of INdAM (Istituto Nazionale di Alta Matematica), Italy. LMV is supported by ANID-Chile through Fondecyt project 1181511 and by Centro de Modelamiento Matemático (CMM), ACE210010 and FB210005, BASAL funds for center of excellence from ANID-Chile. FAC, HDC and LMV are supported by the INRIA Associated Team "Efficient numerical schemes for non-local transport phenomena" (NOLOCO; 2018–2020) and by project MATH-Amsud 22-MATH-05 "NOTION: NOn-local conservaTION laws for engineering, biological and epidemiological applications: theoretical and numerical". HDC was partially supported by the National Agency for Research and Development, ANID-Chile through Scholarship Program, Doctorado Becas Chile 2021, 21210826.
| 1. | Harold Deivi Contreras, Paola Goatin, Luis-Miguel Villada, A two-lane bidirectional nonlocal traffic model, 2025, 543, 0022247X, 129027, 10.1016/j.jmaa.2024.129027 | |
| 2. | Veerappa Gowda G. D., Sudarshan Kumar Kenettinkara, Nikhil Manoj, Convergence of a second-order scheme for non-local conservation laws, 2023, 57, 2822-7840, 3439, 10.1051/m2an/2023080 | |
| 3. | Felisia A. Chiarello, Harold D. Contreras, 2024, Chapter 26, 978-3-031-55263-2, 303, 10.1007/978-3-031-55264-9_26 |
Example 2.
| 0.1 | 0.05 | 0.01 | 0.004 | |
| 2.8e-1 | 1.6e-1 | 3.6e-2 | 1.1e-2 |
Illustration of the model setting
Example 1. Numerical approximations of the problem (2.1). Dynamic of Model 1 vs. Model 2 at (a)
Example 2. Numerical approximations of the problem (2.1) at
Example 3. Numerical approximation at time
Example 4. Dynamic of the model (2.1). Behavior of the numerical solution computed with Algorithm 3.1 by means of Model 1 and Model 2 at time (a)