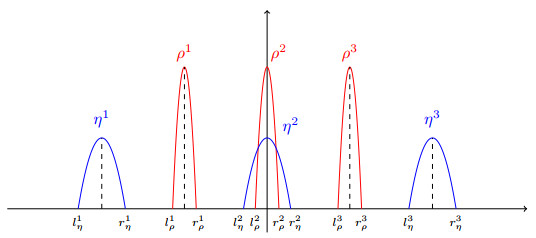
A possible example of a stationary solution to (3) with
We investigate existence of stationary solutions to an aggregation/diffusion system of PDEs, modelling a two species predator-prey interaction. In the model this interaction is described by non-local potentials that are mutually proportional by a negative constant −α, with α>0. Each species is also subject to non-local self-attraction forces together with quadratic diffusion effects. The competition between the aforementioned mechanisms produce a rich asymptotic behavior, namely the formation of steady states that are composed of multiple bumps, i.e. sums of Barenblatt-type profiles. The existence of such stationary states, under some conditions on the positions of the bumps and the proportionality constant α, is showed for small diffusion, by using the functional version of the Implicit Function Theorem. We complement our results with some numerical simulations, that suggest a large variety in the possible strategies the two species use in order to interact each other.
Citation: Simone Fagioli, Yahya Jaafra. Multiple patterns formation for an aggregation/diffusion predator-prey system[J]. Networks and Heterogeneous Media, 2021, 16(3): 377-411. doi: 10.3934/nhm.2021010
| [1] | Simone Fagioli, Yahya Jaafra . Multiple patterns formation for an aggregation/diffusion predator-prey system. Networks and Heterogeneous Media, 2021, 16(3): 377-411. doi: 10.3934/nhm.2021010 |
| [2] | Rinaldo M. Colombo, Francesca Marcellini, Elena Rossi . Biological and industrial models motivating nonlocal conservation laws: A review of analytic and numerical results. Networks and Heterogeneous Media, 2016, 11(1): 49-67. doi: 10.3934/nhm.2016.11.49 |
| [3] | Mostafa Bendahmane . Analysis of a reaction-diffusion system modeling predator-prey with prey-taxis. Networks and Heterogeneous Media, 2008, 3(4): 863-879. doi: 10.3934/nhm.2008.3.863 |
| [4] | Ivano Primi, Angela Stevens, Juan J. L. Velázquez . Pattern forming instabilities driven by non-diffusive interactions. Networks and Heterogeneous Media, 2013, 8(1): 397-432. doi: 10.3934/nhm.2013.8.397 |
| [5] | Marie Henry . Singular limit of an activator-inhibitor type model. Networks and Heterogeneous Media, 2012, 7(4): 781-803. doi: 10.3934/nhm.2012.7.781 |
| [6] | Stefan Berres, Ricardo Ruiz-Baier, Hartmut Schwandt, Elmer M. Tory . An adaptive finite-volume method for a model of two-phase pedestrian flow. Networks and Heterogeneous Media, 2011, 6(3): 401-423. doi: 10.3934/nhm.2011.6.401 |
| [7] | José Antonio Carrillo, Yingping Peng, Aneta Wróblewska-Kamińska . Relative entropy method for the relaxation limit of hydrodynamic models. Networks and Heterogeneous Media, 2020, 15(3): 369-387. doi: 10.3934/nhm.2020023 |
| [8] | Panpan Xu, Yongbin Ge, Lin Zhang . High-order finite difference approximation of the Keller-Segel model with additional self- and cross-diffusion terms and a logistic source. Networks and Heterogeneous Media, 2023, 18(4): 1471-1492. doi: 10.3934/nhm.2023065 |
| [9] | Julien Barré, Pierre Degond, Diane Peurichard, Ewelina Zatorska . Modelling pattern formation through differential repulsion. Networks and Heterogeneous Media, 2020, 15(3): 307-352. doi: 10.3934/nhm.2020021 |
| [10] | Verónica Anaya, Mostafa Bendahmane, Mauricio Sepúlveda . Mathematical and numerical analysis for Predator-prey system in a polluted environment. Networks and Heterogeneous Media, 2010, 5(4): 813-847. doi: 10.3934/nhm.2010.5.813 |
We investigate existence of stationary solutions to an aggregation/diffusion system of PDEs, modelling a two species predator-prey interaction. In the model this interaction is described by non-local potentials that are mutually proportional by a negative constant −α, with α>0. Each species is also subject to non-local self-attraction forces together with quadratic diffusion effects. The competition between the aforementioned mechanisms produce a rich asymptotic behavior, namely the formation of steady states that are composed of multiple bumps, i.e. sums of Barenblatt-type profiles. The existence of such stationary states, under some conditions on the positions of the bumps and the proportionality constant α, is showed for small diffusion, by using the functional version of the Implicit Function Theorem. We complement our results with some numerical simulations, that suggest a large variety in the possible strategies the two species use in order to interact each other.
The mathematical modelling of the collective motion through aggregation/diffusion phenomena has raised a lot of interest in the recent years and it has been deeply studied for its application in several areas, such as biology [9, 39, 47, 48], ecology [35, 42, 43], animal swarming [3, 4, 40, 46] sociology and economics, [49, 50, 51]. One of the common idea in this modelling approach is that a certain population composed by agents evolves according to long-range attraction and short-range repulsion forces between agents. We are interested in modelling the problem of predator-prey interactions, namely we consider two populations that attract (prey) and repel (predators) each others. The pioneering works for this problem are the ones by Lotka, [36] and Volterra[54], which describe the predator-prey interaction via reaction terms in a set of differential equations, possibly combined with diffusion terms, see [41] and the references therein.
As in [21], in this paper we model predator-prey interactions via a transport terms rather than a reaction ones as follows: consider
| {˙Xi(t)=−N∑k=1mkX(∇Sr1(Xi(t)−Xk(t))+∇Sa1(Xi(t)−Xk(t)))−M∑h=1mhY∇K(Xi(t)−Yh(t)),˙Yj(t)=−M∑h=1mhY(∇Sr2(Xi(t)−Xk(t))+∇Sa2(Yj(t)−Yh(t)))+αM∑k=1mkX∇K(Yj(t)−Xk(t)), | (1) |
with
The formal limit when the number of particles tends to infinity leads to the following system of partial differential equations
| {∂tρ=div(ρ∇(d1ρ−Sa1∗ρ−K∗η)),∂tη=div(η∇(d2η−Sa2∗η+αK∗ρ)), | (2) |
where
The goal of this paper is to show that the model above catches one of the main features that occur in nature, namely the formation of spatial patterns where the predators are surrounded of empty zones and the prey aggregates around, that is usually observed in fish schools or in flock of sheeps, see [32, 38]. In the fully aggregative case, namely system (2) with
Existence theory for solutions to system of the form (2) can be performed in the spirit of [10, 20]. In particular, system (2) should be framed in the context of non symmetrizable systems, for which the Wasserstein gradient flow theory developed in [1] and adapted to systems in [22] does not work. In [10, 20, 22], the authors consider different choices for the diffusion part (no diffusion in [22], diagonal nonlinear diffusion in [10] and cross-diffusion with dominant diagonal in [20]), and the existence of solutions is proved via an implicit-explicit version of the JKO scheme [33].
In the following, we reduce our analysis to the one-dimensional setting
| {∂tρ=∂x(ρ∂x(d1ρ−Sρ∗ρ−K∗η))∂tη=∂x(η∂x(d2η−Sη∗η+αK∗ρ)). | (3) |
We are interested in the existence of stationary solutions to (3), which are solutions to the following system
| {0=(ρ(d1ρ−Sρ∗ρ−K∗η)x)x,0=(η(d2η−Sη∗η+αK∗ρ)x)x, | (4) |
as well as their properties, e.g., symmetry, compact support, etc. We shall assume throughout the paper that
| {0=(ρ(θρ−˜Sρ∗ρ−˜K∗η)x)x,0=(η(θη−Sη∗η+˜α˜K∗ρ)x)x. |
The stationary equation for the one species case, i.e.,
| ∂tρ=∂x(ρ∂x(θρ−S∗ρ)) |
is studied several papers, see [2, 7, 11, 16] and therein references. In [7] the Krein-Rutman theorem is used in order to characterise the steady states as eigenvectors of a certain non-local operator. The authors prove that a unique steady state with given mass and centre of mass exists provided that
In this paper we apply the aforementioned approach in order to show that stationary solutions to (3) are composed of multiple Barenblatt profiles. Let us introduce, for fixed
| M={(ρ,η)∈(L∞∩L1(R))2:ρ,η≥0,‖ρ‖L1=zρ,‖η‖L1=zη}. |
Definition 1.1. We say that a pair
●
●
| supp(ρ)=Nρ⋃i=1Iiρandsupp(η)=Nη⋃i=1Iiη, |
respectively and
where, for
Example 1.1. A possible example of steady states as defined above is a steady state
Remark 1.1. We remark that one should be careful with finding a shape of steady state. More precisely, one should choose the numbers
In order to simplify the notations, in the following we will denote with
(A1)
(A2)
(A3)
Note that assumption (A2) together with the sign in front of the nonlocal terms
The main result of the paper is the following
Theorem 1.1. Assume that
(i)
| Bil=Nl∑j=1S′l(cmil−cmjl)zjl+αlNh∑j=1K′(cmil−cmjh)zjh=0, | (5) |
(ii) the following quantities
| Dil=−Nl∑j=1S″l(cmil−cmjl)zjl−αlNh∑j=1K″(cmil−cmjh)zjh, | (6) |
are strictly positive, for all
where
where
● each interval
●
● the solutions
| zρ=Nρ∑i=1ziρandzη=Nη∑i=1ziη, |
respectively.
The paper is structured as follows. In Section 2 we recall the basics notions on optimal transport and we introduce the
We start collecting preliminary concepts on the Wasserstein distance. Let
| Pp(Rn)={μ∈P(Rn):mp(μ)=∫Rn|x|pdμ(x)<∞}. |
For a measure
| ∫Rkf(y)dT#μ(y)=∫Rnf(T(x))dμ(x)forallfBorelfunctionsonRk. |
We endow the space
| Wpp(μ,ν)=infγ∈Γ(μ,ν){∫Rn×Rn|x−y|pdγ(x,y)}, | (7) |
where
Since we are working in a 'multi-species' structure, we consider the product space
| Wpp(μ,ν)=Wpp(μ1,ν1)+Wpp(μ2,ν2), |
with
| uμ(z)≐inf{x∈R:μ((−∞,x])>z},z∈[0,1], | (8) |
see [14].
In the Section 1 we mentioned that the well-posedness of (3) can be stated according to the results in [10, 20] in an arbitrary space dimension
| F[μ,ν](ρ,η)=θ2∫Rnρ2+η2dx−12∫RnρSρ∗ρdx−12∫RnηSη∗ηdx−∫RnρK∗μdx+α∫RnηK∗νdx, |
for a fixed reference couple of measures
Definition 2.1. A curve
(i)
(ii) for almost every
| ddt∫Rnϕρdx=−θ∫Rnρ∇ρ⋅∇ϕdx+∫Rnρ(∇Sρ∗ρ+∇K∗η)∇ϕdx,ddt∫Rnφηdx=−θ∫Rnη∇η⋅∇φdx+∫Rnη(∇Sη∗η−α∇K∗ρ)∇ϕdx. |
Theorem 2.1. Assume that (A1)-(A3) are satisfied. Let
| F[μ0](μ0)<+∞. |
Then, there exists a weak solution to (3) in the sense of Definition 2.1 with
As already mentioned the proof of Theorem 2.1 is a special case of the results in [10, 20] and consists in the following main steps:
1. Let
| μk+1τ∈argminμ∈P2(Rn)2{12τW22(μkτ,μ)+F[μkτ](μ)}. | (9) |
For a fixed
| μτ(t)=(ρτ(t),ητ(t))=μkτt∈((k−1)τ,kτ],k∈N, |
with
2. There exists an absolutely continuous curve
3. There exist a constant
| ∫T0[||ρτ(t,⋅)||2H1(Rn)+||ητ(t,⋅)||2H1(Rn)]dt≤C(T,μ0), | (10) |
and the sequence
| L2((0,T)×Rn)×L2((0,T)×Rn). |
The estimate in (10) can be deduced by using the so called Flow-interchange Lemma introduced in [37], see also [25]. In order to deduce the strong convergence we use the extended version of the Aubin-Lions Lemma in [44].
4. The approximating sequence
| μϵ=(ρϵ,ηϵ)=(Pϵ#ρk+1τ,ηkτ), | (11) |
where
| 0≤12τ[W22(μk+1τ,μϵ)−W22(μkτ,μk+1τ)]+F[μkτ](μϵ)−F[μkτ](μϵ). | (12) |
After some manipulations, sending first
The existence of weak solutions to the purely non-local systems, i.e.,
| {∂tρ=div(ρ∇(Sρ∗ρ+Kρ∗η)),∂tη=div(η∇(Sη∗η+Kη∗ρ)), | (13) |
with generic cross-interaction kernels
| {∂tρ=div(ρ∇(Sρ∗ρ+K∗η)),∂tη=div(η∇(Sη∗η−αK∗ρ)), | (14) |
and its relation with the particle system
| {˙Xi(t)=−N∑k=1mkX∇Sρ(Xi(t)−Xk(t))−M∑k=1mkY∇K(Xi(t)−Yk(t)),˙Yj(t)=−M∑k=1mkY∇Sη(Yj(t)−Yk(t))+αN∑k=1mkX∇K(Yj(t)−Xk(t)). | (15) |
It is proved that stationary states of system (14) are linear combinations of Dirac's deltas, namely
| (ˉρ,ˉη)=(N∑k=1mkXδˉXk(x),M∑h=1mhYδˉYh(x)). | (16) |
where
| {0=N∑k=1∇Sρ(ˉXk−ˉXi)mkX+M∑h=1∇K(ˉYh−ˉXi)mhY0=M∑h=1∇Sη(ˉYh−ˉYj)mhY−αN∑k=1∇K(ˉXk−ˉYj)mkX. | (17) |
for
| Cα=αN∑i=1miXXi−M∑j=1mjYYj | (18) |
that is a conserved quantities, and therefore one would like to produce a unique steady state once the quantity
As a preliminary result, we now prove the existence of one possible shape of steady state, that will be a prototype example for the general case. The steady state is what we can call a mixed steady state, that identifies the case in which the predators can catch the prey, see Figure 2.
The proof of the existence of such steady state follows by using the strong version of the Krein-Rutman theorem, see [26].
Theorem 2.2 (Krein-Rutman). Let
(i) the spectral radius
(ii)
As pointed out in [6], using this strategy we can only obtain existence of stationary states for a diffusion coefficient that depends on the support, without providing any one-to-one correspondence between the diffusion constant (eigenvalue) and the support. Even if non completely satisfactory, the following results give a useful insight on the possible conditions we can expect in order to get existence of steady states, see Remark 3.1.
Let us first introduce a proper definition for mixed steady states as in Figure 2.
Definition 2.2. Let
| Iρ:=supp(ρ)=[−Rρ,Rρ],andIη:=supp(η)=[−Rη,Rη]. |
Let us now assume that
| {θρ(x)−Sρ∗ρ(x)−K∗η(x)=Cρx∈Iρθη(x)−Sη∗η(x)+αK∗ρ(x)=Cηx∈Iη. | (19) |
where
| {θρx=∫Rρ−RρSρ(x−y)ρy(y)dy+∫Rη−RηK(x−y)ηy(y)dyx∈Iρθηx=∫Rη−RηSη(x−y)ηy(y)dy−α∫Rρ−RρK(x−y)ρy(y)dyx∈Iη. | (20) |
By symmetry properties of the kernels
| θρx=∫Rρ0(Sρ(x−y)−Sρ(x+y))ρy(y)dy+∫Rη0(K(x−y)−K(x+y))ηy(y)dy,θηx=∫Rη0(Sη(x−y)−Sη(x+y))ηy(y)dy−α∫Rρ0(K(x−y)−K(x+y))ρy(y)dy. | (21) |
In order to simplify the notations, we set
| ˜G(x,y):=G(x−y)−G(x+y),forG=Sρ,Sη,K. |
Notice that
| {θp(x)=∫Rρ0˜Sρ(x,y)p(y)dy+∫Rη0˜K(x,y)q(y)dyθq(x)=∫Rη0˜Sη(x,y)q(y)dy−α∫Rρ0˜K(x,y)p(y)dy. | (22) |
Proposition 2.1. Assume that
| C<∫Rη0˜Sη(x,y)h(y)dy∫Rρ0˜K(x,y)k(y)dy, | (23) |
for any
| α<min{C,−S′η(Rη)zη−R2ηK″(0)zρ}, |
where
Proof. Let us first introduce the following Banach space
| XRρ,Rη={(p,q)∈C1([0,Rρ])×C1([0,Rη]):p(0)=q(0)=0}, |
endowed with the
| TRρ,Rη[P]:=(f,g)∈C1([0,Rρ])×C1([0,Rη]), |
where
| f(x)=∫Rρ0˜Sρ(x,y)p(y)dy+∫Rη0˜K(x,y)q(y)dyforx∈[0,Rρ],g(x)=∫Rη0˜Sη(x,y)q(y)dy−α∫Rρ0˜K(x,y)p(y)dyforx∈[0,Rη]. |
The assumptions on the kernels ensure that the operator
| KRρ,Rη={P∈XRρ,Rη:p≥0,q≥0}. |
It can be shown that this set is indeed a solid cone in
| HRρ,Rη={P∈KRρ,Rη:p′(0)>0,p(x)>0forallx∈(0,Rρ),andq′(0)>0,q(x)>0forallx∈(0,Rη)}⊂∘KRρ,Rη, |
where
| ∫Rη0˜Sη(x,y)q(y)dy−α∫Rρ0˜K(x,y)p(y)dy>0, | (24) |
if and only if
| ddx|x=0(∫Rη0˜Sη(x,y)q(y)dy−α∫Rρ0˜K(x,y)p(y)dy)=∫Rη0˜Sη,x(0,y)q(y)dy−α∫Rρ0˜Kx(0,y)p(y)dy=∫Rη0(S′η(−y)−S′η(y))q(y)dy−α∫Rρ0(K′(−y)−K′(y))p(y)dy=−2∫Rη0S′η(y)q(y)dy+2α∫Rρ0K′(y)p(y)dy:=A. |
Now, we need to find the condition on
| −2Rη∫Rη0S′η(y)q(y)dy=−2Rη∫Rη0S″η(y)η(y)dy≥(1Rη∫Rη0−S″η(y)dy)(2Rη∫Rη0η(y)dy)=−S′η(Rη)zηR2η. |
Using the concavity assumption of
| −2∫Rρ0K′(y)p(y)dy=−2∫Rρ0K″(y)ρ(y)dy<−K″(0)zρ. |
Thus,
| α<−S′η(Rη)zη−R2ηK″(0)zρ. | (25) |
As a consequence,
| TRρ,Rη[P]=θP, |
with an eigenspace generated by one given nontrivial element
Remark 2.1. Motivated from the purely aggregative case (13), we actually expect a more rich behavior for the possible steady states configurations, such as the separated stationary state in Figure 3. This is expected as a possible winning strategy for the prey, since it corresponds to prey finding a safe distance from the predators. Unfortunately, the symmetrization argument used in the previous proof seems to fail, since in this case we need to require the symmetry around
In this Section we prove the existence and uniqueness of a multiple bumps steady state in the sense of Definition 1 fixing masses and a small diffusion coefficient. Following the approach in [5, 6], we first formulate the problem in terms of the pseudo-inverse functions and then we use the Implicit Function Theorem (cf. [19, Theorem 15.1]).
We start rewriting our stationary system in terms of pseudo-inverse functions. Let
| {0=(ρ(θρ−Sρ∗ρ−αρK∗η)x)x,0=(η(θη−Sη∗η−αηK∗ρ)x)x. | (26) |
where
| ∫Rxρ(x)dx=cmρ,∫Rxη(x)dx=cmη. |
Remember that the only conserved quantity in the evolution, together with the masses, is the joint centre of mass
| CMα=αcmρ−cmη, | (27) |
that we can consider fixed. Define the cumulative distribution functions of
| Fρ(x)=∫x−∞ρ(x)dx,Fη(x)=∫x−∞η(x)dx. |
Let
| ul(z)=inf{x∈R:Fl(x)≥z},l∈{ρ,η}, |
supported on
| supp(ul)=[0,zl]:=Jl,l∈{ρ,η}. |
For
| ∫ρi(x)dx=ziρ,∫ηj(x)dx=zjη,i=1,2,…,Nρ,j=1,2,…,Nη, |
and the centres of masses accordingly,
| ∫xρi(x)dx=cmiρ,∫xηj(x)dx=cmjη,i=1,2,…,Nρ,j=1,2,…,Nη, |
and we can always assume that the centres of masses are ordered species by species, i.e.
| {Nρ∑j=1S′ρ(cmiρ−cmjρ)zjρ+Nη∑j=1K′(cmiρ−cmjη)zjη=0,i=1,…,Nρ,Nη∑j=1S′η(cmiη−cmjη)zjη−αNρ∑j=1K′(cmiη−cmjρ)zjρ=0,i=1,…,Nη, | (28) |
coupled with the conservation of the joint centre of mass
| ul(z)=Nl∑i=1uil(z)1Jil(z),l∈{ρ,η}, |
where
| supp(ul)=[0,zl]=Jl=Nl⋃i=1[i∑k=1zk−1l,i∑k=1zkl]:=Nl⋃i=1[ˆzil,˜zil]:=Nl⋃i=1Jil,l∈{ρ,η}, |
with
| {θ2∂z((∂zuρ(z))−2)=∫JρS′ρ(uρ(z)−uρ(ξ))dξ+αρ∫JηK′(uρ(z)−uη(ξ))dξ,z∈Jρ,θ2∂z((∂zuη(z))−2)=∫JηS′η(uη(z)−uη(ξ))dξ+αη∫JρK′(uη(z)−uρ(ξ))dξ,z∈Jη. | (29) |
The restriction to
| θ2∂z((∂zuil(z))−2)=Nl∑j=1∫JjlS′l(uil(z)−ujl(ξ))dξ+αlNh∑j=1∫JjhK′(uil(z)−ujh(ξ))dξ,z∈Jil. | (30) |
Similar to [5, 6], we suggest the linearization
| uil=cmil+δvili=1,2,…,Nl,andl∈{ρ,η}, |
with
| δ2∂z((∂zvil(z))−2)=Nl∑j=1∫JjlS′l(cmil−cmjl+δ(vil(z)−vjl(ξ)))dξ+αlNh∑j=1∫JjhK′(cmil−cmjh+δ(vil(z)−vjh(ξ)))dξ. | (31) |
Multiplying (31) by
| δ2∂zvil(z)=Nl∑j=1∫JjlSl(cmil−cmjl+δ(vil(z)−vjl(ξ)))dξ+αlNh∑j=1∫JjhK(cmil−cmjh+δ(vil(z)−vjh(ξ)))dξ+Ail,z∈Jil, | (32) |
where
| Ail=−Nl∑j=1∫JjlSl(cmil−cmjl+δ(λil−vjl(ξ)))dξ−αlNh∑j=1∫JjhK(cmil−cmjh+δ(λil−vjh(ξ)))dξ. | (33) |
Next, we set
| δ3z=Nl∑j=1∫JjlGl(cmil−cmjl+δ(vil(z)−vjl(ξ)))dξ+αlNh∑j=1∫JjhH(cmil−cmjh+δ(vil(z)−vjh(ξ)))dξ+Ailδvil(z)+βil,z∈Jil. | (34) |
Let us denote with
| βil=δ3ˉzil−Nl∑j=1∫JjlGl(cmil−cmjl−δvjl(ξ))dξ−αlNh∑j=1∫JjhH(cmil−cmjh−δvjh(ξ))dξ. | (35) |
As a consequence of all above computations, we get the following relation for
| δ3(z−ˉzil)=Nl∑j=1∫JjlGl(cmil−cmjl+δ(vil(z)−vjl(ξ)))−Gl(cmil−cmjl−δvjl(ξ))dξ−δvil(z)Nl∑j=1∫JjlSl(cmil−cmjl+δ(λil−vjl(ξ)))dξ+αlNh∑j=1∫JjhH(cmil−cmjh+δ(vil(z)−vjh(ξ)))−H(cmil−cmjh−δvjh(ξ))dξ−δvil(z)αlNh∑j=1∫JjhK(cmil−cmjh+δ(λil−vjh(ξ)))dξ. | (36) |
If we define, for
| Fil[p;δ](z)=ˉzil−z+δ−3[Nl∑j=1∫JjlGl(cmil−cmjl+δ(vil(z)−vjl(ξ)))−Gl(cmil−cmjl−δvjl(ξ))dξ−δvil(z)Nl∑j=1∫JjlSl(cmil−cmjl+δ(λil−vjl(ξ)))dξ+αlNh∑j=1∫JjhH(cmil−cmjh+δ(vil(z)−vjh(ξ)))−H(cmil−cmjh−δvjh(ξ))dξ−δvil(z)αlNh∑j=1∫JjhK(cmil−cmjh+δ(λil−vjh(ξ)))dξ],z∈Jil, | (37) |
we have that (30) reduces to the equation
| ∫JjlGl(cmil−cmjl+δ(vil(z)−vjl(ξ)))−Gl(cmil−cmjl−δvjl(ξ))dξ=[Sl(cmil−cmjl)δvil(z)+δ22S′l(cmil−cmjl)(vil(z))2+δ36S″l(cmil−cmjl)(vil(z))3]|Jjl|+∫Jjlδ32S″l(cmil−cmjl)(vjl(ξ))2vil(z)dξ+R(S‴l,δ4), | (38) |
where we used the fact that
| −δvil(z)∫JjlSl(cmil−cmjl+δ(λil−vjl(ξ)))dξ=[−Sl(cmil−cmjl)δvil(z)−δ2S′l(cmil−cmjl)λilvil(z)−δ32S″l(cmil−cmjl)(λil)2vil(z)]|Jjl|−∫Jjlδ32S″l(cmil−cmjl)(vjl(ξ))2vil(z)dξ+R(S‴l,δ4). | (39) |
Summing up the contributions in (38) to (39), we get that the self-interaction part in (37) reduces to
| δ3[δ−12S′l(cmil−cmjl)vil(z)(vil(z)−2λil)+16S″l(cmil−cmjl)((vil(z))3−3vil(z)(λil)2)]|Jjl|+R(S‴l,δ4). | (40) |
Similarly, for the cross-interaction part we obtain
| δ3[δ−12K′(cmil−cmjh)vil(z)(vil(z)−2λil)+16K″(cmil−cmjh)((vil(z))3−3vil(z)(λil)2)]|Jjh|+R(K‴,δ4). | (41) |
Putting together the contributions of (40) and (41) in the functional equation (37), we get
| Fil[p;δ](z)=(ˉzil−z)+Dil6(3vil(z)(λil)2−(vil(z))3)+δ−1Bil2vil(z)(vil(z)−2λil)+R(S‴l,K‴,δ4), | (42) |
where we used the notations introduced in (6) and (5), namely
| Dil=−Nl∑j=1S″l(cmil−cmjl)|Jjl|−αlNh∑j=1K″(cmil−cmjh)|Jjh|, |
and
| Bil=Nl∑j=1S′l(cmil−cmjl)|Jjl|+αlNh∑j=1K′(cmil−cmjh)|Jjh|. |
Note that since the values
| (ˉzil−z)+Dil6(3vil(z)(λil)2−(vil(z))3)=0,z∈Jil, | (43) |
that gives a unique solution once the value of
| Λil[p;δ]=Fil[p;δ](˜zil). | (44) |
Performing Taylor expansions similar to the ones in (38) and (39) we get that
| Λil[p;0]=(ˉzil−˜zil)+Dil3(λil)3, | (45) |
and we are now in the position to solve
| {(ˉzil−z)+Dil6(3vil(z)(λil)2−(vil(z))3)=0,(ˉzil−˜zil)+Dil3(λil)3=0. | (46) |
The second equation in (46) admits a solution once we have that
| λil=(3(˜zil−ˉzil)Dil)1/3. | (47) |
By construction
| ˉρi(x)=Diρ2((λiρ)2−(x−cmiρ)2)1Iiρ(x),i=1,…,Nρ,ˉηh(x)=Dhη2((λhη)2−(x−cmhη)2)1Ihη(x),h=1,…,Nη, | (48) |
where the intervals
| likk=cmikk−λikk,rikk=cmikk+λikk,ik=1,…,Nk,k=ρ,η. |
We are now ready to reformulate (36) as a functional equation on a proper Banach space. Consider the spaces
| Ωil={v∈L∞([ˉzil,˜zil))|vincreasing,v(ˉzil)=0},i=1,…,Nl,l∈{ρ,η}, | (49) |
endowed with the
| Ωl=Nl×i=1Ωil,forl∈{ρ,η}. |
We now introduce the space
| Ω=Ωρ×RNρ×Ωη×RNη, | (50) |
with elements
| |||ω|||=Nρ∑i=1(‖viρ‖L∞+|λiρ|)+Nη∑i=1(‖viη‖L∞+|λiη|). | (51) |
For
| |||ω|||γ=|||ω|||+∑l∈{ρ,η}Nl∑i=1supz∈˜Jil|λil−vil(z)|(˜zil−z)γ, | (52) |
and set
| T[ω;δ](z):=(Fρ[ω;δ](z)Λρ[ω;δ]Fη[ω;δ](z)Λη[ω;δ]), | (53) |
where for
| Fl[ω;δ](z)=(F1l[ω;δ](z),…,FNll[ω;δ](z)),Λl[ω;δ](z):=(Λ1l[ω;δ],…,ΛNll[ω;δ]). | (54) |
The operator
| DT[ω;δ]=(DvρFρ(δ)DλρFρ(δ)DvηFρ(δ)DληFρ(δ)DvρΛρ(δ)DλρΛρ(δ)DvηΛρ(δ)DληΛρ(δ)DvρFη(δ)DλρFη(δ)DvηFη(δ)DληFη(δ)DvρΛη(δ)DλρΛη(δ)DvηΛη(δ)DληΛη(δ)), | (55) |
where the components are actually matrices defined by
| DvhFl(δ)=(∂Fil[ω;δ]∂vjh(νjh))Nl,Nhi,j=1,DλhFl(δ)=(∂Fil[ω;δ]∂λjh(ajh))Nl,Nhi,j=1DvhΛl(δ)=(∂Λil[ω;δ]∂vjh(νjh))Nl,Nhi,j=1,DλhΛl(δ)=(∂Λil[ω;δ]∂λjh(ajh))Nl,Nhi,j=1, |
where
| ∂Fil[ω;δ]∂vil(νil)=−δ−2∫Jilνil(ξ)[Sl(δ(vil(z)−vil(ξ)))−δvil(z)S′l(δ(λil−vil(ξ)))−Sl(−δvil(ξ))]dξ+δ−2νil(z)Nl∑j=1∫Jjl[Sl(cmil−cmjl+δ(vil(z)−vjl(ξ)))−Sl(cmil−cmjl+δ(λil−vjl(ξ)))]dξ+δ−2νil(z)αlNh∑j=1∫Jjh[K(cmil−cmjh+δ(vil(z)−vjh(ξ)))−K(cmil−cmjh+δ(λil−vjh(ξ)))]dξ. |
A Taylor expansion around
| ∂Fil[ω;0]∂vil(νil)=Dil2((λil)2−(vil(z))2)νil(z). |
Concerning the other terms in
| ∂Fil[ω;δ]∂vjl(νjl)=−δ−2Nl∑j=1∫Jjlνjl(ξ)[Sl(cmil−cmjl+δ(vil(z)−vjl(ξ)))−Sl((cmil−cmjl−δvjl(ξ))−δvil(z)S′l(cmil−cmjl+δ(λil−vjl(ξ)))]dξ, |
that all vanish in the limit
| ∂Fil[ω;δ]∂λil(ail)=−δ−1vil(z)ail[Nl∑j=1∫JjlS′l(cmil−cmjl+δ(λil−vjl(ξ)))dξ+αlNh∑j=1∫JjhK′(cmil−cmjh+δ(λil−vjh(ξ)))dξ]. |
Then, Taylor expansion w.r.t.
| ∂Fil[ω;0]∂λil(ail)=Dilλilvil(z)ail. |
Since all the entrances in the matrix
| ∂Fil[ω;δ]∂vjh(νjh)=−δ−2αlNh∑j=1∫Jjhνjh(ξ)[K(cmil−cmjh+δ(vil(z)−vjh(ξ)))−K(cmil−cmjh−δvjh(ξ))−δvil(z)K′(cmil−cmjh+δ(λil−vjh(ξ)))]dξ, |
that vanish in the limit
| ∂Λil[ω;δ]∂vjl(νjl)=−δ−2Nl∑j=1∫Jjlνjl(ξ)[Sl(cmil−cmjl+δ(λil(z)−vjl(ξ)))−Sl((cmil−cmjl−δvjl(ξ))−δλilS′l(cmil−cmjl+δ(λil−vjl(ξ)))]dξ. |
The terms in
| ∂Λil[ω;δ]∂vjh(νjh)=−δ−2αlNh∑j=1∫Jjhνjh(ξ)[K(cmil−cmjh+δ(λil−vjh(ξ)))−K(cmil−cmjh−δvjh(ξ))−δλilK′(cmil−cmjh+δ(λil−vjh(ξ)))]dξ, |
and the usual Taylor expansions around
| ∂Λil[ω;δ]∂λil(ail)=−δ−1ailNl∑j=1∫JjlλilS′l(cmil−cmjl+δ(λil−vjl(ξ)))dξ−δ−1ailαlNh∑j=1∫JjhλilK′l(cmil−cmjh+δ(λil−vjh(ξ)))dξ. |
The last Taylor expansion gives
| ∂Λil[ω;0]∂λil(ail)=Dil(λil)2ail. |
We have proved that
| DT[ω;0]=(El1dg(Diρλiρviρaiρ)000dg(Diρ(λiρ)2aiρ)0000El2dg(Diηλiηviηaiη)000dg(Diη(λiη)2aiη)), | (56) |
where
| El1=dg(Diρ2((λiρ)2−(viρ)2)νiρ),El2=dg(Diη2((λiη)2−(viη)2)νiη), |
and
Lemma 3.1. For
Proof. Thanks to the previous computations it is easy to see that
| sup|||ω|||1/2≤11(˜zil−z)|∂Fil∂vil[⋅,δ](νil)−∂Λil∂vil[⋅;δ](νil)−(∂Fil∂vil[⋅;0](νil)−∂Λil∂vil[⋅;0](νil))+∂Fil∂λil[⋅,δ](ail)−∂Λil∂λil[⋅;δ](ail)−(∂Fil∂λil[⋅;0](ail)−∂Λil∂λil[⋅;0](ail))+∂Fil∂vjh[⋅,δ](νjh)−∂Λil∂vjh[⋅;δ](νjh)−(∂Fil∂vjh[⋅;0](νjh)−∂Λil∂vjh[⋅;0](νjh))+∂Fil∂λjh[⋅,δ](ajh)−∂Λil∂λjh[⋅;δ](ajh)−(∂Fil∂λjh[⋅;0](ajh)−∂Λil∂λjh[⋅;0](ajh))|↘0, | (57) |
as
| 1(˜zil−z)[∂Fil∂vjh[⋅,δ](νjh)−∂Λil∂vjh[⋅;δ](νjh)−(∂Fil∂vjh[⋅;0](νjh)−∂Λil∂vjh[⋅;0](νjh))]=−αl(vil(z)−λil)2˜zil−zNh∑j=1∫JjhK″(cmil−cmjh+δ(λil−vjh(ξ)))νjh(ξ)2dξ−δαl(vil(z)−λil)3˜zil−zNh∑j=1∫JjhK‴(˜x(ξ))νjh(ξ)6dξ=−δαl(vil(z)−λil)2˜zil−zNh∑j=1∫JjhK‴(ˉx(ξ))(λil−vjh(ξ))νjh(ξ)2dξ−δαl(vil(z)−λil)3˜zil−zNh∑j=1∫JjhK‴(˜x(ξ))νjh(ξ)6dξ.=−αl((vil(z)−λil)2˜zil−z+(vil(z)−λil)3˜zil−z)O(δ), |
where in the first equality we did a Taylor expansion around the point
| 1(˜zil−z)[∂Fil∂λjh[⋅,δ](ajh)−∂Λil∂λjh[⋅;δ](ajh)−(∂Fil∂λjh[⋅;0](ajh)−∂Λil∂λjh[⋅;0](ajh))]=0. |
The first two rows in (57) can be treated as follows,
| 1(˜zil−z)[∂Fil∂vil[⋅,δ](νil)−∂Λil∂vil[⋅;δ](νil)−(∂Fil∂vil[⋅;0](νil)−∂Λil∂vil[⋅;0](νil))+∂Fil∂λil[⋅,δ](ail)−∂Λil∂λil[⋅;δ](ail)−(∂Fil∂λil[⋅;0](ail)−∂Λil∂λil[⋅;0](ail))]=δ(˜zil−z)[Nl∑j=1∫Jjlδ−2(vil(z)−λil)(νil(z)−ail)S′l(cmil−cmjl+δ(λil−vjl(ξ)))+δ−112(vil(z)−λil)2(νil(z)−νjl(ξ))S″l(cmil−cmjl+δ(λil−vjl(ξ)))+16(vil(z)−λil)3(νil(z)−νjl(ξ))S‴l(˜x1(ξ))dξ+αlNh∑j=1∫Jjhδ−2(vil(z)−λil)(νil(z)−ail)K′(cmil−cmjh+δ(λil−vjh(ξ)))+δ−112(vil(z)−λil)2(νil(z)−νjl(ξ))K″(cmil−cmjh+δ(λil−vjh(ξ)))+16(vil(z)−λil)3(νil(z)−νjl(ξ))K‴(˜x2(ξ))dξ]=(2(νil(z)−ail)(vil(z)−λil)(˜zil−z)+(2νil(z)−1)((vil(z)−λil)3(˜zil−z)+(vil(z)−λil)2(˜zil−z)))O(δ). |
Since the functions
| λil−vil(z)(˜zil−z)1/2, |
are uniformly bounded in
Lemma 3.2. For any
Proof. Given
| DT[ω0;0]ω=w, | (58) |
admits a unique solution
| ||ω||1/2≤C||w||1. |
The determinant of the matrix in (56) is given by
| detDT=(Nρ∏i=1(Diρ)22((λiρ)2−(viρ)2)(λiρ)2)⋅(Nη∏i=1(Diη)22((λiη)2−(viη)2)(λiη)2), | (59) |
that is always different from zero under the condition
| νil(z)=−2σil(z)Dil((vil(z))2−(λil)2)+2λilvil(z)ail(vil(z))2−(λil)2,ail=kilDil(λil)2, |
that implies
| ail−νil(z)(˜zil−z)1/2, |
is uniformly bounded since
We are now in the position of proving the main result of the paper, namely Theorem 1.1, that we recall below for convenience.
Theorem 3.1. Assume that
(i)
| Bil=Nl∑j=1S′l(cmil−cmjl)zjl+αlNh∑j=1K′(cmil−cmjh)zjh=0, | (60) |
(ii) the following quantities
| Dil=−Nl∑j=1S″l(cmil−cmjl)zjl−αlNh∑j=1K″(cmil−cmjh)zjh, | (61) |
are strictly positive, for all
where
where
● each interval
●
● the solutions
| zρ=Nρ∑i=1ziρandzη=Nη∑i=1ziη, |
respectively.
Proof. Consider
| T[ω;δ](z)=0, |
admits a unique solution
| ω=(v1ρ(z),…,vNρρ(z),λ1ρ,…,λNρρ,v1η(z),…,vNηη(z),λ1η,…,λNηη), |
for
Remark 3.1 Note that conditions (ii) in Theorem 3.1 turn to be conditions on the positions of the centres of masses and on the value of
| α<mini=1,…,NηNη∑j=1S″η(cmiη−cmjη)|Jjη|Nρ∑j=1K″(cmiη−cmjρ)|Jjρ|. |
Note that the above conditions are comparable to the one we got in the proof of Section 2 using the Krein-Rutman approach.
In this section, we study numerically solutions to system (3) using two different methods, the finite volume method introduced in [12, 13] and the particles method studied in [23, 28]. We validate the results about the existence of the mixed steady state and the multiple bumps steady states. Moreover, we perform some examples to show the variation in the behaviour of the solution to system (3) under different choices of initial data and the parameter
| {∂tuρ(z)=−θ2∂z((∂zuρ(z))−2)+∫JρS′ρ(uρ(z)−uρ(ξ))dξ+αρ∫JηK′(uρ(z)−uη(ξ))dξ,z∈Jρ∂tuη(z)=−θ2∂z((∂zuη(z))−2)+∫JηS′η(uη(z)−uη(ξ))dξ+αη∫JρK′(uη(z)−uρ(ξ))dξ,z∈Jη, | (62) |
as the following: Let
| {∂tXiρ(t)=θ2N((ρi−1(t))−2−(ρi(t))−2)+1NN∑j=1S′ρ(Xiρ(t)−Xjρ(t))dξ+αρNN∑j=1K′(Xiρ(t)−Xjη(t))dξ,i=1,⋯N,∂tXiη(t)=θ2N((ηi−1(t))−2−(ηi(t))−2)+1NN∑j=1S′η(Xiη(t)−Xjη(t))dξ+αηNN∑j=1K′(Xiη(t)−Xjρ(t))dξ,i=1,⋯N, | (63) |
where the densities are reconstructed as
| {ρi(t)=1N(Xi+1l(t)−Xil(t)),i=1,⋯,N−1,ρ0(t)=0,ρN(t)=0, | (64) |
and the same for the
| ∫Xi+1ρ,0Xiρ,0ρ(t=0)dX=1N−1,i=1,⋯,N−1. |
The second method we use is the finite volume method which introduced in [12] and extended to systems in [13], that consists in a
| ˜ρi(t):=1Δx∫Uiρ(x,t)dx,˜ηi(t):=1Δx∫Uiη(x,t)dx, |
the averages of the solutions
| {d˜ρi(t)dt=−Fρi+12(t)−Fρi−12(t)Δx,d˜ηi(t)dt=−Fηi+12(t)−Fηi−12(t)Δx, | (65) |
where the numerical flux
| Fρi+12=max(ϑi+1ρ,0)[˜ρi+Δx2(ρx)i]+min(ϑi+1ρ,0)[˜ρi−Δx2(ρx)i], | (66) |
where
| ϑi+1ρ=−θΔx(˜ρi+1−˜ρi)−∑j˜ρj(Sρ(xi+1−xj)−Sρ(xi−xj))−αρ∑j˜ηj(K(xi+1−xj)−K(xi−xj)), | (67) |
and
| (ρx)i=minmod(2˜ρi+1−˜ρiΔx,˜ρi+1−˜ρi−12Δx,2˜ρi−˜ρi−1Δx). | (68) |
The minmod limiter in (68) has the following definition
| minmod(a1,a2,…):={min(a1,a2,…),ifai>0∀imax(a1,a2,…),ifai<0∀i0,otherwise. | (69) |
We have the same as the above expresions for
In all the simulations below, we will fix the kernels as a normalised Gaussian potentials
| Sρ(x)=Sη(x)=K(x)=1√πe−x2, |
that are under the assumptions on the kernels (A1), (A2) and (A3). This choice helps us in better understanding the variation in the behavior of the solutions w.r.t. the change in the initial data and the parameter
● in the first row steady states are plotted at the level of density, on the l.h.s. we compare the two methods illustrated above, while on the r.h.s. we show the evolution by the finite volume method,
● in the second row we plot the particles paths for both species obtained with the particles method,
● in the last row we show the pseudo inverse functions corresponding to the steady state densities.
The last example we present shows an interesting traveling waves-type evolution.
The first example is devoted to validating existence of mixed steady state and separated steady state. By choosing the initial data
| (70) |
and fixing
| (71) |
with the same
We then, test two cases where we validate the existence of steady states of more bumps. Let us fix
| (72) |
as initial data and we take
| (73) |
and
Finally, in this example, we detect existence of traveling waves. Indeed, by choosing initial data as
| (74) |
| 1. | Erin Ellefsen, Nancy Rodríguez, Nonlocal Mechanistic Models in Ecology: Numerical Methods and Parameter Inferences, 2023, 13, 2076-3417, 10598, 10.3390/app131910598 | |
| 2. | Swadesh Pal, Roderick Melnik, Nonlocal Models in Biology and Life Sciences: Sources, Developments, and Applications, 2025, 15710645, 10.1016/j.plrev.2025.02.005 |
A possible example of a stationary solution to (3) with
Example of mixed stationary state. Note that by symmetry
An example of a separated stationary state
In this figure, a mixed steady state is plotted by using initial data given by (70),
A separated steady state is presented in this figure. Initial data are given by (71). The parameters are
This figure shows how from the initial densities
A steady state of four bumps is showed in this figure starting from initial data as in (72) with
Starting from initial data as in (73) with
This last figure shows a possible existence of traveling waves by choosing initial data as in (74),