On the role of tumor heterogeneity for optimal cancer chemotherapy

1.   Introduction

We review and discuss some results that can be obtained about the structure of optimal chemotherapy protocols from mathematical models. This question has been addressed at least since the 1970s and 1980s starting with some of the fundamental work by Eisen [13], Swierniak and Kimmel [23,51] and Swan [49,50]. In most of this early work, it is implicitly assumed that the tumor population is homogeneous and consists of chemotherapeutically sensitive cells. Under this assumption it is natural-and this is generally borne out by all these early models as well-to give chemotherapy as early as possible and with as much force as possible. Medically this corresponds to the so-called maximum tolerated dose (MTD) paradigm [47] which still is at the heart of many chemotherapy schedules for the initial induction phase of chemotherapy. MTD is simply "the highest dose of a drug or treatment that does not cause unacceptable side effects" [1]. Generally, the higher the dose, the more harm is caused to the tumor (although this relation, and especially for high doses, is not linear). Since what matters is the marginal benefit, this reasoning, however, critically relies on the assumption of a homogeneous chemosensitive tumor cell population. Heterogeneity blurs this simple understanding.

Genetic instability of cancer cells [16,17] coupled with faster mutation rates and epigenetic abnormalities foster the creation of diverse sub-populations of tumor cells which have widely varying phenotypes and chemotherapeutic sensitivities. In addition, growing tumors often exhibit considerable evolutionary ability to enhance cell survival in an environment that is becoming hostile. According to the Norton-Simon hypothesis [36,37], generally faster replicating cell lines are more susceptible to a chemotherapeutic attack while slower growing ones are more resistant. One widely accepted explanation for this feature is that resistance is achieved through pathways that use up more energy which thus cannot be used for proliferation [14]. Under traditional MTD type chemotherapy, the more sensitive populations will be eradicated allowing the resistant populations to become dominant possibly leading to full resistance and failure of the therapy. Naturally, this world view is a bit oversimplified as the specifics depend on such features as the relative growth rates of the sub-populations. For example, if the resistant population grows exceedingly slow, for all practical and also mathematical purposes, it can be ignored. But it also matters whether drug resistance is intrinsic (i.e., inherent in the sense that there simply is no treatment for it yet) or whether it is acquired. In the later case, interruptions of treatment, so-called drug holidays, may allow for resensitizations to take place which then enable repeated treatments with high doses (rechallenge therapy [57]). Such considerations, combined with ideas about evolution and competition between cell populations [15] have led to the consideration of various alternative chemotherapy dosing schemes in medical practice, most prominently metronomic [2,22], chemo-switch [39] and adaptive chemotherapy [14,15].

Metronomic chemotherapy is "the chronic administration of chemotherapy at relatively low, minimally toxic doses on a frequent schedule of administration, at close regular intervals, with no prolonged drug-free breaks" [2]. It is hoped that by avoiding the limiting toxic side effects of high dose therapy the overall effect of therapy can be improved because of the greatly extended time horizon over which drugs can be given when compared with repeated MTD doses: "concentration $ \times $ time" matters [60]. Another possible benefit of low-dose schedules is the potential of so-to-speak "crowding" the more dangerous resistant cell populations through the relatively more harmless (since chemosensitive) faster growing population. This, and similar evolutionary aspects [8] based on the view of the tumor as an adaptive ecosystem [14] form the basis for adaptive chemotherapy calling for dosing stratagems that "evolve in response to the temporal and spatial variability of [the] tumor microenvironment and cellular phenotype" [15]. In these strategies, the objective-rather than eradicating the tumor-then becomes to make cancer chronic: keep the resistant cell population in check by managing the sensitive population the right way. Obviously, in reality this is a risky and difficult endeavor-primum non nocere.

Mathematical models, on the other hand, can be freely used to explore such ideas. There exist an abundance of mathematical models for chemotherapy under tumor heterogeneity ranging from rudimentary models that just distinguish a small number of sub-populations (e.g., Hahnfeldt et al. [21], Ledzewicz and Schättler [27,29,31]) to models with increasing degrees of resistance (e.g., Swierniak et al. [55,56] or Wang and Schättler [58]) and even a continuum of traits (e.g., Lorz et al. [34,35], Billy and Clairambault [3], Delitalia and Lorenzi [8,10], Lavi, Green et al. [19,24]). Recurrent conclusions that can be drawn from a variety of these models are that, indeed, if conditions are right (i.e., under assumptions on the relative growth rates of the sub-populations and about the effectiveness of the drugs) it is possible to limit cancer growth through a judicious choice of drug administration schedules. If, however, there exists an intrinsically resistant subpopulation which has a significant growth rate, then it is rather difficult, and plainly impossible in some cases to prevent the drug resistant strain from becoming dominant. In such a situation, the only mathematically feasible control problem becomes to delay the onset, respectively, the emerging dominance of the resistant populations.

While it appears rather difficult to develop drugs that will be effective for tumor populations with ever increasing degrees of heterogeneity, for such a case hope may lie with different therapies. One of the hallmarks of cancer therapies is that the body's immune system does not recognize tumor cells as 'foreign' and thus only elicits no or at best a weak and ineffective immune response. With increasing mutations and a greater variety of genetic changes present in tumor cells, however, it becomes more likely that such a response will be provoked in the first place, i.e., that the tumor becomes immunogenic, or that such a response is stronger. Simply put, the chances that cells will be recognized as hostile increases (also, see [9]). The hope then is that, even if the innate immune system response is initiated by specific mutations, its reaction may be a broader attack on the full tumor. In fact, immunotherapies have proven themselves to be quite effective for cancers like melanoma whose cells exhibit a great variety of mutations.

In this paper, we discuss various conclusions that can be drawn about the structure of optimal chemotherapy protocols from an analysis of mathematical models done in our work and we relate the results to some current efforts in medical practice. We review existing models and summarize their findings, but also include some new results in the context of mutations.

2.   MTD therapies: Homogeneous chemosensitive tumor populations

We briefly describe a mathematical model for chemotherapy based on Swierniak's models [52] that can be used as a common framework for both homogeneous and heterogeneous cell populations. In this section, however, we only discuss it as a framework for cell-cycle specific models for cancer chemotherapy of homogeneous chemosensitive tumors. The mathematical model divides the state into compartments which cluster cells in phases of the cell cycle (and, more generally, could represent cells of certain phenotypes in specific cell-cycle compartments). The state space is the first orthant $ \mathbb{P} $ of vectors with positive entries in $ \mathbb{R}^{n} $ and $ N = (N_{1},\ldots,N_{n})^{T} $ denotes the state with $ N_{i} $ the average number of cancer cells in the ith compartment, $ i = 1,\ldots,n $. The control is a vector $ u = (u_{1},\ldots,u_{m})^{T} $ with $ u_{i} $ denoting the concentrations of various drugs in the blood stream. For the sake of simplicity of exposition, in this paper we do not consider pharmacokinetic aspects of drug delivery and identify the drug dose rates with these concentrations. The control set $ U $ thus is a compact $ m $-dimensional interval of the form $ U = [0,u_{1}^{\max}]\times\cdots\times\lbrack0,u_{m}^{\max}] $ with each $ u_{j}^{\max} $ representing the maximum dose rate/concentration and the lower limit $ 0 $ representing that no drugs are administered. Admissible controls are Lebesgue-measurable (respectively, piecewise continuous) functions $ u $ that take values in the control set, $ u:[0,T]\rightarrow U $. The dynamics consists of balance equations (which take the form of a bilinear system) that describe the inflows and outflows between the various compartments and have the general form

with $ A $ and the $ B_{j} $ constant matrices of appropriate dimensions that describe the transitions between the various compartments. Under appropriate conditions on these matrices (which will be satisfied if the modeling is done properly), it is easy to see that the state space $ \mathbb{P} $ is positively invariant under the dynamics, i.e., for any admissible control, the solution to (1) exists for all times $ t\geq 0 $ and remains in $ \mathbb{P} $.

The problem of cancer chemotherapy can then be formulated as an optimal control problem once an appropriate criterion to be minimized is imposed on this dynamics. While there exist many alternatives to do this, we would like to stress that for a meaningful interpretation of side effects and total drug dose, it seems to be imperative to include the controls as linear terms in this formulation. Thus, with $ r = (r_{1},\ldots,r_{n}) $ and $ q = (q_{1},\ldots,q_{n}) $ $ n $-dimensional row-vectors of positive numbers and $ s = (s_{1},\ldots,s_{m}) $ a nonzero $ m $-dimensional row-vector of non-negative numbers, we define the objective in the following form:

The term $ su = \sum_{i = j}^{m}s_{j}u_{j} $ in the integral is a weighted average of the amounts of the various drugs given and the coefficients $ s_{j} $ represent the degrees of toxicity of the drugs. Side effects generally depend on the specific agent and these differences would be reflected in the choice of these weights. Similarly, the second integral term $ qN = \sum_{i = 1}^{n}q_{i}N_{i} $ represents a weighted average of the number of cancer cells in the respective compartments during treatment and the penalty term $ rN(T) = \sum_{i = 1}^{n}r_{i}N_{i}(T) $ represents a weighted average of the number of cancer cells in the respective compartments at the end of treatment.

The formulation of the objective (2) attempts to make a reasonable compromise between minimizing the tumor kill and limiting the side effects of treatment. These are measured indirectly through a weighted average of the total amount of drugs administered. Obviously, these weights are important for the optimal solutions and a biological calibration of these weights always needs to be undertaken to obtain meaningful results. If the weights on the drugs are too small, optimal solutions will simply give drugs all the time at full dose; if the weights are too high, no drugs will be given. Generally, the weight for a strong cytotoxic (killing) agent should be significantly higher than the weight for a cytostatic (blocking) or recruiting agent. Also, if the model differentiates between compartments of drug sensitive and resistant agents (as they will be considered in Section 3), it may be advisable to use higher weights for the resistant compartments. Similarly, if one takes $ q $ too small relative to $ r $, then the emphasis is put on the terminal condition and this may lead to unacceptable behavior during the therapy interval. Thus one needs to stay aware of the fact that the weights in the objective are variables of choice.

Keeping such restrictions in mind, it can be stated that for cell-cycle specific models of homogeneous tumor cell populations, optimal controls apply cytotoxic agents in one full dose segment at the beginning of the therapy interval. Mathematically more precisely, numerous models for cancer chemotherapy with cytotoxic agents have been considered and analyzed in the work of Swierniak et al. [52,53,54] and Ledzewicz and Schättler [25,26,44] and for each of them it has been verified theoretically that optimal controls are bang-bang, i.e., alternate between full dose treatments and rest periods. Generally such statements depend on properties of the matrices $ A $ and $ B_j $, $ j = 1,\ldots,m $, in the dynamics (1) and their commutators (i.e., Lie-brackets). Then, and often for almost any reasonable choice of weights in the objective, the cytotoxic (killing) agent has exactly one switch from full dose to no dose. If other drugs are used as well in combination treatments to modulate the killing effects, e.g., cytostatic (blocking) agents, such drugs also are administered in the form of bang-bang controls, but their timing enhances the actions of the killing agent.

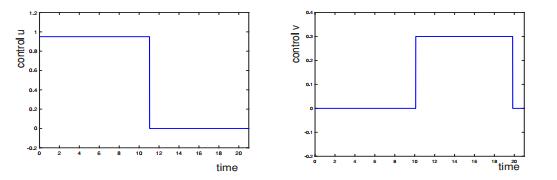
Figure 1 shows a typical example of optimal controls for a $ 3 $-compartment model with cytotoxic agent $ u $ and cytostatic agent $ v $ [32]. The objective was chosen of the form (2) and consisted of a weighted average of all components, i.e., the tumor volumes at the end of therapy, during the therapy interval and the total doses of both agents. The optimal control $ u $ starts with a full dose segment. As it would make no sense to block the flow of cells while a cytotoxic agent is active, the cytostatic agent is inactive at the beginning. It only becomes activated just prior to the termination of the cytotoxic agent and then remains active for most of the time. This simply is a second, less toxic mechanism to slow down the growth of the tumor. The cytostatic agent then is turned off before the therapy interval ends simply since, because of the delays inherent in the cell-cycle dynamics, late administration of the cytotoxic agent would not show up as improvement in reducing the tumor cell count while it would still add to the value of the objective. While the quantitative results (actual values of the switching times etc.) for a given system of course depend on the specific weights chosen in the objective, the qualitative structure of the results shown here is quite robust with respect to changes in these values.

3.   Metronomic and adaptive therapies: Heterogeneous tumor populations with a small number of traits

A bilinear dynamics of the type (1) can also be used to investigate the structure of optimal chemotherapy protocols for a heterogeneous tumor population. In the paper [21], Hahnfeldt, Folkman and Hlatky compare the effects of MTD and metronomic chemotherapy dosings (for bolus type injections) for a 2-compartment model consisting of sensitive and resistant populations. They analyze the maximum asymptotic factor reduction in tumor size in an infinite cycle of periodic therapy periods and come to the conclusion that a metronomic, regular scheduling of the drugs has better long term effects when compared with MTD bolus injections. Alternatively, minimizing an objective of the type (2), one can explore the structure of optimal protocols that minimize the tumor burden as measured by the average over one large therapy interval (e.g., see [27,28]).

For example, the dynamics for a 3-compartmental model that distinguishes between "sensitive" cells, $ S $, "partially sensitive" cells, $ P $, and "resistant" cells, $ R $, can be formulated as follows:

The labels $ S $, $ P $ and $ R $ are simply used to indicate that these three populations have different chemotherapeutic sensitivities towards a specific cytotoxic agent with $ S $ the highest and $ R $ the lowest. We assume that these sub-populations grow at net growth rates $ \alpha_{1}>\alpha_{2}>\alpha_{3} $ consistent with the "Norton-Simon hypothesis". In the model, transitions between the three compartments are allowed and these are described by the coefficients $ \sigma_X $, $ \rho_Y $ and $ \pi_Z $ with $ X,Y,Z \in \{S,P,R\} $. Thus sensitive cells may become more resistant, but also resensitizations are allowed [20] which make cells less resistant to the chemotherapeutic agent. By setting some of these parameters to zero, this can be prohibited. The effectiveness of the drug on killing the respective sub-populations are denoted by $ \varphi_{1}>\varphi_{2}>\varphi_{3}\geq 0 $ with $ \varphi_{3} = 0 $ corresponding to the situation of a fully resistant subpopulation $ R $.

If we denote the proportions of the respective populations by

a direct computation verifies that $ x $, $ y $ and $ z $ (as quotients of solutions to linear differential equations) obey Riccati differential equations and it can be shown that this dynamics has exactly one globally (within the open unit simplex) asymptotically stable equilibrium point $ (x_{\ast},y_{\ast},z_{\ast})\in\Sigma $ which defines the steady-state proportions [44,Appendix B]. Thus, given an estimate on the tumor size at the beginning of therapy, there exists a well-defined initial condition $ (S_{0},P_{0},R_{0}) = (x_{\ast},y_{\ast},z_{\ast})C_{0} $ for the dynamics. As above, we then consider the optimal control problem to minimize an objective of the type (2) with all terms present. Given the problem setting where the sensitive population will be contributing much more to the cell kill count, we assigned higher weights to the more resistant populations in order to counter balance these effects.

Contrary to the models for homogeneous populations, here optimal controls that take values in the interior of the control set are viable alternatives. It follows from the necessary conditions for optimality of the Pontryagin maximum principle [40] (for some more recent texts, see [6,7,43]) that optimal controls $ u_{\ast} $ minimize the Hamiltonian function $ H $,

pointwise over the control set along the optimal trajectory $ N_{\ast} $ and a solution $ \lambda $ (which we write as a row vector) to the adjoint equation

with terminal condition $ \lambda(T) = r $. In this case, the Hamiltonian $ H $ is linear in the control and the control set is a compact interval. If we define the switching function as

then optimal controls satisfy

while the minimization condition a priori gives no information about the optimal control $ u_{\ast}(t) $ if the switching function vanishes, $ \Phi(t) = 0 $. However, if $ \Phi $ vanishes over an open interval, then also all its derivatives on this interval vanish and this often allows to derive formulas for the optimal controls of such intervals. Such controls are called singular.

It follows from general Lie algebraic identities that the control can appear for the first time only in an even derivative when the switching function is differentiated. If this happens in the second derivative, a singular control is said to be of order one. In this case, it is a second-order necessary condition for optimality, the Legendre Clebsch condition that

If this quantity is positive, we say the strengthened Legendre-Clebsch condition holds.

Proposition 1. [29] For the compartmental model defined by equations (3)-(5), singular controls exist, are of order $ 1 $ and the strengthened Legendre-Clebsch condition for minimality is satisfied. Furthermore, the following formula for the singular control is valid:

where the commutator of the matrices $ X $ and $ Y $ is defined as $ [X,Y] = YX-XY $ (according to conventions for the Lie bracket of the associated linear vector fields).

Dividing both numerator and denominator by the total number of cancer cells, we note that the singular control actually does not depend on the values $ S $, $ P $ and $ R $, but only on the proportions $ x $, $ y $ and $ z $. In order to be admissible, the control needs to lie in the control set $ [0,u_{\max}] $.

Figure 2 shows an example of an extremal controlled trajectory starting from proportions given by the steady-state of the uncontrolled dynamics. Initially the control is given by the maximum dose rate, but then, as a certain equilibrium between the proportions of the three populations is reached, administration of the agent switches to a singular control with reduced dose rates adapting to the changed composition of the tumor. In the medical literature, such protocols have been called chemo-switch protocols [39]. But note that this lower dose rate no longer is able to shrink the total tumor size: all three subpopulations grow during the period when the singular control is administered, but at reduced rates. This example illustrates that, as differing chemotherapeutic sensitivities come into play, with time lower dose rates become the better alternative to MTD protocols.

We note that the analysis of the multi-input scenario corresponding to combination treatments with different drugs would be an interesting and relevant extension of this work as in such cases drug holidays indeed have shown to be effective in resensitizing sub-populations that have acquired drug resistance [57]. However, incorporating such effects would also require to make the transition rates in the dynamics to be drug dependent. From the mathematical perspective, additional difficulties will arise as now controls might be simultaneously singular. Necessary conditions for optimality such as the Goh condition also exist for such cases.

4.   Heterogeneous tumor populations with a large number of traits

Some cancers, like melanoma, are characterized by a large number of mutations that can easily go into the hundreds, even thousands. Aside from progressive mutations, a second key reason for the emergence of cellular heterogeneity and drug resistance in cancers of all types are epigenetic abnormalities, i.e., mistakes in the control mechanisms that govern gene expression patterns [12]. This is important from a therapy perspective since reversing such abnormalities appears to be more promising than correcting for mutations. Given such a diversity, it therefore makes sense to also consider distributed mathematical models for phenotypic heterogeneity and drug resistance in tumors that allow for a continuum of possible traits. Such models have been formulated by Lorz, Lorenzi, Clairambault et al. [34,35] and are also considered in the work of Billy and Clairambault [3] and Delitalia and Lorenzi [8,10]. Lavi, Greene et al. [19,24] consider such models as a means to explain the roles played by increasing cell densities and mutations in the emergence of specific traits that become dominant. We briefly recall their formulation.

In the model, a continuum of possible traits/resistance levels $ x $, $ x\in \lbrack 0,1] $, is considered. Let $ n(t,x) $ denote the population density of cells with trait $ x $ at time $ t $ and let $ \bar{N}(t) = \int_{0}^{1}n(t,x)dx $ denote the total number of cancer cells at time $ t $. The time evolution of traits is modelled as

with trait specific replication rates $ r $ and natural death rates $ \mu $. With increasing cell densities, i.e., with increasing $ \bar{N}(t) $, the replication rates actually decrease and the apoptosis rates will increase [18]. These effects are incorporated into the model through a strictly monotonically increasing function $ G $ which arises from a normalization of such effects and subsequent reparameterization of the original time scale $ t $ in the form $ \tau = \tau(t) $ used in (12). The model also includes mutations from one trait to another with $ p(x|y) $ denoting the transition density from trait $ y $ into trait $ x $. For simplicity, it is assumed that a fixed fraction $ \theta $, $ \theta \in (0,1) $, of cells mutate regardless of the originating trait $ y $. This then reduces the reproduction rate $ r $ by $ \theta $ and the total inflow of all mutating cells into $ x $ is given by $ \theta \int_{0}^{1}p(x|y)r(y)n(\tau ,y)dy $. The net effect of the mutations on the growth of the total population is zero and growth of the total population is described by the following differential equation

The incorporation of cell densities, i.e., the addition of the $ G $-term in the dynamics, induces a logistic structure that keeps the total tumor volume bounded. Specifically, we have the following result for the uncontrolled system (c.f., [44,Prop. 3.1.2]):

Proposition 2. Let

and suppose the function $ G:(0,\infty)\rightarrow(0,\infty) $, $ N\mapsto G(N) $, is strictly increasing and satisfies $ \lim_{t \rightarrow \infty} G_{t}>G_{\ast} $. Then there exists a unique population level $ N_{\ast} $ such that $ G(N_{\ast}) = G_{\ast} $ and the total tumor population $ N $ stabilizes at this level in the sense that $ \lim\sup_{\tau\rightarrow\infty}N(\tau) = N_{\ast} $.

Drug treatment can be incorporated into equations (12) and (13) by subtracting trait dependent killing terms. If one considers constant controls, one may model the effects of such terms by still subtracting $ c(x)n(\tau ,x) $ in equation (12) or one could take the point of view that such a term is already taken into account in the trait dependent replication rate $ r(x) $. In these models, and both with or without treatment, as $ \tau \rightarrow \infty $, certain traits $ x $ become dominant. In the absence of mutations ($ \theta = 0 $), it is not difficult to see that phenotypes will concentrate in the long run on specific levels (converge to Dirac distributions) [38] while in the presence of mutations generally some distributions around such Dirac masses appear [19], although for specific simple forms of the function $ G $ Dirac masses may still arise [5].

Here, rather than using a linear log-kill term, we consider a Michealis-Menten type pharmacodynamic model of the form

where $ UC_{50} $ denotes the concentration at which the drug has 50% effect. For simplicity, we also assume $ UC_{50} $ is the same for all traits. (It could easily be made trait dependent in the model, especially if only numerical computations are made, but it would be quite difficult to measure such quantities in reality. Any data would give an average of these values.) An important observation regarding treatment is that although the killing coefficient $ c $ is trait-dependent, the concentration of the agent-and this is the meaning of the control variable-is not, i.e., we have $ u = u(\tau) $, not $ u = u(\tau,x) $.

Optimal control problems of this type are inherently difficult as the aim is to control a large number of distinct cell populations by means of a what in reality are a very small number of controls (the concentrations of just a few drugs, maybe 1 to 4) giving rise to the notion of multi-targeted optimal control problems: a large number of variables needs to be controlled with a small number of inputs. Mathematically, allowing for a continuum of traits in the model gives the problem a distributed aspect and the resulting optimization problem becomes non-standard and of great complexity. This is also attested to by the theoretical analysis given by Pouchol et al. [41] who considered optimal control problems for such systems determined by phenotype-structured equations.

In our work [58], we have taken the approach to approximate this structure by a finite-dimensional model, but with a potentially large dimension. If we discretize the traits and again denote the state by the vector $ N = (N_1, \ldots, N_n)^T $, the dynamics (12) takes the form

with $ C $ and $ M $ diagonal matrices,

and

Using the same type of objective as before, for a fixed terminal time $ T $ we then want to minimize the objective

over all Lebesgue measurable functions $ u:[0,T]\rightarrow\lbrack0,u_{\max}] $ subject to the dynamics (15).

Figure 3 below gives, for various mutation rates $ \theta $, examples of numerically computed optimal controls. We used $ n = 21 $ states corresponding to the levels $ x_i = \frac{i-1}{20} $, $ i = 1, \ldots, 21 $, and the replication rates $ r $ and cytotoxic killing parameter $ \varphi $ are the values of the functions

evaluated at these nodes; we kept the death rate constant, $ \mu \equiv 0.50 $. For the transition probabilities $ p(x|y) $ a modified Gaussian kernel of the form

with variance $ \sigma^2 = 3 $ and normalizing constant $ k(y) $ was used. Also, the control is normalized in terms of its $ UC_{50} $ concentration, i.e., $ UC_{50} = 1 $, and the control limit is $ u_{\max} = 3 $, i.e., up to three times the $ UC_{50} $ value. The weights in the objective $ J $ were $ \alpha = (1, \ldots,1) $, $ \beta = 500\alpha $ and $ \gamma = 5000 $. In all the calculations we chose the initial distribution of cells over the traits to be uniform with value $ n(0,x)\equiv \frac{200}{21} $.

The top row of Fig. 3 shows the optimal controls coded with different colors for different mutation rates $ \theta $, the middle row shows the corresponding evolution of the total tumor volume $ \bar{N} $ and the bottom row shows the profiles $ n(20,x) $ at the terminal time $ T = 20 $. Because of the change in the pharmacodynamic model to (14), in this problem formulation optimal controls are continuous [59] more in line with an interpretation of the controls as concentrations while optimal controls for a linear log-kill model are discontinuous more in line with an interpretation of the controls as dose rates. Note that each solution again is of the chemo-switch type: after an initial period of full dose therapy, the dose rates drop and eventually reach zero; all controls end with a brief period of no dose treatment.

This particular simulation provides only a snapshot of one specific scenario to illustrate some of the comments made above. The bottom figure shows the emergence of a dominant trait. There is only a small group of traits located around $ x = 0.5 $ that is resistant while other traits are sensitive. The replication rate is highest for $ x = 0 $ and then monotonically decreases over the traits, but the killing coefficient follows a similar characteristic. In the net effect, traits for low or large $ x $ values can be eradicated, but for $ x = 0.5 $ this is not possible. A high rate of transitions between the traits, possibly due to epigenetic interventions, is actually beneficial. The reason simply is that these change the more resistant trait into sensitive traits and overall this turns out to be beneficial. Indeed, in this scenario, the least amount of drug is given with the highest mutation rate considered and the best overall result in terms of the total tumor volume is achieved in this case. The reason is that so-to-speak 'bad' traits are constantly changed into 'good' traits which then can be more effectively killed by the agent. Clearly, if mutations are not reversible (as it is implicitly assumed by using a Gaussian kernel to model $ p(x|y) $) this will change. We emphasize that this is just a simulation of one possible scenario to show effects that mutations can have in the mathematical model, both positive and negative. Clearly, if the mutations are not symmetric and have the tendency to move from 'good' to 'bad', the results will look very different. Indeed, as the graphs for $ \theta = 0 $ (no mutations) show, given the relative growth rates and assumed effectiveness of the drug in this case, the resistant population persists and eventually becomes the dominant one, no matter what the control does.

5.   Immunogenic tumors and immunotherapies

Once heterogeneity in tumor cells increases and cells become resistant, the attempt to develop drugs that could deal with each and every possibility becomes futile (e.g., because of exorbitant costs connected with drug development) and it appears that the answer to treating strongly heterogeneous tumors must lie elsewhere. This may be immunotherapies. As abnormalities accumulate, it simply becomes more likely that either the innate immune system recognizes the tumor cells as foreign or that it becomes easier to teach the immune system through outside intervention that these cells are foreign and thus elicit a strong reaction of the immune system. In principle, as with chemotherapies, it may happen that the immune system only reacts to specific mutations which will selectively be killed (immuno-editing [11,45]), but the hope is that the immune reaction will be more systemic and attack the full tumor.

There have been a number of mathematical models that analyze tumor immune interactions starting with the largely influential model by Stepanova [48]. In that model, the main features of tumor immune system interactions are aggregated into just two variables, the tumor volume, $ x $, and the immunocompetent cell densities, $ y $, a non-dimensional, order of magnitude quantity related to various types of immune cells ($ T $-cells) activated during the immune reaction. The basic structure of the model is as follows

with $ F $ a generic growth function and all Greek letters constant coefficients which model the most essential aspects of tumor immune interactions. Most importantly, for small tumors the immune system is stimulated by the anti-tumor antigen which is assumed to be proportional to the tumor volume $ x $ while large tumors suppress the activity of the immune system. These features are expressed through the inclusion of the term $ -\beta x^{2} $ so that $ 1/\beta $ corresponds to a threshold beyond which the immunological system becomes depressed by the growing tumor. The coefficients $ \mu_{I} $ and $ \beta $ are used to calibrate these interactions and in the product with $ y $ collectively describe a state-dependent influence of the cancer cells on the stimulation of the immune system.

Precisely because of its simplicity-a few parameters incorporate many medically important features-the underlying equations have been widely accepted as a basic model which, despite its simplicity, accurately describes essential aspects of tumor immune system interactions. Depending on the parameter values, there exist three possibilities. The dynamics can have a unique globally asymptotically equilibrium point with small tumor volumes, the benign situation, in which the immune system simply is able to control the disease. On the other side of the spectrum lies the scenario when there still exists a unique globally asymptotically equilibrium point, but now with large tumor volumes, the malignant case, when even outside intervention can only move this equilibrium point to lower values that may still be lethal. The third scenario is the medically relevant one and it lies in between these extremes: the dynamics is multi-stable and the system has both a locally asymptotically stable microscopic and macroscopic equilibrium point as well as an unstable saddle point. The tumor volumes are small and the immuno-competent cell densities are upregulated for the microscopic equilibrium point while they are large, almost at their carrying capacity, with depressed immuno-competent cell densities at the macroscopic equilibrium point. Both equilibria are locally asymptotically stable and their regions of attraction are separated by the stable manifold of the saddle which forms the common boundary of these regions. Figure 4 gives a characteristic illustrative example of this structure.

Given the bi-stable character of the underlying dynamics, now the control problem becomes to move the system-through therapy-back into the region of attraction of the microscopic equilibrium point. Note that there is no need to steer the system into the benign equilibrium point itself as this point is locally asymptotically stable. Once the state of the system lies within its region of attraction, possibly with some safe distance from its stability boundary, the system will self-regulate to this point, i.e., the immune system takes over the rest of the treatment. Such a geometric situation naturally leaves a tremendous freedom in the formulation of the objective. We found it especially useful to take relative weights for the variables $ x $ and $ y $ in the penalty term that are determined by the unstable eigenvector of the saddle point, oriented from the benign into the malignant region (as we minimize the objective). In our paper [30] we consider this optimal control problem under chemotherapy and a generic immune boost designed to upregulate the immunocompetent cell densities. For such a formulation, the typical optimal chemotherapy protocol also starts with a brief period of full dose treatment and then lowers the doses following a singular control. It is also quite common that optimal controls still give a short chemotherapy boost at maximum dose after this initial chemo-switch protocol followed by a prolonged rest period [30,33,42]. Interestingly, this is a practice not uncommon in medical treatments. Figure 5 shows a typical such administration schedule. From the mathematical side, we especially point out the paper [42] in which a full synthesis for these optimal control problems is developed.

6.   Conclusion

Progressive mutations and epigenetic abnormalities can lead to great heterogeneity in tumor cell populations which may prevent successful treatment. In this paper, at the hand of some minimally parameterised mathematical models, we discussed effects that tumor heterogeneity has on the structure of optimal chemotherapy protocols. From a practical perspective, these solutions suggest that lower, properly calibrated doses may be more advantageous as drug resistance builds up as they may also be able to control the growth of a more malignant, but slower growing drug resistant strain of cells.

Acknowledgment

The authors would like to express their thanks to two anonymous reviewers of this manuscript whose comments helped us greatly in improving the presentation of the material and who directed us to some relevant literature cited in the paper.