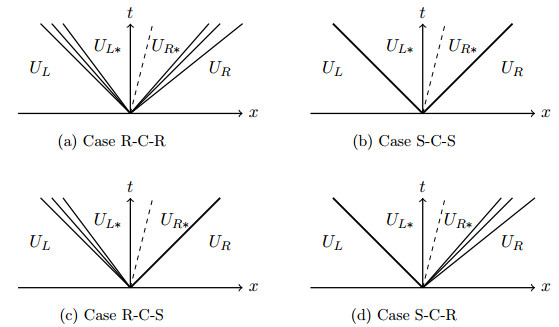
Possible wave patterns in the solution of Riemann problems for the Euler equations: shock (S), contact (C) and rarefaction (R).
.This paper is concerned with a set of novel coupling conditions for the 3× 3 one-dimensional Euler system with source terms at a junction of pipes with possibly different cross-sectional areas. Beside conservation of mass, we require the equality of the total enthalpy at the junction and that the specific entropy for pipes with outgoing flow equals the convex combination of all entropies that belong to pipes with incoming flow. Previously used coupling conditions include equality of pressure or dynamic pressure. They are restricted to the special case of a junction having only one pipe with outgoing flow direction. Recently, Reigstad [SIAM J. Appl. Math., 75:679-702,2015] showed that such pressure-based coupling conditions can produce non-physical solutions for isothermal flows through the production of mechanical energy. Our new coupling conditions ensure energy as well as entropy conservation and also apply to junctions connecting an arbitrary number of pipes with flexible flow directions. We prove the existence and uniqueness of solutions to the generalised Riemann problem at a junction in the neighbourhood of constant stationary states which belong to the subsonic region. This provides the basis for the well-posedness of the homogeneous and inhomogeneous Cauchy problems for initial data with sufficiently small total variation.
Citation: Jens Lang, Pascal Mindt. 2018: Entropy-preserving coupling conditions for one-dimensional Euler systems at junctions, Networks and Heterogeneous Media, 13(1): 177-190. doi: 10.3934/nhm.2018008
| [1] | Jens Lang, Pascal Mindt . Entropy-preserving coupling conditions for one-dimensional Euler systems at junctions. Networks and Heterogeneous Media, 2018, 13(1): 177-190. doi: 10.3934/nhm.2018008 |
| [2] | Gunhild A. Reigstad . Numerical network models and entropy principles for isothermal junction flow. Networks and Heterogeneous Media, 2014, 9(1): 65-95. doi: 10.3934/nhm.2014.9.65 |
| [3] | Gabriella Bretti, Roberto Natalini, Benedetto Piccoli . Numerical approximations of a traffic flow model on networks. Networks and Heterogeneous Media, 2006, 1(1): 57-84. doi: 10.3934/nhm.2006.1.57 |
| [4] | Martin Gugat, Alexander Keimer, Günter Leugering, Zhiqiang Wang . Analysis of a system of nonlocal conservation laws for multi-commodity flow on networks. Networks and Heterogeneous Media, 2015, 10(4): 749-785. doi: 10.3934/nhm.2015.10.749 |
| [5] | Steinar Evje, Kenneth H. Karlsen . Hyperbolic-elliptic models for well-reservoir flow. Networks and Heterogeneous Media, 2006, 1(4): 639-673. doi: 10.3934/nhm.2006.1.639 |
| [6] | Michael Herty, S. Moutari, M. Rascle . Optimization criteria for modelling intersections of vehicular traffic flow. Networks and Heterogeneous Media, 2006, 1(2): 275-294. doi: 10.3934/nhm.2006.1.275 |
| [7] | Michael Herty, Niklas Kolbe, Siegfried Müller . Central schemes for networked scalar conservation laws. Networks and Heterogeneous Media, 2023, 18(1): 310-340. doi: 10.3934/nhm.2023012 |
| [8] | Rinaldo M. Colombo, Francesca Marcellini . Coupling conditions for the $3\times 3$ Euler system. Networks and Heterogeneous Media, 2010, 5(4): 675-690. doi: 10.3934/nhm.2010.5.675 |
| [9] | Dilip Sarkar, Shridhar Kumar, Pratibhamoy Das, Higinio Ramos . Higher-order convergence analysis for interior and boundary layers in a semi-linear reaction-diffusion system networked by a $ k $-star graph with non-smooth source terms. Networks and Heterogeneous Media, 2024, 19(3): 1085-1115. doi: 10.3934/nhm.2024048 |
| [10] | Jan Friedrich, Simone Göttlich, Annika Uphoff . Conservation laws with discontinuous flux function on networks: a splitting algorithm. Networks and Heterogeneous Media, 2023, 18(1): 1-28. doi: 10.3934/nhm.2023001 |
This paper is concerned with a set of novel coupling conditions for the 3× 3 one-dimensional Euler system with source terms at a junction of pipes with possibly different cross-sectional areas. Beside conservation of mass, we require the equality of the total enthalpy at the junction and that the specific entropy for pipes with outgoing flow equals the convex combination of all entropies that belong to pipes with incoming flow. Previously used coupling conditions include equality of pressure or dynamic pressure. They are restricted to the special case of a junction having only one pipe with outgoing flow direction. Recently, Reigstad [SIAM J. Appl. Math., 75:679-702,2015] showed that such pressure-based coupling conditions can produce non-physical solutions for isothermal flows through the production of mechanical energy. Our new coupling conditions ensure energy as well as entropy conservation and also apply to junctions connecting an arbitrary number of pipes with flexible flow directions. We prove the existence and uniqueness of solutions to the generalised Riemann problem at a junction in the neighbourhood of constant stationary states which belong to the subsonic region. This provides the basis for the well-posedness of the homogeneous and inhomogeneous Cauchy problems for initial data with sufficiently small total variation.
We consider the one-dimensional polytropic Euler equations with source terms at a network with one single junction connecting
| $ \partial_t U^{(i)} + \partial_x F(U^{(i)}) = G(x, t, U^{(i)}), (x, t)\in\mathbb{R}^+\times\mathbb{R}^+, $ | (1) |
| $ U^{(i)}(x, 0) = U^{(i)}_0(x), x\in \mathbb{R}^+, $ | (2) |
for
|
$
\label{euler_flux}
U^{(i)} = (ρiρiuiEi) \;\;\mbox{and}\;\;
F(U^{(i)}) = (ρiuiρiu2i+piui(Ei+pi)) .
$
|
(3) |
Each pipe is described by a vector,
| $ E_i = \frac{p_i}{\gamma-1} + \frac12 \rho_iu_i^2 $ | (4) |
with a suitable adiabatic exponent
| $ s_i = c_v\, \ln\left( \frac{p_i}{\rho_i^\gamma}\right) \;\;\mbox{and}\;\; h_i = \frac{E_i+p_i}{\rho_i} $ | (5) |
with the specific (constant) heat capacity
The characteristic eigenvalues of the Euler equations are
| $ \lambda_1(U) = u - c, \;\; \lambda_2(U) = u, \;\; \lambda_3(U) = u + c. $ | (6) |
As usual in the literature, we also restrict our analysis to the subsonic region defined by
| $ D^+ : = \{ U = (\rho, \rho u, E)\in \overset{{}^\circ }{\mathop{\mathbb{R}}}\,^+\times\mathbb{R}\times\overset{{}^\circ }{\mathop{\mathbb{R}}}\,^+: \, \lambda_1(U) < 0 < \lambda_2(U) < \lambda_3(U)\}, $ | (7) |
| $ D^- : = \{ U = (\rho, \rho u, E)\in\overset{{}^\circ }{\mathop{\mathbb{R}}}\,^+\times\mathbb{R}\times\overset{{}^\circ }{\mathop{\mathbb{R}}}\,^+: \, \lambda_1(U) < \lambda_2(U) < 0 < \lambda_3(U)\}, $ | (8) |
with
The main challenge in network modelling is to prescribe a set of coupling conditions at the junction-pipe interfaces of the form
| $ \Phi \left( U^{(1)}(0^+, t), \ldots, U^{(N)}(0^+, t) \right) = \Pi(t), $ | (9) |
where
|
$
(M)∑Ni=1‖νi‖qi(0+,t)=0,t>0(conservation of mass), (E)∑Ni=1‖νi‖(ui(Ei+pi))(0+,t)=0,t>0(conservation of energy), (P)pi(0+,t)=p∗(t),t>0(equality of pressure), (PD)(ρiu2i+pi)(0+,t)=P∗(t),t>0(equality of dynamic pressure), (H)hi(0+,t)=h∗(t),t>0(equality of enthalpy), (S)∑Ni=1‖νi‖(qisi)(0+,t)≥0,t>0(entropy increase),
$
|
where
Colombo and Mauri [10] used coupling conditions that include mass and energy conservation at the junction, the equality of dynamic pressure as well as the entropy increase, i.e., the trace of the solution satisfies
Pressure equality,
In contrast to the isothermal flow, the situation for the compressible Euler equations with subsonic flow conditions is still unsettled and the analysis suffers from the open question: What are further physically sound coupling conditions for which well-posedness of Cauchy problems can be shown for the general case of a junction connecting
In this paper, we consider the equality of the entropy at the junction-pipe interface for pipes with outgoing flow:
| $ (S_o) \;\;\;\; s_i(0^+, t) = s^*(t), \;t > 0, \;i\in\mathbb{I}_o \;\; \mbox{(equality of outgoing entropy)}, $ | (10) |
where the coupling constant
| $ (S_i) \;\;\;\; {\displaystyle s^*(t) = \frac{1}{\sum\limits_{i\in\mathbb{I}_i}\, \|\nu_i\|q_i(0^+, t)} \, \sum\limits_{i\in\mathbb{I}_i}\, \|\nu_i\|(q_is_i)(0^+, t)} \;\;\; \mbox{(entropy mix)}. $ | (11) |
Our choice is motivated by the assumption that gas flows entering a junction mix perfectly, which was also used by Schmidt, Steinbach, and Willert [19] to derive a mixing temperature at junctions and by Gasser and Kraft [12] to formulate an equal inflow boundary condition for all densities of outgoing pipes. A direct consequence of (11) and the conservation of mass is the conservation of entropy per unit volume in smooth flows. In this case, the momentum equation in (1) can be equivalently reformulated to
| $ (S') \;\;\;\; \sum\limits_{i = 1}^{N}\, \|\nu_i\|\, (q_is_i)(0^+, t) = 0, \;t > 0 \;\;\; \mbox{(entropy conservation}). $ | (12) |
The paper is organised as follows. In Sect. 2, we formulate the generalised Riemann problem at a junction with the coupling conditions
In this section, we show the well-posedness of the coupling conditions
Let denote by
We first recall two basic definitions for generalised Riemann problems at junctions.
Definition 2.1. The Riemann problem at a junction with
|
$
∂tY(i)+∂xF(Y(i))=0,(x,t)∈R+×R+,Φ(Y(1)(0+,t),…,Y(N)(0+,t))=ˉΠ,Y(i)(x,0)=ˉY(i)0,x∈R+,
$
|
(13) |
for
Definition 2.2. A
1. There exists a constant state
|
$
\label{prob_crm}
\begin{array}{rll} \partial_t Y^{(i)} + \partial_x F(Y^{(i)}) & = & 0, \\ Y^{(i)}(x, 0) & = & \left\{ \begin{array}{ll} \bar{Y}^{(i)}_0 & \mbox{if }x > 0, \\ Y^{(i)}_\ast & \mbox{if }x < 0. \end{array}
\right.
\end{array}
$
|
(14) |
2. The state
The solution of the standard Riemann problem (14) with initial data
| $ p_\ast = p_{L\ast} = p_{R\ast} \;\;\;\mbox{ and }\;\;\; u_\ast = u_{L\ast} = u_{R\ast}. $ | (15) |
The four sought (constant) variables
| $ u_\ast = u_L-\psi(p_\ast, U_L) = u_R+\psi(p_\ast, U_R), $ | (16) |
| $ \rho_{L\ast} = \phi(p_\ast, U_L), \;\;\; \rho_{R\ast} = \phi(p_\ast, U_R), $ | (17) |
where for
|
$
\psi(p_\ast, U_k) =
{2ckγ−1((p∗pk)γ−12γ−1)if p∗≤pk (rarefaction)(p∗−pk)(1−μ2ρk(p∗+μ2pk))12if p∗>pk (shock)
$
|
(18) |
|
$
\phi(p_\ast, U_k) =
{ρk(p∗pk)1γif p∗≤pk (rarefaction)ρkp∗+μ2pkμ2p∗+pkif p∗>pk (shock)
$
|
(19) |
with
For later use, let
|
$
\mathcal{L}_1(\sigma, U_L) : = (ϕ(σ,UL)ϕ(σ,UL)(uL−ψ(σ,UL))σγ−1+12ϕ(σ,UL)(uL−ψ(σ,UL))2)
$
|
(20) |
Analogously, let
|
$
\mathcal{L}_3(\sigma, U_R) : = (ϕ(σ,UR)ϕ(σ,UR)(uR+ψ(σ,UR))σγ−1+12ϕ(σ,UR)(uR+ψ(σ,UR))2)
$
|
(21) |
We further recall the fact that for the
| $ \mathcal{L}_2(\tau, \bar{U}) : = \bar{U} + \tau \left( 1, \, \bar{u}, \, \frac{1}{2}\bar{u}^2\right)^T $ | (22) |
can be connected to
We can now express the coupling conditions for the
Due to the special parametrisation of the pipes and the restriction to subsonic flow, the contact discontinuity always travels with positive wave speed and, hence, the state
| $ \Phi\left(\left( Y^{(i)}_{L\ast}\right)_{i\in\mathbb{I}_i}, \, \left( Y^{(j)}_{L\ast}\right)_{j\in\mathbb{I}_o}\right) = \bar{\Pi}\in\mathbb{R}^d $ | (23) |
with
| $ Y^{(i)}_{L\ast} = \mathcal{L}_3(\sigma_i, \bar{Y}^{(i)}_0), \;i\in\mathbb{I}_i, \;\;\;\mbox{and}\;\;\; Y^{(j)}_{L\ast} = \mathcal{L}_2(\tau_j, \mathcal{L}_3(\sigma_j, \bar{Y}^{(j)}_0)), \;j\in\mathbb{I}_o. $ | (24) |
Let
Given constant states
|
$
\label{eq_qhs}
fi(σi,τi)=fi(L2(τi,L3(σi,ˉY(i)0))),i=1,…,No,fj(σj)=fj(L3(σj,ˉY(j)0)),j=No+1,…,N,
$
|
(25) |
with
|
$
0 = \Phi(\sigma, \tau) = (∑i=1,…,No‖νi‖qi(σi,τi)+∑j=No+1,…,N‖νj‖qj(σj)hNo+1(σNo+1)−h1(σ1,τ1)⋮hNo+1(σNo+1)−hNo(σNo,τNo)hNo+1(σNo+1)−hNo+2(σNo+2)⋮hNo+1(σNo+1)−hN(σN)s1(σ1,τ1)−s∗(σNo+1,…,σN)⋮sNo(σNo,τNo)−s∗(σNo+1,…,σN))
$
|
(26) |
with
| $ s^\ast = \frac{1}{\sum_{j = N_o+1, \ldots, N}\, \|\nu_j\|q_j(\sigma_j)} \, \sum\limits_{j = N_o+1, \ldots, N}\, \|\nu_j\|(q_js_j)(\sigma_j). $ | (27) |
The regularity of the Lax curves ensures the property
| $ Y^{(i)}_\ast = \mathcal{L}_3(\sigma_i^\ast, \bar{Y}^{(i)}_0), \;i\in\mathbb{I}_i, \;\;\mbox{and}\;\; Y^{(j)}_\ast = \mathcal{L}_2(\tau_j^\ast, \mathcal{L}_3(\sigma_j^\ast, \bar{Y}^{(j)}_0)), \;j\in\mathbb{I}_o. $ | (28) |
We note that due to the special choice in (26) energy and entropy are conserved at the junction, i.e.,
In the case
Lemma 2.3. Let
|
$
U(x, 0) = (\rho, q, E)(x, 0) = {(ˉρ1,ˉq1,ˉE1)forx>0,(ˉρ2,−ˉq2,ˉE2)forx<0.
$
|
(29) |
Then the functions
|
$
Y(1)(x,t)=(ρ1,q1,E1)(x,t)=(ρ,q,E)(x,t)ifx>0,Y(2)(x,t)=(ρ2,q2,E2)(x,t)=(ρ,−q,E)(−x,t)ifx<0
$
|
(30) |
are
Proof. Observe that the assertion holds true if the following equivalence is satisfied:
For the general case of
Theorem 2.4. Let
| $ \|\mathcal{R}^{\Phi}(\tilde{U})-\mathcal{R}^{\Phi}(\bar{U})\|_{{\boldsymbol{\rm{L}}}^\infty(\Omega)} \le K\, \sum\limits_{i = 1}^N\|\tilde{U}^{(i)}-\bar{U}^{(i)}\|. $ | (31) |
Additionally, if
| $ \|\mathcal{R}^{\Phi}_\nu(\tilde{U})-\mathcal{R}^{\Phi}_{\hat{\nu}}(\tilde{U})\|_{{\boldsymbol{\rm{L}}}^\infty(\Omega)} \le K\, \sum\limits_{i = 1}^N\|\nu_i-\hat{\nu}_i\| $ | (32) |
with
Proof. We follow the proof of Theorem 2.7 in [10] and show that (26) has locally a unique solution. Observe
Let us first collect a few derivatives. For incoming pipes, we derive from the second equation in (25)
| $ q_j'(\bar{p}_j) = \frac{\lambda_3(\bar{u}_j)}{\bar{c}_j^2}, \;\; h_j'(\bar{p}_j) = \frac{\lambda_3(\bar{u}_j)}{\bar{c}_j\bar{\rho}_j}, \;\; \partial_{\sigma_j}s^\ast(\bar{p}) = \frac{\|\nu_j\|\lambda_3(\bar{u}_j)}{\bar{c}_j^2 \sum_{i\in\mathbb{I}_i}\|\nu_i\|\bar{q}_i}\left( \bar{s}_j-\bar{s}^\ast\right) $ | (33) |
with
| $ \partial_{\sigma_i}q_i(\bar{p}_i, 0) = \frac{\lambda_3(\bar{u}_i)}{\bar{c}_i^2}, \;\; \partial_{\sigma_i}h_i(\bar{p}_i, 0) = \frac{\lambda_3(\bar{u}_i)}{\bar{c}_i\bar{\rho}_i}, \;\; \partial_{\sigma_i}s_i(\bar{p}_i, 0) = 0, $ | (34) |
| $ \partial_{\tau_i}q_i(\bar{p}_i, 0) = \lambda_2(\bar{u}_i), \;\; \partial_{\tau_i}h_i(\bar{p}_i, 0) = -\frac{\bar{c}_i^2}{(\gamma-1)\bar{\rho}_i}, \;\; \partial_{\tau_i}s_i(\bar{p}_i, 0) = -\frac{\gamma c_v}{\bar{\rho}_i} $ | (35) |
for
| (36) |
Here, we have used the short notations
| $ \hat{q}_{\sigma_i} > 0, \;\hat{q}_{\tau_j} > 0, \;h_{\sigma_i} > 0, \;h_{\tau_j} < 0, \;s_{\tau_i} < 0 \;\;\mbox{for }\;\;i = 1, \ldots, N, \;j = 1, \ldots, N_o. $ | (37) |
Without loss of generality, we choose the numbering of the incoming pipes in such a way that
|
$
D_i = (ˆqσiˆqσNo+1ˆqτi−hσihσNo+1−hτi0−s∗σNo+1sτi)
\;\;\mbox{for }\;\;i = 1, \ldots, N_o,
$
|
(38) |
are regular. Taking into account the signs of all derivatives, we have
| $ \det \left( D_i \right) = \hat{q}_{\sigma_i} (h_{\sigma_{N_o+1}}s_{\tau_i}-h_{\tau_i}s^\ast_{\sigma_{N_o+1}})+ h_{\sigma_i} (\hat{q}_{\sigma_{N_o+1}}s_{\tau_i}+ \hat{q}_{\tau_i}s^\ast_{\sigma_{N_o+1}}) < 0. $ | (39) |
Therefore,
| $ Y_\ast^{(i)} = \mathcal{L}_3(\varphi(\tilde{U})_i, \tilde{U}), \;i\in\mathbb{I}_i, \mbox{ and } Y_\ast^{(j)} = \mathcal{L}_2(\varphi(\tilde{U})_{j+N}, \mathcal{L}_3(\varphi(\tilde{U})_j, \tilde{U}), \;j\in\mathbb{I}_o. $ | (40) |
The Lipschitz estimate (31) follows from the
Remark 1. (energy and entropy conservation) We would like to remember that the coupling conditions ensure conservation of energy and entropy at the junction,
| $ \sum\limits_{i = 1}^{N}\, \|\nu_i\|\, (u_i(E_i+p_i))(0^+, t) = \sum\limits_{i = 1}^{N}\, \|\nu_i\|\, (q_is_i)(0^+, t) = 0. $ | (41) |
It is therefore not necessary to assume that the perturbed initial state
Remark 2. Theorem 2.4 remains valid even if the adiabatic exponent
In this section, we define a weak entropic solution for the general Cauchy problem with source terms at junctions, using the above stated coupling conditions. Further, two main results are formulated: the well-posedness for the homogeneous as well as the inhomogeneous case under the well known assumption that the total variation of the initial data is sufficiently small. Both theorems can be seen in line with Theorem 3.2. from Colombo and Mauri [10] and Theorem 2.3. from Colombo, Guerra, Herty, and Schleper [8]. The key point is the well-posedness of the Riemann problem stated in Theorem 2.4 above, which provides the basis for the proofs.
We first introduce a few notations.
Definition 3.1. Let
|
$
‖Y‖=N∑i=1‖Y(i)‖for Y∈Ω,‖Y‖L1=∫R+‖Y(x)‖dxfor Y∈L1(R+;Ω)TV(Y)=N∑i=1TV(Y(i))for Y∈BV(R+;Ω).
$
|
(42) |
For a constant state
| $ D_\delta(\bar{Y}) = \{ Y \in \bar{Y} + {{\boldsymbol{\rm{L}}}^{\boldsymbol{1}}}(\mathbb{R}^+;\Omega):\;TV(Y)\le \delta\}. $ | (43) |
Let
| $ (G(t, Y))(x) = \left( G(x, t, Y^{(1)}), \ldots, G(x, t, Y^{(N)})\right). $ | (44) |
For the map
|
$
‖G(t,Y1)−G(s,Y2)‖L1≤L1(‖Y1−Y2‖L1+|t−s|)for all Y1,Y2∈Dˉδ(ˉY),TV(G(t,Y))≤L2for all Y∈Dˉδ(ˉY).
$
|
(45) |
This is the usual assumption on
Next we define the Cauchy problem at junctions, which corresponds to our special set of coupling conditions.
Definition 3.2. Let
|
$
∂tU(i)+∂xF(U(i))=G(x,t,U(i)),(x,t)∈R+×R+,i=1,…,N,Φ(U(0+,t))=0,t∈R+,U(x,0)=U0(x),x∈R+,U0∈ˉU+L1(R+;Ω),
$
|
(46) |
is a map
| $ {\displaystyle\sum\limits_{i = 1}^N\left(\int_0^T \int_{\mathbb{R}^+} \left( \rho_i\partial_t\varphi + q_i\partial_x\varphi + G_1(x, t, U^{(i)})\varphi\right)\, dx\, dt \right) \, \|\nu_i\| = 0} $ | (47) |
and
| $ \displaystyle\int_0^T \int_{\mathbb{R}^+} \left( q_i\partial_t\varphi + P_i\partial_x\varphi + G_2(x, t, U^{(i)})\varphi\right)\, dx\, dt = {\displaystyle\int_0^T P_i(0^+, t)\varphi(0, t)\, dt, }\\ \displaystyle\int_0^T \int_{\mathbb{R}^+} \left( E_i\partial_t\varphi + q_ih_i\partial_x\varphi + G_3(x, t, U^{(i)})\varphi\right)\, dx\, dt = {\displaystyle\int_0^T q_i(0^+, t)h^\ast(t)\varphi(0, t)\, dt.} $ | (48) |
for all
The weak solution is entropic if for all non-negative
| $ \int_0^T \int_{\mathbb{R}^+} \left( \rho_is_i\partial_t\varphi + q_is_i\partial_x\varphi + \partial_U(\rho_is_i)G(x, t, U^{(i)})\varphi\right)\, dx\, dt \ge 0. $ | (49) |
We note that multiplying the energy equation with
| $ {\displaystyle\sum\limits_{i = 1}^N\left(\int_0^T \int_{\mathbb{R}^+} \left( E_i\partial_t\varphi + q_ih_i\partial_x\varphi + G_3(x, t, U^{(i)})\varphi\right)\, dx\, dt \right) \, \|\nu_i\| = 0, } $ | (50) |
which means energy conservation in the case
A solution to the Cauchy problem can be constructed by means of the wave front tracking method. In the book of Bressan [3] all necessary steps can be found.
Let us first consider the homogeneous case. We have the following
Theorem 3.3. Let
(1)
(2)
(3) For all
(4) For
| $ \|S_t(\hat{U})-S_s(\tilde{U})\|_{{\boldsymbol{\rm{L}}}^{\boldsymbol{1}}} \le K\, (\|\hat{U}-\tilde{U}\|_{{\boldsymbol{\rm{L}}}^{\boldsymbol{1}}}+|s-t|). $ |
(5) If
Proof. The properties are a direct consequence of a natural extension of the standard Riemann semigroup theory [3,Section 8.3] to junctions. All arguments can be copied from the proof of Theorem 3.2. in [10].
For non-vanishing sources
Theorem 3.4. Let
(1)
(2)
(3)
(4) For all
| $ \mathcal{E}(s_2, t_0+s_1)\circ\mathcal{E}(s_1, t_0) = \mathcal{E}(s_1+s_2, t_0). $ |
(5) For all
(6) For all
| $ \lim\limits_{t\rightarrow 0}\frac{1}{t} \|U(t)-(S_t(U_0)+tG(t_0, U_0))\|_{{{\boldsymbol{\rm{L}}}^{\boldsymbol{1}}}} = 0, $ |
where
(7) For all
| $ \| \mathcal{E}(s, t_0)U-\mathcal{E}(s, t_0)\tilde{U}\|_{{{\boldsymbol{\rm{L}}}^{\boldsymbol{1}}}} \le K \|U-\tilde{U}\|_{{{\boldsymbol{\rm{L}}}^{\boldsymbol{1}}}}.$ |
Proof. The proof can be achieved by following the standard line developed in [8] for
We have proposed a novel set of physically sound coupling conditions at a junction of pipes with possibly different cross-sectional areas for the
This work was supported by the German Research Foundation within the collaborative research center TRR154 "Mathematical Modeling, Simulation and Optimization Using the Example of Gas Networks" (DFG-SFB TRR154/1-2014, TP B01).
| 1. | Sara Grundel, Michael Herty, Hyperbolic discretization of simplified Euler equation via Riemann invariants, 2022, 106, 0307904X, 60, 10.1016/j.apm.2022.01.006 | |
| 2. | Jan Van den Berghe, Bruno R.B. Dias, Yann Bartosiewicz, Miguel A. Mendez, A 1D model for the unsteady gas dynamics of ejectors, 2023, 267, 03605442, 126551, 10.1016/j.energy.2022.126551 | |
| 3. | Pascal Mindt, Jens Lang, Pia Domschke, Entropy-Preserving Coupling of Hierarchical Gas Models, 2019, 51, 0036-1410, 4754, 10.1137/19M1240034 | |
| 4. | Pia Domschke, Oliver Kolb, Jens Lang, Fast and reliable transient simulation and continuous optimization of large-scale gas networks, 2022, 95, 1432-2994, 475, 10.1007/s00186-021-00765-7 | |
| 5. | Sarah‐Alexa Hauschild, Nicole Marheineke, Structure‐preserving methods for a coupled port‐Hamiltonian system of compressible non‐isothermal fluid flow, 2023, 1617-7061, 10.1002/pamm.202300012 | |
| 6. | Damien Furfaro, Jacek Kosek, Andrey Ovcharov, Tyge Schioler, Rossella Rotella, Tim Luce, A new fast and robust thermo-hydraulic code for ITER superconducting magnet simulation, 2024, 00112275, 103978, 10.1016/j.cryogenics.2024.103978 |
Possible wave patterns in the solution of Riemann problems for the Euler equations: shock (S), contact (C) and rarefaction (R).
Connection of the regions