In quasi-periodic homogenization of elliptic equations or nonlinear
periodic homogenization of systems, the cell problem must be in
general set on the whole space. Numerically computing the
homogenization coefficient therefore implies a truncation error, due
to the fact that the problem is approximated on a bounded, large
domain. We present here an approach that improves the rate of
convergence of this approximation.
1.
Introduction
Psychiatric disorders such as depression, anxiety, bipolar disorder, autism spectrum disorder (ASD) and attention deficit hyperactivity disorder (ADHD) may relate to behavioral, cognitive and emotional disturbances which are eventually rooted in disordered brain function [1]. These disorders are linked to dysregulation of various neurotransmitters as well as dysfunction of neuronal networks in brain [1]. Psychiatric disorders have sometimes etiological problems with high mortality, which contributes significantly to the global burden of diseases. [2]. Environmental conditions, genetic background, immune dysregulation and some infectious agents are known to be involved in the pathogenesis of these psychiatric disorders [3],[4]. In particular, infections could enhance inflammatory pathways and consequently may have certain roles in the pathogenesis of psychiatric disorders [5]. Immune responses to the infection have also shown to be involved in the diseases severity and/or treatment outcomes [6]. Further understanding about the pathogenesis of psychiatric disorders would provide a promising therapeutic option in the diseases treatment [7]. Underlying pathogenesis of psychiatric disorders has yet been poorly understood [8], however, growing evidence suggests that gut microbiome in the host could play an important role in the pathogenesis [9]. This gut-brain axis contains a biochemical pathway between the gastrointestinal tract and the central nervous system (CNS) (Figure 1). Although the presence of the gut–brain axis has long been established, several recent studies suggest that gut microbiome-management for individual with psychiatric disorder has often approved promising results [10]. A functional relationship between gut microbiota and brain could play a significant role in neurological diseases and in neurodegenerative diseases [11],[12]. Consistently, it has been shown that gut microbiota affects the brain function of the host behavior in rodent models [13]. In addition, trillions of microbes in the intestine have been suggested to regulate the gut-brain axis [14]. There might be several alterations in gut microbiome among psychiatric disorders in connection with the heterogeneity of neuropsychiatric disorders. In animal models, treatment with definite microorganisms in gut could improve behavioral changes [15]. It is probable that certain gut microbiota is involved in human psychiatric disorders [16]. Microbial diversity of gut might undergo substantial changes during neuropsychiatric disorders. In this review, we have summarized and discussed the gut microbiota in main neuropsychiatric disorders for the future directions of exploration.
2.
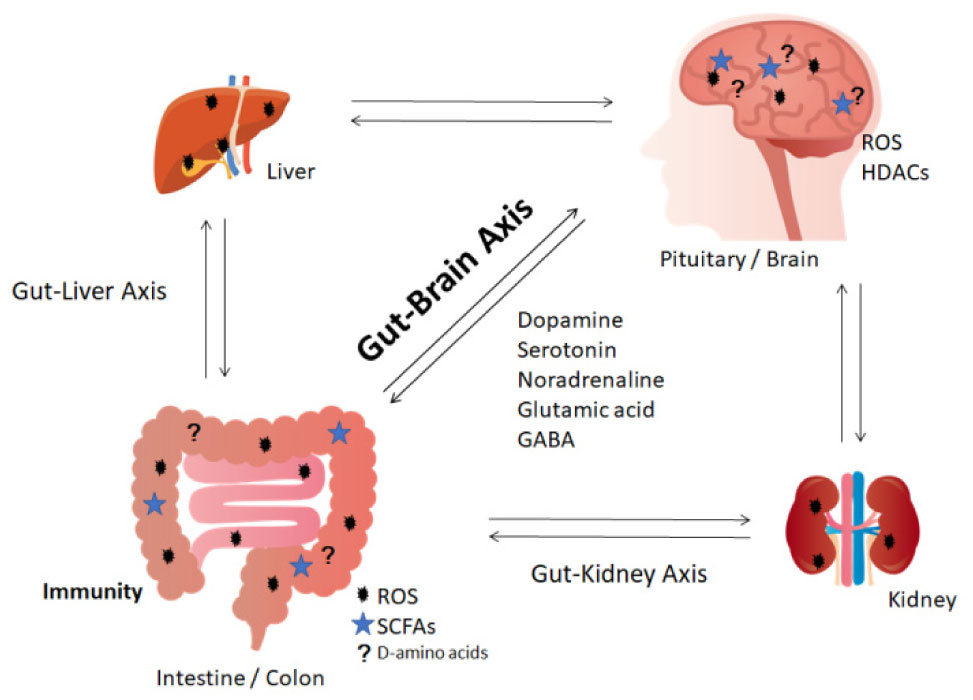
The gut-brain axis
The gut-brain axis characterizes a set of bidirectional communication between gut and brain [17] (Figure 1). This concept includes the interplay between the neurological system and gut microbiota including microorganisms that exist in the gastrointestinal tract. The gut microbiota is affected by various host factors including nutrition, exercise, past illnesses and past use of antibiotics [18]. Studies have shown that dysbiosis of gut microbiota could exacerbate various neuropsychiatric disorders [19], suggesting that the cross-talk of gut-brain axis may play an important role in the pathogenesis of the disorder. In addition, patients with neurological dysfunction often exhibit some of gastrointestinal signs and/or symptoms [20]. Therefore, the gut–brain axis may have a critical role in metabolism, physiology, and homoeostasis for keeping host health [21]. However, the efficacy of targeting the gut microbiota has not yet been established, and needs further investigation [21]. It has been reported that gut microbiota is associated with the pathogenesis of several mental disorders [1],[9],[12],[14],[22]. In addition, it has been suggested the association between psychological stress and dysbiosis of gut microbiota [23]. Furthermore, the effects of antidepressant may be partially reconciled by the restoration of beneficial microbiota [24]. Daily oral administration of an antidepressant fluoxetine to healthy mice significantly decreased the abundance of beneficial Lactobacillus species, suggesting that the positive effects of the fluoxetine may be caused by good alterations in the gut microbiota [25]. Similarly, treatment with another antidepressant such as lithium, aripiprazole or valproate also increases the quantity of several specific beneficial bacteria species [26]. Normal gut microbiota could protect the brain, whereas gut dysbiosis of the microbiota could facilitate the psychiatric disorders [27]. Presumably, the gut-brain axis may be significantly affected by the loss of gut neurons and production of inflammatory cytokines [27]. It has been shown that microbes in gut could stimulate afferent sensory neurons [28]. Alterations in the gut microbial composition have been correlated with altered neurotransmitter expression in the CNS pathways controlling sensory and/or motor functions [29]. Alternatively, gut microbial metabolism may provide several precursors involved in biosynthetic pathways of neurotransmitters or neuromodulators such as dopamine, serotonin, noradrenaline, glutamic acid, and gamma amino butyric acid (GABA) [30] (Figure 1).
3.
Gut microbiota could control ROS, short-chain fatty acids, and D-amino acids in order to keep brain healthy
Diet is known to be an important regulator of gut microbiomes [31]. Consequently, the gut flora can maintain a dynamic balance with the host and can play a unique role in host functional activities such as nutritional metabolism and host immunity [32]. In addition, the gut microbiota is involved in a wide variety of physiological features and interplay of the gut microbiota and cognition has been under focus of recent researches [33]. In this regards, disturbance of the gut microbiota might lead to the occurrence of physical and/or mental diseases. Several studies have highlighted the relationship among the gut microbiota and oxidative stresses [34]. In particular, reactive oxygen species (ROS) production has a defense mechanism that could provoke cytotoxicity against several pathogens and decrease the possibility of severe infections [35],[36]. For example, epithelial cells may accomplish ROS production in response to several harmful bacteria [35]. However, the ROS might be rigorously controlled by the signaling process for appropriate gut immunity [37]. On the other hand, various bacterial species of microbiota may result in diminishing the ROS production in gut [38]. Microbial products could upregulate the activity of superoxide dismutase, which results in a smaller level of ROS and reduces the cellular apoptosis or cell death [39]. For example, the vanillin derivative improves the survival of lethally irradiated mice by promoting intestinal regeneration and increasing the number of surviving crypts [39]. There might be many ROS-sensitive enzymes in gut epithelium, which is affected by alterations of the redox condition in gut. It has been shown that cisplatin-induced ROS generation is responsible for the upregulation of SIRT2, a member of class III HDACs in cell-line cells, which is protecting cells from ROS-damages [40]. The SIRT2 is a critical modulator of aging and could extend life span of animals [40].
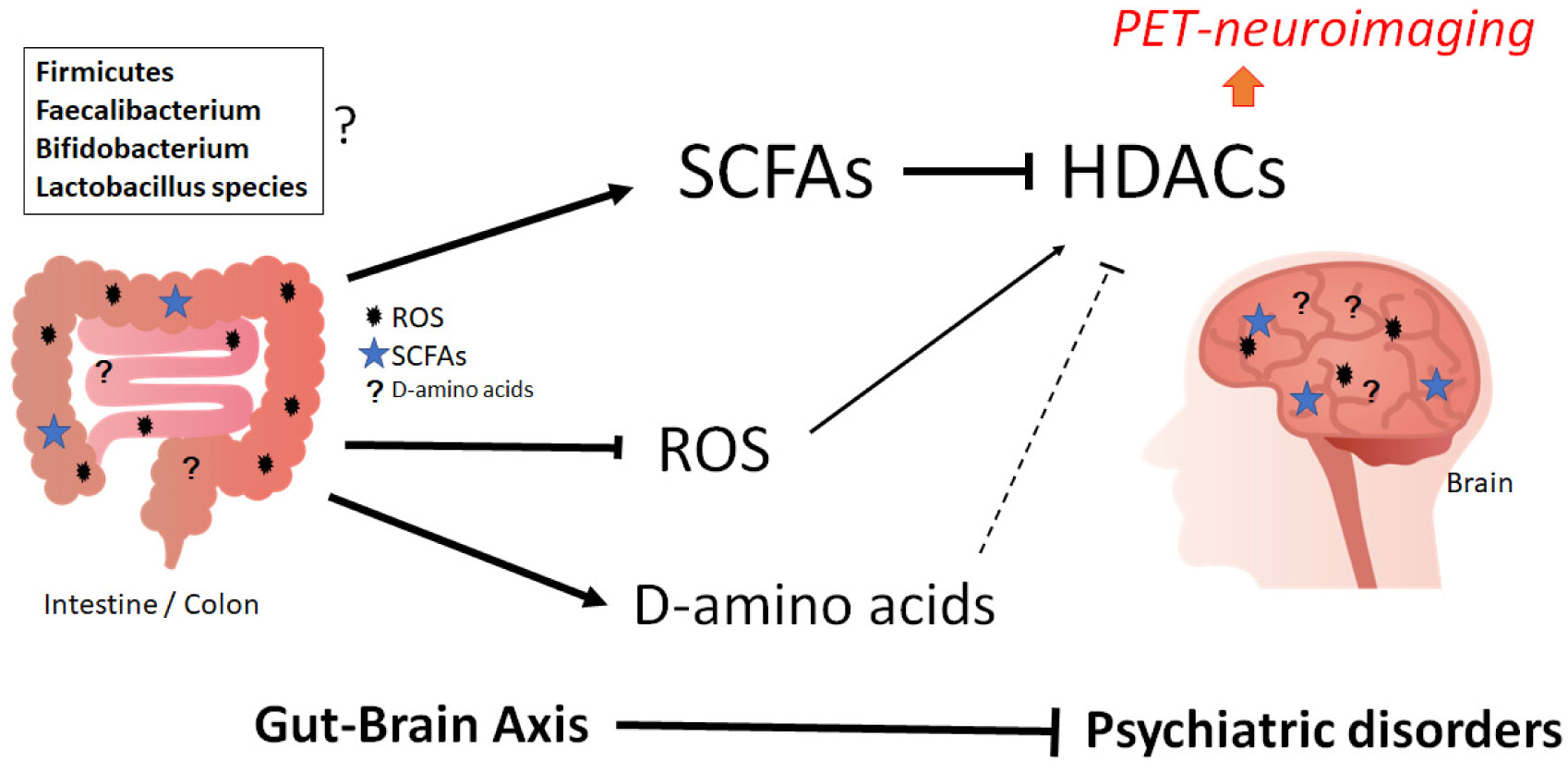
Soluble peptides and fibers which are not degraded by intestinal enzymes in the upper gut are further metabolized by the microbiota in the lower gut. Their main products are short chain fatty acids (SCFAs), including acetate, propionate, and butyrate [41]. SCFAs are fatty acids with fewer than six carbon atoms. Primary source of the SCFAs are the essential gut-microbial derived metabolites formed from dietary composites, while fermented foods themselves could be a secondary source of the SCFAs [42]. SCFAs have been shown regulatory substances with the potential to influence emotional state through the gut–brain axis [43]. In addition, SCFAs may increase the permeability of blood brain barrier (BBB), which demonstrates that SCFAs could directly control brain homeostasis [44]. Parenteral nutrition has been associated with the alteration of microbiota and/or SCFAs production, which could induce gut mucosal atrophy [45]. Certain level of SCFAs produced by the healthy gut microbiota have shown possessing anti-inflammatory properties with the proper regulation of T cell proliferation [46]. These inhibitory effects existing in SCFAs may work at least in part via the regulation of histone deacetylases (HDACs) [47] (Figure 2).
Gut microbiota have a large genetic capacity to metabolize D-amino acids which are utilized as nutrients to support bacterial growth [48]. Many bacterial species encode specific racemases that convert L-amino acids to D-amino acids [49]. Accordingly, possible source of D-amino acids in mammals may mostly be their gut microbiota. For example, D-alanine production is associated with a relative abundance of bacterial species such as Enterococcus and Lactobacillus in the microbiota [50]. In addition, different bacterial species may produce distinct D-amino acids profiles [51]. Higher levels of D-amino acids have been actually associated to the gut microbial mass [52]. D-amino acid oxidase promotes senescence through the ROS production [53]. Conjugation of several fatty acids to the side chains of certain D-amino acids has potential antimicrobial activities [54]. Interestingly, a cyclic peptide (-L-amino acid-D-amino acid-L-Val-D-Pro-) with an -SS- bridge has been shown a potent HDACs inhibitor [55] (Figure 2).
4.
Relationship between gut microbiota, SCFAs and HDACs may be involved in the pathogenesis of neuropsychiatric disorders
Interpretation of neuropsychiatric disorders is complicated due to overlapping symptoms [56]. Alzheimer' disease (AD) is an irreversible type of dementia that causes memory and/or thinking problems, which may finally disturb activities of daily life [57]. The characteristic brain pathology includes amyloid plaque deposition and hyper-phosphorylation of tau protein in the brain-neurons of AD [58]. Recently, it has been hypothesized that AD may be associated with the dysbiosis of gut microbiota and their metabolite SCFAs, whose improvement has been demonstrated to inhibit the progression of AD [59]. In an AD model animal, for example, butyrate treatment increased spatial learning and neural plasticity [44], [60]. In Parkinson's disease, nerves are affected by alpha-synuclein pathology [61]. Symptoms of Parkinson's disease result to a large extent from loss of dopaminergic neurons in the substantia nigra of midbrain [62]. SCFAs in a body differ between patients with Parkinson's disease and age-matched controls [63]. Consequently, the reduction in SCFAs might induce alterations in the nervous system and contribute to gastrointestinal dysmotility in Parkinson's disease [63]. Consistent with this, the applications of propionic acid mostly promote cell survival of dopaminergic cells [64]. Schizophrenia is a neuropsychiatric disorder associated with thinking disorders disturbing perception and social interaction in addition to the symptom of psychosis [65]. Recent studies have also found differences in microbiome composition of gut between healthy controls and schizophrenia patients [66]. Furthermore, SCFAs are reported to have neuroprotective effect and influence gene expression in haloperidol-induced neurite lesions in animal model of schizophrenia [67]. Depression is an unexciting-feeling disease that involves a loss of interest and a feeling of sadness in daily activities [68]. Some SCFAs have been shown considerably decreased in the depression compared to the control in mice model [69]. Instabilities in the gut-microbiota have been associated with the pathophysiology of depressive behavior [70]. The roles of gut microbiota may also be related to autism spectrum disorder [71]. Most of children with autism spectrum disorder have gastrointestinal disorders indicating a relationship between autism spectrum disorder and altered microbiota of the gut [72]. In a stool microbiome analysis, bipolar disorder patients have a decreased richness of Firmicutes and Faecalibacterium spp., which are SCFAs-producing bacteria [73]. Intermediation with Lactobacillus spp. and Bifidobacterium strains has noticeably decreased the psychiatric symptoms, in which an increase of the major SCFA acetate has been shown [74]. In mania and bipolar disorder models, rats treated with butyrate have presented decreased morbid locomotor activity [75]. In addition, it has been reported that treatment with sodium butyrate abolishes lipopolysaccharide–induced depression-like behaviors in mice [76].
SCFAs may protect several organs including brain by inhibiting HDACs [77] (Figure 2). Modulation of individual HDACs could be an important therapeutic approach for neurodevelopmental and/or psychiatric disorders [78]. For example, valproic acid, a class I HDAC inhibitor, is widely used antiseizure medications, which could increase gene expression via the inhibition of HDACs [79]. In animal models of neuropsychiatric disorder, dysregulation of gene transcription could be attributed to the epigenetic enzymes including HDACs [80]. Treatment of HDACs inhibitor sodium butyrate has increased the levels of acetylation on histone H3 enhancing conditioned taste aversion learning in rats [81]. Genetic alterations of HDAC2 may be linked to increased risk for the bipolar disorder [82]. In addition, anti-manic effects of HDAC-inhibition might be related to the function in brain [83]. HDACs inhibitor treatment may also act as a mood-stabilizing drug with effects on behaviors like mania and psychosis [84]. In an autism spectrum disorder model, butyrate treatment has increased long-term memory and histone acetylation [85]. In these ways, HDACs inhibitors could be used as an effective treatment for several psychiatric and neurological disorders [86]. Furthermore, the simultaneous inhibition of HDACs has a synergistic therapeutic effect in AD animal models [87]. Inhibition of specific HDACs would also be a targeted strategy in Parkinson's disease [88]. Studies have defined alterations in histone acetylation in the brains of Parkinson's disease patients in animal models [88],[89]. Besides, α-synuclein accumulation has been related to the alterations in histone acetylation [88],[89]. Therefore, pharmacological strategies aimed at modulating histone acetylation are under examination as new approaches to disease-modification in psychiatric disorders. Recent strategies for the treatment of neurodegenerative disorders have also included HDACs inhibitors [89].
An imaging study has demonstrated that microbiota-derived acetate, a SCFA, could alter hypothalamic gene expression [90]. Butyrate, a SCFA, has been shown to be associated with increased expression of the tight junction protein occludin in the frontal cortex and hippocampus [91]. BBB permeability is associated with reduced expression of the occludin which are known to regulate barrier function in endothelial tissues [91]. These SCFAs are predominantly produced by gut microbiota fermentation, and serves as an important neuromodulator in the central nervous system. SCFAs may be an endogenous ligand for two orphan G protein-coupled receptors, GPR41 and GPR43 [92]. As mentioned above, those SCFAs act as a potent inhibitor of HDACs, which might regulate genes expression important for neuroplasticity associated with the psychiatric disorders [93]. It is possible that altered HDACs expression contributes to emotional disturbances through altered neuroplasticity. In fact, altered HDAC expression (not a HDAC-inhibition) has impacts on emotion-regulation and attention-regulation [94]. HDAC expression levels might modulate attention and emotion regulation.
5.
Application to diagnostics of patient with psychiatric disorders
Due to a lack of definite treatments, the psychiatric disorders are public health concern [95]. A principal goal in basic neuroscience research is to develop knowledge and techniques that could be extended from animal model to the human brain, which might enable early detection and/or early treatment for the psychiatric disorders. In this meaning, translational tools that can visualize brain function are predominantly useful. However, visualizing brain function is a major challenge given that the human brain is difficult to examine directly. Recently, HDACs inhibitors have been developed as an imaging agent for the psychiatric disorders. In particular, positron emission tomography (PET)-neuroimaging has revealed the dysregulation of HDACs in schizophrenia [96]. The PET would be an ideal tool to measure and quantification of HDACs expression in a non-invasive way. This tool will be a critical addition to ex vivo methods to evaluate in CNS dysfunction [97]. The basis to examine the role of HDACs for using PET has been clinically provided in human cognition [96]. In addition, the development of neuronal PET tracers for the HDACs in brain would be progressing as an epigenetic brain marker [98]. It has been shown by the PET-neuroimaging that HDACs activity both of hippocampus and white matter in brain associates to the emotional alteration [99] (Figure 2).
The analysis of the SCFAs concentration could serve as an indirect way to analyze microbiota composition [100]. Beneficially, it would also be a non-invasive way to examine. Actually, SCFAs concentration of feces correlates to the severity of depressive symptoms [43],[101]. In addition, the levels of fecal acetate, propionate, and butyrate in multiple sclerosis have been shown significantly lower than those in healthy controls [102]. Besides, fecal concentration of SCFAs (ex. butyrate and propionate) have been shown significantly reduced in anorexia nervosa [103]. The gut dysbiosis could take part in the anorexia nervosa neurobiology [103]. The metabolites could also increase the absorption of glucose and change the permeability of the intestinal barrier [104]. In addition, it has been shown that mix of butyrate-producing bacteria improves epithelial barrier integrity in vitro [104].
6.
Perspectives and concluding remarks
Alterations of gut microbiota may modulate the gut–brain communication, which could lead to the development of neuropsychiatric disorders. Therefore, the use of compounds that improve the microbiota including prebiotics and/or probiotics appears to be a promising way to improve neuropsychiatric disorders [105]. For example, the disturbed gut microflora function and the fecal SCFA pattern in childhood celiac disease are normalized after gluten-free diet [106]. The gluten-free diet could suppress several harmful intraluminal intestinal events [107]. There seem to be some possibilities for shaping the dysregulated gut homeostasis in individuals with celiac disease and/or neurodegeneration [108]. The growing interest in this area will lead to more insights into the precise mechanisms underlying gut–microbiome–brain communication. It will provide a new microbiome-based diagnostic and therapeutic strategies that could help to treat the neuropsychiatric disorders. Interestingly, gut microbiota transplantation has been reported to be sufficient both for the microglial activation in the brain and for the behavioral changes [109]. Of course, there should be a requirement for the concepts produced in animal models to be translated to the human in the future. An increase in the translocation of gut bacteria is detected in depression-patients, which might support the activation of immune responses [110]. Obviously, the gut microbiota could alter the function of the brain indirectly through the change of the inflammatory and/or immune conditions. Evaluation for intensive experiments should be compulsory to obtain further insights. Also, noninvasive neuroimaging should be more revolutionized for the understanding of brain function in a breathing human. Finally, long-term studies are mandatory to clarify the efficacy in the status from hatred to reconciliation of the psychiatric disorders.









 DownLoad:
DownLoad: