1. Introduction
The administration of cancer chemotherapy has for a long time followed established principles based on dose intensity and dose effect. Although the resulting schedules have at times been questioned [23,51], it is only more recently that these principles are being reexamined in view of new biological approaches and medical considerations. In traditional therapy protocols, cytotoxic agents are administered at maximum tolerated doses (MTD) to counteract disease progression and to kill as many cancer cells as possible. This approach requires treatment breaks to let the body recover from treatment induced toxicity. On the other hand, some experimental and clinical studies attest that "more is not necessarily better" (e.g., [20]). Alternative types of protocols which take into account the highly complex interactions of a tumor with its microenvironment may give a better outcome or may be able to control a resistant tumor. In this context, the concept of metronomic chemotherapy was introduced in 2000 (e.g., see [6,9,20,24]). Metronomic chemotherapy (MC) is the administration of chemotherapeutic agents at lower than maximum doses without prolonged breaks [2,3]. It has been shown that aside from lower cytotoxic effects, such schedules also exhibit antiangiogenic and pro-immune effects (see [21] for a comprehensive summary of the medical literature on this topic). These are both very important aspects of a tumor's microenvironment which usually have been analyzed and modelled separately (e.g., see [10,18,30,50]). Another aspect that should be taken into account in designing cancer therapy protocols is the effect it has on heterogeneous tumor populations. According to the Norton-Simon hypothesis, the population of cells which are sensitive to a specific chemotherapy drug grow faster than the ones which are resistant [39,40]. In part, this may be because of the strategies developed by clones to become resistant (i.e., by activating or upregulating pathways that use up energy that then cannot be used, for instance, for proliferation) [11,12]. While the higher proportions of sensitive cells implies that the majority of cells can be killed, this may turn into a disadvantage when an unsuitable type of therapy protocol is administered. For example, the application of MTD type chemotherapy leads to the selection of resistant strains through the annihilation of sensitive ones. This in turn leads to drug resistant strains becoming dominant and then therapy is no longer effective [13,14].
In this paper, we address this topic from a mathematical modeling and optimal control point of view. We briefly recall a mathematical model for evolving drug resistance that was introduced by Lorz et al. in [35,36] and expanded upon by Greene et al. in [16,25]. In this model, various sub-populations of cells indexed by a variable x∈[0,1] are considered. This variable x merely labels these groups which may have different replication or death rates and/or other distinguishing features such as varying chemotherapeutic sensitivities with respect to anti-cancer drugs considered in the model. Such properties may be related to different fitness properties of these cells, but no specific mechanism is assumed here. For such a model, we formulate an optimal control problem with the objective to minimize the total number of cancer cells, both at the end of therapy and over the therapy interval, while at the same time minimizing the toxicity of the drugs. Optimal solutions then achieve a balance between these two competing objectives. The optimal control problem obtained in this way is infinite-dimensional and has a mathematical structure for which a solution cannot be given with the use of classical tools or methods. Therefore we consider finite-dimensional approximations. Indeed, it is one of the main conclusions of the work of Lorz et al. [35,36] and Greene et al. [16,25] that evolutionary principles will lead to a selection of those sub-populations that have the highest net proliferation rates in a given environment. These will become dominant and outperform those sub-population that have lower performance parameters. In view of this observation, there actually are good reasons to look at problems with a finite number of levels. The most rudimentary approach is to consider a single drug and only account for two main classes, populations that are resistant and sensitive with respect to this drug's actions. Below, such a model, which is based on equations originally formulated by Hahnfeldt et al. in [19] is considered. An analysis of this model as an optimal control problem was given in [32] and an extension that also included a third class of partially resistant cells was presented in [27]. In either model, as the resistant population achieves a certain level, optimal controls favor lower dose administrations. In this paper, we put these results within the framework of the more general model briefly mentioned above and relate them to the ideas of chemo-switch protocols and metronomic chemotherapy. Optimal protocols coming from our analysis support the thesis that "more is not necessarily better" by highlighting the role of what in the mathematical literature are called singular controls. These represent treatment protocols with lower partial doses. More specifically, it is shown that the choice of the dosage depends on the whole biological condition of the system. There exists a region corresponding to tumor volumes with a high fraction of sensitive cells where MTD (full dose) treatment protocols are the optimal choice. However, once the sensitive cell population becomes depleted beyond a certain threshold, singular controls become optimal. This corresponds to the medical concept of "chemo-switch" protocols when an initial period of full dose chemotherapy session is followed by a prolonged period of low dose metronomic chemotherapy [42].
2. Optimal control for chemotherapy under tumor heterogeneity
We briefly describe a mathematical model for phenotypic heterogeneity and drug resistance in solid tumors that considers a continuum of possible traits. This model was originally formulated in the work of Lorz et al. [35,36] and then expanded upon by by Greene et al. [16,25] as a means to explain the roles that increasing cell densities and mutations play in the emergence of specific traits which become dominant. Essentially, as a response to different net growth rates, the 'fitter' phenotypes (in the model these simply are the ones that have the highest net proliferation rates) crowd the less fit cells and limit their growth. We recall this model.
2.1. An optimal control problem with a continuum of traits
In the model, a continuum of possible traits (phenotypes) x, x∈[0,1], is considered. If n(t,x) denotes the population density of cells with trait x at time t, then the total number N(t) of cancer cells at time t is given by
The variable x merely indicates that there exist sub-populations that have distinguishing features such as different replication and/or apoptosis rates or may react differently to specific chemotherapeutic drugs. Thus the replication rate r and the natural death rate μ of cancer cells are taken as functions of x, r=r(x) and μ=μ(x). Some of these functions could be constant on some subsets of [0,1] or even on all of it. The main reason for considering sub-populations x lies in modeling the effects of chemotherapy. Making the linear log-kill hypothesis, we denote the cytotoxic killing parameter under treatment with a specific chemotherapeutic agent by φ=φ(x) depending on the trait x of the sub-population. Thus, and using a model of exponential growth for the cells, one arrives at the following dynamics:
|
∂n∂t(t,x)=(r(x)−φ(x)c(t)−μ(x))n(t,x).
|
(2)
|
Most cytotoxic agents merely prevent further cell divisions and for this reason the killing terms are subtracted from the reproduction rate r.
More realistically, the rates for cell division and apoptosis not only depend on the trait x, but also on the cell density which itself is closely related to the total tumor mass N [15]. Taking this into account, Greene et al. [16] modify equation (2) to become
|
∂n∂t(t,x)={f(N(t))(r(x)−φ(x)c(t))−g(N(t))μ(x)}n(t,x)
|
(3)
|
with f=f(N) and g=g(N) positive, non-dimensional functions of the total tumor size N. Mathematically, equation (3) can be simplified by rescaling the time variable t. Let G(N)=g(N)/f(N) and define a new time variable τ, τ:t↦τ(t), as τ(t)=∫t0f(N(s))ds. Setting ˜n(τ,x)=n(t(τ),x) and ˜c(τ)=c(t(τ)), one obtains the simpler expression
|
∂˜n∂τ(τ,x)={r(x)−φ(x)˜c(τ)−G(N(τ))μ(x)}˜n(τ,x).
|
(4)
|
This new time-scale has the advantage that only the apoptosis rates are changed. But note that the new time scale no longer is linear, so it does not contain units such as [days], [weeks] etc. These only make sense after reverting to the original scale.
The model is nonlinear with the right-hand side exhibiting similar features as a logistic term of the form (a−bN)N. If one assumes that the growth rate f decreases with increasing cell density while the apoptosis rate g increases—and these are reasonable assumptions—then the scaling factor G is monotonically increasing. As this term offsets the balance between growth and apoptosis, the population will stabilize. Thus, while (2) represents a model of exponential growth that generates unbounded total populations, incorporating cell densities into the model in (3) introduces a logistic structure that generates finite carrying capacities [16,45].
We are interested in the following optimal control problem. For notational convenience we revert to the original labeling with t and n.
[Het]: With α, β and γ row vectors of positive weights, minimize
|
J=J(u)=αN(T)+∫T0(βN(t)+γu(t))dt
|
(5)
|
over all Lebesgue measurable functions u=(u1,…,um)T, ui:[0,T]→[0,umaxi], subject to the dynamics
|
∂n∂t(t,x)=[r(x)−m∑i=1φi(x)ci(t)−G(N(t))μ(x)]n(t,x),
|
(6)
|
In this formulation, we consider a multi-input optimal control problem that allows for combinations of various drugs. Each of them is endowed with its own drug specific sensitivities of the subpopulations with trait x defined by the functions φi(x). In principle, some traits x may be sensitive to drug 1, but less sensitive or even resistant to drug 2. Equation (7) is the standard one compartment linear pharmacokinetic model for the concentration of the ith agent if the dose rate is given by ui. The dependence of the model on the traits x makes this a highly unconventional problem that has a distributed aspect to it. At the same time, x-dependent controls, the natural choice for the mathematical structure, are not a realistic description of the underlying medical problem. The different effects that drugs have on cells of trait x are modelled by means of the functions φi(x), but drug administration is open-loop based on information at the beginning of therapy, i.e., ui=ui(t). In fact, for an optimal control problem of this type, it is not even clear how necessary conditions for optimality look. It therefore makes sense to start its analysis with finite-dimensional approximations.
2.2. Emergence of traits under cell density and mutations
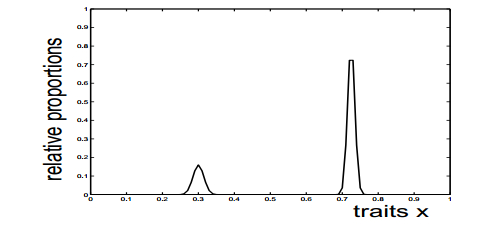
It is one of the main findings in the papers by Greene et al. [16,25] that with time specific traits emerge and become dominant. For the model described by equation (2), and also assuming a constant concentration c(t)≡c, if the function Δ(x)=r(x)−φ(x)c−μ(x) attains its maximum M in a finite number of points xi, i=1,…,k, then (and making some continuity and positivity assumptions) the total number of cells N(t) grows exponentially and the relative proportions of traits, ρ(t,x)=n(t,x)N(t), has a well-defined steady-state distribution given by a weighted average of Dirac δ-distributions at the traits with the fastest net growth rates [16,25].
As mutations are included into the modeling, these distributions 'smear' and have a larger support around these traits, but otherwise the same qualitative picture arises (see Fig. 1). Mutations are described through transition probabilities from one trait to another. For x,y∈[0,1], let p(x|y) denote the transition density of a change from trait y into trait x. Thus, for every y∈[0,1], p(⋅|y) is a nonnegative function that integrates to 1. For example, if one wants to capture the effect that small mutations are more likely than others, then a modified Gaussian kernel of the form
|
p(x|y)=k(y)exp(−12(x−yσ)2)
|
with σ the standard deviation and k(y) a normalizing constant is adequate. If, for simplicity, it is also assumed that at a given instant in time a fixed fraction θ, θ∈(0,1), of cells mutate, then this reduces the reproduction rate r by θ and the total flow of all mutating cells cells is given by
Hence the dynamics (4) with mutations takes the form
|
∂n∂t(t,x)={r(x)(1−θ)−φ(x)c(t)−G(N(t))μ(x)}n(t,x)+θ∫10p(x|y)r(y)n(t,y)dy.
|
(8)
|
The net effect of mutations on the growth of the total population thus is zero and the total growth is still described by the same differential equation as before,
|
dNdt(t)=∫10{r(x)(1−θ)−φ(x)c(t)−G(N(t))μ(x)}n(t,x)dx+∫10(θ∫10p(x|y)r(y)n(t,y)dy)dx
|
(9)
|
In particular, the total tumor population remains bounded.
Summarizing the results of Lorz et al. [35,36] and Greene et al. [16,25], in the long run (steady-state), specific traits, possibly with small variations, emerge and become dominant as an evolutionary response to different rates for growth and apoptosis, increasing cell densities and mutations. In the presence of mutations, this occurs regardless of whether these traits were present originally or not.
3. Optimal control for a mathematical model of sensitive and resistant populations
In view of the mathematically difficult problem formulation for the optimal control problem with a continuum of traits, it therefore makes sense to look at finite-dimensional approximations and, in fact, even models with a small number of compartments become illustrative. In the most extreme simplification, one can just consider "sensitive" and "resistant" populations (e.g., see [19,29]). Mathematically, however, we only assume that the 'resistant' population has a lower sensitivity to the chemotherapeutic agent that is being applied, not necessarily that there is none. We denote the populations of sensitive cells (total numbers of cells or volume) by S and the population of resistant cells by R. In the model, it is allowed that sensitive cells mutate into resistant ones, but also that resistant ones resensitize. The latter fact is well-documented in the literature on cancer as acquired drug resistance can be lost in a drug free environment (e.g., see [17,22]) whereas naturally such transitions are less likely or do not occur in case of intrinsic drug resistance. Thus a simple 2-compartment model for the evolution of sensitive and resistant populations takes the following form
|
˙S=(r1−θ1−φ1c)S+θ2R,S(0)=S0,
|
(10)
|
|
˙R=θ1S+(r2−θ2−φ2c)R,R(0)=R0,
|
(11)
|
where c denotes the concentration of the chemotherapeutic agent. The constants r1 and r2 are the replication rates of the respective populations and θ1 and θ2 describe the exchange between the two subpopulations. Here, as a simplifying assumption, the apoptosis rate has been set to zero, i.e., increasing cell densities are not included in the model. Cell kill is modelled using the standard linear log-kill hypothesis and the coefficients φ1 and φ2 define the effects of the drug on the two subpopulations (pharmacodynamics). According to the labeling of the populations, we assume that φ1>φ2≥0 with the case φ2=0 corresponding to the situation of a fully resistant second subpopulation. The concentration c may either be considered as the control in the system [29] or it may be modelled as a third state variable by including a pharmacokinetic model. In the simplest case, as above, this is given by the standard model of exponential growth and decay,
with k=ln2T and T the half-life of the agent.
3.1. Formulation as optimal control problem and numerical analysis
We consider the problem to minimize the tumor burden over a fixed therapy interval [0,T] through administration of chemotherapy. Toxicity of the treatment is taken into account indirectly by including the integral ∫T0u(t)dt, which denotes the total dose of drugs given over the interval [0,T], as a penalty term in the objective. Under the log-kill hypothesis the damage done to cells is proportional to the concentration of drugs given and thus this term represents the toxic side effects of treatment. We consider the following optimal control problem:
[C]: For a fixed therapy horizon [0,T], minimize the objective
|
minJ=α1S(T)+α2R(T)+∫T0(β1S(t)+β2R(t)+u(t))dt
|
(13)
|
over all Lebesgue-measurable functions u:[0,T]→[0,umax] subject to the dynamics (10)-(12).
In the objective, α1, α2, β1 and β2 are positive coefficients that represent weights; umax denotes the maximum drug dose rate. It is convenient to introduce a compact notation for the state, but we wish to separate the concentration c of the chemotherapeutic agent from the vector denoting the cancer cells. Let z=(S,R)T and denote by A and B the matrices
|
A=(r1−θ1θ2θ1r2−θ2)andB=(−φ100−φ2),
|
so that equations (10) and (11) take the bilinear matrix form
We also write α=(α1,α2) and β=(β1,β2) for the row vectors in the objective which then takes the form
|
J=αz(T)+∫T0(βz(t)+u(t))dt.
|
(15)
|
First order necessary conditions for optimality are given by the Pontryagin maximum principle [43]. (For some more recent references on optimal control, see [7,8,34,44]). Essentially, these conditions assert that if u∗:[0,T]→[0,umax] is an optimal control with corresponding trajectory (z∗,c∗), then there exist multipliers λ=(λ1,λ2):[0,T]→(R2)∗ (which we write as a row vector) and μ:[0,T]→R that satisfy the adjoint equations
|
˙λ=−∂H∂z=−β−λ(A+c∗B),λ(T)=α,
|
(16)
|
|
˙μ=−∂H∂c=−λBz∗+kμ,μ(T)=0,
|
(17)
|
and are such that the optimal control u∗ minimizes the Hamiltonian function H defined by
|
H=H(λ,μ,z,c,u)=βz+u+λ(A+cB)z+μ(−kc+u),
|
(18)
|
in u over the control set [0,umax] along (λ(t),μ(t),z∗(t),c∗(t)).
Any controlled trajectory ((z,c),u) for which there exist multipliers λ and μ such that these conditions are satisfied, is called an extremal and the triple ((z,c),u,(λ,μ)) is an extremal lift. Since the Hamiltonian H is linear in the control u, it is clear that the minimization property gives us that
|
u∗(t)={0if Φ(t)>0,umaxif Φ(t)<0.
|
(19)
|
where Φ is the so-called switching function given by
Whenever the switching function does not vanish, optimal controls are given by either full dose treatment or no treatment at all. However, optimal controls may take values in the interior of the control set if Φ vanishes identically over some open interval. Such controls are called singular while controls which only take values in the boundary points of the control interval are called bang-bang controls. Whenever Φ(τ)=0 and ˙Φ(τ)≠0, then the optimal control switches between umax and 0 depending on the sign of the derivative, ˙Φ(τ), which gives the switching function its name. Optimal controls typically consist of concatenations of bang and singular structures that need to determined through an analysis of the properties of the switching function.
3.2. On the structure of optimal controls
Except for degenerate situations, singular controls can be determined by differentiating the switching function in time until the control u explicitly appears in the formula. It follows from general facts of Lie algebra that this can only happen for the first time in an even numbered derivative. If this is the 2k-th derivative, then the control is said to be of intrinsic order k. (For details we refer the reader to [44]). It is then a necessary condition for optimality for the minimization problem, the so-called generalized Legendre-Clebsch condition [7,44], that
|
(−1)k∂∂ud2kdt2k∂H∂u(λ(t),μ(t),z∗(t),c∗(t),u∗(t))=(−1)k∂∂uΦ(2k)(t)≥0.
|
(21)
|
If this condition is violated, singular controls locally maximize the objective.
For the model considered here, because a linear pharmacokinetic model is included for the drug actions, it can be shown that singular controls are of intrinsic order 2 [31,32] and a direct computation verifies that the strengthened Legendre-Clebsch condition for optimality is satisfied. Specifically,
|
∂∂ud4dt4∂H∂u=−λ(t)[B,[A,B]]z(t)+βB2z(t)=(φ1−φ2)2(λ2(t)θ1S(t)+λ1(t)θ2R(t))+(β1φ21S(t)+β2φ22R(t))>0
|
(22)
|
where we use the facts that both the multipliers λ1 and λ2 and the states S and R are positive [32]. We thus have the following result:
Proposition 1. [32] Singular controls are of order 2 and the Legendre-Clebsch condition for minimality is satisfied.
Further analysis of the derivatives of the switching function shows that optimal controls necessarily are bang-bang if the fraction of sensitive cells is high. Specifically, the following result holds:
Proposition 2. [32] If the state (S,R) of the system lies in the set
|
BB={(R,S):((φ1−φ2)kθ2−β2φ1φ2S(t))R(t)≤β1φ21S(t)2},
|
(23)
|
then the corresponding optimal control is bang-bang with at most one switching from full dose, u≡umax, to no dose, u≡0. Especially this holds while the number of sensitive cells exceeds the threshold
If we choose the weights β1 and β2 in a way that makes the weighted populations of sensitive and resistant cells comparable in size, say β1S∼β2R, then equation (23) induces an approximately linear relation on S and R. In this case, it can be concluded that optimal controls are bang-bang if the percentage of sensitive cells lies above a certain threshold. As the proportion of sensitive cells decreases, lower partial dose rates for the control become viable. In fact, this result points to the following structure of controls as optimal: initially, as there is a high percentage of sensitive cells, give full dose therapies. This simply represents the case of a high tumor burden when immediate action becomes necessary. Later on, as the fraction of sensitive cells diminishes, switch to lower dose rates determined by the singular control. Note that we always have that μ(T)=0 at the end of the therapy interval and thus the switching function is positive at the terminal time T. This implies that optimal controls end with an interval when no drugs are given any more. Singular controls are a viable alternative for the intermediate section between full and no dose treatments.
Mathematically, however, a simple strategy of the form umax/using/0,
|
˜u(t)={umaxfor 0≤t≤τ1,usingfor τ1<t≤τ2,0for τ2<t≤T,
|
(25)
|
(consisting of full dose therapy followed by lowering the dose rates to the singular control and a restperiod at the end), although intuitive, cannot be optimal for the optimal control problem [C]. The reason lies in the fact that it is well-known in optimal control theory (e.g., see [44]) that concatenations of constant controls with singular controls of order 2 are not optimal. Indeed, optimal concatenations are accomplished by so-called chattering controls that switch between the extreme values umax and 0 infinitely many times (the so-called Fuller or Zeno phenomenon [31]). Clearly, for the underlying practical problem such concatenations are not feasible. On the other hand, simple approximations of the optimal chattering sequences, such as the intuitive sequence umax/using/0 generally do very well and often come close to the optimal values (e.g., see [28]). Thus control strategies based on equation (25) provide simple and generally excellent suboptimal approximations.
3.3. Numerical simulations of suboptimal approximations
We give some examples of suboptimal control strategies that follow this structure and initially give full dose treatment over an interval of length τ and then switch to the singular control for the rest of the therapy horizon, i.e., are of the form
|
uτ(t)={umaxfor 0≤t≤τ,usingfor τ<t≤T.
|
(26)
|
Mathematically, these controls represent simple heuristic approximations of what the theory suggests to be the optimal structure. Similar types of protocols that follow full dose therapy sessions with lower, reduced doses have been tested in medical trials and are referred to as "chemo-switch" protocols in the medical literature [20].
The values for our numerical simulations are summarized in Table 1. These values are only meant to illustrate the qualitative behavior of the system. As such we have selected numbers from a reasonable range given the meaning of the variables and parameters, but they are not based on medical data. Specifically, for the growth rates of the sensitive and resistant compartment we picked r1=3.5 and r2=1 reflecting a significantly higher growth rate for the more sensitive compartment. For the interchange between the compartments, we chose θ1=0.15 and θ2=0.02. This corresponds to a situation where it is much more likely that sensitive cells become resistant than it is that resistant cells resensitize. But this possibility is included and matters for the structure of solutions. We are assuming that the cytotoxic agent is able to kill a much larger fraction of the sensitive cells than of the resistant population and chose φ1=5 and φ2=1. So we still have a positive, though much lower cell kill for the population R in the model. For the chemotherapeutic agent we have taken as example the pharmacokinetic data for Taxol which has a half-life of 5.6 hours. If this is used to compute the clearance rate for the drug in days we get the value k=2.9706 shown in the table. But, once more, this is merely one representative value. The maximum dose rate was set to umax=10 which then leads to a maximum concentration of cmax=umaxβ=3.366. As initial conditions we chose a total tumor burden of 1010 cells and distributed the cells according to the steady state proportions of the uncontrolled dynamics. These simply are the limits for the solutions of the Riccati differential equation induced on the fraction σ=SS+R by the dynamics (e.g., see [45,Chapter 2]). Since the dynamics (10)-(11) is linear in S and R, this value can be normalized. In the objective, and in accordance with the normalization of the coefficient at the control to 1, we selected the coefficients β1 and β2 equal to 10−10 so that the initial term β1S(0)+β2R(0) is comparable to the highest dose rate. The therapy horizon for the simulations is given by T=21 or T=42 and could be thought of as [days].
Table 1. Values for the initial data and parameters used in numerical computations.
| parameters |
interpretation |
value |
| S0 |
initial condition of sensitive cells |
9:4051 × 109 |
| R0 |
initial condition of resistant cells |
0:5949 × 109 |
| r1 |
growth rate of sensitive population |
3:5 |
| r2 |
growth rate of resistant population |
1 |
| θ1 |
rate at which sensitive cells become resistant |
0:15 |
| θ2 |
rate at which resistant cells become resensitized |
0:02 |
| ψ1 |
log-kill coefficient for sensitive population |
5 |
| ψ2 |
log-kill coefficient for resistant population |
1 |
| k |
clearance rate of drug [Taxol] |
2:9706 |
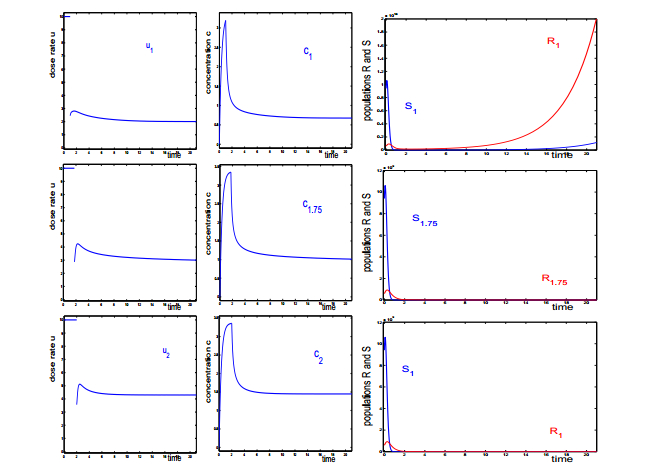
For these data, the initial condition lies in the region BB where optimal controls are bang-bang. If the initial segment τ is too short, the lower dose rates are not able to control the population size. While the sensitive population gets eradicated by the subsequent administration of drugs, the resistant population simply takes over (top row in Fig. 2). If the time τ is increased to τ=1.75, both populations decrease during administration of the singular dose rate. At the end of the initial MTD session, the sensitive cancer cells have been reduced significantly, S1.75(τ)=93153, but there remains a sizable resistant population, R1.75(τ)=5.112⋅107. Although resensitization expressed by the coefficient θ2 is small, combined with the fact that it is still assumed that the chemotherapeutic agent has some cytotoxic effect on the less sensitive compartment, the much lower dose rates are then able to control the cancer volume over the therapy interval (middle row in Fig. 2)). If the time τ is increased to τ=2, the sensitive population is almost eliminated (bottom row in Fig. 2)). The residual numbers of cancer cells after the MTD session are given by S2(τ)=51145 and R2(τ)=2.8244⋅107.
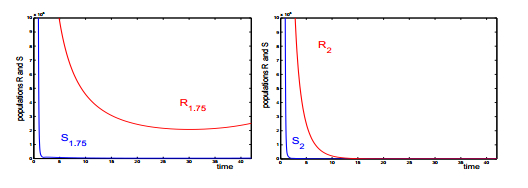
If a longer time horizon is considered, then the control which administers the maximum dose for time τ=1.75 and then switches to the singular control leads to an increase in the resistant population later on. Figure 3 shows a comparison of the strategies uτ for τ=1.75 and τ=2 over a time horizon of 42 days and while the population of resistant cells starts to slowly increase after about T=30, for τ=2 this does not happen. The reason lies in the overall growth rates for the total cancer population. If we define the time-varying growth rate χ(t) for the total cancer population C=S+R by ˙C(t)/C(t), then, with σ(t)=S(t)/C(t) and ρ(t)=R(t)/C(t), we have that
|
χ(t)=(r1−φ1c(t))σ(t)+(r2−φ2c(t))ρ(t).
|
(27)
|
In the case τ=2, the singular control and concentration actually reach a constant steady-state and the instantaneous growth rate stabilizes at the negative value χ=−0.4661. In the case τ=1.75, however, while the growth rate at time T=21 is negative, χ(21)=−0.0299, the system does not reach a steady-state, but rather increases over longer time intervals and we have that χ(42)=0.0319 and even χ(63)=0.1063. In this case the resistant and thus also the total population will eventually grow exponentially. This behavior, which is shown in Fig. 3, illustrates the importance of the initial full dose segment.
4. Extensions of results to multiple compartments
Similar results are valid when more, but still a small number of compartments, are considered. In fact, in [27] a 3-compartment model was analyzed that distinguished three levels of chemotherapeutic sensitivities, but allowed for transitions between all these compartments by means of gene amplifications or other mutation type events. In this case, and different from the results above, partial dose rates become an option for optimal controls from the onset. However, for these results an important aspect is that exchanges between the compartments are possible that make the overall dynamics resemble the behavior and properties of an ergodic Markov chain.
Since there is a qualitatively different behavior in the form of solutions, it is of interest to extend the analysis above to models with a large number of compartments. Returning to the model formulation in Section 2, if one considers n distinct traits and a single control u=u(t), and now writing N=(N1,…,Nn)T for the state of the system (the numbers of cancer cells for the specified finite numbers of traits), this leads to the following optimal control problem:
[Het-a]: with α, β and γ row vectors of positive weights, minimize
|
J=J(u)=αN(T)+∫T0(βN(t)+γu(t))dt
|
(28)
|
subject to the dynamics
|
˙Ni(t)={ri−ciu(t)−G(ˉN(t))μi}Ni(t),whereˉN(t)=1nn∑i=1Ni(t).
|
(29)
|
We can write the dynamics in matrix notation in the form
|
˙N(t)={R−Cu(t)−G(ˉN(t))M}N(t)
|
where R, C and M are diagonal matrices. In principle, this is a standard, nonlinear optimal control problem and generally such problems are difficult to solve if the dimension is high. In this case, however, the dynamics has special structure since all the matrices are diagonal and this simplifies the analysis. If one takes the weights β in the objective (28) equal, β=ˉβ(1,…,1), then singular controls can explicitly be computed [49] as feedback functions (i.e., functions that only depend on the states, but not on the multipliers),
|
using(t)=β(R−G(ˉN(t))M)N(t)βCN(t).
|
(30)
|
and they satisfy the Legendre-Clebsch necessary condition for optimality if the function G is increasing and concave [49]. Interestingly, the singular control has the property that it keeps the total population of cancer cells constant, i.e.,
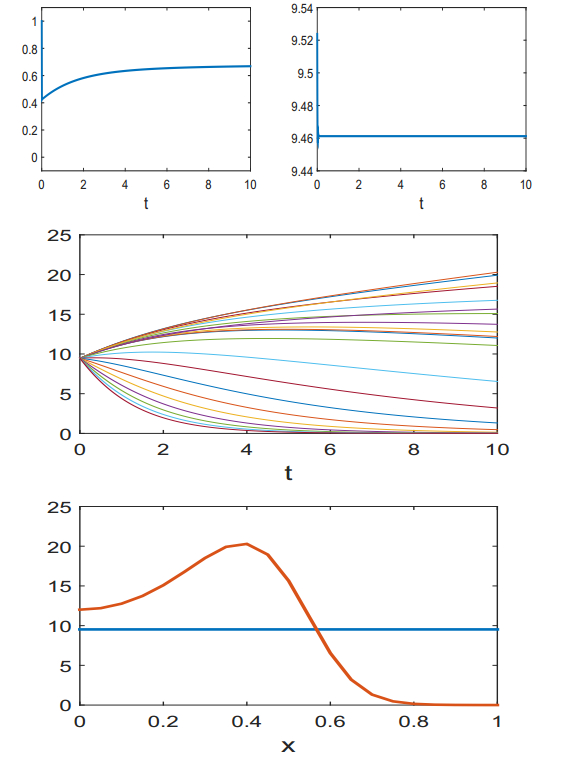
This feature is illustrated in Figs. 4 and 5 where we show the behavior of the system for controls that start with a full dose control over an initial interval [0,τ] and then switch to a singular control for the remaining period [τ,T]. The graphs shown in the figures give the result when this structure has been optimized over τ for n=21 traits. In the computations, the following functions were used in the dynamics:
|
r(x)=21.1+2x5,φ(x)=11+x2,μ(x)≡0.50.
|
(32)
|
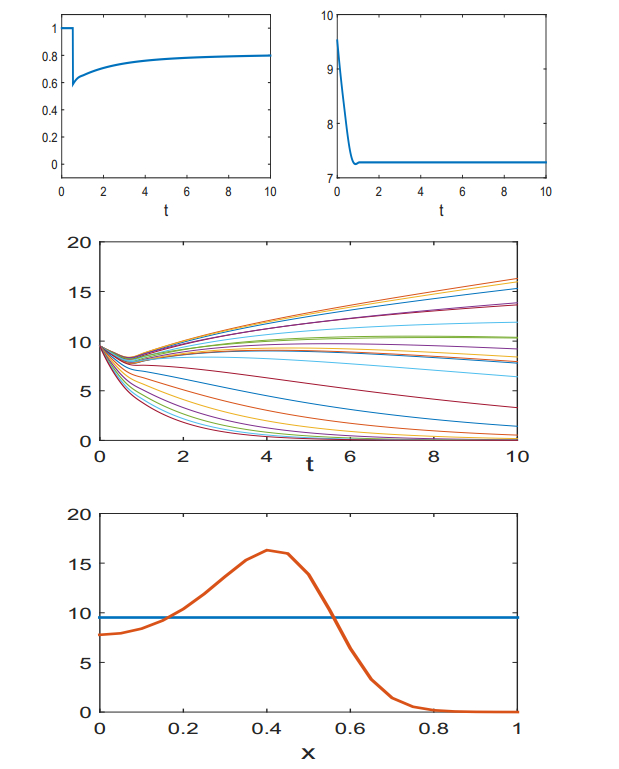
These functions simply represent replication rates and chemotherapeutic sensitivities that decrease in x [16]. No pharmacokinetic model has been used in these calculations, i.e., c=u. In each case, the weights in the objective favor the use of the singular control and there are only short initial periods of full dose therapy. In the first case, Fig. 4, the control is singular for almost all the interval and thus the total population remains basically constant. While some of the traits decrease, others increase and the panel at the bottom shows how the initial density, which was chosen to be uniform, changes under the control. For the functions given in (32) the sub-populations with highest x values are the ones that are diminished the most albeit these have the lowest drug sensitivities. The reason lies in the fact that these are also the slowest growing populations and the sensitivity to the drug is still high enough to eradicate these sub-populations. The net balance is the worst for x=0.4 and this population grows the strongest, i.e., has the worst overall therapy effect under this specific drug concentration. This example illustrates how the balance between replication rate and cytotoxic activities of the drug at a specific concentration interact to determine the dominant trait under treatment. Full dose therapy leads to a reduction in all traits, but for this particular objective side effects are judged more severe and thus the control becomes singular. In the second example, Fig. 5, the weight β in the Lagrangian term has been increased and thus more emphasis is put on the tumor size during the interval. As a result, the value of the singular control increases and, in fact, if β is increased beyond 15 the singular control exceeds the preset upper limit and becomes inadmissible. Essentially, in such a case the size of the tumor is the most important feature and the control becomes identically 1, the preset full dose.
Generally, the weights α, β and γ are variables of choice that need to reflect the underlying objectives of therapy balancing the need for tumor reduction with controlling side effects. The examples shown here give but one facet of the overall picture and are only intended to illustrate the effect that singular controls have in keeping the total population constant and thus controlling the tumor size. Clearly, in a practical case it may be difficult to obtain precise information about the functions r(x), φ(x) and μ(x), but qualitative information of the type that certain traits respond to one drug, but are resistant to another one, in principle can be incorporated and qualitative results about the structure of administration protocols are the main objective of this research.
5. Discussion and conclusions
Over the last years, clonal heterogeneity has been put on center stage as it is an important factor contributing to resistance to anticancer treatments and, most importantly, targeted therapies [38]. It has even been envisioned as the potential frontier to targeted therapies [47]. Here, using a simple model with one sensitive and one resistant clone, it is shown that a strategy that combines an initial MTD chemotherapy segment followed by metronomic chemotherapy, also called chemo-switch, results in effective control of the tumor. This approach has already been validated in vivo and in vitro [5,37,42].
The model presented in this paper can be developed further in various directions to be made more realistic. These include, for instance, taking into account more than two clones with different levels of resistance, different mechanisms of resistance and more than one anticancer agent. Such a model has been formulated in problem [Het]. Eventually, all components of the microenvironment, which includes the vessels that form the tumor vasculature or immune cells, need to be integrated. (A first attempt has been made in [26,46].) The resulting optimal treatment is expected to necessitate not only to adjust doses and schedules of one agent beyond what are chemo-switch regimens, but to generate a more complex, evolving treatment that anticipates and adjusts to evolutions of heterogenous clones. For the clinician this might result in an approach that would comprise combinations of drugs relying on an ever evolving mixture of the following therapeutic concepts: "dose effect", "dose intensity", "adaptive therapy" and "metronomics". This kind of unconventional treatment would result in a seemingly chaotic therapy that is not reachable with our current empirical approach. Combination of mathematics, biology and pharmacology though computational pharmacology is mandatory to be able to design such treatments [1,4].
Acknowledgments
The research of U. Ledzewicz, H. Schättler and S. Wang is based upon work partially supported by the National Science Foundation under collaborative research Grants Nos. DMS 1311729/1311733. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation. N. André, M.A. Heng and E. Pasquier thank "LNlavie", "Les copains de Charles" for their support.









 DownLoad:
DownLoad: