Finite-time stabilization of nonlinear systems with partially known states via aperiodic intermittent control and event-triggered impulsive control

1.   Introduction

In recent years, nonlinear systems have become a research hotspot in control theory due to their theoretical significance and practical applications in the synchronization of networked systems, digital signal processing, and stabilization of dynamical systems (see e.g., ^[1,2,3,4]). Among the many research directions of nonlinear systems, the problems of finite-time stabilization (FTS) and finite-time convergence stabilization (FTCS) have aroused widespread attention. FTS emphasizes that the system state will stabilize within a bounded region that is larger than the range of the initial state in a finite time (see e.g., ^[5,6,7,8]), while FTCS further emphasizes that the system state can converge to a bounded region smaller than the initial state range within a specified time (see e.g., ^[9,10,11]).

In engineering practice, control signals are crucial for maintaining the desired state of complex systems. Traditionally, continuous control strategies have been predominantly employed. However, as an innovative discontinuous control strategy, intermittent control (IC) offers significant advantages over continuous strategies. IC divides the time between two adjacent control signals into a "control interval" (operation) and a "rest interval" (no operation), thereby reducing redundant and unnecessary control actions and extending the lifespan of the equipment. Depending on whether the control signal is applied at fixed time intervals, IC can be classified into periodic intermittent control (PIC) (see e.g., ^[12,13]) and aperiodic intermittent control (APIC) (see e.g., ^{[14,15,16,17,18,19]}). In ^[13], the Halanay inequality and PIC were used to handle differential inequalities, thus successfully achieving the stability of highly nonlinear stochastic coupled systems. The theoretical results not only encompassed previous findings, but also provided theoretical support for the design and analysis in the field of nonlinear stochastic systems. However, the fact that the control signals in PIC are predefined and unchangeable restricts its flexibility for different applications. Therefore, a more flexible APIC is proposed, which adjusts the starting time sequence and control width to achieve a more efficient control. In ^[17], the input-to-state stability (ISS) of semi-linear systems was achieved through APIC, and the results indicated that the width of the control interval has a positive impact on the ISS of the system. In ^[19], further research on APIC led to the following conclusions: PIC and time-triggered APIC both belong to strong control schemes and achieve system stability more quickly than event-triggered APIC. However, event-triggered IC outperforms time-triggered IC in terms of the control number, control cost, and control rate. From the studies reported above, it is clear that APIC is a very powerful control tool.

In addition, impulsive control (IMC) is a discontinuous control method with extensive applications across diverse sectors including communication systems, automation, and aerospace (see e.g., ^{[20,21,22,23,24]}). Its main characteristic is the use of short-duration, high-intensity control inputs at specific discontinuous moments to regulate the system behavior. Traditional impulse sequences (IMS) are typically preset and essentially act as a time-triggered mechanism. However, unnecessary impulsive actions may occur during information transmission, thus resulting in a low control performance. Recently, event-triggered impulsive control (ETIMC) has emerged as a new research approach that combines event-triggered control (ETC) with IMC (see e.g., ^[25,26,27]). ETC is a mechanism that triggers control actions based on changes in the system state, rather than relying on fixed time intervals. In this way, the IMS in ETIMC is dynamically determined by an event-triggered mechanism (ETM), which closely links IMC to the system state. In ^[28], three event-triggered conditions were designed to achieve synchronization in chaotic dynamical systems. Similarly, in ^[29], a novel switching ETIMC was proposed, and an appropriate Lyapunov function was constructed to achieve quasi-synchronization in memristive neural networks with communication delays. Furthermore, in ^[30], a distributed ETIMC method was developed and was used to investigate the leader-following consensus problem in multi-agent systems. These control methods not only achieve a state consensus, but also effectively reduce the resource consumption.

It should be noted that a obtaining a complete system state in practical applications is often challenging due to external disturbances and technical limitations. Therefore, the design and implementation of control strategies based on the system state must fully take these practical difficulties into account. To address situations where only partially states is available, in ^[31], the problem of synchronization of neural networks with unmeasurable states was investigated using observers and state-feedback control to explore two scenarios: Unmeasurable states in the drive neural network and unmeasurable states in the response neural network. In ^[32], a dimensionality reduction technique was applied to separate known and unknown states, and the exponential stability of a switching system with partially unmeasurable states was achieved through a state feedback control. It is worth noting that the methodology to achieve FTS and FTCS in nonlinear systems with partially known states is still a complex problem and is insufficiently explored.

Based on the previous discussion, this paper proposes a novel hybrid control strategy that combines APIC and ETIMC to address the FTS and FTCS problems of nonlinear systems with partially known states. The key contributions of this paper are outlined below:

$(i)$ In the case of mismatched dimensions between the known and unknown states, we discuss two scenarios. By using dimension extension techniques, the dimensions of the known and unknown states are made equal, thereby facilitating the effective application of the results.

$(ii)$ We design a targeted impulsive control strategy that uses information from the known states to design impulsive control gains for the unknown states, thereby achieving state transitions at impulse moments and ensuring that the system meets the desired performance.

$(iii)$ Within the framework of FTS and FTCS, a close relationship is established between the event-triggered parameters, the intermittent control width, and the boundary parameters, thus preventing the occurrence of Zeno-behavior and ensuring the effectiveness and feasibility of the novel hybrid control strategy.

The paper is structured as follows: Section 2 introduces some necessary prerequisites; Section 3 focuses on several key conclusions and presents some critical conditions to support the FTS and the FTCS; Section 4 verifies the proposed conclusions using two simulation examples; and finally, Section 5 concludes the paper by summarizing the main content.

Notations: Let $\mathbb{R}$ and $\mathbb{N}$ signify the sets of real numbers and natural numbers, respectively. $\mathbb{R}^{n}$ and $\mathbb{R}^{n\times m}$ denote the $n$-dimensional real space and the $n\times m$-dimensional real space, respectively. $\lambda_{\max}(A)$ and $\lambda_{\min}(A)$ represent the maximum and minimum eigenvalues of matrix $A$, respectively. $A > 0$ (or $A < 0$) denotes that $A$ is a symmetric positive definite (or negative definite) matrix. $I$ and $O$ denote the identity matrix and the zero matrix of appropriate dimensions, respectively. $\star$ denotes the symmetric block of a symmetric matrix. $PC([-\tau, 0], \mathbb{R}^{n})$ denotes the set of right-continuous piecewise functions $\phi: [-\tau, 0] \to \mathbb{R}^{n}$ with the norm defined as $\left\| \phi\right\| _{\tau} = \sup_{-\tau\leq s\leq0}\left\| \phi(s)\right\|$. $C(S, L)$ denotes the family of continuous functions $\vartheta : S\to L$. For $\vartheta(t)\in C(S, L)$, $D^{+}\vartheta$ denotes the upper right-hand Dini derivative: $D^{+}\vartheta(t) = \underset{\vartriangle\to 0^{+}}{\lim }(\sup(\vartheta(t+\vartriangle)-\vartheta(t)))/\vartriangle$.

2.   Model description and preliminaries

Consider the following nonlinear time-delay system:

where $x(t)\in \mathbb{R}^n$ denotes the system state, and $\dot{x} \left (t \right)$ denotes the right-hand derivative of $x(t)$. $\tau$ is time delay, which is constant, and $\psi \in \mathrm{PC} [(-\tau, 0), \mathbb{R}^n]$. $A$ and $B$ $\in \mathbb{R}^{n\times n}$ are system matrices. The function $F(x) = \left(f_{1}\left(x_{1}\right), f_{2}\left(x_{2}\right), \cdots, f_{n}\left(x_{n}\right)\right)^{T}: \mathbb{R}^{n} \rightarrow \mathbb{R}^{n}$, ${{f}_{i}}\left(0 \right) = 0$, and positive constant ${{l}_{i}}$ meets

$C \in \mathbb{R}^{n\times r}$ is the coefficient matrix, and $u(t)$ is APIC, which is characterized as follows:

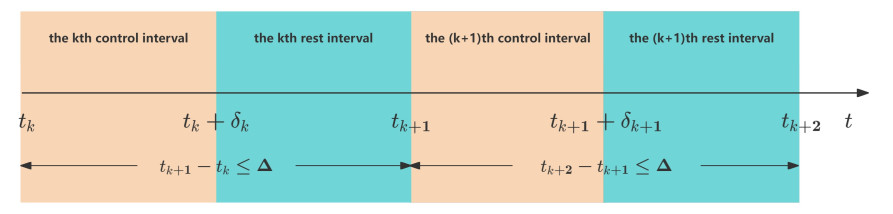
where $Z\in {{\mathbb{R}}^{r\times n}}$ is the gain matrix of APIC, $\{t_{k}: k\in {\mathbb{N}_{+}}\} = \{t_{k}\}$ is the IMS, as determined by the ETIMC devised later, and ${\delta }_{k}$ represents the control width of the APIC, which satisfies the relation $0 < {\delta }_{k} < t_{k+1}-t_{k}$. It is worth noting that controller (2.2) only carries out the input of the control signals in the control interval.

Upon introducing APIC (2.2) into system (2.1), one obtains the following:

where $K = CZ$.

Disturbances in the external environment, limitations in measurement techniques, and the complexity of the system structure make it possible that the states of a nonlinear system may not be completely known. In view of this, assume that system (2.3) has $m$ known states, where $0 < m < n$. Let $\Omega _{1} = \left \{ \jmath_{1}, \jmath_{2}, \dots, \jmath_{m}\right \}$ and $\Omega _{2} = \left \{ \jmath_{m+1}, \jmath_{m+2}, \dots, \jmath_{n}\right \}$ denote the set of subscripts of the known states and the set of subscripts of the unknown states, respectively. By a transition matrix $J$ to make $y = Jx = (x_{\jmath _{1} }, x_{\jmath _{2} }, \dots, x_{\jmath _{n} })^{T}$, then system (2.3) is transformed into the following:

where $A_{y} = JAJ^{-1}$, $K_{y} = JKJ^{-1}$, $B_{y} = JBJ^{-1}$, $\psi_{y} = J\psi$, $y = (y_{1}, y_{2})^{T}$, and $y_{1}\in \mathbb{R}^{m}$ and $y_{2}\in \mathbb{R}^{n-m}$ represent the portions that correspond to the known states and unknown states, respectively.

Remark 2.1. In recent years, hybrid control methods that combine APIC and ETIMC have been explored in ^{[25,26,27,28,29,30]}. However, these methods presuppose that the state information of the system is completely known. As a result, these aforementioned methods become inapplicable when only the partial state information is available. In this paper, we integrate APIC with ETIMC to study the FTS and FTCS of system (2.4), thereby extending the existing results. Specifically, we address two scenarios: one where the number of known states is greater than or equal to the number of unknown states, and the other where the number of known states is less than the number of unknown states.

Definition 2.1. ^[9] For the given positive constants $\mathcal{T}$, $\varrho_{1}$, and $\varrho_{2}$, where $0 < \varrho_{1} < \varrho_{2}$, system (2.4) is said to be FTS with respect to (w.r.t.) $(\mathcal{T}, \varrho_{1}, \varrho_{2})$ if there exists a controller such that, given $||y(0)|| \leq \varrho_{1}$, the trajectory of system (2.4) satisfies $||y(t)|| \leq \varrho_{2}$ for all $t \in [0, \mathcal{T}]$. Moreover, under the above conditions, if there exist positive constants $\mathcal{T^{0}}$ and $\varrho$ such that $0 < \mathcal{T^{0}} < \mathcal{T}$ and $0 < \varrho < \varrho_{1} < \varrho_{2}$, and the trajectory of system (2.4) satisfies $||y(t)|| \leq \varrho$ for $t \in [\mathcal{T}-\mathcal{T^{0}}, \mathcal{T}]$, then system (2.4) is said to be FTCS w.r.t. $(\mathcal{T}, \varrho_{1}, \varrho_{2}, \varrho, \mathcal{T^{0}})$.

Remark 2.2. According to ^[9,25], FTS describes the "boundedness" of a system whose state is stabilized in a bounded region that is larger than the initial state range for a finite period of time. In contrast, FTCS emphasizes that the system trajectory must remain within a smaller region than the initial boundary for a defined period time. In other words, FTCS not only reflects the "boundedness" of the system, but also demonstrates the "contraction" of the system.

Lemma 2.1. ^[33] For $t\in (-\tau, +\infty)$, if the continuous function $y\geq 0$ meets

then

Lemma 2.2. ^[34] For any real matrices $\mathcal{G} > 0$ and scalar $\iota > 0$, the following relevant inequality holds:

Lemma 2.3. ^[35] For a given symmetric matrix $\mathcal{M} = \left [ \begin{matrix} \mathcal{M}_{11} & \mathcal{M}_{12} \\ \mathcal{M}_{12}^{T} & \mathcal{M}_{22}\end{matrix} \right ]$, where $\mathcal{M}_{11}\in \mathbb{R} ^{s\times s}$, the following three conditions are equivalent:

$(i)$ $\mathcal{M} < 0,$

$(ii)$ $\mathcal{M}_{22} < 0, \mathcal{M}_{11}-\mathcal{M}_{12}\mathcal{M}_{22}^{-1}\mathcal{M}_{12}^{T} < 0,$

$(iii)$ $\mathcal{M}_{11} < 0, \mathcal{M}_{22}-\mathcal{M}_{12}^{T}\mathcal{M}_{11}^{-1}\mathcal{M}_{12} < 0.$

3.   Main results

Since there are partially unknown states in system (2.4), the designed ETM can only rely on the partially known states. Based on this, the corresponding ETM design scheme is proposed:

the forced impulse sequence (FIMS) $\{t_{k}^{\diamond}\}$ satisfies

and the event-triggered function

where $V_{1}(t)$ denotes the Lyapunov function, which depends on the known state $y_{1}$. $\Delta$ stands for the forced impulse interval, which is usually set to a sufficiently large constant. $a_{k} > 0$ represents the parameters of the ETM.

Remark 3.1. Zeno-behavior occurs when the designed trigger condition is continuously satisfied. To prevent Zeno-behavior, a uniform positive lower bound should be set for the impulse intervals (see e.g., ^[25,36,37]). Combining (2.2) and (3.2), it follows that $0 < {\delta }_{k} < t_{k+1}-t_{k}\le\Delta$. Let $\delta = \underset{k\in \mathbb{N}}{\inf }\{\delta_{k}\}$; then $0 < {\delta } < t_{k+1}-t_{k}\le\Delta$, thereby excluding Zeno-behavior in the ETIMC.

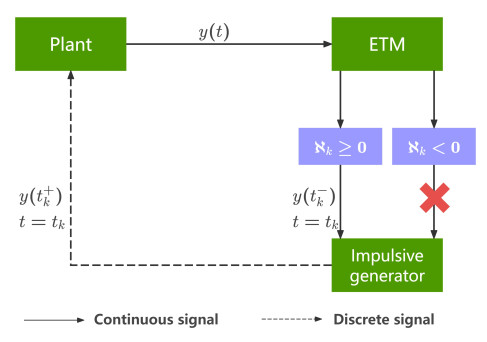
Remark 3.2. Figure 1 shows the cyclic process of hybrid control, where dashed and solid lines represent discrete and continuous signals in the system, respectively. The ETM is used to detect whether predefined events occur. When $\aleph_{k} \geq 0$, the predefined event occurs, and the system receives the transmission value $y(t_{k}^{-})$. After calculation by the impulsive generator, $y(t_{k}^{+})$ is transmitted to the system. At this point, the system will enter the next cycle in accordance with the revised data conditions. When $\aleph _{k} < 0$, the predefined event does not occur, and no signal is transmitted to the system. Figure 2 presents the framework of hybrid control, which introduces forced impulse instants on top of traditional impulse signal release, aiming to prevent the ETM from remaining inactive for an extended period, thus ensuring the system meets the desired performance objectives.

Next, we will discuss the FTS and FTCS in system (2.4) under a hybrid control in two cases based on the quantitative relationship between the known and unknown states.

3.1.   The number of known states is greater than or equal to the number of unknown states

When $m \geq n-m$, let $y = (y_{1}, y_{2})^{T}$, where $y_{1} = (y_{1}^{1}, y_{1}^{2})^{T}$, ${y}_{1}^{1} = {{({{x}_{{\jmath}_{1}}}, {{x}_{{\jmath }_{2}}}, \cdots, {{x}_{{\jmath}_{n-m}}})}^{T}}\in \mathbb{R}^{n-m}$, ${y}_{1}^{2} = {{({{x}_{{\jmath }_{n-m+1}}}, {{x}_{{\jmath }_{n-m+2}}}, \cdots, {{x}_{{\jmath }_{m}}})}^{T}}\in \mathbb{R}^{2m-n}$, ${y}_{2} = {{({{x}_{{\jmath }_{m+1}}}, {{x}_{{\jmath}_{m+2}}}, \cdots, {{x}_{{\jmath }_{n}}})}^{T}}\in \mathbb{R}^{n-m}$. $F = \left (F_{1}, F_{2}\right)^{T}$, where $F_{1} = (F_{1}^{1}, F_{1}^{2})^{T}$, $F_{1}^{1} = (f(x_{\jmath_{1} }), f(x_{\jmath_{2} }), \cdots, f(x_{\jmath_{n-m} }))^{T}\in \mathbb{R}^{n-m}$, $F_{1}^{2} = (f(x_{\jmath _{n-m+1} }), f(x_{\jmath _{n-m+2} }), \cdots, f(x_{\jmath_{m} }))^{T}\in \mathbb{R}^{2m-n}$, $F_{2} = (f(x_{\jmath _{m+1} }), f(x_{\jmath_{m+2} }), \cdots, f(x_{\jmath_{n} }))^{T}\in \mathbb{R}^{n-m}$. Then, system (2.4) is given as follows:

where $y_{1}^{1}, y_{1}^{2} \in y_{1}$, $y_{1}$ is the known state, and $y_{2}$ is the unknown state.

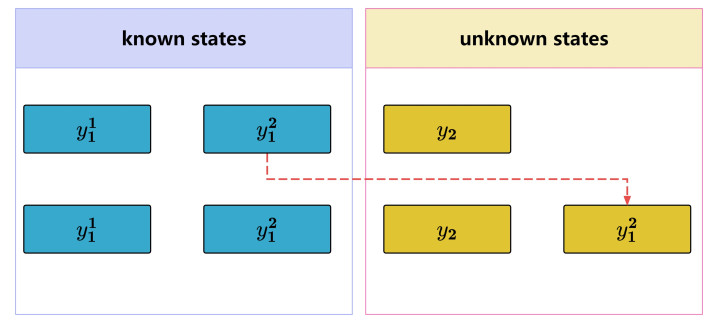
For $m > n-m$, as shown in Figure 3, we construct an augmentation term to make the number of known states equal to the number of unknown states. Let $\bar{y} = (\bar{y}_{1}, \bar{y}_{2})^{T}$, $\bar{y}_{1} = y_{1} = (y_{1}^{1}, y_{1}^{2})^{T}$, $\bar{y}_{2} = (y_{2}, y_{1}^{2})^{T}$, $\bar{F} = (\bar{F}_{1}, \bar{F}_{2})^{T}$, $\bar{F}_{1} = F_{1}$, and $\bar{F}_{2} = (F_{2}, F_{1}^{2})^{T}$. $\bar{y}_{1}$ and $\bar{y}_{2}$ represent the known and unknown parts of the states, respectively, and both have the same dimension. For $m = n-m$, system (3.3) does not perform a dimensional expansion and directly obtains $\bar{y}_{1} = y_{1}$, $\bar{y}_{2} = y_{2}$, $\bar{F}_{1} = F_{1}$, and $\bar{F}_{2} = F_{2}$. Hence, system (3.3) with ETIMC is updated as follows:

where

Remark 3.3. Unlike traditional impulsive controllers, which assume that all the system states are known, our design relies only on the partially known states at the impulsive moments. In other words, the impulsive jumps of the unknown states $\bar{y}_{2}$ are adjusted based on the known states $\bar{y}_{1}$.

Therefore, the analysis of the FTS and FTCS problems for system (2.1) is transformed into the analysis of the FTS and FTCS for system (3.4). For system (3.4), the IMS $\{t_{k}\}$ is dynamically determined by ETM (3.1), where $V_{1}(t) = {\bar{y}_{1}}^{T}(t)P_{1}\bar{y}_{1}(t)$, and $P_{1} \in \mathbb{R}^{m\times m}$ is a positive definite matrix. In the following, we will show that system (3.4) is the FTS and FTCS.

Theorem 3.1. Suppose there exist $m\times m$ real matrices $P_{1} > 0$, $P_{2} > 0$, $2m\times 2m$ real diagonal matrices $Q$, $M$, $m\times m$ real matrices $S_{1}$, $S_{2}$, and positive constants $\alpha_{1}$, $\alpha_{2}$, $\beta_{1}$, $\beta_{2}$, $\xi_{1}$, $\xi_{2}$, $\mathcal{T} > \mathcal{T^{0}} > 0$, $\varrho_{2} > \varrho_{1} > \varrho > 0$, and $\hbar > 1$, satisfying the following:

$(I_1)$ $\left (\begin{matrix} H\bar{A}+\bar{A}^{T}H-\alpha _{1}H-N-N^{T} & H\bar{B}\\ \star & -Q \end{matrix} \right) \le 0,$

$(I_2)$ $\left (\begin{matrix} H\bar{A}+{\bar{A}^{T}H-\alpha _{2}H} & H\bar{B}\\ \star & -M \end{matrix} \right) \le 0,$

$(I_3)$ $\left (\begin{matrix} -\hbar P_{1} & S_{1}&S_{2}\\ \star & -P_{1} & 0 \\ \star & \star & -P_{2} \end{matrix} \right) \le 0,$

$(I_4)$ $\xi_{1}I\leq H\leq\xi_{2}I,$

$(I_5)$ ${N(0, t)\ln\hbar+\sum\limits_{i = 0}^{N(0, t)}{{{a}_{i}}}+({{\alpha }_{2}}+{{\beta }_{2}})t_{N(0, t)+1}-({{\alpha }_{2}}+{{\beta }_{2}}-(\alpha_{1}+\beta_{1}))\sum\limits_{i = 0}^{N(0, t)}{{{\delta }_{i}}}}\leq \ln (\xi _{1}\varrho_{2}^{2})-\ln (\xi _{2}\varrho_{1}^{2}),$

where $H = \left (\begin{matrix} P_{1}+P_{2} & -P_{2} \\-P_{2} &P_{2}\end{matrix} \right)$, $L = diag\left \{ l_{\jmath_{1}}, \cdots, l_{\jmath_{n}}, l_{\jmath_{n-m+1}}, \cdots, l_{\jmath_{m}} \right \}$, $\beta_{1} = \lambda _{\max}(LQLH^{-1})$, $\beta_{2} = \lambda _{\max}(LMLH^{-1})$. Then, system (3.4) is FTS w.r.t $(\mathcal{T}, \varrho_{1}, \varrho_{2})$ under a hybrid control. Furthermore, if $t\in [\mathcal{T}-\mathcal{T^{0}}, \mathcal{T}]$, and

$(I_6)$ ${N(0, t)\ln\hbar+\sum\limits_{i = 0}^{N(0, t)}{{{a}_{i}}}+({{\alpha }_{2}}+{{\beta }_{2}})t_{N(0, t)+1}-({{\alpha }_{2}}+{{\beta }_{2}}-(\alpha_{1}+\beta_{1}))\sum\limits_{i = 0}^{N(0, t)}{{{\delta }_{i}}}}\leq \ln (\xi _{1}\varrho^{2})-\ln (\xi _{2}\varrho_{1}^{2})$

holds, then system (3.4) is FTCS w.r.t $(\mathcal{T}, \varrho_{1}, \varrho_{2}, \varrho, \mathcal{T^{0}})$ under a hybrid control. Besides, $N(0, t)$ delegates the number of control periods on $[0, \mathcal{T}]$, $\mathcal{T}\ne t_{k}$. The IMC gain matrices $G_{1}$ and $G_{2}$ are given by $G_{1} = P_{1}^{-1}S_{1}^{T}$, $G_{2} = P_{1}^{-1}S_{1}^{T}+P_{2}^{-1}S_{2}^{T}$, and the APIC gain matrix is given by $\bar{K} = H^{-1}N$.

Proof. For the given $0\le \left\| y(0)\right\|\leq\varrho_{1}$, let $y(t) = y(t, 0, \psi)$ be the solution of system (3.4) through $(0, \psi)$. Construct a Lyapunoov function as follows:

where $V_{1} = {\bar{y }_{1}}^{T}(t)P_{1}\bar{y }_{1}(t)$, $V_{2} = {\bar{y}_{2}(t)-\bar{y}_{1}}(t))^{T}P_{2}(\bar{y}_{2}(t)-\bar{y}_{1}(t))$.

For $t\in [t_{k}, t_{k}+\delta_{k}), k\in \mathbb{N}$, one obtains the following:

where $\beta_{1} = \lambda _{\max}(LQLH^{-1})$, $N = H\bar{K}$. From Lemma 2.1, one has the following:

When $t\in \left[ t_{k}+\delta_{k}, t_{k+1}\right)$, $k\in \mathbb{N}$, the following holds:

where $\beta_{2} = \lambda _{\max}(LMLH^{-1})$. From Lemma 2.1, one obtains the following:

Moreover, when $t = t_{k}, k\in \mathbb{N}_{+}$, the following holds:

In fact, when $t\in \left[ 0, \delta_{0}\right)$, from (3.7), one obtains the following:

Therefore,

For $t\in \left[\delta_{0}, t_{1}\right)$, combining (3.1) and (3.12), the following holds:

and

Next, we will claim that

For $t\in \left[t_{1}, t_{1}+\delta_{1}\right)$, combining (3.7), (3.10), and (3.14), one has the following:

and

For $t\in \left[t_{1}+\delta_{1}, t_{2}\right)$, combining (3.9) and (3.17), yields the following:

and

Thus, (3.15) holds for $k = 1$. Assume that (3.15) holds for $k = l$. When $t\in \left[t_{l}, t_{l+1}\right)$, it holds that

Then, we will show that (3.15) holds for $k = l+1$. From (3.20), we have the following:

Therefore, when $t\in [{{t}_{l+1}}, {{t}_{l+1}}+{{\delta }_{l+1}})$, we derive

and

For $t\in \left[t_{l+1}+\delta_{l+1}, t_{l+2}\right)$, combining (3.9) and (3.23), one obtains the following:

This is, (3.15) is satisfied for $k = l+1$. Therefore, (3.15) holds for all $k\in N(0, t)$. It holds that

By ($I_{4}$) and ($I_{5}$), we can easily obtain the following:

which signifies $\left\| y(t)\right\| \leq \varrho_{2}$; thus, $\left\| y(t)\right\| \leq \varrho_{2}$ holds on $[0, \mathcal{T}]$. Therefore, system (3.4) is FTS, meaning that system (2.1) can achieve FTS under a hybrid control. When $t\in [\mathcal{T}-\mathcal{T^{0}}, \mathcal{T} ]$, if $(I_{5})$ is satisfied, then from (3.25), we have the following:

which shows that $\left\| y(t)\right\| \leq \varrho$, for all $t\in [\mathcal{T}-\mathcal{T^{0}}, \mathcal{T} ]$. Therefore, system (3.4) is the FTCS, that is, system (2.1) can achieve FTCS under a hybrid control. □

3.2.   The number of known states is less than the number of unknown states

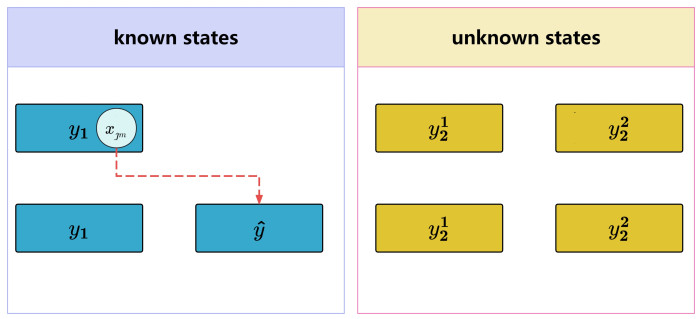
When $m < n-m$, let $y = (y_{1}, y_{2})^{T}$, where ${y}_{1} = {{({{x}_{{\jmath }_{1}}}, {{x}_{{\jmath}_{2}}}, \cdots, {{x}_{{\jmath}_{m}}})}^{T}}\in \mathbb{R}^{m}$, $y_{2} = (y_{2}^{1}, y_{2}^{2})^{T}$, ${y}_{2}^{1} = {{({{x}_{{\jmath }_{m+1}}}, {{x}_{{\jmath}_{m+2}}}, \cdots, {{x}_{{\jmath}_{2m}}})}^{T}}\in \mathbb{R}^{m}$, ${y}_{2}^{2} = {{({{x}_{{\jmath }_{2m+1}}}, {{x}_{{\jmath }_{2m+2}}}, \cdots, {{x}_{{\jmath }_{n}}})}^{T}}\in \mathbb{R}^{n-2m}$. $F = \left (F_{1}, F_{2}\right)^{T}$, where $F_{1} = (f(x_{\jmath_{1} }), f(x_{\jmath _{2} }), \cdots, f (x_{\jmath_{m} }))^{T}\in \mathbb{R}^{m}$, $F_{2} = (F_{2}^{1}, F_{2}^{2})^{T}$, $F_{2}^{1} = (f (x_{\jmath _{m+1} }), f(x_{\jmath_{m+2} }), \cdots, f (x_{\jmath_{2m} }))^{T}\in \mathbb{R}^{m}$, $F_{2}^{2} = (f (x_{\jmath_{2m+1} }), f(x_{\jmath _{2m+2} }), \cdots, f(x_{\jmath_{n} }))^{T}\in \mathbb{R}^{n-2m}$. Then, system (2.4) is given as follows:

where $y_{1}$ is the known state, $y_{2}^{1}, y_{2}^{2} \in y_{2}$, and $y_{2}$ is the unknown state. For $m < n-m$, as shown in Figure 4, we construct an augmentation term to make the number of known states equal to the number of unknown states. Expending the dimension of $y_{1}$ with $x_{\jmath_{m} }$, it leads to $\tilde{y}_{1} = (y_{1}, \hat{y})^{T}$, $\tilde{F}_{1} = (F_{1}, \hat{F})^{T}$, where $\hat{y} = (x_{\jmath_{m} }, x_{\jmath_{m} }, \cdots, x_{\jmath_{m} })^{T}\in \mathbb{R}^{n-2m}$, and $\hat{F} = (f(x_{\jmath_{m} }), f(x_{\jmath_{m} }), \cdots, f(x_{\jmath_{m} }))^{T}\in \mathbb{R}^{n-2m}$. Let $\tilde{y} = (\tilde{y}_{1}, \tilde{y}_{2})^{T}$, $\tilde{y}_{1} = (y_{1}, \hat{y})^{T}$, $\tilde{y}_{2} = y_{2}$, $\tilde{F} = (\tilde{F}_{1}, \tilde{F}_{2})^{T}$, $\tilde{F}_{1} = (F_{1}, \hat{F})^{T}$, and $\tilde{F}_{2} = F_{2}$. $\tilde{y}_{1}$ and $\tilde{y}_{2}$ denote the known and unknown parts of the states, respectively, with the same dimension. System (3.28) with ETIMC is updated as follows:

where

Therefore, the analysis of the FTS and FTCS problems for system (2.1) is transformed into the analysis of the FTS and FTCS for system (3.29). For system (3.29), the IMS $\{t_{k}\}$ is dynamically determined by ETM (3.1). For ETM (3.1), take $V_{1}(t) = {\tilde{y }_{1}}^{T}(t)P_{1}\tilde{y }_{1}(t)$, and $P_{1}\in \mathbb{R}^{(n-m)\times (n-m)}$ is a positive definite matrix. In the following, we will show that system (3.29) is the FTS and FTCS.

Theorem 3.2. Suppose there exist $(n-m)\times (n-m)$ real symmetric matrices $P_{1} > 0$, $P_{2} > 0$, $2(n-m)\times 2(n-m)$ real diagonal matrices $Q$, $M$, $(n-m)\times (n-m)$ real matrices $S_{1}$, $S_{2}$, and positive constants $\alpha_{1}$, $\alpha_{2}$, $\beta_{1}$, $\beta_{2}$, $\xi_{1}$, $\xi_{2}$, $\mathcal{T} > \mathcal{T^{0}} > 0$, $\varrho_{2} > \varrho_{1} > \varrho > 0$, and $\hbar > 1$, satisfying the following:

$(I_7)$ $\left (\begin{matrix} H\tilde{A}+\tilde{A}^{T}H-\alpha _{1}H-N-N^{T} & H\tilde{B}\\ \star & -Q \end{matrix} \right) \le 0,$

$(I_8)$ $\left (\begin{matrix} H\tilde{A}+{\tilde{A}^{T}H-\alpha _{2}H} & H\tilde{B}\\ \star & -M \end{matrix} \right) \le 0,$

$(I_9)$ $\left (\begin{matrix} -\hbar P_{1} & S_{1}&S_{2}\\ \star & -P_{1} & 0 \\ \star & \star & -P_{2} \end{matrix} \right) \le 0,$

$(I_{10})$ $\xi_{1}I\leq H\leq\xi_{2}I,$

$(I_{11})$ ${N(0, t)\ln\hbar+\sum\limits_{i = 0}^{N(0, t)}{{{a}_{i}}}+({{\alpha }_{2}}+{{\beta }_{2}})t_{N(0, t)+1}-({{\alpha }_{2}}+{{\beta }_{2}}-(\alpha_{1}+\beta_{1}))\sum\limits_{i = 0}^{N(0, t)}{{{\delta }_{i}}}}\leq \ln (\xi _{1}\varrho_{2}^{2})-\ln (\xi _{2}\varrho_{1}^{2})$,

where $H = \left (\begin{matrix} P_{1}+P_{2} & -P_{2} \\-P_{2} &P_{2}\end{matrix} \right)$, $L = diag\left \{ l_{\jmath_{1}}, \cdots, l_{\jmath_{m}}, \cdots, l_{\jmath_{m}}, l_{\jmath_{m+1}}, \cdots, l_{\jmath_{n}} \right \}$, $\beta_{1} = \lambda _{\max}(LQLH^{-1})$, $\beta_{2} = \lambda _{\max}(LMLH^{-1})$. Then, system (3.29) is FTS w.r.t ($\mathcal{T}, \varrho_{1}, \varrho_{2}$) under a hybrid control. Furthermore, if $t\in [\mathcal{T}-\mathcal{T^{0}}, \mathcal{T}]$, and

$(I_{12})$ ${N(0, t)\ln\hbar+\sum\limits_{i = 0}^{N(0, t)}{{{a}_{i}}}+({{\alpha }_{2}}+{{\beta }_{2}})t_{N(0, t)+1}-({{\alpha }_{2}}+{{\beta }_{2}}-(\alpha_{1}+\beta_{1}))\sum\limits_{i = 0}^{N(0, t)}{{{\delta }_{i}}}}\leq \ln (\xi _{1}\varrho^{2})-\ln (\xi _{2}\varrho_{1}^{2})$

holds, then system (3.29) is FTCS w.r.t $(\mathcal{T}, \varrho_{1}, \varrho_{2}, \varrho, \mathcal{T^{0}})$ under a hybrid control. Besides, $N(0, t)$ delegates the number of control periods on $[0, \mathcal{T}]$, $\mathcal{T}\ne t_{k}$. The IMC gain matrices $G_{1}$ and $G_{2}$ are given by $G_{1} = P_{1}^{-1}S_{1}^{T}$, $G_{2} = P_{1}^{-1}S_{1}^{T}+P_{2}^{-1}S_{2}^{T}$, and the APIC gain matrix is given by $\tilde{K} = H^{-1}N$.

Proof. The proof process of Theorem 3.3 follows similarly to that of Theorem 3.1, which is omitted here. □

Remark 3.4. The conditions $(I_{5})$, $(I_{6})$, $(I_{11})$, and $(I_{12})$ in Theorems 3.1 and 3.2 reveal the intricate interplay between the control interval width, the event-triggered parameter, and the boundary parameters. The results indicate that as the event-triggered parameter increases, the corresponding value of the IMS also increases, which can lead to the failure of the ETM. As a result, the IMS is entirely composed of the FIMS, thus preventing the system from reaching FTS and FTCS under the given conditions. Additionally, the values of $\alpha_{2}$ and $\beta_{2}$ must increase as the event-triggered parameter and impulse sequence values increase to ensure that conditions $(I_{5})$, $(I_{6})$, $(I_{11})$, and $(I_{12})$ hold.

4.   Numerical examples

To demonstrate the validity of the hybrid control method, two numerical examples are provided.

Example 4.1. For system (2.1), where function $f(x_{i}) = 0.3(|0.85x_{i}(t-\tau)+2|-|0.85x_{i}(t-\tau)-2|), i = 1, 2$, $\tau = 0.5$ and

Now, consider system (2.1), where $x_{2}$ is a known state, while $x_{1}$ is unknown state. A transition matrix $J$ can be constructed such that the transformed states are expressed as $y_{1} = x_{2}, y_{2} = x_{1}$. The transition matrix $J$, along with the transformed system matrices $A_{y}$ and $B_{y}$, are given by the following:

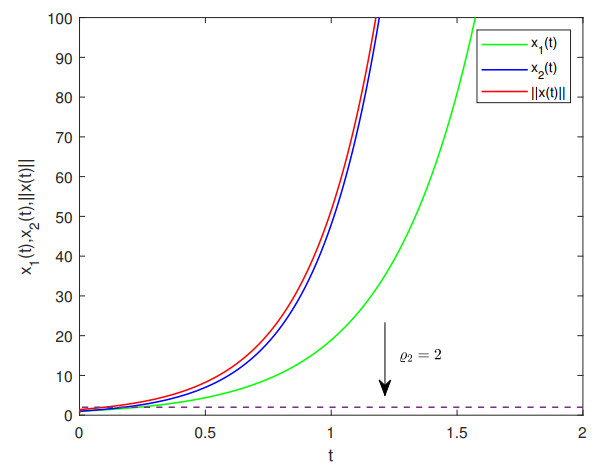
Let $y(0) = [1, 1]^{T}$, and the parameters be $\varrho_{1} = 1.3$, $\varrho_{2} = 2$, $\mathcal{T} = 3$. Based on the trajectories of system (2.1), as shown in Figure 5, system (2.1) is not FTS w.r.t. (3, 1.3, 2) without hybrid control.

Since $m = n - m = 1$, there is no need to construct an augmentation term. Therefore, under the hybrid control, system (2.1) is given as follows:

where $\bar{y}_{1} = y_{1}$ and $\bar{y}_{2} = y_{2}$ represent the known and unknown states, respectively. $\bar{F}_{1} = f(x_{2})$, $\bar{F}_{2} = f(x_{1})$, $\bar{A} = A_{y}$, and $\bar{B} = B_{y}$. Choose $P_{1} = 2.4$, $P_{2} = 2.2$, $\alpha_{1} = 1.5$, $\alpha_{2} = 9.6$, $\hbar = 1.04$, $\xi_{1} = 1$, and $\xi_{2} = 3.5$. Under condititions $(I_{1})$–$(I_{3})$ of Theorem 3.1, using the MATLAB toolbox, one can obtain the following:

Let $a_{k} = 8$, $\delta_{k} = 1.3$, and $\Delta = 3$; the ETM can be constructed by the following:

Therefore, the impulse instants are obtained as $t_1 = 1.3995$, $t_2 = 2.7992$, and $t_3 = 4.1989$. Furthermore, for $t \in [0, 3]$, the IMS $\{t_{k}\}$ satisfies the following:

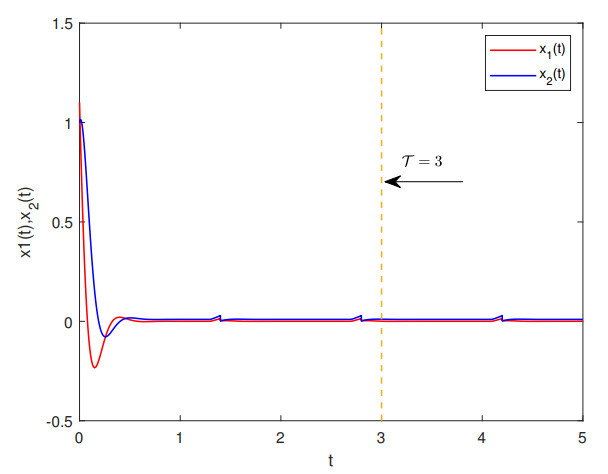
From Theorem 3.1, system (4.1) is FTS w.r.t (3, 1.3, 2) under the hybrid control strategy. For $\bar{y}(0) = [1.1, 1]^{T}$, the state trajectories of $x_{1}(t)$ and $x_{2}(t)$ are illustrated in Figure 6. Furthermore, let $\mathcal{T^{0}} = 1$, $\varrho = 0.2$; when $t\in [\mathcal{T}-\mathcal{T^{0}}, \mathcal{T}]$, the IMS $\{t_{k}\}$ satisfies the following inequality:

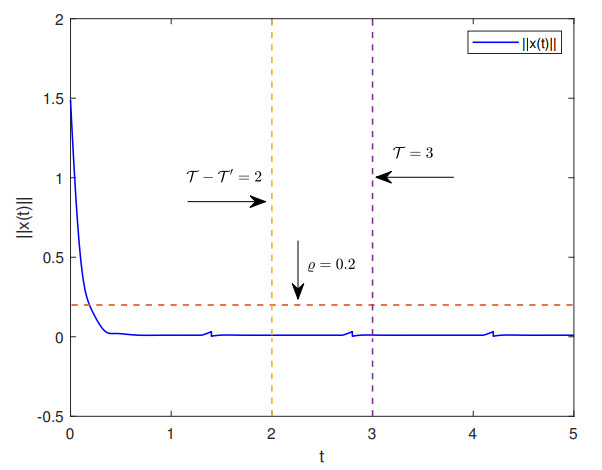
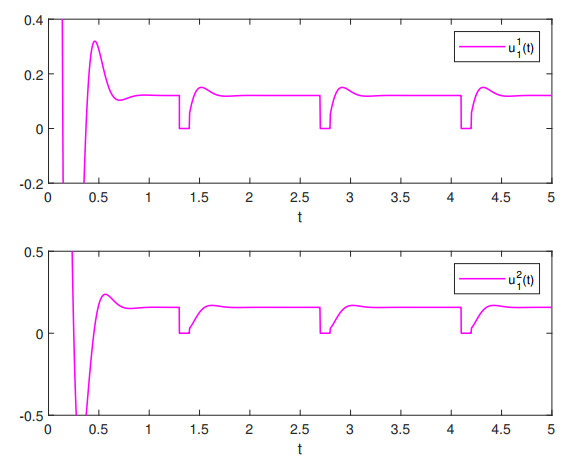
Moreover, according to Theorem 3.1, system (4.1) is FTCS w.r.t (3, 1.3, 2, 0.2, 1) under the hybrid control strategy. Let $\bar{y}(0) = [1.1, 1]^{T}$. Figure 7 illustrates the trajectory of the norm $\left\| x(t)\right\|$, while Figure 8 depicts the trajectories of $u_{1}$.

Example 4.2. For system (2.1), where function $f(x_{i}) = 0.3(|0.85x_{i}(t-\tau)+2|-|0.85x_{i}(t-\tau)-2|), i = 1, 2, 3$, $\tau = 0.5$ and

Now, consider system (2.1), where $x_{3}$ is a known state, while $x_{1}$ and $x_{2}$ are unknown states. A transition matrix $J$ can be constructed such that the transformed states are expressed as $y_{1} = x_{3}^{T}, y_{2} = (x_{1}, x_{2})^{T}$. The transition matrix $J$, along with the transformed system matrices $A_{y}$ and $B_{y}$, are given by the following:

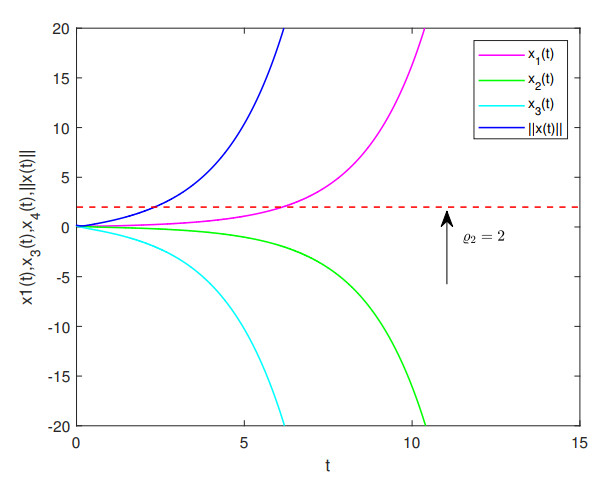
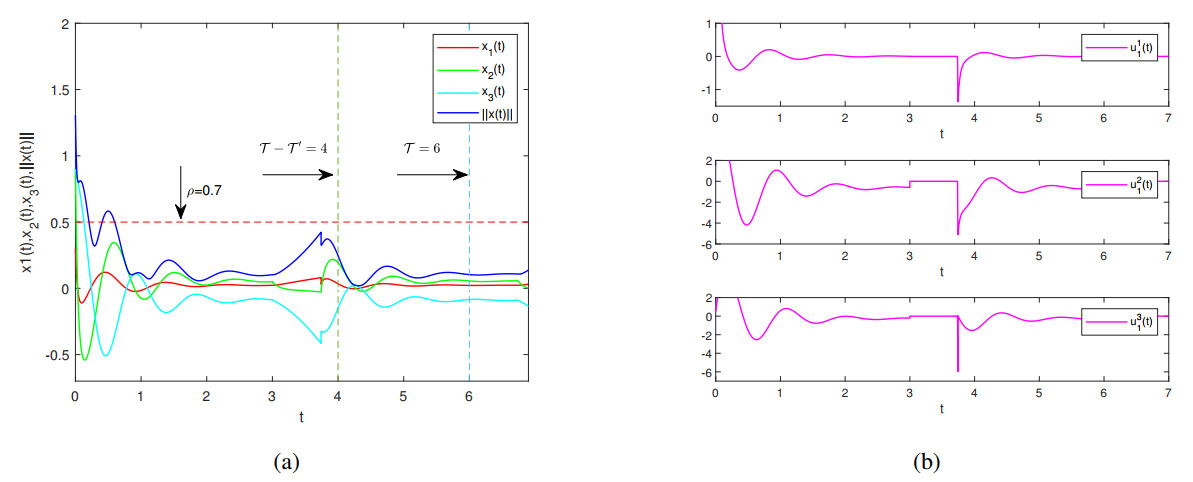
Let $y(0) = [0.1, 0.1, 0.1]^{T}$, and the parameters be $\varrho_{1} = 1.3$, $\varrho_{2} = 2$, $\mathcal{T} = 6$. Based on the trajectories of system (2.1), as shown in Figure 9, system (2.1) is not FTS w.r.t. (6, 1.3, 2) without a hybrid control.

Since $m < n - m$, we construct an augmentation term of $y_{1}$ using the known state $x_{3}$. Therefore, under the hybrid control, system (2.1) is given as the following:

where $\tilde{y}_{1} = (x_{3}, x_{3})^{T}$ and $\tilde{y}_{2} = (x_{1}, x_{2})^{T}$ are the known states part and unknown states part, respectively. Additionally, $\tilde{F}_{1} = (f(x_{3}), f(x_{3}))^{T}$, $\tilde{F}_{2} = (f(x_{1}), f(x_{2}))^{T}$, and

Choose $P_{1} = diag\{3, 2.4\}$, $P_{2} = diag\{2.37, 2.2\}$, $\alpha_{1} = 9.4$, $\alpha_{2} = 30$, $\hbar = 1.1$, $\xi_{1} = 1$, and $\xi_{2} = 4$. Under condititions $(I_{7})-(I_{9})$ of Theorem 3.3, using the MATLAB toolbox, one can obtain the following:

Let $a_{k} = 3.1$, $\delta_{k} = 3$, and $\Delta = 9$; the ETM can be constructed by the following:

Therefore, the impulse instants are obtained as $t_1 = 3.7418$, $t_2 = 7.5089$. Furthermore, for $t \in [0, 6]$, the IMS $\{t_{k}\}$ satisfies the following:

By Theorem 3.3, system (4.3) is FTS w.r.t (6, 1.3, 2) under the hybrid control strategy. Moreover, take $\mathcal{T^{0}} = 2$, $\varrho = 0.7$; when $t\in [\mathcal{T}-\mathcal{T^{0}}, \mathcal{T}]$, the IMS $\{t_{k}\}$ satisfies the following inequality:

Moreover, by Theorem 3.3, system (4.3) is FTCS w.r.t (6, 1.3, 2, 0.7, 2) under the hybrid control strategy. Let $\tilde{y}(0) = [0.3, 0.9, 0.9]^{T}$. Figure 10(a) illustrates the trajectories of $x_{1}(t)$, $x_{2}(t)$, and $\left\| x(t)\right\|$ are depicted in Figure 10(a), while Figure 10(b) depicts the trajectories of $u_{1}$.

5.   Conclusions

To address the limitation of traditional control methods that require the system state information to be completely known, this paper proposed a hybrid control strategy that combined IC and ETIMC to study the FTS and FTCS problems of nonlinear systems with partially known states. By employing impulsive differential inequalities and dimension extension techniques, impulsive control gains based on partially known states information were designed, and sufficient conditions to achieve FTS and FTCS were provided. Future research will focus on how to relax some restrictions in the theoretical criteria, thereby extending the applicability of the proposed method to a broader class of nonlinear systems.

Author contributions

Huiling Li: Writing-original draft; Jin-E Zhang: Supervision, writing-review and editing; Ailong Wu: Writing-review and editing. All authors have read and approved the final version of the manuscript for publication.

Use of Generative-AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this paper.

Acknowledgments

This work is supported by the National Natural Science Foundation of China under Grant 62476082.

Conflict of interest

The authors declare that there are no conflicts of interest.