Electromagnetic waves propagation in thin heterogenous coaxial cables. Comparison between 3D and 1D models

1.   Introduction and motivation

An electrical cable is a structure whose transverse dimensions are smaller than the longitudinal one. In particular, a co-axial cable is a dielectric material that surrounds metallic inner-wires and is surrounded by a metallic shield. A dielectric material is characterised by its dielectric permittivity $\varepsilon$ and its magnetic permeability $\mu$. The study of the propagation of electromagnetic waves along such a cable is an important issue in many industrial applications, such as wire troubleshooting. See ^[2] for a general review of wire troubleshooting, ^[1] for the detection of soft fault diagnosis in a simplified transmission line, and ^[5] for reconstruction of the underline graph of an unknown network. The simplest way to models a coaxial cable is to consider a 1D model called the telegrapher model, which deals with the propagation of the voltage $V^{\delta, 0}$ and the current $I^{\delta, 0}$ along infinitesimal LC quadripoles:

where the variable $z$ represents the longitudinal variable of the cable, $C$ the capacitance, and $L$ the inductance.

However, the real propagation of electromagnetic waves is governed by the 3D Maxwell equations. Solving the 3D Maxwell's equation is a not a trivial task: complex geometry due to defaults, or the 3D mesh for the thin cable. Indeed, performing such 3D simulations when the cable is thin can be a numerical challenge. One of computational difficulties comes from the fact that the transversal scale of the mesh must be small compared to the thickness $\delta$ of the cable, whereas the longitudinal scale of the mesh must be small in regard to the typical wavelength of input. The practical regime

implies that

In ^[9], we proposed an efficient numerical method to solve the 3D Maxwell equations in an elongated cylindrical coaxial cable. We used an anisotropic prismatic mesh, with a transverse mesh and a longitudinal mesh, which is consistent with the thin cable geometry, while relying on a hybrid implicit-explicit scheme. However, as the simulations are costly, engineers are not usually interested in the full electromagnetic fields, but rather in the electrical voltage and current that are 1D quantities. On the other hand, one could derive 1D models, called the telegrapher models. This leads to a good approximation of the solution of our 3D problem (see ^[4,15]). It is also worthwhile to mention that such models can be extended to the multi-conductors case: see ^[20] in the electromagnetism literature or ^[6] for a more rigorous approach. The simplified 1D models have been derived by performing an asymptotic analysis of the 3D Maxwell equations as the thinness of the cable tends to zero. In this asymptotic analysis, we assumed that the electromagnetic fields can be expanded in powers of $\delta$ where $\delta$ is the thinness parameter. The derivation of the simplified 1D models gives an explicit way to compute the effective inductance $L(z)$ and the effective capacitance $C(z)$ at each point $z$ from the geometry of the cross-section at point $z$ and the characteristic of the dielectric material. Unfortunately, this model cannot be used for fine wire troubleshooting since it is blind to some geometrical defaults and neglects some dispersive effects that are measured in practical experiments. Indeed, coefficients $L$ and $C$ are invariant under a conformal mapping, i.e, for two sections connected by a conformal map, $L$ and $C$ are the same. We expect a 1D model that takes into account all the geometrical defaults, or at least crushing, but it will require further analysis so as to have a model that is as exhaustive as necessary. A more accurate model was derived in chapter 5 of ^[4] by considering the second order terms in the asymptotic expansion. In that case, the electrical capacitance $C$ and inductance $L$ become spatial differential operators. More precisely, (1.1) must be replaced by

In the particular case where the permittivity and the permeability do not depend on the longitudinal variable $z$, the capacitance and inductance operators are second order elliptic operators given by

where $\kappa_e$ and $\kappa_m$ are computed from the geometry of the cross-section at point $z$ and the characteristic of the dielectric material. Note that when $\kappa_e$ and $\kappa_m$ are constants, one finds the equations of the linear ABCD-Boussinesq's model of shallow water-wave propagation (see ^[11]). We could not find any case in the classical literature on coaxial cables ^[20] where our new effective coefficients are introduced. This is because in the aforementioned literature the standard telegrapher's model is only valid for cylindrical cables with constant permittivity and permeability. In fact, under these hypotheses, our new effective coefficients $\kappa_e$ and $\kappa_m$ vanish. The coefficient $\kappa_e$ cannot vanish in the case where,

● the cable is made of cylindrical, concentric, different layers of homogenous dielectric material, known as an onion-like structure (from now on),

● the velocity of electromagnetic waves is not homogeneous.

In that case, the dispersion effect due to $\mathcal{C}^{\delta, 2}$ cannot be neglected. From $1$D models, one can reconstruct electromagnetic fields whith explicit formulae in order to make some comparisons with the 3D Maxwell equations. In particular we will see that the usual Transverse Electro-Magnetic (TEM) hypothesis is no longer true. This hypothesis states that the electric (and magnetic) field lines are all restricted to perpendicular directions to the direction of propagation. This is widely used to justify 1D models in the classical literature ^[20]. In ^[9], we also made comparisons between numerical simulations of (1.1) and between numerical simulations of the 3D Maxwell's equations. But, we have not shown the order of convergence with respect to $\delta$, which is to say

Moreover, as we have already stated, one expects more efficient approximations that take into account dispersives effects. The aims of the paper are threefold:

(1) We will be presenting the second order 1D model as well as a way to calculate the characteristic coefficients involved in the equations. Moreover, we will show that it is a well-posed problem (see Theorem 2.1).

(2) We will give a formal derivation of this second order model in the context of onion-like structures (see Theorem 3.1).

(3) We perform numerical comparaisons between the 1D model and the 3D Maxwell's equations in a periodic domain. More precisely, we aim to show (1.3) and

We are able to perform numerical simulations of the 3D Maxwell's equations only in the cylindrical case. This is why we will only consider cylindrical cables in this paper. Moreover, we will assume that the inner-wire and the shield are perfect conducting materials. That is, the electromagnetic waves are confined in the dielectric part of the cable so that we can neglect the skin-effect. See ^[7] for the derivation of the resistance from the skin-effect in the 1D model.

Notations: The usual Sobolev spaces are denoted by $H^r$, and $H^1_{/ \mathbb{R} }$ refers to Sobolev space with null average, i.e.,

2.   3D and 1D models of waves propagation in a co-axial cable

A cylindrical co-axial cable is a waveguide

such that all cross sections $S \times \{ x_3 \}$ are identical, and each cross section has a closed inner hole ${\mathcal{O}}$ with non-null area included in a bounded disk $\mathcal{B}$ of $\mathbb{R}^2$. Therefore, the domain $S$ has a boundary made of two connected parts

that assume to be Lipschtiz continuous. The boundary $\partial_{-} S$ is usually called the inner boundary, whereas $\partial_{+} S$ is usually called the outer boundary. The cable $\Omega$ is made of a dielectric material characterised by the electric permittivity and magnetic permeability

that are piecewise regular bounded positive functions.

2.1.   Wave propagation in a thin co-axial cable

A thin co-axial cable $\Omega^\delta$ is a co-axial cable $\Omega$ on which we apply a transverse scaling

parametrized by a small parameter $\delta \ll 1$ which refers to the thickness of the cable. More precisely, one has

Moreover, the characteristic coefficients of the thin cable $\Omega^{\delta}$ are obtained from the reference cable $\Omega$ by $\rho^\delta = \rho \circ \mathcal{G}_\delta^{-1}$, where $\rho = \varepsilon, \mu$. The notation $x_3 \in \mathbb{R}$ will always refer to the longitudinal variable, whereas $x_T = (x_1, x_2) \in \mathbb{R}^2$ will always refer to the transverse variables. The propagation of electromagnetic waves along the thin cable is described by the electromagnetic fields

which solve the 3D Maxwell equations

with initial conditions

where $\nabla_{(x_T, x_3)} \times$ stands for the usual 3D curl operator.

Note that we have made the three following simplifications:

(1) (Dielectric conductivity) We assume that there is no loss in the dielectric material. If we want to take it into account, we shall consider $\varepsilon^{\delta} \partial_t {E}^{\delta} + \sigma^{\delta} {E}^{\delta}- \nabla_{(x_T, x_3)} \times \, {H}^{\delta}$ instead of $\varepsilon^{\delta} \partial_t {E}^{\delta} - \nabla_{(x_T, x_3)} \times \, {H}^{\delta}$ where $\sigma^{\delta}$ is the electrical conductivity. For a practical cable, this conductivity is very small, i.e., of order $O(\delta^2)$. However, if the cable is wetted the conductivity, could be of order $O(1)$. This work was conducted in ^[6] when the $\delta^2$ terms are neglected.

(2) (Metallic conductivity) The boundary condition ${E}^{\delta} \times n = 0$ means that we consider the inner-wire and the metallic shields as perfect conducting materials. A more realistic model should consider highly conductive material instead of perfect conducting material. See ^[7] where the $\delta^2$ terms are neglected.

(3) (Easy data) The hypotheses on the initial conditions are not necessary, but they are just given for sake of simplicity. One could consider more general initial conditions.

(4) (Sole inner-wire) We consider only one inner hole ${\mathcal{O}}$. The case of several inner wires is treated in ^[6].

To compare with practical experiments, one can extract the voltage $V^\delta(x_3, t)$ and the current $I^\delta(x_3, t)$ from the electromagnetic fields. The way to extract it will be detailed in (6.1). Given the difficulty in solving the Maxwell equations, one can consider a 1D model of wave propagation. In this model, the unknowns are not the electromagnetic fields, but the voltage $V^{\delta, 2}(x_3, t)$ and the current $I^{\delta, 2}(x_3, t)$ which solve the following telegrapher's equations:

Here, the generalised capacitance $\mathcal{C}^{\delta, 2}$ and inductance $\mathcal{L}^{\delta, 2}$ operators are differential operators that will be defined later.

Let us note some consequences of the four simplifications we made:

(1) (Dielectric conductivity) If there is electrical conductivity of order $O(1)$, then we shall consider $\mathcal{C}^{\delta, 2}(x_3, \partial_{x_3}, \partial_t) \, \partial_t V^{\delta, 2} + GV^{\delta, 2} + K \ast_t V^{\delta, 2}$ instead of $\mathcal{C}^{\delta, 2}(x_3, \partial_{x_3}) \, \partial_t V^{\delta, 2}$ in the first equation of (2.3). The operator $\mathcal{C}^{\delta, 2}(x_3, \partial_{x_3}, \partial_t)$ becomes non-local in time, but the expression is complex These are described in Fourier frequency space in chapter 5 of ^[4].

(2) (Metallic conductivity) Considering highly conductive material instead of perfect conducting material leads to replacing $\mathcal{L}^\delta(x_3, \partial_{x_3}) \, \partial_t I^{\delta, 2}$ by $\mathcal{L}^\delta(x_3, \partial_{x_3}) \, \partial_t I^{\delta, 2} + \delta R \partial_t^{1/2} I^{\delta, 2} - \delta^2 L_{sk} I^{\delta, 2}$, where the resistance $R$ is described in ^[7], the fractional derivative $\partial_t^{1/2}$ stands for the Fourier multiplier associated to $\sqrt{i \omega}$ in Fourier frequency space, and the coefficient $L_{sk}$ is described in chapter 7 of ^[4] (see Theorem 7.5.2).

(3) (Easy data) If we consider general initial conditions, we need to add a source term in the 1D model (see chapter 5 of ^[4]).

(4) (Sole inner-wire) If we consider several inner wires, then the electrical voltage and current become vectors whose dimension coincide with the number of inner wires.

With the electrical voltage $V^{\delta, 2}$ and current $I^{\delta, 2}$, one can reconstruct an approximation $({E}^{\delta, 2}, {H}^{\delta, 2})$ of the electromagnetic field $({E}^{\delta}, {H}^{\delta})$ (see section 2.4). Note that if we formally take $\delta = 0$ into (2.3), one has the usual telegrapher Eq (1.1) whose solutions are denoted by $V^{\delta, 0}$ and $I^{\delta, 0}$. One can also reconstruct an approximation $({E}^{\delta, 0}, {H}^{\delta, 0})$ of the electromagnetic field $({E}^{\delta}, {H}^{\delta})$ from $V^{\delta, 0}$ and $I^{\delta, 0}$. In ^[4], some error estimates are proved in the case where the characteristic coefficients of the dielectric $\varepsilon^\delta$ and $\mu^\delta$ are continuous. Our aim is to illustrate such error estimates with numerical simulations when $\varepsilon^\delta$ and $\mu^\delta$ are piecewise constant.

Main result 1. Numerical results of (1.1), (2.2) and (2.3) satisfy

whereas

Finally, our results justify the use of 1D models instead of the full 3D Maxwell equations. Moreover, they also justify the preference for the second order 1D model (2.3) instead of the usual model (1.1).

2.2.   Harmonic potential and description of the effective capacitance and inductance

To define the generalised capacitance and inductance operators, one needs to introduce the harmonic potentials

which are the solutions of the following elliptic equations in the reference geometry

and

where:

● the differential operator $\nabla$ and $\mbox{div}$ refer to the usual 2D gradient and divergence operators on the cross-section $S$,

● the artificial cut $\Gamma$ is any artificial 1D curve which links the inner $\Sigma^{\frac{1}{2}}$ to the outer $\Sigma^{N+\frac{1}{2}}$ boundaries, and $[ \cdot ]_\Gamma$ the jump through the cut. Even if we can take any cut, we choose $\Gamma: = S \cap e_1$, where $e_1$ is the abscissa axis. Since the gradient of $\psi(\rho)$ has null jump through the cut, we can extend $\nabla \psi(\rho)$ on S. Then, if the harmonic potential $\psi(\rho)$ depends on the artificial cut, its gradient does not. This is why we say that $\Gamma$ is artificial. This property can be seen in the fundamental example of the case where the cross section is a circular annulus and $\rho$ is radial. Indeed, in that case one has in polar coordinate system $(e_r, e_\theta)$

First, note that neither $\psi(\rho)$ nor $\nabla \psi(\rho)$ depend on the weight.

They are called harmonic potentials since they span the harmonic spaces. More precisely, one can show that (see chapter 1 of ^[4])

and

where

and

These two harmonic potentials are conjugated in the sense that they satisfy the Cauchy-Riemann-like relations

where the 2D vectorial rotational $\nabla^{\perp}$ stands for

We will use extensively this conjugation relation (see chapter 1 of ^[4] for the proof).

We can take as weight $\rho$ the electric permittivity (respectively the magnetic permeability) which yields an harmonic potential $\varphi_e$ of electrostatic type (respectively $\psi_m$ of magneto-static type) and its conjugated potential $\psi_e$ (respectively $\varphi_m$). More precisely, one has

We also define the oscillating part

Definition 2.1. The capacitance and inductance coefficients are defined by

The effective capacitance and inductance operators are defined by the bilinear form

for all $V, U \in H^1$, and

for all $I, J \in H^1$.

First, we notice that the definitions of the effective capacitance and inductance operators are still valid when there is a variable cross-section, i.e., the cable is not cylindrical. In that case, $\partial_{x_3} \varphi_e$ must be interpreted as the Eulerian shape derivative $\varphi_e$ with respect to the variation of the shape of each cross-section. In that case, one needs to assume that the cross-sections are more regular than Lipschitz continuous. We refer the readers to ^[12] for the definition of Eulerian shape derivative. The explicit computation of $\partial_{x_3} \varphi_e$ is given in proposition 4.1.4 in ^[4].

In the particular case where the permittivity and the permeability satisfy the property

the capacitance and inductance operators are second order elliptic operators given by

where

are constants. Indeed, in that case, one gets $\partial_{x_3} \varphi_e = 0$, and $\partial_{x_3} \widetilde{\psi_m} = 0$ and thus with an integration by parts in the definition of $\mathcal{C}^{\delta, 2}$ and $\mathcal{I}^{\delta, 2}$, one has the expected expressions. The new coefficients $\kappa_e$ and $\kappa_m$, are respectively the electric and magnetic dispersion coefficients. If the electromagnetic wave velocity $c = 1/ \sqrt{\varepsilon \mu}$ is constant, then the dispersion coefficients $\kappa_e$ and $\kappa_m$ are null. Indeed, $\varphi_e = \varphi_m$ and $\psi_e = \psi_m$ as a consequence of

which ensure that $\varphi_e$ solves the problem satisfied by $\varphi_m$ (and so on for $\psi_e$ that solves the problem satisfied by $\psi_m$). In the following we shall be interested in cables for which dispersion occurs. One important class of dispersive media is provided by cables whose internal structure is made of finitely many materials structured in an onion-like manner. By this we mean that the coefficients are piecewise constant in successive concentric layers. This is the topic of the following subsection.

First, we want to underline that, under suitable geometric assumptions, the capacitance $C$ and the inductance $L$ are bounded from above and below. Indeed, in the case of a circular annulus of inner radius $r_-$ and outer radius $r_+$ and constant permittivity and permeability, one gets $C = \varepsilon 2 \pi / \ln(r_+ /r_-)$ and $L = \mu \ln(r_+ /r_-)/ (2 \pi)$ by directly solving Eqs (2.4) and (2.5) in the polar coordinate system $(e_r, e_\theta)$. In more general cases, see the following proposition:

Proposition 2.1. (i) Suppose that the hole $\mathcal{O}$ has a positive area $|\mathcal{O}|$, then

where $C_-: = \lambda_D \, |\mathcal{O}| > 0$ and $\lambda_D$ denotes the lowest eigenvalue for the Dirichlet problem associated to the Laplace operator in the domain $S \cup \mathcal{O}$.

(ii) Suppose that there exists an ellipse $\mathcal{E}_-$ with semi-major axis $a_-$ and semi-minor axis $b_-$ that surround the hole $\mathcal{O}$ without touching the exterior boundary. We denote by

where

where $D$ is the distance between the center of the ellipse $\mathcal{E}_-$ and the point of $\mathcal{E}_-$ which is the closed to the exterior boundary. One gets

Proof. (ⅰ) This is a consequence of Lemma 5.3 of ^[6]. (ⅱ) For the higher bound of $C$, we need to remark that the elliptic annulus $\mathcal{E}^\ast$ of the inner ellipse $\mathcal{E}_-$ (respectively outer ellipse $\mathcal{E}_+$) characterized by semi-major axis $a_-$ (respectively $a_+: = a_- + d_{\ast}$), semi-minor axis $b_-$ (respectively $b_+: = \sqrt{2a_- d_{\ast} + d_{\ast}^2 + b_-^2}$) is included in S. Thus, by the Dirichlet principle, we have $C \leq \sup(\varepsilon) Cap^{\ast}$ where $Cap^{\ast} = \int_{\mathcal{E}^\ast} | \nabla \varphi^\ast|$ is the capacity of the potential $\varphi^\ast$ solution of

Since $\mathcal{E}_-$ and $\mathcal{E}_+$ have the same focal $c = \sqrt{a_-^2-b_-^2} = \sqrt{a_+^2-b_+^2}$, the Joukowsky transform

maps conformally $\mathcal{E}^\ast$ to the circular annulus of inner radius $(a_-+b_-)$ and outer radius $(a_++b_+)$. Thus, since the capacity is invariant by conformal mapping, we have

which concludes the proof for the higher bound of $C$. The lower bound of $L$ is a consequence of the conjugation relationship (2.11).

It was shown in ^[6] that the capacitance $C$ and the inductance $L$ become positive-definite matrices when we consider several inner wires.

Remark 2.1. This proposition implies that the effective capacitance and inductance operators are non-negative:

We can do better by showing that the operators are in fact coercive on appropriate spaces.

Proposition 2.2. One has for all $V, U \in H^1(\mathbb{R})$

where

Proof. For all $V, U \in H^1(\mathbb{R})$, one gets

By integration by parts with respect to the longitudinal variable $x_3$, one has

and thus we have the expected formula.

Remark 2.2. In order to show that $\mathcal{C}^{\delta, 2}$ is a coercive operator from $H^1(\mathbb{R})$ to $H^1(\mathbb{R})$, one needs to assume that $C + \delta^2 (\eta_e- \partial_{x_3} \chi_e) \geq 0$ (which is in accordance with the smallness of $\delta$) and to show that $\kappa_e$ does not degenerate. As we will see later, this is indeed the case in the onion-like structure.

2.3.   Simplification in onion-like structure

We will assume that our cable has an onion-like structure whenever

● the cross-section $S$ is made of $N$ concentric layers $S^n$ such that

and such that

are 1D regular loops with non null perimeter that surround the inner-hole and never touch each other,

● for any $x_3 \in \mathbb{R}$, the electric permittivity $\varepsilon(x_T, x_3)$ and magnetic permeability $\mu(x_T, x_3)$, are transversely piecewise constant according to the partition (2.14), i.e., for any $x_3$ there exist positive bounded coefficients $(\varepsilon^n(x_3), \mu^n(x_3))$ such that

We want to show that under appropriate hypotheses, the effective telegrapher's Eq (2.3) is well-posed and deals with dispersive media.

Hypotheses 2.1. $(H1)$ The cable $\Omega$ has the onion-like structure as described above.

$(H2)$ The velocity $c = 1/\sqrt{\varepsilon \mu}$ is not constant with respect to the transversal coordinate.

$(H3)$ The hole $\mathcal{O}$ has a positive area, and there exists an ellipse that surrounds the hole $\mathcal{O}$ without touching the exterior boundary.

$(H4)$ The functions $x_3 \mapsto \varepsilon^n(x_3)$ and $x_3 \mapsto \mu^n(x_3)$ are bounded, regular, positive, and have non-null minima.

The main result of this section is the following:

Theorem 2.1. Assume hypotheses 2.1, and that the parameter $\delta$ is small enough such that $C + \delta^2 (\eta_e- \partial_{x_3} \chi_e) \geq 0$. Let $r \geq 0$ be a real number, and let $(I_0^{\delta, 2}, V_0^{\delta, 2}) \in H^{r}(\mathbb{R}) \times H^{r+1}(\mathbb{R})$ be initial conditions. Then, problem (2.3) is globally well-posed in $C^\infty(\mathbb{R}_+, H^{r}(\mathbb{R}) \times H^{r+1}(\mathbb{R}))$.

The dispersion plays a significant role. On the one hand, if the dispersion is neglected ($\delta = 0$), then (2.3) becomes the usual wave equation. Then, accordingly to the usual Lummer-Phillips theorem, the solution has the following regularity:

if the initial condition lies in $H^{r}(\mathbb{R}) \times H^{r+1}(\mathbb{R})$. To gain one temporal regularity, one must pay one spatial derivative. On the other hand, when there is dispersion, the solution has the following regularity

To prove Theorem 2.1, one needs to introduce a mapping that lets us work in the simplest geometry, which is a circular annulus. We denote by $\frak{v}^n$ the volume of each layer $S^n$ and by $2r_\ast$ the diameter of $S$. We construct a piecewise volume-preserving mapping

such that the restrictions $\mathcal{T}_v^n: = \mathcal{T}_v \Big |_{S^n}$ transform each layer $S^n$ into an annulus $C^n: = C(r^{n-\frac{1}{2}}, r^{n+\frac{1}{2}})$ where the radii are finding through the following induction:

The annuli $C^n$ are constructed such that area($S^n$)$=$area($C^n$).

Proposition 2.3. In the onion-like structure, one gets

where $\psi$ is the solution of the harmonic problem

Proof. We denote by

the solution of

We remark that $\hat{\psi} = (1- \frac{\theta}{2 \pi})$ satisfies system (2.17), which admits a unique solution. Consequently, $\psi_m$ depends only on the geometry and not on the permability $\mu$. The same reasoning holds for $\psi_e$. Moreover, one has

Thus, since ${\mathcal{T}}_v$ is a piecewise volume-preserving mapping, one gets

and therefore

In particular, the effective inductance operator is just the inductance coefficient, namely

Moreover, the conjugation relationship (2.11) becomes

Remark 2.3. The level set of $\varphi_e$ and $\varphi_m$ are always orthogonal to the level-set of $\psi$

This remark is a consequence of the previous proposition and the conjugation relation (2.11). Indeed, one has

Proposition 2.4. Under hypotheses 2.1 and assuming $C + \delta^2 (\eta_e- \partial_{x_3} \chi_e) \geq 0$, one has that, for all $V \in H^1(\mathbb{R})$,

where $C_- > 0$ is given in proposition (2.1) and $\kappa_0: = \min_{x_3}\, {\kappa_e(x_3)}$ is a positive constant.

Proof. Let $V \in H^1$.

Step 1. Proposition 2.2 implies, together with $C + \delta^2 (\eta_e- \partial_{x_3} \chi_e) \geq 0$,

Then, using proposition 2.1, one gets

Step 2. We show that there exits a positive constant $\kappa_0$ such that

when $c = 1/\sqrt{\varepsilon \mu}$ is not constant with respect to the transversal coordinate (hypothesis (H2)).

We notice that (2.19) is invariant under volume-preserving maps. Thus, we can work under the simple geometry given by the transformation $\mathcal{T}_v$. The harmonic potential satisfies (see step 3)

where the coefficients $B^n(\rho)$ are given by the sequence

where, initially,

is the solution to (2.4) under this simple geometry. This will be shown in Step 3. Then, one has

and thus after straightforward (but tedious) calculations, one gets

Moreover, one can show by induction that $\left(B^n(\varepsilon) - B^n(\mu^{-1}) \right)$ is null if and only if $\left(\frac{C}{\varepsilon^n} - \frac{\mu^n}{L}\right) = 0$.

Thus, (2.21) is null if and only if, for all $n$, one has $LC = \varepsilon^n\mu^n$.

Step 3. (2.20) is indeed the solution of (2.4) in $\mathcal{T}_v S$.

The function

satisfies $\Delta \varphi(\rho) = 0$ on each layer $\mathcal{T}_v S^n$. It remains to find the expression of $A^n$ and $B^n$. Moreover, we have with the jump of the normal derivative at each $r^{n+ \frac{1}{2}}$

such that $A^n(\rho) = A(\rho)$. In polar coordinates $(e_r, e_\theta)$, one gets,

and we deduce that

which is the expected expression. Taking the jump of $\varphi(\rho)$ at $r^{n+ \frac{1}{2}}$, we have

Taking the value of $\varphi(\rho)$ on the boundaries, we have

Proposition 2.4 with the Lax-Milgram theorem shows that $\mathcal{C}^{\delta, 2}: H^{r+2} \to H^r$ is a linear invertible operator for every real number $r \geq 0$. This is the keystone to ensure well-posedness.

Proof of Theorem 2.1. Let $r \geq 0$, and initial conditions $(I_0^{\delta, 2}, V_0^{\delta, 2}) \in H^{r}(\mathbb{R}) \times H^{r+1}(\mathbb{R})$.

Using the fact that $(\mathcal{C}^{\delta, 2})^{-1}: H^r(\mathbb{R}) \to H^{r+2}(\mathbb{R})$ is a regularized operator of order 2, we can write the telegrapher Eq (2.3) as the ODE

where $\frak{L}: H^{r}(\mathbb{R}) \times H^{r+1}(\mathbb{R}) \to H^{r}(\mathbb{R}) \times H^{r+1}(\mathbb{R})$ is the linear Lipschitz field on Banach spaces defined by

The local well-posedness is a consequence of the Cauchy-Lipshitz theorem.

An energy estimate

is obtained by multiplying the first equation of (2.3) by $V^{\delta, 2}$, the second by $I^{\delta, 2}$, summing both, and integrating over $\mathbb{R}_{x_3}$. In particular, it implies that it is globally well-posed.

If we remove assumptions (H1), (H2), and $C + \delta^2 (\eta_e- \partial_{x_3} \chi_e) \geq 0$, the problem (2.3) is still well-posed in $C^0(\mathbb{R}_+, L^2(\mathbb{R}) \times H^{1}(\mathbb{R}))$. The proof is more complicated since $\kappa_e$ can degenerate. This may be found in ^[4].

2.4.   1D model as good approximation of 3D model

We say that the 1D model is a good approximation of the 3D Maxwell equations since we can reconstruct the electromagnetic fields $({E}^{\delta}, {H}^{\delta})$ from the 1D voltage $V^{\delta, 2}$ and current $I^{\delta, 2}$ and the harmonic potentials through the formulae

and

for all $(x_T^\delta, x_3^\delta) \in \Omega^\delta$ where

while

and

where, for all $f \in L^2(S)$, the potentials $\xi[f] \in H^1(S)$ and $\zeta[f] \in H^1(S)$ are the solutions to the following elliptic problems:

Such reconstruction formulae will be derived in section 3, and a rigorous justification in Theorem 3.1.

An important feature for troubleshooting is that the electromagnetic wave could not be TEM of order $O(\delta)$, not even if the multilayer cable is cylindrical. In fact, we will see in the next section, that it can never be TEM if as the characteristic coefficients are different on each layer. Taking $\delta = 0$ in (2.22) and (2.23), one has that, for all $(x_T^\delta, x_3^\delta) \in \Omega^\delta$,

which are a less accurate approximation of the 3D Maxwell equations.

3.   Derivation of effective telegrapher equation

In order to derive a $1$D model, we first transform the $3$D Maxwell's Eq (2.2) to $1$D and $2$D considerations. So, the reader must be careful with the differential operators: some are $3$D ($\nabla_{(x_T, x_3)}, \nabla_{(x_T, x_3)} \times$), others are $2$D ($\nabla, \mbox{div}, \nabla^\perp, \mbox{rot}$). We have postulated in ^[6] an Ansatz of the electromagnetic fields in the form of a polynomial series of power $\delta$

where each coefficients

are given by injecting Ansatz (3.1) into the Maxwell's equations. This was done in ^[6]. We will just recall the cascade of equations to determine $({E}^{p+1}, {H}^{p+1})$ from $({E}^p, {H}^p)$. To do that, we separate for each 3D fields, the tangential component and the longitudinal one

We consider the fields $\mathbf{T}$ in $H(\mbox{div}, S)$ and $\varphi$ in $H^1(S)$. In this context, the operators $(\mbox{div}, \mbox{rot})$ are duals of $(\nabla, \nabla^{\perp})$ in the sense of Green's formulae as follows:

One also gets

We can see that the 2D rotational and gradient are linked by a rotation of $\pi/2$

The cascade of equations is the following:

$\qquad \bullet$ transverse electric fields

$\qquad \bullet$ transverse magnetic fields

$\qquad \bullet$ longitudinal magnetic fields

$\qquad \bullet$ longitudinal electric fields

with the convention

The Eqs (3.8) and (3.9) have meaning if and only if we can write

as a 2D vectorial rotational $\nabla^\perp$. Since they both be free-divergence fields, we need to prove that every divergence-free fields can be a rotational of 1D fields as consequence of (3.6) and (3.7) . It is obvious for simply connected domains, but one must check it in a non-simply connected domain like $S$.

Lemma 3.1. Any fields $u \in L^2(S)$ such that $\mathit{\mbox{div}}(\rho u) = 0$ can be written as a vectorial 2D rotational

with $\psi(\rho^{-1})$ defined in (2.5) and $\zeta$ the solution of the following elliptic problem:

Proof. One gets

such that

By the definition of $\tilde{u}$, we have

From Green's formula (3.2) and $\mbox{div}\; (\rho \, u) = 0$, one has

Moreover, one has with the conjugation relationship (2.11)

Thus,

which concludes the proof.

3.1.   Order 0 in the polynomial series Ansatz

3.1.1.   The longitudinal fields of order 0

Equations (3.8) and (3.9) with $p = -1$ show that the limit electromagnetic field is transversely polarized, namely

as it is usually assumed in the engineering literature (see ^[20]).

3.1.2.   Structure of the transverse fields of order 0

Equations (3.6) and (3.7) for $p = 0$ show that (see (2.7) and (2.8)) there exists functions

representing the electric voltage and electric current respectively, such that for all $(x_T, x_3) \in S \times \mathbb{R}$ one has

where we recall that $\psi_m = \psi$ (see proposition 2.3) in the onion-like structure.

3.1.3.   Equations for the electric voltage and current

The first equations of (3.8) and (3.9) with $p = 0$ do not provide closed equations for $(E_T^0, H_T^0)$ due to the presence of $(E_3^1, H_3^1)$. To get rid of them, as in ^[6] we take the scalar product in $L^2(S)$ of (3.9) and (3.8) with $\nabla \varphi_e$ and $\nabla \psi$, respectively. Using the expression (3.12) of $E_T^0$ and $H_T^0$, the Remark 2.3 and the definition (2.11) of coefficients $C$ and $L$, we then get

Finally, we remark that the terms involving $E_3^1$ and $H_3^1$ in the above equations vanish. Indeed, using Green's formula (3.3) and the fact that $\varphi_e$ is constant on each connected part $\partial S$, one has

Again, using Green's formula (3.3) and the fact that $E_3^1 = 0$ on $\partial S$ (see (3.9) with $p = 0$), one has

Finally, one gets the telegrapher's equation

with initial condition

This 1D wave problem is of course well-posed. More precisely, for any $r \geq 0$ if $V_0 |_{t = 0} \in H^{r+1}(\mathbb{R})$ then one has

3.2.   Order 1 in the polynomial series Ansatz

3.2.1.   The longitudinal fields of order 1

The Eqs (3.9) and (3.8) with $p = 0$ and the expression of $(E_T^0, H_T^0)$ given in (3.12) become

and

Using the conjugation relationship (2.18), one has

Finally, using the telegrapher's Eq (3.14), $E_3^{1} = 0$ on $\partial S$ and $\int_{S} \mu H_3^{1} = 0$ one has

We can first notice that the electromagnetic field cannot be transversely polarized since, in an onion-like structures, one has $\int_{S} \varepsilon | \varphi_e - \varphi_m | > 0$.

3.2.2.   The transverse fields

Equations (3.6) and (3.7) for $p = 1$ show that (see (2.7) and (2.8)) there exists functions $V_1: \mathbb{R} \rightarrow \mathbb{R}$ and $I_1: \mathbb{R} \rightarrow \mathbb{R}$ such that, for all $(x_T, x_3) \in S \times \mathbb{R}$, one gets

Applying the same reasoning as in section 3.1.3 with Eqs (3.8) and (3.9) with $p = 1$ instead of $p = 0$, one has

with null intial conditions. Thus, one has

and finally

The structure of first order fields $({E}^1, {H}^1)$ are completely different from the one at limit order $({E}^0, {H}^0)$. On one hand, the limit order field is transversely polarized. On the other hand, the first order field is longitudinally polarized.

3.3.   Order 2 in the polynomial series Ansatz

3.3.1.   The longitudinal fields of order 2

Using $(E_T^1, H_T^1) = (0, 0)$, the Eqs (3.9) and (3.8) with $p = 1$ become

Thus, one has

3.3.2.   Structure of transversal fields of order 2

Equations (3.6) and (3.7) for $p = 2$ give

and

We introduce

and

where, for all $f \in L^2(S)$, the potential $\xi[f] \in H^1(S)$ and $\zeta[f] \in H^1(S)$ are the solutions of the elliptic problems (2.24).

Thus, there exists functions

representing the electric voltage and electric current respectively, such that one has

3.3.3.   Equations for the electric voltage and current

The first equations of (3.8) and (3.9) with $p = 2$ do not provide closed equations for $(E_T^2, H_T^2)$ due to the presence of $(E_3^3, H_3^3)$. To get rid of them, as it was done in section 3.1.3, we take the scalar product in $L^2(S)$ of (3.9) and (3.8) with $\nabla \varphi_e$ and $\nabla \psi$, respectively. Using expression (3.12) of $E_T^2$ and $H_T^2$, Remark 2.3, and the fact that (same reasoning as in section 3.1.3)

and the fact that

we then get

By algebraic calculus, one gets

On one hand, using Green's formula (3.3) and Eqs (3.22), one gets

On the other hand,

which becomes

since by the orthogonality relation and conjugation relation

Then, using Green's formula (3.3) and the fact that $\partial_{x_3} \varphi_e = \varphi_e-\varphi_m = 0$ on $\partial S$, one gets

Thus, with (3.23), one has

where $\kappa_e$, $\eta_e$, and $\chi_e$ are defined in proposition 2.2. To sum up, one has one gets the telegrapher's equation

This 1D wave problem is of course well-posed. More precisely, for any natural numbers $s \geq 0$ and $r \geq s+2$ if $V_0 \in C^s \big(\mathbb{R}_+, H^{r+1-s}(\mathbb{R}) \big)$, one has

3.4.   Error estimates

In the previous sections, closed equations to compute $({E}^p, {H}^p, V^p, I^p)$ for $p = 0, 1, 2$. We can then compute

These aim at being good approximations of the approximate models $({E}^{\delta, 2}, {H}^{\delta, 2})$ and the electromagnetic fields $({E}^{\delta}, {H}^{\delta})$

in the sense that we have the following error estimates

Note that since $E_{\text{trunc}}^{\delta, 2}$ is defined in the reference geometry $\Omega$ whereas $({E}^{\delta}, {E}^{\delta, 2})$ are defined in the thin geometry $\Omega^\delta$, one needs the scaling $\mathcal{G}_\delta$ to compare them. The global estimation (3.30c) is the expected estimation and the consequence of (3.30a) and (3.30b). The proof of (3.30b) is beyond the scope of this paper, and was shown in ^[4]. We only show the modelling error estimation and illustrate with numerical simulation that we get an error of order $O(\delta^2)$. The main theorem of this section is the following:

Theorem 3.1. Take natural numbers $r \geq 3$ and $s \in [1, r-2]$ and initial condition $V_0 |_{t = 0} \in H^{r+1}(\mathbb{R})$. One has for the electrical voltage and current

One also has for the transverse electromagnetic fields

and

and for the longitudinal electromagnetic fields

and

Note that if one considers more general initial conditions and source terms, then one has $O(\delta^3)$ estimates instead of $O(\delta^4)$.

Proof.

The effective telegrapher's Eq (2.3) takes into account the telegrapher's Eqs (3.14), (3.18) and (3.27) that gives the electrical voltage and current at each order. Indeed, the combination

and the proposition 2.2 gives an equation on the modelling error

which is

With $r \geq 3$ and initial condition $V_0 |_{t = 0} \in H^{r+1}(\mathbb{R})$, (3.15) and (3.28) imply that $V_2 \in C^{s} \big(\mathbb{R}_+, H^{r+1-s-2}(\mathbb{R}) \big)$. Then, since $(\mathcal{C}^{\delta, 2})^{-1}$ is a regularised operator of order 2, one has

and thus

Similarly, the combinations

give

and

Thus, using the estimates on $\mathcal{V}$, one can conclude the expected modelling error estimates.

4.   Space-time discretization of the 3D model

For the 1D-3D comparisons, we will use the method that we introduced in ^[9]. The only purpose is to point out that, in the algebraic formulation of the problem, the matrices are affected by the small parameter $\delta$ representing the transverse dimension of the cable and to emphasize once more the fact that the CFL stability condition is independent of $\delta$. Practical cables are thin in the sense that $\delta \ll 1$. As mentioned in the introduction, this impies some numerical difficulties. In the considered applications, the wavelength is large compared to the diameter of the cross-section, but small compared to the size of the cable. This feature has two impacts on the time discretization:

$•$ an implicit scheme would be too costly given the size of the problem,

$•$ an explicit scheme is to be avoided because the corresponding CFL condition would be too constraining.

To take care of this, we use an anisotropic prismatic spatial mesh and a hybrid implicit-explicit scheme for the time discretization. This method has some similarities with the ADI schemes proposed by Fornberg and Lee (see ^[14,17,18] for an analysis). A prismatic spatial mesh means that $h_T \ll h$ where $h_T$ is the transverse step size $h_T$ and $h$ is the longitudinal step size $h$. To implement this method, the first step is to make a longitudinal discretization of the cable, then a transverse discretization of each section, and finally a discretization in time. We do not want to discretize a thin coaxial cable $\Omega^\delta$, we introduce the rescaled electric field $\widetilde{E}^\delta = (\widetilde{E}_T^\delta, \widetilde{E}_3^\delta)$ and magnetic field $\widetilde{H}^\delta = (\widetilde{H}_T^\delta, \widetilde{H}_3^\delta)$ that are casted in the reference cable $\Omega$. They are defined by

Thus, the electric field is the solution of

The details of computation from Maxwell's Eq (2.2) to the second order formulation of the rescaled Maxwell's Eq (4.1) are given in ^[9]. The discretization is performed in the reference geometry $\Omega$.

$•$ For the discretization in the longitudinal variables, we decomposed the cable $\Omega$ into small cylindrical cells

These cells of size $h$ in the $x_3$ direction are separated by transverse cross sections $S_j$ for all $j \in \mathbb{Z}$, where, by definition, ${\cal S}_{\nu} = \{ (x_T, \nu h), x_T \in S \},$ for all $\nu \in \mathbb R$.

$•$ For the discretization in the transverse variables, we introduced a conforming triangular mesh $\cal T$ of the section $S$ with step size $h_T$.

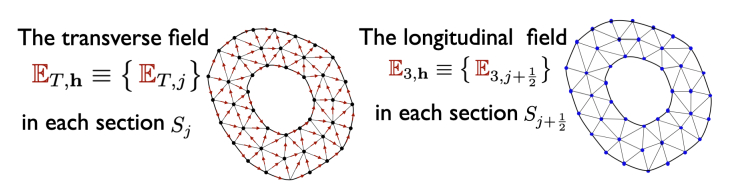
The transverse field $\widetilde{E}_T$ will then be approximated by Nedelec elements in each section $S_j$ and by piecewise affine elements along the longitudinal direction. On the other hand, the longitudinal field $\widetilde{E}_3$ field will be approximated by $\mathbb{P}_1$ elements on each $S_{j+1/2}$ section and by $\mathbb{P}_0$ discontinuous elements along the longitudinal direction (See Figure 1).

The fully semi-discrete variational problem reads: find $\big(\widetilde{E}_{T, {\mathbf h}}, \widetilde{E}_{3, {\mathbf h}}\big) \in {\mathbf V}_{\mathbf h}$ such that for any $\big({E}_{T, {\mathbf h}}, {E}_{3, {\mathbf h}}\big) \in {\mathbf V}_{\mathbf h}$,

where the space ${\mathbf V}_{\mathbf h}$ is the space of prismatic edge elements, namely,

with

${\cal P}_{K, j} = K \times [jh, (j+1)h ], \mbox{where } K \mbox{ is a triangle in the triangular mesh } {\cal T},$

${\cal T}_{3D}: = \big\{ {\cal P}_{K, j} \; / \; \, K \in {\cal T}, j \in \mathbb{Z} \big\}, \mbox{ such that } \Omega = \bigcup_{K, j} {\cal P}_{K, j},$

${\cal R} = \big\{ {E} = ({E}_T, E_3) \; | \; {E}_T(\cdot, x_3) \in \mathbb{P}_1(\mathbb{R}; \mathcal N_{2D}), \; E_3(\cdot, x_3) \in \mathbb{P}_0(\mathbb{R}; \mathbb{P}_1(\mathbb{R}^2)) \big\} \subset \mathbb{P}_1^3.$

To write the problem in an algebraic form, we introduce the (infinite) vector of degrees of freedom (see Figure 1), namely,

where $\mathbb{V}_{{\mathbf h}, T}$ and $\mathbb{V}_{{\mathbf h}, 3}$ are, respectively, the Hilbert spaces

Thus, (4.2) admits the algebraic form

where ${\mathbf M}_{\mathbf h}$ and ${\mathbf K}_{\mathbf h}$ are the mass and stiffness matrices in $\mathbb{V}_{\mathbf h}$. According to the decomposition of ${\mathbf V}_{\mathbf h}$ between transverse and longitudinal fields, the mass matrix ${\mathbf M}_{\mathbf h}$ has the following block diagonal form

and, in particular, thanks to the numerical quadrature, ${\mathbf M}^T_{\mathbf h}$ (${\mathbf M}^3_{\mathbf h}$) is block diagonal by sections. The numerical quadrature corresponds to a weighted trapezoidal rule, which is fundamental to the efficiency of our method (partial lumping) (for more details see Remark 2.1 in ^[9].) On the other hand, the stiffness matrix ${\mathbf K}_{\mathbf h}$ can be written, according to (4.2), as

We used bold (normal) letters when they apply to transverse (longitudinal) fields. The index $\cdot_{T}$ means that only transverse derivatives are involved, while the index $\cdot_{3}$ means that only $x_3$-derivatives are involved. Oppositely, ${\mathbf C}_{3T, \mathbf h}$ couples the transverse and longitudinal fields and mixes the $x_3$ and transverse derivatives.

This method uses a tricky decomposition of the stiffness matrix ${\mathbf K}_{\mathbf h} = {\mathbf K}_{\mathbf h}^i + {\mathbf K}_{\mathbf h}^e$, where

The interest of the decomposition lies in the following two observations:

$\bullet$ ${\mathbf K}_{\mathbf h}^i$ is adapted to implicit time discretization since the matrix is positive and, thanks to $x_3$ quadrature, block diagonal by section, and thus easy to invert.

$\bullet$ ${\mathbf K}_{\mathbf h}^e$ is adapted to explicit time discretization since it corresponds to the discretization of the differential operators in the $x_3$ direction; this matrix couples all the interfaces and has no sign.

As a consequence, we propose the following scheme

It was shown in ^[9] (Theorem 2.3) that discrete scheme (4.8) is stable under $\theta > \mbox{ $\frac{1}{4}$ }$ and the following CFL condition

where $c^+: = \sup (\varepsilon\, \mu)^{-\frac{1}{2}}$ is the maximum velocity of the electromagnetic wave and is independent of $\delta$.

5.   Numerical resolution of 1D effective telegrapher's model

5.1.   Computation of effective coefficients

This preliminary step consists of computing an approximation of the coefficients $C(x_3), L(x_3), \kappa_e(x_3), \eta_e(x_3)$, and $\chi_e(x_3)$. To do so, one needs to solve for each $x_3$ the 2D elliptic problems (2.4) and (2.5) whose solutions are $\varphi(\rho(x_3))$ and $\psi(\rho(x_3))$, respectively. Since the cable is cylindrical, $x_3$ that plays the role of a parameter. We recall that, in the context of an onion-like structure, one has $\psi(\rho) = \psi$ that does not depend on $x_3$.

The potentials $\varphi(\rho(x_3))$ and $\psi$ are first approximated as a result of a $\mathbb{P}_1$ finite-elements approximation of the boundary value problems (2.4) and (2.5) with a triangular mesh of the cross section $S$ with step-size $h_T$

where $V_{0, h_T}$ and $\widetilde V_{\Gamma, h_T}$ are the Galerkin approximation sub-spaces for $H^1_0(S)$ and $H^1_{/ \mathbb{R}}(S \backslash \Gamma)$, respectively. Then, $C(x_3), L(x_3), \kappa_e(x_3), \eta_e(x_3)$, and $\chi_e(x_3)$ are approximated by

5.2.   Resolution of the 1D evolution problem

In order to compare the 3D and 1D simulations, we will also write the 1D telegrapher's Eq (2.3) in the second order formulation

5.2.1.   The semi-discretization in space

The semi-discretization in space of the 1D model (5.2) is done using 1D finite elements (for instance continuous $\mathbb{P}_1$), and mass lumping with a uniform mesh of step-size $h$. The resulting algebraic problem takes the form

where $\mathbb{V}_h(t) = \big(V_j(t)\big)$ is the vector of degrees of freedom at time $t$ for the semi-discrete voltage ${V}_h(t) \in H^1(\mathbb R)$ (the nodal values at the points $jh$),

is the effective mass matrix, and ${\mathbf K}_h$ is the stiffness matrix. More precisely, one has

$\bullet$ ${\mathbf M}^0_{h} = \mbox{diag} \big(m_{j}\big) > 0$ is the diagonal mass (like) matrix (divided by $h$ for homogeneity) such that

$\bullet$ ${\mathbf K}_h: = \big(k_{i, j}\big)_{i, j\in\mathbb{Z}}$ is the stiffness (like) matrix, which is symmetric and positive, such that

$\bullet$ ${\mathbf D}_h: = \big(d_{i, j}\big)_{i, j\in\mathbb{Z}}$ is the dispersive matrix witch is symmetric and non-negative defined by

where $(u_i)_{i\in \mathbb{Z}}$ is the basis of

5.2.2.   The time discretization

For the time discretization, we use a leap-frog scheme with a constant time step $\Delta t$

where $\mathbb{V}_h^{n}$ is the vector of degrees of freedom of ${V}_h^{n} \in H^1(\mathbb R)$, an approximation of $V_h(n \Delta t)$. We use the same scheme for the discretization of the zero-order model (1.1) with $\delta = 0$, i.e.,

where $\mathbb{V}_h^{\delta, 0, n}$ is the vector of degrees of freedom of ${V}_h^{\delta, 0} \in H^1(\mathbb R)$ (an approximation of $V^{\delta, 0}_h(n \Delta t)$). In ^[8], the ODE structure explained in the proof of Theorem 2.1 is used to propose a scheme different from (5.4). Indeed, by inversion of $\mathcal{C}^{\delta, 2}$, one can write equations as a conservative law with non-local flux. We have decided not to use this strategy since we want to use the same type of scheme for the second-order model and the first-order model. This is done with (5.4) and (5.5).

5.2.3.   Stability analysis of the fully discrete scheme

Theorem 5.1. The numerical scheme (5.4) is $L^2$-stable under the sufficient CFL condition

where $c_{h_T}$ is the velocity of 1D waves such that, for all $x_3 \in \mathbb R$,

and $\lambda^-$ is the minimum of the eigenvalues of the matrix ${\mathbf D}_h$.

Note that when $\delta$ vanishes, one has the usual CFL condition for the leap-frog scheme (5.5) adapted for the 1D waves (1.1).

Proof. We needs to introduce the factor

where the notation $\oint_ \mathbb R {f}$ refers to a quadrature formula in $x_3$. More precisely, for ${f} \in C^0\big(\mathbb{R}\big) \cap L^1\big(\mathbb R \big),$ we set

The proof is done in two steps using an energy approach.

Step 1. Lower bound on the dispersive matrix.

We first want to show that, for ${\mathbf U}_{h} \in \mathbb{P}_{h, 1}$ associated with the vector ${\mathbb U}_{h} \in \mathbb{P}_{1}$, ${\mathbf D}_h$ satisfies

where $\beta^- = {\inf_{x_3\in \mathbb R}} \dfrac{\lambda^-}{C_{h_T}}\geq 0$.

We shall introduce the notation $\big(\cdot, \cdot \big)$ for inner products in $\mathbb{P}_1$,

Let ${\mathbf U}_{h} \in \mathbb{P}_{h, 1}$ be associated with the vector ${\mathbb U}_{h} \in \mathbb{P}_{1}$, then we have that ${\mathbf D}_h$ is a positive symmetric matrix, which allows us to deduce the inequality

where, $\lambda^-\geq 0$ is the minumum of the eigenvalue of the matrix ${\mathbf D}_h$.

We define

Thus, we obtain

Step 2. Discrete energy conservation.

We use this standard key identity:

This allows us to rewrite our scheme as a perturbation of the $\frac{1}{4}$ -scheme

where we have set

Taking the scalar product (in $\mathbb{P}_{1}$) of the above equation with $\frac{{\mathbb V}_{h}^{n+1}-{\mathbb V}_{h}^{n-1}}{2\Delta t}$, we classically deduce, thanks to the symmetry of all matrices, the conservation of the discrete energy

Step 1. Derivation of the sufficient stability condition (5.6).

This will be simply obtained from showing the positivity of the discrete energy ${ \cal E}_h^{n + \frac{1}{2}}$, that amounts to the positivity of the modified mass matrix ${\mathbf M}^\delta_h(\Delta t)$.

Since ${\mathbf K}_h$ is positive, using (5.10) we have for any vector ${\mathbb U}_{h} \in \mathbb{P}_{1}$

where

We control the matrix ${\mathbf K}_h$ with the help of the mass matrix ${\mathbf M}^0_h$ that appears in the lower bound (5.13). This is where the space step $h$ will appear via $\alpha_h$. More precisely, let ${\mathbf U}_{h} \in \mathbb{P}_{h, 1}$ be associated with the vector ${\mathbb U}_{h} \in \mathbb{P}_{1}$, and by definition of ${\mathbf K}_h$,

By definition (5.8) of $\alpha_h$, and since each function ${\mathbf U}_{h}$ belongs to ${\mathbb P}_{1, h}$, one has

so that

Joining (5.13) and (5.14) with definition (5.12) of ${\mathbf M}^0_h (\Delta t)$, we obtain

The stability condition is obtained by writing

In addition, for any $u_h \in \mathbb{P}_{1, h}$ and by definition (5.7) of $c_{h_T}^+$, we obtain

We define

Since $u'_h$ is piecewise constant, we have, with $u_j: = u_h(jh)$ and by definition (5.17) of $C_{h_T, j+\frac{1}{2}}$,

By $|u_{j+1}-u_j|^2 \leq 2 \, \big(|u_{j+1}|^2 + |u_j|^2 \big)$, we deduce,

Finally, using (5.16) and (5.18), we get the CFL condition (5.6).

5.3.   Reconstruction of the 3D electric field

Once the discrete voltage $V_h^n(x_3)$ is computed, using the formula (2.22), one can reconstruct the rescaled 3D electric field at time $n \Delta t$ as the $\mathbb{P}_1$-interpolant of the following transverse fields, defined for each $j$, namely,

where

6.   Comparison between 3D and 1D calculations.

We notice that from definition (2.22) of field $\widetilde{E}^{\delta, 2}({x}, t)$, one has

This suggests that we define the 1D voltage $V^\delta(x_3, t)$ for the 3D problem as

For the comparisons of the rescaled electric field, we can compare the 3D fields, ${E}^{\delta, 2}$ (issued for the effective 1D model) with $\widetilde{E}^{\delta}$ (issued for the 3D model), or we can compare the 1D voltages, $V^{\delta, 2}$, the solution of problem (5.2), with the voltage $V^\delta$ obtained by post-processing the 3D solution ${E}_T^\delta$.

We define the relative space-time error $\vert\Vert\cdot \Vert\vert$, that we will use for the comparison between 3D and 1D calculations as

where $T$ is the time of the simulations and $L$ is the longitudinal size of the considered domain. In the simulations of this paper, one takes $T = 6$ and $L = 12$.

6.1.   Problem's data

For the numerical computations, one considers a finite cylindrical coaxial cable

with periodic boundary condition at the left end $x_3 = 0$ and right end $x_3 = 12$.

One assumes that the cross section $S$ is made of three layers $S = S^1 \cup S^2\cup S^3$.

Concerning the characteristic coefficients of the model, we consider a heterogeneous onion-like structure cylindrical cable:

where $(\varepsilon^n, \mu^n)$ for $n\in\{1, 2, 3\}$ are taken as

and $p$ can be seen as a perturbation in the longitudinal direction, in the numerical experiments, we shall take

so that the velocity of electromagnetic waves, i.e., $c = (\varepsilon \mu)^{-\frac{1}{2}}$, satisfies

and is in particular heterogeneous (we recall that the heterogeneity of the velocity of electromagnetic waves is essential to have a 1D dispersive model).

We also take initial conditions that are localised near $x_3 = 6$ and are well prepared with respect to the expected asymptotic result (5.19). More precisely, $\widetilde{H}_0(x_T, x_3) = 0$ and

The time interval for the numerical experiments is $[0, T]$ with $T = 6$, so that, taking (6.4) into account, it implies that the waves will not reach the transverse boundaries $x_3 = 0$ and $x_3 = 12$ before the final time $T$. In other words, the periodic boundary conditions in $x_3$ will not play any role. If one considers a longer final time such that the waves can reach the boundaries, then one cannot use periodic boundary conditions. In that case, one needs to (artificially) bound the domain of computation. To do this, one can use perfectly matched layer (PML) techniques. More precisely, one encloses the computational domain with an absorbing layer. One perfectly matched layer is such an absorbing layer such that there is no reflection at the interfaces between the layer and the domain of computation. It is easy to build such a PML for the 1D dispersive telegrapher's Eq (2.3) if one considers $\kappa_e$ constant for $|x| > L$ with $L$ finite since (2.3) is similar to Boussinesq-Abbott equations for $|x| > L$. In ^[10] a stable PML was proposed for Boussinesq-Abbott equations. However, we can not succeed in building a stable PML for the 3D Maxwell's Eq (2.2) in the case of non-homogeneous velocity ^[3].

6.2.   Discretization parameters

6.2.1.   Data for the transverse discretization

The cross section $S$ is meshed by a triangular mesh represented Figure 2. In particular, there are 40 mesh points along the cut $\Gamma$, and the typical diameter of each triangle in the mesh is $h_T \simeq 0.04.$ This mesh is used not only for the $2D$ transverse problems (2.4) and (2.5) for computing the potentials $(\varphi_e, \varphi_m, \psi_m, \psi_e)$ and the coefficients $\big(C, L, \kappa_e, \eta_e, \chi_e\big)$, but also for the 3D computations (4.8).

6.2.2.   Data for the longitudinal discretization

We consider $h = 0.06$ for the longitudinal step size. This is well adapted to the discretization of the Gaussian ${\cal F}$. This same longitudinal mesh is used for the discretization of the 1D problem (5.4) (cf. (5.2)) and for the 3D computations. As already said, the 3D computations are more restrictive in terms of the longitudinal step size. We use the same for performing comparaison between 1D and 3D simulations.

6.2.3.   Data for the time discretization

For the comparison between the 1D and 3D results, we shall use the same time step $\Delta t$ for both 1D and 3D computations. The choice of $\Delta t$ will be constrained by the 3D condition (4.9), which is more restrictive than the 1D condition (see Theorem 5.1). For the 3D computations, we shall take $\theta = {1}/{3}$, in which case the CFL (4.9) becomes $c^+\Delta t/{h} \leq 1/2$. In practice, we choose $\Delta t = 0.95 \; \, {h }/{(2 \; c^+)}$.

7.   Numerical results

7.1.   The potentials

We show in Figure 3 the computed potentials $\varphi_e$ and $\psi_m$ in the first cable section. The right picture shows the level lines of $\varphi_e$ (which are "parallel" to the boundaries), and those of $\psi_m$ (which intersect the boundaries). This illustrates Remark 2.3.

Figure 4 shows $(\psi_e-\psi_m)$ and $(\varphi_e-\varphi_m)$. The numerical results proves that $\kappa_e > 0$ and the two potentials $\psi_e$ and $\psi_m$ are equal (this is a numerical interpretation of Proposition 2.3).

7.2.   Comparisons of voltages

In Figure 5, we compare the evolution of the 1D voltage $V^{\delta, 2}$ issued from the numerical resolution of the 1D model (5.2) to the 1D voltage $V^\delta$ for the 3D problem, defined by (6.1).

More precisely, we compare the above functions in space for different values of $\delta$. The solution $V^{\delta, 2}(x_3, T)$ is in red, while $V^\delta(x_3, T)$ is in blue. Numerical results confirm that the approximation of $V^{\delta}(x_3, t)$ by $V^{\delta, 2}(x_3, t)$ improves with the decrease of $\delta$. We observe that $V^{\delta, 2}$ and $V^\delta$ already almost coincide for $\delta = 0.05$. It is also important to note that the main effect of local perturbations $p$ is the appearance of reflection phenomena.

7.3.   Comparison of the transverse electric fields

In Figures 6 and 7, we represent for different values of $\delta$ the Euclidean norms $|{\widetilde{E}}_T^\delta|$ and $|{\widetilde{E}}_T^{\delta, 2}|$ at final time $T = 6$ on the boundary $\partial \Omega$. We observe that the result obtained with $\delta = 0.075$ cannot be distinguished from the one obtained with the 1D model (${\widetilde{E}}_T^{\delta, 2})$, while a substantial difference exists for $\delta = 0.15$. As found in the 1D results, we also observe that the electric wave is reflected because of the perturbation $p$ localised at $x_3 = 8$.

7.4.   Comparison of the longitudinal electric fields

Finally, in order to check the asymptotic transverse polarisation of the electric field, we show in Figures 8 and 9, again along $\partial \Omega$ at time $T = 6$, the longitudinal electric fields $\widetilde{E}_3^\delta$ and $\widetilde{E}_3^{\delta, 2}$. We observe that the two longitudinal fields tend to $0$ when $\delta$ tends to $0$. On the other hand, for $\delta = 0.15$ we see that these fields are really non-transversely polarised.

7.5.   Error between 3D and 1D models: order of convergence.

In Figure 10, we show in red the relative error between the voltage $V^{\delta}$ obtained by the 3D computations with the voltage $V^{\delta, 2}$ of the second-order 1D model (5.2) for different values of $\delta$ and at a final time $T$. On the same figure we display in blue the relative error between the electric voltage $V^{\delta}$ obtained by the 3D computations with the solution voltage of the 1D limit model $V^{\delta, 0}$ (the solution of (5.2) when $\delta = 0$).

The numerical results obtained in Table 1 show that the second-order model is a better approximation with respect to $\delta$ than the limit model ($\delta = 0$). More precisely, its convergence is of order two, whereas the convergence of the limit model is of order one.

In the Figure 11, we show in red the relative error between $E^{\delta}$ and $E^{\delta, 2}$, and in blue the relative error between $E^{\delta}$ and $E^{0}$, for different values of $\delta$ at a final time $T = 6$. As for the electrical voltage, the simulations show that the second-order is a better approximation with respect to $\delta$ (see Table 2). The error between the electric field solution of the 3D Maxwell equations and the reconstruction of the electric field from the second-order model is of order $O(\delta^2)$, whereas one gets only $O(\delta)$ for the limit model.

8.   Conclusions

We have presented a second-order effective 1D model that takes into account dispersive effects. We have also developed a stable numerical scheme for its space-time discretization. Finally, we have carried out and performed the validation of this new effective model by comparing its results with those obtained for the 3D Maxwell model for small values of $\delta$. Our numerical results illustrate the interest of this new dispersive 1D model compared to the usual one. However, it is important to note that all the results obtained in this paper are only valid for cylindrical coaxial cables. For this reason, it will be interesting to study the extension of these ideas to the case of non-cylindrical coaxial cables.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Conflict of interest

The authors declare that there are no conflicts of interest regarding the publication of this paper.