Dispersive optical soliton solutions with the concatenation model incorporating quintic order dispersion using three distinct schemes

1.   Introduction

Different dispersion characteristics can be designed into modern optical fibers. Thus, it is not as absurd as it might first appear to think that some predictions might allow for experimental confirmations. Realistically, when pulses are near 20 ps in length, fifth-order concatenation model dispersion does affect current laser studies ^[1]. A universal paradigm for modelling wave dynamics in many nonlinear systems is the nonlinear Schrö dinger equation (NLSE). The only two terms in the NLSE that permit bright and dark soliton-type pulse propagation in anomalous and normal dispersion regimes for picosecond light pulses are the self-phase modulation and the group velocity dispersion (GVD), which are well-known in the fiber ^[2,3,4,5]. For instance, the $\chi ^{5}$ nonlinearity (cubic-quintic medium) should be included in the NLSE at high light intensities. Be aware that semiconductor double-doped optical fibers can realize the competing cubic-quintic nonlinearity. Additionally, it has been shown that higher-order effects in nonlinear media become significant for pulses shorter than 100 femto-seconds.

The study of solitons in nonlinear models has become increasingly common in engineering and science, emerging as a dynamic and quickly advancing field of research. Researchers from different fields have investigated this area of study in recent years, leading to its rapid growth and progress. The NLSE describes the behavior of optical solitons in optical fiber. This equation is considered integrable, meaning it can be solved exactly. It is worth noting that different dispersion regions give rise to distinct types of optical solitons. The NLSE-types are formulated as a theoretical framework within the field of quantum mechanics. This model has become one of the most widely used to study solitons in different media types, such as plasma, water waves, and optical fibers. Multiple governing models can be utilized to investigate the transmission of solitons across optical fibers. However, there has been a recent development in this specific field that involves combining existing models to construct new structures for efficiently controlling the flow of solitons over vast distances between continents ^{[6,7,8,9,10,11,12,13,14,15,16]}.

Note that the NLSE with higher order elements has undergone substantial numerical and theoretical study ^{[17,18,19,20]}, making it a model with physical importance. Having optical soliton solutions is the most crucial aspect of nonlinear science. There are numerous schemes created by authors, such as the extended auxiliary equation method ^[21,22], new mapping method ^{[23,24,25,26]}, an addendum to Kudryashov's method ^{[27,28,29,30]}, the enhanced Kudryashov's method ^[31,32], unified Riccati equation expansion method ^[33,34], unified Auxiliary equation ^[33], Jacobi elliptic function method ^[35], and so on. However, because of the unique differential equation structure, the previously successful method of constructing exact solutions using the logistic function is insufficiently effective in constructing the optical solitons that are defined by generalized Schrödinger equations ^{[36,37,38,39,40,41,42]}.

In dimensionless form, the quintic operator, Lakshmanan-Porsezian-Daniel operator ^[6,7,8], Hirota operator ^[43,44,45], and nonlinear Schrödinger operator are four well-known nonlinear models that make up the fifth-order concatenation model. The notation for this concatenation model is ^{[46,47,48,49,50,51,52]}:

where $q(x, t)$ is a complex envelope of the waves; $q^{\ast }(x, t)$ is the complex conjugate; $\ x$ is the propagation variable, and $t$ is the transverse variable; $\iota^{2} = -1$; and $\alpha, \gamma$, and $\delta$ are non-zero constants. The coefficient of $\alpha$ is the Hirota operator, the coefficient of $\gamma$ is the Lakshmanan-Porsezian-Daniel (LPD) operator, and the coefficient of $\delta$ is the quintic operator. If $\alpha = \gamma = \delta = 0,$ then Eq (1.1) can be reduced to the standard NLSE which describes the propagation of picosecond pulses in optical fibers. If $\gamma = \delta = 0,$ then Eq (1.1) can be reduced to the Hirota equation. If $\alpha = \delta = 0,$ then Eq (1.1) can be reduced to the LPD equation. If $\alpha = \gamma = 0,$ then Eq (1.1) can be reduced to quintic NLSE. Eq (1.1) has been discussed in ^[46] when $\alpha, \gamma,$ and $\delta$ are non-zero constants using the ansatz approach. The authors have found just one solution, via bright soliton. Equation (1.1) has also been discussed in ^[50] when $\delta = 0$ and in ^[48] when $\alpha = \gamma = 0.$ In this paper, Eq (1.1) is solved when the parameters $\alpha, \gamma,$ and $\delta$ are non-zero constants. The novelty of Eq (1.1) is unique because it is a combination of four well-known equations that describe the propagation of soliton dynamics through optical fibers across inter-continental distances. Equation (1.1) with $\alpha, \gamma,$ and $\delta$ as non-zero constants is also unique in the sense that all the perturbations and dispersive effects describe the soliton propagations dynamics.

The following is the organization of this project: In Section 2, the governing model is provided. Section 3 introduces the mathematical analysis. The fifth-order concatenation model (1.1) is solved in Section 4 by the Weierstrass type projective Riccati equation expansion method. Using the Kudryashov method addendum, we solve the fifth-order concatenation model (1.1) in Section 5. Using the new mapping strategy, we solve the fifth-order concatenation model (1.1) in Section 6. Several numerical simulations that were obtained are shown in Section 7. Section 8 presents the conclusions.

2.   Mathematical analysis of the governing equation

For solving Eq (1.1), set

where $w$ is the wave number, $\theta _{0}$ is the phase constant, $V$ is the shift of the soliton's inverse group velocity, and $\kappa$ is the soliton frequency. The shape of the pluse is represented by $\varphi (\xi)$, which is a valued function of $\xi$, where $\xi$ is the traveling coordinate. Plugging (2.1) into Eq (1.1) with the real and imaginary parts separated, we have the ordinary differential equation (ODE):

and

Integrating (2.2) with zero constant of integration, we get:

Equations (2.2) and (2.4) are equivalent if the following conditions are satisfied:

We obtain

provided $\omega \neq \frac{1}{3}.$ Equation (2.2) can be written in the form:

where

provided $\delta \neq 0,$ $\delta \neq \gamma,$ $\omega \neq \frac{1}{3}.$ Let us now solve the ODE (2.7) using the following three mathematical methods, the Weierstrass type projective Riccati equation expansion method, an addendum to Kudryashov's method, and the new mapping approach.

3.   Weierstrass type projective Riccati equation expansion method

To apply the Weierstrass method ^[53,54] to Eq (2.7), we first balance $\varphi ^{\left(4\right) }\left(\xi \right)$ with $\varphi ^{5}\left(\xi \right)$ to get the balance number $n = 1$. The solution of Eq (2.7) is:

where $a_{0}, a_{1}$, and $b_{1}$ are constants that need to be found, $a_{1}^{2}+b_{1}^{2}\neq 0;$ and $F\left(\xi \right)$ and $G\left(\xi \right)$ are solutions of the projective Riccati equations

such that $p, q,$ and $r$ are constants. Weierstrass elliptic solutions to Eqs (3.2) are known in reference ^[53]. They are as follows:

Set 1:

Set 2:

Set 3:

where $g_{2}$ and $g_{3}$, the invariants, are provided by

Furthermore, the Weierstrass function ($\wp$) satisfies the relations

Type 1: Add Eqs (3.1), (3.2), and (3.3) to Eq (2.7); collect each coefficient of $F^{i}\left(\xi \right) G^{j}\left(\xi \right)$ $(i = 1, .., 5, j = 0, 1)$; and then set them to zero, then we have the following algebraic equations:

Using Maple to solve the algebraic Eqs (3.8) yields:

provided $pq(\sqrt{\Delta _{3}+24\Delta _{2}}-\Delta _{3}) < 0, (\Delta _{3}+24\Delta _{2}) > 0.$ Substituting (3.9), (3.3) into Eq (3.1) by using (2.1) we derive the travelling wave solution of the Weierstrass type of Eq (1.1) as:

provided $q(\sqrt{\Delta _{3}+24\Delta _{2}}-\Delta _{3}) < 0.$ By substituting the conversion formula (3.7) with $\theta = -pq$ into Eq (3.10), the dark soliton solution is:

and the singular soliton solution:

provided $pq < 0, p(\sqrt{\Delta _{3}+24\Delta _{2}}-\Delta _{3}) > 0.$

Type 2: Substite Eqs (3.1), (3.2), and (3.4) into Eq (2.7); collect each coefficient of $F^{i}\left(\xi \right) G^{j}\left(\xi \right)$ $(i = 1, .., 5, j = 0, 1)$; set them to zero. Then, we get these algebraic equations, we can solve with Maple, to get

provided $\Delta _{1} < 0, q > 0,$ $\epsilon = \pm 1.$ Substituting Eqs (3.13) and (3.4) into Eq (3.1), the following Weierstrass type travelling wave solution is obtained:

where $g_{2}$ and $g_{3}$, the invariants, are provided by

Substituting the conversion formula (3.7) with $\theta = -pq = \frac{16\Delta _{1}}{9}$ into Eq (3.14), we get the following solitary wave solutions:

provided $\Delta _{1} < 0, p < 0, \epsilon = \pm 1.$

Type 3: Substite Eqs (3.1), (3.2), and (3.5) into Eq (2.7); collect every coefficient of $F^{i}\left(\xi \right) G^{j}\left(\xi \right)$ $(i = 1, .., 5, j = 0, 1)$, and then set them to zero. Then, we get these algebraic equations that we can solve using Maple to obtain:

Substituting Eqs (3.18) and (3.5) into Eq (3.1), the following Weierstrass type travelling wave solution is obtained:

where $(\sqrt{\Delta _{3}+24\Delta _{2}}-\Delta _{3}) < 0, (\Delta _{3}+24\Delta _{2}) > 0, \; p > 0,$ and $\epsilon = \pm 1.$ Substituting the conversion formula (3.7) with $\theta = -pq$ into Eq (3.19), we get the following straddled soliton solutions:

provided $(\sqrt{\Delta _{3}+24\Delta _{2}}-\Delta _{3}) < 0, (\Delta _{3}+24\Delta _{2}) > 0, pq < 0, \epsilon = \pm 1.$

4.   An addendum to Kudryashov's method

Using this technique ^{[27,28,29,30,31,32]}, Eq (2.7) has the formal solution:

where $B_{j}$ $\left(j = 1, 2, ..., M\right)$ are constants, such that $B_{M}\neq 0,$ and $R\left(\xi \right)$ represents the auxiliary equation's solution:

where $\chi$ is a constant. It is simple to demonstrate that the solution to Eq (4.2) is:

where $A$ is a constant that is not zero, p is a positive constant and $\exp _{K}\left(p\xi \right) = K^{p\xi }$. Balancing $\varphi ^{\left(4\right) }\left(\xi \right)$ with $\varphi ^{5}\left(\xi \right)$ in Eq (2.7), we get:

Now, the following are different cases that arise: Case–1. If we choose $p = 1$, then $M = 1$. Thus, we deduce that:

Substituting Eqs (4.5) and Eq (4.2) where $p = 1$ into Eq (2.7), assembling every power of a coefficient of $\left[ R(\xi)\right] ^{q_{1}}$ $\left[ R^{\prime }(\xi)\right] ^{q_{2}}, \left(q_{1} = 0, 1, 2, ...5, { \ } q_{2} = 0, 1\right),$ and setting each of these coefficients to zero, the following results are the outcome of Maple solving the algebraic equations:

and

provided $\chi > 0.$ Substituting Eqs (4.6) and (4.3) into Eq (4.5), one gets the solutions of Eq (1.1) in the forms:

It is easy to see that Eq (4.8) reduces to the straddled soliton solution:

In particular, if we set $\chi = 4A^{2}$ in Eq (4.9), then we have the bright soliton solutions of Eq (1.1) as

Under the conditions (4.7), the solutions (4.8)–(4.10) exist.

Case–2. If we choose $p = 2,$ then $M = 2.$ Thus, Eq (2.7) has the formal solution:

Substituting Eqs (4.11) and Eq (4.2) where $p = 2$ into Eq (2.7), collecting all coefficients for every power of $\left[ R(\xi)\right] ^{q_{1}}$ $\left[ R^{\prime }(\xi)\right] ^{q_{2}}, \left(q_{1} = 0, 1, 2, ...10, \text{ } q_{2} = 0, 1\right),$ and setting these coefficients to zero, we get an algebraic equation system that we can solve with Maple to get

and

provided $\chi > 0.$ The solutions of Eq (1.1) can be obtained by substituting Eqs (4.12) and (4.3) into Eq (4.11).

It is easy to see that Eq (4.14) reduces to the straddled soliton solution in the form

In particular, if we set $\chi = 4A^{2}$ in Eq (4.15), we have the bright soliton solution of Eq (1.1):

Under the condition (4.13), the solutions (4.14)–(4.16) exist.

Similar to that, we can find a variety of solutions by selecting various values for $p$ and $M$; however, for simplicity, those solutions have been excluded here.

5.   New mapping approach

With the new mapping method ^{[23,24,25,26]}, the solution to Eq (2.7) is as follows:

where $\alpha _{0}, \alpha _{1}$ and $\alpha _{2}$ are constants which will be determined, also $\alpha _{2}\neq 0,$ the function $Z\left(\xi \right)$ satisfies the first order equation:

Let $r$, $p$, $q$, and $s$ be constants, where $s$ is not equal to zero. By substituting Eqs (5.1) and (5.2) into Eq (2.7), and gathering the coefficients of each power of $Z^{h}\left(\xi\right) \left[Z^{\prime}\left(\xi\right)\right]^j, \; (h = 0\to10, \; j = 0, 1)$, we can analyse the resulting expression. By setting these coefficients to zero, the following algebraic equations are obtained.

With reference to ^{[23,24,25,26]}, algebraic equations can be solved by three cases.

Case 1.The following are the results of substituting $s = \frac{3q^{2}}{16p},$ $r = \frac{16p^{2}}{27q}$ into the system of algebraic equations (5.3) and solving them by Maple or Mathematica:

and

provided $\Delta _{1} < 0.$ From Eqs (5.1) and (5.4), the straddled soliton solutions have been obtained as follows:

and

where $\epsilon = \pm 1.$ Under the conditions (5.5), solutions (5.6) and (5.7) are possible.

Case 2.Inserting $s = \frac{3q^{2}}{16p},$ $r = 0$ into the algebraic equations (5.3) and solving them by Maple or Mathematica, we obtain the following results:

and

provided $(-2\Delta _{3}+\Delta _{1}) > 0.$ From Eqs (5.1) and (5.8), the dark soliton solution is

and the singular soliton solution is

With the constraint conditions (5.9), the solutions (5.10) and (5.11) exist.

Case 3.Inserting $r = 0$ into the system of algebraic equations (5.3), if we extract those equations and solving them by Maple, we get

and

provided $s\Delta _{1} < 0.$ From Eqs (5.1) and (5.12), we get the straddled soliton solutions:

provided $s > 0, \Delta _{1} < 0, M = \left(9q^{2}+\frac{12s\Delta _{1}}{5}\right) > 0,$ and $\epsilon = \pm 1.$Under the constraint conditions (5.13), the solutions (5.14)–(5.19) are valid.

6.   Graphical representation

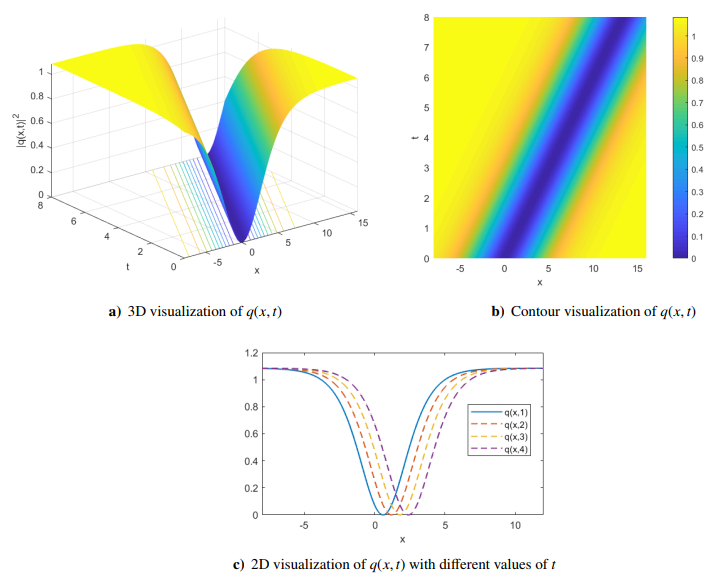
Visual representation is the most efficient technique for understanding the visible bodily movements of real-life situations. The graphs in this section depict solitons retrieved with the concatenation model having quintic-order dispersion. We obtain solutions of the Weierstrass type projective Riccati equation expansion approach by employing the Weierstrass type. These solutions can be further reduced using the conversion formula to yield dark, singular, and straddled soliton solutions. We utilize the dark soliton solution (3.11) to generate Figure 1 by carefully selecting appropriate values for the parameters $\Delta_2 = 0.96, \Delta_3 = 0.59, p = 1.45, q = -0.27,$ and $v = 0.5$. By employing the addendum to Kudryashov's method, we obtain closed-form expressions for exact solutions. These solutions can be simplified to bright soliton solutions. To demonstrate this, we select solution (4.10) and plot it with specific parameter values $K = 1.661$ and $v = 0.5$, as depicted in Figure 2. Finally, by employing the new mapping method, we can obtain explicit dark and straddled soliton solutions. In contrast, for the straddled soliton solution (5.6), we utilize the values $\Delta_1 = -1.5$ and $v = 0.5$ which correspond to bright soliton solutions (refer to Figure 3). We select the values $\Delta_1 = 1.7$, $\Delta_3 = -1.72$, and $v = 0.5$, for the dark soliton solution (5.10) (refer to Figure 4).

7.   Conclusions

This work has successfully derived various types of solitons, including bright solitons, dark solitons, and combo straddled solitons, for the fifth-order concatenation model with four combined well-known nonlinear NLSE-type models. The study has also identified the novel Weierstrass-type traveling wave solutions, which can be reduced to optical soliton solutions using the conversion formula. These findings contribute to the understanding of soliton dynamics and have implications for various fields of research. Three distinct methods have been employed in this study to obtain solutions for the model at hand. These include the Weierstrass-type projective Riccati equation expansion method, the addendum to Kudryashov's method, and the new mapping methods. These approaches have contributed to the advancement of research in this field.

The findings of this research provide substantial evidence and accuracy in elucidating various physical phenomena and provide a comprehensive overview of the requirements for the existence of soliton solutions. The listed criteria serve as crucial guidelines for identifying and understanding the behaviour of solitons in various physical systems. By establishing these conditions, researchers can effectively analyze and predict the presence and characteristics of solitons, contributing to advancements in fields such as nonlinear optics, fluid dynamics, and quantum mechanics. The behaviour of the solutions (3.11), (4.10), (5.6), and (5.10) has been visually represented through the plotting of their 2D, 3D, and contour plots in Section 6. These figures provide valuable insights into the characteristics and patterns exhibited by these solutions. The findings validate the advantages and applicability of the employed methodologies. Furthermore, the approaches described are reliable and applicable to a wide range of nonlinear models in mathematical physics. Finally, the obtained results were validated through the utilization of Maple, as satisfied by the verification of Eq (1.1).

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgements

This work was supported by the Technology Innovation Program (20018869, Development of Waste Heat and Waste Cold Recovery Bus Air-conditioning System to Reduce Heating and Cooling Load by 10%) funded By the Ministry of Trade, Industry & Energy (MOTIE, Korea).

Conflict of interest

The authors declare that they have no competing interests.