Positive solutions for a critical quasilinear Schrödinger equation

1.   Introduction

Numerous researchers have analyzed fractional evaluation equations in the last decade because of their enormous usefulness in multiple domains of development in science and engineering. Eventually, these fractional evaluation equations can describe a wide range of essential effects in quantum mechanics, hydrodynamics, chaos, fibers, bifurcation, acoustics, thermodynamics, aquifers, and material science, among other disciplines ^[1,2,3,4]. Furthermore, approximate findings of fractional evaluation equations are of considerable worth. Various initiatives can also be conducted to evaluate the dynamic behaviour of fractional systems. By employing linearization or series solutions, these analytical approaches are susceptible to achieving an estimated result. In this flow, several new definitions and fractional operators are introduced by numerous analysts, such as Caputo, Hadamard, Hilfer, Riez, Caputo-Fabrizio, and Atangana-Baleanu, that can portray physical phenomena accurately with memory depending on power law, exponential, and Mittag-Leffer as a kernel, see ^{[5,6,7,8,9,10,11,12,13,14,15]} and the references cited therein.

Finding an effective fractional PDE in the framework of numerical techniques is a challenging task. It necessitates a comprehension of the underlying physical processes. On the other hand, realistic physical processes are always tempered with vagueness. This is evident when interacting with "living" resources like soil, water, and microbial communities. When a real physical phenomenon is modelled by a fractional generic EW model, it comprises the following structure for long waves in the positive ${\bf{y}}$ direction ^{[16,17,18,19,20,21,22,23]}:

where $\sigma, \; \epsilon$ and $\mu$ are the positive integrer and constants, respectively, that needs the boundary conditions (BCs) $\Theta\mapsto0$ as ${\bf{y}}\mapsto\pm\infty$ while $\varphi$ denotes the fractional-order. The derivatives are comprehended in CFD and AB in the Caputo sense, whereas $\Theta({\bf{y}}, \lambda)$ signifies the probability density function with $({\bf{y}}, \lambda)$ are the spatial and temporal coordinates. This equation has a parameter $\varphi$ that specifies the fractional derivative order.

In this investigation, we will provide periodic BCs for a space $a_{1}\leq{\bf{y}}\leq a_{2}.$ The initial wave will be designed in such a way that $\vert\Theta\vert$ is relatively small at significant regions from the wave and follows the free space BCs $\Theta = 0.$ Also, $\Theta$ correlates to the vertical displacement of the fluid surface in the fluid problem, and $\Theta$ is the negative of electrostatic potential in the plasma problem. There is a solitary wave result to the fractional-order general EW model. Model (1.1) has fertile application in fluid mechanics and magnetic fields. Therefore, several developments have been incorporated by researchers to explore various kind of models for physical purposes, see ^{[24,25,26,27]}. The following are a few of these research findings: Wazwaz ^[28] devised a number of different sorts of accurate MEW solutions. In ^[29], Lu contemplated the variational iteration method (VIM) for estimating the solutions similar to (1.1), Esen and Kutluay ^[30] established the solitary wave solutions by the finite difference method (FDM), Esen ^[31] expounded lumped Galerkin method for the numerical treatment of the MEW equation. Moreover, Rui et al. ^[32] obtained the traveling wave solutions of (1.1) employing the integral bifurcation approach, Taha and Noorani ^[33] established the exact solutions of the MEW equation via the $G/G^{'}$-expansion method, Goswami et al. ^[34] proposed the homotopy perturbation method for finding the solution analogs to (1.1), Fourier spectral method ^[35], Exp-function method ^[36] and the method of dynamical systems ^[37] has been used for finding the solution to (1.1).

An estimated analytical approach has the advantages of being able to solve complex problems without ascribing motives to numerical solutions to the precise solution to assess its validity. It also has quick estimation accuracy. In ^[38], a Chinese mathematician, J. H. He, developed the homotopy perturbation method (HPM) premised on homotopy in topology ^[39]. In HPM, the approximate result is represented as a series that rapidly converges to the exact solution. The versatility of HPM allows it to yield approximate and exact solutions to both linear and nonlinear problems without the necessity for discretization and linearization, as with analytical methods ^[40]. Various studies have extensively used the HPM to analyze linear and nonlinear PDEs ^[34].

The initial value in (1.1), for instance, may not be clearly recognized. On the other hand, conventional mathematics is incapable of dealing with this circumstance. As a result, alternative theories are required in order to address this problem. There are several frameworks for explaining this scenario, the most prominent of which is the fuzzy set theory ^{[41,42,43,44,45,46]}.

Chang and Zadeh ^[47] were the first to suggest the fuzzy derivative notion, which was quickly adopted by numerous other researchers ^[45,46,48]. Hukuhara's publication ^[49] is the main focus of the concept of set valued DEs and fuzzy DEs. The Hukuhara derivative served as the foundation for the investigation of set DEs and, thereafter, fuzzy fractional DEs. Recently, Agarwal et al. ^[50] have made an attempt to identify the paradigm of solution for fuzzy FDEs in order to accomplish a more accurate version which was the basic foundation for the theme of fuzzy fractional derivatives. This discovery has inspired a number of scholars to come up with certain inferences about the existence and uniqueness of solutions (see ^[51,52]). Allahviranloo et al. ^[53] addressed explicit solutions to unpredictable fractional DEs under Riemann-Liouville $\mathcal{H}$-differentiability incorporating Mittag-Leffler mechanisms in ^[54], and formed fuzzy fractional DEs under Riemann-Liouville $\mathcal{H}$-differentiability incorporating fuzzy Laplace transforms. They demonstrated two novel existence theorems for fuzzy fractional differential equations using Riemann-Liouville generalized $\mathcal{H}$-differentiability and fuzzy Nagumo and Krasnoselskii-Krein criteria ^[55]. Bushneq et al. ^[56] explored the findings of a fuzzy singular integral equation with an Abel's type kernel using a novel hybrid method. In ^[57], Zia et al. adopted a semi-analytical technique for obtaining the solutions of fuzzy nonlinear integral equations. Salahshour et al. ^[58] expounded the $\mathcal{H}$-differentiability with Laplace transform to solve the FDEs. Ahmad et al. ^[59] studied the third order fuzzy dispersive PDEs in the Caputo, Caputo-Fabrizio, and Atangana-Baleanu fractional operator frameworks. Shah et al. ^[60] presented the evolution of one dimensional fuzzy fractional PDEs.

Numerical and analytical research into the fuzzy EW, MEW and VMEW equations are limited and lacking. In 2019, the Shehu transform method was first introduced and implemented by two mathematician Shehu Maitama and W. Zhao ^[66] as an efficient integral transform method in solving differential equations ^[65].

In this research, we employ a hybrid approach of the Shehu transform connected with the homotopy perturbation method to find the applicability of the fuzzy fractional EW, MEW, and VMEW models of the type based on prior work. The main objective of this study is to expand the implementation of the SHPTM to develop numerical solutions for fractional EW, MEW, and VMEW models via fuzziness. The findings of the fractional-order with uncertainty factor are examined by advanced techniques and methods. The strength of SHPTM is that its value comes from its ability to combine two powerful strategies for obtaining numerical findings from complex equations. Some comparison plots illustrate the supremacy of the Hukuhara generalized fractional derivative of CFD and ABC operators. It is worth noting that the proposed algorithm is capable of reducing the amount of computing costs as compared to conventional systems while maintaining good numerical accuracy as maintained by the uncertain term $\hbar\in[0, 1].$ Several physical phenomena can be addressed by the projected method. Additionally, this method hopes to broaden series solutions by reducing homotopies in determining the desired unknown coefficients of these solutions, which probably resulted in solutions in rapidly convergent series forms without the necessity for linearization or any restrictions on the complexity of the topic or its categorization.

2.   Basic notions of fractional and fuzzy calculus

This section clearly exhibits some major features connected to the stream of fuzzy set theory and FC, as well as certain key findings about the Shehu transform. For more details, we refer ^[61].

Definition 2.1. (^[62,63]) We say that $\nabla:\mathbb{R}\mapsto[0, 1]$ is a fuzzy set, then it is known to be fuzzy number, if it holds the subsequent assumptions:

1. $\nabla$ is normal: there exists ${\varkappa}_{0}\in\mathbb{R}$ such that $\nabla(\varkappa_{0}) = 1$,

2. $\nabla$ is upper semi continuous,

3. $\nabla({\bf{y}}_{1}\mu+(1-\mu){\bf{y}}_{2})\geq\big(\nabla({\bf{y}}_{1})\wedge\nabla({\bf{y}}_{2})\big)\; \forall\mu\in[0, 1], \; {\bf{y}}_{1}, {\bf{y}}_{2}\in\mathbb{R},$ i.e $\nabla$ is convex;

4. $cl\big\{{\bf{y}}\in\mathbb{R}, \nabla({\bf{y}}) > 0\big\}$ is compact.

Definition 2.2. (^[62]) We say that a fuzzy number $\nabla$ is $\hbar$-level set described as

where $\hbar\in(0, 1]$ and $\Theta\in\mathbb{R}.$

For a fuzzy number $\nabla$, its $\hbar$-cuts are closed intervals in $\mathbb{R}$ and we denote them by $[\nabla]^{\hbar} = [a^{\hbar}, b^{\hbar}].$

Definition 2.3. (^[62]) The parameterized version of a fuzzy number is denoted by $\big[\underline{\nabla}(\hbar), \bar{\nabla}(\hbar)\big]$ such that $\hbar\in[0, 1]$ satisfies the subsequent assumptions:

1. $\underline{\nabla}(\hbar)$ is non-decreasing, left continuous, bounded over $(0, 1]$ and left continuous at $0.$

2. $\bar{\nabla}(\hbar)$ is non-increasing, right continuous, bounded over $(0, 1]$ and right continuous at $0.$

3. $\underline{\nabla}(\hbar)\leq\bar{\nabla}(\hbar).$

Moreover, $\hbar$ is known to be crisp number if $\underline{\nabla}(\hbar) = \bar{\nabla}(\hbar).$

Definition 2.4. (^[61]) For $\hbar\in[0, 1]$ and $\Upsilon$ be a scalar. Assume that there are two fuzzy numbers $\tilde{\gamma_{1}} = (\underline{\gamma_{1}}, \bar{\gamma_{1}}), \; \tilde{\gamma_{2}} = (\underline{\gamma_{2}}, \bar{\gamma_{2}}),$ then the addition, subtraction and scalar multiplication, respectively are stated as

1. $\tilde{\gamma_{1}}\oplus\tilde{\gamma_{2}} = \big(\underline{\gamma_{1}}(\hbar)+\underline{\gamma_{2}}(\hbar), \bar{\gamma_{1}}(\hbar)+\bar{\gamma_{2}}(\hbar)\big),$

2. $\tilde{\gamma_{1}}\ominus\tilde{\gamma_{2}} = \big(\underline{\gamma_{1}}(\hbar)-\underline{\gamma_{2}}(\hbar), \bar{\gamma_{1}}(\hbar)-\bar{\gamma_{2}}(\hbar)\big),$

3. $\Upsilon\odot\tilde{\gamma_{1}} = \begin{cases} (\Upsilon\underline{{\gamma_{1}}}, \Upsilon\bar{\gamma_{1}})\; \; \Upsilon\geq0, \\(\Upsilon\bar{\gamma_{1}}, \Upsilon\underline{\gamma_{1}})\; \; \Upsilon < 0. \end{cases}$

Definition 2.5. (^[58]) Suppose a fuzzy mapping ${\bf{H}}:\tilde{E}\times\tilde{E}\mapsto\mathbb{R}$ having two fuzzy numbers $\tilde{\gamma_{1}} = (\underline{\gamma_{1}}, \bar{\gamma_{1}}), \; \tilde{\gamma_{2}} = (\underline{\gamma_{2}}, \bar{\gamma_{2}}),$ then ${\bf{H}}$-distance between $\tilde{\gamma_{1}}$ and $\tilde{\gamma_{2}}$ is represented as

Definition 2.6. (^[58]) Consider a fuzzy mapping $f:\mathbb{R}\mapsto\tilde{E},$ if for any $\epsilon > 0\; \exists\; \delta > 0$ and fixed value of $\mu_{0}\in[a_{1}, a_{2}],$ we have

then $\mu$ is known to be continuous.

Definition 2.7. (^[64]) Let $\delta_{1}, \delta_{2}\in\tilde{E},$ if $\delta_{3}\in\tilde{E}$ and $\delta_{1} = \delta_{2}+\delta_{3}.$ The $\mathcal{H}$-difference $\delta_{3}$ of $\delta_{1}$ and $\delta_{2}$ is denoted as $\delta_{1}\ominus^{\mathcal{H}}\delta_{2}.$ Observe that $\delta_{1}\ominus^{\mathcal{H}}\delta_{2}\neq\delta_{1}+(-1)\delta_{2}.$

Definition 2.8 (^[64]) Suppose that $\mu:(b_{1}, b_{2})\mapsto\tilde{E}$ and $\varpi_{0}\in(b_{1}, b_{2}).$ Then $\mu$ is said to be strongly generalized differentiable at $\varpi_{0}$ if $\mu^{\prime}(\varpi_{0})\in\tilde{E}$ exists such that

(ⅰ) $\mu^{\prime}(\varpi_{0}) = \lim\limits_{\hbar\mapsto 0}\frac{\mu(\varpi_{0}+\hbar)\ominus^{g\mathcal{H}}\mu(\varpi_{0})}{\hbar} = \lim\limits_{\hbar\mapsto 0}\frac{\mu(\varpi_{0})\ominus^{g\mathcal{H}}\mu(\varpi_{0}-\hbar)}{\hbar},$

(ⅱ) $\mu^{\prime}(\varpi_{0}) = \lim\limits_{\hbar\mapsto 0}\frac{\mu(\varpi_{0})\ominus^{g\mathcal{H}}\mu(\varpi_{0}+\hbar)}{-\hbar} = \lim\limits_{\hbar\mapsto 0}\frac{\mu(\varpi_{0}-\hbar)\ominus^{g\mathcal{H}}\mu(\varpi_{0})}{-\hbar}.$

Throughout this investigation, we use the notation $\mu$ is $(\textbf{1})$-differentiable and $(\textbf{2})$-differentiable, respectively, if it is differentiable under the assumption (ⅰ) and $\textbf{(ii)}$ defined in the above definition.

Theorem 2.9. (^[61]) Consider a fuzzy valued function $\mu:\mathbb{R}\mapsto\tilde{E}$ such that $\mu(\varpi_{0};\hbar) = \big[\underline{\mu}(\varpi_{0};\hbar), \bar{\mu}(\varpi_{0};\hbar)\big]$ and $\hbar\in[0, 1].$ Then

I. $\underline{\mu}(\varpi_{0};\hbar)$ and $\bar{\mu}(\varpi_{0};\hbar)$ are differentiable, if $\mu$ is a (1)-differentiable, and

II. $\underline{\mu}(\varpi_{0};\hbar)$ and $\bar{\mu}(\varpi_{0};\hbar)$ are differentiable, if $\mu$ is a (2)-differentiable, and

Definition 2.10. (^[58]) Assume that a fuzzy mapping $\Theta_{g\mathcal{H}}^{(r)} = \Theta^{(r)}\in \mathbb{C}^{F}[0, s]\bigcap\mathbb{L}^{F}[0, s].$ Then, fuzzy Caputo generalized Hukuhara derivative (for short ($g\mathcal{H}$)-derivative) of order $0 < \varphi\leq1$ is represented as

Therefore, the parameterized versions of $\Theta = \big[\underline{\Theta}_{\hbar}(\lambda), \bar{\Theta}_{\hbar}(\lambda)\big], \; \hbar\in[0, 1]$ and $\lambda_{0}\in(0, s),$ then CFD in fuzzy generalized Hukuhara sense is stated as

and that $\Theta$ is $(ii)-g\mathcal{H}$-differentiable at $\lambda_{0}$ if

Definition 2.11. Assume that a fuzzy mapping $\tilde{\Theta}(\lambda)\in\tilde{\mathbb{H}}^{1}(0, T)$ and $\varphi\in[0, 1],$ then fuzzy $g\mathcal{H}$-fractional Atangana-Baleanu differentiabilty of fuzzy-valued mapping is represented as

Thus, the parameterized formulation of $\Theta = \big[\underline{\Theta}_{\hbar}(\lambda), \bar{\Theta}_{\hbar}(\lambda)\big], \; \hbar\in[0, 1]$ and $\lambda_{0}\in(0, s),$ then the fuzzy Atangana-Baleanu derivative in Caputo sense is stated as

where

where $\mathbb{B}(\varphi)$ denotes the normalize function that equals to 1 when $\varphi$ assumed to be $0$ and $1$. Also, we suppose that type $(i)-g\mathcal{H}$ exists. So here is no need to consider $(ii)-g\mathcal{H}$ differentiability.

Definition 2.12. (^[65]) Consider a continuous real-valued mapping $\tilde{\Theta}$ and there is an improper fuzzy Riemann-integrable mapping $\exp\big(\frac{-\mu}{\varrho}\big)\odot\tilde{\Theta}(\lambda)$ on $[0, \infty).$ Then, the integral $\int\limits_{0}^{\infty}\exp\big(-\frac{\mu}{\varrho}\big)\odot\tilde{\Theta}(\lambda)d\lambda$ is known to be fuzzy Shehu transform and is stated over the set of mappings:

as

Remark 1. In (2.14), $\tilde{\Theta}$ fulfilled the assumption of the decreasing diameter $\underline{\Theta}$ and increasing diameter $\bar{\Theta}$ of a fuzzy mapping $\Theta.$ If $\varrho = 1,$ then fuzzy Shehu transform reduces to fuzzy Laplace transform.

Using the fact of Salahshour et al. ^[54], we have

Also, considering the classical Shehu transform ^[66], we get

and

Then, the aforesaid expressions can be written as

Next we will define the fuzzy Shehu transform of Caputo generalize Hukuhara derivative $\, _{g\mathcal{H}}^{c}\mathcal{D}_{\lambda}^{\varphi}\Theta(\lambda),$ see ^[65].

Definition 2.13. (^[65]) Suppose there be an integrable fuzzy-valued mapping $\, _{g\mathcal{H}}^{c}\mathcal{D}_{\lambda}^{\varphi}\tilde{\Theta}(\lambda),$ and $\Theta(\lambda)$ is the primitive of $\, _{g\mathcal{H}}^{c}\mathcal{D}_{\lambda}^{\varphi}\tilde{\Theta}(\lambda)$ on $[0, \infty),$ then CFD of order $\varphi$ is presented as

Again, using the fact of Salahshour et al. ^[54], we have

Bokhari et al. ^[67] defined the ABC fractional derivative operator in the Shehu sense. Further, we extend the idea of fuzzy ABC fractional derivative in a fuzzy Shehu transform sense as follows:

Definition 2.14. Consider $\Theta\in \mathbb{C}^{F}[0, s]\bigcap\mathbb{L}^{F}[0, s]$ such that $\tilde{\Theta}(\lambda) = \big[\underline{\Theta}(\lambda, \hbar), \bar{\Theta}(\lambda, \hbar)\big], \; \hbar\in[0, 1],$ then the Shehu transform of fuzzy ABC of order $\varphi\in[0, 1]$ is described as follows:

Further, using the fact of Salahshour et al. ^[54], we have

3.   Description of the fuzzy SHPTM

In this section, we exhibit the basic formulation of the fuzzy SHPTM to derive the generic solution for the one-dimensional fuzzy fractional equal width equation.

Here, we employ the following generic form of time-fractional fuzzy PDE to implement this technique:

subject to

The parameterized formulation of (3.1) is exhibited as

where $\, _{0}^{\ast}\mathcal{D}_{\lambda}^{\varphi}$ represents the CFD or ABC fractional derivative and the linear term is denoted by $\mathcal{L}\langle.\rangle$ and nonlinear factor is signified by $\mathcal{N}\langle.\rangle.$ Taking into consideration the fuzzy Shehu transform elaborated in Definition 2.13 and 2.14, respectively, we characterize the recursive techniques for the solution of (3.1). For this, we proceed with the first case of (3.3) and transformed mappings for the fuzzy CFD operator, then for fuzzy ABC fractional derivative as

Also, the transformed function in the fuzzy ABC derivative sense

It follows that

and

where $\mathcal{G}_{1}({\bf{y}}, \lambda; \hbar) = \big(\frac{\varrho}{\mu}\big){\underline{\Theta}}({\bf{y}}, 0)+\big(\frac{\varrho}{\mu}\big)^{\varphi}{\bf{S}}\big[\theta({\bf{y}}, \lambda; \hbar)\big]$ and $\mathcal{G}_{2}({\bf{y}}, \lambda; \hbar) = \big(\frac{\varrho}{\mu}\big){\underline{\Theta}}({\bf{y}}, 0)+\Big(\frac{1-\varphi+\varphi\big(\frac{\varrho}{\mu}\big)^{\varphi}}{\mathbb{B}(\varphi)}\Big){\bf{S}}\big[\theta({\bf{y}}, \lambda; \hbar)\big],$ respectively. By employing the perturbation method, we acquire the solution of the first case of (3.3) as

Non-linearity factors in (3.3) can be computed as

and the components of $\underline{\bf{F}}_{\kappa}({\bf{y}}, \lambda; \hbar)$ are the He's polynomials ^[68,69] as

Plugging (3.6) and (3.7) into (3.4), we achieve the recursive factors which produce the solution for the fuzzy fractional CFD operator:

and again, plugging (3.6) and (3.8) into (3.5), we achieve the recursive factors which produce the solution for fuzzy ABC fractional derivative operator:

Then, by examining the like powers of $\varkappa$ in (3.9), we calculate the subsequent CFD homotopies:

Moreover, by examining the like powers of $\varkappa$ in (3.10), we calculate the subsequent ABC operator homotopies:

After applying the inverse Shehu transform, the components of $\underline{\Theta}_{\kappa}({\bf{y}}, \lambda; \hbar)$ easily computed to the convergence series form, when $\varkappa\rightarrow1,$ so, we attain the approximate solution of (3.1),

Repeating the same procedure for the upper case of (3.3). Therefore, we mention the solution in parameterized version as follows:

4.   Functioning of the SHPTM and mathematical findings

Here, we elaborate on the pair of numerical solutions of fuzzy fractional EW, MEW, and VMEW models via the Shehu homotopy perturbation transform method involving the fuzzy fractional CFD and ABC derivative operators, respectively. Throughout this investigation, the MATLAB 2021 software package has been considered for the graphical representation processes.

Example 4.1. If $\epsilon = \sigma = 1$ along with $\mu = 1$, then we have the fuzzy time-fractional equal width model

subject to fuzzy ICs

where $\tilde{\Upsilon}(\hbar) = [\underline{\Upsilon}(\hbar), \bar{\Upsilon}(\hbar)] = [\hbar-1, 1-\hbar]$ for $\hbar\in[0, 1]$ is fuzzy number.

The parameterized formulation of (4.1) is presented as

Case Ⅰ. Firstly, taking into consideration the CFD coupled with the Shehu homotopy perturbation transform method on the first case of (4.3).

In view of the process stated in Section 3, we have

In view of fuzzy IC and making use of the inverse Shehu transform implies

Now implementing the HPM, we have

Non-linearity factors represented by He's polynomial $\mathcal{H}_{\kappa}(\Theta)$, (see ^[68,69]).

Therefore, He's polynomials are denoted by

Few of the terms of He's polynomials are prescribed as

Equating the coefficients of the same powers of $\varkappa,$ we have

The series form solution is presented as follows:

implies that

Finally, we have

Case 2. Now, we employ the fuzzy ABC derivative operator on the first first case of (4.3) as follows:

In view of the process stated in Section 3, we have

In view of fuzzy IC and making use of the inverse Shehu transform implies

Now implementing the HPM, we have

where $\sum\limits_{\kappa = 0}^{\infty}\varkappa^{\kappa}\underline{\mathcal{H}}_{\kappa}(\underline{\Theta}) = \underline{\Theta}\frac{\partial}{\partial{\bf{y}}}\underline{\Theta},$ represents the He's polynomials that can be dealt by (4.5).

Equating the coefficients of the same powers of $\varkappa,$ we have

The series form solution is presented as follows:

implies that

Finally, we have

Figure 1 illustrates the three-dimensional comparison between the lower and upper solutions of $\tilde{\Theta}({\bf{y}}, \lambda; \hbar)$ for Example 4.1 when $\varphi = 1$ and uncertainty factor $\hbar\in[0, 1]$ by means of $g\mathcal{H}$-differentiability of Caputo and AB fractional derivative operator in the Caputo sense subject to fuzzy ICs. The SHPTM solution exhibits a strong correlation with both fractional-order derivatives. From Figure 2, it can be shown that increasing the spatial variable causes wavelike motion in the $({\bf{y}}, \lambda; \hbar)$ for waves in plasma at $\lambda = 0.2.$ Figure 3 illustrates the interactions of two wave solutions of various fractional orders. Interaction started at about time $\lambda = 0.5$ overlapping processes occurred between times $\lambda = 0$ and $\lambda = 0.5$ and, waves started to resume their original shapes after time $\lambda = 0.5$. At $\lambda = 0.5$, the wave with the larger amplitude is on the downward side, while the wave with the smaller amplitude is on the upward side.The larger wave catches up with the smaller one at the minimum time.

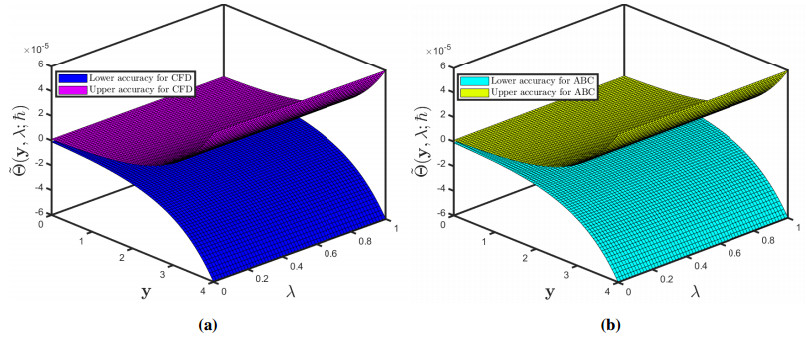
In Figure 4 represents the comparison of absolute error for the lower accuracies between the fuzzy CFD and fuzzy ABC fractional derivative operators. In Figure 5 demonstrates the comparison of absolute error for the upper accuracies between the fuzzy CFD and fuzzy ABC fractional derivative operators.

The important element is that SHPTM has provided pairs of solutions for the EW equation, which is one of the most significant models in fluid dynamics, with limited computational intricacy and concentration. When the constants in these solutions acquire a particular interpretation, they can be used to describe fluid dynamics and physical occurrences. This will be especially useful for fluid dynamics researchers.

Example 4.2. If $\epsilon = 3, \sigma = 2$ along with $\mu = 1$, then we have the fuzzy time-fractional modified equal width model

subject to fuzzy ICs

where $\tilde{\Upsilon}(\hbar) = [\underline{\Upsilon}(\hbar), \bar{\Upsilon}(\hbar)] = [\hbar-1, 1-\hbar]$ for $\hbar\in[0, 1]$ is fuzzy number.

The parameterized formulation of (4.1) is presented as

Case Ⅰ. Firstly, taking into consideration the CFD coupled with the Shehu homotopy perturbation transform method on the first case of (4.8).

In view of the process stated in Section 3, we have

In view of fuzzy IC and making use of the inverse Shehu transform implies

Now implementing the HPM, we have

Non-linearity factors represented by He's polynomial $\mathcal{G}_{\kappa}(\Theta)$, (see ^[68,69]).

Therefore, He's polynomials are denoted by

Few of the terms of He's polynomials are prescribed as

Equating the coefficients of the same powers of $\varkappa,$ we have

The series form solution is presented as follows:

implies that

Finally, we have

Case 2. Now, we employ the fuzzy ABC derivative operator on the first first case of (4.8) as follows:

In view of the process stated in Section 3, we have

In view of fuzzy IC and making use of the inverse Shehu transform implies

Now implementing the HPM, we have

where $\sum\limits_{\kappa = 0}^{\infty}\varkappa^{\kappa}\underline{\mathcal{G}}_{\kappa}(\underline{\Theta}) = \underline{\Theta}^{2}\frac{\partial}{\partial{\bf{y}}}\underline{\Theta},$ represents the He's polynomials that can be dealt by (4.10).

Equating the coefficients of the same powers of $\varkappa,$ we have

The series form solution is presented as follows:

implies that

Finally, we have

Figure 6 illustrates the three-dimensional comparison between the lower and upper solutions of $\tilde{\Theta}({\bf{y}}, \lambda; \hbar)$ for Example 4.2 when $\varphi = 1$ and uncertainty factor $\hbar\in[0, 1]$ by means of $g\mathcal{H}$-differentiability of Caputo and AB fractional derivative operator in the Caputo sense subject to fuzzy ICs. The SHPTM solution exhibits a strong correlation with both fractional-order derivatives. From Figure 7, it can be shown that increasing the spatial variable causes wavelike motion in the $({\bf{y}}, \lambda; \hbar)$ for waves in plasma at $\lambda = 0.2.$

The interactions of two wave solutions of different fractional orders are depicted in Figure 8. Interaction started at about time $\lambda = 0.5$ overlapping processes occurred between times $\lambda = 0$ and $\lambda = 0.5$ and, waves started to resume their original shapes after time $\lambda = 0.5$ and continued to be overlapped for fractional order $\varphi = 0.6$ in the CFD case, but began to wave patteren in the ABC fractional case. This means that the memory effect of the ABC fractional operator is stronger than the CFD. At $\lambda = 0.5$, the wave with the larger amplitude is on the downward side, while the wave with the smaller amplitude is on the upward side. The larger wave catches up with the smaller one at the minimum time.

In Figure 9 represents the comparison of absolute error for the lower accuracies between the fuzzy CFD and fuzzy ABC fractional derivative operators. In Figure 10 demonstrates the comparison of absolute error for the upper accuracies between the fuzzy CFD and fuzzy ABC fractional derivative operators.

The important element is that SHPTM has provided pairs of solutions for the MEW equation, which is one of the most significant models in fluid dynamics, with limited computational intricacy and concentration. When the constants in these solutions acquire a particular interpretation, they can be used to describe fluid dynamics and physical occurrences. This will be especially useful for fluid dynamics researchers.

Example 4.3. Assume the fuzzy time-fractional variant of modified equal width model

subject to fuzzy ICs

where $\tilde{\Upsilon}(\hbar) = [\underline{\Upsilon}(\hbar), \bar{\Upsilon}(\hbar)] = [\hbar-1, 1-\hbar]$ for $\hbar\in[0, 1]$ is fuzzy number.

The parameterized formulation of (4.1) is presented as

Case Ⅰ. Firstly, taking into consideration the CFD coupled with the Shehu homotopy perturbation transform method on the first case of (4.14).

In view of the process stated in Section 3, we have

In view of fuzzy IC and making use of the inverse Shehu transform implies

Now implementing the HPM, we have

Non-linearity factors represented by He's polynomial $\underline{\mathcal{Q}}_{\kappa}(\Theta)$ and $\underline{\mathcal{U}}_{\kappa}(\Theta)$, (see ^[68,69]).

Therefore, He's polynomials are denoted by

Few of the terms of He's polynomials are prescribed as

Equating the coefficients of the same powers of $\varkappa,$ we have

The series form solution is presented as follows:

implies that

Finally, we have

Case 2. Now, we employ the fuzzy ABC derivative operator on the first first case of (4.3) as follows:

In view of the process stated in Section 3, we have

In view of fuzzy IC and making use of the inverse Shehu transform implies

Now implementing the HPM, we have

where $\sum\limits_{\kappa = 0}^{\infty}\varkappa^{\kappa}\underline{\mathcal{Q}}_{\kappa}(\underline{\Theta}) = \big(\underline{\Theta}^{6}\big)_{{\bf{y}}{\bf{y}}\lambda}$, and $\sum\limits_{\kappa = 0}^{\infty}\varkappa^{\kappa}\underline{\mathcal{U}}_{\kappa}(\underline{\Theta}) = \big(\underline{\Theta}^{6}\big)_{{\bf{y}}}$, are represents the He's polynomials that can be dealt by (4.16).

Equating the coefficients of the same powers of $\varkappa,$ we have

The series form solution is presented as follows:

implies that

Finally, we have

Figure 11 illustrates the three-dimensional comparison between the lower and upper solutions of $\tilde{\Theta}({\bf{y}}, \lambda; \hbar)$ for Example 4.3 when $\varphi = 1$ and uncertainty factor $\hbar\in[0, 1]$ by means of $g\mathcal{H}$-differentiability of Caputo and AB fractional derivative operator in the Caputo sense subject to fuzzy ICs. The SHPTM solution exhibits a strong correlation with both fractional-order derivatives. From Figure 12, it can be shown that increasing the spatial variable causes wavelike motion in the $({\bf{y}}, \lambda; \hbar)$ for waves in plasma at $\lambda = 0.2.$

In Figure 13 represents the comparison of absolute error for the lower accuracies between the fuzzy CFD and fuzzy ABC fractional derivative operators. In Figure 14 demonstrates the comparison of absolute error for the upper accuracies between the fuzzy CFD and fuzzy ABC fractional derivative operators.

The important element is that SHPTM has provided pairs of solutions for the VMEW equation, which is one of the most significant models in fluid dynamics, with limited computational intricacy and concentration. When the constants in these solutions acquire a particular interpretation, they can be used to describe fluid dynamics and physical occurrences. This will be especially useful for fluid dynamics researchers.

5.   Conclusions

In this research, we have attained pairs of numerical solutions for EW, MEW, and VMEW models via the fuzzy SHPTM under the generalized Hukuhara differentiability of Caputo and AB fractional derivatives in the Caputo sense have been established. Advanced methodology was utilized in the development of these findings. The merits and demerits of supplied strategies are examined. The findings elaborate on the similarities and differences between the two fuzzy fractional operators' methodologies. The SHPTM method is pragmatic for reducing the computational costs. This technique was implemented explicitly, avoiding the requirement for unphysical constraining conditions, linearization, by identifying adequate fuzzy initial estimates to achieve the estimated solution in the series formulation with accurately determined components. The pattern behaviour was presented graphically and numerically at various fractional orders and $\hbar$-level values. The findings showed that for the specified expressions and variables, the approximate responses are in agreement. According to the illustrated findings, the respective bounds of fuzzy solutions form a relatively symmetric triangle around the core symmetry at $\hbar = 1$. Finally, we may further deduce from our findings that the presented scheme is a comprehensive and appropriate methodology for addressing and solving various initial value problems under unpredictability, with considerable promise in scientific and physical domains.

Acknowledgments

This research was supported by Taif University Research Supporting Project Number (TURSP-2020/326), Taif University, Taif, Saudi Arabia.

Conflict of interest

The authors declare that they have no competing interests.