Coronavirus dynamics, infections and preventive interventions using fractional-calculus analysis

1.   Introduction

It is significant that the World Health Organization (WHO) has identified the infection of COVID-19 as a global epidemic. This viral infection is dangerous and has symptoms that range from those of an ordinary cold to disastrous respiratory disorders. It is also reported that the coronavirus infection principally affects blood pressure. The central nervous system, skin, pregnancy, urinary system, gastrointestinal tract, endocrine system, peripheral nervous system, cardiovascular system and immunological system are all affected by this virus ^[1]. The acute respiratory syndrome (SARS-Cov-2) is caused by the COVID-19 virus, which targets the respiratory system. These are viruses that affect the respiratory system. In December, it was introduced for the first time in China. In January 2020, the WHO proclaimed SARS-Cov-2 to be pandemic ^[2]. Mathematical modeling is the ideal instrument for studying and understanding this complicated and demanding undertaking in order to cope with the epidemic. Because of the spreading characteristics of such occurrences, mathematical modeling has received a lot of interest. Many researchers have developed numerous models to investigate the temporal dynamics of communicable illness. Infectious diseases are the second-leading source of death on the planet ^[3,4]. The authors in ^[3] considered an epidemic model with nonlinear incidence and relapse while the authors in ^[4] focused on the analysis and multi-model selection of COVID-19 infection.

Mathematical modeling is critical for studying disease management and dynamics, especially when the illness is in its early stages or there is no vaccine. The study of biological models of infectious illnesses has received a lot of interest in recent research articles. Stability theory and current system solutions are best described by mathematical language in optimizing epidemiological systems ^[5,6]. In the case of COVID-19, numerous studies have been carried out to conceptualize different aspects of this viral infection. The virus might resurface if social separation is relaxed ^[7]. An effective, safe and widely used vaccine would eliminate the need for social isolation, but creating a COVID-19 vaccine is fraught with difficulties ^[8], and one is unlikely to be ready until spring 2021 at the earliest ^[9]. Until then, non-pharmaceutical measures such as social distancing, diagnostic testing, contact tracing and patient isolation will be used to successfully control COVID-19 ^[10]. In ^[11], the authors introduced the dynamics of COVID-19 and simulate the disease's phase-based transmissibility, moreover, they determine the threshold parameter and examine the system. Khan and Atangana ^[12] presented a mathematical model for the coronavirus infection and evaluated the disease's dynamical characteristics by detailing the interactions between bats and unknown hosts in brief detail ^[13,14]. In ^[15], an epidemic model is presented for the investigation of the effectiveness of control policies through the use of a genetic algorithm. A novel approach has been used by the researchers for the investigation of the approximate solution of the dynamics of COVID-19 infection ^[16]. Here, we formulate the intricate dynamics of COVID-19 with treatment, reinfection and vaccination to study the intricate phenomena of this viral infection.

Fractional calculus is an extended version of classical calculus. Non-integer operators can be utilized to better comprehend physical phenomena and provide insight into mathematical models. The fractional-order derivatives are utilized to better understand the nonlocal behavior and memory. The highest levels of precision and measurement are likewise provided by fractional-order derivative models ^[17,18]. It is reported that the dynamics of infection can be better understood by utilizing fractional derivatives ^[19,20]. A number of fractional operators with non-singular and singular kernels have been identified in recent investigations; moreover, these operators are successfully applied to different problems ^[21,22]. In ^[23], the researchers formulated an epidemic model through the use of non-integer derivatives and showed that the results of fractional calculus are more accurate than ordinary systems. The stochastic dynamics of COVID-19 infection has been studied through the use of a fractional operator in a recent study ^[24]. The researchers in ^[25] examined the dynamics of COVID-19 by using of stochastic and deterministic model by applying a non-integer framework with optimized vaccination. They considered the real data of Saudi Arabia and inspected different vaccination scenarios with the help of numerical schemes. Due to the reported extraordinary properties of fractional operators, we have opted to represent the infection process of COVID-19 through the fractional framework.

The rest of the paper is organized follows. In Section 2, we present some concepts and definitions about fractional theory that are used in this work. We formulate a COVID-19 model in Section 3 and then represent the dynamics with the help of Caputo-Fabrizio (CF) derivatives. The basic reproduction number is calculated, symbolized by $\mathcal{R}_0$ and equilibria are investigated in the same section. We carried out numerical simulations to visualize the significance of the input factors to $\mathcal{R}_0$. In Section 4, by using fixed-point theory, the uniqueness and existence of the solution is discussed. Finally, the research is concluded in Section 5 of this article.

2.   Fractional concepts

For the examination of our COVID-19 dynamics, we shall explain the principal notion and findings of the CF fractional operator. Below are the definitions of these key ideas:

Definition 2.1. Let us take a function $g \in H^1(a, b)$; then, the CF fractional operator ^[26] with normality $\mathcal{W}(\tau)$ is given by

where $b > a$ and $\hbar \in [0, 1]$. If $g \notin H^1(a, b)$, then we get

Remark 2.1. If $\sigma = \frac{1-\hbar}{\hbar}\in [0, \infty)$ and $\hbar = \frac{1}{1+\sigma}\in [0, 1]$, then from (2.2), one can get

furthermore, the below is obtained:

where $M(0) = M(\infty) = 1.$

Definition 2.2. ^[27] The integral of the above fractional operator is defined as follows:

where $0 < \hbar < 1$ and indicates integral order:

Remark 2.2. The above Eq (2.2) yields the following:

where $\mathcal{W}(\hbar) = \frac{2}{2-\hbar}$. From ^[27], we have

3.   Formulation of COVID-19 dynamics

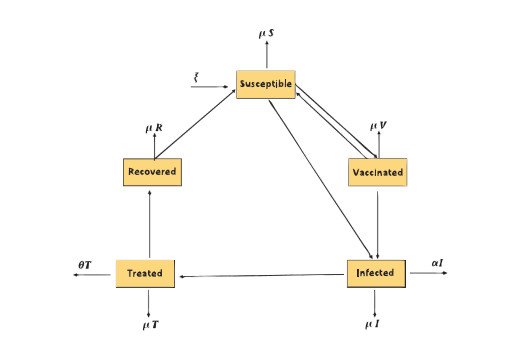
We propose a mathematical model for the transmission of COVID-19 with treatment and immunization in this portion of the study, where $\mathcal{N}(t)$ is the whole population and the population has been divided into five classes: $\mathcal{S}(t)$ indicates the susceptible individuals, $\mathcal{V}(t)$ indicates the vaccinated individuals, $\mathcal{I}(t)$ indicates the infected individuals, $\mathcal{T}(t)$ indicates the treated individuals and $\mathcal{R}(t)$ denotes the recovered individuals at time t. Susceptible individuals are those who have not been infected with COVID-19, whereas infected individuals are those who have been diagnosed with COVID-19 and have transmitted the virus to the susceptible ones. People who have been treated for the illness are known to have been treated; these assumptions leads us to the following:

with

and

The initial values of the state variables and the values of parameters are listed in the following Table 1 for numerical purposes. The flow chart of the transmission phenomena of our model is illustrated in Figure 1.

Mathematical biology is one of the many uses of fractional theory in technology and science. Fractional frameworks have been shown to be more precious rather than traditional derivatives for diseases. It is reported that the recently developed CF derivative describes the nonlocal behavior of biological processes more accurately. Therefore, we represent our model of COVID-19 infection by using a CF fractional operator as follows

where $\hbar$ is the CF fractional operator's order. Next, we focus on the positive invariant region for our fractional model of Covid1-19 infection which can be easily proven by applying analytic skills ^[28].

Theorem 3.1. Let us take $\Xi = \{ (\mathcal{S}, \mathcal{V}, \mathcal{I}, \mathcal{T}, \mathcal{R}) \in R^5_+: 0 \leq \mathcal{S}+\mathcal{V}+\mathcal{I}+\mathcal{T}+\mathcal{R} \leq \mathcal{M} \}$ where $\mathcal{M}$ is a positive constant; then, the set $\Xi$ is positive-invariant for the above-mentioned system (9) of COVID-19.

Investigation of the model

Now we will focus on the analysis of the suggested COVID-19 model (9) including equilibria, stability, reproduction parameter and sensitivity analysis. We indicate the disease-free equilibria by $\mathcal{E}_{0}$ and it is given by the following values

The reproduction parameter of the system can be determined by the methods mentioned in ^[29,30] as follows

which implies that

Thus, the required reproduction number is given by

Theorem 3.2. If $\mathcal{R}_0 < 1$, then the DFE $\mathcal{E}_0(\mathcal{S}^{0}, \mathcal{V}^{0}, \mathcal{I}^{0}, \mathcal{T}^{0}, \mathcal{R}^{0})$ of the system (9) is stable in the local domain and unstable in other cases.

$\mathit{Proof \; 3.2}.$ In this case, we take the Jacobian matrix of our recommended system of COVID-19 as

simplifying the above Eq (3.3) at the disease-free equilibrium $\mathcal{E}_0(\mathcal{S}^{0}, \mathcal{V}^{0}, \mathcal{I}^{0}, \mathcal{T}^{0}, \mathcal{R}^{0})$, we obtain

Now, we find the roots of (3.4) as follows:

Solving (3.5), we get

Here, the eigenvalues $-(\gamma + \mu), -(\beta_2 + \mu), -(\beta_1 +\mu)$ and $-(\theta +\psi + \mu)$ are negative. To fulfill the condition of stability, we take

which implies that

from the above, we have

which implies that the last eigenvalue $\lambda$ is negative for $\mathcal{R}_{0} < 1$. As a result of this, the DFE $\mathcal{E}_0(\mathcal{S}^{0}, \mathcal{V}^{0}, \mathcal{I}^{0}, \mathcal{T}^{0}, \mathcal{R}^{0})$ of the system (9) is stable in the local domain if $\mathcal{R}_{0} < 1$.

Let the endemic state be denoted by $\mathcal{E}_1 = (\mathcal{S}^{*}, \mathcal{V}^{*}, \mathcal{I}^{*}, \mathcal{T}^{*}, \mathcal{R}^{*})$. $\mathcal{E}_1$ is obtained by setting all equations of model (9) equal to zero and solving the model; we have the following:

and

Theorem 3.3. In the case of $\mathcal{R}_{0} > 1$, the endemic steady-state $\mathcal{E}_{1}$ of (9) is stable in the local domain at $\mathcal{E}_{1} = ({\mathcal{S}^{*}, \mathcal{V}^{*}, \mathcal{I}^{*}, \mathcal{T}^{*}, \mathcal{R}^{*}})$.

$\mathit{Proof\ 3.3}$. In this case, we use the Jacobian matrix at endemic steady state as

The fifth-order polynomial equation for $\mathcal{J}_{\mathcal{E}_{1}}$ is given as

Here, we get

and

with the following assumptions:

Using the Routh-Hurwitz method we get the criteria for stability:

As a result, the required proof is completed.

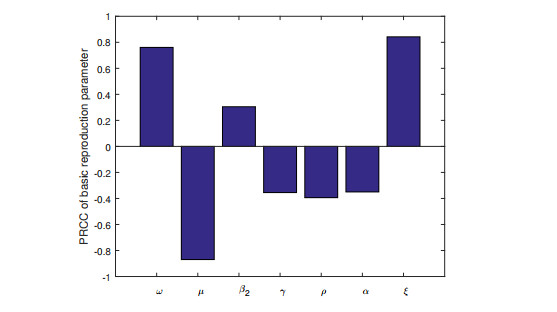
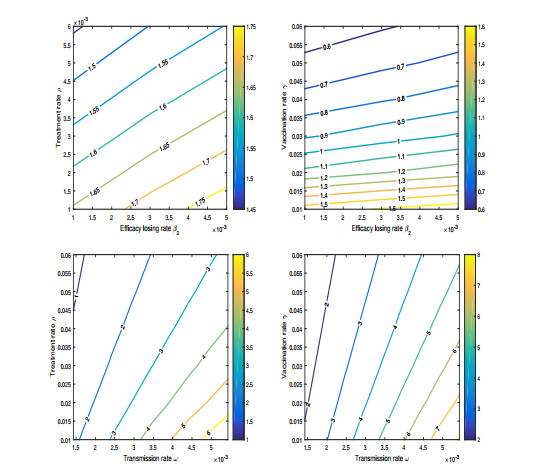
Next, we show the impact of the input factors on the reproduction number of the system $\mathcal{R}_0$ by employing a partial ranked correlation coefficient method (PRCC). The outcomes of the PRCC significance test is illustrated in Figure 2 with PRCC values of $0.7609, -0.8697,$ $0.3049,$ $-0.3549,$ $-0.3940,$ $-0.3499$ and $0.8422$ for the parameters $\omega, \mu, \beta_2, \gamma, \rho, \alpha$ and $\xi$, respectively. This implies that the parameters $\mu, \xi, \omega$ and $\rho$ are the most sensitive parameters of $\mathcal{R}_0$ followed by the other parameters. We performed different simulations to check the results of $\mathcal{R}_0$. The outcomes of the reproduction number are checked against variation of the transmission rate, treatment rate, vaccination rate and immunity loss rate, as can be seen in Figure 3.

4.   Solution investigation

The examination of the solutions of our COVID-19 model is the subject of this study. The presence of a solution will be investigated by using fixed-point theory (9). We will proceed as follows:

Using the result of ^[29], we have the below

Therefore,

Theorem 4.1. The kernels $P_1, P_2, P_3, P_4$ and $P_5$ satisfy the contraction and Lipschitz condition if the following is satisfied:

Proof. For the required result, we take $\mathcal{S}$ and $\mathcal{S}_1$ and proceed from $P_1$ as follows

On solving (4.4), we get that

Let $Q_1 = (\omega M + \gamma + \mu)$, where $\| \mathcal{I} \|\leq M$ due to boundedness; we obtain

As a consequence of this, we demonstrate the Lipschitz condition for $P_1$, as well as the contraction resulting from the condition $0\leq (\omega M + \gamma + \mu) < 1$. We may also determine the Lipschitz conditions in the same way.

Further, solving (4.2) shows that

Thus, the above equations yield

It has the following initial conditions:

The difference terms are given by

Also, we have the following:

Similarly, we get that

In addition, solving the above Eq (4.13) leads to

Therefore,

Similarly, we get the results listed below.

Theorem 4.2. In the case that the below holds true

then one can have the exact coupled solutions of the model (9) of COVID-19.

Proof. We observed that the Lipschitz condition is satisfied and the boundedness of $\mathcal{S}(t)$, $\mathcal{V}(t)$, $\mathcal{I}(t), \mathcal{T}(t)$ and $\mathcal{R}(t)$ are ensured. Thus, from Eqs (4.15) and (4.16), we get that

From Eq (4.17), we get the existence and continuity of the solution. Now we have to prove Eq (4.17) is a solution of system (9); we start the preceding as follows:

Now, we take

Therefore,

We attain the following result at time $t_0$:

Proceeding in a similar way and using (4.21), we obtain

Similarly, we get that $N2_n(t), N3_n(t), N4_n(t)\; and\; N5_n(t)$ approaches $0$ as $n$ approaches $\infty$.

To show that the solution of system (9) is unique, let $(\mathcal{S}_{1}(t)$, $\mathcal{V}_{1}(t)$, $\mathcal{I}_{1}(t)$, $\mathcal{T}_{1}(t)$, $\mathcal{R}_{1}(t))$ be any other solution of system (9); then,

Taking the norm on both sides of Eq (4.22), we get

Using the Lipschitz condition, we attain

Hence, we get that

Theorem 4.3. If the following condition is satisfied:

then the system (9) has a unique solution.

Proof. Let us suppose that Eq (4.26) holds; then, Eq (4.25) yields the following result:

Which implies that

Similarly we obtain the below listed results

To grasp the dynamical behavior of our COVID-19 model, we chose to run multiple simulations for the suggested fractional system by changing the input parameter values. For simulation proposals, the parameter values listed in Table 1 were utilized, with certain values being assumed in these simulations $\mathcal{S} = 800, \mathcal{V} = 50, \mathcal{I} = 30, \mathcal{T} = 100$ and $\mathcal{R} = 20$, which are the values of state variables.

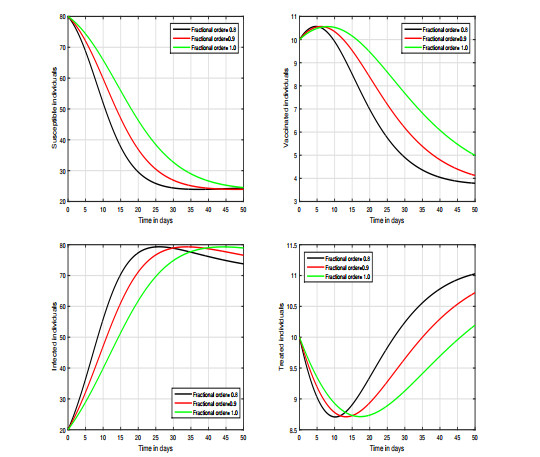
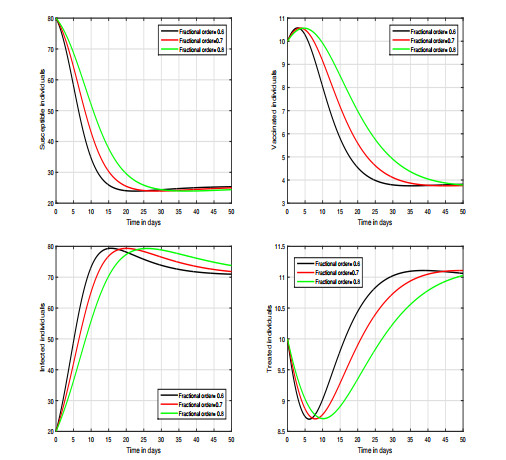
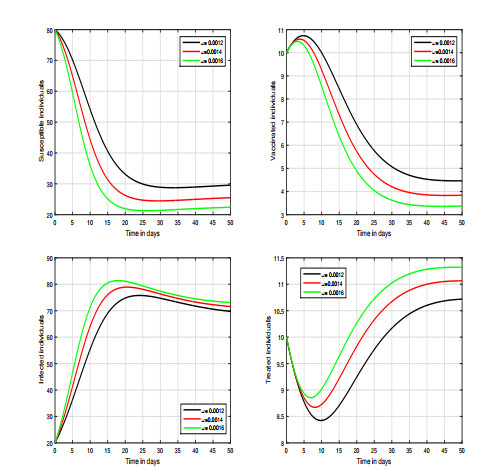
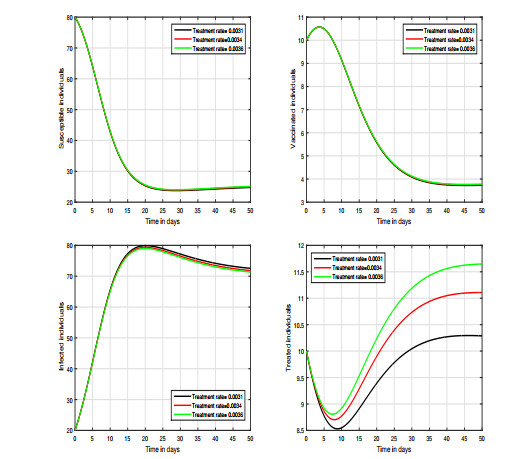
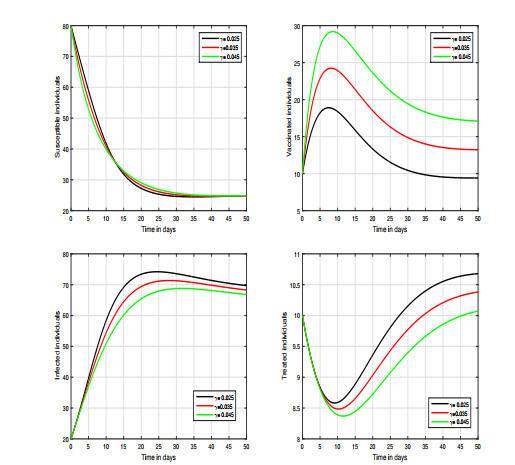
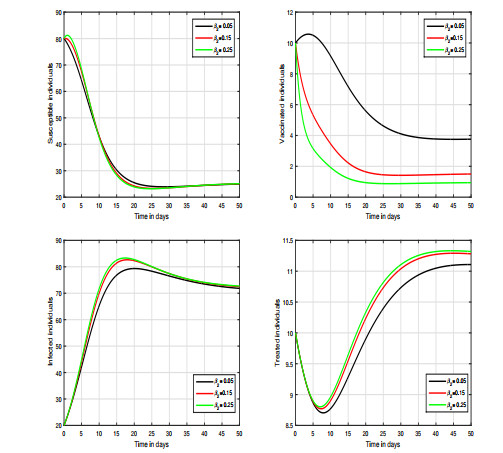
We ran four distinct scenarios to see how different settings affect the system's output. Our major goal was to detect the level of infection and the volatility of these values, as well as to anticipate appealing control measures for COVID-19 infection prevention. In the first instance, we show how fractional order affects the system shown in Figures 4–5. In these simulations, we primarily focused on the system's variation in response to changes in the index of memory. We observed that this input factor has a significant influence on the system and can effectively decrease the level of infection in the community. In Figure 6, we varied the value of the transmission rate $\omega$; thus, we can observe the fluctuation of the dynamics in the second scenario. In the third and fourth scenarios respectively presented in Figures 7 and 8, we show the dynamical behavior of the hypothesized model with the variation in treatment and vaccination rates $\rho$ and $\gamma$, respectively; we noticed the influence of each of these parameters on the infected individuals in the COVID-19 model. In our results, we observed that the vaccination rate has an attractive influence on the system in terms of its ability to reduce the level of infection; thus, it can be used as a control parameter. Finally, regarding in the last scenario, the efficacy loss rate of vaccination is illustrated in Figure 9 which shows that this factor is critical and can increase the risk of infection.

5.   Conclusions

In the context of the CF derivative, we introduced a mathematical model for the COVID-19 transmission process incorporating vaccination and therapy components. For the examination of the recommended dynamics, we represented the fundamental findings of fractional theory. We examined the steady states of the system and the reproduction parameter $\mathcal{R}_{0}$ was calculated via a next-generation matrix approach. The infection-free equilibrium of the suggested system has been determined to be locally asymptotically stable if $\mathcal{R}_{0} < 1$ and unstable in all other cases. It has been proved that the endemic steady state is locally asymptotically stable for $\mathcal{R}_{0} > 1$. The system's reproduction parameter has been quantitatively explored by varying various factors. In addition to this, we established results for the existence and uniqueness of the solution for the proposed COVID-19 infection model. The tracking path behavior of our model has been analyzed by using a numerical method. Numerical simulations with different input parameters have been used to show the system's dynamical behavior. The influence of various factors of the system has been conceptualized for the solution pathways. For infection control, the most significant scenario of the system has been proposed to the public health. In the future work, the dynamics of COVID-19 infection will be examined through the use of stochastic differential equations. Moreover, we will also apply real data to the dynamics of COVID-19 infection for further predictions.

Acknowledgments

The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University for funding this work through the Research Groups Program [grant number R.G.P.2/25/44].

Conflict of interest

The authors stated that there are no conflicts of interest regarding this work.