Global properties of delayed models for SARS-CoV-2 infection mediated by ACE2 receptor with humoral immunity

1.   Introduction

The coronavirus disease 2019 (COVID-19) began in China in December 2019; it then turned into a global pandemic ^[1]. According to the World Health Organization report of August 27, 2023, there were over 770 million confirmed cases and 6.9 million deaths globally ^[2]. The world has also seen economic losses as a result of this sickness. COVID-19 originated from an infection with a virus called severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2). It is a single-stranded RNA virus in the coronaviridae family. SARS-CoV-2 attacks the epithelial (target) cells by binding its spike protein, S, to the angiotensin-converting enzyme 2 (ACE2) receptor on the surface of epithelial cells ^[3,4]. ACE2 receptors of epithelial cells play a crucial role in cellular entry in humans, which may provide worthy input for the development of possible receptor-targeted vaccines and drugs ^[4,5]. Some of the symptoms that may appear in COVID-19 patients are like include headaches, fatigue, fever, myalgia, dry cough, nausea, abdominal pain, vomiting and diarrhea. Recognition of COVID-19 is essential because it enables the introduction of effective infection control measures and potentially helpful antiviral therapy. The adaptive immune response has an effective role in resisting and fighting viruses that attack the human body. B cells and cytotoxic T lymphocytes (CTLs) are two main players in the adaptive immune response. B cells generate antibodies to neutralize the SARS-CoV-2, while CTLs kill the epithelial cells infected by SARS-CoV-2.

Since the beginning of the spread of this disease, scientists and researchers from all fields have united their massive efforts to study and understand the mechanism between the virus and host cells in order to produce treatments and vaccines for this virus. Experimental evaluation of interactions between SARS-CoV-2, epithelial cells and immune cells can be difficult and expensive. Studying the dynamics of SARS-CoV-2 infection within the host by performing mathematical modeling may facilitate understanding of the dynamic behavior of the virus and its target cells, as well as immune cells. This type of study also helps in understanding the effectiveness of medications, whether individually or in combination. A within-host SARS-CoV-2 infection model with target-limited cells was given in ^[6]. Li et al. ^[7] included the production and death of the epithelial cells in a model of SARS-CoV-2 infection. Some biological processes were incorporated into the SARS-CoV-2 infection models by considering the effect of the immune response ^{[8,9,10,11,12,13,14,15,16]}, drug therapies ^{[17,18,19,20]} and time delay ^[21]. In these works, the dynamics of ACE2 receptors of epithelial cells were not considered. In ^{[22,23,24,25]}, the authors modeled the effect of the dipeptidyl peptidase 4 receptor on the Middle East respiratory syndrome coronavirus (MERS-CoV) infection. Chatterjee and Al Basir ^[26] presented a SARS-CoV-2 model with ACE2 receptors. The authors studied the local stability of equilibria. Lv and Ma ^[27] formulated a system of delay differential equations (DDEs) for SARS-CoV-2 infection, as mediated by ACE2 receptors, as follows:

The variables $E(t)$, $I(t), S(t)$ and $A(t)$ represent, respectively, the concentrations of per unit volume of uninfected epithelial cells, infected cells, SARS-CoV-2 particles and ACE2 receptors at time $t$. $\Psi(A)$ is the probability of successful entry of the SARS-CoV-2 into the epithelial cell mediated by the ACE2 receptors. When the concentration of ACE2 receptor is lower (higher), then $\Psi(A)\thicksim0\; (\thicksim1)$ ^[27]. Here, $\tau_{1}$ is the time from the SARS-CoV-2 particles making contact with uninfected epithelial cells to them becoming actively infected cells. The factor $e^{-\alpha_{1} \tau_{1}}$ is the probability of survival of infected cells during the delay period of $[t-\tau_{1}, t]$. Note that the term $\eta \Psi(A)ES$ denotes a decrease in uninfected epithelial cells (due to free virions), and the average number of ACE2 receptors carried by each uninfected epithelial cell is $A/E$. Therefore, the decrease in ACE2 receptors due to the decrease in uninfected epithelial cells (caused by free virions) is $\kappa \eta \Psi(A)ES = \kappa \eta \Psi(A)ES\times(A/E) = \kappa \eta \Psi (A)AS,$ where $\kappa$ is a constant ^[27].

The model described by Eqs (1.1)–(1.4) does not take the immune system's response to SARS-CoV-2 infection into account. Furthermore, the model ignores the maturation delay and only takes into account one type of discrete-time (constant) delay, $\tau_{1}$. Therefore, our aim in this paper is to extend the model given by Eqs (1.1)–(1.4) by including the role of the humoral immune response and considering two classes of delays: (ⅰ) Delay in the SARS-CoV-2 infection of epithelial cells, and (ⅱ) delay in the maturation of recently released SARS-CoV-2 virions. In the first model, we consider discrete-time delays which are generalized in the second model by considering distributed-time delays. We first look into the fundamental characteristics of the DDEs; then, we find all equilibria and discuss their existence and global stability. We construct suitable Lyapunov functions and use LaSalle's invariance principle (LIP) to investigate the global asymptotic stability of all equilibria. We use numerical simulations to demonstrate the theoretical findings. Finally, we discuss the obtained results.

2.   Model with discrete delays

2.1.   Model formulation

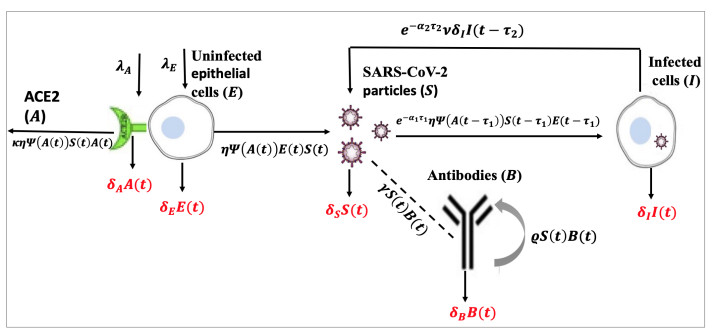
We formulate a system of DDEs for SARS-CoV-2 infection, as mediated by ACE2 receptors. We consider two discrete-time delays and the humoral immune response:

where $B(t)$ denotes the concentration of antibodies at time $t$. The antibodies are stimulated at a rate of $\varrho SB$, die at a rate of $\delta_{B}B$ and neutralize the SARS-CoV-2 particles at a rate of $\gamma SB$. Here, $\tau_{2}$ is the maturation time of new virions. Factor $e^{-\alpha_{2}\tau_{2}}$ represents the probability of survival of SARS-CoV-2 particles during their delay period of $[t-\tau_{2}, t]$. Usually, $\Psi(A)$ is chosen as the classic Hill function: $\Psi(A) = \frac{A^{n}}{\mathcal{A}_{s}^{n}+A^{n}},$ where $\mathcal{A}_{s}$ is the half-saturation constant and $n > 0$ is the Hill coefficient ^[27,28]. The function $\Psi(A)$ is continuously differentiable on $[0, \infty)$ and strictly monotonically increasing. All parameters of model (2.1) are positive. A schematic representation of the model given by (2.1) is illustrated in Figure 1.

Let $\tau^{\ast} = \max \{ \tau_{1}, \tau_{2}\},$ and consider the initial conditions for model (2.1) as follows:

where $\phi_{i}\in C([-\tau^{\ast}, 0], \mathbb{R} _{\geq0})$ is the Banach space of continuous functions mapping from $[-\tau^{\ast}, 0]$ to $\mathbb{R} _{\geq0}$ with the norm $\left \Vert \phi_{i}\right \Vert = \sup \limits_{-\tau ^{\ast}\leq \theta \leq0}\left \vert \phi_{i}(\theta)\right \vert$ for $\phi_{i}\in C,$ $i = 1, 2, ..., 5.$ We note that system (2.1) with the initial conditions given by Eq (2.2) has a unique solution ^[29].

2.2.   Basic qualitative properties

This subsection proves the non-negativity and boundedness of the solutions of system (2.1).

Lemma 1. The solutions of model (2.1) with the initial conditions given by Eq (2.2) are non-negative and ultimately bounded.

Proof. We have that $\dot{E}\mid_{E = 0} = \lambda_{E} > 0,$ $\dot{A}\mid _{A = 0} = \lambda_{A} > 0$ and $\dot{B}\mid_{B = 0} = 0.$ Hence, $E(t), A(t), B(t)\geq0$ for all $t\geq0$ (see Proposition B.7 of ^[30]). From the second and third equations of system (2.1), we have

for all $t\in \lbrack0, \tau^{\ast}]$ ^[31]$.$ Hence, by recursive argumentation, we obtain that $I(t), S(t)\geq0$ for all $t\geq0.$ Hence, $E, I, S, A$ and $B$ are non-negative.

Now, we prove the ultimate boundedness of $E(t),$ $I(t),$ $S(t),$ $A(t)$ and $B(t)$. From the first equation of system (2.1), we have that $\lim \limits_{t\rightarrow \infty}\sup E(t)\leq \frac{\lambda_{E}}{\delta_{E}} = \omega_{1}.$ To prove the ultimate boundedness of $I(t),$ we define

Then, we obtain

where $p_{1} = \min \{ \delta_{E}, \delta_{I}\}$. Therefore, $\lim \limits_{t\rightarrow \infty}\sup \Pi_{1}(t)\leq \frac{\lambda_{E}}{p_{1}} = \omega_{2}$. Since $E(t)\geq0$ and $I(t)\geq0,$ then $\lim \limits_{t\rightarrow \infty}\sup I(t)\leq \omega_{2}$. Now, let us define

Then, we obtain

where $p_{2} = \min \{ \delta_{S}, \delta_{B}\}$. Therefore, $\lim \limits_{t\rightarrow \infty}\sup \Pi_{2}(t)\leq \frac{\delta_{I}\nu \omega_{2} }{p_{2}} = \omega_{3}$, $\ $and then $\lim \limits_{t\rightarrow \infty}\sup S(t)\leq \omega_{3}$ and $\lim \limits_{t\rightarrow \infty}\sup B(t)\leq \frac{\varrho}{\gamma}\omega_{3} = \omega_{5}$. Finally, from the fourth equation of system (2.1), we have that $\lim \limits_{t\rightarrow \infty}\sup A(t)\leq \frac{\lambda_{A}}{\delta_{A}} = \omega_{4}.$ Then, $E, I, S, A$ and $B$ are ultimately bounded.

From Lemma 1, we can establish that $\Gamma = \{(E, I, S, A, B)\in C_{\geq0} ^{5}:\left \Vert E\right \Vert \leq \omega_{1},$ $\left \Vert I\right \Vert \leq \omega_{2},$ $\left \Vert S\right \Vert \leq \omega_{3},$ $\left \Vert A\right \Vert \leq \omega_{4},$ $\left \Vert B\right \Vert \leq \omega_{5}\}$ is positively invariant for system (2.1).

2.3.   Equilibria

This subsection is a derivation of all equilibria of model (2.1) and the threshold parameters that determine the existence of the equilibria. First, we compute the basic infection reproduction number $\Re_{0}$ for system (2.1) by using the next-generation matrix method ^[32]. Define the matrices $F$ and $V$ as follows:

where $E_{0} = \lambda_{E}/\delta_{E}$ and $A_{0} = \lambda_{A}/\delta_{A}.$ Then, $\Re_{0}$ can be derived as the spectral radius of $FV^{-1},$ as follows:

Second, let $\Delta = (E, I, S, A, B)$ be any equilibrium of system (2.1); we have

Equation (2.8) has two solutions, $B = 0$ and $S = \frac{\delta_{B}}{\varrho}$. When $B = 0$, then, from Eq (2.6), we get

Substituting Eq (2.9) into Eq (2.5), we get

and then we have

If $S = 0,$ then, from Eqs (2.4), (2.5) and (2.7), we have that $E = \lambda_{E}/\delta_{E}$, $I = 0$ and $A = \lambda_{A}/\delta_{A}.$ Then, we obtain the uninfected equilibrium $\Delta_{0} = (E_{0}, 0, 0, A_{0}, 0)$.

If $S\neq0$, then $I\neq0$ and

Therefore, we obtain

Substituting Eq (2.11) into Eq (2.5), we have

Since $I\neq0,$ then

We define a function $G(I)$ as follows:

We have

and

So, we have

Then, there exists a unique $I_{1}\in \left(0, \frac{\lambda_{E}}{\delta_{I} }e^{-\alpha_{1}\tau_{1}}\right)$ that satisfies that $G(I_{1}) = 0.$

Therefore, there exists a unique infected equilibrium without humoral immunity $\Delta_{1} = (E_{1}, I_{1}, S_{1}, A_{1}, 0)$ when $\Re_{0} > 1,$ where $E_{1} = \frac{\lambda_{E}-e^{\alpha_{1}\tau_{1}}\delta_{I}I_{1}}{\delta_{E}} \in \left(0, \frac{\lambda_{E}}{\delta_{E}}\right), \ S_{1} = \frac {e^{-\alpha_{2}\tau_{2}}\delta_{I}\nu I_{1}}{\delta_{S}}\in \left(0, \frac{\lambda_{E}\nu}{\delta_{S}}e^{-\alpha_{1}\tau_{1}-\alpha_{2}\tau_{2} }\right) \ $ and $A_{1} = \frac{\lambda_{A}}{\delta_{A}+\kappa e^{\alpha_{1} \tau_{1}}\delta_{I}I_{1}/E_{1}}\in \left(0, \frac{\lambda_{A}}{\delta_{A} }\right).$

If $B\neq0$ and $S = \frac{\delta_{B}}{\varrho}$, we therefore obtain

Substituting Eq (2.13) into Eq (2.5), we obtain

Define a function $G^{\ast}(I)$ as follows:

We have

Moreover,

So, we have

Hence, there exists a unique $I_{2}\in \left(0, \frac{\lambda_{E}}{\delta_{I} }e^{-\alpha_{1}\tau_{1}}\right)$ that satisfies that $G^{\ast}(I_{2}) = 0.$ Consequently, there exists a unique infected equilibrium with humoral immunity $\Delta_{2} = (E_{2}, I_{2}, S_{2}, A_{2}, B_{2})$ when $\Re_{1} > 1,$ where $E_{2} = \frac{\lambda_{E}-e^{\alpha_{1}\tau_{1}}\delta_{I}I_{2}}{\delta_{E}} \in \left(0, \frac{\lambda_{E}}{\delta_{E}}\right),$ $\ S_{2} = \frac {\delta_{B}}{\varrho}, \ \ A_{2} = \frac{\lambda_{A}}{\delta_{A}+\kappa e^{\alpha_{1}\tau_{1}}\delta_{I}I_{2}/E_{2}}\in \left(0, \frac{\lambda_{A} }{\delta_{A}}\right)$ and $B_{2} = \frac{\delta_{S}}{\gamma}\left(\Re _{1}-1\right),$ where

Here, $\Re_{1}$ represents the humoral immunity activation number.

We have that $\Psi(A_{2}) < \Psi(A_{0})$ and $E_{2} < E_{0}$. Therefore,

Now, we can state the following lemma:

Lemma 2. For system (2.1), there exist two threshold parameters $\Re_{0}$ and $\Re_{1}$ such that the following conditions hold:

(ⅰ) If $\Re_{0}\leq1$, then the uninfected equilibrium $\Delta_{0} = (E_{0}, 0, 0, A_{0}, 0)$ is the only equilibrium.

(ⅱ) If $\Re_{1}\leq1 < \Re_{0}$, then there exists two equilibria, $\Delta_{0}$ and the infected equilibrium without humoral immunity $\Delta_{1} = (E_{1}, I_{1}, S_{1}, A_{1}, 0)$.

(ⅲ) If $\Re_{1} > 1$, then there exist three equilibria, $\Delta_{0}$, $\Delta_{1}$ and the infected equilibrium with humoral immunity $\Delta_{2} = (E_{2}, I_{2}, S_{2}, A_{2}, B_{2})$.

2.4.   Global stability

This subsection describes the use of the Lyapunov method to study the global asymptotic stability of the equilibria. We define a function $\Phi(x) = x-1-\ln x.$ Clearly, $\Phi(1) = 0$ and $\Phi(x)\geq0$ for $x > 0.$ Let $\tilde{\Omega}_{j}$ be the largest invariant subset of

where $\Lambda_{j}(E, I, S, A, B)$ is a Lyapunov function candidate. Denote $(E, I, S, A, B) = (E(t), I(t), S(t), A(t), B(t))$ and $(E_{\tau}, I_{\tau}, S_{\tau }, A_{\tau}) = (E(t-\tau), I(t-\tau), S(t-\tau), A(t-\tau))$. Subsequent to the studies of ^[33] and ^[44], we construct Lyapunov functions in the following theorems.

Theorem 1. For system (2.1), if $\Re_{0}\leq1$, then $\Delta _{0}$ is globally asymptotically stable (G.A.S), and it is unstable when $\Re_{0} > 1$.

Proof. Define

We note that $\Lambda_{0}(E, I, S, A, B) > 0$ for all $E, I, S, A, B > 0$ and $\Lambda _{0}(E_{0}, 0, 0, A_{0}, 0) = 0$. We evaluate $\frac{d\Lambda_{0}}{dt}$ along the solutions of system (2.1) as follows:

Using system (2.1), we get

Collecting terms, we get

Using the equilibrium condition of $\lambda_{E} = \delta_{E}E_{0}$, as well as $\lambda_{A} = \delta_{A}A_{0}$, we get

Since $\Psi(A)$ is strictly monotonically increasing, then $\left(\Psi(A)-\Psi(A_{0})\right) (A_{0}-A)\leq0$. Therefore, $\frac{d\Lambda_{0} }{dt}\leq0$ for all $E, S, A, B > 0$ when $\Re_{0}\leq1$. In addition, $\frac{d\Lambda_{0}}{dt} = 0$ when $E = E_{0},$ $A = A_{0}$ and $S = B = 0.$ Solutions of system (2.1) converge to $\tilde{\Omega}_{0},$ which contains elements ^[37]. Since $\tilde{\Omega}_{0}$ is invariant with respect to (2.1), on $\tilde{\Omega}_{0}$, we have

Therefore, $\tilde{\Omega}_{0} = \left \{ \Delta_{0}\right \}$ and, applying the LIP (see ^[29,39]), we obtain that $\Delta_{0}$ is G.A.S.

To show the instability of $\Delta_{0},$ we calculate the characteristic equation of system (2.1) at $\Delta_{0}$ as follows:

Define a function where $\mathcal{T}(c)$ as follows:

which is continuous on $[0, \infty)$. We have

Hence, $\mathcal{T}(c)$ has a positive real root and $\Delta_{0}$ is unstable.

To confirm the result on the dynamics of $\Delta_{1}$, we require additional assumptions ^[38]:

Theorem 2. Consider system (2.1) and suppose that assumption (A) is satisfied and $\Re_{1}\leq1 < \Re_{0}$; then, $\Delta_{1}$ is G.A.S.

Proof. Define

Note that $\Lambda_{1}(E, I, S, A, B) > 0$ for all $E, I, S, A, B > 0$ and $\Lambda _{1}(E_{1}, I_{1}, S_{1}, A_{1}, 0) = 0$. We evaluate $\frac{d\Lambda_{1}}{dt}$ as follows:

Using system (2.1), we get

Collecting terms, we get

Using the equilibrium condition for $\Delta_{1}$, i.e.,

we obtain

Using the equalities

we obtain

We have that $\left(\Psi(A)-\Psi(A_{1})\right) (A_{1}-A)\leq0$, and, from Assumption (A), we have that $S_{1}-\frac{\delta_{B}}{\varrho}\leq 0$. Thus, $\frac{d\Lambda_{1}}{dt}\leq0$ for all $E, I, S, A, B > 0$. In addition, $\frac{d\Lambda_{1}}{dt} = 0$ when $E = E_{1},$ $A = A_{1}$, $B = 0$ and

All solutions of system (2.1) are attracted to $\tilde{\Omega }_{1}$. Since $\tilde{\Omega}_{1}$ is invariant with respect to (2.1), on $\tilde{\Omega}_{1}$, we have

and, from Eq (2.21), we get that $I(t) = I_{\tau_{2}} = I_{1}$ for any $t$. Therefore, $\tilde{\Omega}_{1} = \left \{ \Delta_{1}\right \}$, and by applying the LIP, we obtain that $\Delta_{1}$ is G.A.S.

Theorem 3. Consider system (2.1) and let $\Re_{1} > 1$; then, $\Delta_{2}$ is G.A.S.

Proof. Consider

We note that $\Lambda_{2}(E, I, S, A, B) > 0$ for all $E, I, S, A, B > 0$ and $\Lambda _{2}(E_{2}, I_{2}, S_{2}, A_{2}, B_{2}) = 0$. We calculate $\frac{d\Lambda_{2}}{dt}$ as follows:

From system (2.1), we get

Collecting terms, we get

Using the equilibrium condition for $\Delta_{2}$, i.e.,

we obtain

Using the equalities

we obtain

If $\Re_{1} > 1$, we get that $\frac{d\Lambda_{2}}{dt}\leq0$ for all $E, I, S, A > 0$. Further, $\frac{d\Lambda_{2}}{dt} = 0$ when $E = E_{2}$, $A = A_{2}\ $ and

Trajectories of system (2.1) converge to $\tilde{\Omega}_{2},$ where $E = E_{2}$ and $A = A_{2}$; then,

and, from Eq (2.24), we get that $I(t) = I_{\tau_{2}} = I_{2}$ for any $t$. Moreover, the third equation of system (2.1) yields

Hence, $\tilde{\Omega}_{2} = \left \{ \Delta { _{2} }\right \}$ and the LIP implies that $\Delta_{2}$ is G.A.S.

3.   Model with distributed delays

In the previous section, we assumed that the time between the virus entering the cell and the production of new immature virions ($\tau_{1})$ is fixed for each cell. Moreover, the maturation time ($\tau_{2})$ for each virus is fixed. Several viral infection models were developed by taking into account the time delay as a random variable drawn from the probability distribution function in order to avoid such an (biologically implausible) assumption (see, e.g., ^[34,35,36]). In this section, we study a SARS-CoV-2 infection model with distributed-time delay. It is worth pointing out that the distributed delay is one of various time delays, and it is more general than discrete delay. In various nonlinear systems, other types of time delays have been examined, including proportional delay ^[40], time-varying delay ^[45,46] and state-dependent delay ^[47].

3.1.   Model formulation

We formulate a SARS-CoV-2 infection system with two kinds of distributed delays as follows:

Here, $\tau$ is a random variable from a probability distributed function $f_{i}(\tau)$ over the interval $\left[ 0, h_{i}\right],$ where $h_{i}$ is the limit superior of the delay period, and $i = 1, 2$. The factor $f_{1} (\tau)e^{-\alpha_{1}\tau}$ represents the probability that uninfected epithelial cells contacted by the SARS-CoV-2 at time $t-\tau$ survive $\tau$ time units and become infected at time $t.$ The factor $f_{2}(\tau)e^{-\alpha_{2}\tau}$ is the probability that an immature SARS-CoV-2 at time $t-\tau$ survives $\tau$ time units to become mature SARS-CoV-2 at time $t$. The function $f_{i}(\tau)$ satisfies the following conditions:

Let $\chi_{i}(\tau) = f_{i}(\tau)e^{-\alpha_{i}\tau}$ and $\zeta_{i} = \int _{0}^{h_{i}}\chi_{i}(\tau)d\tau$; thus, $0 < \zeta_{i}\leq1$, $i = 1, 2$. Because $f_{i}(\tau)$ is a general distribution, it is possible to model a variety of delay distributions by using model (3.1). The initial conditions for model (3.1) are the same as those given by Eq (2.2), where $\tau^{\ast} = \max \{h_{1}, h_{2}\}$.

3.2.   Basic qualitative properties

This subsection proves the non-negativity and boundedness of the solutions of system (3.1).

Lemma 3. Solutions of model (3.1) with the initial conditions given by Eq (2.2) are non-negative and ultimately bounded.

Proof. We have that $\dot{E}\mid_{E = 0} = \lambda_{E} > 0,$ $\dot{A}\mid _{A = 0} = \lambda_{A} > 0$ and $\dot{B}\mid_{B = 0} = 0.$ Thus, $E(t)\geq0,$ $A(t)\geq0$ and $B(t)\geq0$ for all $t\geq0$ (see Proposition B.7 of ^[30]). In addition, we have

for all $t\in \lbrack0, \tau^{\ast}]$ ^[31]. Hence, by recursive argumentation, we get that $I(t), S(t)\geq0$ for all $t\geq0.$ Hence, $E, I, S, A$ and $B$ are non-negative.

Now, we prove that $E,$ $I,$ $S,$ $A$ and $B$ are all ultimately bounded. From the first equation of system (3.1) we have that $\lim \limits_{t\rightarrow \infty}\sup E(t)\leq \frac{\lambda_{E}}{\delta_{E}} = \omega_{1}.$ To investigate the ultimate boundedness of $I,$ we define

Then, we obtain

where $p_{1} = \min \{ \delta_{E}, \delta_{I}\}.$

It follows that $\lim \limits_{t\rightarrow \infty}\sup \Pi_{1}(t)\leq \frac{\lambda_{E}}{p_{1}} = \omega_{2}$. Since $E\geq0$ and $I\geq0,$ then $\lim \limits_{t\rightarrow \infty}\sup I(t)\leq \omega_{2}$. Now, let us define $\Pi_{2} = S+\frac{\gamma}{\varrho}B$. Then, we obtain

where $p_{2} = \min \{ \delta_{S}, \delta_{B}\}$. Hence, $\lim \limits_{t\rightarrow \infty}\sup \Pi_{2}(t)\leq \frac{\delta_{I}\nu \omega_{2} }{p_{2}} = \omega_{3}.$ Since $S\geq0$ and $B\geq0,$ then $\lim \limits_{t\rightarrow \infty}\sup S(t)\leq \omega_{3}$ and $\lim \limits_{t\rightarrow \infty}\sup B(t)\leq \frac{\varrho}{\gamma}\omega _{3} = \omega_{5}$. Finally, from the fourth equation of system (3.1), we have $\lim \limits_{t\rightarrow \infty}\sup A(t)\leq \frac{\lambda_{A}}{\delta_{A} } = \omega_{4}.$ Then, $E, I, S, A$ and $B$ are ultimately bounded.

From Lemma 3, we can demonstrate that $\Gamma = \{(E, I, S, A, B)\in C_{\geq0} ^{5}:\left \Vert E\right \Vert \leq \omega_{1},$ $\left \Vert I\right \Vert \leq \omega_{2},$ $\left \Vert S\right \Vert \leq \omega_{3},$ $\left \Vert A\right \Vert \leq \omega_{4},$ $\left \Vert B\right \Vert \leq \omega_{5}\}$ is positively invariant for system (3.1).

3.3.   Equilibria

First, we compute the basic reproduction number $\bar{\Re_{0}}$ for system (3.1). Define $\bar{F}$ and $\bar{V}$ as follows:

where $E_{0} = \lambda_{E}/\delta_{E}$ and $A_{0} = \lambda_{A}/\delta_{A}$. Then, $\bar{\Re_{0}}$ can be computed as the spectral radius of $\bar{F}\bar{V} ^{-1}$, as follows:

Second, let $\Delta = (E, I, S, A, B)$ be any equilibrium of system (3.1) such that

Equation (3.8) has two solutions, $B = 0$ and $S = \frac{\delta_{B}}{\varrho}$. When $B = 0$, then, from Eq (3.6), we get

Substituting Eq (3.9) into Eq (3.5), we obtain

and then we have

If $S = 0,$ then, from Eqs (3.4), (3.5) and (3.7), we have that $E = \lambda_{E}/\delta_{E},$ $I = 0$ and $A = \lambda_{A}/\delta_{A}.$ Then, we obtain the uninfected equilibrium $\Delta_{0} = (E_{0}, 0, 0, A_{0}, 0)$.

If $S\neq0$, then $I\neq0$ and

Therefore, we obtain

Substituting Eq (3.12) into Eq (3.5), we have

Since $I\neq0,$ then

We define a function $G_{1}(I)$ as follows:

We have

and

So, we have

Hence, there exists a unique $I_{1}\in \left(0, \frac{\lambda_{E}}{\delta_{I} }\zeta_{1}\right)$ satisfying that $G_{1}(I_{1}) = 0.$

Therefore, there exists a unique infected equilibrium without humoral immunity $\Delta_{1} = (E_{1}, I_{1}, S_{1}, A_{1}, 0)$ when $\bar{\Re}_{0} > 1,$ where $E_{1} = \frac{\lambda_{E}-\zeta_{1}^{-1}\delta_{I}I_{1}}{\delta_{E}}\in \left(0, \frac{\lambda_{E}}{\delta_{E}}\right), \ S_{1} = \frac{\zeta_{2}\delta_{I}\nu I_{1}}{\delta_{S}}\in \left(0, \frac{\lambda_{E}\nu}{\delta_{S}}\zeta_{1} \zeta_{2}\right) \ $and $A_{1} = \frac{\lambda_{A}}{\delta_{A}+\kappa \zeta _{1}^{-1}\delta_{I}I_{1}/E_{1}}\in \left(0, \frac{\lambda_{A}}{\delta_{A} }\right)$.

If $B\neq0$ and $S = \frac{\delta_{B}}{\varrho}$, we therefore obtain

Substituting Eq (3.14) into Eq (3.5), we obtain

Define a function $G_{1}^{\ast}(I)$ as follows:

We have

Moreover,

So, we have

Then, there exists a unique $I_{2}\in \left(0, \frac{\lambda_{E}}{\delta_{I} }\zeta_{1}\right)$ such that $G_{1}^{\ast}(I_{2}) = 0.$ It follows that there exists a unique infected equilibrium with humoral immunity $\Delta_{2} = (E_{2}, I_{2}, S_{2}, A_{2}, B_{2})$ when $\bar{\Re}_{1} > 1,$ where $E_{2} = \frac{\lambda_{E}-\zeta_{1}^{-1}\delta_{I}I_{2}}{\delta_{E}}\in \left(0, \frac{\lambda_{E}}{\delta_{E}}\right),$ $\ S_{2} = \frac{\delta_{B}} {\varrho}, \ \ A_{2} = \frac{\lambda_{A}}{\delta_{A}+\kappa \zeta_{1}^{-1} \delta_{I}I_{2}/E_{2}}\in \left(0, \frac{\lambda_{A}}{\delta_{A}}\right)$ and$\ B_{2} = \frac{\delta_{S}}{\gamma}\left(\bar{\Re}_{1}-1\right),$ where

Here, $\bar{\Re}_{1}$ represents the antibody activation number.

We have that $\Psi(A_{2}) < \Psi(A_{0})$ and $E_{2} < E_{0}$. Therefore,

Now, we can state the following lemma:

Lemma 4. For system (3.1), there exist two threshold parameters $\bar{\Re}_{0}$ and $\bar{\Re}_{1}$ such that the following conditions hold:

(ⅰ) If $\bar{\Re}_{0}\leq1$, then the uninfected equilibrium $\Delta _{0} = (E_{0}, 0, 0, A_{0}, 0)$ is the unique equilibrium.

(ⅱ) If $\bar{\Re}_{1}\leq1 < \bar{\Re}_{0}$, then there exists two equilibria, $\Delta_{0}$ and the infected equilibrium without humoral immunity $\Delta _{1} = (E_{1}, I_{1}, S_{1}, A_{1}, 0)$.

(ⅲ) If $\bar{\Re}_{1} > 1$, then there exist three equilibria, $\Delta_{0}$, $\Delta_{1}$ and the infected equilibrium with humoral immunity $\Delta_{2} = (E_{2}, I_{2}, S_{2}, A_{2}, B_{2})$.

3.4.   Global stability

This subsection proves the global stability of the equilibria of model (3.1) by using the Lyapunov method. Let $\bar{\tilde{\Omega}}_{j}$ be the largest invariant subset of

where $\bar{\Lambda}j(E, I, S, A, B)$ is a Lyapunov function candidate. Subsequent to the studies of ^[33,34,36], we construct Lyapunov functions in the following theorems.

Theorem 4. Consider system (3.1) and let $\bar{\Re}_{0}\leq1$; then, $\Delta_{0}$ is G.A.S. Moreover, if $\bar{\Re}_{0} > 1$, then $\Delta_{0}$ is unstable.

Proof. Define

We note that $\bar{\Lambda}_{0}(E, I, S, A, B) > 0$ for all $E, I, S, A, B > 0$ and $\bar{\Lambda}_{0}(E_{0}, 0, 0, A_{0}, 0) = 0$. We evaluate $\frac {d\bar{\Lambda}_{0}}{dt}$ as follows:

Using system (3.1), we get

Collecting terms, we get

Using the equilibrium condition $\lambda_{E} = \delta_{E}E_{0}$, as well as $\lambda_{A} = \delta_{A}A_{0}$, we get

Since $\bar{\Re}_{0}\leq1$ and $\left(\Psi(A)-\Psi(A_{0})\right) (A_{0}-A)\leq0,$ then $\frac{d\bar{\Lambda}_{0}}{dt}\leq0$ for all $E, S, A, B > 0$. In addition, $\frac{d\bar{\Lambda}_{0}}{dt} = 0$ when $E = E_{0},$ $A = A_{0}$ and $S = B = 0.$ Trajectories of system (3.1) converge to $\bar{\tilde{\Omega}}_{0}$, where $S = 0$ and $\dot{S} = 0$. The third equation of system (3.1) gives

Therefore, $\bar{\tilde{\Omega}}_{0} = \left \{ \Delta_{0}\right \}$ and by using the LIP, we obtain that $\Delta_{0}$ is G.A.S.

To show the instability of $\Delta_{0}$, we calculate the characteristic equation of system (3.1) at $\Delta_{0}$ as follows:

where $\bar{\zeta_{i}} = \int_{0}^{h_{i}}f_{i}(\tau)e^{-(c+\alpha_{i})\tau} d\tau, \; i = 1, 2$. Define a function $\mathcal{\bar{T}}(c)$ as follows:

which is continuous on $[0, \infty)$. We have

this shows that $\mathcal{\bar{T}}(c)$ has a positive real root; therefore, $\Delta_{0}$ is unstable.

Theorem 5. Consider system (3.1) and suppose that Assumption (A) is satisfied and $\bar{\Re}_{1}\leq1 < \bar{\Re}_{0}$; then, $\Delta_{1}$ is G.A.S.

Proof. Define

Clearly, $\bar{\Lambda}_{1}(E, I, S, A, B) > 0$ for all $E, I, S, A, B > 0$ and $\bar {\Lambda}_{1}(E_{1}, I_{1}, S_{1}, A_{1}, 0) = 0$. We obtain $\frac{d\bar{\Lambda }_{1}}{dt}$ as follows:

Using system (3.1), we get

Collecting terms, we get

Using the equilibrium condition for $\Delta_{1}$, i.e.,

we obtain

Using the equalities

we obtain

We have that $\left(\Psi(A)-\Psi(A_{1})\right) (A_{1}-A)\leq0$, and, from Assumption (A), we have that $S_{1}-\frac{\delta_{B}}{\varrho}\leq 0$. It follows that $\frac{d\bar{\Lambda}_{1}}{dt}\leq0$ for all $E, I, S, A, B > 0$. In addition, $\frac{d\bar{\Lambda}_{1}}{dt} = 0$ when $E = E_{1}$, $A = A_{1}$, $B = 0$ and

All solutions of system (3.1) are attracted to $\bar {\tilde{\Omega}}_{1}$. Since $\bar{\tilde{\Omega}}_{1}$ is invariant with respect to (3.1), on $\bar{\tilde{\Omega}}_{1}$, we have

and, from Eq (3.22), we get that $I(t) = I_{\tau} = I_{1}$ for any $t$. Therefore, $\bar{\tilde{\Omega}}_{1} = \left \{ \Delta _{1}\right \}$, and by applying the LIP, we obtain that $\Delta_{1}$ is G.A.S.

Theorem 6. For system (3.1), let $\bar{\Re}_{1} > 1$; then, $\Delta_{2}$ is G.A.S.

Proof. Define

Obviously, $\bar{\Lambda}_{2}(E, I, S, A, B) > 0$ for all $E, I, S, A, B > 0$ and $\bar{\Lambda}_{2}(E_{2}, I_{2}, S_{2}, A_{2}, B_{2}) = 0$. We calculate $\frac{d\bar{\Lambda}_{2}}{dt}$ as follows:

From system (3.1), we get

Collecting terms, we get

Using the equilibrium condition for $\Delta_{2}$, i.e.,

we obtain

Applying the equalities of (3.20) for $i = 2$, we obtain

If $\bar{\Re}_{1} > 1$, we get that $\frac{d\bar{\Lambda}_{2}}{dt}\leq0$ for all $E, I, S, A > 0$. Further, $\frac{d\bar{\Lambda}_{2}}{dt} = 0$ when $E = E_{2},$ $A = A_{2}$ and

All solutions of system (3.1) are attracted to $\bar {\tilde{\Omega}}_{2}$. Since $\bar{\tilde{\Omega}}_{2}$ is invariant with respect to (3.1), on $\bar{\tilde{\Omega}}_{2}$, we have

and, from Eq (3.25), we get that $I(t) = I_{\tau} = I_{2}$ for any $t$. The third equation of system (3.1) yields

Hence, $\bar{\tilde{\Omega}}_{2} = \left \{ \Delta { _{2} }\right \}$ and, by utilizing the LIP, we get that $\Delta_{2}$ is G.A.S.

4.   Comparison results

Let us compare our proposed model (2.1) and the model given by Eqs (1.1)–(1.4), which was studied in ^[27]. We consider the administration of a treatment to inhibit the virus replication with a drug efficacy $\epsilon_{I}\in \lbrack0, 1]$ ^[43]. Then, model (2.1) becomes

The basic reproduction number of system (4.1) is given by

where $\Re_{0}$ is the basic reproduction number of system (2.1) (i.e., there is no treatment). Assume that $\Re_{0} > 1$; then, the uninfected equilibrium $\Delta_{0}$ for system (2.1) is unstable. Now, we want to determine the range of medication efficacy, $\epsilon_{I}$, that stabilizes system (4.1)'s equilibrium $\Delta_{0}$ and makes $\Re_{0}^{\epsilon_{I}}\leq1$:

On the other hand, the model given by Eqs (1.1)–(1.4) under the effect of treatment becomes

and the basic reproduction number of system (4.4) is given by

where $\hat{\Re}_{0}$ is the basic reproduction number of the system given by Eqs (1.1)–(1.4), which is assumed to be $\hat{\Re}_{0} > 1$. We determine the drug efficacy $\epsilon_{I}$ that makes $\hat{\Re} _{0}^{\epsilon_{I}}\leq1$ and stabilizes the uninfected equilibrium, $\bar{\Delta}_{0}$, of system (4.4) as follows:

Since $\tau_{2} > 0$, then

It follows from Eqs (4.3) and (4.5) that $\epsilon_{I}^{\min} < \hat{\epsilon}_{I}^{\min}$. As a result, adding the maturation delay $\tau_{2}$ to the system will lessen the amount of medication required to stabilize it at the uninfected equilibrium $\Delta_{0}$ and eradicate SARS-CoV-2 from the body. Thus, designing overflow antiviral medications will result from neglecting the maturation delay in SARS-CoV-2 infection models.

When we look at our proposed model (2.1) and the model given by Eqs (1.1)–(1.4), we can see that our model admits three equilibria, uninfected equilibrium ($\Delta_{0}$): infected equilibrium without humoral immunity ($\Delta_{1}$) and infected equilibrium with humoral immunity ($\Delta_{2}$). On the other hand, the model given by Eqs (1.1)–(1.4) admits only two equilibria:

(ⅰ) Uninfected equilibrium, $\bar{\Delta}_{0} = (E_{0}, 0, 0, A_{0})$, where the SARS-CoV-2 infection is cleared.

(ⅱ) Infected equilibrium $\bar{\Delta}_{1} = (E_{1}, I_{1}, S_{1}, A_{1})$, where the SARS-CoV-2 infection is present.

This shows that ignoring the effect of humoral immunity in the SARS-CoV-2 infection model may not accurately describe SARS-CoV-2 infection. Thus, our proposed models are more relevant as a tool to describe the within-host dynamics of SARS-CoV-2 infection than the model presented in ^[27].

The above comparisons underscore the significance of including both the humoral response and maturation delay in the SARS-CoV-2 infection paradigm.

5.   Numerical simulations

In this section, we describe the numerical simulation for model (2.1) to illustrate the theoretical findings. We performed sensitivity analysis for the model. We demonstrate here the effect of humoral immunity and time delays on the SARS-CoV-2 dynamics. The system of DDEs were solved numerically by using the dde23 solver in MATLAB version R2022a. Table 1 contains the values of some parameters of model (2.1). The other values were chosen just for numerical purposes. We chose the function $\Psi$ as $\Psi(A) = \frac{A^{n}}{\mathcal{A}_{s}^{n}+A^{n}}$ ^[27,28]. Then $\Re_{0}$, given by Eq (2.3) becomes

5.1.   Stability of the equilibria

To show the global stability of the equilibria of system (2.1), we applied the following three initial conditions:

where $\theta \in \left[ -\max \left \{ \tau_{1}, \tau_{2}\right \}, 0\right].$ Here, we set $\tau_{1} = \tau_{2} = 0.9$ and selected the values of $\eta$ and $\varrho$ as follows:

State 1. (Stability of $\Delta_{0}$) $\eta = 0.003$ and $\varrho = 0.001$. These values give $\Re_{0} = 0.826494 < 1$. Figure 2 shows that the trajectories tend to the equilibrium $\Delta _{0} = (50, 0, 0, 10, 0)$ for all initial conditions C1–C3. This shows that $\Delta_{0}$ is G.A.S according to Theorem 1. In this state, SARS-CoV-2 particles are eventually cleared.

State 2. (Stability of $\Delta_{1}$) $\eta = 0.01$ and $\varrho = 0.001$. With such a selection, we obtain that $\Re_{1} = 0.923507 < 1 < 2.75498 = \Re_{0}$ and $S_{1} = 88.157 < \frac{\delta_{B}}{\varrho } = \frac{0.1}{0.001} = 100$. The equilibrium point $\Delta_{1}$ exists with $\Delta_{1} = (23.3341, 10.8416, 88.157, 7.44692, 0)$. Figure 3 shows that the trajectories tend, eventually, to $\Delta_{1}$ for all initial conditions, and this is in agreement with Theorem 2. This state describes an infected individual when humoral immunity is not activated.

State 3. (Stability of $\Delta_{2}$) $\eta = 0.01$ and $\varrho = 0.005$. This gives $\Re_{1} = 1.65788 > 1$. The numerical results show that $\Delta_{2} = \left(38.1854, 4.8035, 20, 9.1506, 2.3824\right)$ exists. Figure 4 displays that the trajectories converge eventually to $\Delta_{2}$ for all initial conditions and this is consistent with Theorem 3. This state describes an infected individual with active humoral immunity.

5.2.   Impact of the delays on SARS-CoV-2 dynamics

We show the effects of time delays $\tau_{1}$ and $\tau_{2}$ on solutions of the system, as well as the stability of $\Delta_{0}$. We can see from Eq (5.1) that $\Re_{0}$ is reduced by increasing the delay parameters $\tau_{1}$ and $\tau_{2}$$\ $when all other parameters are fixed. Therefore, the stability of $\Delta_{0}$ can significantly be changed based on $\tau_{1}$ and $\tau_{2}$. Let us fix $\eta = 0.003,$ $\varrho = 0.01$ and vary $\tau_{1}$ and $\tau_{2}$ as follows:

D1: $\tau_{1} = \tau_{2} = 0,$

D2: $\tau_{1} = \tau_{2} = 0.79,$

D3: $\tau_{1} = \tau_{2} = 1,$

D4: $\tau_{1} = \tau_{2} = 2.$

Further, we consider the following initial condition:

Assume that $\tau = \tau_{1} = \tau_{2}$; then, $\Re_{0}$, in the case of $n = 1$, is given by

We see that $\Re_{0}$ is a decreasing function of $\tau$. Let $\tau_{cr}$ be such that $\Re_{0}(\tau_{cr}) = 1$. Consequently,

Hence, $\Delta_{0}$ is G.A.S when $\tau \geq \tau_{cr} = 0.804719$. Therefore, we have the following cases:

(ⅰ) If $\tau \geq \tau_{cr},$ then $\Re_{0}\leq1$ and $\Delta_{0}$ is G.A.S. Therefore, when $\tau$ is large enough, then $\Delta_{0}$ can be stabilized.

(ⅱ) If $\tau < \tau_{cr},$ then $\Re_{0} > 1$ and $\Delta_{0}$ will be unstable.

Figure 5 shows the effect of time delay on the system's trajectories. It is clear that, as $\tau$ is increased, the population of the uninfected epithelial cells and ACE2 receptors are increased, while the populations of infected epithelial cells, SARS-CoV-2 particles and antibodies are decreased.

5.3.   Impact of humoral immunity on the SARS-CoV-2 infection

This subsection addresses the effect of the stimulated rate constant $\varrho$ on the dynamics of system (2.1). We fix the parameters $\eta = 0.01$ and $\tau_{1} = \tau_{2} = 0.9$ and vary the parameter $\varrho$ as follows: $\varrho = 0.001,$ $\varrho = 0.003,$ $\varrho = 0.005$ and $\varrho = 0.007$. Further, we consider the following initial condition:

The impact of humoral immunity on SARS-CoV-2 infection can be seen in Figure 6. We observe that, as $\varrho$ is increased, the concentrations of uninfected epithelial cells, antibodies and ACE2 receptors are increased, while concentrations of infected cells and SARS-CoV-2 particles are decreased. We note that $\Re_{0}$ does not depend on the humoral immune parameters; therefore, humoral immunity plays the role of controlling the infection, but not clearing it. This may help to develop drug therapies with the ability to stimulate the humoral response.

5.4.   Sensitivity analysis

Sensitivity analysis is crucial in pathology and epidemiology when modeling complex interactions ^[41]. Sensitivity analysis can help us to assess how well we are able to prevent the progression of the disease between hosts and within the host. Three techniques may be used to determine sensitivity indices: Directly by direct differentiation, with the use of a Latin hypercube sampling technique or by linearizing the system and resolving the resultant equations ^[41,42]. With the use of direct differentiation, the indices in this study may be stated analytically. When variables fluctuate according to the parameters, one may get the sensitivity index by using partial derivatives. The normalized forward sensitivity index of $\Re_{0}$ is written in terms of the parameter $m$:

Using the values given in Table 1 and $\eta = 0.003$, $\varrho = 0.001$ and $\tau_{1} = \tau_{2} = 0.9$, we present the sensitivity index $\mathcal{S} _{m}$ in Table 2 and Figure 7. Obviously, $\lambda_{E},$ $\eta,$ $\lambda_{A}$ and $\nu$ have positive indices. Clearly, $\lambda_{E},$ $\eta$ and $\nu$ have the most positive sensitivity index. In this state, there is a positive relationship between the progression of COVID-19 and the parameters $\lambda_{E},$ $\eta,$ $\lambda_{A}$ and $\nu$ when all other parameters are fixed. The parameters $\delta_{E},$ $\delta_{S},$ $\delta_{A},$ $\tau_{1}, \ \tau_{2},$ $\alpha_{1},$ $\alpha_{2}$ and $\mathcal{A}_{s}$ have negative indices, meaning that, when the values of these parameters rise, the value of $\Re_{0}$ declines. Obviously, $n$, $\delta_{E}$ and $\delta_{S}$ have the most negative sensitivity index.

6.   Discussion

Since the beginning of the outbreak of SARS-CoV-2 at the end of 2019, many researchers have formulated and developed mathematical models to characterize the dynamics of the virus within the host. Most of these models neglect the role of ACE2 receptors in the infection. In this paper, we studied two SARS-CoV-2 infection models which describe the within-host dynamics of SARS-CoV-2 by considering the role of ACE2 receptors. The effects of humoral immunity and time delays on the SARS-CoV-2 infection was included.

The model admits three equilibrium points, as follows:

● The uninfected equilibrium, $\Delta_{0}$, usually exists. Moreover, $\Delta_{0}$ is G.A.S when $\Re_{0}\leq1$, and it is unstable otherwise. In this state, the number of SARS-CoV-2 particles eventually converges to 0 and the COVID-19 patient will recover. Different control strategies can be applied to realize

These strategies are provided for example:

(ⅰ) Reducing the parameter $\eta$ as $(1-\epsilon_{B})\eta$ by applying treatment to block the virus binding with drug efficacy $\epsilon_{B}\in \lbrack0, 1]$ ^[43].

(ⅱ) Reducing the parameter $\nu$ as $(1-\epsilon_{I})\nu$ by using treatment to inhibit the virus replication with drug efficacy $\epsilon_{I}\in \lbrack0, 1]$ ^[43].

(ⅲ) Enlarging the length of delay periods $\tau_{1}$ and $\tau_{2}$ ^[44].

(ⅳ) Inhibiting the proliferation rate of ACE2 receptors, $\lambda _{A}$ ^[27].

(ⅴ) Increasing the degradation rate of ACE2 receptors, $\delta_{A}$ ^[27].

We observe that model (2.1) may be seen as a nonlinear control system with drug efficacies (e.g., $\epsilon_{B}$ and $\epsilon_{I}$) serving as the control inputs when medicines are used. Then, a variety of control design techniques, including feedback control ^[49], model predictive control ^[50,51] and optimal control ^[19,48], may be applied.

● The infected equilibrium without humoral immunity, $\Delta_{1}$, exists when $\Re_{0} > 1$. Further, $\Delta_{1}$ is G.A.S when $\Re_{1}\leq1 < \Re_{0}$ and $S > \delta_{B}/\varrho$. In this case, the infection is present, but with an inactive immune response. The reason for this is that the amount of viruses present in the body is small, that, is $S\leq \delta_{B}/\varrho$, and it may be insufficient to activate the immune system's reaction.

● The infected equilibrium with humoral immunity, $\Delta_{2}$, exists and is G.A.S when $\Re_{0} > 1$. In this case, the amount of viruses present in the body is sufficient to activate (i.e., $S > \delta_{B}/\varrho$) the immune system's reaction.

The main limitation of our research is that we were not able to use real data from COVID-19 patients to estimate the values of the model's parameters. The following are the reasons: (ⅰ) Real data from infected people are still lacking; (ⅱ) comparing our findings to a small number of real studies may not be very accurate; (ⅲ) it is challenging to collect real data from patients who are SARS-CoV-2-infected; and (ⅳ) conducting experiments to obtain real data is outside the scope of this study.

7.   Conclusions

In this paper, we studied two SARS-CoV-2 infection models which describe the within-host dynamics of SARS-CoV-2 by considering the role of ACE2 receptors. The effect of humoral immunity on the SARS-CoV-2 infection was included. Two time-delays were incorporated: (ⅰ) Delay in the SARS-CoV-2 infection of epithelial cells, and (ⅱ) delay in the maturation of recently released SARS-CoV-2 virions. In the first model, we consider discrete-time delays, which are generalized in the second model by considering distributed-time delays. We first showed the fundamental properties of the solutions, non-negativity and boundedness. Then, we established that the models have three equilibria. On the basis of the two threshold parameters, $\Re _{0}$ and $\Re_{1}$, we proved the existence and global stability of the equilibria. We constructed suitable Lyapunov functions and used the LIP to prove the global asymptotic stability of the three equilibria. We solved the model numerically, presented the results graphically and found agreement between the numerical and theoretical findings. We discussed the respective impacts of humoral immunity, time delay and ACE2 receptors on the SARS-CoV-2 dynamics. We showed that humoral immunity plays the role of controlling the infection, but it does not ultimately clear SARS-CoV-2 particles. Further, increasing the time delay length can significantly decrease $\Re_{0}$ and then inhibit COVID-19 progression. This opens the door for the creation of some treatments that will prolong the delay period. We discussed the mediated effect of the ACE2 receptors. We found that $\Re_{0}$ is affected by the proliferation and degradation rates of ACE2 receptors, and this may serve as worthy insight for the development of possible receptor-targeted vaccines and drugs. Finally, we performed the sensitivity analysis to establish how the values of the model's parameters affect $\Re_{0}$.

Our suggested model may be expanded in several ways by incorporating (ⅰ) latently infected cells ^[6], (ⅱ) immune response delay ^[10], (ⅲ) the CTL response, the other component of the adaptive immune response ^[12], (ⅳ) stochastic interactions ^[52,53], (ⅴ) reaction diffusion ^[16,54] and (ⅵ) immunologic memory by formulation of the model using fractional differential equations ^[48]. By assuming that the generic functions provide the production/stimulation, infection and clearance rates of compartments, our models can be made more widely applicable ^[16]. In future work, we will examine the modeling and analysis of coinfections between two SARS-CoV-2 variants, such as Omicron and Delta ^[55,56]. It is possible to direct future research to incorporate the impact of vaccinations and antiviral medications into the model. We also want to compare the outcomes with data from infected patients.

Use of AI tools declaration

The authors declare that they have not used artificial intelligence (AI) tools in the creation of this article.

Acknowledgments

This research work was funded by Institutional Fund Projects under grant no. (IFPIP: 1103-130-1443). The authors gratefully acknowledge the technical and financial support provided by the Ministry of Education and King Abdulaziz University, DSR, Jeddah, Saudi Arabia.

Conflict of interest

The authors declare no conflict of interest.