State feedback stabilization problem of stochastic high-order and low-order nonlinear systems with time-delay

Nomenclature

1.   Introduction

Lie group transformation or scaling group transformation has elements which are arbitrary close to the identity transformation, which means that the identity transformation is a transformation that changes nothing at all. When two mechanisms contributing to the density diffuse at different rates, convective waves can arise in a steadily stratified liquid. Sophus Lie's ^[1] was developed a differential invariant similarity for the Lie-group. His work was almost forgotten because of the growth of group theory and differential geometry to study differential equations ^[2]. Using Jeffrey and cross fluid models Bhatti et al. ^[3] and Sumer et al. ^[4] analysed importance of momentum with Lie group transformation. Numerical simulation of a thermally enhanced electro-magnetohydrodynamic (EMHD) flow of a heterogeneous micropolar mixture comprising (60%)-ethylene glycol, (40%) water, and copper oxide nanomaterials was studied by Shah et al. ^[5] and MHD heat transfer in thermal slip using semi-infinite domain and Carreau fluid has been discussed by Rehman et al. ^[6]. In recent year, so many researchers made their studies on Lie group transformation ^[7,8,9]. A two-component modeling for non-Newtonian nanofluid slips flow and heat transfer over sheet discussed by Rana et al. ^[10]. They observed that the heat transfer is decreases with increase in Brownian motion and thermophoresis parameters. Amanulla et al. ^[11] studied the numerical analysis of magnetohydrodynamic Williamson nanofluid over an isothermal sphere in the presence of momentum and thermal slip effects. Zhang et al. ^[12] proposed a new multi-view clustering model called Consensus Multi-view Clustering (CMC) model, and it is based on non-negative matrix factorization for predicting the multiple stages of Arithmetic design progression. The proposed CMC model performs multi-view learning to fully capture data features with limited medical images, analyzes similarity relations between different entities, addresses the shortcoming of multi-view fusion that requires manual setting parameters, and further acquires a consensus representation containing shared features and complementary knowledge of multiple view data. Later, Batool et al. ^[13] performed a numerical analysis of heat and mass transfer in micropolar nanofluids flow through a lid-driven cavity by using the finite volume method. They found that a high vortex viscosity parameter produces a weak concentration field and has significant behaviour when the Reynolds number is significant. Maneengam et al. ^[14] analyzed the entropy generation in a two-dimensional Lid-Driven porous container in the presence of obstacles of different shapes and under the influences of buoyancy and Lorentz forces. They concluded that the triangular shape of the baffle is the best in terms of thermal activity and also they observed that increasing the number of lower-wall waves reduces thermal activity. Bhutta et al. ^[15] experimentally investigated the development of novel hybrid two-dimensional and three-dimensional graphene oxide diamond microcomposite polyimide films to ameliorate electrical and thermal conduction. They found that the hybrid fillers with high thermal and low electrical conductivities were responsible for synergistic improvements in the experimental results.Rasool et al. ^[16] performed a numerical investigation of electromagnetohydrodynamic nanofluid flows over a convectively heated Riga pattern positioned horizontally in a Darcy-Forchheimer porous medium. They observed that Darcy-Forchheimer's and Lorentz's forces strengthen the resulting frictional factor at the Riga surface. Rasool et al. ^[17] reported on the Darcy-Forchheimer flow of water conveying multi-walled carbon nanoparticles through a vertical Cleveland z-staggered cavity subject to entropy generation. They found that the velocity of incompressible Darcy-Forchheimer flow at the middle vertical Cleveland Z-staggered cavity declines with a higher Reynolds number.

The phenomena of heat and mass transport associated with entropy production describe the triple diffusion process, which can be found in metallurgy, oceanography, and geophysics. When more than one salt is used in a combined heat and mass transfer, the salts interact and cause coupling effects. In recent years tremendous research activity has been dedicated to developing various fluid models by using the triple diffusive effect: for examples with numerous geometries and multiple body forces, the reader is referred to Arif et al. ^[18], Patil et al. ^[19], Nawaz et al. ^[20] and Manjappa et al. ^[21]. Such techniques used to investigate momentum, thermal and various effects have been discussed by Patil et al. ^[22]; also the roughness of a surface with the nanofluid is studied by Patil et al. ^[23].

The numerical studies incorporated for thermal and momentum slips by Xiong et al. ^[24] and Beg et al. ^[25]. Su et al. ^[26] investigated that increasing flow and convective heat transmission were explored numerically inside circular and parallel-plates micro channels. The slip flow of conductive viscoelastic flow past a permeable radiated shrinking or stretching surface with mass transpiration has been illustrated by Sneha et al. ^[27]. The significance of nanoparticle shape and thermo-hydrodynamic slip constraints on MHD alumina-water nanoliquid flows over a rotating heated disk has been discussed by Sabu et al. ^[28]. Numerous researchers Koriko et al. ^[29], Eleni Seid et al. ^[30], Turkyilmazoglu ^[31], Felipe et al. ^[32], Majeed et al. ^[33] and Zeeshan et al. ^[34] are carried out for different fluid model with various surfaces to analyse the influence of momentum and thermal slips.

No research work has been done using Lie group transformation analysis to analyze the significance of triple diffusive convective flow by considering thermal and momentum slips, as per the authors' knowledge of the literature in most practical uses; however, the components of mass and heat are inextricably linked. The heat and mass diffusion components, on the other hand, are invariably coupled in most real-world applications. Triple diffusion of a fluid has practical applications in many bioengineering and medical sciences. For instance, aqueous suspensions of DNA contain more than two independently diffusing constituents with dissimilar diffusivities and medical drug manufacturing methods etc. However, triple diffusion in the presence of an applied magnetic field has significant applications in metallurgy, solar physics, geophysics, cosmic fluid dynamics, polymer industry, in the motion of the earth's core. This fact prompts us to investigate the combined impact of mass diffusion heat on magnetohydrodynamic free-convective flow in the boundary layer. As far as we can tell, the findings of this work appear to be perfectly consistent with previous research and, due to their simplicity, easily transferable to relevant applications.

2.   Mathematical model and formulation

We perform the analysis of the steady triple diffusive hydromagnetic flow of heat and mass transmission of a viscous, electrically conducting fluid. The flow is supposed to be in the x-direction and y-axis perpendicular to it. A uniform magnetic field of strength B is offered perpendicular to the flow direction. It is also considered that all fluid possessions are fixed excluding the impact of the density deviation with temperature and concentration. The surface is retained at a fixed temperature T_w, which is greater than the constant.

For this study, we have considered a triple diffusive free convective MHD incompressible flow with momentum and thermal slip conditions for a fluid model with the help of Lie group transformation analysis. Also, suppose that the flow generation is estimated for a linear widening surface. Additionally, the flow is restricted to the region $y>0$ and equivalent with the plane $y>0$.

Under the pre-defined assumptions mentioned above, the governing system of continuity, energy, momentum and concentration are expressed as follows:

Given the following boundary conditions:

Now, we need to transform the above Eqs (1) to (6) into non-dimensional form. To perform this, the following similarity dimensionless transformations are considered.

We substitute the above non-dimensional quantities of (7) in Eqs (1) to (5) along with the boundary conditions of Eq (6) and then complete the simplification results by using the following non-dimensional differential equations :

with the following boundary conditions :

where $\lambda = \frac{{g{\beta _T}\Delta T}}{{a\sqrt {av} }}, {\Lambda _1} = \frac{{g{\beta _{{C_1}}}\Delta {C_1}}}{{a\sqrt {av} }}, {\Lambda _1} = \frac{{g{\beta _{{C_2}}}\Delta {C_2}}}{{a\sqrt {av} }}$.

3.   Scaling transformations

First, the stream function $\psi$ is taken as mentioned below before applying scaling transformations.

We introduce the stream functions (14) to (8)–(12) together with the boundary conditions of (13). Obviously, Eq (8) is satisfied by them. And the remaining equations will be converted in terms of the stream function $\psi$ as below period:

with the following boundary conditions:

Consider $\varepsilon$ as a small parameter of the scaling transformation. Then, the transformation $F$ (a specified set of Lie group analysis) is taken as mentioned below period:

Where, ${r_1}, {r_2}, {r_3}, {r_4}, {r_5}\, {\text{and}}\, {r_6}$ are any real arbitrary constant parameters The point conversion defined through (21) transmuted the co-ordinates $\left({x, y, \psi, {\phi _1}, {\phi _2}} \right)$ into $\left({{x^*}, {y^*}, {\psi ^*}, {\phi _1}^*, {\phi _2}^*} \right)$. With the help of Lie group analysis mentioned through (15), Eqs (15)–(18) are transformed as

If the exponent of the above converted equations fulfills the below linear equations, then the set of Eqs (22)–(25) will remain invariant under the folowing transformation

By solving the above linear equations (26)–(29) simultaneously, we find

Replacing the above values of (30) into the scaling transformations given in (21), we get

The Taylor series expansions are

A simple algebraic expression for the above transformations given by (31) with the help of Taylor series expansion leads to a mono-parametric group of transformations in the form of the characteristic equation given below period

From (32), we can easily obtain new similarity transformations as

where, $\eta$ is the similarity variable and $f, \theta, {\phi _1}, {\phi _2}$ are the dependent variables. Now, we substitute the above quantities specified in (33) into PDEs (16) to (18) then, by applying the boundary conditions mentioned in (19), we attain the set of ordinary differential equations as

Together with the boundary situations;

Here, $\, {\alpha _1} = L\sqrt {\frac{a}{v}}$ is the momentum slip parameter and $\, {\alpha _2} = {D_1}\sqrt {\frac{a}{v}}$ is the thermal slip parameter.

with the following predefined parameters:

The physical measures requiring engineering attention are the local friction factor; local Nusselt number and Sherwood number which are defined as follows:

where, $\tau_{w}, q_{w}, h_{1 m} \& h_{2 m}$ symbolize the shear stress, heat and mass flux change, respectively:

The dimensionless friction factor, Nusselt number and Sherwood number are defined as

Where, ${{Re} _x} = \sqrt {\frac{a}{{vl}}} x$.

4.   Results and discussions

The collected results show the impact of non-dimensional regulating parameters such as $L{e_1}, L{e_2}, {\Lambda _1}, {\Lambda _2}, {\alpha _1}, {\alpha _2}$ on and $f'\left(\eta \right), \theta \left(\eta \right), {\phi _1}\left(\eta \right), {\phi _2}\left(\eta \right)$(See Figures 1–16). In the simulations, the pertinent parameter values were $\Pr = 0.72, \, \lambda = - 0.5, L{e_1} = 1, L{e_2} = 1, {\Lambda _1} = 0.5, {\Lambda _2} = 0.5, {\alpha _1} = 0.2, {\alpha _2} = 0.2$. These variables were kept constant throughout the inquiry, with the exception of the various values given in the associated figures. The results are compared with already divulged results and presents excellent correlation with the Ferdows et al. ^[35] results.

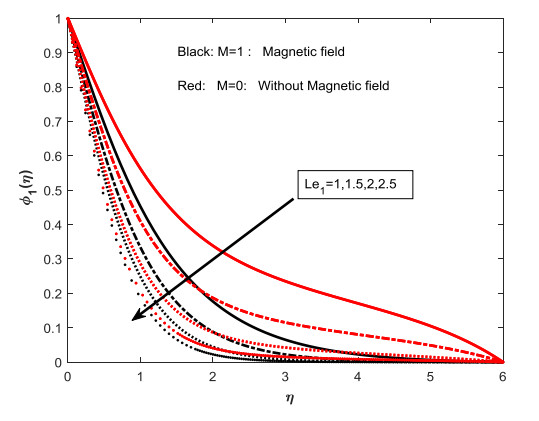
The variation in salt 1 and 2 concentration distributions ${\phi _1}$ and ${\phi _2}$ as a result of varying the regular Lewis numbers $L{e_1}$ and $L{e_2}$ in the presence and absence of the magnetic field parameter are shown in Figures 1–4. It was designed to observe the impact of Lewis numbers on salt 1 and 2 concentrations. Decreases in the solutal concentration profiles ${\phi _1}\, {\text{and}}\, {\phi _2}$ is occurred due to the Lewis number. Physical explanation of such decline in the variations of ${\phi _1}\, {\text{and}}\, {\phi _2}$ can be justified on the fact that $L{e_1}\, {\text{and}}\, L{e_2}$ capture the reverse relation with species diffusion, that is when $L{e_1}\, {\text{and}}\, L{e_2}$ are maximum, species diffusion is lower, which leads to the decrement of the resulting solutal concentrations.

The thermal buoyancy ratio parameter ${\Lambda _1}$ reduces $f'\left(\eta \right), \theta \left(\eta \right), {\phi _1}\left(\eta \right), {\phi _2}\left(\eta \right)$ for both the presence and absence of a magnetic field. The concentration buoyancy ratio parameter ${\Lambda _2}$ enhances $\theta \left(\eta \right)$ in the presence of a magnetic field but slowly decelerates it in the absence of a magnetic field case (Figure 10). The effect of thermal the buoyancy ratio parameter ${\Lambda _1}$ is depicted in Figure 5. From this, we observed that with the increase of the velocity and temperature, Salt 1 and 2 concentration distributions decreased because molecular forces dominated the thermal buoyancy forces. Therefore, the velocity in the momentum boundary layer depreciates in the flow region when the buoyancy forces act in the opposite direction.

The momentum and concentration boundary layer thicknesses decreased the values of ${\Lambda _2}$ in both cases (see Figures 9, 11 and 12).

Figures 13–15 show the influence of the momentum slip parameter ${\alpha _1}$ on the velocity, temperature and Salt 1 concentration distributions. It is clear that the velocity is a decreasing function of the slip parameter. Physically, when slip occurs, the fluid velocity near the surface is no longer equal to the surface velocity, that is, a velocity slip exists with such an increase in a slip velocity. Furthermore, increasing the value of slip will decrease the flow velocity because, under the slip condition, the pulling of the surface can be only partly transmitted to the fluid. The same phenomena can be observed in the temperature and Salt 1 concentration fields. Figure 16 demonstrates the effect of the thermal slip parameter ${\alpha _2}$ on temperature. As the thermal slip parameter increases, less heat is transformed from the surface to the fluid and consequently the temperature decreases.

Figure 17 represents the surface plot of the momentum slip parameter $\alpha_1$ given the skin friction coefficient $f''\left(0 \right)$, Nusselt number $\theta '\left(0 \right)$ and Sherwood number ${\phi ^\prime }\left(0 \right)$ in the absence of the magnetic field parameter $M = 0$ and presence of the magnetic field parameter $M = 1$. Figure 17 shows that the rate of friction factor is −4.256939 in the absence of a magnetic field and −1.454855 in the presence a of magnetic field case. From this we observed that the friction factor coefficient continuously decreases. The opposite phenomena can be observed in the cases of the Nusselt and Sherwood numbers for both the $M = 0$ and $M = 1$ cases (Figures 18–20). Figure 21 represents the thermal slip parameter ${\alpha _2}$ on $f''\left(0 \right), \, \theta '\left(0 \right), {\phi ^\prime }\left(0 \right)$ for both absence and presence of magnetic field parameter cases. Figures 21 and 22 show that ${\alpha _2}$ elevates the rate of heat transfer but decelerates the skin friction coefficient for both cases.

The concentration buoyancy ratio parameter ${\Lambda _2}$ escalates the Salt 1 Sherwood number (Figure 23) and thermal buoyancy ratio parameter ${\Lambda _1}$ also enhances the friction factor coefficient (Figure 24) for the $M = 0\, {\text{and}}\, M = 1$ cases. Figure 25 shows that the Lewis number $L{e_1}$ reduces the Nusselt number in the $M = 0$ case and increases the Nusselt number in the case of $M = 1$ the same phenomena can be observed in Figure 27 Salt 2 Sherwood number. But the skin friction coefficient increases for both cases of magnetic field parameter settings, as shown in Figure 26. Finally, from Figures 28 and 31 we observed that $L{e_2}$ reduces the skin friction coefficient but upsurges the Salt 2 Sherwood number; meanwhile $L{e_2}$ in the absence of a magnetic field and increase in the presence of a magnetic field for the Nusselt number Salt 1 concentration, as shown in Figures 29 and 30.

5.   Concluding remarks

A theoretical study has been conducted for laminar incompressible triple diffusive boundary layer flow in the presence and absence of a hydromagnetic fluid. Momentum and thermal slip effects have been incorporated into model. The transformed boundary layer equations for heat and momentum conservation have been solved by using Lie group transformation analysis. The present investigation has shown the following:

1. The momentum slip parameter ${\alpha _1}$ improve the Nusselt number and Salt 1 and 2 Sherwood number in the presence and absence of a magnetic field.

2. The thermal slip parameter increases, less heat is transformed from the surface to the fluid and consequently the temperature decreases.

3. The momentum slip parameter reduces the skin friction coefficient for $M = 0$, but increases in the case of $M = 1$.

4. The Lewis number $L_{e_{1}}$ enhances the Salt 1 Sherwood number for $M = 0\, {\text{and}}\, M = 1$. The opposite behavior can be observed for the Salt 2 Sherwood number.

5. The thermal slip parameter ${\alpha _2}$ enhances the Nusselt number in both the presence and absence of the magnetic field parameter.

6. The thermal and concentration buoyancy ratio parameters are upsurge the friction factor, Nusselt number and Salts 1 and 2 Sherwood numbers in both cases of magnetic field the parameter $M = 0\, {\text{and}}\, M = 1$.

7. With the increase of the velocity and temperature, Salt 1 and 2 concentration distributions decreased because molecular forces dominate the thermal buoyancy forces.

Conflict of interest

The authors declare that they have no competing interests.