Numerical solution of MHD Casson fluid flow with variable properties across an inclined porous stretching sheet

1.   Introduction

The importance of non-Newtonian fluid boundary layer flow in industrial applications has lately piqued the interest of significant scholars.The rheological equations for this sort of fluid are typically complex, posing a number of obstacles for engineers and scientists to solve. The Casson fluid (visco-inelastic) have received greater attention among all other non-Newtonian fluids. It is a visco-inelastic fluid having yield stress which classify Casson fluid as blood. Therefore, the non-Newtonian nature of fluids is due to yield stress. The applications of such fluids are seen in food processing, polymer processing and many more. In 2015, Mahanta and Shaw ^[1] explored the analysis of Casson fluid flow in three dimensions that passes through a penetrable linearly stretching sheet. Kataria and Patel ^[2] reported Casson fluid movement with contributions from the radiation mode of heat transmission as well as chemical reactions through an oscillating vertical lamina. Ramana Reddy et al. ^[3] probed the Casson and also Maxwell fluids in the midst of cross diffusion and a heat source/sink that isn't uniform. Awais et al. ^[4] recently examined the dynamics of Casson fluid motion through penetrable channel. By altering the thermal conductivity and viscosity of fluids, Idowu and Falodun ^[5] emphasized on the simultaneous flow of fluids such as Casson and Walters-B.

Magnetohydrodynamics (MHD) has high significance in MHD pumps, astrophysical plasmas, MHD meters to name few. In the same vein, MHD is proved to be affective in diagnostics of diseases which makes it to step into bio-engineering applications. Shanmugapriya et al. ^[6] examined the enhancement of MHD hybrid nanofluid motion together with activation energy. Panigrahi et al. ^[7] studied MHD Casson nanofluids dynamics in a porous channel. Bhattacharyya ^[8] researched the MHD stagnation-point involving Casson fluid motion past an extendable membrane subjected to electromagnetic radiation.Waleligh et al. ^[9] examined dynamics of MHD Casson nanofluid past an inclined stretchable cylinder with chemically reactive and thermally radiative effects. Mat Noor et al. ^[10] delved into squishing action of Jeffrey nanofluid in MHD along a horizontal axis. Mahabaleshwar et al. ^[11] took up the MHD non-Newtonian nanofluid flow as well as the study of mass transfer as a result of super-linear strecthable lamina. Wang et al. ^[12] assessed the magnetohydrodynamics of a Williamson nanofluid flowing on top of a thin elastic lamina. ^[13] investigated the dynamics of nanofluids on electrically conducting fluids using the Soret-Dufour mechanism. A study of Kalteh ^[14] examined nanoparticle and base fluid types. The study concluded that the heat transport coefficient is highest for water alumina/water nanoliquid particle magnitude on thermal conductivity. Jin-Kyeong ^[15] examined the impact of nanoparticles in bubble absorption and its activeness in a binary fluid. The impact of thermophoresis on nanoparticle distribution has been investigated by Bahiraei ^[16]. It was found out in the study that the presence of large particles gives non-uniformity in concentration distribution. Seferis et al. ^[17] studied Grain's size together with the shape reliance of luminescence efficiency. The method of sedimentation was used, and the rod similar grain screens show together with a reduction in efficiency of luminescence values. The recent exploration of Bowers ^[18] presented the heat transport behavior of nanofluids flows in microchannels. It was found out in their study that much viscosity of nanofluids in comparison to water, power pumping which is required in the driving flow of nanofluid in microchannels elevate. Krishna et al. ^[19] researched thermal transport in an unsteady state of Powell-Eyring fluid through a sloped elastic membrane. Mahato et al. ^[20] presented an analytical study on the effects of Hall current, magnetic field, and chemical change on an unsteady MHD free convection heat and mass transmission of viscous incompressible, electrically conducting Casson fluid past a virtually unlimited vertical channel with heat source and sink. Kumar et al. ^[21] discussed dual formulations of Williamson fluid MHD flow across a curvy membrane. Musa et al. ^[22] explored the unsteady magnetohydrodynamics flow of nanofluids in the presence of heat radiation and chemical reactivity with variable fluid properties past an angled elastic membrane. Alghamdi et al. ^[23] looked at the Beale-kato-majda's criterion for magnetohydrodynamic equations with zero viscosity. Sunthrayuth et al. ^[24] by considering an unsteady MHD flow for fractional Casson channel fluid in a porous medium: An application of the Caputo-Fabrizio time-fractional derivative. Zhang et al. ^[25] evaluated the heat transport phenomena for the Darcy-Forchheimer flow of Casson fluid over stretching sheets with electro-osmosis forces and Newtonian heating. Computational modelling of multiphase fluid flow behaviour over a stretching sheet in the presence of nanoparticles was studied by Rabbi et al. ^[26]. Khan et al. ^[27] considered the numerical simulation of a non-linear nanofluidic model to characterize the MHD chemically reactive flow past an inclined stretching surface. ^[28] explored the multiple slip effects on unsteady MHD Casson nanofluid flow over a porous stretching sheet. ^[29] claimed an explicit finite difference analysis of an unsteady MHD flow of a chemically reacting Casson fluid past a stretching sheet with Brownian motion and thermophoresis effects.

The present paper deals with end results of radiation produced by electromagnetic waves on unsteady transportation of both heat and mass of Casson fluid with persistant viscosity along with viscous dissipation, a magnetic field, and buoyancy forces. Upon extensive literature survey it has been found that very few researchers worked on the present problem. Effects of elecromagnetic radiation and viscous dispersion has numerous applications in industrial engineering such as separation of isotopes, heat exchangers, petroleum reservoirs etc. Due to these applications, hence the need for this study.

2.   Mathematical formulation

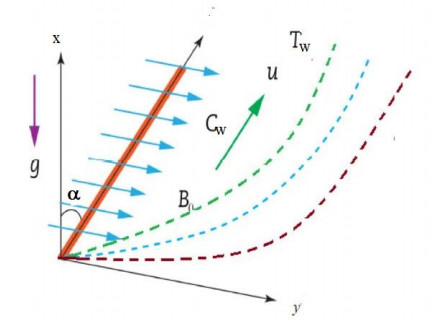
Consider a permeable angular elongated porous sheet with an unstable 2-directional laminar boundary layer of viscous incompressible MHD Casson fluid movement. Elastic sheet with holes and concentration of chemical species are considered and observed that heat is supplied by these to Casson nanofluid uniformly. The density variation with temperature and concentration is assumed to influence only the body force term. Thus, buoyancy forces aroused by the changes in temperature and concentration. Porous stretching sheet is subjected to uniform magnetic field normal to its surface. Another assumption made is with respect to the chemical reaction that is of homogeneous first order type with electromagnetic radiation happening in the move. It is presumed that (x, t) is the velocity of the porous elongated lamina acting along x-axis same as the direction of the force applied and v_w(t) is transfer of mass acting in the normal direction to the porous stretching lamina as shown in the physical model in Figure 1. Also, assumed that T(x, t) be the surface temperature, C(x, t) be the sheet concentration, T_∞ be the uniform temperature at a far-off distance from the lamina and C_∞ be the concentration considered at an appreciable distance away from the sheet. The fluid thermal properties such as conductivity as well as diffusivity are supposed to change linearly with temperature at the molecular level.

The mathematical expression for the Casson fluid is:

where ${\tau _{ij}}$ represents the ${\left({i, j} \right)^{th}}$ stress tensor component, ${\mu _B}$ stands for synthetic absolute viscosity of non-Newtonian fluid, ${p_y}$ indicates fluid's yield stress, and $\pi$ indicates the component of deformation rate multiplied by itself that is laid down as $\pi = {e_{ij}}{e_{ij}},$ and ${e_{ij}}$ stands for the ${\left({i, j} \right)^{th}}$ component of deformation rate, and ${\pi _c}$ is taken as the critical value of $\pi$ based on a non-Newtonian model created. The governing equations for Boussinesq and flow separation approximations were indeed specified by Eqs (2) to (5), that are based on above assertions ^[23]:

The boundary constraints are defined as in (6):

and as

where time is symbolized by t, whilst velocity components in the x-y plane are denoted by u and v and β is Casson fluid parameter. K represents porous medium specification, g stands for gravity acceleration, ρ stands for fluid density, and ν is fluid kinematic viscosity, σ represents electrical conductivity, α is thermal conductivity, T represents fluid temperature, C denotes fluid concentration, and Cp stands for specific heat at constant pressure. D_M is factor of molecular diffusion, Kr is chemical reaction parameter.

The vitality condition (4) can be reduced by employing the Rosseland dispersion approach for the radiative flux as ^[13]:

here σ* is Stefan-Boltzmann consistent and k* is the mean ingestion. If the temperature distinct inside the stream is very small, expanding T⁴ in Taylor's approach around T, while higher terms are avoided,

Heat flux can be estimated as

With the help of Eq (9), the energy equation (4) can appear as

The below mentioned similarity transformation was initiated to reduce the mathematical analysis:

by using the similarity transformation equation (11) for a nonlinear ordinary differential equations (ODE) system, the governing equations (3), (5), and (10) are transcribed in a non-dimensional form:

The corresponding dimensionless form of boundary conditions are given by the equation:

where β, A, K, M, Gr, Gm, Pr, R, Kr, Ec, and Sc are the Casson fluid parameter, unsteadiness parameter, porous medium parameter, magnetic parameter, thermal Grashof number, solutal or concentration Grashof number, Prandtl number, thermal radiation parameter, chemical reaction parameter, Eckert number, and the Schmidt number, respectively.

The skin-friction coefficient, Nusselt number (Nu), and Sherwood number (Sh) are the three basic physical characteristics that are taken into account:

Substituting Eq (11) into (16) to obtain the final dimensional form:

where ${{Re} _x} = \frac{{c{x^2}}}{{\nu \left({1 - \lambda t} \right)}}$ stands for local Reynolds number, C_f is the local skin friction, Nu is the local Nusselt number and Sh is the local Sherwood number.

The dynamic of fluid parcels is described with the help of Newton's second law. An accelerating parcel of fluid is subject to inertial effects. The Reynolds number is a dimensionless quantity which characterizes the magnitude of inertial effects compared to the magnitude of viscous effects. A low Reynolds number (Re≪1) indicates that viscous forces are very strong compared to inertial forces. In such cases, inertial forces are sometimes neglected; this flow regime is called Stokes. In contrast, high Reynolds numbers (Re≫1) indicate that the inertial effects have more effect on the velocity field than the viscous effects. In high Reynolds number flows, the flow is often modeled as an inviscid flow, an approximation in which viscosity is completely neglected. Eliminating viscosity allows the Navier-Stokes equations to be simplified into the Euler equations. The integration of the Euler equations along a streamline in an inviscid flow yield Bernoulli's equation. When, in addition to being inviscid, the flow is irrotational everywhere, Bernoulli's equation can completely describe the flow everywhere. Such flows are called potential flows, because the velocity field may be expressed as the gradient of a potential energy expression. This idea can work fairly well when the Reynolds number is high. However, problems such as those involving solid boundaries may require that the viscosity be included. Viscosity cannot be neglected near solid boundaries because the no-slip condition generates a thin region of large strain rate, the boundary layer, in which viscosity effects dominate and which thus generates vorticity. Therefore, to calculate net forces on bodies (such as wings), viscous flow equations must be used: Inviscid flow theory fails to predict drag forces, a limitation known as the d'Alembert's paradox. A commonly used model, especially in computational fluid dynamics, is to use two flow models: The Euler equations away from the body, and boundary layer equations in a region close to the body. The two solutions can then be matched with each other, using the method of matched asymptotic expansions.

3.   Numerical solution of the problem

To solve the system of ordinary differential equations (12)–(14) with their corresponding initial and boundary conditions (15) numerically, the domain [0, ∞) has been substituted by the bounded domain [0, η_∞] where η_∞ is a suitable finite real number that should be chosen in such a way that the solution satisfies the domain. Also (12)–(14) form a highly nonlinear coupled initial boundary value problem of third and second order ordinary differential equations. For this reason, (12)–(14) have been reduced to a system of seven initial problems of the first order of seven unknowns following the supposition in:

Thus, we develop the most effective numerical shooting technique in line with the fourth order Runge-Kutta method. To solve this system, we require seven initial conditions whereas we have only four initial conditions for $f\left(0 \right), f'\left(0 \right), \theta \left(0 \right){\text{ and }}\phi \left(0 \right), {\text{ }}$ while the other three $f''\left(0 \right), \theta '\left(0 \right){\text{ and }}\phi '\left(0 \right)$ and ϕ(0), were not given; hence, we employ numerical shooting technique where these three initial conditions are guessed to produce the required three ending boundary conditions. The step size $\Delta \eta = 0.001$ is used to obtain the numerical solution with six decimals (1×10⁻⁶) as a criterion of convergence.

4.   Results and discussion

This study examined heat and mass transportation's impacts on the movement of MHD Casson nanofluid with variable properties. The transformed equations (12)–(14) with the associated boundary conditions in Eq (15) has been mathematically resolved by utilizing the Runge-Kutta techniques along with the shooting techniques. All flow parameters' contributions such as unsteadiness parameter (A), Casson parameter $\left(\beta \right)$, magnetic specification (M), radiative Grashof number (Gr), mass Grashof number (Gm), Prandtl number (Pr) and so on are represented using graphs.

Figure 2 depicts, how the Casson parameter ($\beta$) affects the velocity contour. The velocity distributions are observed to decrease as the (β) value increases. This is true because the moment $\left(\beta \right)$ enlarges, the yield stress Py of the Casson fluid parameter $\left(\beta \right)$ degenerates that lead to improve plastic dynamic fluid flow rate. As the plastic absolute viscosity increases, it causes fluid flow resistance by reducing the velocity contour. Figures 3–5 describes the extent of unsteadiness variable (A) on the flow speed, temperature, and concentration proportions. A spike in the unsteadiness variable causes a reduction in flow speed, temperature, and concentration proportions. The yield exhibiting Casson nanofluid dominate viscosity which is accountable for the degeneration of fluid flow speed, temperature, and concentration contours. Physically, significant amount of A leads to the degradation of boundary layers thickness.

Figure 6 depicts the implications of a porous medium specification (K) on velocity contour. A rise in (K), the porous medium specification is noticed to cause reduction in fluid velocity contour. A random mixing of the Casson nanoparticles together with the imposed magnetic field strength causes the penetration of fluids to be very slow. Physically, the porous medium allows the passage of fluid particles within the boundary layer but plastic dynamic viscosity of the yield exhibiting fluid slows down its motion. Figure 7 indicates outcome of magnetic specification on velocity contour. An increase in magnetic specification's value has been observed to decrease the distribution of velocity. A huge M value originates the Lorentz force which can degenerate the motion of an electrically conducting fluids. Physically, the multiplication of electrical conductivity $\left(\sigma \right)$ and magnetic force's magnitude possess electromagnetic force which drag back the fluid motion.

In Figure 8, the contribution of the radiative Grashof number (Gr) to the flow speed contour is shown. The fluid velocity profile is improved by an improvement in Gr. By increasing the velocity contour, the buoyancy force acts on the fluid, causing a rapid flow within the layer. The contribution of the mass Grashof (Gc) on the flow speed contour is seen in Figure 9. A significant amount of Gm causes the flow speed contour to accelerate. In the model, the mass Grashof number is physically responsible for mass transfer. As a result, as Gc rises, the mass buoyancy force rises, causing the velocity distribution to widen.

The function of Prandtl number (Pr) on the temperature contour is seen in Figure 10. The temperature distributions degenerate as the value of Pr rises significantly. Pr is noted to be the inverse of thermal diffusivity in the model of heat transfer. When Prandtl number, Pr < < 1 it shows that thermal conductivity manages the nature of flow while Pr > > 1 means momentum diffusivity command the flow. Figure 11 outlines the impact of the Eckert number on temperature profiles. The temperature contour is lowered as Ec rises. Because of the plastic dynamic viscosity and magnetic field strength, this is true. The significance of Schmidt number (Sc) as well as the chemical change parameter (Kr) on the concentration proportion is shown in Figurers 12 and 13. A substantial amount of both Sc and Kr degenerates the concentration contours. Figure 14 highlights the influence of electromagnetic radiation variable (R) on the temperature distributions. A large R value appears to raise the fluid temperature. This aids the fluid's thermal state and has uses in thermal engineering. Figure 15 shows the flow chart for implementing the numerical technique.

In order to validate our modern-day consequences and to determine the accuracy of the existing evaluation, comparisons with to be had results of the skin friction coefficient for the unsteady flow of viscous incompressible Newtonian fluid are finished. In Table 1, we compare our results of the skin friction coefficient generated by way of Chamkha et al. ^[30] and Mabood et al. ^[31]. In this desk, we examine that there may be an extraordinary agreement among our effects, and those look at on this table that the skin friction coefficient increases with the increasing values of the stretching parameter. In Table 2, we observe that there is an excellent agreement among our present consequences with the ones previously received by using Mabood and Das ^[32] and Mabood et al. ^[31]. We also observe in this table that, because the magnetic parameter M will increase, the pores and skin friction substantially increase due to the Lorentz drag pressure resulting from electromagnetism increases.

5.   Conclusions

Heat and mass are examined for transport of MHD Casson nanofluid movement by considering constant physical properties past a stretchable sheet has been explored in this paper. The flow is stretchable within the boundary layer through the penetrable medium. The present outcomes portray that constant viscosity and thermal conductivity elevates thermal buoyancy force. The Runge-Kutta technique alongside shooting method is found to be efficient because it solves the highly nonlinear differential equations numerically. The following are the key findings:

(ⅰ) A large value of the visco-inelastic parameter $\left(\beta \right)$ is found to degenerates the velocity profile.

(ⅱ) The Lorentz force is constructed by the applied field of attraction. The Lorentz force gains its strength when the magnetic specification is increased, giving rise to the electromagnetic force.

(ⅲ) Raising the unsteadiness parameter (A) causes the velocity, temperature, and concentration proportions to degenerate.

(ⅳ) By raising the temperature contour, a boost in thermal radiation variable raises the fluid thermal condition.

(ⅴ) An improvement of Schmidt number (Sc) and chemical change variable is found to degenerate fluid concentration.

Acknowledgments

The authors R. Jarra, H. Shanak and J. Asad would like to thank Palestine Technical University-Kadoorie for supporting this work financially.

Conflict of interest

The authors declare no conflicts of interest in this paper.

Nomenclature

x: Coordinate along the stretching sheet

y: Distance normal to the stretching sheet

c: Initial stretching rate

b: Constants

t: Time

u: Velocity along the x− direction

v: Velocity along the y− direction

u_w(x, t): Velocity of the stretching sheet

v_w(t): Velocity of the mass transfer

F: Force applied along the x− axis

T_w(x, t): Temperature of the sheet at the wall

C_w(x, t): Concentration of the fluid at the wall

T_∞: Uniform temperature far from the sheet

C_∞: Uniform concentration far from the sheet

B₀: Magnetic induction

Cp: Specific heat at constant pressure

Kr: Chemical reaction parameter

Ec: Eckert number

Sc: Schmidt number

Cf: Skin friction coefficient

Nu_x: Nusselt number

Sh_x: Sherwood number

q_w: Heat flux

Rex: Reynolds number

K: Thermal conductivity

D: Molecular diffusivity

T: Temperature of the species

C: Concentration of the species

g: Acceleration due to gravity

q_r: Radiation heat flux

v₀: Constant

K_∞: Thermal conductivity of the ambient

D_M: Diffusion coefficient of the ambient

M: Magnetic parameter

A: Unsteadiness parameter

Gr: Thermal Grashof number

Gc: Solutal or concentration Grashof number

Pr: Prandtl number

R: Thermal Radiation parameter

S: Suction/Injection parameter.

Greek Symbols

α: Inclination angle

λ: Constant

ψ: Stream function

σ^*: Stefan- Boltzmann constant

β₁: Variable thermal conductivity

β₂: Variable diffusion coefficient

τw: Shear stress

K: Porous medium parameter

ν: Kinematic viscosity

μ: Coefficient of viscosity

ϕ: Dimensionless concentration function

β_T: Coefficient of thermal expansion

β_C: Volumetric concentration coefficient

θ: Dimensionless temperature function

η: Dimensionless space variable

ρ: Fluid density

σ: Electrical conductivity.

Subscripts

∞: Free stream condition

w: Properties at the plate