1.
Introduction
Startups and small and medium-sized enterprises (SMEs) account for a significant share of the global market for human capital but are often constrained in their growth potential, as they have difficulty accessing capital markets (Carpenter & Peterson, 2002). Blockchain-based initial coin offerings (ICOs) promised to provide a new source of financing for such firms. The phenomenon dates back to 2013. Since then, the number and funding of projects has been growing exponentially, with over $20 billion raised by December 2018 (Coinschedule, 2018). While ICOs provide a promising financing option for certain companies utilizing decentralized business models or blockchain protocols, they typically do not suit regular businesses, since the blockchain-based token are often of no use outside of the ICO itself and the token does not grant any right of ownership or dividends. In addition, ICOs and cryptocurrencies are often associated with crimes like fraud, money laundering, hacks or theft (Ante, 2018), which is why companies approach them with caution.
Token offerings evolved over time and, more recently, also include the category of security tokens that promise to better fit firms' and investors' needs and fill the role that ICOs failed to meet. While security tokens are also blockchain-based tokens they—contrary to tokens sold in ICOS—represent securities, as defined by the relevant jurisdiction. In security token offerings (STOs), companies sell tokenized traditional financial instruments, like equity, debt, revenue sharing rights or any other mechanism in the form of a cryptographic token. Compared to traditional securities, this has a number of advantages: (1) Tokens are immediately transferable and can be traded 24/7 on secondary markets, (2) clearing and settlement is a matter of only a few minutes, (3) tokens can be held personally, i.e. brokers and custody accounts are no longer required and (4) the underlying blockchain ensures transparency of all transactions. STO participants classify as investors with the respective rights derived from the financial instrument, whereas ICO participants may legally only classify as donors with very limited rights. STOs are thus not a subset of ICOs (Lambert et al., 2020).
Adhami et al. (2018) analyze 253 ICO campaigns and find that code availability, presales, and specific services (like profit sharing) raise the probability of campaign success. Profit sharing may be indicative of a security, so this paper potentially addresses a partial aspect of security tokens. Fisch (2019) uses a dataset in which he classifies 17% of the tokens as security tokens and tests campaign success for a utility token dummy variable (i.e., no security token) that shows a negative but insignificant influence on ICO success. In the first published paper dealing only with STOs, Mazzorana-Kremer (2019) highlights the differences to ICOs and the potential of reduced intermediary and transactions costs compared to regular securities. She concludes that while STOs are likely to grow as an alternative to IPOs, private equity and crowdfunding to finance SMEs, their success will strongly depend on the quality of their issuers and secondary markets platforms. Lambert et al. (2020) give the most comprehensive theoretical and empirical analysis of STOs and investigate a dataset of 106 STOs. They find that 30% of the issuers are incorporated in the USA, around 9% in UK and Cayman Islands, 8% in Switzerland and the rest widely dispersed around the globe. On average, $6.4 million are raised with a maximum of $134 million. Defining STO success as the amount raised, Lambert et al. (2020) find that giving voting rates is a success factor for STOs, while the use of a softcap (minimum amount to be raised), a Swiss and UK incorporation show a significant and strong negative and a presence on telegram a small negative association with amount raised. Alternative success factors, "the ratio of amount of capital raised in the STO to the target" and "softcap achieved", show similar results. By use of a theoretical model, Gryglewicz et al. (2019) compare tokens issued by digital platforms with and without security aspects and show that while security features foster network effects and adoption, they also dilute developers' incentives. Roth et al. (2019) analyze the advantages and disadvantages of equity crowdfunding (ECF) via tokens and argue that it can lower costs of secondary market trading and reduces the power of intermediaries, while it can create information asymmetries, raise regulatory issues, and be more energy consumptive if issued on a proof-of-work blockchain.
We add to the literature on entrepreneurial finance by analyzing empirically whether cheap signals of quality are used in STOs and whether they have an effect on funding success. We define success in STOs as the amount of funding a venture is able to collect. Cheap signals do not require costly efforts for firms and could therefore potentially be exploited by firms in order to influence their funding success. For instance, fake social information represents a clear thread to the provision of trust and credibility of web content (Luca & Zervas, 2016). Based on a sample of 495 token offerings Momtaz (2020) argues that ICO projects have incentives of moral hazard in quality signaling, as there are no institutions in place that verify or enforce trust in signals. Biased signals may not be identified by the market during the financing process but only backfire once the token is listed on secondary markets and more information is available. For our analysis, we distinguish four signal categories: (1) human capital, (2) external networks, (3) project elaboration, and (4) social media and analyze a dataset of 151 tokenized offerings that started between April 2017 and October 2018 in regard to these signals and other indicators. By analyzing investors' behavior in STOs, we provide insights for firms as to which variables they could focus on to signal their quality to potential investors and if it might be concerning for investor protection.
2.
Blockchain-based financing: ICOs and STOs
Blockchain technology is a secure and transparent way to transfer value on the internet. It comprises a mixture of existing technologies, like hashing, peer-to-peer networks, time-stamping and merkle trees (Merkle, 1989), that generates a secure distributed ledger for transactions that is updated at regular intervals (Ante, 2020a; Steinmetz et al., 2020). While Bitcoin (Nakamoto, 2008) only represents some specific use cases, like e-money or store of value, and is mostly used for trading purposes (e.g. Zheng & Kaizoji, 2019), the underlying technology has various other applications. One particular use case is tokenization on top of the blockchain infrastructure through the use of so-called smart contacts. Smart contracts are computer code that is automatically executed in a decentralized way based on specific events (Buterin, 2013; Wood, 2014; Ante, 2020b). These tokens can represent any form of value and can be transacted on the blockchain ledger. Three different token forms can be distinguished, but hybrid instruments also exist (FINMA, 2018): (1) Payment tokens are cryptocurrencies with no other functions or links to specific projects. They are used as a means of payment (e.g. Bitcoin). (2) Utility tokens provide digital access to an application or a service (e.g. a software license or a voucher). (3) Asset tokens (or security tokens) represent underlying, assets for example companies, income streams, or an entitlement to dividends or interest payments. Their functions are analogous to traditional financial instruments like equities, bonds or derivatives.
An increasing number of startups in the blockchain ecosystem have been using ICOs to raise early-stage financing since the first ICO that was conducted in 2013. Instead of going for an IPO or ECF, which may be more expensive and more tightly regulated, startups issue utility tokens and distribute them to investors in proportion to their respective investment. In the case of utility tokens, startups exploit the light regulation in that utility tokens are typically not subject to securities regulation, as contributions to an ICO may not be classified as investments but as donations. The decentralized nature of the blockchain technology allows the tokens to be immediately exchanged on secondary markets, in theory providing ICO contributors with instant liquidity and, unintended by regulators, room for speculation (Ante, 2019; Ante & Meyer, 2019; Meyer & Ante, 2020; Bogusz et al., 2020). ICOs for utility or payment tokens have raised over $20 billion to date. However, with their necessity to sell a utility token, ICOs are unsuited for firms that do not plan to actually provide services or products that can be obtained in exchange for such a token. As ICOs represent a rather young phenomenon, the academic research on the topic is limited.
Amsden & Schweizer (2018) show in their sample of 1009 projects between 2015 and 2017 that ICO success depends negatively on venture uncertainty and positively on venture quality. Overall, the term "success" is somewhat ambiguous, as it can be applied to funding success, venture success, secondary market access, or return on investment. In a sample of 278 ICOs, Ante et al. (2018) find that human capital characteristics, business model quality, project elaboration, and social media activity determine funding success—defined as the size of funding received—in both ICOs and crowdfunding. Three of these signals could be classified as cheap, as signals of human capital by listing team members or advisors on the project's website, whitepaper characteristics and social media reach can theoretically be faked or artificially inflated. A study by EY (2017) claims that 10% of all ICO funds are effectively lost as a result of hacking attacks. Shifflet & Jones (2018) evaluate the documentation of 1450 ICOs, of which investors claimed losses amounting to $273 million based on the information from law suits and other actions. A total of 18.69% of the projects used documentation that are classified as "red flags". Such red flags involve plagiarism, identity theft and promises of improbable returns.
In contrast, security tokens are "digital representation[s] of an investment product, recorded on a distributed ledger, subject to regulation under securities laws" (Lambert et al., 2020). Hence, STOs fall under the financial regulation of the specific jurisdiction where they are issued rendering them different from ICOs. The technical protocols for security tokens, legal structures and secondary markets continue to evolve. As tokens can represent all kinds of things, a security token can in theory also (additionally) serve as a means of payment or as a utility token. The financing round thus allows the issuer to gain direct access not only to investors but also to potential customers.
In the US, the Securities and Exchange Commission (SEC) applies the Howey test to determine whether an asset qualifies as a security. Essentially, investments are considered securities if (1) money is invested, (2) the investment is expected to yield a profit, (3) the money is invested in a common enterprise and (4) any profit comes from the efforts of a promoter or third party (SEC, 1946). In 2017, the SEC determined that the tokens issued by the project The DAO were securities that would have required a prospectus (SEC, 2017a), and it issued a cease-and-desist order on Munchee Inc. for its tokens being securities (SEC, 2017b). While TheDAO was structured as a decentralized venture capital fund that would distribute profits to investors, Munchee "only" promised its investors that the value of the token could increase due to the company's work and the token being listed on secondary markets. It lacked mechanisms such as dividends or buybacks. The Munchee ruling was surprising, as the company complied with the Simple Agreement for Future Tokens (SAFT), a concept which was developed expressly to tackle practical problems with utility tokens and the Howey test. In short, SAFT argues that the status of tokens changes over time, from a security while the token network does not yet exist to a utility token once the network is operational. Investors make use of convertible loans to access their tokens when the network goes live (Batiz-Benet et al., 2017). On a European level, the Authority (ESMA) has not yet determined how (security) toke legal certainty of (security) token offerings is less pronounced, as the European Securities and Markets ns fit into European prospectus rules and financial instruments under the 2nd Markets in Financial Instruments Directive (MiFID II). On a national level, the German financial supervisory authority BaFin (2017) has stated that tokens will be classified on a case-by-case basis.
The basic mechanism of STOs—to collect capital from the public in return for equity (or other financial instruments)—is by no means new, as IPOs or ECF do just the same. The main benefit of security tokens consists in the underlying blockchain technology, which provides transparency, pseudo-anonymity, finality and security. Transactions are broadcasted transparently to the network, so that ownership of each token is known at all times. Settlement of transactions is final, enabling much faster and more efficient clearing and settlement compared to traditional processes that take up to three business days (Mills et al., 2016; Fiedler et al., 2018). A blockchain-based security clearance system updates the register of ownership instantly, which could save stock markets up to $1.2 billion annually (Pinna & Ruttenberg, 2016) and could prevent abuse in the form of dividend stripping, like so called cum-ex deals (Büttner et al., 2018), as ownership is always clear and transfers are semi-transparent. The semi-transparency is due to the public and private key structure of blockchain systems like Ethereum. Public keys represent addresses that may receive transactions without permission being given. However, issuing send transactions from an account requires the private key (i.e. a password). Therefore, the public key can be publicly known, while the private key must remain private. Public keys are strings of letters and numbers that generally cannot be associated with the owner. Once the holder of a public key becomes known, all historic transactions can be accessed. Blockchains like Bitcoin or Ethereum are thus considered pseudo-anonymous (Koshy et al., 2014).
The success of ICOs can be explained by the instant liquidity that comes with the listing of blockchain tokens on one of the many cryptocurrency exchanges that have emerged since 2011 alongside the growing interest in Bitcoin and other crypto currencies. The biggest promise of security tokens is that this type of liquidity will be carried over to the market for STOs. Yet such development is anything but certain, as liquidity usually requires mature assets and a market. Brunnermeier & Pedersen (2008) state that traders of an asset provide liquidity to a market, while their liquidity depends on the availability of funding. This funding in turn depends on the liquidity of the asset on the market. Their model shows that liquidity in security markets can evaporate immediately, has correlations between securities, relates to volatility, has flight-to-quality effects and moves with overall market developments. Therefore, a highly liquid market for security tokens will require existing infrastructure and firm quality. Tokenized securities provide the advantages that they can potentially be traded 24/7 and investors can hold their assets without a need for brokers or custody solutions.
To this date there is no regulated exchange offering trading for securities, yet. Secondary markets for security tokens are being developed from various sides: Cryptocurrency exchanges are working to obtain the relevant licenses to list security tokens (Zhao, 2018a) and are partnering with stock exchanges (Baydakova, 2018). New startups are building secondary markets (e.g. tzero.com). At the same time, traditional stock markets are experimenting with blockchain technology, although they mostly focus on the clearing and settlement of traditional securities, rather than on STOs (Deutsche Börse, 2018).
3.
Literature & hypotheses development
3.1. Startup financing
Corporate financing is subject to risk and startup financing is usually subject to high risk (Hannan & Freeman, 1989) and high information asymmetry alike (Petersen & Rajan, 1995), which limits the firms' financing options. Startups are often not able to signal their quality at an early stage of development in the absence of collateral, past cash-flows and data on new markets. Hence, debt financing is often not available to ventures (Cosh et al., 2009; Schwienbacher & Larralde, 2010), leaving them with the option of equity funding. Business angels, venture capital or crowdfunding offer startups ways to finance themselves. Business angels are wealthy individuals without familial ties to the entrepreneur who invest money and their experience in the venture (Deakins & Freel, 1998). They provide the startup with knowledge, funds and contacts (Macht & Robinson, 2009). Venture capitalists devote significant resources to understanding new markets and identifying startups. They provide initial funding to ventures and offer guidance and contacts (Davila et al., 2003; Macht & Robinson, 2009). According to Hellmann & Puri (1999), startups that are financed through venture capital are more innovative and enter the market faster than startups that use alternative financing alternatives. Venture capitalists bundle resources from larger investors and invest them in startups based on their investment thesis. Average venture capital investments in startups amount to below three or four million dollars (Kim & Wagman, 2016). These financing forms play an important role in startup financing but do not come without limitations, especially high transaction costs and barriers to access.
Innovative financing instruments like leasing, credit scoring or factoring provide SMEs with greater flexibility, as these instruments rely less on formal financing institutions. Crowdfunding is a recent additional example, where retail investors pool resources to fund a specific project on the internet (Ahlers et al., 2015). It has become a common source of capital for early stage startups in recent years (Hornuf & Schwienbacher, 2017). Four forms of crowdfunding can be distinguished (Griffin, 2012): (1) donation-based, without any actual rewards, (2) rewards-based, with non-financial rewards in the form of promotion or services, (3) lending-based, with a financial return like interest payments, or (4) equity-based with financial returns like dividends. Crowdfunding campaigns usually offer signals to potential contributors regarding the relevance and market potential of their product or service (Schwienbacher & Larralde, 2010). Investors are financially motivated: Cholakova & Claryssee (2015) show that the probability of a pledge being honored is positively related to equity investments, whereas there is no significant association with non-financial motives. A shortcoming of crowdfunding campaigns is their need to attract investors who contribute comparatively small amounts in return for a small stake in the company (Malmendier & Shanthikumar, 2007). Compared to business angels and venture capitalists, these investors lack experience and face high information costs, as a small investment does not warrant in-depth research into the project or company (Ahlers et al., 2015). The most severe limitation to the financing potential of crowdfunding is the fact that many jurisdictions impose a cap on the profit for investors, who receive an instrument that is only similar to equity. Hornuf & Schwienbacher (2017) use the term "quasi-equity" to describe the mezzanine financial instruments, like subordinated profit-participating loans or silent partnerships, that are used in ECF on the German market. Blockchain-based financing might be a promising alternative to crowdfunding, venture capital and IPOs.
3.2. Information asymmetry and signaling theory
Available information provides a basis for decision-making processes. It can be divided into freely accessible public information and private information that is only available to a specific group. Therefore, information asymmetry exists when "different people know different things" (Stiglitz, 2002), e.g., a specific group holding private information. In the context of corporate financing, the management of a project is able to decide on the degree of information it wants to provide to the public or specific groups. Stiglitz (2000) specifically highlights the importance of information about quality and intent as particularly important. In terms of quality, this relevance derives from the lack of awareness in regards to specific characteristics of the other party. In terms of intent, information asymmetry has a high relevance due to concerns about the behavior and intentions of the other party (Elitzur & Gavious, 2003).
Signaling theory (Spence, 1973) postulates that signals can alleviate asymmetric information. For example, if a seller possesses much more information about a product than a prospective buyer, sales can be increased if the seller signals the value of the product to the buyer. Consumer uncertainty is of specific relevance for electronic markets, as consumers are not able to directly evaluate a product or serve but require external information. This information is often provided by a seller that can in theory fake or misinform the consumer (Mavlanova et al., 2012; Wessels, 2015). Such mechanisms can lead to problems of adverse selection for consumers, as they may use prices as signal and not signaled quality (Akerlof, 1970). To be effective and credible, signals should be costly to imitate or sent by trusted third parties (Sanders & Boivie, 2004; Fischer & Reuber, 2007). In the context of corporate finance, signals like debt (Ross, 1973) or dividends (Bhattacharya, 1979) have been identified as relevant and costly signals of quality, as only firms of high quality are able to constantly pay out dividends and interest.
Signals do not have to be costly or honest in order to have an effect on the decision process of investors. In the case that party does not possess a specific quality but realizes that the presumed benefits of a signal outweigh the related costs of producing such signal, the party may be incentivized to falsely communicate or fake the signal. Such actions allow parties to provide false signals of quality until a counterparty leans about it and effectively ignores the signal for the decision process. Therefore, signals should be structured so that dishonesty does not pay off for misbehaving parties (Connelly et al., 2011). Smith (1994) shows that in theory there are circumstances where even cost-free signals can provide a reliable basis when two participating entities rank possible results from an outcome in the same rank order, whereas the degree of this preference is not relevant. Johnstone & Grafen (1993) argue that inferior signalers are incentivized to produce dishonest signals to attract signal receivers, as the interests of the two involved parties compete. Firms signaling future stock repurchase programs without actually realizing them in the future represents an example for dishonest signals (Westphal & Zajac, 2001).
The signaling environment can also have a relevant effect on the degree of relevance of a signal. Environments that a signaler can easily influence, like a website or social media channels, may indicate biased or potentially faked signals, while the chance of independent external parties falsely signaling seems less probable. In the case of unclarity on the interpretation of a signal, receivers may orientate towards imitations of the signal for their decision-process (Sliwka, 2007). Yet such second-level signals may result in different outcomes, as press releases act as credible signals (Carter, 2006), while reports about press releases result in potential informative distortions (Connelly et al., 2011).
In the following, academic research in the context of signaling theory will be introduced for human capital, network size, project elaboration and social media that represent the basis for our different hypotheses.
3.2.1. Human capital signals
Ahlers et al. (2015) argue that smaller investors use human capital as an important input for their investment decision in ECF; large project teams create the impression that a firm can easily interest employees in its mission. Mollick (2013) similarly assumes a positive relationship between team size and project success in the context of venture capital. Based on the literature on corporate finance in the form of venture capital, ECF and ICOs, we posit a positive effect of human capital characteristics on STO success, since human capital serves as a signal for venture capital investment (Hsu, 2007; Gimmon & Levie, 2010). Human capital as a signal for venture capitalists' investment decisions is especially important in young industries (Hsu, 2007). Carpenter et al. (2003) show that staff size has a positive effect on IPO performance in the technology sector. Blockchain, tokens and especially security tokens are very young technology, so we should expect human capital to be an important signal. Ante et al. (2018) identify a positive effect of team and network size on funding success in a sample of 278 ICO projects. We distinguish between team size and team quality. Team size is a quantitative variable that is rather easy to influence by inflating the number of pictures and names supposed to be working for the company on a website or at LinkedIn. We thus categorize team size as a cheap signal whereas team quality is not a cheap signal and not in the focus of our study.
3.2.2. Network size signals
Third party endorsement helps reduce the information gap between startups and other third parties like potential investors (Stuart et al., 1999). Relationships with prominent entities like universities (Colombo et al., 2019), venture capital firms (Megginson & Weiss, 1991; Gulati & Higgins, 2003), underwriters (Carter & Manaster, 1990) or auditors (Beatty, 1989) serve as a quality signal for IPOs. Certo (2003) suggests that IPOs utilize board prestige structures to reduce the disadvantage of being new to the market and to signal their quality to potential investors. In ECF, external certification and quality signaling through established partnerships signal a higher level of reputation to a project and its team (Mollick, 2014; Ahlers et al., 2015). The size of the advisory council has a positive effect on ICO funding (Ante et al., 2018). We distinguish between the quantity of the advisor board and partnerships and their quality and consider the mere quantity to be a cheap signal, since projects are able to list all types of advisors and partnerships on their websites without communicating the actual relevance of the business connections. We do not focus on the quality of advisors and partnerships, since we do not consider this a cheap signal.
3.2.3. Project elaboration signals
A whitepaper, business plan or other project descriptions and forecasts can help external parties to evaluate the risks and opportunities of a venture and thus to reduce information asymmetries. A startup that lacks such documentation signals uncertainty (Mollick, 2013; Ahlers et al., 2015). The preparation of such documents can be costly and can therefore signal the management team's commitment and professionalism (Chen et al., 2009). Pitch quality has been identified as associated to funding success in crowdfunding, as it signals quality and preparedness of a project (Mollick, 2014; Fondevila-Gascón et al., 2015; Hobbs et al., 2016; Mollick & Nanda, 2016). Gafni et al. (2018) show that sound textual descriptions of crowdfunding projects (similarly to a whitepaper for an STO) have a positive effect on project success. Precise communication promotes crowdfunding success (Davis et al., 2017; Parhankangas & Renko, 2017). In their sample of 1009 ICO projects between 2015 and 2017, Amsden and Schweizer (2018) show that ICO success declines with venture uncertainty and increases with venture quality. The existence of a whitepaper has also been identified as a driver of ICO funding (Ante et al., 2018). Shifflet & Jones (2018) show that a high degree of ICOs made use of plagiarized documents. Projects actually directly copied entire text sections from other whitepapers to describe metrics like security aspects or technical features. Based on the startup financing literature, we anticipate a positive effect of the existence and quality of project documentation in the form of a whitepaper. Again, we distinguish between the quantitative and the qualitative part of the signal and break down the quantitative signal as (1) the pure existence of a whitepaper and (2) the size and number of citations of a whitepaper. These quantitative signals are cheap to influence, while the actual quality of a whitepaper is not considered a cheap signal.
3.2.4. Social media signals
Firms can use simple metrics such as "likes" to evaluate the potential demand for an idea through social media (Moisseyev, 2013). And yet the effects of corporate social media use may prove to be uncontrollable, as a single message can create an outrage and severely damage the firm's image (Scovotti & Jones, 2011; Pfeffer et al., 2014). A larger social media network (Kromidha & Robson, 2016) and increased social media activity have positive effects (Nevin et al., 2017) on crowdfunding campaigns. Research on ICO success shows positive effects of Telegram group size and Twitter followers (Howell et al., 2018). Fraudulent crowdfunding projects are less likely to use social media channels (Cumming et al., 2017). For crowdfunding, positive effects on campaign success have been identified for the number of Facebook friends and likes (Mollick, 2012; Moisseyev, 2013; Hong et al., 2015), as well as for Twitter influence (Jin et al., 2017). Yang & Berger (2017) show that the number of social media followers on Facebook and Twitter tends to raise the amount of venture capital received by startups. Social information can provide consumers with substantial information for their decision making and can lead to informational cascade effects (Duan et al., 2009; Tucker & Zhang, 2011). Wessel et al.(2015, 2016) tackle fake social information in crowdfunding and show that faked Facebook likes on the Kickstarter crowdfunding platform have a short but positive effect on funding success that turns negative over time. Based on the assembled evidence, we expect that social media channel size has a positive influence on STO success. The absolute size of social media networks does not necessarily represent the actual social network of a company, as followers or likes can be purchased to make the network look bigger than it actually is. The signal can therefore be classified as comparatively cheap.
3.3. Hypotheses
Our general hypothesis is that investors of STOs and traditional financial markets invest according to similar signals that disclose information about fundamentals of a company in the form of human capital, network size, project elaboration and social media characteristics. We hypothesize that investors make use of costly signals to evaluate the quality of a project and disregard cheap signals in their decision process. If our hypothesis is correct, we should find that funding success (i.e. the attractiveness of a project for investors) is not systematically related to cheap signals. Based on the literature on signals in the context of venture financing we build four sub-hypotheses for the four different characteristics.
We hypothesize that the amount of funds raised in an STO is:
● (Hypothesis 1) unrelated to cheap human capital signals;
● (Hypothesis 2) unrelated to cheap advisory and/or partnership signals;
● (Hypothesis 3) unrelated to cheap project elaboration signals;
● (Hypothesis 4) unrelated to cheap social media signals;
We operationalize the respective cheap signals as follows:
● Cheap human capital signals: (a) the number of team members mentioned on the project website and (b) the number of employees listed in the project's LinkedIn profile.
● Cheap advisory and/or partnership signals as (a) the number of advisors and (b) the number of partnerships mentioned on the project website.
● Cheap project elaboration signals as (a) the availability of a whitepaper and as (b) a whitepaper score, which is calculated as the number of pages and citations of each document.
● Cheap social media signals as the number of followers on (a) Twitter, (b) Telegram and (c) LinkedIn, (d) the number of Facebook page likes.
4.
Data collection, variables and empirical methodology
4.1. Data collection
Projects that sold tokens under security regulation were identified by manual research via Google search, the SEC's EDGAR search tool (sec.gov/edgar) and various STO listing sites: tokenmarket.com, token.security, stocheck.com and stoscope.com. Once the projects were identified, we collected all the necessary information on the teams, advisors, partners, funding amount, whitepaper, social media channels, etc. from the project's website and the above sources. We selected the four social media channels that the projects used most often: Facebook, Telegram, Twitter and LinkedIn. Companies utilize social media channels based on their target market (Stelzner, 2010), which is why the four prevalent channels of the respective market should display a fitting record of social media across STOs. All social media data was collected through API calls or manual lookup for LinkedIn. Ethereum price data was retrieved from coinmarketcap.com. All time-sensitive information, like social media followers or data on team, partners and advisors were collected at the time prior to the start of the public financing campaign. We were able to identify both the start and closing dates for only 56 of the projects. We were not able to collect data on the underlying security structures for many tokens, as offering documents did not provide exact details.
The dataset comprises 151 projects (1) that sold tokens as securities, (2) that were able to collect financing in the relevant period and (3) for which the bulk of the information we use in our analyses was available. The term security token may refer to either equity or debt instruments. Only three of the projects showed signs of failure: two websites were no longer accessible and one project was shut down by the authorities. We selected only projects that sold tokens as securities in order to rule out any uncertainty as to whether a campaign should be considered an STO or an ICO. We thus excluded a number of projects that sold tokens to the public that could (or must) be classified as securities but did not declare this in their communication, The Dao being the most prominent example (SEC, 2017a).
4.2. Variables
Dependent variable.
Funding is our dependent variable, as it provides an indicator for the success of a funding campaign. To account for the skewedness of the variable, we use the natural logarithm of the amount raised. Similar studies in crowdfunding (Mollick, 2014) or ICOs (Ante et al., 2018; Fisch, 2019) have relied on the same dependent variable.
Independent variables: Team size (website) signifies natural logarithm of the number of team members presented on a project's website, while Team size (LinkedIn) is the logarithms of the number of employees who are associated with the project on LinkedIn. Whitepaper exists is a dummy variable that indicates whether a project whitepaper is available. For ICOs, whitepapers are what business plans and prospectuses are for IPOs. This is due in part to the fact that very successful cryptocurrencies like Bitcoin or Ethereum issued whitepapers, setting a standard for the ecosystem (Nakamoto, 2008; Buterin, 2013; Wood, 2014). Whitepaper score in turn is our proxy for the cheap signal of whitepaper quantity. It is calculated as the sum of the number of pages and the number of references of each whitepaper. The variables Facebook Likes, Telegram Followers, Twitter Followers and LinkedIn Followers capture the natural logarithm of a project's absolute number of likes or followers on each social media platform. Projects that did not show specific social media channels or had zero followers or likes on their channels were assigned the smallest positive value of the absolute numbers of each specific channel before the natural logarithm was applied. Advisors and Partners indicate the logarithm of the number of advisors and partners, respectively, that are mentioned on the website.
Control variables: The Ethereum blockchain has been the most widely-used infrastructure for token sales. Ether (ETH) is the native token of the Ethereum blockchain and has been used for a major portion of all ICOs (Ante et al., 2018). Discussing risk-taking in the context of prior gains and losses, Thaler & Johnson (1990) introduce the house money effect and show that risk seeking increases with prior gains. Accordingly, an increase in the price of ETH may raise the willingness of potential investors to reinvest their capital in ETH-based projects. Ethereum price equals of the price of Ethereum at the starting date of the security token offering for each project. Ethereum 30d represents the relative price change of Ethereum of the 30 days prior to the start of the STO.
Various projects set maximum funding amounts, for instance to signal reasonable planning or scarcity of the investment, or in order not to appear immodest. Funding Cap equals the natural logarithm of the amount of any such limitation in US-Dollars. The variable represents the funding target of the company, which is why it can act as a representation for unobserved variables, like asset size.
Furthermore, the dataset was divided into a number of industry sectors: Information Technology, Financial, Gaming & Gambling, Healthcare & Medicine and Real Estate are dummies for the five most common industry sectors. Regulations differ across jurisdictions, and so do the conditions for projects that are looking to raise money (Chen et al., 2009; Stuart & Sorenson, 2007).
A feature of crowdfunding, ICOs and STOs is that geographical limitations are reduced (Stuart & Sorenson, 2003; Agrawal et al., 2010). Legal certainty in the sale of (security) tokens is greatest in the US while countries like Switzerland or Singapore are lagging behind. Tax havens provide a legal framework but lack financial accessibility. Mollick (2014) showed that in crowdfunding, geography matters both to the number of projects proposed and the success of funding campaigns. Amsden & Schweizer (2018) failed to find any effect of tax havens on ICO success. Fisch (2019) also used location dummies and found a positive effect for the US on the amount raised in ICOs. In the present study, Tax Haven indicates that a firm is incorporated in a tax haven.1 The variables United States, Switzerland and Singapore indicate incorporation the respective country—which need not be the country in which the token was registered or issued. For instance, we identified six companies located in Singapore, whereas the Monetary Authority of Singapore said in September 2018 that it had not approved a token that represents a security to date (Zhao, 2018b).
1 Location: tax haven comprises the following countries and territories: Bahamas, Barbados, Bermuda, Cayman Islands, Gibraltar, Guernsey, Malta, and Virgin Islands. Being home to 61.9% of the companies in this group, the Cayman Islands are the most popular "tax haven".
4.3. Empirical methodology
After individually estimating the log-transformed amount of funding on the each independent and control variable (univariate regressions), we estimate funding on the set of independent variables, as shown in Equation (1):
Next, we extent the model by adding control variables on the target and the jurisdiction (tax haven, USA, Swiss and Singapore) of the venture (Equation (2)):
Third, we add industry dummy control variables to the model (Equation (3)) and lastly market characteristics, i.e. Ethereum price and Ethereum 30d (Equation (4)).
5.
Results
5.1. Descriptive results
Table 1 provides an overview of the dataset. The 151 projects in the dataset were able to collect $1.95 billion in total, ranging from $10k to $204 million, for an average of $13.4 million raised. The average funding cap was at $31.7 million, or 2.37 times the average actual funding. These non-log-transformed results are not reported in Table 1.
As for the human capital characteristics, there is a marked difference between the size of the team as shown on a project's website and the number of individuals who associated themselves with the project on LinkedIn. It is rather easy to lie on LinkedIn about being employed at a certain company. For example, the CEO of the cryptocurrency exchange Binance, Changpeng Zhao, tweeted that the majority of "Binance employees" on LinkedIn are fake (Twitter, 2018). Individuals are impersonating Binance staff for fraudulent reasons. Furthermore, larger companies are looking to protect their human capital from head hunters by not disclosing their staff on the website, whereas smaller firms need to signal their quality with human capital (Hsu, 2007). It seems plausible that LinkedIn lists more team members than regular company websites. The 151 companies showed a total of 1952 employees or team members on their websites, or 12.93 employees per company on average. The largest number shown was 200, while 25 companies did not show any team members at all. A total of 5996 persons associated with these companies were listed on LinkedIn, or 43.77 per company on average. The highest number of employees for a single company was 1823 linked persons, while three companies showed 0 employees.
The average and maximal number of advisors and number of partners were relatively similar, as projects had an average of 4.38 advisors and 4.06 partnerships listed on their website. The highest number was 34 for advisors 35 for partnerships. We were able to identify a whitepaper for 113 projects (74.8%), with 30.31 pages and 7.15 literature references on average. The highest identified whitepaper score is 129, the average score is 27.99. Across all 151 projects, 106 Facebook accounts (70.2%), 105 Telegram channels (69.5%), 131 Twitter accounts (86.6%) and 137 LinkedIn sites (90.7%) were identified. On average, the projects had 11,300 Facebook likes, 11,444 Telegram followers, 11,472 Twitter followers and 780 LinkedIn followers. The Ethereum price at the start of a funding period was $586.71 on average, ranging between $42.6 and $1363.19. The price rose by 18% ($24.39) on average over the 30 days before the start date, with a range from -56% (a loss of $487.93) to 132% (a gain of $674.67).
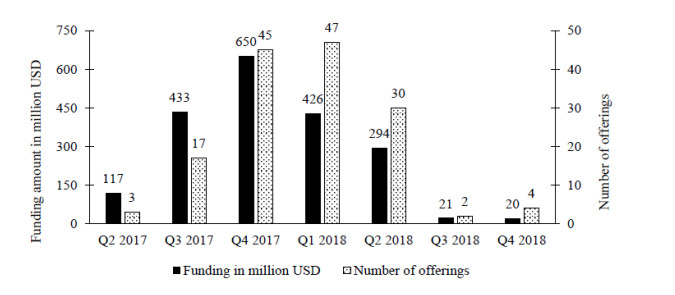
We were able to identify exact starting dates of the offering periods for 147 projects, as shown in Figure 1. Most projects were conducted from Q2 2017 to Q2 2018. The average number of funds raised constantly decreases over time. The three projects that started their STO in Q2 2017 raised an average of $39 million and the 17 projects in Q3 2017 were able to raise an average of $25 million. For the first three quarters of 2018, STOs raised on average between $9-10.5 million and the three projects in Q4 2018 raised a total of $20 million.
Around a third (35.8%) of the firms can be assigned to the information technology sector, 25.2% are in the financial industry and 8.6% in media and entertainment. Smaller sectors include gaming/gambling (7.3%), real estate (3.3%), healthcare and medicine (3.3%), internet of things (1.9%), and science and education (1.9%). In terms of location, 67.5% of the companies are incorporated in the US, which may be explained by the comparatively high level of legal certainty compared to other jurisdictions. In second place are the Cayman Islands (8.6%), followed by Switzerland (4.6%) and Singapore (4%). The United Kingdom and Canada each account for 2%.
5.2. Correlations
Correlations and variance inflation factors for the variables are displayed in Table 2. All correlations are below the critical level of 0.7 (Mukaka, 2012). Some variables show significant correlations, which may (1) be explained by the limited number of observations of the dataset and (2) by the fact that social media presence correlates across platforms. Yet, the variance inflation factors signal that multicollinearity should not have a relevant effect for the dataset and the multivariate results, as all factors rank below 3, far off from the critical level of 10. The two team size variables do not show a high correlation to each other and can therefore be used in the same models.
5.3. Multivariate results
We perform univariate regressions and stepwise regressions with backward elimination for the available samples. The dependent variable is the log of funds raised. Constants were included but are not reported in the table (cf. Equations 1 through 4). The four different model specification were chosen in order for model 1 to evaluate the results for the independent variables, model 2 to test for additional effects of jurisdictions, model 3 to test additional effects for industry sectors and model 4 to test all existing variables.
Multivariate results are shown in Table 3. Coefficients and standard errors are shown for each model. At the bottom of each model, the R2 (adjusted) and the number of observations is shown. The stepwise regression model is executed with the logic of p ≥ 0.20, which means that for each model all variables are regressed and the factor with the highest p ≥ 0.20 is eliminated. The model is then run again and again another factor is excluded. This logic is repeated until a state of p ≥ 0.20 for all remaining factors occurs, which represents the final model. The model specification of p ≥ 0.20 is based on the recommendation of Wang et al. (2007) for stepwise regression models with backwards elimination.
Model 1 provides a R2 of 0.26 suggesting a comparatively low fit. The R2 of the models 2, 3 and 4 are all 0.40, suggesting a better fit that can likely be explained by the highly significant results for the variable target that acts as a proxy for unobserved variables, like asset size.
The variable Twitter has a highly significant positive effect on funding success in all four models. Model 1 shows the highest coefficient (0.242; p < 0.01) and model 2 the lowest (0.147; p < 0.01). The only other social media channel ending in a final model is telegram in model 2 with a negative but insignificant result. Variables regarding project elaboration end up in the final models 1, 3 and 4. The existence of a whitepaper has insignificant negative coefficients and WP score shows a positive effect (0.015; p = 0.1).
Across all four models, we identify positive effects for Team (website), whereas only three models are significant, with coefficients ranging from.376 (p < 0.05) to.425 (p < 0.05). The variable Team (LinkedIn) has a comparatively lower positive effect and is only significant at p < 0.05 in model 1 and p < 0.10 in model 2. Advisors show negative significant results in all four models. Partners does not end up in any final model.
The jurisdiction-specific control variable Singapore remains in the final models 2. The variable has hardly significant positive at p < 0.10 (1.223). We only identify a significant positive effect of the industry sector Finance in model 4 (0.435; p < 0.01). In model 3, the variable additionally has an insignificant positive effect and Gaming/gambling has a negative but insignificant coefficient. The variable ETH price does not end up in the final state of model 4 but the variable Ethereum 30d has a significant negative effect on funding success (-001; p < 0.1).
5.4. Robustness checks and further results
Our dependent variable, the log-transformed funding (in USD), is normally distributed, as validated via the Shapiro-Wilk test for non-normality (Shapiro & Wilk, 1965). Yet, the p value of the test is close (0.042) to the chosen alpha level of 0.05. In line with literature on crowdfunding and ICOs (e.g. Anglin et al., 2018; Fisch, 2019), we use a generalized linear regression model (GLM) to test the robustness of our results. In the GLM model, estimations are calculated via maximum likelihood estimation and the dependent variable can have an error distribution. The results of the GLM model are presented in model 1 of Table 4. In the line with the previous results, we identify variables like Twitter (0.214; p < 0.05), team (LinkedIn) (0.001; p < 0.10), team (website) (0.025; p < 0.10) and target (0.367; p < 0.01) as determinants of funding success.
Large residuals or outliers may distort the results. Therefore, the second alternative estimation technique is a robust regression, where distortions that are caused by outliers can be accounted for (Rousseeuw & Leroy, 1987). In the used model, one outlier is removed based on Cook's distance (Cook, 1977). The results of the robust regression are shown in model 2 of Table 4. The team (LinkedIn) variable does not have a significant effect on funding success in this model, which may be an indicator that the eliminated outlier caused this effect.
Projects from the United States represent the highest share (67.5%) of the data set. Models 3 and 4 are stepwise regressions with backwards elimination predicting STO funding success for U.S. projects only. The results indicate that the Twitter variable of special relevance for this market, as the significant coefficient are much higher compared to the overall models. The team variables show similar effects, while a gaming/gambling sector has a significant negative effect (-1.672; p > 0.05) on STOs from the United States. The existence of a whitepaper (-1.081; p > 0.10) has a negative effect in model 3, while the whitepaper score (-0.164; p > 0.05) has a positive effect.
The models 5 and 6 predict funding success for projects that started their offering period in 2017, while models 7 and 8 do the same for projects that started in 2018. We are able to identify clear differences between the years. For 2017, the variable Twitter does not show a significant effect but LinkedIn (0.268; p < 0.05) and Telegram (-0.109; p < 0.10) do so. In 2018, Twitter as a highly significant positive effect but no other social media channels do so. We identify significant negative effects for advisors and highly positive effects for partnerships in models 7 and 8, while the variables are eliminated in the regression process for models 5 and 6. For the year 2017 (model 6), Ethereum price (0.005; p < 0.01) and Ethereum 30d (-0.007; p < 0.10) show significant effects, while the variables are eliminated for the year 2018 (model 8).
6.
Discussion
The public communication of the size of the project team on project websites as a cheap signal for human capital seems to be a relevant signaling source in the context of STOs. This finding corresponds to the existing literature on startups and venture capital in terms of human capital (Hsu, 2007; Gimmon & Levie, 2010), ICOs (Ante et al., 2018) and ECF (Ahlers et al., 2015). Our alternative measure of team size relies on mentions of the companies on LinkedIn, which may not represent the number of employees a company wants to signal, or may even be biased by fraud, as described above. The results also show a comparatively lower positive effect compared to the projects' communicated team size. Therefore, we reject both hypotheses 1a and 1b.
We found a significant negative impact of the communicated number of advisors on STO success, a result which is in in contrast with the existing research on venture capital (Florin et al., 2003; Stuart et al., 1999), ICOs (Ante et al., 2018; Fisch, 2019) and ECF (Ahlers et al., 2015). Yet we do not find an influence of the number of a project's partnerships on venture success, at odds with research on IPOs (Certo, 2003) and crowdfunding (Mollick, 2014; Ahlers et al., 2015). Citing external advisors on the project's website constitutes an ineffective signal in the STO context, as it does not necessarily represent a costly signal. The results additionally indicate seasonality, as the effects apply for projects that started in 2018, while we do not find effects for the year 2017. We thus reject hypothesis 2a, while we accept 2b.
Project elaboration in terms of the existence of a whitepaper does not have a significant effect on STO. These findings are at odds with research on ICOs (Ante et al., 2018; Fisch, 2019) or crowdfunding (Gafni et al., 2018). Yet, when only testing US-based projects, we identify a negative effect of the variable. The score variable we built from the length of the document and the number of citations has a positive effect on funding success in the main results. Yet, we lack accordance when testing the robustness of the results. The variable is not sufficiently sophisticated to truly capture quality, as both size and citations can be inflated, and therefore represents a cheap signal. We reject hypothesis 3.
For social media channels, Twitter shows a significant positive effect across all four models, while the other channels do not end up in any final model. A positive effect of Twitter network size is in line with the results by Jin et al. (2017) in the context of crowdfunding. Across all four models, eliminated coefficients for the channel Facebook were negative, LinkedIn positive and, in line with Lambert et al. (2020), Telegram negative. In addition to that, we identify that effects for LinkedIn and Telegram are significant for the year 2017, which indicates that the relevance of social media channels shifts over time. We therefore reject hypotheses 4. Our findings suggest social media network size can act as a cheap sign of quality for STO projects and projects may therefore have an incentive to devote resources to social media when looking to attract funding.
The jurisdiction Singapore represents the only country variable for which we identified a hardly significant positive effect for STOs. We find evidence that the industry sector makes a difference to funding success, as projects from the financial sector show a positive effect on STO funding. This finding is robust for both observed years. For the year 2017, projects from the information technology sector additionally have a positive effect on funding. We find no evidence on an effect of the price of Ethereum on the funding success of STOs in the main models but for the relative price development 30 days prior to the STO. The Ethereum price development has a negative effect on STO funding success. When testing for year samples, both Ethereum variables only have significant effects for the year 2017, the price positive and the 30-day price development negative. This may be an indicator that they market correlation between cryptocurrency, like Ethereum, and STOs decreases, as more fiat gateways exist and markets mature.
6.1. Implications for theory
This study extends the entrepreneurial finance literature by looking at security tokens as a new instrument for capital markets and STOs as a new form of financing. The work in particular adds to the recent research on crowdfunding (Ahlers et al., 2015), IPOs (Carpenter et al., 2003), ICOs (Ante et al., 2018; Fisch, 2019) and especially morally hazardous signaling in blockchain-based token sales (Momtaz, 2020). Providing an initial understanding of the mechanisms of security tokens, the present study can serve as the basis for future research in the fields of entrepreneurial finance, capital structure and capital markets. We add to the literature on entrepreneurial finance by applying signaling theory to STOs to explore relevant (cheap) signs of quality for this new type of corporate financing. Our findings provide an indication as to specific success factors for STOs in terms of funding success. These factors especially tackle cheap signals that can theoretically be faked or inflated by projects, as has been shown for ICOs (Momtaz, 2020). As security tokens represent regulated financial instruments, cheap signals should theoretically have no or a rather low effect on funding success. Yet our models show that this is not always the case. In line with Johnstone & Grafen (1993), this suggests that projects are incentivized to dishonestly signal quality through cheap signals. The theory of crime and punishment (Becker, 1968, 1993) implies that the probability of fraudulent behavior decreases based on the probability and severity of punishment and increases with the level of personal gains for involved individuals. The misuse of cheap signals may in many cases not represent fraud but "only" cheating, which is why the expected consequences in the form of punishment are very limited. Additionally, the market for security tokens is rather young and immature and critical problem cases have not yet been identified. Therefore, investors may lack precautions when analyzing projects. Future research should examine the phenomenon from the perspective of investors, platform providers, regulation/law and society and additionally test models that involve both cheap and costly signals of quality. Additionally, the signal environment should be considered to test for differences between direct signals (e.g. project websites) and third-party signals (e.g. information portals).
Security tokens can be both debt and/or equity. Based on the cost and ease of utilization of debt or equity, firms' decisions in favor of either route may be of great interest to capital structure theory. Capital markets play a major role in the financial structure of firms (Carpenter & Peterson, 2002), which is why increased access may yield new insights for capital structure theory with regard to SMEs, such as the pecking order hypothesis. STOs may reduce the cost of issuing equity or debt for SMEs and thus result in different capital structure decisions. Theoretically, smaller firms may even gain a cost advantage in issuing equity, as some jurisdictions waive the requirement for a costly prospectus below certain thresholds.2 This possibility could be evaluated empirically in future research. While no relevant secondary markets for security tokens exist as yet, they may be expected to form in the near future, which will enable research on secondary market returns or underpricing of STOs and the actual impact of this new form of financing on the capital structure puzzle (Myers, 1984).
2 REGULATION (EU) 2017/1129 states that no prospectus is required if less than €1 million is issued over a 12-month period. Furthermore, EU member states may extend the prospectus waiver to offers of less than €8 million.
Market timing theory refers to the practice of firms issuing equity at high prices and buying it back later at lower prices. The theory assumes that managers align their company's financing strategy with current capital market conditions. It further assumes that companies have a target capital structure that adapts to capital market conditions (Merton, 1981; Baker & Wurgler, 2002). As security tokens promise to give SMEs broad access to the capital market for the first time, market timing may be a determinant for managers, as they see funding capital that wants to access this new market. Once this funding pressure diminishes, they may be able to buy back the issued tokens at lower prices. We find that a growth in the price of Ethereum has an effect on the success of STO funding. Therefore, projects may use favorable market conditions (i.e. growth in the price of Ethereum) to influence their financing success. The analysis of on-blockchain data (Ante & Fiedler, 2020; Ante 2020c) can be a starting point for future research in this respect.
In the ICO market, overall funding increased as market conditions improved, as evidenced for example by the exponential price increases experienced by Ethereum and Bitcoin in 2017 (Corbet et al., 2018). This success in raising funds via ICOs may have been due to house money effects (Thaler & Jonson, 1990), as early investors reaped profits of thousands of percent and were looking to reinvest that money. The social meaning of money theory (Zelizer, 2017) assumes that money is treated differently depending on the context of usage. Money gained from comparatively small investments in cryptocurrencies is more easily invested in projects that are based on cryptocurrency or blockchain technology. Given the close similarities between ICOs and STOs, it could be suggested that STO projects exploit overall (crypto) market conditions to gain favorable deals. However, for STOs, the development of markets for Bitcoin or Ethereum should play less of a role compared to ICOs, since the value of securities can be determined by fundamentals and the house money effect may be much smaller. Compared to ICOs, in which payment typically does not occur in fiat money, a larger audience is targeted in STOs. On the other hand, Ethereum, being the most common platform for token issuance, may be of special relevance. Having tested for an influence of (changes in) the Ethereum price, we find evidence that indicates such behavior. A growth of the Ethereum price leads to an increased size of STO funding.
6.2. Implications for practice
Our results indicate that team size as communicated via a project's website provides a perceived signal of quality to potential investors. This suggests that projects should show or mention their entire team on their website, instead of just showing the management team or no team information at all. These results enforce the adverse selection problem, as companies have an incentive to misuse the cheap signal of team size to influence investor decisions.
As the number of advisors are negatively correlated with funding success, STO projects are incentivized not to communicate existing advisors and not to look for new ones. External advisors may indicate future business relationships, expertise or other relevant signals to potential investors. Yet potential investors are most likely not able to assess the relevance of an advisor for a project, i.e. if the advisor is really supporting the project (free of charge) or if the advisor is simply paid for being used as a signal. This high level of information asymmetry bears substantial problems, as consumers are not able to effectively differentiate between real and fake signals. Our findings show that the market penalizes the communication of a high number of advisors. This suggests that investors may have learnt to effectively evaluate this signal as cheap or dishonest, as it represented a relevant signal for the ICO market (Ante et al., 2018). While our analysis is limited to the overall number of partnerships and advisors on a project's website, the IPO literature shows that specific partnerships like universities (Colombo et al., 2019), venture capital firms (Megginson & Weiss, 1991; Gulati & Higgins, 2003), underwriters (Carter & Manaster, 1990) or auditors (Beatty, 1989) provide effective signals, which may also apply to STOs.
Based on our results, projects should focus on the growth of their Twitter social media channel to signal the size of their network to the public, though this preference for Twitter might change over time. The fact that we failed to identify a relevant effect for the Telegram messenger, which has become a leading medium for crypto enthusiasts and ICOs (Amsden & Schweizer, 2018), might be explained by projects exaggerating mechanisms like so-called airdrops (giveaways) or bots to obviously inflate the size and activity of their social media channel. Projects might be well advised to use several social networks so that they are less vulnerable to changes in market sentiment and relevance of specific networks. Time series data is of great value to investigating the interaction between social media and financial offerings. The development of both the size and activity levels of social networks before, during and after offering periods may provide valuable insights on the effects of social media on funding success or price development on secondary markets but also on the use of fake and/or paid traffic. Future research should control for both social media size and (unique) activity. Ideally, fake users could be excluded (Cresci et al., 2015), or rather used as a unique variable in a dataset to fully measure the effect of fake social media signals. Crowdfunding platforms like Kickstarter can be considered social networks in their own right. Such platforms are currently also emerging for STOs.
Summarized, STO projects are able to use cheap signals and are therefore incentivized to exaggerate, fake or inflate such metrics. Yet the negative effect of the cheap advisor signal may indicate that the market will be punish projects that make use of vague, dishonest or cheap signals once understanding the irrelevance of the signal. As security tokens represent regulated financial instruments, regulators should closely monitor the development of the market to apply countermeasures for such behavior in order to protect investors. Institutions or institutional investors may be able to resolve information asymmetry, i.e. false assessment of signals for STO projects, as has been shown for ICOs (Fisch & Momtaz, 2020).
Our results indicate that team size as communicated via a project's website provides a perceived signal of quality to potential investors. This suggests that projects should show or mention their entire team on their website, instead of just showing the management team or no team information at all. These results enforce the adverse selection problem, as companies have an incentive to misuse the cheap signal of team size to influence investor decisions.
As the number of advisors are negatively correlated with funding success, STO projects are incentivized not to communicate existing advisors and not to look for new ones. External advisors may indicate future business relationships, expertise or other relevant signals to potential investors. Yet potential investors are most likely not able to assess the relevance of an advisor for a project, i.e. if the advisor is really supporting the project (free of charge) or if the advisor is simply paid for being used as a signal. This high level of information asymmetry bears substantial problems, as consumers are not able to effectively differentiate between real and fake signals. Our findings show that the market penalizes the communication of a high number of advisors. This suggests that investors may have learnt to effectively evaluate this signal as cheap or dishonest, as it represented a relevant signal for the ICO market (Ante et al., 2018). While our analysis is limited to the overall number of partnerships and advisors on a project's website, the IPO literature shows that specific partnerships like universities (Colombo et al., 2019), venture capital firms (Megginson & Weiss, 1991; Gulati & Higgins, 2003), underwriters (Carter & Manaster, 1990) or auditors (Beatty, 1989) provide effective signals, which may also apply to STOs.
Based on our results, projects should focus on the growth of their Twitter social media channel to signal the size of their network to the public, though this preference for Twitter might change over time. The fact that we failed to identify a relevant effect for the Telegram messenger, which has become a leading medium for crypto enthusiasts and ICOs (Amsden & Schweizer, 2018), might be explained by projects exaggerating mechanisms like so-called airdrops (giveaways) or bots to obviously inflate the size and activity of their social media channel. Projects might be well advised to use several social networks so that they are less vulnerable to changes in market sentiment and relevance of specific networks. Time series data is of great value to investigating the interaction between social media and financial offerings. The development of both the size and activity levels of social networks before, during and after offering periods may provide valuable insights on the effects of social media on funding success or price development on secondary markets but also on the use of fake and/or paid traffic. Future research should control for both social media size and (unique) activity. Ideally, fake users could be excluded (Cresci et al., 2015), or rather used as a unique variable in a dataset to fully measure the effect of fake social media signals. Crowdfunding platforms like Kickstarter can be considered social networks in their own right. Such platforms are currently also emerging for STOs.
Summarized, STO projects are able to use cheap signals and are therefore incentivized to exaggerate, fake or inflate such metrics. Yet the negative effect of the cheap advisor signal may indicate that the market will be punish projects that make use of vague, dishonest or cheap signals once understanding the irrelevance of the signal. As security tokens represent regulated financial instruments, regulators should closely monitor the development of the market to apply countermeasures for such behavior in order to protect investors.
6.3. Limitations
Following, we want to highlight the foremost severe limitations of this study. First, the present study suffers from limited data quality and availability. There is no suitable database on STO projects; existing projects only disclose limited information and the STO market is just emerging. Much of the data used in this study was collected manually from a range of (third-party) sources, and a number of other variables that may also affect STO funding success never made it into the analysis for lack of data. For example, costly signals like the founders' experience or financial information, like historic balance sheets or external variables, like the degree of legal protection, the existence of institutions or investor control may also be of interest. As this study focuses on tokens regulated as securities, i.e. tokens that must not necessarily act like securities, we were not able to control for underlying mechanisms such as assigned (financial) rights.
Second, we have defined security tokens as blockchain-based tokens that represent a security in the relevant jurisdiction—though they may not be considered a security in another jurisdiction. In future research, tokens could instead be classified on the basis of their underlying mechanisms, like payments, debt, participation in profits or revenue, dividends or equity, while bearing in mind that as hybrid instruments, tokens can contain multiple mechanisms. These underlying mechanisms and the relative amount of equity (or profit etc.) shared may also serve as a signal for investors.
Third, we use the term cheap signals, whose meaning is not clearly defined. While signaling theory uses terms like veracity, reliability, credibility, fit, honesty or reliability (Connelly et al., 2011), we use the term cheap to describe signals that may possess a certain degree of honesty but can also be faked (e.g. by buying fake Twitter followers or by inflating the team size on the website). For instance, social media followers will very unlikely be 100% fake but the level of dishonesty could vary from 99% to 0%. As we cannot identify this level of dishonesty for each observation, we classify the signals as cheap (to fake). There is no definition of what makes a signal cheap or not, as processes are continuums and distinctions are arbitrary. We thus chose to focus on signals that are easy to agree upon (to be cheap). Of course, other signals should be addresses by future research. Additionally, theory could be developed on what makes a signal cheap or hazardous or not.
Fourth, we could not gather information on voting rights for our dataset. This can be potentially limiting to our results, since Lambert et al. (2020) found positive relationship between voting rights and STO success and it is possible that some of our results, for example on jurisdiction, might be explained by voting rights. However, it does not seem plausible that our results on cheap signals are related to voting rights.
Lastly, the unclear results for most control variables, like industries, jurisdictions or the Ethereum price, may be due to the limited data set or the immaturity of the market. As the ecosystem grows, the availability of data on security tokens will increase. This will allow researchers to further investigate these variables and determine their impact on STO success.
7.
Conclusion
This study provides an overview of security tokens and the STO model for corporate financing. Our analysis investigates security tokens from the perspective of a firm looking to raise capital. It adds to the existing research by introducing this new ecosystem and comparing it to existing signals for IPOs, ICOs, venture capital and crowdfunding financing. We analyzed success determinants of 151 STO projects that raised funds between 2017 and 2018. The findings suggest overall similarities between the emerging market for STOs and comparable markets, as even cheap signals of human capital, external advisors and social media serve as signals of quality to investors. The type of signals influencing funding success indicate that the market is still immature, as projects have a clear incentive to enlarge the level of asymmetric information between them and potential investors by taking advantage of cheap quality signals. The anticipated level of punishment for misusing cheap signaling is low, as the mechanism does not represent fraud but "cheating". This is a concern in regards to investor protection. Projects may exploit cheap signals until the market learns to not consider these characteristics as indicators of quality.
Conflict of interest
The authors declare no conflict of interest.









 DownLoad:
DownLoad: