Discrete Temimi-Ansari method for solving a class of stochastic nonlinear differential equations

1.   Introduction

Stochastic differential equations have an important role in explaining some phenomena such as population dynamics ^[1], optimal pricing in economics ^[2], motions of ions in crystals ^[3], and thermal noise ^[4]. Finding the exact solution of such stochastic differential equations is difficult in many cases. Thus, numerical and semi-analytic methods have been developed. Like, Euler-Maruyama method ^[5,6], Finite difference schemes ^[7,8], theta methods ^[9], nite element approaches ^[10,11,12], Homotopy analysis method ^[13], wavelets collocation method ^[14], Picard method ^[15], hat function operational matrix method ^[16], operational matrix of based on Chebyshev polynomials ^[17,18], B-spline collocation method ^[19,20] and mean-square dissipative method ^[21]. Additionally, many theoretical studies about the existence and uniqueness have been conducted by researchers in the literature ^[22,23,24].

The main contribution of the current paper is to implement a numerical technique based on Temimi and Ansari (TAM) ^[25] to solve the following model of stochastic nonlinear differential equations:

where ${\text{ }}u{\text{(t)}}$ is the unknown function, $t$ represents the independent variable, $F{\text{(}}t{\text{, }}u{\text{)}}$ and $G{\text{(}}t{\text{, }}u{\text{)}}$ are linear or nonlinear functions and ${\text{ }}n{\text{(t) }}$ is Gaussian white noise. The relation between the Wiener process $w(t)$ and the Gaussian white noise ${\text{ }}n{\text{(t) }}$ is defined by

the expectation $E[n(t)] = 0$, and finite variance $Var[n(t)] = {\varsigma ^2}$.

The Temimi and Ansari method (TAM) has been successfully applied to solve many classes of differential equations, such as nonlinear second-order multipoint boundary value problems ^[25], ordinary differential equations ^[26], Fokker-Planck's equations ^[27], and korteweg-de Varies equations ^[28]. In this paper, we modified the Temimi-Ansari method called the discrete Temimi-Ansari method DTAM to handle the stochastic nonlinear differential Eq (1). The proposed method provides a prodigious performance by merging the traditional TAM with the finite difference numerical scheme. To test the proposed method, we solve four stochastic models. These models are stochastic Langevin's equation, Ginzburg-Landau equation, Davis-Skodje, and Brusselator systems. These problems illustrate the accuracy of the proposed method as compared with the stochastic Runge Kutta method (SRK), and semi-analytic methods.

This work is structured as follows: Section 2, introduces the discrete Temimi-Ansari method (DTAM). In the third section, the stochastic models were solved using the proposed method. Finally, conclusions are presented in Section 4.

2.   Discrete Temimi-Ansari method and convergence analysis

Consider the following differential equation in the form is

with initial conditions:

where $L$ and $N$ represent the linear and nonlinear operators, respectively, and $g\left(t\right)$ represents the inhomogeneous term. The Temimi-Ansari method was used to solve differential Eq (3) as follows:

First consider the initial approximate function ${u}_{0}$ (t), which is the solution of the following initial value problem

To nd the next approximate function ${u}_{1}$ (t), the following problem must be solved

The n^th approximate functions ${u_n}(t)$ can be evaluated in the same way. Then

In this method, it is very serious to note that each of $u{}_n(t)$ is separately a solution to model (3a). We document that this scheme is easy to implement and has the distinction that each solution is a refinement of the previous iteration. Sequential solutions must be verified versus the previous iteration to confirm the convergence of solutions. The analytical solution converges to the exact solution as the number of iterations increases. Depending on this, an analytical solution can be obtained with good agreement with the exact solution as

An error analysis of a single nonlinear ordinary differential equation, generalization of these theorems applied to systems of differential equations, and a complete study of convergence criteria for the TAM iterative scheme are presented in ^[26,29,30].

To supply the convergence analysis for the proposed method in this paper, we begin by submitting the following steps for the proposed approximate analytical scheme:

The operator $\Phi [u(t)]$ is defined as

where the term ${u_n}(t)$ is the analytical solution of the TAM.

According to these criteria, appropriate conditions for the convergence of this technique are studied with the following theorems.

Theorem 1. The series solution $u(t) = \sum\limits_{i = 0}^\infty {u{}_i(t)}$ will represent the exact solution to the given nonlinear problem if this series solution is convergent.

Proof. Fruition ^[29,30].

Theorem 2. Suppose that $\Phi$ defined in Eq (9), is an operator from ${\rm H}$ to ${\rm H}$, where ${\rm H}$ is a Hilbert space. The series solution $u(t) = \sum\limits_{i = 0}^n {u{}_i(t)}$ converges if $\exists {\text{ 0 < }}\gamma < {\text{ }}1{\text{ }}$ such that $\left\| {\Phi [{\eta _0} + {\eta _1} +.....} \right.\left. { + {\eta _n}]} \right\| \leqslant \gamma \left\| {\Phi [{\eta _0} + {\eta _1} +.....} \right.\left. { + {\eta _{n -1}}]} \right\|, {\text{ }}\forall \gamma \in \mathbb{N} \cup \left\{ 0 \right\}.$

This theory is a special case of fixed-point theory and it is sufficient to prove the convergence of TAM.

Proof. Fruition ^[29,30].

Theorem 3. If the series solution $\sum\limits_{i = 0}^\infty {{u_i}(t)}$ is convergent to ${\text{ }}u(t)$, then the maximum error ${E_n}(t)$ is given by

where the tailless series $\sum\limits_{i = 0}^{n - 1} {{u_i}(t)}$ is used as a way to solve the presented nonlinear problem.

Proof. Fruition ^[29,30].

The solution obtained by TAM converges to the exact solution provided that: $\exists {\text{ }}0{\text{ < }}\gamma {\text{ < }}1{\text{ }}$ such that

when $0{\text{ }} \leqslant {B_{n - 1}}{\text{ < }}1{\text{ }}, {\text{ }}\forall n = 1, 2, 3, ..$ the power series solution $\sum\limits_{n = 0}^\infty {{u_n}(t)}$ converges to the exact solution ${u_{}}(t).$

The TAM approach can be used to solve the differential Eq (1) with a random function excitation. However, only a few iterations can be calculated due to the difficulty of integrating random functions. We adopted discrete Temimi-Ansari (DTAM) to solve stochastic nonlinear differential Eq (1) as follows:

Suppose: $0{\text{ < }}{t_{\text{1}}}{\text{ < }}{t_{\text{2}}}....{\text{ < }}{t_{\text{n}}} = T{\text{ }}$ is a uniform mesh of $[0, T]$ with ${t_{\text{i}}} - {t_{{\text{i - 1}}}} = P, {\text{ }}1 \leqslant i \leqslant n.$ Let $h \in (0, P]$ be a given constant. For a given $h$, the nite difference formulas to approximate $\frac{{d{u_0}({t_{i + 1}})}}{{dt}}$ and $\frac{{dw({t_{i + 1}})}}{{dt}}$ are given by

where ${u_0}({t_{i + 1}}) = u_0^{i + 1}, {u_0}({t_j}) = u_0^i, w({t_{i + 1}}) = {w_{i + 1}}{\text{ }}and{\text{ }}w({t_i}) = {w_i}$. Therefore, the first iterative equation to discretize the initial approximate function ${u_0}({t_{i + 1}})$ is

and by using

The next discrete approximate function ${u_1}({t_{i + 1}})$ and the n^th discrete approximate functions ${u_n}({t_{i + 1}})$ can be computed as follows

The Wiener process $w(t)$ is a random function, so the solution must be based on $k$ runs with different samples of the Wiener process $w(t)$. Then the iterative Eqs (13) and (15) can be written in the following form:

The time step $h$ should be used to warrant convergence of systems (16a)–(16c). Applying the convergence standard of the fixed-point iteration by differentiating the right-hand side of Eq (16b) concerning $u_{0, k}^{}$ we obtain

Let ${f_1} = \frac{{\partial G({t_i}, u_{0, k}^i)}}{{\partial u_{0, k}^i}}, {f_2} = \frac{{\partial F({t_i}, u_{0, k}^i)}}{{\partial u_{0, k}^i}}$ then we have:

The condition $h{\text{ < - }}\varsigma {\text{ }}\frac{{{f_1}}}{{{f_2}}}({w_{i + 1, k}} - {w_{i, k}})$ is a sufficient condition for the time step used in FDM for convergence. Due to similarity in the other two Eqs (16a) and (16c), the same condition can be also used in the numerical FDM approximations.

Finally, by taking the mean and the variance of the solution sequences { ${u}_{n, 1}, {u}_{n, 2}, {u}_{n, 3}, \dots., {u}_{n, k}$ } we obtain the mean and the variance of the solution. This elegant combination of the traditional TAM and finite difference numerical scheme produces a fast and effective tool in handling stochastic nonlinear differential equations and this is one of its uncountable merits. Thus, we simply calculate many iterations without time consumption in comparison with traditional methods such as HAM, WHEP, and even TAM which are unable to perform many iterations due to the complexity of calculations of the mean and the variance.

3.   Numerical simulation and discussion

3.1.   Numerical simulation

In this section, four examples are given to illustrate the applicability of the proposed method, and all of them are performed on a computer by using the Mathematica program.

Example 1. Consider the stochastic Langevin's equation ^[31] of the form:

The constructed iterative scheme (16) for stochastic Langevin's Eq (20) at $\varsigma = 1$ is

By choosing ${\text{ }}h = 0.01$, Figure 1 displays the expectation of sequences { ${u}_{\mathrm{5, 1}}, {u}_{\mathrm{5, 2}}, {u}_{\mathrm{5, 3}}, \dots., {u}_{\mathrm{5, 1000}}$ } and the solution by the stochastic Runge Kutta method (SRK), which was built in Mathematica software. The variance by the proposed scheme and stochastic Runge Kutta method (SRK) after 5 and 6iterations are shown in Figures 2 and 3, respectively. These gures confirmed that the resulting numerical scheme solutions (21) are compatible with the stochastic Runge Kutta method (SRK) in a good manner. Additionally, the proposed solutions illustrated the accuracy compared with WHEP, Pickard, HPM, and HAM ^[31].

Example 2. Consider the following scalar stochastic Ginzburg-Landau equation ^[23]:

where $\eta \geqslant 0, \sigma, \lambda > 0$. Eq (22) from the theory of superconductivity is derived by Ginzburg and Landau to describe a phase transition in a deterministic sense ^[32,33]. By choosing $\eta = 1.5$, $\sigma = \lambda = 1$ and $h = 0.01$, the proposed iterative Eq (16) for the Ginzburg-Landau Eq (22) are

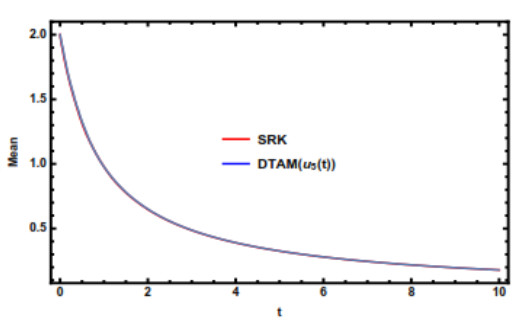
By choosing $u\left(0 \right) = 2$ and $k = 5000$ runs with different samples of the Wiener process $w\left(\text{t}\right)$, the expectation and the variance of the proposed method and stochastic Runge Kutta method are shown in Figures 4 and 5, respectively. These gures confirmed that the presented solutions are compatible with the stochastic Runge Kutta method in a good manner.

Example 3. Consider Davis-Skodje system is ^[33]

The chemical reaction system (24) introduced in ^[34] and if $\gamma > 1{\text{ }}$ gives a measure for the spectral gap or stiffness of the system. This system is simulated when $\mu = \sigma = 0.01$ and $\gamma = 1000$, and the proposed iterative scheme is given by

The stable equilibrium point for the nonlinear system (24) is (0, 0) proven in ^[34]. Figure 6 simulates the nonlinear system (24) for $0 \leqslant t \leqslant 10$ using $k = 100$ samples with initial position $\left({u\left(0 \right), v\left(0 \right)} \right) = \left({6, 0.85} \right)$ by using the proposed scheme (25). We can see that the current method converges toward the asymptotic solution (0, 0).

Example 4. Consider a stochastic version of the Brusselator system ^[35]:

This nonlinear system is unforced periodic oscillations in certain chemical reactions. We simulate this system when $\alpha = 1.9$ and $\gamma = 0.1$, and the proposed iterative scheme of it is given by

where $n = 2, 3, 4, ....$ On the interval $t \in [0,125]$ with $h = 0.025$ and starting with $\left({u\left(0 \right), v\left(0 \right)} \right) = \left({ - 0.1, 0} \right)$ as in [36]. Figure 7 shows that the approximate trajectories of the proposed scheme (27) remain close to the origin replicating the behavior of the correct solution.

3.2.   Discussion

The TAM approach can solve the differential Eq (1) with a random function excitation. However, only a few iterations can be calculated because of the stiffness of integrating random functions. We suggested discrete Temimi-Ansari (DTAM) to solve the stochastic nonlinear differential equation. We establish an unusual stochastic method to approximate a wide class of stochastic differential equations by combining the classical TAM with the finite difference numerical scheme.

The ability of the proposed scheme has been illustrated by several nonlinear stochastic differential equations. In particular, Figures 1–5 show that the proposed method is able to solve the nonlinear stochastic Langevin's equation (20) and Ginzburg-Landau (22). Also, calculating the amount of the convergence parameter ${B}_{n}$ for Eqs (20) and (22) as in (11) is shown in Tables 1 and 2. These tables refer to the values of ${B}_{n}$ less than one and verify that the proposed solutions are convergent. In Figures 6 and 7, we examine the behavior of the stochastic Davis-Skodje system (24) and the Brusselator system (26). It can be seen that the proposed method solutions tend to the solution (0, 0). The results reveal that the proposed method is reliable and can be applied to stiff stochastic problems in applied sciences. This wonderful scheme produces a fast and functional approach in treating the stochastic nonlinear differential equations and this is one of its uncountable advantages. The classical semi-analytic method needs a huge time and effort to reach an acceptable solution because of the complexity of mean and variance solutions. Our proposed method beats this shortage simply. We can expand the above analysis to many random parameters besides the noise enjoined in the previous examples.

4.   Conclusions

In some cases, the traditional TAM is not suitable to solve the stochastic nonlinear differential Eq (1), and we devolved this method to handle this class. The DTAM had been successfully applied to find the solutions of the stochastic nonlinear differential equations. The efficiency and accuracy of the proposed method were demonstrated by solving stochastic Langevin's equation, Ginzburg-Landau equation, Davis-Skodje, and Brusselator systems. Through the figures, it can be seen clearly that the discrete TAM solutions converge when the number of iterations is increased. The motivation of our work is achieved by comparing the stochastic Runge Kutta method with DTAM. Future directions might include solving various complicated stochastic linear and nonlinear differential equations, partial stochastic differential equations, fractional differential equations, fractional stochastic differential equations, delayed fractional stochastic differential equations, and fuzzy differential equations.

Conflict of interest

The authors declare that there is no conflict of interests regarding the publication of this paper.