On a problem of dynamical input reconstruction for a system of special type under conditions of uncertainty

1.   Introduction

Input reconstruction problems for controlled systems based on inaccurate/incomplete information on phase states arise in many scientific studies and applications (in flight mechanics and guidance theory, in financial and actuarial mathematics, for designing engineering and technological processes, in ecology and medicine, etc.) and attract a great attention in recent time. The first publications concerning this field go back to the 60's of the previous century ^[1,2,3], when some criteria of the unique solvability of inverse problems and of the continuous "input/output" dependence for systems described by ordinary differential equations were obtained under the conditions of sufficiently smooth inputs. The key definition of an invertible dynamical system was introduced in ^[2].

Input reconstruction problems can be treated as the special case of identification problems. They fall into the range of inverse problems of dynamics of controlled systems and, as a rule, are ill-posed (due to the nonuniqueness of the desired characteristic, as a consequence of inaccuracies, and/or due to the discontinuity of the inverse operator) and require the application of regularizing procedures.

The huge amount of works is devoted to different statements of identification problems, where solving approaches are based on a posteriori character of desired regularizing algorithms using the whole history of output measurements. We list only some of monographs containing detailed reviews and bibliography. In the classical monograph ^[4], the emphasis is on different classes of recurrent methods for the identification of nonstationary objects, including the theoretical analysis and experimental verification. The work ^[5] contains the introduction to identification theory. Algorithms for estimating time-varying inputs acted upon linear systems are considered in ^[6]. The monographs ^[7,8,9] are devoted to the foundations of the theory of inverse and ill-posed problems.

One specific solution approach named the method of dynamic inversion was proposed and developed by Kryazhimskii, Osipov, and their colleagues, see ^{[10,11,12,13]}. It is extremely important in cases when there is the necessity to reconstruct some characteristics dynamically and preferably in real time, for example, to make an urgent control decision. The approach is based on the combination of principles of the theory of positional control ^[14,15] and ideas of the theory of ill-posed problems ^[7,8,9]. A reconstruction problem is reduced to a feedback control problem for an auxiliary dynamical system called a model. The goal is to find an appropriate control law for this model in such a way that the adaptation of the model controls to the results of current observations provides an approximation (in a desired sense) to the unknown inputs. In addition, solving algorithms should be both dynamic and stable. As the dynamic property, we understand the property that the algorithm uses current input and output values in real time to provide some operative reaction during the process. In its turn, the stability property means that the algorithm produces an approximation that is as precise as one likes if the observations are sufficiently accurate.

First, the method of dynamic inversion was realized for systems described by ordinary differential equations (ODEs) ^[10,11,12], then, for functional differential equations ^[16,17], equations and variational inequalities with distributed parameters ^[13,18,19]. The problem of tracking a solution under the action of an unknown input on an arbitrarily long time interval was considered in ^[20].

As to the application of the theory of dynamic inversion to stochastic objects, the problem of positional simulation of a stochastic control was formulated for the first time in ^[21], where the authors considered a deterministic system of ODEs under the action of an unknown random control, for which one of possible realizations should be reconstructed with the use of measurements of the whole phase state (actually, of the whole random process). The present paper deals with a quite different statement; it continues the investigations (in the framework of the theory of dynamic inversion) of the problems of reconstructing unknown deterministic characteristics of a linear and a quasi-linear (with diffusion depending on the phase state) stochastic differential equation (SDE). In ^[22], the problem of dynamical reconstruction of a disturbance entering the Ito integral and characterizing the amplitude of a random noise was considered in the case of measuring realizations of the whole phase vector. In ^[23], a similar statement supplemented by the simultaneous reconstruction of disturbances both in the deterministic and stochastic terms was discussed for a quasi-linear equation. As is shown in ^[22,23], the problem for a SDE can be reduced to an inverse problem for the system of ODEs describing the mathematical expectation and covariance matrix of the process. The main advantage of this approach is in the applicability of algorithms for reconstructing unknown parameters developed earlier for systems of ODEs ^[10,11,12]. This applicability was substantiated, appropriate finite-step software-oriented modifications were proposed, and estimates for their convergence rate with respect to the number of measurable realizations were obtained.

It should be noted that all the classical dynamical reconstruction algorithms elaborated within the framework of the theory of dynamic inversion and applied in the works cited above were developed in accordance with the similar schemes (a two step procedure: the choice of an appropriate model and an appropriate control law). In this paper, we study a specific reconstruction problem under conditions of incomplete information; therefore, we describe (in more detail) additional aspects concerning such problems, for which stable algorithms operating for some classes of partially observed systems were designed. In the case of a finite-dimensional system, the role of input signals can be played by measurements of a part of coordinates of the phase vector, whereas, in the case of an infinite-dimensional system, this role is played by values of a solution on some subsets of the domain of definition.

The study of inverse dynamical problems under conditions of incomplete information was started from the case when an unknown control entered the measured component of an ODE ^[24]. The elaborated algorithm was based on the possibility of formal resolution of the equation describing the observed part of the phase state with respect to disturbance. This algorithm used the construction of an appropriate model reproducing both the unmeasured component (call this part Block 1) and the unknown disturbance (Block 2). The technique got the further development; similar reconstruction problems for partially observed ODE systems were considered in different statements (see review ^[12]). In ^[25], the problem of guaranteed control of a partially observed ODE system was firstly solved for the case when a disturbance entered the unmeasured component.

By analogy with the statements above, the problem of dynamical input reconstruction in a linear/quasi-linear SDE was extended by the possibility of measuring a part of coordinates of the stochastic process, see ^[26]. The novelty of the present paper consists in considering, for the first time, the specific statement of the inverse problem for a dynamical system of hybrid type, where a disturbance (acted upon an ODE) to be restored is subject to geometrical restrictions and does not enter the measured component being a SDE. The solution algorithm is essentially based on the results from ^[27,28], where a similar inverse problem was investigated for a system of ODEs.

It is important that the practical application of inversion/control algorithms of such kind is technically rather difficult due to the necessity of adjusting the algorithm to a specific dynamical system. The matter is that up to now there is no a universal procedure for fitting parameters of algorithms of dynamical reconstruction even in the case of a fully observed ODE, see the discussions on numerical examples in ^[11,12,17]. In ^[29], we made a first attempt to fill this gap by developing an empirical procedure for the automatic tuning of algorithm's parameters in order to get best approximation results. This idea is applied for the problem under consideration, too.

The paper is organized as follows. In Section 2, we give the statement of the dynamical input reconstruction problem for a hybrid type system. Section 3 is devoted to the description of the solution idea via the flowchart of the algorithm for the dynamical reconstruction under incomplete information. The procedure of reducing the problem for the original system to the problem for a system of ODEs is outlined. A constructive algorithm for solving the latter problem, a feedback controlled model, and an estimate of the convergence rate of the algorithm are presented in Section 4. In Section 5, a model example illustrating the method proposed and the calibration of its parameters are discussed. In Conclusions, we resume the results obtained and mention some directions for perspective investigations.

2.   Dynamical input reconstruction problem

Simple stochastic linearized models can be useful, for example, when studying the change of the size of a biological population in a stochastic medium or the processes of chaotic motion of one-type particles. At that, additional ordinary equations can simultaneously describe some deterministic noises influencing different characteristics of the phenomena under investigation. In this context, we consider a linear system consisting of SDE and ODE:

Here, $t\in T = [0, \vartheta]$; $(x(\cdot, \omega), \, y(\cdot))$ is the phase trajectory, $x(t, \omega) \in \mathbb{R}^{n_1}$, $y(t) \in \mathbb{R}^{n_2}$; $(x_0, \, y_0)$ is a known deterministic initial state; $\xi(t, \omega) \in \mathbb{R}$ is a standard scalar Wiener process (i.e., a process starting from zero with zero mathematical expectation and dispersion equal to $t$; $\omega \in \Omega$, $\Omega$ is the set of possible outcomes; $m(t) = Mx(t, \omega)$ is the mathematical expectation; $u(\cdot)$ is an external disturbance with values from a given compact set $S_u \in \mathbb{R}^{m}$ and with bounded variation on $T$; $A$, $B$, $C$, $D$, $E$, and $F$ are constant matrices of corresponding dimensions; vector functions $f_0(\cdot)$ and $f_1(\cdot)$ are square integrable on $T$.

A solution of Eq (2.1) is defined as a stochastic process satisfying (for any $t$ with probability 1) the corresponding integral identity containing the stochastic Ito integral on the right-hand part:

As is known, under the above assumptions, there exists a unique solution $x(t, \omega), \, t\in T$, which is a normal Markov process with continuous realizations, see ^[30], Theorem 5.2.1. A solution of Eq (2.2) is understood in the sense of Carathéodory; $y(\cdot)$ is assumed to be absolutely continuous.

The problem under discussion consists in the following. An unknown disturbance $u(t)$ acting upon the system is a part of the second equation only, whereas, at discrete, frequent enough, times $\tau _{i} \in T$, $\tau _{i} = i\delta$, $\delta = \vartheta /l$, $i \in [0:l]$, the information on some number $N$ of realizations of the first phase component, stochastic process $x(\tau _i)$, is received.

It is required to design an algorithm for the dynamical reconstruction of the unknown disturbance $u(t)$ from the available information. The probability of an arbitrarily small deviation of the approximation from the desired input in $L_{2}(T; \mathbb{R}^{m})$-metric should be close to 1 for sufficiently large $N$ and the time discretization step $\delta = \delta(N) = \vartheta /l(N)$ concordant with $N$ in an appropriate way. Such a statement can be useful in the situation when we want to reconstruct some unknown characteristics of outer noises influencing the collective behavior of one-type species or particles on the basis of measurements of a number of their trajectories.

3.   Solution idea–transformation of the problem

The solution algorithm is constructed within the framework of the theory of dynamic inversion ^[10,11,12]. In connection with the informational incompleteness, according to the methods elaborated for solving such inverse problems ^[12], first, we should construct a block of dynamical reconstructing the unknown coordinate $y(t)$ (Block 1), which is treated as a provider of the information on the whole current phase state of the system. This information is operatively fed onto a block forming, by the feedback principle, a model control approximating the real disturbance (Block 2). The work of Block 1 and Block 2 should be synchronized in time.

The novelty of the present paper consists namely in considering the specific statement of the inverse problem for a dynamical system of hybrid type, where a disturbance to be restored is subject to geometrical restrictions and does not enter the measured component being a SDE.

Let us discuss the subproblem from Block 1 (the reconstruction of $y(t)$). The specific properties of SDE (2.1) admit the reduction (by analogy with the method of moments, see ^[31]) of the problem formulated for system (2.1), (2.2) to a problem for the system consisting of an additional ODE describing the mathematical expectation of the desired process and original ODE (2.2). It is easily seen that the equation describing the mathematical expectation of the process has the form

It actually replaces Eq (2.1), thus composing system of ODEs (3.1), (2.2). Now we can organize an auxiliary procedure for the reconstruction of the unknown function in the right-hand part of (2.1). Following ^[22,23,26], we reduce the reconstruction problem for system (2.1)–(2.2) to an analogous problem for new system (3.1), (2.2). Thus, the subproblem for the SDE with measuring its trajectories is transformed into the subproblem for the ODE with measuring its phase state. Nowadays, the latter problem has become classical ^[10,11,12].

To obtain measurements appropriate for Eq (3.1), we need

Lemma ^[23]. The standard estimates $m_{i}^{N}$ of the mathematical expectations $m(\tau _i)$ constructed from $N$ realizations of the random variables $x(\tau_{i})$ by the standard rule ^[32]:

provide the validness of the relation

where $l(N)\rightarrow \infty$, $h(N), \, g(N) \rightarrow 0$ as $N\rightarrow \infty$.

Now, using the inaccurate measurements $m_{i}^{N}$ of the phase state of Eq (3.1), finally, we have to reconstruct the unknown disturbance $u(t)$ acting on Eq (2.2).

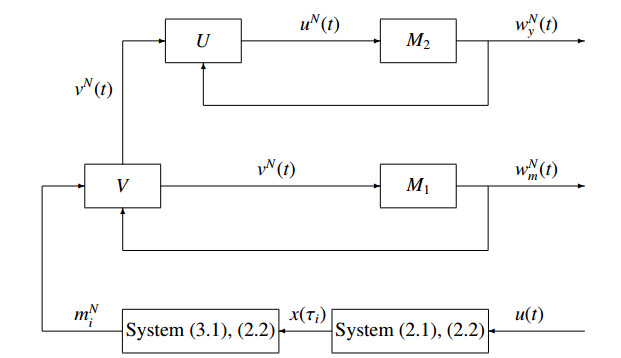
The outline of the solving algorithm is shown in Figure 1. According to this scheme, system (2.1), (2.2) is transformed to system (3.1), (2.2); the latter is accompanied by an auxiliary artificial feedback control system (a model $M$, to be constructed), which consists of two systems, $M_1$ and $M_2$. This model, functioning on the time interval $T$ synchro with the original system, has unknown inputs (treated as controls) $v^N(t)$ and $u^N(t)$ and outputs $w_m^N(t)$ and $w_y^N(t)$. Such a notation emphasizes the dependence of all the input/output parameters of the algorithm on the number $N$ of available trajectories of Eq (2.1). Because of the fact that only the part $x(\tau_i)$ (or $m(\tau_i)$) of the phase state of the original system is measured, the algorithm for solving the problem should include two blocks: Block 1 providing the information on the current phase state $y(t)$ of Eq (2.2) and Block 2 forming (on the basis of the data received from Block 1) an approximation to $u(t)$. According to Figure 1, Block 1 includes the system $M_1$ and control law $V$, whereas Block 2 consists of the system $M_2$ and control law $U$.

After choosing the model feedback control laws, the process of synchronous operation of the original system and systems $M_1$ and $M_2$ is organized on the interval $T$. This process is decomposed into $l(N)-1$ identical steps. At the $i$-th step carried out on the time interval $[\tau_i, \tau_{i+1})$, the following actions are performed. First, at the time $\tau_i$, according to the chosen rules $V$ and $U$, the controls $v^N(t)$ and $u^N(t)$, $t\in [\tau_i, \tau_{i+1})$, are calculated. Then, they are fed onto the systems $M_1$ and $M_2$, respectively. The values of $w_m^N(\tau_{i+1})$ and $w_y^N(\tau_{i+1})$ influencing the feedback controls result from the algorithm at the $i$-th step. Thus, all the complexity of solving the problem is reduced to the appropriate choice of the model $M$ and the rules $V$ and $U$ in order to approximate the unknown input function $u(t)$ by $u^N(t)$.

4.   Realization of solution algorithm

Let us make Block 1, Block 2, and the model controls more precise.

Denote the fundamental matrices of the systems $\dot m(t) = A m(t)$ and $\dot y(t) = D y(t)$ by the symbols $M(t) = \exp(At)$ and $Y(t) = \exp(Dt)$, respectively. Note that, in virtue of the properties of matrix exponential, one can specify constants $\omega$ and $\hat \omega$ such that

We need the special condition restricting the right-hand part of the systems.

Condition. Assume that $m \le n_2 \le n_1$ and there exist numbers $d_1 > 0$ and $d_2 > 0$ such that $\|B y\|_{n_1} \ge d_1\|y\|_{n_2}$ and $\|F u\|_{n_2} \ge d_2\|u\|_{m}$ for all $y\in \mathbb{R}^{n_2}$ and $u\in \mathbb{R}^{m}$, respectively.

This condition is valid, for example, in the case of quadratic nondegenerate matrices $B$ and $F$.

At the initial time $\tau _{0} = 0$, we fix a number $N$; then, in accordance with Lemma, determine the values $l(N)$, $h(N)$, and $g(N)$ and construct the uniform partition of the interval $T$ with the step $\delta(N) = \vartheta /l(N)$: $\tau_{i} = i\delta(N)$, $i\in [0:l(N)]$. Note that $\delta(N), \, h(N), \, g(N) \rightarrow 0$ as $N\rightarrow \infty$.

Let us present the model consisting of two blocks in the discrete form:

Here, $w^N_m(\tau_i) \in \mathbb{R}^{n_1}$, $w^N_y(\tau_i) \in \mathbb{R}^{n_2}$ are model variables; $v^N(\tau_i) \in \mathbb{R}^{n_2}$, $u^N(\tau_i) \in \mathbb{R}^{m}$ are model controls. In addition, we choose functions $\alpha(N), \, \hat\alpha(N) : \mathbb{N} \to \mathbb{R}^{+}$ (treated as regularizers) such that $\alpha(N) \to 0$, $\hat\alpha(N) \to 0$ as $N \to \infty$. The control process for the model introduced is organized as follows. The work of the algorithm is decomposed into $l(N)$ identical steps. At the $i$th step performed on the interval $[\tau_{i}, \, \tau_{i+1})$, $i \in [0:(l(N)-1)]$, the input data for calculations are the estimate $m^N_i$ and the model state $w^N_m(\tau_{i})$, $w^N_y(\tau_{i})$ formed till this moment. The following operations are fulfilled. First, Block 1, using the values of $m^N_i$ and $w^N_m(\tau_{i})$, computes the vector

where

Here, $y(t; t_0, x_0, y_0, u(\cdot))$ is the bundle of solutions of Eq (2.2) starting from the fixed initial point for any admissible control $u(\cdot)$. Evidently, the number $d$ exists. Then, Block 2, on the basis of the approximation $v_i^N$ and the value $w^N_y(\tau_{i})$, finds the vector

where

After that, according to formulas (4.1), the model state is recalculated to the values $w^N_m(\tau_{i+1})$ and $w^N_y(\tau_{i+1})$. At the next, $(i+1)$th step, the similar actions are fulfilled. Thus, two piece-wise constant controls

are formed as a result of the procedure above. The process stops at the terminal time $t = \vartheta$. Let us formulate the main result of the paper.

Theorem. Under some feasible conditions of concordance of algorithm's parameters and the number of measured trajectories $N$, the estimate is valid:

where $H(N), \, G(N) \rightarrow 0$ as $N\rightarrow \infty$ and can be written explicitly.

Proof. As is shown in ^[23], the values from (3.2) are the following: $l(N) = C_1N^{\epsilon_1}$, $\delta(N) = C_2/N^{\epsilon_1}$, $h(N) = C_3/N^{1/2-\epsilon_2}$, and $g(N) = C_4/N^{1-\epsilon_1}$, $0 < \epsilon_1 < 1$, $0 < \epsilon_2 < 1/2$; here and below, $C_i$ are some positive constants, which can be written explicitly. Introduce the functions

The main result of ^[28] obtained for the above algorithm applied to the system of ODEs (3.1), (2.2) gives us the estimate

Using estimate (3.2), which is uniform with respect to all $l(N)$ measurements, and its probability, we conclude that procedure (4.1)–(4.6) provides the validness of estimate (4.7), at that $G(N) = g(N)$. It remains to verify that $H(N) \to 0$ under some appropriate concordance conditions. First, we have to get $\rho(N) \to 0$. Toward this aim, we assume that $h(N)$ and $\delta(N)$ have the same order of smallness with respect to the value $1/N$, i.e. $\epsilon_1 = 1/2-\epsilon_2$, and set $\alpha(N) = (h(N))^{k_1}, 0 < k_1 < 1$. In this case, we should write $k_1/2 = 1-k_1$, $k_1 = 2/3$. Then, $\rho(N)$ has the same order as $(h(N))^{1/3}$. Pass to the relation $H(N) \to 0$. Analogously, considering $\hat\alpha(N)) = (h(N))^{k_2}, 0 < k_2 < 1/6$, we obtain $k_2/2 = 1/6-k_2$, $k_2 = 1/9$. Then, $H(N)$ has the same order as $(h(N))^{1/18}$. Thus, the step $\delta(N)$ has the order as $1/N^{1/2-\epsilon_2}$, the probability characteristic $G(N)$, as $1/N^{1/2+\epsilon_2}$ (both asymptotically close to $1/2$), whereas the approximation accuracy $H(N)$ is equivalent to $1/N^{(1/2-\epsilon_2)/18}$. The latter order is important for proving convergence (4.7) but its optimality is not investigated. In addition, the obtained estimate allows us to make a conclusion on the uniqueness of the desired disturbance (actually, this fact is substantiated by Condition).

5.   Illustrative example

The work of the elaborated algorithm and the convergence rate in (4.7) are tested by a model, rather artificial, example. For all examples, we plan to find optimal values of algorithm's parameters with the help of the tuning procedure suggested in ^[29]. In the experiment described below, we vary the key parameters, taking

where $K_1$ and $K_2$ are some positive constants to be determined for the best approximation. These constants depend on the parameters of the given system, on a priori constraints on the unknown functions, but should be independent of the realizations of these functions. Then, we assume that desired relations between parameters can be determined empirically through a solution of the following simple extremal problem, see ^[29]:

Here, the notation $u^{N}_{K_{1}, K_{2}}(\cdot)$ emphasizes the dependence of algorithm's output on the constants $K_1$ and $K_2$; $I^{N}$ is the set of chosen values of $N$, $\beta^{N}$ are weighting coefficients, $\sum_{N \in I^{N}} \beta^{N} = 1$; $S_{K}$ is some set of admissible values of the vector $(K_{1}, \, K_{2})$, as a rule, it is a rectangle in the positive quadrant. We fix all the constraints imposed on the admissible inputs, introduce a uniform grid with respect to $K_{1}$, $K_{2}$ and then solve problem (5.2) by exhaustive search for some admissible model disturbance $u^{*}(\cdot)$, which is typical for the original system.

To simulate the dynamics of Eq (2.1) in order to get measurements $m^N_i$, we apply the Euler method with the substitution of a sequence of random impulses for the Wiener process (the detailed description of the approximation scheme can be found, for example, in ^[33]). The mean square accuracy order of this method for a quasi-linear SDE is equal to $O(\delta_s)$, where $\delta_s$ is a simulation step. This step is, as a rule, rather small comparing with the step $\delta^{N}$ of receiving the information on the realizations and, correspondingly, of reconstructing the unknown function $u(t)$. Thus, two time grids are involved into the scheme of the tuning of algorithm's parameters for a specific system. The simulations with the smaller step take place only at the stage of tuning; when solving a real problem, the input information should come from "outer space". Note that the probabilistic character of convergence estimate (4.7) assumes the algorithm's output averaging over a series of runs for a fixed set of parameters.

Let us pass to the description of the model example. Consider a quasi-linear SDE describing a stochastic process, which can be treated as a "spoiled" mean-reverting Ornstein–Uhlenbeck process ^[30] and a simple linear ODE:

Here, $u_1(t)$ and $u_2(t)$ are unknown bounded disturbances to be reconstructed, $u_1, u_2 \in [-1, 3]$; $\xi(t)$ is a standard scalar Wiener process. Realizations of $x(t)$ are measured at discrete times. The condition from Section 4 imposed on the right-hand part of the system (namely, on the matrices $B$ and $F$) is valid.

Equations like (5.3) are used, in particular, in some simplest models describing the dynamics of relatively stable biological populations. In this case, the value $x(t) = (x_1(t), \, x_2(t))$ represents the current size of two interacting biological species; the structure of the deterministic part of the equation defines some sizes (for example, averages for some previous interval), which are the aim of "subconscious" return of the populations. Such a return can be prevented by the neighbors as well as by the action of external factors via the functions $y_1(t)$ and $y_2(t)$ influencing the mathematical expectation of the process. The latter functions, in their turn, are disturbed by $u_1(t)$ and $u_2(t)$ to be reconstructed. Realizations of $x(t)$ corresponding to different colonies are measurable at discrete times.

The application of procedure (5.2) allowed us to get the values providing the best approximation results for specific disturbances (we chose zero functions). Here they are: $K_{1} = 0.9$, $K_{2} = 0.5$. In the computational experiment, as the unknown disturbances in the latter equations of (5.3), we chose the following functions:

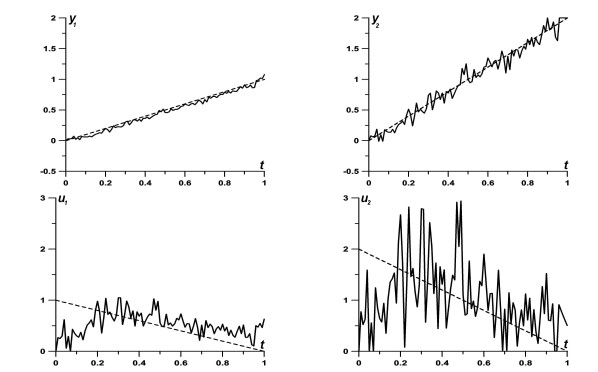
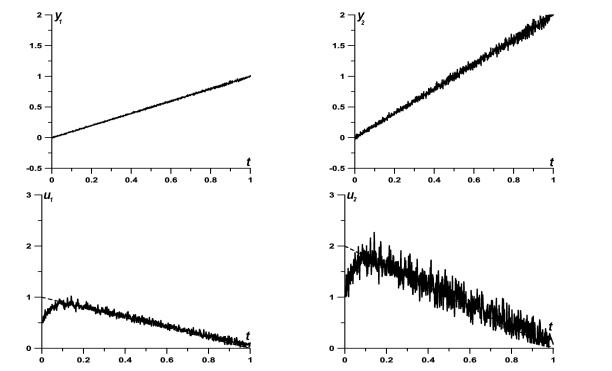
In this case, $y_1(t) = t$ and $y_2(t) = 2t$. The reconstruction results for optimal $K_{1}$, $K_{2}$ and different $N$ are presented in Figures 2 and 3. In both figures, the upper row is for the functions $y_1$ and $y_2$ (to be reconstructed by Block 1) and the lower row is for the disturbances $u_1$ and $u_2$ (to be reconstructed by Block 2), the real functions are shown by dashed line, and results of their reconstruction, by solid line; the horizontal and vertical axes correspond to time $t$ and to the values of functions, respectively. Figure 2 corresponds to $N = 10^{4}$; in this case, according to (5.1), $\delta(N) = 0.01$, $\alpha(N) = 0.04$, $\hat\alpha(N) = 0.3$. Figure 3 corresponds to $N = 10^{6}$; here, $\delta(N) = 0.001$, $\alpha(N) = 0.009$, $\hat\alpha(N) = 0.023$.

The results are definitely in agreement with convergence (4.7): the larger is the amount of measurable trajectories $N$, the smaller are the values of reconstruction accuracies.

6.   Conclusions

In the present paper, the input reconstruction problem for a differential system of special type is investigated. The first equation of the system is a linear stochastic Ito equation, the second one is a linear ordinary equation containing an unknown disturbance. The statement when the reconstruction is performed from discrete measurements of several realizations of the stochastic process being a solution of the first equation is considered. The problem is reduced to an inverse problem for the system of ordinary differential equations, which includes, instead of the stochastic equation, the equation describing the dynamics of the mathematical expectation of the original process. To solve the latter problem, from the viewpoint of the approach of the theory of dynamic inversion, the feasible reconstruction algorithm based on the method of auxiliary feedback controlled models is elaborated; the estimate for its convergence rate with respect to the number of measured realizations is presented. The main result of the paper is in an attempt to develop a procedure for solving the specific and technically complicated inverse problem for a dynamical system of hybrid type, where an unknown disturbance does not enter the measured component being a stochastic differential equation. The simple illustrating example is considered, the calibration of algorithm's parameters is fulfilled. As a perspective research direction, first of all, we have to note the necessity to construct an example of the system of hybrid type with evident practical importance, then to apply the method elaborated in the paper. It seems that the investigation of the optimality order for the convergence rate estimate will be also challenging.

Acknowledgments

The author would like to thank the generous support from the Krasovskii Institute of Mathematics and Mechanics, Yekaterinburg. Useful comments from the editor and reviewers are very appreciated.

Conflict of interest

The author declares no conflicts of interest in this paper.