Prescribed-time adaptive stabilization of high-order stochastic nonlinear systems with unmodeled dynamics and time-varying powers

1.   Introduction

This study presents a stochastic nonlinear plant in the form of non-strict feedback, as described below:

where $x = [x_1, \ldots, x_n]^{\top}\in R^{n}$, $\nu \in R$, and $x_{0}\in R$ are the system state, input, and initial value, respectively. $z \in R^{n_0}$ is the stochastic state unmodeled dynamics portion. System power $p_i(t)$: $R^+ \rightarrow R^+$ is defined as an unknown time-varying function. It is worth mentioning that when $p_i(t)\geq1$, we call system (1.1) a high-order system. We denote $[\cdot]^p = \text{sign}(\cdot)|\cdot|^p$ for any real number $p > 0$. $\omega(t)$ represents an $m$-dimensional standard Wiener process. $\Gamma_i(\cdot)$ represents nonlinear dynamic disturbances. $q(\cdot)$, $h_i(\cdot)$, $\Gamma_i(\cdot)$, $f_i(\cdot)$, and $g_{i}(\cdot)$ indicate unknown locally Lipschitz continuous functions. The input unmodeled dynamics subsystem is listed as

where $\bar{z} \in R^{n_1}$ denotes the input unmodeled dynamics, $a_\Gamma$ indicates a globally Lipschitz smooth function vector, $b_\Gamma$ indicates a constant vector, $c_\Gamma(\bar{z})$ indicates a smooth function, $d_\Gamma$ indicates a constant, and $u\in R$ indicates the system input.

Many practical applications require severe time response constraints due to security reasons, or simply to improve productivity. Hence, finite-time and further fixed-time stability problems have been intensively studied, see ^{[1,2,3,4,5,6]} and the references therein. In recent decades, due to the widespread application of stochastic nonlinear control in the fields of economics and engineering, the design of stability time for their systems has become a hot topic. Some results have been achieved on the asymptotic stability ^[7,8,9], finite-time stability ^[5,11], and fixed-time stability ^[12,13,14] of stochastic nonlinear systems with $p_i(t) = 1$. It must be clarified that the aforementioned control strategies can only determine the upper limit of the stable time through a complex mathematical function composed of multiple control parameters. In many engineering applications, it is necessary not only to achieve the desired control performance within a specified time frame but also without being constrained by initial conditions. In this regard, ^[15] introduced the concept of prescribed time for normal-form nonlinear systems, which utilizes state scaling methods, allowing users to pre-determine a convergence time independent of other control parameters. Taking into account the frequent occurrence of stochastic disturbances in practical systems, ^[16] further applied the concept of prescribed-time stability to the inverse optimal control problem of stochastic nonlinear systems. In continuation of previous research in ^[16], subsequent research in ^[17] founded a way to ease the burden of control efforts. Additionally, a new non-scaling output-feedback control scheme was developed in ^[18] for stochastic nonlinear systems with or without sensor uncertainty. Taking a step further, when $p_i(t) = p_i > 1$, that is, system (1.1) is a stochastic high-order nonlinear system, there poses a challenge to the control design since the presence of high powers impedes the achievement of feedback linearization or controllability through Jacobian linearization, as discussed in ^[19]. For such systems, the prescribed-time mean-square stability was discussed in ^[20], addressing both state-feedback control and parameter uncertainty issues.

However, the aforementioned research outcomes are primarily based on an assumption that the powers of system (1.1) are constants and precisely known. In real engineering applications, the powers of many systems may undergo variations influenced by factors such as engineering data and operating conditions. For instance, the power of a boiler turbine unit might be adjusted according to actual demand in ^[21] and nonlinear springs in unstable mechanical systems could lead to changes in dynamic characteristics in ^[22]. These situations need to be considered during system modeling. Furthermore, factors such as external disturbances, modeling errors, and model simplifications may negatively impact the stability of controlled systems, thereby degrading control performance. Although some scholars investigated finite-time or fixed-time control of stochastic nonlinear systems with unmodeled dynamics and dynamic disturbances, and proposed some meaningful conclusions in ^{[23,24,25,26]}, these studies have not yet addressed the issue of prescribed-time control. It is worth emphasizing that the adaptive neural network/fuzzy control method excels in addressing unknown nonlinearities. For example, ^[27] proposed an event-triggered adaptive fuzzy control scheme that effectively addresses stochastic nonlinear time-delay systems by handling delays using the Lyapunov-Krasovskii function and simplifying uncertainty modeling with fuzzy logic, significantly reducing data transmission and communication burdens. Additionally, ^[28] introduced an adaptive neural network event-triggered asymptotic tracking control strategy that effectively tackles state constraints and unknown dynamics in multi-input/multi-output (MIMO) nonlinear systems, utilizing barrier Lyapunov functions and neural networks to achieve safe control and dynamic modeling, thereby enhancing control efficiency and reducing data transmission. However, as far as we are aware, there are still some challenges in directly applying this method to achieve prescribed-time stability for stochastic nonlinear systems. Thus, these facts prompt us to raise an interesting question: can we develop an adaptive neural prescribed-time controller to stabilize stochastic nonlinear systems with unmodeled dynamics and unknown time-varying powers $p_i(t)$?

To address this critical issue, this article provides a new constructive control strategy for prescribed-time stabilization in probability. Prior to the controller design, the concept of semi-global practical prescribed-time stability in probability is first introduced. Then, dynamic signal function, normalized signals, dynamic surface control, and the parameter separation technique are used in every phase of the iterative design to solve the issue of differential explosion of the virtual control and to eliminate the effects of multiple unknown uncertainties. Radial basis function neural networks (RBFNNs) are deployed to estimate the uncertainty functions and the backstepping technique is manipulated to design the controller. Based on the bounded control gain function, the virtual controller does not tend to infinity during operation and the suggested control scheme enables the system to persist operation after a specified time, thus ensuring the performance of the closed-loop system. Compared with existing findings, this article incorporates its primary contributions as follows:

(1) The framework of system (1.1) is more prevailing. In comparison with recent literature on prescribed-time control ^{[16,17,18,20]}, this is the first study of the adaptive neural prescribed-time control problem for stochastic high-order nonlinear systems with unknown time-varying powers.

(2) This paper expands upon previous research on stochastic nonlinear systems with unknown time-varying powers, as discussed in ^{[29,30,31,32,33]}, by additionally considering unmodeled dynamics in both input and state. These dynamics have the potential to negatively impact control performance and potentially lead to instability in the closed-loop system. On this basis, the control algorithm avoids the repeated differentiation of the virtual controller by dynamic surface control, ensures the system signal will achieve more effective prescribed finite-time stability, and adopts the minimum learning parameter method where only one adaptive parameter needs to be adjusted dynamically to reduce the computation.

(3) Even though stochastic nonlinear systems in ^{[16,17,18,20]} can operate stably within the prescribed-time range, the control algorithm relies heavily on the unbounded gain signal $\frac{T}{t-T}$ at $t = T$, where $T$ is the prescribed stabilization time. This situation presents difficulties for the control system's execution. Considering that any dynamic interference can lead to the controller approaching infinity, which can harm the system response, inspired by ^[34], this article overcomes the shortcomings of existing prescribed-time control methods when there is multiple interference in the system, and ensures the continuous operation of the closed-loop system.

2.   Problem statement and preliminaries

2.1.   Problem statement

The aim of this thesis is formulated as to develop an adaptive neural prescribed-time control scheme for system (1.1), which ensures the convergence of all closed-loop system signals to a specified small region after the predetermined moment.

To ensure continuous operation of the control system, we introduce the function $\aleph(t)$ as

where $t_p$ indicates a specific moment in time that meets the criteria of $t_p < T$, $\mu(t) = \left(\frac{T}{T-t}\right)^s$, $s \geq 1$ indicates a constant, and $T > 0$ indicates the liberally predetermined time parameter.

Assumption 1. There exist positive constants $\bar p$ and $\underline p$ such that $1 \leq \underline p \le p_{i}(t) \le \bar p$, $i = 1, \ldots, n$.

Assumption 2. There exist known smooth positive functions $\underline{h}_i(\bar{x}_i)$, $\bar{h}_i(\bar{x}_i)$ such that $\underline{h}_i(\bar{x}_i) \leq |h_i(\bar{x}_i)| \leq \bar{h}_i(\bar{x}_i)$, $i = 1, \ldots, n$.

In order to address the nonlinear dynamic disturbance $\Gamma_i$ induced by the state unmodeled dynamical system $\text{d}z = q(z, x)\text{d}t$ and the influence of the input unmodeled dynamical subsystem (1.2), some assumptions need to be outlined.

Assumption 3. The dynamic disturbance $\Gamma_i$ of system (1.1) satisfies

where $\psi_{i1}(\cdot)$ denotes an uncertain non-negative smooth function, and $\psi_{i2}(\cdot)$ denotes an unknown monotone increasing non-negative smooth function.

Assumption 4. The unmodeled dynamic $z$ is exponentially input-state-practically stable, meaning that for $d z = q(z, x)$, there exists a Lyapunov function $V_0(z)$ such that

where $\alpha_1(\cdot)$, $\alpha_2(\cdot)$, and $\lambda(\cdot)$ are all $\mathcal{K}_\infty$ functions, $l_0 > 0$ and $l_1 > 0$ represent two known constants, and $\chi \in (0, 1)$.

Assumption 5. If $d_\Gamma > 0$ in (1.2), the following relation holds

where $b_0$ is an unknown non-negative constant.

Assumption 6. There exists a Lyapunov function $V_w(\bar{z})$ such that

where $H_1$, $H_2$, and $H_3$ are positive constants and $e_0$ represents a known positive constant.

2.2.   Preliminaries

Consider the stochastic nonlinear system described below:

We list some definitions and lemmas below for the following design and analysis process.

Definition 1. For system (2.2), the stochastic differential operator $\mathcal{L}$ is listed as

where $\text{Tr}\{g^T\frac{\partial^2{V}}{\partial^2{x}}g\}$ represents the Hessian item.

Definition 2. ^[35] If the solution of the nonlinear stochastic system (2.2) satisfies the following conditions, the system is considered to be semi-global practical prescribed-time stable in probability.

(1) For any stochastic initial value $x_0$, a unique solution is guaranteed.

(2) For initial values $x_0$, there exist a positive scalar $\zeta$ and a setting time $t_p(\zeta, x_0) < T$ to make $E\{\|x(t)\|^2\} \leq \zeta$, $\forall$$t \geq t_0+t_p < T$, where $T$ indicates a predetermined prescribed time independent of the initial value.

Lemma 1. If the continuous function $R(t)$ satisfies

then $R(t)\leq 0$ for $\forall t \geq 0$.

Lemma 2. For system (2.2), if a continuously differentiable (i.e., $C^2$), positive definite, and radially unbounded quadratic function $V(x)$ exists along with $\mathcal{K}_\infty$ functions $\bar{\alpha}_1(\cdot)$ and $\bar{\alpha}_2(\cdot)$, constants $C > 0, 0 < \chi < 1$, $P_1 > 0$, and $P_2 > 0$, such that

then system $(2.2)$ is semi-global practical prescribed-time stable in probability, where $\aleph(t)$ is the bounded function defined in (2.1).

Proof. First, since $V (x) \geq 0$ and $\mathcal{L}V (x) \leq \aleph(t)P_1+P_2$ hold for all $x_0$, according to the proof of Theorem 4.1 in ^[1], it can be inferred that a unique strong solution of system (2.2) exists.

According to (2.3), there exists a constant $0 < \pi \leq 1$, and the following inequality holds:

where $P = P_1+P_2$. Applying the It$\hat{o}$ formula, one has

where $E$ indicates the mathematical expectation.

Let $\Omega = \{x|EV(x) \leq (\frac{P}{(1-\pi)C})^{\frac{1}{\chi}}\}$, and in the sequel, the following two situations are contemplated.

Situation 1. if the signals do not satisfy $\Omega$, according to (2.3) and applying Jensen's inequality, one has

Therefore, it is obvious that

Moreover, the following inequality exists:

Denote $EV(x(t)) = G(x(t))$ and construct the auxiliary function $R(x(t))$ as

According to (2.4) and Lemma 1, one has

Furthermore, the following inequality is listed:

According to ^[34], we define function $\beta(t) = \pi C(1-\chi)\int_0^t \aleph(\varsigma)d(\varsigma)$ that is a prescribed-time function. Thus, there exists a time $t_p = \beta^{-1}(\frac{1}{C\pi(1-\chi)}(G^{1-\chi} (x(0))-(\frac{P}{(1-\pi)C})^{\frac{1-\chi}{\chi}})) < T$ such that $\beta(t_p) = G^{1-\chi}(x(0))-(\frac{P}{(1-\pi)C})^{\frac{1-\chi}{\chi}}$. Next, for $t\leq t_p$, we get $G(x(t)) \leq (\frac{P}{(1-\pi)C})^{\frac{1}{\chi}}$. In addition, when $t > t_p$, $\aleph(t) = \mu(t_p)$ becomes a positive constant such that $\aleph(t)$ is bounded. Then there is a finite time $t_f = \frac{1}{C\aleph(t)\pi(1-\chi)}(G^{1-\chi}(x(t_p))-(\frac{P}{(1-\pi)C})^{\frac{1-\chi}{\chi}})$ such that $G(x(t)) \leq (\frac{P}{(1-\pi)C})^{\frac{1}{\chi}}$ for $\forall \; t \geq t_p$.

Situation 2. if the signals satisfy $\Omega$, according to the Lasalle invariance principle, the track of $x(t)$ remains within the set $\Omega$. In sum, the time to arrive at the set $\Omega$ is bounded as $t_p$ which is less than $T$. Therefore, one has $EV(x(t)) \leq (\frac{P}{(1-\pi)C})^{\frac{1}{\chi}}$.

Remark 1. In comparison with the prescribed-time stable in probability control strategies proposed in ^{[16,17,18,19,20]}, the selection of a power index $\chi \in (0, 1)$ in (2.3) ensures the existence of a time $0 \leq t_p < T$ such that $E(x^2)\leq 2(\frac{P}{(1-\pi)C})^{\frac{1}{2\chi}}$ for $t \geq t_p$, resolving the issue that controllers containing the prescribed time function $\mu(t)$ do not involve infinite gain. For system (1.1), a globally stable state within the prescribed settling time $T$ is realized. Moreover, since RBFNNs can infinitely approximate unknown nonlinear functions through online learning, the combination of prescribed-time control with adaptive neural networks allows for its application to stochastic nonlinear systems.

Lemma 3. ^[37] If (2.2) holds for system $\text{d}z = q(z, x)$, then for any constant $\bar a \; \in \; (0, a_0)$, any initial condition $z_0 = z_0(0)$, and any function $\bar \lambda$ satisfying $\bar \lambda(\|x\|) \geq \lambda(\|x\|)$, there exists a finite time $T_0 = \max \{0, \ln(\frac{V_w(z_0)}{r_0})/(a_0-\bar a)\}$, a non-negative function $B(t_0, t)$ given for $t\geq t_0$, and the signal depicted by

such that $B(t_0, t) = 0$ for $t \geq t_0+T_0$ and $V(z(t))\leq r(t)+B(t_0, t)$. Without compromising generality, we select $\bar\lambda(\|x\|) = \lambda(\|x\|)$.

Lemma 4. ^[38] If Assumption 6 holds and $u$ belongs to $L_\infty$, the first-order system is defined by $d \hbar = - \aleph e_0\hbar+ |u|$ for the subsystem (1.2) such that

where $q_1 > 0$, and $q_2 \; > \; 0$ are constants.

Lemma 5. ^[39] Let $p \ge 1$, and the relation can be obtained as

Lemma 6. ^[40] Let $p\geq 1$, and then

Lemma 7. ^[41] Let $\wp > 0$, $\rho_1 > 0$, and $\rho_2 > 0$. Then

Lemma 8. ^[42] $p(t)$ is a real-valued function satisfying $0 < \underline{p} \leq p(t) \leq \bar p$ with known constant $\underline p$ and $\bar p$. Then

To approximate the successive unknown nonlinear function $F(\Psi):R^q \rightarrow R$ over a compact set $\Omega_\Psi \subset R^q$ in the design process, we further introduce the RBFNNs defined by

in the context of the adaptive control problem, where the input vector $\Psi \in \Omega_\Psi \subset R^q$ is described, $\Omega_\Psi$ is compact, $W = [w_1, \ldots, w_d]^\top \in R^d$ is the weight vector, $d > 1$ indicates the node number of the hidden layer, the vector of basis function $\Phi(\Psi) = [\phi_1(\Psi), \ldots, \phi_d(\Psi)]^\top \in R^d$ is denoted, the Gaussian function $\phi_i(\Psi)$ is described as

where the center vector $z_i = [z_{i1}, \ldots, z_{iq}]^T$ is represented, and the width of the Gaussian function $e_1$ is represented. If $F(\Psi)$ is a continuous function on a compact set $\Omega_\Psi \subset R^q$ with sufficiently large node number $d$, then it can be approximated by the RBFNN as

where $\varepsilon(\Psi)$ with $|\varepsilon(\Psi)| < \varepsilon^*$ indicates the approximation deviation, and $\varepsilon^* > 0$ indicates an unknown constant. The optimal weight vector, denoted as $W^*$, is expressed as

Lemma 9. ^[43] If the basis function vector of the RBFNNs is expressed by $\Phi(\Psi_n) = [\phi_1(\Psi_n), \cdots, \phi_d(\Psi_n)]^T$ with $\Psi_n\in R^n$, then $\|\Phi(\Psi_n)\|^2 \leq \|\Phi(\Psi_m)\|^2, m \leq n.$

Remark 2. It is worth noting that the nonlinear functions $f_i(x)$ and $g_i(x)$ in system (1.1) include all state variables, which is a non-strict-feedback structure. This is also true for some devices in practical applications, such as uncertain robot systems and hyperchaotic inductive capacitor oscillation circuit systems. If the control algorithm adopts the traditional backstepping method, its virtual controller will inevitably contain the state variables of system (1.1), which will lead to algebraic loop problems in simulation. Therefore, based on the definition of $\phi_i(\Psi)$ and $\Phi(\Psi)$ in RBFNNs, we utilize the properties of Gaussian functions in Lemma 9 and the approach of segregating variables to reduce the number of variables in the controller. Moreover, the restrictive conditions on $f_i$ and $g_i$ in ^{[29,30,31,32,33]} where stochastic disturbances and time-varying powers also exist in the studied system are no longer needed in this paper.

3.   Main results

This section introduces a cohesive neural adaptive prescribed-time control strategy. The recursive design process comprises $n$ steps involving dynamic surface control and the backstepping technique. The design of the $n$-step backstepping is rooted in the following coordinate transformation:

where $s_i$ denotes error surfaces, $\alpha_{i-1}$ denotes virtual controllers, $x_{id}$ denotes the first-order filter output signal which can be obtained through the input $\alpha_{i-1}$, and $\alpha_{i-1}$ will be specified later.

3.1.   Controller design

Step $1$. Consider the two equations of (1.1) and (3.1), and we have

Take the following Lyapunov function candidate into account:

Applying Assumption 3 and Definition 1, it is not difficult to obtain that

Building upon Young's inequality, Assumption 3, and Lemma 3, it holds that

where $d_1 > 0$ represents a constant.

Then, one has

where the unknown nonlinear function $\bar{f_1}(X_1) = f_1 +\frac{3}{4}d_1^{-2}\xi_1\|g_1(x)\|^4 +\frac{3}{4}\xi_1(\psi_{11}^{\frac{4}{3}}(\|x\|)+\psi_{12}^{\frac{4}{3}}(\alpha^{-1}_1(r+B(t_0, t))))$ with $X_1 = (x, r)^\top$. Building upon the RBFNNs, a neural network represented as $W_1^{*\top}\Phi_1(X_1)$ is utilized to approximate $\bar{f_1}(X_1)$ with $X_1 \in \Omega_{X_1}$ in a manner that

with any given constant $\varepsilon_1^* > 0$.

Using Lemma 9 and Young's inequality, one has

where $Z_1 = [x_1]^\top$, $\Theta^* = \max\{\|W_i^*\|^{\frac{3+\bar p}{3}} i = 1, \ldots, n \}$, and $\varrho_1$ indicates a design positive parameter.

Then, the formula (3.6) can be rewritten as

The first intermediate control signal is constructed as follows:

where $k_1 > 0$ is a design parameter. Furthermore, from Lemmas 5 and 8, we get

Thus, $\mathcal{L}V_{1}$ can be obtained as

where $D_1 = \frac{1}{2}+\frac{3}{4}d_1^2+\varepsilon_1^{\ast\frac{3+\bar{p}}{\bar{p}}} +\varrho_1^{-\frac{3+\bar{p}}{\bar{p}}}$.

According to Assumptions 1 and 2, and Lemmas 6–8, we have

where $\varphi_{21} = 2^{\bar{p}+2}(\bar{p}(2^{\bar{p}-2}+1))^{\bar{p}+3} |\bar{h_1}\xi_1^{3}|^{3+\bar{p}}(2+|\xi_2+s_2|^{(\bar{p}+3)(\bar{p}-1)}+|\alpha_1|^{(\bar{p}+3)(\bar{p}-1)})$ and $\varphi_{22}$ are known $C^1$ functions independent of $p_1(t)$, and $M_0 = \frac{2+\bar{p}}{3+\bar{p}}(3+\bar{p})^{-\frac{1}{2+\bar{p}}}+\frac{3}{4}4^{-\frac{1}{3}}$.

From Lemma 8 and Assumption 1, it holds that

Substituting (3.13) and (3.14) into (3.12) results in

Step $i$ $(i = 2, \ldots, n-1)$. Based on It$\hat{o}$'s differentiation rule and (3.1), we have

Select the Lyapunov function candidate as

Then, the infinitesimal generator of $V_{i}$ indicates

In order to circumvent the need for repetitive differentiation of $\alpha_{i-1}$, the first-order filter can be described as

where $\tau_i$ is a positive constant.

By using the definition of $s_i = x_{id}-\alpha_{i-1}$, we have $\dot{x}_{id} \; = \; -\aleph\frac{s_i}{\tau_i}$, and the differential of $s_i$ is

From (3.20) and Young's inequality, one concludes

where $d \alpha_{i-1} = \sum_{j = 1}^{i-1}\frac{\partial{\alpha}_{i-1}}{\partial{x}_{j}} (h_{j-1}[x_{j}]^{p_{j-1}(t)}+f_{j-1}-\Gamma_{j-1}) +\frac{\partial{\alpha}_{i-1}}{\partial{\hat\Theta}}\dot{\hat\Theta} +\frac{\partial{\alpha}_{i-1}}{\partial{t}}$ +$\frac{1}{2}\sum_{k, l = 1}^{i-1}\frac{\partial^{2}\alpha_{i-1}}{\partial{x}_k\partial{x}_l}g_k^\top g_l$ +$\frac{\partial\alpha_{i-1}}{\partial x_{i-1d}}\dot{x}_{i-1d}$ and $\eta_i \geq \frac{3}{4}((\sum_{j = 1}^{i-1}\frac{\partial{\alpha}_{i-1}}{\partial{x}_{j}}g_{j}(x))^\top (\sum_{j = 1}^{i-1}\frac{\partial{\alpha}_{i-1}}{\partial{x}_{j}} g_{j}(x)))^2 +\frac{1}{4}(d\alpha_{i-1})^4$ is a non-negative continuous function.

With the help of the same estimation method in step $1$, we have

Similar to (3.13), one has

Then, the dynamic equation of $V_i$ is

where $\bar{f}_i(X_i) = f_i(x) +\frac{3}{4}d_i^{-2}\xi_i\|g_i\|^4 +\frac{3}{4}\xi_i(\psi_{i1}^{\frac{4}{3}}(\|x\|)+\psi_{i2}^{\frac{4}{3}}(\alpha^{-1}_1(r+B(t_0, t)))) -\dot{x}_{id}+[\xi_{i}]^{\bar{p}}\varphi_{i1}$ with $X_i = (x, x_{id}, \dot{x}_{id}, \hat{\Theta}, r)^\top$ being an unknown nonlinear function. Then, for a given positive constant $\varepsilon_i^*$, the neural network $W_i^{*\top}\Phi_i(X_i)$ with $X_i \in \Omega_{X_i}$ can be utilized for approximating $\bar{f}_i(X_i)$ in the following manner:

Using Young's inequality and Lemma 9 yields

where $Z_i = [x_1, \ldots, x_i, \hat{\Theta}]^\top$, and $\varrho_i > 0$ is a given design parameter.

Then, it can be obtained that

where $D_i = \frac{3}{4}d_i^2 +\frac{1}{2} +\varrho_i^{-\frac{3+\bar p}{\bar p}} +\varepsilon_i^{*\frac{3+\bar p}{\bar p}} +M_0$.

Next, the virtual controller can be specified as

Substituting (3.28) into (3.27), it can be derived that

Step $n$. In this step, a real control law $u$ will be constructed. Choose the Lyapunov function and compact set $\Omega_n$ as

where $\xi = [\xi_1, \ldots, \xi_n]$, $s = [s_2, \ldots, s_n]$, $\gamma > 0$, $\gamma_1 > 0$, and $\gamma_2 \; > \; 0$ are the design parameters, and $(\tilde{\cdot})(t) = (\cdot)^*-(\hat \cdot)(t)$ with $(\hat \cdot)$ being the estimation of $(\cdot)^*$.

From Assumption 5 and Lemma 4, we obtain

where $\Lambda_m = \max \{b_0 q_1(\|\bar{z}(0)\|+|\hbar(0)|), b_0 q_2\}$.

Thus, we have

where $\Lambda = \frac{\Lambda_a}{\varsigma}$, $\Lambda_a = \frac{\bar p}{3+\bar p}(\frac{\bar{h}_n(\bar{x}_n)}{d_\Gamma}\Lambda_m)^{\frac{3+\bar p}{\bar p}}$, and $d_n > 0$ and $\varsigma > 0$ are constants.

Furthermore, the expression of $\mathcal{L}V_n$ is

where $\bar{f}_n(X_n) = \frac{1}{d_\Gamma}(f_n(x)-\dot{x}_{nd}) +\frac{3}{4d_\Gamma^2}\xi_n\|g_n\|^4 +\frac{3}{4}\xi_nd_\Gamma^{-\frac{4}{3}}(\psi_{n1}^{\frac{4}{3}}(\|x\|) +\psi_{n2}^{\frac{4}{3}}(\alpha^{-1}_1(r+B(t_0, t))))$ with $X_n = (x, x_{nd}, \dot{x}_{nd}, \hat{\Theta}, r)^\top$ being an unknown nonlinear function. Then $\bar{f}_n(X_n) = W_n^{*\top}\Phi_n(X_n)+\varepsilon_n(X_n), |\varepsilon_n(X_n)| \le \varepsilon_n^*$ with the neural network $W_n^{*\top}\Phi_n(X_n)$ and a positive constant $\varepsilon_n^*$.

Utilizing Young's inequality and Lemma 9, one has

where $Z_n = [x_1, \ldots, x_n, \hat\Theta]^T$ and $\varrho_n$ indicates a given design positive parameter.

Then, by substituting (3.34) into (3.33), one has

where $D_n = \frac{3}{4}d_n^2+\frac{1}{2} +\varrho_n^{-\frac{\bar p+3}{\bar p}} +\varepsilon_n^{*\frac{\bar p+3}{\bar p}}$.

Now, the control law and the parameter update laws are devised as

where $k_n$, $\delta$, and $\delta_1$ are positive design parameters.

Therefore, we can get

3.2.   Stability analysis

Theorem 1. Under the controllers and parameter adaptive laws (3.10), (3.28), and (3.36), stochastic system (1.1) satisfying Assumptions 1–6 exhibits the following characteristics: (1) All internal signals within the closed-loop system (1.1) remain bounded. (2) The equilibrium point of the system is prescribed-time stable in probability.

Proof. Next, it is evident from the structure of $V_n$ in (3.30) that $V_n$ is a positive definite, radial unbounded, and quadratic continuously differentiable function. Referring to Lemma $4.3$ in ^[44], there exist $\mathcal{K}_\infty$ functions $\bar{\alpha}_1(\cdot)$ and $\bar{\alpha}_2(\cdot)$ such that

By defining $\Theta^\ast$ and $\Lambda^\ast$, one obtains

With the aid of Lemma 7 and (3.14), one has

From (3.40), choose $\pi = \min\{k_1, \ldots, k_{n}, \delta, \delta_1, e_0\}$, let $\chi = \frac{\bar{p}-1}{\bar{p}+1}$ and $k_n \geq \frac{3}{3+\bar p}+\pi(\frac{1}{d_\Gamma})^\chi$, and rewrite (3.37) as

According to Lemma 7, one obtains

Since $\varphi_{j2}$, $\eta_j$, $|u|$, and $|(1-\frac{\xi_n^{3+\bar p}}{\varsigma})(1+|\hbar(t)|)^{\frac{3+\bar p}{\bar p}}\Lambda_a|$ are non-negative continuous functions, and $V_n(\Delta)$ is bounded, there exist known positive constants $\bar{\varphi}_{j2}$, $\bar{\eta}_j$, $\bar{H}_1$, and $N_1$ such that $\varphi_{i2} \leq \bar{\varphi}_{i2}$, $|u| \leq N_1$, $\eta_i \leq \bar{\eta}_i$, and $|(1-\frac{\xi_n^{3+\bar p}}{\varsigma})(1+|\hbar(t)|)^{\frac{3+\bar p}{\bar p}}\Lambda_a| \; \leq \; \bar{H}_1$. Hence, by choosing $\frac{1}{\tau_j} \geq \bar{\varphi}_{j2} + \frac{3}{2}$ and $\frac{1}{\tau_n} \geq \frac{3}{2}$, (3.41) becomes

where $C = \min\{ 4^\chi\pi, \pi^\chi, (4(\frac{1}{\tau_j}-\frac{3}{2}-\bar{\varphi}_{j2}))^\chi, (4(\frac{1}{\tau_n}-\frac{3}{2}))^\chi \}$, $P_1 = \delta\frac{1}{2\gamma}\Theta^{*T}\Theta^{*} +\delta_1\frac{1}{2\gamma_1}\Lambda^{*T}\Lambda^{*} +(n+3)(1-\chi)\chi^{\frac{\chi}{1-\chi}} +(1-\frac{4(\bar{p}-1)}{(\bar{p}+1)(3+\bar{p})})(\sum_{j = 1}^{n-1}k_j(n-1)+k_n-\frac{3}{3+\bar p})$, and $P_2 = \sum_{j = 1}^{n}D_j+\sum_{j = 2}^{n}\bar{\eta}_i +N_1+\bar{H}_1$. Therefore, we can obtain

where $P = P_1+P_2$. Consequently, it is deduced from (3.30) and (3.44), in conjunction with Lemma 1, that the $\Delta$-system attains semi-global practical prescribed-time stability in probability. Taking the proof procedure of Lemma 2 and (3.44) into consideration, it can be concluded that all signals are confined within a compact set $\Omega = \{\Delta|EV_n \leq (\frac{P}{(1-\pi)C})^{\frac{1}{\chi}} \}$ as

where $\gamma_{\max} = \max\{\gamma, \gamma_1\}$.

Remark 3. We further elucidate the challenges presented in this thesis as follows:

(1) In this paper, due to the joint role of unknown time-varying powers, stochastic disturbances, unknown control coefficients, and unmodeled dynamics, to handle the high nonlinearity in the design procedure is not an easy task.

(2) Since the adaptive neural network control is incorporated into the design process to address cases involving an unknown nonlinear function encompassing all state variables, which inherently results in the diversity of variables and the complexity of coefficient functions, therefore, how to overcome this problem to prevent the difficult execution of the controller becomes a challenging task.

(3) How to analyze the semi-global practical prescribed-time stability in probability of system (1.1) with unknown time-varying powers, stochastic disturbances, unknown control coefficients, and unmodeled dynamics is not easy work.

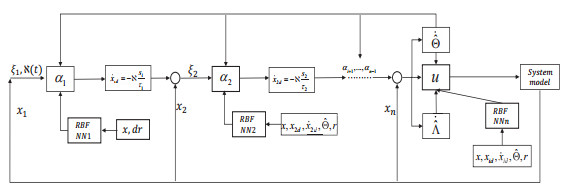
The design procedure of the proposed control scheme can be depicted by Figure 1.

4.   Simulation examples

To validate the effectiveness and feasibility of the proposed adaptive control project, this section presents a numerical example and a practical application case.

4.1.   Example 1

The following second-order stochastic high-order non-strict-feedback nonlinear system is considered:

where $p_{1}(t) = p_{2}(t) = \frac{7}{6}+\frac{1}{6}\sin t$, $\bar p = \frac{4}{3}$, $\underline p = 1$, $\underline{h}_i = \bar{h}_i = 1$, $f_1(x) = x_1\cos (x_2)$, $f_2(x) = x_1x_2^2$, $\Gamma_1 = 0.1z \sin(x_1x_2)$, $\Gamma_2 = zx_1^2x_2$, $g_1(x) = 15x_1^2x_2$, and $g_2(x) = 16x_2 e^{-x_1^2}$.

By adhering to the design methodology elucidated in this thesis, the virtual controller $\alpha_1$, the controller $u$, and adaptive laws $\dot{\hat\Theta}$ and $\dot{\hat\Lambda}$ can be obtained in the following form:

In simulation, we choose the prescribed settling time $T = 4$ and the initial values are designated as $[x_1(0), x_2(0)] = [4, −5]$, $\hat{\Theta}(0) = 0.9$, $\hat{\Lambda}(0) = -0.9$, $\hbar(0) = 0.9$, $z(0) = 1.5$, and $\bar{z}(0) = [0.1, 0.1]^T$. The design parameters are selected in intermediate control functions as $\tau_2 = 0.4$, $k_1 = k_2 = 0.5$, $\varrho_1 = \varrho_2 = 0.2$, $\delta = \delta_1 = 0.3$, $\gamma = \gamma_1 = 0.1$, $e_0 = 5$, and $s = 2$. To establish the basis vector function $\Phi_j(Z_j)$, for the backstepping steps, we designate the center of the receptive field as $z = [-1.5, -1, -0.5, 0, 0.5, 1, 1.5]^T$ and determine the Gaussian functions width as $e = \sqrt{2}$.

Thus, the outcomes of the simulation are shown by Figures 2–4. Figure 2 shows the curve of the system states $x_1$ and $x_2$. Figure 3 illustrates the curves of control signal $u$. Figure 4 depicts that the trajectories of the adaptive parameters $\hat{\Theta}$ and $\hat{\Lambda}$ are bounded. As shown in these figures, we know that the suggested adaptive neural control scheme ensures that the closed-loop system is continuously stable after a preset time $T = 4$ (s).

In order to verify Assumptions $4$–$6$, we select input unmodeled dynamics $\bar{z } = [\bar{z}_1, \bar{z}_2]^T$, $V_w = \bar{z}^T\bar{z}$, and $V_0(z) = z^2$. By employing Young's inequality, one obtains

By selecting $H_1 = 0.6$, $H_2 = 1.7$, and $H_3 = 2$, one has

Let $\alpha_1 = 0.3z^2$ and $\alpha_2 = 1.5z^2$. Then

According to (4.3)–(4.5), it can be observed that input and state unmodeled dynamics satisfy the requirements of Assumptions 4–6.

Remark 4. In order to further study the impact of the control parameters on system response, we choose two groups of different cases for Example $1$ in Table 1. In addition, both groups of data is operated with the same other design parameters of $\tau_2 = 0.4$, $\delta = \delta_1 = 0.3$, $\gamma = \gamma_1 = 0.1$, and $e_0 = 5$. The final simulation results are shown in Figures 5 and 6. By comparing the responses of the two cases, we can see that the dynamic response of case $1$ is better than that of case $2$. On the other hand, by Lemma $2$ and (3.44), one can see that the small and convergence rate of system response are affected by the design parameters $k_i$, $\varrho_i$, $T$, and $s$. When we choose larger prescribed control parameters $T$ and $s$, then the $\aleph(t)$ in $\alpha_1$ and controller $u$ are very large. At this time, the values of parameters $k_i$ and $\varrho_i$ in the controller can be selected to be small. Hence, from the perspective of practical application, we need to tradeoff the boundedness of the controller and the convergence time by selecting large $k_i$, small $T$, and appropriate $\varrho_i$ and $s$.

4.2.   Example 2

This example is a simplified model representing a boiler-turbine unit in ^[21] as follows:

where $x_1$ and $x_2$ indicate the drum and reheater pressures, respectively. $u$ represents the placement of the control valve, the unknown systems orders are indicated as $1 \leq p_i(t) \leq \frac{7}{5}$, $i = 1, 2, \; p_1(t) = \frac{8}{7}+\frac{1}{7}\sin t$, $p_2(t) = \frac{6}{5}+\frac{1}{5}\sin t$, $\bar{p} = \frac{7}{5}$, $\underline p = 1$, $\underline{h}_1 = \bar{h}_1 = 1$, $\underline{h}_2 = 1$, $\bar{h}_2 = 1+ x_1^2$, $\Gamma_1 = z\sin(x_1x_2)$, and $\Gamma_2 = 0.5zx_1x_2$.

According to (3.36), the controller, the adaptive law, and the basis functions of NNs are consistent with the structure of Example 1. The design parameters and the initial values are taken as $\tau_2 = e^{-t}+0.01$, $k_1 = k_2 = 0.7$, $\varrho_1 = \varrho_2 = 0.1$, $\gamma = \gamma_1 = 0.1$, $\delta = \delta_1 = 0.3$, $e_0 = 3$, $s = 2$, $T = 3$, $x_1(0) = 0.5$, $x_2(0) = 0.2$, $\hat{\Theta}(0) = 0.8$, $\hat{\Lambda}(0) = -1$, $\hbar(0) = 0.2$, $z(0) = 1.3$, and $\bar{z}(0) = [0.1, 0.1]^T$. The control effects are shown by Figures $7$–$9$. Specifically, Figure 7 provides the trajectories of $x_1$ and $x_2$ within the prescribed settling time. Figure 8 depicts the actual control input $u$ that can compensate for the effects of the stochastic disturbance and dynamic uncertainties. Figure 9 expresses the curve of adaptive laws $\hat{\Theta}$ and $\hat{\Lambda}$.

5.   Conclusions

The importance of this thesis lies in its pioneering exploration of the adaptive prescribed-time stabilization issue in stochastic high-order nonlinear systems, where unknown time-varying powers and dynamic uncertainty are prevalent. This study represents the first comprehensive discussion of this challenging problem. A neural predetermined time-varying feedback controller is crafted to avoid the differentiation of virtual controllers and reduce computational burden through the dynamic surface control. The results indicate that all internal signals of the closed-loop system are continuous and bounded, and the equilibrium point is semi-global practical prescribed-time stable in probability. There are still some unresolved issues at present:

(1) We need to find a more comprehensive control scheme that enables the system to achieve global stability without relying on initial values and design parameters, eliminating the impact of unbounded gains.

(2) Note that the dynamic surface control method can generate significant filtering errors and cannot achieve good stability effects. Another future work is to combine command filtering control and eliminate the residual term generated by adaptive control to achieve zero tracking error.

Author contributions

Yihang Kong: Conceptualization, formal analysis, methodology, validation; software, writing original draft, writing review editing. Xinghui Zhang: Conceptualization, formal analysis, methodology, funding acquisition, validation, investigation, writing original draft, writing review editing. Yaxin Huang: Investigation, funding acquisition, validation. Ancai Zhang: Funding acquisition, resources, validation. Jianlong Qiu: Funding acquisition, resources, validation. All authors have read and agreed to the published version of the manuscript.

Acknowledgments

This work was supported in part by the Taishan Scholar Program of Shandong Province under Grant No. tsqn202211240, the Natural Science Foundation Program of Shandong Province under Grant No. ZR2019YQ28, the Development Plan of Youth Innovation Team of University in Shandong Province under Grant No. 2019KJN007, the Yunnan Provincial Science and Technology Plan Project under Grant No. 202302AD080006, and the China Postdoctoral Science Foundation under Grants No. 2020M682226, 2021T140424.

Conflict of interest

The authors declare no conflicts of interest.