On irregularity descriptors of derived graphs

1.   Introduction

Graph theory has become a significant and essential part of the predictive toxicology and drug discovery, as it performs a vital role in the analysis of structure-property and structure-activity relationships. That is, different properties of molecules rely on their structures and therefore, quantitative structure activity property toxicity relationships (QSAR/QSPR/QSTR) research has become visible as a productive field of research in the characterization of physico-chemical properties, biological and pharmacological activities of materials and chemical compounds. These studies have been extensively used to toxicology, pharmacokinetics, pharmacodynamics, chemometrics, and so on ^[1].

Topological descriptors catch symmetry of compounds and provide the information in the numerical form about the molecular size, presence of heteroatoms, shape, multiple bonds, and branching. Topological descriptors have secured appreciable significance, due to the ease of generation and the speed with which these calculations can be performed. There are many graph-related numerical descriptors, which have confirmed their importance in theoretical chemistry and nanotechnology. Thereby, the computation of these topological descriptors is an interesting and attractive line of research. Some productive classes of topological descriptors of graphs are distance-based, counting-related, and degree-based; among these, degree-based indices have the most eye-catching position and can perform the prominent role to characterize the chemical compounds and forecast their different physicochemical properties like density, molecular weight, boiling and melting points, etc. A valuable subclass of degree-based topological descriptors are the irregularity indices that tell us about the irregularity of the graph in question. The topological descriptor $TI (\Gamma)$ of the graph $\Gamma$ is said to be an irregularity index if $TI (\Gamma) \ge 0$ and $TI (\Gamma) = 0,$ if and only if, it is regular graphics. Prior to the documentation, I cite ^[2] that irregularity indices were not considered to play a significant role in predicting the physicochemical properties of chemical structures. In ^[2], a regression analysis is performed to investigate and determine the application of various irregularity indicators to evaluate the physicochemical properties of octane isomers. They submitted that using the non-uniformity indices, the properties of octane isomers such as Accentric Factor (AcenFac), Evaporation Enthalpy (HVAP), Entropy, and Standard Evaporation Enthalpy (DHVAP) can be estimated with a correlation coefficient greater than $0.9$. For the detail discussion of different types of indices and their related results, we refer the interested reader to ^{[3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18]}.

Throughout the article, the vertex and edge sets of a graph $\Gamma$ are represented by ${\rm{V}}(\Gamma)$ and ${\rm{E}}(\Gamma)$ respectively. We denote the degree of a vertex ${\rm{q}}$ of a graph $\Gamma$ by $d_{\Gamma}({\rm{q}})$, and it is defined as the number of edges incident with ${\rm{q}}$. If in a graph, all its vertices have the same degree, then it said to be a regular graph, otherwise, it is an irregular graph. Let the order and size of $\Gamma$ are ${\rm{n}}$ and ${\rm{m}}$ respectively and with ${\rm{V}}(\Gamma) = \{{\rm{q}}_{1}, \dots, {\rm{q}}_{n}\}$. A sequence $s_{1}, \dots, s_{{\rm{n}}}$, where $s_i\in \mathbb{Z}^+$ for all $i = 1, \ldots, {\rm{n}}$, is said to be a degree sequence of a graph $\Gamma$, and $d_{\Gamma}({\rm{q}}_{l}) = s_{l}$. Let ${\rm{q}}_{l}$ represents the number of vertices of degree $l$, where $l = 1, 2, 3, \dots, {\rm{n}}-1$. Let ${\rm{e}} = {\rm{q}}_1{\rm{q}}_2\in {\rm{E}}(\Gamma)$, the imbalance of ${\rm{e}}$ is described as $imb({\rm{e}}): = |d_{\Gamma}({\rm{q}}_1)-d_{\Gamma}({\rm{q}}_2)|$. In $1997$, the idea of the irregularity of a graph $\Gamma$ was given by Albertson ^[19] in the following way:

The Zagreb indices have appreciable applications in chemistry. In 1972, Gutman et. al ^[20] proposed the first Zagreb index based on the degree of vertices of a graph $\Gamma$. The first and second Zagreb indices of a graph $\Gamma$ can be defined in the following way:

Inspired by the Zagreb indices, Furtula and Gutman ^[21] introduced the forgotten index of $\Gamma$ as follows:

Recently, Gutman et al. ^[22] brought in the idea of the $\sigma$ irregularity index of a graph $\Gamma$, which is defined as:

Different properties of $\sigma$ irregularity index have been discussed in ^[23,24]. If the size and order of $\Gamma$ are ${\rm{m}}$ and ${\rm{n}}$ respectively, then the variance of $\Gamma$ is defined by ^[25] in the following way:

The irregularity measure discrepancy of a graph $\Gamma$ was introduced in ^[26,27] as follows:

For the comprehensive discussions about these graph descriptors, we refer the readers to ^{[28,29,30,31,32,33]}.

2.   Derived graphs

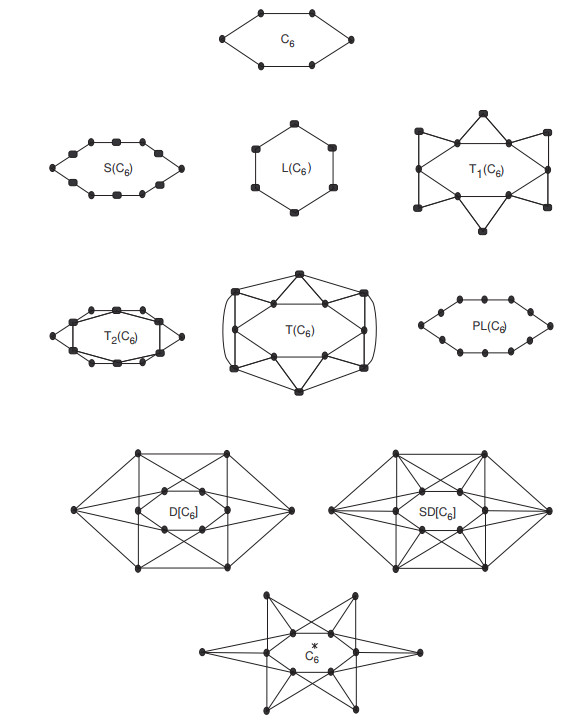
Definition 2.1. Subdivision graph: For a graph $\Gamma$, its subdivision graph is constructed by adding a vertex of degree $2$ in each edge. Therefore, $|{\rm{V}}({\rm{S}}(\Gamma))| = {\rm{n}}+{\rm{m}}$, $|{\rm{E}}({\rm{S}}(\Gamma))| = 2{\rm{m}}$ and

Definition 2.2. Line Graph: For a graph $\Gamma$, its line graph denoted by ${\rm{L}}(\Gamma)$ is the graph such that ${\rm{V}}({\rm{L}}(\Gamma)) = {\rm{E}}(\Gamma)$ and there is an edge between a pair vertices of ${\rm{L}}(\Gamma)$ if and only if the corresponding edges are incident in $\Gamma$. Clearly, $|{\rm{V}}({\rm{L}}(\Gamma))| = {\rm{m}}$ and by using hand shaking-lemma one can easily see that $|{\rm{E}}({\rm{L}}(\Gamma))| = \dfrac{M_1(\Gamma)}{2}-{\rm{m}}$, and for all ${\rm{q}} = {\rm{q}}_1{\rm{q}}_2\in {\rm{E}}(\Gamma)$, we have

Definition 2.3. Semi-total point graph ^[34]: For a graph $\Gamma$, its semi-total point graph is represented by $\mathcal{T}_1(\Gamma)$ and it is formed by inserting a new vertex to each edge of $\Gamma$ and then joining it to the end vertices of the corresponding edge. Thus, $|{\rm{V}}(\mathcal{T}_1(\Gamma))| = {\rm{n}}+{\rm{m}}$, $|{\rm{E}}(\mathcal{T}_1(\Gamma))| = |{\rm{E}}({\rm{S}}(\Gamma))|+{\rm{m}} = 2{\rm{m}}+{\rm{m}} = 3{\rm{m}}$ and

Definition 2.4. Semi-total line graph ^[34]: For a graph $\Gamma$, its semi-total line graph is represented as $\mathcal{T}_2(\Gamma)$ and it is formed by placing a new vertex at each edge of $\Gamma$, linking those new vertices by edges whose related edges are incident in $\Gamma$. We have $|{\rm{V}}(\mathcal{T}_2(\Gamma))| = {\rm{n}}+{\rm{m}}$, $|{\rm{E}}(\mathcal{T}_2(\Gamma))| = {\rm{m}}+\dfrac{M_1(\Gamma)}{2}$ and

Definition 2.5. Total Graph: The union of semi-total point graph and semi-total line graph is called total graph of a graph $\Gamma$. It is denoted by $\mathcal{T}(\Gamma)$. Also, $|{\rm{V}}(\mathcal{T}(\Gamma))| = {\rm{n}}+{\rm{m}}$, $|{\rm{E}}(\mathcal{T}(\Gamma))| = {\rm{m}}+|{\rm{E}}({\rm{S}}(\Gamma))| +|{\rm{E}}({\rm{L}}(\Gamma))| = 2{\rm{m}}+\dfrac{M_1(\Gamma)}{2}$ and

Definition 2.6. Paraline Graph: This graph $\rm{PL}(\Gamma)$ is the line graph of subdivision graph represented by $\rm{PL}(\Gamma) = {\rm{L}}({\rm{S}}(\Gamma))$. Also $|{\rm{V}}(\rm{PL}(\Gamma))| = |{\rm{E}}({\rm{S}}(\Gamma))| = 2{\rm{m}}$ and $|{\rm{E}}(\rm{PL}(\Gamma))| = \dfrac{M_1({\rm{S}}(\Gamma))}{2}-2{\rm{m}}$, where $M_1({\rm{S}}(\Gamma)) = M_1(\Gamma)+4{\rm{m}}$, therefore $|{\rm{E}}(\rm{PL}(\Gamma))| = \dfrac{M_1(\Gamma)}{2}$.

Definition 2.7. Double Graph: Let $\Gamma$ be a graph with ${\rm{V}}(\Gamma) = \{{\rm{q}}_1, {\rm{q}}_2, \dots, {\rm{q}}_{\rm{n}}\}$, and the vertex set of double graph $\rm{D}[\Gamma]$ are given by the two sets $\Gamma_1 = \{{\rm{x}}_1, {\rm{x}}_2, \dots, {\rm{x}}_{\rm{n}}\}$ and $\Gamma_2 = \{{\rm{y}}_1, {\rm{y}}_2, \dots, {\rm{y}}_{\rm{n}}\}$. For ${\rm{q}}_i\in {\rm{V}}(\Gamma)$, there are two vertices ${\rm{x}}_i$ and ${\rm{y}}_i$ in ${\rm{V}}(\rm{D}[\Gamma])$. The double graph $\rm{D}[\Gamma]$ consists of the original edge set of every copy of $\Gamma$, and for ${\rm{q}}_i {\rm{q}}_j\in {\rm{E}}(\Gamma)$, two more edges ${\rm{x}}_i {\rm{y}}_j$ and ${\rm{x}}_j {\rm{y}}_i$ are added.

Definition 2.8. Strong double Graph: Let $\Gamma$ be a graph with ${\rm{V}}(\Gamma) = \{{\rm{q}}_1, {\rm{q}}_2, \dots, {\rm{q}}_{\rm{n}}\}$, and the set ${\rm{V}}(\rm{SD}[\Gamma])$ is converted into $\Gamma_1 = \{{\rm{x}}_1, {\rm{x}}_2, \dots, {\rm{x}}_{\rm{n}}\}$ and $\Gamma_2 = \{{\rm{y}}_1, {\rm{y}}_2, \dots, {\rm{y}}_{\rm{n}}\}$ sets. For each ${\rm{q}}_i\in {\rm{V}}(\Gamma)$, there are ${\rm{x}}_i$ and ${\rm{y}}_i$ type vertices in ${\rm{V}}(\rm{SD}[\Gamma])$. The strong double graph $\rm{SD}[\Gamma]$ consists of the original edge set of every copy of $\Gamma$, and for ${\rm{q}}_i {\rm{q}}_j\in {\rm{E}}(\Gamma)$, more edges ${\rm{x}}_i{\rm{y}}_j$, ${\rm{x}}_j {\rm{y}}_i$ and ${\rm{x}}_i{\rm{y}}_i$ are added.

Definition 2.9. Extended double cover: Let $\Gamma$ be a graph with ${\rm{V}}(\Gamma) = \{{\rm{q}}_1, {\rm{q}}_2, \dots, {\rm{q}}_{\rm{n}}\}$. The extended double cover of $\Gamma$, represented by $\Gamma^*$ is the bipartite graph with bipartition $(\Gamma_1, \Gamma_2)$ where $\Gamma_1 = \{{\rm{x}}_1, {\rm{x}}_2, \dots, {\rm{x}}_{\rm{n}}\}$ and $\Gamma_2 = \{{\rm{y}}_1, {\rm{y}}_2, \dots, {\rm{y}}_{\rm{n}}\}$ such that ${\rm{x}}_i$ and ${\rm{y}}_j$ are linked if and only if either ${\rm{q}}_i$ and ${\rm{q}}_j$ are linked in $\Gamma$ or $i = j$.

The different derived graphs of a graph $\Gamma = C_{6}$ are illustrated in Figure 1.

3.   Main results

In this section, we present our main results. First of all, we deduce the results related to the variance of derived graphs.

3.1.   The variance index of derived graphs

Theorem 3.1. The variance of the subdivision graph ${\rm{S}}(\Gamma)$ of $\Gamma$ is

Proof. By using Eq 2.1 in formula (1.4), we get

This finishes the proof.

Theorem 3.2. The variance of ${\rm{L}}(\Gamma)$ of $\Gamma$ is

Proof. By using Eq 2.2 in formula (1.4), we obtain

This accomplishes the proof.

Theorem 3.3. The variance of the semi-total point graph $\mathcal{T}_1(\Gamma)$ of $\Gamma$ is given by

Proof. By using Eq 2.3 in formula (1.4), we have

This completes the proof.

Theorem 3.4. The variance of the semi-total line graph $\mathcal{T}_2(\Gamma)$ of $\Gamma$ is

Proof. By using Eq 2.4 in formula (1.4), we get

Thus we obtain the required result.

Theorem 3.5. The variance of the total graph $\mathcal{T}(\Gamma)$ of $\Gamma$ is

Proof. By using Eq 2.5 in formula (1.4), we have

This finishes the proof.

Theorem 3.6. The variance of the paraline graph $\rm{PL}(\Gamma) = {\rm{L}}({\rm{S}}(\Gamma))$ of $\Gamma$ is given by

Proof. From Theorem 3.2 and $|{\rm{V}}(\rm{PL}(\Gamma))| = |{\rm{V}}({\rm{L}}({\rm{S}}(\Gamma)))| = 2{\rm{m}}$, we get

Since $F({\rm{S}}(\Gamma)) = F(\Gamma)+8{\rm{m}}$, $M_2({\rm{S}}(\Gamma)) = 2M_1(\Gamma)$, $M_1({\rm{S}}(\Gamma)) = M_1(\Gamma)+4{\rm{m}}$, and $|{\rm{E}}({\rm{S}}(\Gamma))| = 2{\rm{m}}$. Therefore

This completes the proof.

Theorem 3.7. The variance of the double graph $\rm{D}[\Gamma]$ of $\Gamma$ is

Proof. By using $d_{\rm{D}[\Gamma]}({\rm{q}}) = 2d_{\Gamma}({\rm{q}})$ in formula (1.4), we get

This accomplishes the proof.

Theorem 3.8. The variance of the strong double graph $\rm{SD}[\Gamma]$ of $\Gamma$ is

Proof. By using $d_{\rm{SD}[\Gamma]}({\rm{q}}) = 2d_{\Gamma}({\rm{q}})+1$ in formula (1.4), we have

Thus we have the desired result.

Theorem 3.9. The variance of extended double cover of $\Gamma^*$ of $\Gamma$ is

Proof. By using $d_{\rm{D}[\Gamma]}({\rm{q}}) = d_{\Gamma}({\rm{q}})+1$ in formula (1.4), we get

This finishes the proof.

3.2.   The $\sigma$ index of the derived graphs

In this part, we present the results related to the $\sigma$ index of the derived graphs.

Theorem 3.10. The $\sigma$ index of the subdivision graph ${\rm{S}}(\Gamma)$ of $\Gamma$ is

Proof. By using Eq 2.1 in formula (1.3), $\sigma$ index can be computed in the following manner:

This accomplishes the proof.

Theorem 3.11. The $\sigma$ index of the semi-total point graph $\mathcal{T}_1(\Gamma)$ of $\Gamma$ is

Proof. Using Eq 2.2 in formula (1.3), we get

This completes the proof.

Theorem 3.12. The $\sigma$ index of the semi-total line graph $\mathcal{T}_2(\Gamma)$ of $\Gamma$ is

Proof. By using Eq 2.3 in formula (1.3), $\sigma$ index can be computed in the following manner:

Theorem 3.13. The $\sigma$ index of the total graph $\mathcal{T}(\Gamma)$ of $\Gamma$ is

Proof. By using Eq 2.4 in formula (1.3), $\sigma$ index can be computed in the following manner:

Theorem 3.14. The $\sigma$ index of the double graph $\rm{D}[\Gamma]$ of $\Gamma$ is

Proof. By the definition of double graph, it is easy to follows that $d_{\mathcal{D}[\Gamma]}({\rm{x}}_i) = d_{\mathcal{D}[\Gamma]}({\rm{y}}_i) = 2d_\Gamma({\rm{q}}_i)$, where ${\rm{q}}_i\in \rm{V}(\Gamma)$ and ${\rm{x}}_i, {\rm{y}}_i\in \rm{V}(\rm{D}[\Gamma])$ are the corresponding clone vertices of ${\rm{q}}_i$. Therefore, the $\sigma$ index of $\rm{D}[\Gamma]$ is

Theorem 3.15. The $\sigma$ index of the strong double graph $\rm{SD}[\Gamma]$ of $\Gamma$ is

Proof. By the definition of strong double graph, it is easy to see that $d_{\rm{SD}[\Gamma]}({\rm{x}}_i) = d_{\rm{SD}[\Gamma]}({\rm{y}}_i) = 2d_\Gamma({\rm{q}}_i)+1$, where ${\rm{q}}_i\in {\rm{V}}(\Gamma)$ and ${\rm{x}}_i, {\rm{y}}_i\in {\rm{V}}(\rm{SD}[\Gamma])$ are the corresponding clone vertices of ${\rm{q}}_i$. Therefore, the $\sigma$ index of $\rm{SD}[\Gamma]$ is

Theorem 3.16. The $\sigma$ index of the extended double cover graph $\Gamma^*$ of $\Gamma$ is

Proof. By the definition of extended double cover graph, it is easy to observe that $d_{\Gamma^*}({\rm{x}}_i) = d_{\Gamma^*}({\rm{y}}_i) = d_\Gamma({\rm{q}}_i)+1$, where ${\rm{q}}_i\in {\rm{V}}(\Gamma)$ and ${\rm{x}}_i, {\rm{y}}_i\in {\rm{V}}(\Gamma^*)$ are the related clone vertices of ${\rm{q}}_i$. Therefore, the $\sigma$ index of $\Gamma^*$ is

3.3.   The discrepancy of derived graphs

Finally, we give the results related to the discrepancy of derived graphs.

Theorem 3.17. The discrepancy of subdivision graph ${\rm{S}}(\Gamma)$ of $\Gamma$ is given by

Proof. By using Eq 2.1 in formula (1.5), we get

Since $|\rm{a}|-|\rm{b}|\leq|\rm{a}-\rm{b}|\leq|\rm{a}|+|\rm{b}|$. Thus we have

Similarly

This accomplishes the proof.

Theorem 3.18. The discrepancy of line graph ${\rm{L}}(\Gamma)$ of $\Gamma$ is

Proof. By using Eq 2.2 in formula (1.5), we get

Since $|\rm{a}|-|\rm{b}|\leq|\rm{a}-\rm{b}|\leq|\rm{a}|+|\rm{b}|$. Thus we have

Similarly

This finishes the proof.

Theorem 3.19. The discrepancy of semi-total point graph $\mathcal{T}_1(\Gamma)$ of $\Gamma$ is

Proof. By using Eq 2.3 in formula (1.5), we get

Since $|a|-|b|\leq|a-b|\leq|a|+|b|$. Thus we have

Similarly

This accomplishes the proof.

Theorem 3.20. The discrepancy of semi-total line graph $\mathcal{T}_2(\Gamma)$ of $\Gamma$ is

Proof. By using Eq 2.4 in formula (1.5), we get

Since $|\rm{a}|-|\rm{b}|\leq|\rm{a}-\rm{b}|\leq|\rm{a}|+|\rm{b}|$. Thus we have

Similarly

This finishes the proof.

Theorem 3.21. The discrepancy of total graph $\mathcal{T}(\Gamma)$ of $\Gamma$ is

Proof. By using Eq 2.5 in formula (1.5), we get

Since $|\rm{a}|-|\rm{b}|\leq|\rm{a}-\rm{b}|\leq|\rm{a}|+|\rm{b}|$.

Similarly

This accomplishes the proof.

Theorem 3.22. The discrepancy of the paraline graph $\rm{PL}(\Gamma)$ of $\Gamma$ is given by

Proof. From formula (1.5), we get

Since $|a|-|b|\leq|a-b|\leq|a|+|b|$.

Similarly

Since $M_1({\rm{S}}(\Gamma)) = M_1(\Gamma)+4{\rm{m}}$.

This finishes the proof.

Theorem 3.23. The discrepancy of the double graph $\rm{D}[\Gamma]$ of $\Gamma$ is given by

Proof. From formula (1.5), we get

Since $|\rm{a}|-|\rm{b}|\leq|\rm{a}-\rm{b}|\leq|\rm{a}|+|\rm{b}|$.

Similarly

Theorem 3.24. The discrepancy of the strong double graph $\rm{SD}[\Gamma]$ of $\Gamma$ is given by

Proof. From formula (1.5), we get

Since $|\rm{a}|-|\rm{b}|\leq|\rm{a}-\rm{b}|\leq|\rm{a}|+|\rm{b}|$.

Similarly

This accomplishes the proof.

Theorem 3.25. The discrepancy of extended double cover graph $\Gamma^*$ of $\Gamma$ is

Proof. From formula (1.5), we get

Since $|\rm{a}|-|\rm{b}|\leq|\rm{a}-\rm{b}|\leq|\rm{a}|+|\rm{b}|$.

Similarly

Thus we have the required result.

4.   Conclusions

The analysis of graphs by using numerical graph invariants is a successful strategy, which plays an appreciable role in predicting the physico-chemical properties of the given chemical structure. Thereby, the computation of topological descriptors is an interesting and attractive line of research. In this paper, we have provided the expressions for the variance of vertex degrees, $\sigma$ irregularity index and the discrepancy index of subdivision graph, vertex-semi total graph, edge-semi total graph, total graph, line graph, paraline graph, double graph, strong double graph and extended double cover of a graph.

Conflict of interest

The authors declare no conflict of interest.