Elastic transformation method for solving the initial value problem of variable coefficient nonlinear ordinary differential equations

1.   Introduction

Elasticity is originally a physical term used to reflect the ability of an object to be strained by an outside force, that is, the property of an object deformed under a force to return to its original state after the outside force is withdrawn ^[1]. And in economics, elasticity is an important tool for micro analysis. In the middle of the 19th century, British economist Muller noticed the interrelationship between demand and price in his research, which gave rise to the concept of demand elasticity ^[2]. Zhang ^[3] further comprehensively introduced the concept of elastic coefficient. At the beginning of this century, Marshall ^[4] gave the definition of elasticity in economics for the first time, using elasticity to describe how intensely consumers and producers react to price changes. After that, Woods et al. ^[5] gave the mathematical expression of elasticity. Since then, elasticity has been widely used in physics ^[6,7], economics ^[8,9,10,11], mechanics ^[12,13,14] and other fields.

The development of differential equation theory has gone through hundreds of years, and many basic laws of physics or chemistry can be written in the forms of differential equations. The initial interest in the study of differential equations is to find the solutions of the equations ^[15]. Previous scholars have studied many methods (Separation of variables ^[16,17], Constant variation method ^[18,19,20], Integrating factor method ^[21], Power series method ^[22,23,24], etc.) to find general solutions of differential equations, but only a small part of special forms of differential equations can find general solutions. Especially for nonlinear differential equations and differential equations with variable coefficients, it is more difficult to find their solutions. For the solution of nonlinear differential equations, Fatoorehchi et al. proposed the improved differential transf method (IDTM) ^[25] and the extended Laplace transform method (ELTM) ^[26] for solving nonlinear differential equations based on the theorem of Adomian polynomials, and solved many famous nonlinear equations, including Riccati equation, Clairaut equation, Blasius equation, etc. They also obtained explicit and numerical solutions to three diffusion-convection-reaction (DERC) equations using the Adomian decomposition method (ADM) ^[27], and proposed a time-advanced version of the Adomian decomposition method, called the multi-level Adomian decomposition method (MADM) ^[28]. For the solution of variable coefficient equations, the variational iteration method (VIM) and the homotopy perturbation method (HPM) are two very effective methods. Yulita et al. ^[29] applied the variational iteration method to obtain the analytical solutions of fractional heat wave-like equations with variable coefficients. The comparison with the Adomian decomposition method shows that VIM is a powerful method for solving linear and nonlinear fractional differential equations. Oezis et al. ^[30] solved the heat-like and wave-like equations using the homotopy perturbation method, and tested the method on various examples, revealing its effectiveness and simplicity. With the rapid development of computational mathematics, some scholars also use numerical calculation software to find numerical solutions of differential equations: In 2012, Das et al. ^[31] proposed a numerical scheme to solve the singularly perturbed reaction-diffusion problem with Robin boundary conditions and provided numerical experiments to verify the theoretical results. In 2019, Chandru et al. ^[32] established a parametric uniform numerical method for two-parameter singularly perturbed parabolic partial differential equations with discontinuous convection coefficients and source terms. In 2020, Das et al. ^[33,34] used the homotopy perturbation method to solve the approximate solution of the fractional Volterra-Fredholm integral-differential equation, and discussed the convergence of the method. The results showed that the approximate solution converges to the exact solution even for higher-order fractional differential equations. However, differential equations are widely used in physics, biology, engineering and other fields, and are the theoretical basis for us to establish mathematical models. Therefore, it is necessary to explore new methods to find accurate analytical solutions and expand the solvable classes ^[35] of differential equations.

According to the expression of elasticity, Li et al. ^[1,36,37] introduced elasticity into the reservoir seepage model and established the reservoir seepage model under the condition of elastic outer boundary ^[38] to better reflect the real situation of the reservoir formation. Peng studied the boundary value problems of second-order homogeneous linear ordinary differential equations under elastic outer boundary conditions, and obtained similar structures for the solutions of several types of special equations. Luo et al. ^[39] used the elastic transformation method to transform a class of first-order and a class of third-order variable coefficient nonlinear ordinary differential equations into Laguerre equations ^[40] and found the general solutions. The Russian mathematician Chebyshev first proposed the Chebyshev equation and gave the specific form of its general solution, namely the Chebyshev polynomials ^[41]. Chebyshev polynomials are widely used in function approximation. Using Chebyshev polynomials zero-point interpolation can avoid Runge phenomenon ^[42] and provide the best uniform approximation of continuous functions. Hafez et al. ^[43,44] introduced a numerical algorithm for dealing with two-dimensional mixed Volterra-Fredholm integral equations by using the properties of the shifted Chebyshev polynomials. The integral equations were transformed into matrix equations and solved. Tang et al. ^[45] used the properties of Chebyshev polynomials to study the expression of solution to a class of boundary value problems of Chebyshev equation, and obtained the similar structure of its solution.

Based on the above research, an elastic transformation method for solving nonlinear ordinary differential equations with variable coefficients is proposed in this paper according to the definition and expression of elasticity in order to obtain accurate analytical solutions of nonlinear ordinary differential equations and expand the solvable classes of ordinary differential equations. By elastic transformation, a class of first-order and a class of third-order nonlinear differential equations are transformed into Chebyshev equations. According to the solutions of Chebyshev equations and initial conditions, the solutions to the initial value problems of the original first-order and third-order equations are obtained. The second chapter introduces the basic knowledges of elasticity and the properties of Chebyshev equations and Chebyshev polynomials. The third chapter uses the elastic upgrading transformation method to solve the initial value problems of a class of first-order nonlinear ordinary differential equations with variable coefficients. The fourth chapter uses the elastic reduction transformation method to solve the initial value problems of a class of third-order nonlinear ordinary differential equations with variable coefficients. Chapter 5 summarizes the steps and flowchart of solving nonlinear differential equations by elastic transformation method based on the knowledge of Chapters 2 and 3. Finally, the conclusions of this article are summarized in the last Chapter.

2.   Preliminary knowledge

2.1.   Definition of elasticity

In a differentiable non-zero function $y = f\left(x \right)$, the elasticity of the dependent variable $y$ to the independent variable $x$ is defined as:

In a physical sense, the derivative $\frac{dy}{dx}$ represents the absolute rate of change of the dependent variable $y$ to the independent variable $x$, while the elasticity $\frac{Ey}{Ex}$ represents the relative rate of change of the dependent variable $y$ to the independent variable $x$. Similarly, in a non-zero differentiable multivariate function $y = f\left({{x}_{1}}, {{x}_{2}}, ..., {{x}_{n}} \right)$, the elasticity of the dependent variable $y$ to any independent variable ${{x}_{i}}$ can be defined as:

2.2.   Elastic representation of the derivative

According to the elastic expression (2.1), it can be known that:

2.3.   Elastic inverse transformation

Lemma 1. If the elasticity of a certain function is known, we can find the original function according to the elastic expression. That is to say: assuming that the elasticity of $y$ to $x$ is $\eta \mathit{{\rm{ = }}}\frac{Ey}{Ex}$, then, the original function $y\left(x \right)$ is:

2.4.   Chebyshev equation

The equation of the following form:

is called Chebyshev equation, where $\mu$ is a parameter, and when $\mu {\rm{ = }}{{n}^{2}}{\rm{ }}\left(n = 0, 1, 2, ... \right)$, the general solution of the Chebyshev equation is ^[39]

where $A$, $B$ are arbitrary constants, and

is called Chebyshev polynomial ^[40] of the first kind. The upper bound $\left[\frac{n}{2} \right]$ of the summations is a floor function with respect to $\frac{n}{2}$, representing the largest integer not greater than $\frac{n}{2}$.

is another solution that is linearly independent of ${{T}_{n}}\left(x \right)$ and is called Chebyshev polynomial of the second kind. The upper bound $\left[\frac{n-1}{2} \right]$ of the summations is a floor function with respect to $\frac{n-1}{2}$, representing the largest integer not greater than $\frac{n-1}{2}$.

2.5.   Properties of Chebyshev polynomial

1) The Chebyshev polynomial has the following recurrence formulas ^[39]:

2) Orthogonality of Chebyshev Polynomials: ^[42]

The set of Chebyshev polynomials $\left\{ {{T}_{k}}\left(x \right) \right\}$ is orthogonal with a weight factor $\rho \left(x \right) = 1/\sqrt{1-{{x}^{2}}}$, and

In fact, let $x = \cos \theta$, then $dx = -\sin \theta d\theta$, so

3.   Elastic upgrading transformation method for solving the initial value problem of a class of first-order nonlinear ordinary differential equation with variable coefficient

3.1.   Solving process

For the initial value problem of a class of first-order nonlinear ordinary differential equation with variable coefficient:

Solution: Regarding $y$ as the elasticity of a certain non-zero function $z$ to $x$, according to elastic expression, we have:

Replacing $y$ and ${y}'$ in (3.1) with the form of (3.2) and (3.3), then the equation in (3.1) is transformed into:

and according to $y{\rm{ = }}\frac{x}{z}\frac{dz}{dx}$, we know $z = {{e}^{\int{\frac{y}{x}dx}}}$, take $z{\rm{ = }}{{z}_{0}}{{e}^{\int_{{{x}_{0}}}^{x}{\frac{y}{x}dx}}}$ (${{z}_{0}}$ is a arbitrary constant), then, we get $z\left\vert_{x = {{x}_{0}}} \right. = {{z}_{0}}$. From

we get

Therefore, the initial value condition $y\left\vert _{x = {{x}_{0}}} = {{y}_{0}} \right.$ of Eq (3.1) can be transformed into the initial value conditions of Eq (3.4):

Therefore, the initial value problem (3.1) of the first-order nonlinear ordinary differential equation with variable coefficient can be transformed into the initial value problem:

of the second-order Chebyshev equation through the elastic upgrading transformation.

For the initial value problem (3.6), according to Eq (2.8), the general solution is $z = A{{T}_{n}}\left(x \right)+B{{U}_{n}}\left(x \right)$. Substituting the initial value conditions into the general solution, we get:

From the properties (2.11) and (2.12) of Chebyshev polynomials, the above equations are transformed into:

According to Cramer's law, the values of $A$ and $B$ can be calculated as:

Therefore, according to the elastic expression (2.1), the solution of the initial value problem (3.1) of the original first-order nonlinear ordinary differential equation with variable coefficient is:

According to the recurrence formulas (2.11) and (2.12) of the Chebyshev polynomial, the above formula is transformed into

Let $C = \frac{B}{A}$, the above formula simplifies to

where

It can be seen from Eqs (3.13) and (3.14) that the value of ${{z}_{0}}$ only has effect on the initial value problem (3.6) of the Chebyshev equation obtained after elastic upgrading transformation, but has no effect on the solution of the original initial value problem (3.1) of the original first-order nonlinear equation.

Example 1. For example, when $n = 1$, for the initial value problem of a first-order nonlinear ordinary differential equation:

According to the above steps, the initial value problem (3.15) is transformed into the initial value problem

of Chebyshev equation through elastic upgrading transformation. From the expression of Chebyshev equation and Chebyshev polynomials, the general solution of the Eq (3.16) is:

Therefore, ${z}' = A-\frac{Bx}{\sqrt{1-{{x}^{2}}}}$, and the value of ${{z}_{0}}$ has no effect on the initial value problem (3.15), for the convenience of calculation, we take ${{z}_{0}} = 1$, then

Solving the above equations gives $A = -\frac{7}{2}$ and $B = -\frac{\sqrt{3}}{2}$, so the solution of the initial value problem (3.16) is:

According to (3.2), the solution to the initial value problem of the original first-order nonlinear ordinary differential Eq (3.15) is:

It can be obtained in the same method that when we take ${{z}_{0}} = 2$, there is:

The solution is $A = -7$, $B = -\sqrt{3}$, so $z = -7x-\sqrt{3}\sqrt{1-{{x}^{2}}}$, and

The result is the same as the Eq (3.20). It can be seen that the value of ${{z}_{0}}$ has no effect on the solution of the initial value problem (3.15).

3.2.   Curve analysis

1) The effect on functions $z$ and $y$ when ${{z}_{0}}$ takes different values.

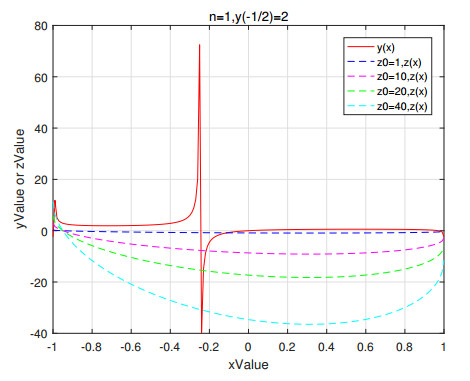
In Figure 1, the red solid line indicates the curve of $y\left(x \right)$ in the initial value problem (3.1) when $n = 1$, the initial value condition is $y\left\vert _{x = -\frac{1}{2}} \right. = 2$, and ${{z}_{0}}$ takes different values. It can be found that no matter what the value of ${{z}_{0}}$ is, the image of $y\left(x \right)$ is always the same curve. Therefore, the value of ${{z}_{0}}$ has no effect on the solution of the initial value problem (3.1). The four dotted lines of blue, pink, green, and cyan represent the function curves of $y\left(x \right)$ when ${{z}_{0}} = 1, 10, 20, 40$ in turn. It can be found that in the interval $\left(-1, 1 \right)$, the four curves all fall first and then rise, and the function $y\left(x \right)$ is a convex function. As the value of ${{z}_{0}}$ increases, the extreme point of the function $z\left(x \right)$ gradually moves to the negative semiaxis of the $x$ axis. Although the value of ${{z}_{0}}$ has an influence on the solution $z\left(x \right)$ of the initial value problem (3.6), it does not change the general direction of the curve $z\left(x \right)$.

2) The influence of different initial value conditions on solution.

In Figure 2, the four curves of cyan, pink, blue and red represent the images of $y\left(x \right)$ in the initial value problem (3.1) when $n = 1$, ${{z}_{0}} = 1$ and the initial value conditions are $y\left\vert _{x = -\frac{1}{2}} \right.{\rm{ = }}8, 6, 4, 2$. It can be seen from the figure that the four curves have roughly the same shape and have two extreme points. As the initial value ${{y}_{0}}$ increases, the extreme point of the function $y\left(x \right)$ will move to the negative semiaxis of the $x$ axis.

3) The influence of different parameters $n$ on solution $y\left(x \right)$.

In Figure 3, the curves of the four colors of red, blue, green and pink represent the images of the function $y\left(x \right)$ when the initial value conditions are all $y\left\vert _{-\frac{1}{2}} \right. = 4$, but the parameter $n$ is equal to $1$, $2$, $3$, or $4$ in the initial value problem (3.1). It can be seen from the figure that the function $y\left(x \right)$ has a periodic upward and downward trend, and as the value of $n$ increases, the period gradually shortens.

In summary, the initial value ${{y}_{0}}$ mainly affects the position of the inflection point of the function $y\left(x \right)$, and the value of the parameter $n$ mainly affects the periodicity of the function $y\left(x \right)$. The value of ${{z}_{0}}$ only affects the solution $z\left(x \right)$ of the initial value problem (3.6) of the Chebyshev equation after elastic upgrading transformation, but has no effect on the solution $y\left(x \right)$ of the initial value problem (3.1) of the original first-order nonlinear differential equation.

4.   Elastic reduction transformation method for solving the initial value problem of a class of third-order nonlinear ordinary differential equation with variable coefficient

4.1.   Solving process

For the initial value problem of a class of third-order nonlinear ordinary differential equation with variable coefficient:

Solution:

It is easy to see that $y = C$ ($C$ is an arbitrary constant) is a solution of the equation in (4.1), so if ${{y}_{0}} = {{y}_{1}} = {{y}_{2}} = 0$, then $y\equiv 0$ is a solution that satisfies the initial value condition in (4.1). If $y$ is a non-zero function, the elasticity of the function $y$ to $x$ can be set as $\mu$, that is, $\mu = \frac{x}{y}\frac{dy}{dx}$, according to the elastic representation of the derivative (2.3)–(2.5), we have:

Replace ${y}'$, ${y}''$, ${y}'''$ in the equation (4.1) with the form of (4.2)–(4.4), then we get:

This is a Chebyshev equation of order $n$, and its general solution is $\mu = A{{T}_{n}}\left(x \right)+B{{U}_{n}}\left(x \right)$.

According to Eqs (4.2) and (4.3), the initial value condition $\left\{ \begin{aligned} & {y}'\left\vert _{x = {{x}_{0}}} \right. = {{y}_{1}} \\ & {y}''\left\vert _{x = {{x}_{0}}} \right. = {{y}_{2}} \\ \end{aligned} \right.$ can be transformed into $\left\{ \begin{aligned} & \frac{y}{x}\mu \left\vert _{x = {{x}_{0}}} \right. = {{y}_{1}}, \\ & \frac{y}{x}\left[{\mu }'+\frac{1}{x}\mu \left(\mu -1 \right) \right]\left\vert _{x = {{x}_{0}}} \right. = {{y}_{2}}.\\ \end{aligned} \right.$

After simplification, we get:

Substituting the initial value condition (4.6) into the general solution $\mu = A{{T}_{n}}\left(x \right)+B{{U}_{n}}\left(x \right)$, we get:

According to the properties (2.11) and (2.12) of Chebyshev polynomials, the above equations become:

According to Cramer's law, the values of $A$ and $B$ can be calculated as:

Then calculate the following initial value problem from the elastic inverse transformation according to formula (2.6):

and the solution of the initial value problem (4.1) can be easily obtained as:

Example 2. For example, when $n = 1$, for the initial value problem:

Assuming that the elasticity of the function $y$ to $x$ is $\mu$, that is, $\mu = \frac{x}{y}\frac{dy}{dx}$, then according to the above steps, the equation and the second and third initial value conditions can be transformed into:

This is a Chebyshev equation whose general solution is $u = Ax+B\sqrt{1-{{x}^{2}}}$. Substituting the general solution into the boundary conditions, we get $\left\{ \begin{aligned} & -\frac{1}{2}A+\frac{\sqrt{3}}{2}B = -\frac{1}{2} \\ & A+\frac{\sqrt{3}}{3}B = 1 \\ \end{aligned} \right.$, and the solution is $\left\{ \begin{aligned} & A = 1 \\ & B = 0 \\ \end{aligned} \right.$, so the solution of the initial value problem (4.14) is

Substituting it into (4.11), we get

Solving this equation, we get the solution of the initial value problem (4.13) is

4.2.   Curve analysis

1) The effect of ${{y}_{0}}$ taking different values on the functions $y\left(x \right)$ and $\mu \left(x \right)$.

In Figure 4, the four solid lines of red, blue, green and cyan represent the curves of the solution to the initial value problem (4.1) when $n = 1$, ${y}'\left(-\frac{1}{2} \right) = {y}''\left(-\frac{1}{2} \right) = 1$ remain unchanged, and the initial value $y\left(-\frac{1}{2} \right)$ is equal to $1$, $2$, $3$, and $4$ respectively. It can be seen from the figure that the four curves in the interval $\left(-1, 1 \right)$ are monotonically increasing, and as the value of ${{y}_{0}}$ increases, the curves gradually become flat. The four dotted lines represent the curves of the solution $\mu \left(x \right)$ to the initial value problem of the Chebyshev equation after elastic reduction transformation. It can be seen from the figure that the four dotted curves in the interval $\left(-1, 1 \right)$ are monotonically increasing, and intersect at a point. As the value of ${{y}_{0}}$ increases, the curves gradually become flat.

2) The effect of ${{y}_{1}}$ taking different values on the functions $y\left(x \right)$ and $\mu \left(x \right)$.

In Figure 5, the three solid lines of red, blue and green represent the curves of the solution to the initial value problem (4.1) when $n = 1$, $y\left(-\frac{1}{2} \right) = {y}''\left(-\frac{1}{2} \right) = 1$ remain unchanged, and the initial value ${y}'\left(-\frac{1}{2} \right)$ is equal to $1$, $2$, $3$, and $4$ respectively. It can be seen that as the initial value ${{y}_{1}}$ increases, the inflection point of the function $y\left(x \right)$ gradually moves to the positive axis of the $y$ axis, and the image becomes steeper. The three dotted lines in corresponding colors represent the curves of the solution $\mu \left(x \right)$ to the initial value problem of the corresponding Chebyshev equation after elastic reduction transformation. It can be seen that the three dotted lines intersect at one point, showing a monotonically increasing trend. As the initial value ${{y}_{1}}$ increases, the image of the function $\mu \left(x \right)$ gradually becomes steeper.

3) The effect of ${{y}_{2}}$ taking different values on the functions $y\left(x \right)$ and $\mu \left(x \right)$.

In Figure 6, the four solid lines of red, blue, green and cyan represent the curves of the solution to the initial value problem (4.1) when $n = 1$, $y\left(-\frac{1}{2} \right) = {y}'\left(-\frac{1}{2} \right) = 1$ remain unchanged, and the initial value ${y}''\left(-\frac{1}{2} \right)$ is equal to $1$, $2$, $3$, and $4$ respectively. It can be seen from the figure that with the increase of the initial value ${{y}_{2}}$, the value of the function $y\left(x \right)$ near the left endpoint $x = -1$ gradually increases, while the value near the right endpoint $x = 1$ gradually decreases. The function $y\left(x \right)$ gradually changes from a monotonically increasing function to a convex function that first decreases and then increases. The four dotted lines in corresponding colors represent the curves of the solution $\mu \left(x \right)$ to the initial value problem of the corresponding Chebyshev equation after elastic reduction transformation. It can be seen that the four dotted lines intersect at one point. And the same as $y\left(x \right)$, as the initial value ${{y}_{2}}$ increases, the value of the elastic function $\mu \left(x \right)$ near the left endpoint $x = -1$ gradually increases, while the value near the right endpoint $x = 1$ gradually decreases. The function $\mu \left(x \right)$ gradually changes from a monotonically increasing function to a convex function that first decreases and then increases.

5.   Steps and flow chart of the elastic transformation method

5.1.   Steps of solving a class of first-order nonlinear ordinary differential equations through elastic upgrading transformation

By analyzing and summarizing the Chapter 3, we conclude that the steps to solve a kind of initial value problem of first-order nonlinear ordinary differential equations with variable coefficient of $y$ to $x$ through elastic upgrading transformation are as follows:

Step 1: Think of $y$ as the elasticity of a non-zero function $z$ to $x$, and play an elastic upgrading transformation to $y$, that is, let $y = \frac{x}{z}\frac{dz}{dx}$.

Step 2: Take the derivative of $y$, and substitute $y$ and ${y}'$ in the form of containing $z$, ${z}'$ and ${z}''$ into the equation to transform the original first-order nonlinear equation to the second-order Chebyshev equation.

Step 3: Transform the original initial value condition $y\left\vert _{x = {{x}_{0}}} = {{y}_{0}} \right.$ into the initial value condition $\left\{ \begin{aligned} & z\left\vert _{x = {{x}_{0}}} \right. = {{z}_{0}}, \\ & {z}'\left\vert _{x = {{x}_{0}}} \right. = \frac{{{y}_{0}}}{{{x}_{0}}}{{z}_{0}}. \\ \end{aligned} \right.$ of the second-order Chebyshev equation through the elastic upgrading transformation.

Step 4: Use the general solution and initial value condition of Chebyshev equation to find it's definite solution $z\left(x \right)$ under the initial value condition.

Step 5: Take the derivative of $z\left(x \right)$, according to the elastic expression, the solution to the initial value problem of the original first-order nonlinear ordinary differential equation with variable coefficient is: $y(x) = \frac{x}{z(x)}\frac{dz(x)}{dx}, (z(x)\ne 0)$.

5.2.   Steps of solving a class of third-order nonlinear ordinary differential equations through elastic reduction transformation

By analyzing and summarizing the Chapter 4, we conclude that the steps to solve a kind of initial value problem of third-order nonlinear ordinary differential equations with variable coefficient of $y$ to $x$ by elastic reduction transformation are as follows:

Step 1: Find the elastic function $\mu \left(x \right)$ of $y$ to $x$ according to the elastic expression.

Step 2: Calculate the ${y}'$, ${y}''$ and ${y}'''$ expressed in the form of the elastic function $\mu \left(x \right)$ and substitute them into the equation to transform the original third-order nonlinear equation of $y$ to $x$ into the Chebyshev equation of $\mu$ to $x$.

Step 3: Convert the original initial value conditions $\left\{ \begin{aligned} & {y}'\left\vert _{x = {{x}_{0}}} \right. = {{y}_{1}} \\ & {y}''\left\vert _{x = {{x}_{0}}} \right. = {{y}_{2}} \\ \end{aligned} \right.$ to the initial value conditions $\left\{ \begin{aligned} & \mu \left\vert _{x = {{x}_{0}}} \right. = \frac{{{x}_{0}}{{y}_{1}}}{{{y}_{0}}} \\ & {\mu }'\left\vert _{x = {{x}_{0}}} \right. = \frac{{{x}_{0}}{{y}_{2}}}{{{y}_{0}}}-\frac{{{x}_{0}}{{\left({{y}_{1}} \right)}^{2}}}{{{\left({{y}_{0}} \right)}^{2}}}+\frac{{{y}_{1}}}{{{y}_{0}}} \\ \end{aligned} \right.$ of the second-order Chebyshev equation by elastic reduction transformation.

Step 4: Use the general solution and initial value conditions of Chebyshev equation to find its definite solution $\mu \left(x \right)$ under the initial value condition.

Step 5: Play the elastic inverse transformation on $\mu \left(x \right)$, find the original function $y{\rm{ = }}{{e}^{\int{\frac{u}{x}}dx}}$ whose elasticity is $\mu$, and combine with the initial value condition $y\left\vert _{x = {{x}_{0}}} \right. = {{y}_{0}}$, then obtain the solution to the initial value problem of the original third-order nonlinear variable coefficient ordinary differential equation is: $y\left(x \right){\rm{ = }}{{y}_{0}}{{e}^{\int_{{{x}_{0}}}^{_{x}}{\frac{\mu }{x}}dx}}$

5.3.   Flow chart

The flow chart of the steps for solving the initial value problems of a class of first-order and a class of third-order ordinary differential equations with variable coefficients by elastic transformation method is as follows in Figure 7.

6.   Conclusions

1) In this paper, a class of first-order nonlinear ordinary differential equations with variable coefficient are transformed into second-order Chebyshev equations through elastic upgrading transformation, and the initial value problems of such first-order nonlinear equations are solved according to the Chebyshev polynomial. A class of third-order nonlinear ordinary differential equations with variable coefficient are converted to second-order Chebyshev equations through elastic reduction transformation, and the initial value problems of such third-order nonlinear equations are solved through the Chebyshev polynomial.

2) The elastic transformation method can not only upgrade a equation, but also reduce a equation. Therefore, it is possible to convert low-order nonlinear differential equations into solvable higher-order linear differential equations by using elastic upgrading transformation, and transform high-order nonlinear differential equations into solvable low-order linear differential equations by using elastic reduction transformation. Even we can successively use elastic upgrading transformation to upgrade low-order nonlinear differential equations multiple times to solve, or continuously use elastic reduction transformation to reduce high-order nonlinear differential equations multiple times to solve.

3) However, the definition of elasticity is only applicable to non-zero differentiable functions, so not all nonlinear differential equations can be transformed into linear equations by using elastic transformation method. Moreover, the linear equations obtained after elastic transformation are not all solvable.

4) Applying the concept of elasticity to the field of mathematics to solve differential equations is a novel, feasible and innovative method. The introduction of the elastic transformation method provides us with new ideas for solving nonlinear differential equations, expands the solvable classes of ordinary differential equations, and brings convenience to future scholars in the study of differential equations.

Acknowledgments

This work was initiated while Lin was studying in Institute of Applied Mathematics, Xihua University as a Master during the year 2020–2022, who would like to thank the teachers for their warm help and support.

Conflict of interest

The authors declare that there is no conflict of interest in this paper