Global attractivity for uncertain differential systems

1.   Introduction

In 1940s, for dealing with dynamic stochastic systems, stochastic differential equations involving Wiener process were proposed by It$\hat{o}$ for the first time. And they have played a very important role in many branches of science and industry. Ruelle ^[1] initiated the study of global random attractors. In 2004, for a kind of higer order nonlinear difference equation, The literature ^[2] considered global attractivity. In particular, for neutral SPDEs, Liu and Li ^[3] analyzed global attracting set, exponential decay and stability in distribution. Recently, much research has been done for various differential systems ^[4,5,6].

An uncertain differential system (U-D-S) ^[7] involving the canonical Liu process ^[8] was proposed for the first time. Then Chen and Liu made an in-depth analysis of the U-D-S and obtained the existence and uniqueness theorem ^[9]. After that, The U-D-Ss have been applied in more and more fields. For instance, they have been applied to uncertain optimal control ^[10,11,12], and uncertain financial market ^[7,13,14].

Since Liu ^[15] presented the definition of stability, many scholars have done a lot of research. For instance, existence and uniqueness theorem for uncertain differential equations ^[16,17,18], Stability in mean for uncertain differential equation ^[19], and stability for multi-dimensional uncertain differential equation ^[20,21]. In 2021, Some new stability theorems of uncertain differential equations with time-dependent delay were studied by Jia and Liu ^[22].

From the perspective of application, attractive domain estimation has been applied to many fields, such as in power system. If the voltage disturbance exceeds a certain level, it may cause a large area of power failure of the entire grid, or even make the whole grid collapse. Therefore, it is particularly important to determine the allowable value of deviation from the stable state, that is, the size of the attractive domain of the stable fixed point. For example, in an ecosystem, the initial population density range, namely the size of the viable attractive region, is determined to ensure that the system will not become extinct or explode under the given parameters. Therefore, the estimation of the attractive region has strong practical value. Tao and Zhu ^[23,24] studied attractivity and got some the judgement conditions for U-D-Ss.

In this paper, our aim is to study global attractivity for U-D-Ss. Furthermore, we will deduce some judging conditions for linear U-D-Ss. In Section $2$, Several basic uncertainty definitions and theorems will be reviewed. Section $3$ will present several global attractivity concepts for U-D-Ss. In Section $4$, for linear U-D-Ss, we will deduce some sufficient conditions. Furthermore, we will find the relationship of of global attractivity between the solution of the U-D-S and its $\alpha$-path. In Section $5$, we will present some examples having locally but not globally attractivity. Last, Section $6$ will show an interest rate model with uncertainty, which is a global attractive in mean.

2.   Preliminary

Definition 2.1. (^[25]) $\zeta$ defined on uncertainty space ($\Gamma$, $\mathcal{L}$, $\mathcal{M}$) is an uncertain variable. If at least one of the two integrals is finite, then

is called the expected value $E[\zeta]$ of $\zeta$.

Definition 2.2. (^[7]) Let $f_{1}$ and $f_{2}$ be two given binary functions, and $C_{t}$ be a canonical process. Then

is called a U-D-S.

Definition 2.3. (^[26]) Suppose a number $\alpha$ satisfies $0 < \alpha < 1$. If $Y_{t}^{\alpha}$ solves

In the above equation, $\Phi^{-1}(\alpha)$ is the inverse uncertainty distribution of standard normal uncertain variable, and

Then U-D-S (2.1) is said to have an $\alpha$-path $Y_{t}^{\alpha}$.

Definition 2.4. (^[23]) Let $Y_{t}$ and $Z_{t}$ satisfy U-D-S (2.1), and their initial values be $Y_{0}$ and $Z_{0}$, respectively. Then the U-D-S (2.1) is called

(i) attractive in measure (i.e., locally attractive in measure) if for any given $\varepsilon > 0$, here exists $\sigma > 0$ satisfying when $|Y_{0}-Z_{0}| < \sigma$, we can get

(ii) attractive almost surely (i.e., locally attractive almost surely) if here exists $\sigma > 0$ satisfying when $|Y_{0}-Z_{0}| < \sigma$, one can obtain

(iii) attractive in mean (i.e., locally attractive in mean) if there exists $\sigma > 0$ satisfying when $|Y_{0}-Z_{0}| < \sigma$, we can get

(iv) attractive in distribution (i.e., locally attractive in distribution) if $Y_{t}$ and $Z_{t}$ have uncertainty distributions $\Upsilon_{t}(x)$ and $\Psi_{t}(x)$, respectively. And here exists $\sigma > 0$ satisfying when $|Y_{0}-Z_{0}| < \sigma$, we can get

Theorem 2.1. (^[25]) Let $\zeta$ be an uncertain variable. Then, the following inequality holds.

provided that $f$ is a even function with $f\geq 0$ and increasing on $[0, \infty)$.

Theorem 2.2. (^[9]) Suppose that $Y_{t}$ defined on $[a_{1}, a_{2}]$ is an integrable uncertain process, $C_{t}$ is a canonical process, and the sample path $C_{t}(\gamma)$ has the Lipschitz constant $K(\gamma)$. Then, the following inequality holds.

Theorem 2.3. (^[26]) Let $Y_{t}$ and $Y_{t}^{\alpha}$ satisfy (2.1) and (2.2), respectively. Then at each time $t$,

is said to be an inverse uncertainty distribution of $Y_{t}$.

3.   Some global attractivity concepts

In this section, several global attractivity definitions are given for the U-D-S

We suppose that $Y_{t}$ and $Z_{t}$ satisfy the above system (3.1), and the initial values are $Y_{0}$ and $Z_{0}$, respectively.

Definition 3.1. If for any $0 < \sigma < +\infty$ and for any $\varepsilon > 0$, when $|Y_{0}-Z_{0}| < \sigma$, the following equation

holds. Then the U-D-S (3.1) is called globally attractive in measure.

Example 3.1. Assume that U-D-S has the below form

It follows that

Thus

For any given $\sigma > 0$ and $\varepsilon > 0$. We prove it in two cases. Case 1: Assume $0 < \sigma\leq \varepsilon$. When $|Y_{0}-Z_{0}| < \sigma$, it is easy to see that $\ln\frac{\varepsilon}{|Y_{0}-Z_{0}|} > \ln\frac{\varepsilon}{\sigma}\geq 0$. According to $\int_{0}^{t}-\exp(2s){{{{\rm{d}}}}}s = \frac{1}{2}-\frac{1}{2}\exp(2t) < 0$, where $t > 0$. By the Theorem 2.1, we can obtain

as $t\rightarrow +\infty$. Case 2: Assume $\sigma > \varepsilon$. When $|Y_{0}-Z_{0}| < \sigma$, it is easy to see that $\ln\frac{\varepsilon}{\sigma} < \ln\frac{\varepsilon}{|Y_{0}-Z_{0}|} < 0$. Then there exists $T_{0} = \frac{1}{2}\ln\left(2+2|\ln\frac{\varepsilon}{\sigma}|\right) > 0$, such that when $t > T_{0}$, we can obtain $\ln\frac{\varepsilon}{|Y_{0}-Z_{0}|}+\frac{1}{2}\exp(2t)-\frac{1}{2} > 0$. It follows from Theorem 2.1 that

as $t\rightarrow +\infty$. Thus the U-D-S (3.2) is globally attractive in measure.

Definition 3.2. The U-D-S (3.1) is called globally attractive almost surely if for any $\sigma$ with $0 < \sigma < +\infty$, when $|Y_{0}-Z_{0}| < \sigma$, we get

Definition 3.3. The U-D-S (3.1) is called globally attractive in mean if for any $0 < \sigma < +\infty$, when $|Y_{0}-Z_{0}| < \sigma$, we get

Definition 3.4. Suppose $Y_{t}$ and $Z_{t}$ have uncertainty distributions $\Upsilon_{t}(x)$ and $\Psi_{t}(x)$, respectively. Then the U-D-S (3.1) is called globally attractive in distribution if for any $0 < \sigma < +\infty$, when $|Y_{0}-Z_{0}| < \sigma$, one can obtain

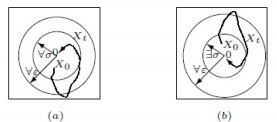
Remark 3.1. Global attractivity in measure implies local attractivity in measure of the uncertainty solutions. However the reverse implication may not hold (Several other definitions have similar results). For the global and local attractivity of zero solution, Figure 1 shows us an intuitional comprehension. (a) Global attractivity means for any $0 < \sigma < +\infty$, If $Y_{0}$ is in the $\sigma$-neighborhood of zero, the state $Y_{t}$ with initial value $Y_{0}$ converges to 0 ($t\rightarrow +\infty$). (b) Local attractivity describes here exists $0 < \sigma < +\infty$, if $Y_{0}$ is in the $\sigma$-neighborhood of zero, then $Y_{t}$ with initial value $Y_{0}$ converges to 0 ($t\rightarrow +\infty$).

4.   Some results

Firstly, this section studies the global attractivity of linear U-D-Ss, and deduces several sufficient and necessary conditions for global attractivity. Secondly, global attractivity relationships between the solution and $\alpha$-path are discussed.

Assuming that $A_{1}(t)$, $A_{2}(t)$, $B_{1}(t)$, $B_{2}(t)$ are continuous functions on $[0, +\infty)$. For the linear U-D-S

we suppose that $Y_{t}$ and $Z_{t}$ satisfy the above system (4.1), and the initial values are $Y_{0}$ and $Z_{0}$, respectively.

Theorem 4.1. The linear U-D-S (4.1) is globally attractive in measure if

and here exists one number $p > 1$ that satisfies

Proof: According to the system (4.1), It is easy to see that

Thus

For any given $\sigma > 0$ and $\varepsilon > 0$. We prove it in two cases. Case 1: Assume $\sigma\leq \varepsilon$. When $|Y_{0}-Z_{0}| < \sigma$, it is easy to see that $\ln\frac{\varepsilon}{|Y_{0}-Z_{0}|} > \ln\frac{\varepsilon}{\sigma}\geq 0$. According to the (4.3), here exists $\tau > 0$ satisfying when $t > \tau$, it can be seen $\int_{0}^{t}A_{1}(s){{{{\rm{d}}}}}s < 0$. From Theorem 2.1, (4.2) and (4.3), if $t\rightarrow +\infty$, we can get

Case 2: Assume $\sigma > \varepsilon$. When $|Y_{0}-Z_{0}| < \sigma$, it is easy to see that $\ln\frac{\varepsilon}{\sigma} < \ln\frac{\varepsilon}{|Y_{0}-Z_{0}|} < 0$. According to the (4.3), here exists $\tau > 0$ such that when $t > \tau$, the inequality $\ln\frac{\varepsilon}{\sigma} -\int_{0}^{t}A_{1}(s){{{{\rm{d}}}}}s > 0$ holds. By the Theorem 2.1, (4.2) and (4.3), we can get

as $t\rightarrow +\infty$. Thus the linear U-D-S (4.1) is globally attractive in measure.

Example 4.1. Analyze a following linear U-D-S

Obviously $A_{1}(t) = -4t^{3}$ and $B_{1}(t) = t,$ then it is easy to get

Thus $dY_{t} = -4t^{3}Y_{t}{{{{\rm{d}}}}}t+tY_{t}{{{{\rm{d}}}}}C_{t}$ is globally attractive in measure by Theorem 4.1.

Theorem 4.2. The linear U-D-S (4.1) is globally attractive almost surely if and only if

Proof: Since $Y_{t}$ and $Z_{t}$ both satisfy the linear U-D-S (4.1), the following equation holds

According to $\int_{0}^{t}B_{1}(s){{{{\rm{d}}}}}C_{s}\sim \mathcal{N}(0, \int_{0}^{t}|B_{1}(s)|{{{{\rm{d}}}}}s)$, $\int_{0}^{t}|B_{1}(s)|{{{{\rm{d}}}}}s\leq \int_{0}^{+\infty}|B_{1}(s)|{{{{\rm{d}}}}}s < +\infty$. Let $K(\gamma)$ be the Lipschitz constant of $C_{t}(\gamma)$. From the Theorem 2.2, we can get

It is easy to see that

For any given $\sigma > 0$, when $|Y_{0}-Z_{0}| < \sigma$, we know that

The linear U-D-S (4.1) is globally attractive almost surely if and only if

Example 4.2. Analyze a following linear U-D-S

Since $A_{1}(t) = -(t^{2}+t)$ and $B_{1}(t) = \exp(-3t),$ the following equations

and

hold. Thus ${{{{\rm{d}}}}}Y_{t} = -(t^{2}+t)Y_{t}{{{{\rm{d}}}}}t+\exp(-3t)Y_{t}{{{{\rm{d}}}}}C_{t}$ is globally attractive almost surely.

Theorem 4.3. Suppose that $\int_{0}^{+\infty}|B_{1}(s)|{{{{\rm{d}}}}}s < \frac{\pi}{\sqrt{3}}.$ Then the linear U-D-S (4.1) is globally attractive in mean if and only if

Proof: We can get easily the following equation from (4.1)

For the above equation, by taking the expected value, we can obtain

Now that $\int_{0}^{t}B_{1}(s){{{{\rm{d}}}}}C_{s}\sim \mathcal{N}(0, \int_{0}^{t}|B_{1}(s)|{{{{\rm{d}}}}}s)$.

Since

According to the ^[27], we can obtain

For any given $\sigma > 0$, when $|Y_{0}-Z_{0}| < \sigma$, it is easy to see that

Obviously,

is equivalent to

Hence (4.1) is globally attractive in mean if and only if

Example 4.3. For the linear U-D-S with following form

Note that $A_{1}(t) = -\frac{1}{t+1}$ and $B_{1}(t) = \frac{1}{t^{2}+1},$ we immediately obtain

Thus ${{{{\rm{d}}}}}Y_{t} = -\frac{1}{t+1}Y_{t}{{{{\rm{d}}}}}t+\frac{1}{t^{2}+1}Y_{t}{{{{\rm{d}}}}}C_{t}$ is globally attractive in mean.

Next, global attractivity on the solutions and $\alpha$-paths for U-D-Ss will be studied.

Theorem 4.4. The U-D-S (3.1) is globally attractive in distribution if and only if the differential system (2.2) is globally attractive.

Proof: Suppose $\Upsilon_{t}(x)$ and $\Psi_{t}(x)$ are corresponding regular distributions of $Y_{t}$ and $Z_{t}$, respectively. Let $Y_{t}^{\alpha}$ and $Z_{t}^{\alpha}$ satisfy (2.2), and their initial values be $Y_{0}$ and $Z_{0}$, respectively.

If (3.1) is globally attractive in distribution, In other words, for any given $0 < \sigma < +\infty$, when $|Y_{0}-Z_{0}| < \sigma$, we can get

Then

By Yao-Chen Formula (Theorem 2.3), the following equation holds.

with $|Y_{0}-Z_{0}| < \sigma$. Hence, (2.2) is globally attractive.

Each of these steps is reversible. Then the proof has been completed.

Example 4.4. Let us analyze the following linear system

Suppose $Y_{t}^{\alpha}$ is an $\alpha$-path and the initial value is $Y_{0}$, i.e., it satisfies the ordinary differential system

Since the differential system (4.4) and ${{{{\rm{d}}}}}Y_{t}^{\alpha} = -(Y_{t}^{\alpha})^{3}{{{{\rm{d}}}}}t$ have the same as attractivity, we only study ${{{{\rm{d}}}}}Y_{t}^{\alpha} = -(Y_{t}^{\alpha})^{3}{{{{\rm{d}}}}}t$. By solving the equation, we get $Y_{t}^{\alpha} = Y_{0}[1+2(Y_{0})^{2}t]^{-\frac{1}{2}}$ with the initial value $Y_{0}$. For any $\sigma > 0$ and $\varepsilon > 0$, here exists $T_{1} = \frac{1}{\varepsilon^{2}} > 0$ such that when $|Y_{0}| < \sigma$ and $t > T_{1}$, one can obtain

Thus ${{{{\rm{d}}}}}Y_{t}^{\alpha} = -(Y_{t}^{\alpha})^{3}{{{{\rm{d}}}}}t$ is globally attractive. It follows from the globally attractivity of ${{{{\rm{d}}}}}Y_{t}^{\alpha} = -(Y_{t}^{\alpha})^{3}{{{{\rm{d}}}}}t$ that (4.4) is globally attractive. According to the Theorem 4.4, the uncertain differential system ${{{{\rm{d}}}}}Y_{t} = -Y_{t}^3{{{{\rm{d}}}}}t+\sigma {{{{\rm{d}}}}}C_{t}$ is globally attractive in distribution.

Corollary 4.1. The U-D-S (3.1) is not globally attractive in distribution if here exists $0 < \alpha < 1$ such that the differential system (2.2) is not globally attractive.

Proof: We suppose $\alpha_{0}\in(0, 1)$ and the differential system

is not globally attractive. By the Theorem 4.4, the U-D-S (3.1) is not globally attractive in distribution.

5.   Examples having local but not global attractivity

In this section, we give some examples to show that local attractivity does not implies global attractivity.

Example 5.1. (Locally but not globally attractive in measure) Let us consider the following form of system

We have

If we integrate both sides, we can obtain

That is

We know that $0$ satisfies (5.1) with the initial $Y_{0} = 0$. For any given $0 < \varepsilon < 1$, let $|Y_{0}| < 1$. We can prove it in two cases. Case 1: If $0\leq Y_{0} < 1$, it follows that

as $t\rightarrow +\infty$.

Case 2: Assume $-1 < Y_{0} < 0$, we can easily obtain

as $t\rightarrow +\infty$. No matter what case happens, we always have

That is to say that (5.1) is locally attractive in measure. However if $Y_{0} = 1$, $Y_t = 1$ is the solution of (5.1). Then we have

Thus (5.1) is not globally attractive in measure.

Example 5.2. (Locally but not globally attractive almost surely) Analyze the U-D-S

It is easy to see that $0$ is the solution of (5.2) and the initial is $Y_{0} = 0$. It can be obtained that

From Theorem 2.2, we can deduce

where $K(\gamma)$ is the Lipschitz constant of $C_{t}(\gamma)$. It is easy to see that

Then we have

It follows that

for $|Y_0| < 1$. Thus (5.2) is locally attractive almost surely. But if $Y_{0} = -1$, we have $Y_t = -1$ and then

Then (5.2) is not globally attractive almost surely.

Example 5.3. (Locally but not globally attractive in mean) Supposed the U-D-S is

We know that $0$ is the solution of (5.3) if the initial is $Y_{0} = 0$. In addition, we can obtain

Obviously,

Taking integral on both sides, we get

Thus

Note that $\int_{0}^{t}\frac{1}{s^{2}+1}{{{{\rm{d}}}}}C_{s}\sim \mathcal{N}(0, \int_{0}^{t}\frac{1}{s^{2}+1}{{{{\rm{d}}}}}s)$. Hence

Since

from ^[27], we have

When $|Y_{0}| < 1$, we have

as $t\rightarrow +\infty$. So (5.3) is locally attractive in mean. But if $Y_{0} = 1$, (5.3) has a solution $Y_t = 1$, and then we have

Thus (5.3) is not globally attractive in mean.

Example 5.4. (Locally but not globally attractive in distribution) Analyze the U-D-S with the following form

Let $Y_{t}^{\alpha}$ be an $\alpha$-path of the above system and the initial value is $Y_{0}$, i.e., it satisfies the ordinary differential system

Since the differential system (5.4) and ${{{{\rm{d}}}}}Y_{t}^{\alpha} = (-Y_{t}^{\alpha}+(Y_{t}^{\alpha})^{2}) {{{{\rm{d}}}}}t$ have the same attractivity, we only study ${{{{\rm{d}}}}}Y_{t}^{\alpha} = (-Y_{t}^{\alpha}+(Y_{t}^{\alpha})^{2}) {{{{\rm{d}}}}}t$, which has zero solution and a solution $Y_{t}^{\alpha} = \frac{Y_{0}\exp(-t)}{Y_{0}\exp(-t)-Y_{0}+1}$ with initial value $Y_{0}$. Let $|Y_0| < 1$, we can prove it in two cases. Case 1: Let $0\leq Y_{0} < 1$.

as $t\to +\infty$. Case 2: Assume $-1 < Y_{0} < 0$. Then

as $t\to +\infty$. No matter what case happens, the ordinary differential system ${{{{\rm{d}}}}}Y_{t}^{\alpha} = (-Y_{t}^{\alpha}+(Y_{t}^{\alpha})^{2}) {{{{\rm{d}}}}}t$ is locally attractive. But if $Y_{0} = 1$, then $Y_t^{\alpha} = 1$ and we have

Thus the ordinary differential system ${{{{\rm{d}}}}}Y_{t}^{\alpha} = (-Y_{t}^{\alpha}+(Y_{t}^{\alpha})^{2}) {{{{\rm{d}}}}}t$ is not globally attractive. we obtain that the ordinary differential system (5.4) is locally attractive but not globally attractive. By ^[23], the uncertain differential system

is locally attractive in distribution but not globally attractive in distribution by Corollary 4.1.

6.   Interest rate model with uncertainty

The real interest rate has not kept unchanged. Assumed that the interest rate follows an U-D-S, Chen and Gao ^[14] introduced a following model

where $a, b, \sigma$ are all positive numbers. $Z_{t}$ and $Y_{t}$ are assumed to satisfy (6.1) with initial values $Z_{0}$ and $Y_{0}$, respectively. It is easy to get the following equation

Thus

For any $0 < \sigma < +\infty$, when $|Z_{0}-Y_{0}| < \sigma$, we can easily obtain the following result

as $t\rightarrow +\infty$. Thus

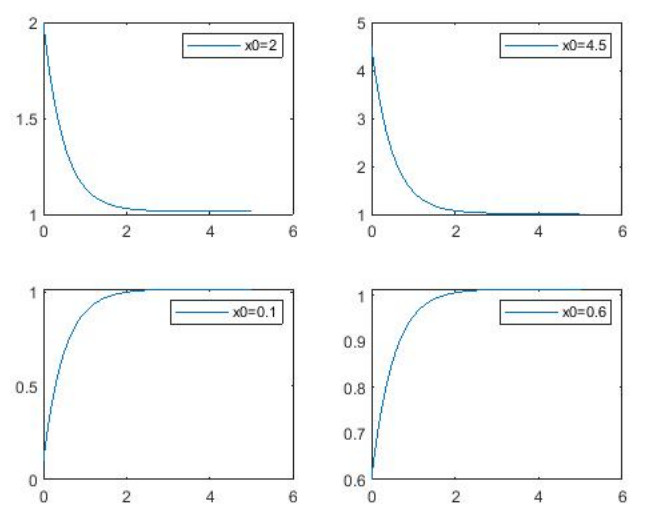
as $t\rightarrow +\infty$. Therefore, this model (6.1) is globally attractive in mean.

The above result shows that if $Z_{0}$ is higher than $\frac{b}{a}$, the drift of (6.1) is negative, and the interest rate will drop down in the $\frac{b}{a}$ direction. Similarly, if $Z_{0}$ is less than $\frac{b}{a}$, the drift of (6.1) is positive, so the rate will rise in the direction of $\frac{b}{a}$.

Next, let $a = 2, b = 2, \sigma = 1$, using MATLAB, Figure 2 shows the simulation diagram of $E(X_{t})$ with several different initial values.

7.   Conclusions

This article gave several concepts of global attractivity. Global attractivity (in measure, in mean, almost surely, in distribution) implies local attractivity (in measure, in mean, almost surely, in distribution). However the reverse implication may not hold. We gave some locally but not globally attractive examples. For linear U-D-Ss, some sufficient conditions of global attractivitywere presented. Furthermore, this paper found the relationship of attractivity and stability between the solution of the U-D-S and its $\alpha$-path. The attractivity and stability of the general differential system solution can be determined by constructing Lyapunov function, thus the difficulty of determining the attractivity and stability of the U-D-Ss is greatly reduced. Last, an uncertain interest rate model which is global attractive in mean was considered. It is deduced that the solution of the model is attractive in mean. Future work will focus on the application of stability and attractivity.

Acknowledgments

This work is supported by the Key Scientific Research Projects of Henan Higher Education Institutions (No.18B11012).

Conflict of interest

No potential conflict of interest was reported by the author(s).